二年级奥数 巧数图形

巧数图形
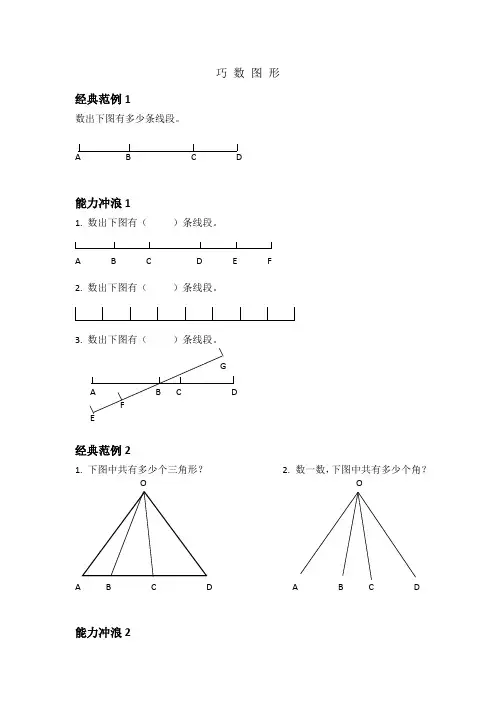
经典范例1
数出下图有多少条线段。

A B C D
能力冲浪1
1. 数出下图有（）条线段。

A B C D E F
2. 数出下图有（）条线段。

3. 数出下图有（）条线段。

G
A B C D
F
E
经典范例2
1. 下图中共有多少个三角形？
2. 数一数，下图中共有多少个角？
O O
A B C D A B C D 能力冲浪2
1. 下图中共有（）个三角形？
2. 数一数，下图中共有（）个角？
O
A
B
C
D
0 E
F 3. 数一数，下图中有多少个三角形？
经典范例3
数出下列各图中长方形的个数分别是多少个？
C
F
A B
能力冲浪3
1. 下列各图中分别有多少个长方形或平行四边形。

2. 数出下图中带有☆ 的长方形共有多少个？
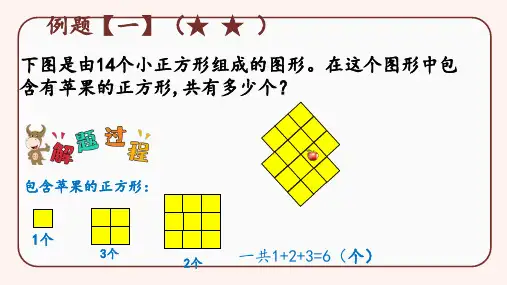
经典范例4
下图中有个（ ）正方形（每个小格都是正方形）。

能力冲浪4
下列各图中分别有多少个正方形（每个小格都是正方形）？
经典范例5
数一数，下图中一共有（ ）个三角形。

能力冲浪5
1. 数一数，图中有（ ）个长方形。

2. 下图中一共有（ ）个正方形（除5、6外，每个小格都是正方形，5、6长是宽的2倍）。

3. 下图中分别有多少个三角形。

A
B C
F。

二年级奥数：巧数图形体系所属体系板块：第三级上能力培养：分类思考、数形结合思想体系对接：第一级下《有趣的平面图形》第三级下《飞速图形计数》预热知识一、分类法1、打枪法2、恰含法3、分大小【例】下图你能数出多少条线段？【例】下图共有多少个长方形？【解析】分类法（打枪法）【解析】分类数（恰含法）总：4+3+2+1=10（个）总：3+2+1=6（个）答：共10个。

答：共6个。

【例】下图你能数出多少个正方形？【解析】分类数（大小）1个小正方形：4个4个小正方形：1个总：4+1=5（个）答：共5个。

二、巧数图形（分层数）1、总数=每层个数相加每层个数=上层个数+看得见【例】下图中的小方块有几个？【解析】巧数图形（分层数）总：1+4+5=10（个）答：有10个。

课前思考1、正方形如何计数呢？2、小方块如何计数呢？3、如何利用学过的乘法来进行计数？4、一年级秋季要求背的1-10的三角形数还记得吗？数数中的枚举知识点精讲知识点总结一、数字：0、1、2、3、4、5、6、7、8、9（共10个）数：由数字组成的（无数个）二、组数（最高位不为0）1.确定几位数2.确定从哪位开始写注：①“比”后为目标②“相差”：2种情况3.确定顺序（从小到大/从大到小）4.有无特殊要求反序数下降数（上升数）例题精讲1.根据条件组数——有序的排列（例2）你能根据下面的要求，写出所有符合条件的两位数吗？（1）十位上的数字比个位上的数字大2；（2）十位上的数字与个位上的数字相差2。

解析：（1）先确定要题目要求我们写的是两位数，再确定从哪一位开始写——通过比较，发现先写出“比”字后面的，再写前面的思考起来更容易，所以一般我们把“比”字后面的当做是目标。

在这里也就是“个位上的数字”为目标，先写出来个位可能是几，再寻找十位上比个位上大2的数字即可组成我们需要的两位数。

个位上可能是：0、1、2、3、4、5、6、7、8、9。

而十位上最大是9，十位上的数字比个位上的数字大2，所以个位上最大是7。

二年级奥数：有趣的图形计数知识点总结一、平面图形计数1.规则图形——跑火车基本图形数依次加到12.不规则图形——分层数分类（大小分类，方向分类）3.方法：观察规律，变加为乘二、立体图形计数——分层数每层个数=上层个数+本层露出头顶的个数二、染色问题1重合2不染知识点精讲一、平面图形1、规则图形公式法（跑火车）（适用于数线段、数角、数三角形等）例数线段分析：有3条基本线段（火车头是3），所以一共有3+2+1=6（条）线段例数角分析：有3个基本角，共有3+2+1=6（个）角例数三角形分析：有4个基本三角形，共有4+3+2+1=10（个）三角形（2）不规则图形①分层数例数多层长方形（分层数）分析：每层有3+2+1=6（个），有3层，所以共有6╳3=18（个）也可以，长边上线段总数3+2+1=6（个）宽边上线段总数2+1=3（个）总共有：3×6=18（个）例图中有多少个三角形?解析：观察本图不是规则图形，不能直接用公式.但可以将它分成2层（中间横线以上是一层，去掉横线是一层），且每层都是一个规则的数三角的图形.每层个数：3+2+1=6（个）层数：2层总个数6×2=12（个）②分类数：大小、方向例数三角形方法：标号法（适用于任何基本的平面图形，建议重点掌握）分析：用标号法如图小三角形有6个，两个小三角形拼成的有（2,3）（4,5）（6,1）3个三个小三角形拼成的有（1,2,3）（2,3，4）（3,4,5）（4,5,6）（5,6,1）（6,1,2）6个六小三角形拼成的有1个共6+3+6+1=16（个）二、其它平面图形计数1、数棋盘：细观察，找规律，变加为乘2、数方块: 补、拆三、立体图形计数1、数立方体推荐方法：从上往下一层一层的数每层个数=上层个数+本层露出头顶的个数例数一数下图有多少块立方体?分析：如图，从上往下，一层一层的数即1+3+6+10=20（块）2、补成大正方体/长方体推荐方法：要补的块数=总数-现有的块数例至少添加多少个小正方体可以组成一个较大的正方体?分析：先观察发现这幅图有4层，那么要想拼出一个大正方体，那么每层应该有4行4列，所以拼成的大正方体至少得4╳4╳4=64块，现在有3+4+5+7=19块，所以至少得补64-19=45块3、染色问题简单情况可使用观察法没被染色的面即为粘在一起的面（重合面），粘一处少两个面，（两个方块各少一个面）例下面是用小正方体堆成的图形，现在把这个图形的表面涂上红色，数一数有多少个小正方形没有被涂色?分析：“横着”粘的：第一层+第二层的块数1+2=3处。

二年级奥数专题-数数图形王牌例题1 数一数,下图中共有多少条线段？A B C D E【思路导航】我们知道,每条线段都有两个端点,以相邻两个端点间的线段为1条基本线段,图中有AB、BC、CD、DE 4条,由两条基本线段组成的线段有：AC、BD、CE 3条,由三条基本线段组成的线段有AD、BD 2条,由四条基本线段组成的线段有：AE 1条,因此,图中共有线段：4＋3＋2＋1=10（条）。

由此可见：一条大线段上的基本线段总条数之间的关系是：线段总条数是从1开始的一串自然数之和,其中最大的自然数等于基本线段条数。

列式如下：4＋3＋2＋1=10（条）答：此图共有10条线段。

疯狂操练11．数一数,下图中共有多少条线段？A B C D E F 2．观察下图,数一数图中共有多少条线段？3．上海到南京的汽车,除起点、终点外,还要停靠6个站,汽车公司要准备几种车票？王牌例题2 数出下面图形有多少条线段？【思路导航】线段都是直的,因此我们在数的时候,必须将这幅图分成A -B ；B -E ；E -F ；H -G 这四个部分。

每一部分用例1的方法数一数,A -B 只有一条线段；B -E 有3＋2＋1=6（条）线段；E -F 有1条线段；H -G 有2＋1=3（条）线段。

因此这幅图共有1＋6＋1＋3=11（条）线段。

列式如下：1＋（1＋2＋3）＋1＋（1＋2）=11（条）答：此图共有11条线段。

疯狂操练21．数一数,下图共有多少条线段？2．观察下图,数一数图中共有多少条线段？ A B C D E FG H3．小红在纸上画了一条线段,小亮又拿起笔,在小红画的线段上点了5个点,然后问小红：“你知道现在这条线段上又多出了多少条线段吗？”小明一会儿就说出了结果。

聪明的小朋友,你知道小明说的是几吗？王牌例题3 数一数,下图中共有多少个三角形？【思路导航】先数上层,有三角形3＋2＋1=6（个）,再数两层合起来的大三角形,有3＋2＋1=6（个）,所以一共有6×2=12（个）三角形。

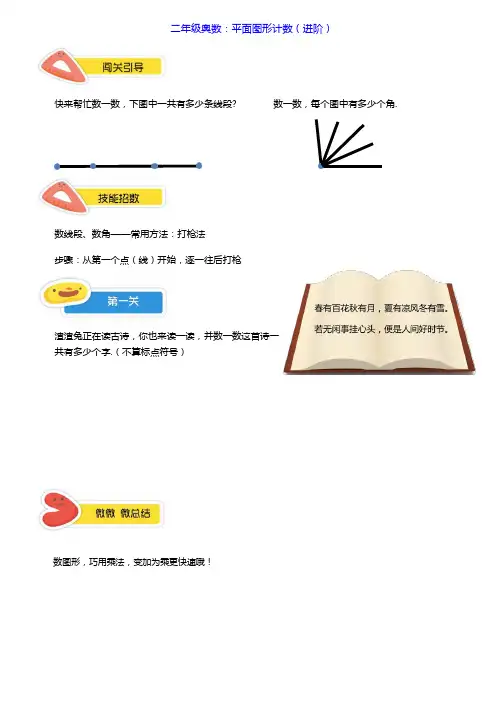
二年级奥数：平面图形计数（进阶）快来帮忙数一数，下图中一共有多少条线段? 数一数，每个图中有多少个角.数线段、数角——常用方法：打枪法步骤：从第一个点（线）开始，逐一往后打枪渣渣兔正在读古诗，你也来读一读，并数一数这首诗一共有多少个字.（不算标点符号）数图形，巧用乘法，变加为乘更快速哦！渣渣兔玩起了火柴棒，快来数数它用了多少根火柴棒呢！数图形①分类数，比如方向：横、竖、斜②找出相同的部分，数一数，用乘法轻松搞定注意：特殊的部分要别漏算了如果火柴棒变成了这样的造型，你再数数一共有多少根.微微老师也用火柴棒摆了一些图形，你来数一数.①观察下图，第 7 个三角形数是多少?②观察下图，第 8 个正方形数是多少?特殊数①三角形数——第几个数，就是从 1 加到几的和②正方形数——第几个数，就是几乘几的积一、数图形①分类数，比如方向：横、竖、斜②找出相同的部分，数一数，用乘法轻松搞定二、特殊数：三角形数、正方形数（1）这是（）.（打一动物）（2）罗网中心有一个点.织到第一层，一共有（）个点；织到第二层一共有（）个点……（3）现在这个网上一共有多少个点?（4）如果织到第八层，一共有多少个点?【练习 1】小朋友们看下面这首古诗，去掉标点，这首诗共有几个字?敕勒川，阴山下. 天似穹庐，笼盖四野.天苍苍，野茫茫.风吹草低见牛羊.【练习 2】下图这样摆出一个长方形，一共多了多少根小棒?【练习 3】下面的木板上，摆着一些火柴棒，小朋友请你数一数，这些火柴棒一共有多少根?【练习 4】数一数，下图中共有几个正方形.【练习 5】你知道跳棋棋盘上有多少个囿洞吗?数一数.。