下载文档原格式
第五章 电气设备的选择5-1 电气设备选择的一般原则是什么?答：电气设备的选择应遵循以下3项原则：(1) 按工作环境及正常工作条件选择电气设备a 根据电气装置所处的位置,使用环境和工作条件,选择电气设备型号；b 按工作电压选择电气设备的额定电压；c 按最大负荷电流选择电气设备和额定电流。
(2) 按短路条件校验电气设备的动稳定和热稳定 (3) 开关电器断流能力校验5-2 高压断路器如何选择？ 答：（1）根据使用环境和安装条件来选择设备的型号。
（2）在正常条件下，按电气设备的额定电压应不低于其所在线路的额定电压选择额定电压，电气设备的额定电流应不小于实际通过它的最大负荷电流选择额定电流。
（3）动稳定校验(3)max shi i ≥ 式中，(3)sh i 为冲击电流有效值，max i 为电气设备的额定峰值电流。
（4）热稳定校验2(3)2th th ima I t I t ∞≥式中，th I 为电气设备在th t 内允许通过的短时耐热电流有效值；th t 为电气设备的短时耐热时间。
（5）开关电器流能力校验对具有分断能力的高压开关设备需校验其分断能力。
设备的额定短路分断电流不小于安装地点最大三相短路电流，即(3).max cs K I I ≥5-3跌落式熔断器如何校验其断流能力?答：跌落式熔断器需校验分断能力上下限值,应使被保护线路的三相短路的冲击电流小于其上限值,而两相短路电流大于其下限值。
5-4电压互感器为什么不校验动稳定，而电流互感器却要校验？答：电压互感器的一、二次侧均有熔断器保护，所以不需要校验短路动稳定和热稳定。
而电流互感器没有。
5-5 电流互感器按哪些条件选择？变比又如何选择？二次绕组的负荷怎样计算？ 答：(1）电流互感器按型号、额定电压、变比、准确度选择。
( 2）电流互感器一次侧额定电流有20，30，40，50，75，100，150，200，400，600，800，1000，1200，1500，2000（A ）等多种规格，二次侧额定电流均为5A ，一般情况下，计量用的电流互感器变比的选择应使其一次额定电流不小于线路中的计算电流。
概率论习题解答（第5章）第5章习题答案三、解答题1. 设随机变量X 1，X 2，…，X n 独⽴同分布，且X ～P (λ)，∑==ni i X n X 11，试利⽤契⽐谢夫不等式估计}2|{|λλ<-X P 的下界。
解：因为X ～P (λ)，∑∑===?===n i i n i i n nX E n X n E X E 111)(1)1()(λλλλn n nX D n X n D X D n i i n i i 11)(1)1()(2121====∑∑==由契⽐谢夫不等式可得nn X P 4114/1}2|{|-=-≥<-λλλλ 2. 设E (X ) = – 1，E (Y ) = 1，D (X ) = 1，D (Y ) = 9，ρ XY = – 0.5，试根据契⽐谢夫不等式估计P {|X + Y | ≥ 3}的上界。
解：由题知()()()Y X Y X E E E +=+=()11+-=0Cov ()Y X ,=()()Y D X D xy ??ρ=()915.0??-= -1.5()()()()()75.1291,2=-?++=++=+Y X Cov Y D X D Y X D所以{}{}97303≤≥-+P =≥+)(Y X Y X P 3. 据以往经验，某种电器元件的寿命服从均值为100⼩时的指数分布．现随机地取16只，设它们的寿命是相互独⽴的．求这16只元件的寿命的总和⼤于1920⼩时的概率．解：设i 个元件寿命为X i ⼩时，i = 1 ,2 , ...... , 16 ，则X 1 ，X 2 ，... ，X 16独⽴同分布，且 E (X i ) =100，D (X i ) =10000，i = 1 ,2 , ...... , 16 ，4161161106.1)(,1600)(?==∑∑==i i i i D E X X ，由独⽴同分布的中⼼极限定理可知：∑=16i iX近似服从N ( 1600 , 1.6?10000)，所以>∑=1920161i i X P =≤-∑=19201161i i X P ???-≤?--=∑=16000016001920100006.116001161i i X P()8.01Φ-==1- 0.7881= 0.21194. 某商店负责供应某地区1000⼈商品，某种商品在⼀段时间内每⼈需要⽤⼀件的概率为0.6，假定在这⼀时间段各⼈购买与否彼此⽆关，问商店应预备多少件这种商品，才能以99.7%的概率保证不会脱销（假定该商品在某⼀时间段内每⼈最多可以买⼀件）．解：设商店应预备n 件这种商品，这⼀时间段内同时间购买此商品的⼈数为X ，则X ~ B （1000，0.6），则E (X ) = 600，D (X ) = 240，根据题意应确定最⼩的n ，使P {X ≤n }= 99.7%成⽴. 则P {X ≤n })75.2(997.0)240600(240600240600ΦΦP ==-≈-≤-=n n X 所以6.64260024075.2=+?=n ，取n =643。
第五章 汇编语言程序设计1、画图说明下列语句所分配的存储器空间及初始化的数据值。
难度：2(1) BYTE_VAR DB ‘BYTE’，12，-12H ，3 DUP(0，2 DUP(1，2)，7) (2) WORD_VAR DW 3 DUP(0，1，2)，7，-5，’BY’，’TE’，256H 答：（1） （2）07H BYTE_V AR 42H WORD_V AR 00H 00H 59H 00H FBH 54H 01H FFH 45H 00H 59H 0CH 02H 42H EEH 00H 45H 00H 00H 54H 01H 00H 56H 02H 01H 02H 01H 00H 02H 02H 07H 00H 00H 00H 01H 00H 02H 01H 01H 00H 02H 02H 07H 00H 00H 00H 01H 00H 02H 01H 01H 00H 02H 02H07H00H2、假设程序中的数据定义如下： PARTNO DW ?PNAME DB 16 DUP(?) COUNT DD ? PLENTH EQU $- PARTNO 问：PLENTH 的值为多少？他表示什么意义？ 答：PLENTH 的值为22，它表示当前已分配单元空间。
《微型计算机原理》第5章习题与解答3、有符号定义语句如下：难度：2BUF DB 1，2，3，’123’EBUF DB 0L EQU EBUF-BUF问：L的值是多少？答：L的值为6；4、假设成序中的数据定义如下：难度：2LNAME DB 30 DUP(?)ADDRESS DB 30 DUP(?)CITY DB 15 DUP(?)CODE_LIST DB 1,7,8,3,2(1)用一条MOV指令将LNAME的偏移地址存入BX。
(2)用一条指令将CODE_LIST的头两个字节的内容放入SI。
(3)写一条伪指令定义符使CODE_LENGTH的值等于 CODE_LIST域的实际长度。
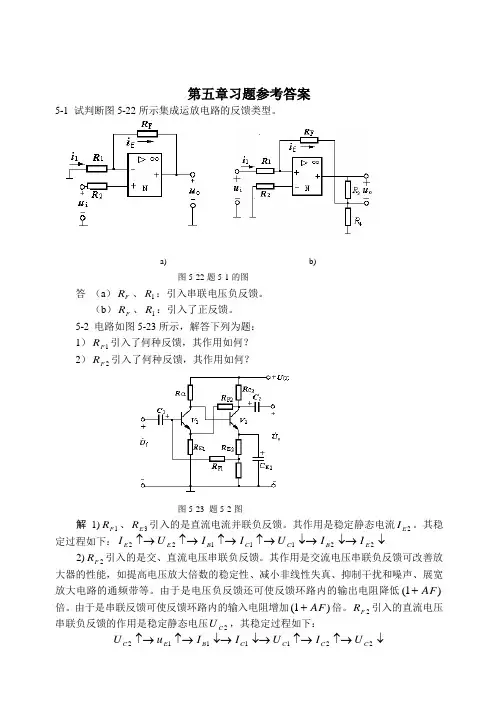
第五章习题参考答案5-1 试判断图5-22所示集成运放电路的反馈类型。
a) b)图5-22题5-1的图答 （a ）F R 、1R ：引入串联电压负反馈。
（b ）F R 、1R ：引入了正反馈。
5-2 电路如图5-23所示，解答下列为题： 1）1F R 引入了何种反馈，其作用如何？ 2）2F R 引入了何种反馈，其作用如何？图5-23 题5-2图解 1)1F R 、3E R 引入的是直流电流并联负反馈。
其作用是稳定静态电流2E I 。
其稳定过程如下：↓↓→↓→↑→↑→↑→↑→2211122E B C C B E E I I U I I U I2)2F R 引入的是交、直流电压串联负反馈。
其作用是交流电压串联负反馈可改善放大器的性能，如提高电压放大倍数的稳定性、减小非线性失真、抑制干扰和噪声、展宽放大电路的通频带等。
由于是电压负反馈还可使反馈环路内的输出电阻降低)1(AF +倍。
由于是串联反馈可使反馈环路内的输入电阻增加)1(AF +倍。
2F R 引入的直流电压串联负反馈的作用是稳定静态电压2C U ，其稳定过程如下：↓↑→↑→↓→↓→↑→↑→2211112C C C C B E C U I U I I u U5-3 在图5-24所示的两级放大电路中，（1）那些是直流负反馈；（2）哪些是交流负反馈，并说明其类型；（3）如果F R 不接在T 2的集电极，而是接在C 2与L R 之间，两者有何不同？（4）如果F R 的另一端不是接在T 1的发射极，而是接在它的基极，有何不同，是否会变为正反馈？5-24 题5-3图解 1)1E R 、2E R 直流串联电流负反馈，F R 、1E R 直流电压串联负反馈。
2)F R 、1E R 交流电压串联负反馈。
3)如果F R 不接在T 2的集电极，而是接在C 2与L R 之间，则F R 、1E R 只有交流电压串联负反馈，没有直流反馈。
4)如果F R 的另一端不是接在T 1的发射极，而是接在它的基极，则变为正反馈。
习 题 五1. 设V 是数域F 上向量空间，假如V 至少含有一个非零向量α，问V 中的向量是有限多还是无限多？有没有n (n ≥ 2)个向量构成的向量空间？ 解 无限多；不存在n (n ≥ 2)个向量构成的向量空间(因为如果F 上一个向量空间V 含有至少两个向量, 那么V 至少含有一个非零向量α , 因此V 中含有α , 2α , 3α , 4α , …,这无穷多个向量互不相等,因此V 中必然含有无穷多个向量).2. 设V 是数域F 上的向量空间，V 中的元素称为向量，这里的向量和平面解析几何中的向量α，空间解析几何中的向量β有什么区别？解 这里的向量比平面中的向量意义广泛得多,它可以是多项式,矩阵等,不单纯指平面中的向量.3. 检验以下集合对所指定的运算是否构成数域F 上的向量空间.（1）集合：全体n 阶实对称矩阵；F ：实数域；运算：矩阵的加法和数量乘法；（2）集合：实数域F 上全体二维行向量；运算： (a 1, b 1)+ (a 2, b 2)＝(a 1＋a 2, 0) k • (a 1, b 1)＝(ka 1, 0)（3）集合：实数域上全体二维行向量；运算： (a 1, b 1)+ (a 2, b 2)＝(a 1＋a 2, b 1＋b 2)k •( a 1, b 1)＝(0, 0)解 (1) 是; (2) 不是(因为零向量不唯一);(3) 不是(不满足向量空间定义中的(8)).4. 在向量空间中，证明，(1) a (－α)=－a α=(－a ) α ,(2) (a -b )α＝a α－b α ,a ,b 是数，α是向量.证明 (1) a a a a =+-=+-))(()(αααα 0= 0ααa a -=-∴)(又 ==+-=+-a a a a a 0))(()(ααα 0ααa a -=-∴)(综上, .)()(αααa a a -=-=-(2) ααααααb a b a b a b a -=-+=-+=-)())(()(.5. 如果当k 1＝k 2＝…＝k r ＝0时，k 1α1＋k 2α2＋…＋k r αr ＝0, 那么α1, α2, …, αr 线性无关. 这种说法对吗？为什么?解 这种说法不对. 例如设α1=(2,0, -1), α2=(-1,2,3), α3=(0,4,5), 则0α1+0α2+0α3=0. 但α1, α2, α3线性相关, 因为α1+2α2－α3=0.6. 如果α1, α2, …, αr 线性无关，而αr ＋1不能由α1, α2, …, αr 线性表示，那么α1, α2,…, αr , αr ＋1线性无关. 这个命题成立吗？为什么？ 解 成立. 反设α1, α2,…, αr , αr ＋1线性相关,由条件α1, α2, …, αr 线性无关知αr ＋1一定能由α1, α2, …, αr 线性表示,矛盾.7. 如果α1, α2, …, αr 线性无关，那么其中每一个向量都不是其余向量的线性组合. 这种说法对吗？为什么？解 对. 反设 αi = k 1α1+k 2α2+…k i -1αi-1+k i+1αi ＋1 +…+k r αr ,则 k 1α1+k 2α2+…k i -1αi-1+(－1) αi +k i+1αi ＋1 +…+k r αr =0. 由于－1≠0, 故α1, α2, …, αr 线性相关.8. 如果向量α1, α2, …, αr 线性相关，那么其中每一个向量都可由其余向量线性表示. 这种说法对吗？为什么？解 不对. 设α1=(1,0) , α2=(2,0) , α3=(0,1) , 则α1, α2, α3线性相关, 但α3不能由α1, α2线性表示.9. 设α1＝ (1, 0, 0), α2＝ (1, 2, 0), α3＝(1, 2, 3)是F 3中的向量，写出α1, α2, α3的一切线性组合. 并证明F 3中的每个向量都可由{α1, α2, α3}线性表示.解 k 1α1+k 2α2+k 3α3 k 1, k 2 , k 3∈F .设k 1α1+k 2α2+k 3α3=0,则有⎪⎩⎪⎨⎧==+=++030220332321k k k k k k , 解得 k 1= k 2 =k 3=0.故α1, α2, α3线性无关.对任意(a,b,c)∈F 3, (a,b,c)=3213)32())322((αααc c b c ba +-+--,所以F 3中的每个向量都可由{α1, α2, α3}线性表示.10. 下列向量组是否线性相关(1) α1＝ (1, 0, 0), α2＝ (1, 1, 0), α3＝(1, 1, 1)；(2) α1＝(3, 1, 4), α2＝(2, 5, -1), α3＝(4, -3, 7).解 (1) 线性无关; (2) 线性无关.11. 证明，设向量α1, α2, α3线性相关，向量α2, α3, α4线性无关，问：(1) α1能否由α2, α3线性表示？说明理由；(2) α4能否由α1, α2, α3线性表示？说明理由.解 (1)因为α2, α3线性无关而α1, α2, α3线性相关,所以α1能由α2, α3线性表示;(2)反设α4能由α1, α2, α3线性表示,但α1能由α2, α3线性表示,故α4能由α2, α3线性表示,这与α2, α3, α4线性无关矛盾,所以α4不能由α1, α2, α3线性表示.12. 设α1＝ (0, 1, 2), α2＝ (3, －1, 0), α3＝(2, 1, 0)，β1＝ (1, 0, 0), β2＝ (1, 2, 0), β3＝(1, 2, 3)是F 3中的向量. 证明，向量组{α1, α2, α3}与{β1, β2, β3}等价.证明 (β1, β2, β3)=(321,,εεε)A(α1, α2, α3)= (321,,εεε)B其中A=⎪⎪⎪⎭⎫ ⎝⎛300220111, B=⎪⎪⎪⎭⎫ ⎝⎛-002111230.易验证A , B 均可逆, 这样 (β1, β2, β3) = (α1, α2, α3 )(B -1A )(α1, α2, α3) = (β1, β2, β3)(A -1B ) ,故向量组{α1, α2, α3}与{β1, β2, β3}等价.13. 设数域F 上的向量空间V 的向量组{α1, α2, …, αs }线性相关，并且在这个向量组中任意去掉一个向量后就线性无关. 证明，如果∑=s i i ik 1α＝0 (k i ∈F )，那么或者k 1＝k 2＝…＝k s ＝0, 或k 1，k 2，…，k s 全不为零.证明 由条件∑=s i i ik 1α＝0 (k i ∈F )知k i αi = - (k 1α1+k 2α2+…k i -1αi-1+k i+1αi ＋1 +…+k s αs ) （*）(1) 当k i =0时,（*)式左边等于零,故k 1α1+k 2α2+…k i -1αi-1+k i+1αi ＋1 +…+k s αs =0. 由于这s -1个向量线性无关,所以k 1＝k 2＝…＝k s ＝0.(2) 当k i ≠0时, αi = -ik 1(k 1α1+k 2α2+…k i -1αi-1+k i+1αi ＋1 +…+k s αs ),下证对于任意i j s j ≠∈},,2,1{ 时k j ≠0. 反设k j =0, 则αi 可由s -2个向量线性表示.这与任意s -1个向量线性无关矛盾,所以此时k 1,k 2，…，k s 全不为零.14. 设α1＝(1, 1), α2＝(2, 2), α3＝(0, 1) , α4＝(1, 0)都是F 2中的向量. 写出{α1, α2, α3, α4}的所有极大无关组.解 α1, α3 ; α1, α4 ; α2 ,α3 ; α2 ,α4 ; α3 ,α4 .15. 设A 1＝⎪⎪⎭⎫ ⎝⎛-2001,A 2＝⎪⎪⎭⎫ ⎝⎛-0021, A 3＝⎪⎪⎭⎫ ⎝⎛0120,A 4＝⎪⎪⎭⎫ ⎝⎛-2142∈M 2×2(F ). 求向量空间M 2×2(F )中向量组{A 1, A 2,A 3, A 4}的秩及其极大无关组. 解 秩{A 1, A 2,A 3, A 4}=3, {A 1, A 2,A 3}是向量组{A 1, A 2, A 3, A 4}的一个极大无关组.16．设由F 4中向量组｛α1=(3，1，2，5)，α2＝(1，1，1，2)，α3＝(2，0，1，3)，α4 =(1，－1，0，1)，α5 =(4，2，3，7)｝. 求此向量组的一个极大无关组.解 (α1,α2,α3,α4,α5)= (4321,,,εεεε)A , 其中A=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-71325301122101141213, 则秩A =2. 又(α1,α2 )= (4321,,,εεεε)B , 其中B =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛25121113. 秩B =2, 故{α1,α2}线性无关, 它是向量组{α1,α2,α3,α4,α5}的一个极大无关组.17. 证明，如果向量空间V 的每一个向量都可以唯一表成V 中向量α1, α2, …, αn 的线性组合，那么dim V ＝n .证明 由条件零向量可唯一的表示成α1, α2, …, αn 的线性组合, 这说明α1, α2, …, αn 线性无关, 故可作为V 的基, 从而dim V ＝n .18. 设β1, β2，…，βn 是F 上n (>0)维向量空间V 的向量，并且V 中每个向量都可以由β1, β2，…，βn 线性表示. 证明, {β1, β2，…，βn }是V 的基.证明 由条件标准正交基{ e 1, e 2, …,e n }可由β1, β2，…，βn 线性表示, 反过来β1, β2，…，βn 又可由{ e 1, e 2, …,e n }线性表示,所以{ e 1, e 2, …,e n }和{β1, β2，…，βn }等价. 由{ e 1, e 2, …,e n }线性无关知{β1, β2，…，βn }线性无关,又因V 中每个向量都可以由β1, β2，…，βn 线性表示, 由基的定义知{β1, β2，…，βn }是V 的基.19. 复数集C 看作实数域R 上的向量空间（运算: 复数的加法，实数与复数的乘法）时，求C 的一个基和维数.解 基为{1, i }； dim C ＝2.20. 设V 是实数域R 上全体n 阶对角形矩阵构成的向量空间（运算是矩阵的加法和数与矩阵的乘法）. 求V 的一个基和维数.解 基为E ii (i =1,2, …,n )； dim V ＝n .21. 求§5.1中例9给出的向量空间的维数和一个基.解 任意一个不等于1的正实数都可作为V 的基； dim V ＝1.22. 在R 3中，求向量α＝(1, 2, 3)在基ε1＝(1, 0, 0)，ε2＝(1, 1, 0)，ε3＝(1, 1, 1)下的坐标.解 (-1,-1,3)T .23. 求R 3中由基{α1, α2, αs }到基{β1, β2, β3 }的过渡矩阵，其中α1＝(1, 0, -1), α2＝(-1, 1, 0), α3＝(1, 2, 3)，β1＝(0, 1, 1), β2＝(1, 0, 1), β3＝(1, 1, 1).解 所求过渡矩阵为⎪⎪⎪⎭⎫ ⎝⎛-32204230061. 24. 设{α1, α2,…, αn }是向量空间V 的一个基，求由这个基到基{α3, α4, …, αn ，α1, α2}的过渡矩阵.解 所求过渡矩阵为⎪⎪⎭⎫ ⎝⎛-0022n I I . 25. 已知F 3中向量α关于标准基ε1＝(1, 0, 0)，ε2＝(0, 1, 0) ，ε3＝(0, 0, 1)的坐标是(1, 2, 3)，求α关于基β1＝(1, 0, 1), β2＝(0, 1, 1), β3＝(1, 1, 3)的坐标.解 (1,2,0)T .26. 判断R n 的下列子集哪些是子空间(其中R 是实数域，Z 是整数集).(1) {(a 1, 0, …, 0, a n )| a 1, a n ∈R };(2) {(a 1, a 2, …, a n )|∑==ni i a 10，a 1, a 2, …, a n ∈R };(3) {(a 1, a 2, …, a n )|a i ∈Z , i ＝1, 2, …, n };解 (1) 是; (2) 是; (3) 不是(数乘不封闭).27. 设V 是一个向量空间，且V ≠{0}. 证明，V 不能表成它的两个真子空间的并集.证明 设W 1与W 2是V 的两个真子空间(1) 若21W W ⊆，则W 1⋃W 2= W 2≠V ;(2) 若21W W ⊇,则W 1⋃W 2= W 1≠V ;(3) 若21W W ⊄且12W W ⊄, 取1W ∈α但2W ∉α,2W ∈β但1W ∉β, 那么1W ∉+βα,否则将有1)(W ∈=-+βαβα,这与1W ∉β矛盾, 同理2W ∉+βα, 所以V 中有向量21W W ∉+βα,即V ≠21W W .28. 设V 是n 维向量空间，证明V 可以表示成n 个一维子空间的直和.证明 设{α1, α2,…, αn }是向量空间V 的一个基, (α1), (α2) ,…, (αn )分别是由α1, α2,…, αn 生成的向量空间, 要证(α1+α2+…+αn )= (α1)⊕ (α2)⊕…⊕ (αn )(1) 因为{α1, α2,…, αn }是V 的一个基, 所以V 中任一向量α都可由α1, α2,…, αn 线性表示, 此即(α1+α2+…+αn )= (α1)+ (α2)+…+ (αn ).(2) 对任意i ≠j ∈{1,2,…, n },下证 (αi )∩ (αj )={0}. 反设存在0 ≠∈x (αi )∩ (αj ),由∈x (αi )知存在k F ∈使得x =k αi ； 由 x ∈ (αj )知存在F l ∈使得x =l αj , 从而αi =kl αj , 即α1与α2线性相关, 矛盾, 所以 (αi )∩ (αj )={0}. 综上, (α1+α2+…+αn )= (α1)⊕ (α2)⊕…⊕ (αn ).29. 在R 3中给定两个向量组α1＝(2, -1, 1, -1), α2＝(1, 0, -1, 1),β1＝(-1, 2, -1, 0), β2＝(2, 1, -1, 1).求 (α1, α2)＋ (β1, β2) 的维数和一个基.解 取R 4的标准正交基{4321,,,εεεε},于是(α1, α2, β1, β2)= (4321,,,εεεε)A ,其中 A =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------1011111112012112 , 秩A = 4. 故α1, α2, β1, β2线性无关, 又因为 (α1, α2)∩ (β1, β2)={0},所以dim (α1, α2) + dim (β1, β2)= 4,{ α1, α2, β1, β2}是它的基.30. 设W 1, W 2都是向量空间V 的子空间，证明下列条件是等价的：(1) W 1⊆W 2;(2) W 1∩W 2＝W 1;(3) W 1＋W 2＝W 2.证明 (i) (1)⇒(2) 因为W 1⊆W 2 , 所以W 1∩W 2＝W 1. (ii) (2)⇒(3) W 1＋W 2 ={α1+α2 | α1∈W 1, α2∈W 2} 由(2)知对任意α∈W 1, 都有α∈W 2 , 所以W 1＋W 2 ={α1+α2 | α1, α2∈W 2}=W 2 .(iii) (3)⇒(1) W 1＋W 2 ={α1,+α2 | α1∈W 1, α2∈W 2}=W 2 , 说明对任意α∈W 1, 都有α∈W 2 , 此即W 1⊆W 2 .31. 设V 是实数域R 上n 阶对称矩阵所成的α2向量空间；W 是数域R 上n 阶上三角矩阵所成的向量空间，给出V 到W 的一个同构映射.解 对∈∀A V (A =(a ij )且a ij = a ji )和B ∈W (B =(a ij ),当i>j 时, a ij =0) 定义f : V → WA B 易验证f 是V 到W 的一个同构映射.32. 设V 与W 都是数域F 上的向量空间，f 是V 到W 的一个同构映射，证明{α1, α2, …, αn }是V 的基当且仅当{f (α1), f (α2), …, f (αn )}是W 的基.证明 设{α1, α2, …, αn }是V 的基.(1) 由α1, α2, …, αn 线性无关知f (α1), f (α2), …, f (αn ) 线性无关.(2) 任取∈ηW , 由f 是同构映射知存在∈ξV 使得f (ξ)=η.但ξ=∑=n i i ia 1α, a i ∈F , f (ξ)=f (∑=n i i i a 1α)=)(1∑=n i i i f a α=η. 由η的任意性知{f (α1), f (α2), …, f (αn )}是W 的基.反过来, {f (α1), f (α2), …, f (αn )}是W 的基(1) 由f (α1), f (α2), …, f (αn )线性无关知α1, α2, …, αn 线性无关.(2) 任取∈ξV , 由f 是同构映射知存在∈ηW 使得f (ξ)=η.但η=∑=n i i i f k 1)(α= f (∑=n i i i k 1α), k i ∈F , 从而ξ=∑=ni i i k 1α, k i ∈F .由ξ的任意性知{ α1, α2, …, αn }是V 的基.补 充 题1. 设W 1, W 2是数域F 上向量空间V 的两个子空间. α,β是V 的两个向量，其中α∈W 2，但α∉ W 1，β∉W2. 证明：（1）对于任意k ∈F ，αβk +∉W 2；（2）至多有一个k ∈F ，使得αβk +∈W 1.证明 (1)反设存在k 1∈F 使得αβ1k +∈W 2 , 又α∈W 2 , 因此β=β+ k 1α-k 1α∈W 2 , 这与β∉W 2矛盾. 所以对于∀k ∈F ，αβk +∉W 2 .(2)若有k 1, k 2∈F , k 1≠k 2使得αβ1k +, αβ2k +∈W 1, 那么。
第5章：运输层1、试说明运输层在协议栈中的作用？运输层的通信和网络层的通信有什么重要的区别？为什么运输层是必不可少的？答：（1）首先，从通信和信息处理的角度来看，运输层向它上面的应用层提供通信服务，并为高层用户屏蔽了下层通信通信子网的细节。
其次，运输层的另一个重要功能就是复用和分用功能。
第三，运输层对传输的报文提供了差错检测机制。
第四，根据应用的不同，运输层还采用不同的运输层协议提供不同的服务。
（2）网络层为主机之间提供逻辑通信，而运输层为应用进程之间提供端到端的逻辑通信，如下图所示：（3）虽然无连接的运输服务和无连接的网络服务十分相似，但是运输层依然有它存在的必要性，因为：事实上，网络层是通信子网的一个组成部分，假设网络服务质量不可靠，频繁地丢失分组，网络层系统崩溃或不停的发出网络重置，这将发生什么情况呢？因为用户不能对通信子网加以控制，所以无法采用更好的通信处理机来解决网络层服务质量低劣的问题，更不可能通过改进数据链路层纠错能力来改善低层的条件。
因此，解决这一问题的唯一可行的办法就是在网络层的上面增加一层，即运输层。
运输层的存在使得运输服务比网络服务更可靠，分组的丢失、残缺，甚至网络重置都可以被运输层检测到，并采用相应的补救措施，而且由于运输服务独立于网络服务，故可以采用一个标准的原语集提供运输服务。
2、网络层提供数据报或虚电路服务对上面的运输层有何影响？答：如果下层的网络十分可靠，例如提供虚电路服务，那么用于完成数据传输的运输层协议就不需要做太多的工作。
当网络层仅使用提供不可靠的数据报服务时，运输层就需要使用一些复杂的协议，以便能够提供更优质的服务。
3、当应用程序使用面向连接的TCP和无连接的IP时，这种传输是面向连接的还是面向连接的？答：在网络层IP提供的是无连接的服务，但是在运输层TCP提供的服务是面向连接的。
但是最终，该应用程序使用的还是面向连接的传输服务。
4、试用画图解释运输层的复用。
画图说明许多个运输用户复用到一条运输连接上，而这一条运输连接又复用到IP 数据报上。
答：答案见辅导材料P155页。
5、试举例说明有些应用程序愿意采用不可靠的UDP,而不愿意采用可靠的TCP。
答：6、接收端收到有差错的UDP用户数据报时应如何处理？答：简单的进行丢弃，其他的什么也不做。
7、如果应用程序愿意使用UDP完成可靠的传输，这可能吗？请说明理由？答：不可能。
因为UDP是无连接的，只提供尽最大可能的交付。
并且UDP没有拥塞控制，当很多主机同时向网络发送高速率的数据时，网络就会产生拥塞，结果会致使大家都收不到正确的数据。
8、为什么说UDP是面向报文的，而TCP是面向字节流的？答：在发送方，UDP对应用层送交下来的报文既不合并，也不拆分，按照原样发送，即UDP一次发送一个报文；在接收方，UDP对IP层交上来的UDP数据报，在除去首部后就原封不动的交付给上层的应用进程，即,UDP一次交付一个报文。
TCP是面向字节流的：TCP仅把应用程序交下来的数据看成一连串的无结构的字节流，并不知道所传输的字节流的含义，也不保证接收方应用程序收到的数据块和发送方发送的数据块的大小是否具有对应关系。
即：TCP可能把应用层交下来的数据块分成几个部分发送出去，也可能把几个数据块合并成一个发送出去。
在接收端也同样。
9、端口的作用是什么？为什么端口号要划分为三种？答：端口的作用：发送端：让应用层的各种应用进程都能将其数据通过端口向下交付给运输层，以便组成TPDU；接收端：运输层收到IP层交上来的数据后，要根据目的端口号决定应当通过哪个端口将数据交付给应用层中的相应的进程。
从这个意义上讲，端口是用来标志应用层的进程。
把端口号分成三种不同的类型是为了方便不同的应用程序使用：熟知端口号（系统端口号）：其数值标号为0~1023,把它们指派给TCP/IP最重要的一些应用程序使用，让所有的用户都知道。
当一种新型的应用程序出现后，IANA必须要为它指派一个熟知端口号，否者因特网上的其它应用程序就无法和它进行通信。
登记端口号：是为了给没有熟知端口号的应用程序使用的。
客户端使用的端口号：这类端口号仅在客户进程运行时才动态选择的，是留给客户进程选择暂时使用的。
10、试说明运输层中伪首部的作用。
答：伪首部既不向上也不向下传送，仅仅是为了计算检验和。
11、某个应用进程使用运输层的用户数据UDP,然后继续向下交给IP层后组成IP数据报。
既然都是数据报，是否可以跳过UDP直接交给IP层？哪些功能UDP提供了但是IP没有提供？答：虽然都是数据报，但是应用进程不能跳过UDP直接交给IP层，因为IP数据报只能找到目的主机而无法找到目的进程。
UDP提供了IP 所不能提供的复用和分用功能；UDP可以对数据报做包括数据段在内的差错检测，而IP只对其数据报的头部做差错检测。
12、一个应用程序用了UDP，到了IP层之后把数据报再分为4个数据报片发送出去，结果是前两个数据报片丢失，后两个到达了目的站，过了一段时间，应用程序重传UDP,而IP层仍然划分为4个数据报片来传送，结果这次的前两个到达了目的站而后两个丢失了。
试问：在目的站能否将这四个数据报片组装成一个完整的数据报？假设在目的站第一次收到的后两个数据报片仍然保存在目的站的缓存中》答：不行。
重传时，IP数据报的标识字段会有另一个标识符。
仅当标识符相同的数据报片才能组成一个数据报。
前两个数据报片的标识符和后两个数据报片的标识符不同，所以不能组成一个IP数据报。
13、一个UDP用户数据报的数据字段为8192字节，在链路层要使用以太网来传送，试问应当划分为几个IP数据报片？说明每个IP数据报片的长度和片偏移字段的值？答：以太网帧的数据字段的最大长度是1500字节。
UDP数据报的首部是8个字节，所以整个UDP数据报的长度是8200字节。
假定IP数据报的首部没有选项，即首部长度是20字节。
而IP数据报的片偏移量指出了一个片在原IP数据分组中的相对位置，单位是8字节。
通过以上分析，可将UDP数据报分为6个数据报片，前5个的长度是1480字节（IP数据报是1500字节），最后一个的长度是800字节（IP 数据报是820字节），片偏移量分别是：0，185，370，555，740，925.14、一个UDP用户数据报的首部的十六进制表示是：06 32 00 45 00 1C E2 17 。
试求源端口，目的端口，用户数据报的总长度、数据部分长度。
这个用户数据报是从客户发送给服务器的，还是服务器发送给客户的？使用UDP的这个服务器程序是什么？答：把UDP数据报的首部各字段如下（每个字段都是2字节）：因此：源端口是1586，目的端口是69，UDP用户数据报总长度是28字节，数据部分是20字节。
此UDP用户数据报是从客户发给服务器的，因为目的端口号69<1023,是熟知端口。
服务程序是TFTP。
（查熟知端口表就会知道）。
15、使用TCP对实时话音数据的传输有没有什么问题？使用UDP在传输数据文件时会有什么问题？答：UDP不保证可靠交付，但是UDP比TCP的开销要小。
因此，只要应用程序接受这样的服务质量就可以使用UDP。
如果话音不是实时数据（边接收边播放）就可以使用TCP,因为TCP传输可靠。
接收端用TCP将话音数据接收完毕后，可以在以后的任何时间进行播放。
但假定是实时传输，则必须使用UDP.16、在停止等待协议中，在什么情况下确认帧可以不使用序号？在停止等待协议中，如果不使用编号是否可行？为什么？答：（1）在停止等待协议中，仅当数据帧和确认帧在传输的过程中既不会丢失也不会有差错的情况下，确认帧才可以不使用序号（其实，如果在传输的过程中既不丢失也无差错时，根本就不用确认了）。
（2）然而在现实的数据传输中，很难保证数据的传输既不丢失也不出现差错，所以在停止等待协议中应当使用序号。
17、在停止等待协议中，如果收到重复的报文段时不予理睬（即悄悄地丢弃它，其他什么也不做）是否可行？试举出具体的例子。
答：不行。
如下图所示：若对收到的重复的报文不进行重传确认，就会让发送方一直认为它所发送的数据没有正确到达接收端，而继续重传下去；当重传达到一定的次数时，就会认为网络出现了故障。
18、假定在运输层使用停止等待协议。
发送方在发送报文段M0后在设定的时间内未收到确认，于是重传M0，但是M0又迟迟不能到达接收方。
不久，发送方收到了迟到的对M0的确认，于是发送下一个报文段M1，不久就收到了对M1的确认。
接着发送方发送新的报文段M0，但是这个新的M0在传送的过程中丢失了。
正巧，一开始就滞留在网络中的M0现在到达了接收方。
接收方无法分辨M0是旧的。
于是收下了M0，并发送确认。
显然，接收方后来收到的M0是重复的，协议失败了。
试画出类似于图5-9所示的双方交换报文段的过程。
答：见教材P38319、试证明：当用n比特进行分组的编号时，若接收窗口等于1（即只能按序接收分组），则仅在发送窗口不超过2n-1时，连续ARQ协议才能正确运行。
窗口的单位是分组。
答：如下图所示：设发送窗口记为W T ,接收窗口记为W R .假定用3个比特进行编号，设接收窗口正好在7号分组处（有阴影的分组）。
发送窗口W T的位置不可能比②更靠前，也不可能比③更靠后，也可能不是这种极端位置，如①。
对于①和②的情况，在W T的范围内无重复序号，即W T≦2n。
对于③的情况，在W T+W R的范围内无重复序号，即W T+W R≦2n。
现在W R =1，故发送窗口的最大值W T≦2n-1。
图见教材P38320、在连续ARQ协议中，若发送窗口等于7，则发送端在开始发送时可以连续发送7个分组，因此，每一个分组发送出去后，都要设置一个超时计时器。
现在计算机中只有一个硬时钟。
设这7个分组发出的时间分别是：t0 ,t1 ,t2 ,t3 ,t4 ,t5 ,t6 ,且t out都一样大，试问如何实现这7个超时计时器（这叫软时钟法）？答：用相对发送时间实现一个链表，见P383图A-5。
21、假定使用连续ARQ协议，发送窗口大小是3，而序号的范围是【0，15】，而传输媒体保证在接收方能够按序收到分组，在某个时刻，在接收方，下一个期望收到的序号是5.试问：（1）在发送方的发送窗口中可能出现的序号组合有哪几种？（2）接收方已经发送出去的、但是在网络中（即还没有到达发送方）的确认分组可能有哪些？说明这些确认分组是用来确认哪些序号的分组？答：（1）接收方期望收到的分组序号是5，说明前5个分组都已经收到了。
若这些确认都已经到达了发送方，则发送窗口的范围是【5，7】。
接收方期望收到序号为5的分组，说明序号为0，1，2，3，4的分组都已经收到，并且发出了确认。
并且对序号为0，1的分组的确认肯定被发送方收到了，否则不可能发送4号分组。
