19 全因子实验设计

820 112 40 144 140 132 138.667820 120 50 125 127 140 130.667810 116 45 92 136 83 103.667810 116 45 129 119 87 111.667800 112 50 91 79 94 88.000820 120 40 116 121 94 110.333800 120 50 118 98 90 102.000820 112 50 135 149 137 140.333820 112 50 131 140 142 137.667820 112 40 113 110 136 119.667800 120 40 82 116 113 103.667820 120 50 99 159 118 125.333800 112 40 82 101 87 90.000800 120 40 107 126 116 116.333820 120 40 159 118 108 128.333800 112 40 114 92 109 105.000800 120 50 116 111 71 99.333810 116 45 134 132 130 132.0002。

第二阶段；分析因子设计。

目的：得到Y=f(x),确定哪些因子值得存在函式内。

结果: 第1次实验MINITAB路径：统计-DOE-因子-因子分析设计拟合因子: Y 与压力, 密度, 温度Y 的效应和系数的估计（已编码单位）系数标项效应系数准误 T P常量 114.211 2.179 52.42 0.000压力 29.917 14.958 2.374 6.30 0.000密度 1.167 0.583 2.374 0.25 0.810温度 -0.167 -0.083 2.374 -0.04 0.973压力*密度 -11.583 -5.792 2.374 -2.44 0.033（P0.05,接受HO:交互作用对Y没有影响）压力*温度 9.417 4.708 2.374 1.98 0.073（P0.05,接受HO:交互作用对Y 没有影响）密度*温度 -0.167 -0.083 2.374 -0.04 0.973（P0.05,接受HO:交互作用对Y没有影响）压力*密度*温度 -0.417 -0.208 2.374 -0.09 0.932（P0.05,接受HO:交互作用对Y没有影响）S = 9.49770 PRESS = 2630.73R-Sq = 81.86% R-Sq（预测）= 51.91% R-Sq（调整）= 70.32%对于Y 方差分析（已编码单位）来源自由度 Seq SS Adj SS Adj MS F P主效应 3 3585.58 3585.58 1195.19 13.25 0.0012因子交互作用 3 891.50 891.50 297.17 3.29 0.0623因子交互作用 1 0.69 0.69 0.69 0.01 0.932残差误差 11 992.27 992.27 90.21弯曲 1 8.75 8.75 8.75 0.09 0.772纯误差 10 983.52 983.52 98.35合计 18 5470.05从上图可以看出，P0.05,接受HO:交互作用对Y没有影响，可以通过缩减再观察P值Y 的效应和系数的估计（已编码单位）系数标项效应系数准误 T P常量 114.211 2.571 44.42 0.000压力 29.917 14.958 2.802 5.34 0.000密度 1.167 0.583 2.802 0.21 0.838（P0.1,接受HO:因子对Y没有影响）温度 -0.167 -0.083 2.802 -0.03 0.977（P0.1,接受HO:因子对Y没有影响）S = 11.2085 PRESS = 2995.55R-Sq = 65.55% R-Sq（预测） = 45.24% R-Sq（调整） = 58.66%对于 Y 方差分析（已编码单位）来源自由度 Seq SS Adj SS Adj MS F P主效应 3 3585.58 3585.58 1195.19 9.51 0.001 残差误差 15 1884.46 1884.46 125.63弯曲 1 8.75 8.75 8.75 0.07 0.802失拟 4 892.19 892.19 223.05 2.27 0.134纯误差 10 983.52 983.52 98.35合计 18 5470.05通过上图可以看出，密度和温度P值0.1,接受HO:因子对Y没有影响。

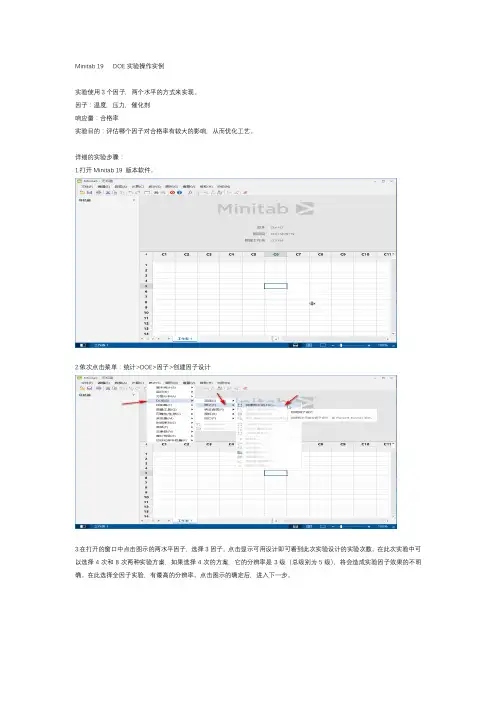
Minitab 19 DOE实验操作实例实验使用3个因子，两个水平的方式来实现。

因子：温度，压力，催化剂响应量：合格率实验目的：评估哪个因子对合格率有较大的影响，从而优化工艺。

详细的实验步骤：1.打开Minitab 19 版本软件。

2.依次点击菜单：统计>DOE>因子>创建因子设计3.在打开的窗口中点击图示的两水平因子，选择3因子。

点击显示可用设计即可看到此次实验设计的实验次数。

在此次实验中可以选择4次和8次两种实验方案，如果选择4次的方案，它的分辨率是3级（总级别为5级），将会造成实验因子效果的不明确。

在此选择全因子实验，有最高的分辨率。

点击图示的确定后，进入下一步。

4.点击设计菜单，按照图示点击设置相关参数之后，点击确定。

角点的仿行数设置为2，表示给实验参数重复两次。

中心点数0表示：没有设置高和低水平之间的中间水平或者理解为当前现实参数。

区组数1：只有一组实验。

5.点击因子菜单，即可对因子及水平具体的输入：按照图示样式输入实验参数后，点击确定。

6.在图示的选项及结果菜单中，默认参数即可。

7.点击确定之后，即可看到软件自动生成的实验方案，详细的实验次数，因子分组，实验顺序等，如右图所示。

保存实验方案，待实验后输入数据。

8.按照上述方案完成实验后，打开上次的实验表格，输入合格率数据如图示。

9. 依次点击菜单：统计>DOE>因子>分析因子设计10.在响应栏中选择合格率，再点击图形，在打开的菜单中，按照图示设置参数后，依次点击两次确定。

11. 在效应图中我们可以看到图示显示红色的ABC 的交互作用和C因子的作用是有明显的影响，即是我们需要重点关注的因子。

12.经过上一步分析得出ABC和C是我们的重要因子，现在继续对重要因子分析，列出因子图更加直观的看到因子对合格率影响效果。

依次点击菜单：统计>DOE>因子>因子图13.在打开的因子窗口中，如图所示设置，点击确定。

全因子设计方法全因子设计方法，听起来有点高大上，对吧？其实没那么神秘啦。

就好比你做饭，你有好多食材，每种食材不同的处理方式组合起来就会做出各种各样的菜，全因子设计方法就有点像这个道理。

全因子设计是一种在实验设计里特别有用的方法呢。

它主要就是考虑所有可能的因子组合。

啥是因子呢？就像我们刚刚说做饭里的食材啊，不同的食材就是不同的因子。

比如说你要做个汤，有鸡肉、香菇、萝卜这几个因子，鸡肉你可以选择新鲜的或者冷冻的，香菇可以是干香菇或者鲜香菇，萝卜可以是白萝卜或者红萝卜，这每个不同的状态就是因子的水平。

那全因子设计就是把这些鸡肉、香菇、萝卜的不同状态都组合起来去考虑，看看哪种组合做出来的汤最好喝。

这种方法有啥好处呢？嘿，那可多了去了。

它能让你把所有的可能性都看个遍。

这就好比你去逛街买衣服，你想找一件最适合自己的衣服。

如果有好几个牌子，每个牌子又有不同的款式和颜色，你要是用全因子设计的思想，你就会把每个牌子的每个款式每个颜色都试一遍，这样肯定能找到最适合你的那一件，对不对？在实际的生产、研究或者其他很多事情里也是一样的。

你要是能把所有可能影响结果的因子和它们的水平组合都研究了，那你就能找到最好的解决方案。

不过呢，全因子设计也不是完美无缺的。

因为它要考虑所有的组合，当因子和水平比较多的时候，这个组合的数量就会变得超级多。

就像你要是有10种食材，每种食材还有3种不同的状态，那组合起来可不得了，你要做的实验或者研究的情况就太多了，这得花多少时间和精力啊。

这就像你要从一个超级大的衣柜里找一件衣服，衣柜里衣服太多了，你可能找得都快晕头转向了。

那在实际操作全因子设计方法的时候要怎么做呢？这就需要你先确定好你的因子和它们的水平。

还是拿做饭来说，你得先想好你要用哪些食材，这些食材有哪些不同的状态。

然后呢，你就要把这些因子和水平列出来，就像写个清单一样。

接着，你就按照这个清单把所有的组合都做一遍。

这过程可能很繁琐，但是为了找到最好的结果，就得有耐心。

全因子实验设计及实例操作全因子实验设计是一种多因素实验设计方法，可以同时考虑多个因素对实验结果的影响。

它通过对所有可能的因素水平组合进行测试，以确定各个因素的主效应和交互效应。

以下是全因子实验设计的实例操作步骤：1. 确定需要考察的因素：首先明确需要研究的因素，并确定每个因素的水平。

2. 确定实验设计类型：根据实验目标和可行性，选择适合的实验设计类型，如完全随机设计、组块设计等。

3. 构建试验方案：根据选定的实验设计类型，构建完整的试验方案。

根据因素的水平组合，生成试验样本，并确定试验的随机化顺序。

4. 进行实验：按照试验方案进行实验操作，记录各个因素的水平和实验结果。

5. 数据分析：使用统计分析方法，如方差分析（ANOVA），分析实验结果，得到各个因素的主效应和交互效应。

6. 结果解释和优化：根据数据分析结果，解释各个因素的影响程度，并进行优化设计。

例如，假设我们要研究对某种产品的质量影响的因素有温度（三个水平：低、中、高）、压力（两个水平：低、高）和时间（两个水平：短、长）。

我们选择完全随机设计。

1. 确定因素：温度、压力、时间。

2. 确定实验设计类型：完全随机设计。

3. 构建试验方案：生成所有可能的因素水平组合，例如，6个试验样本可以是：低温、低压力、短时间；中温、低压力、短时间；高温、低压力、短时间；低温、高压力、短时间；中温、高压力、短时间；高温、高压力、短时间。

4. 进行实验：按照试验方案进行实验操作，记录各个因素的水平和产品质量结果。

5. 数据分析：使用方差分析等统计方法，分析实验结果，得到各个因素的主效应和交互效应。

6. 结果解释和优化：根据数据分析结果，解释各个因素对产品质量的影响程度，并进行优化设计，例如确定最佳的温度、压力和时间组合来提高产品质量。

通过全因子实验设计，我们可以全面地了解多个因素对实验结果的影响，从而进行优化和改进。

全因子实验设计及实例操作全因子实验设计是一种广泛应用于工程、科学和质量控制领域的实验设计方法。

它通过在所有可能的因子水平组合上进行实验，从而充分探索各种因素对实验结果的影响，以期找出最佳的因子组合。

下面将详细介绍全因子实验设计的原理和操作步骤，并结合一个实际案例进行解析。

一、全因子实验设计原理全因子实验设计是一种多因素实验设计方法，它要求对每一个可能影响结果的因子和水平进行考虑和实验，以全面地了解它们对实验结果的影响。

在实际操作中，因子的水平一般是离散的，可以是两个水平或多个水平。

对于每个因子的每个水平，都要进行实验，这就意味着实验设计的规模可能会随着因子数量和水平数量的增加而变得很大。

全因子实验设计的优点在于可以充分研究各种因子之间的相互作用，找出最佳因子组合，从而优化实验结果。

二、全因子实验设计的操作步骤1.确定因子和水平：需要明确定义实验中需要考虑的因子，以及每个因子可能的水平。

这一步需要对研究的问题有清晰的认识和界定，确定哪些因子是需要考虑的，并且估计每个因子可能的水平数量。

2.确定实验设计表：根据确定的因子和水平，可以利用全因子实验设计表格来安排所有可能的水平组合。

这些表格通常是根据二进制码（0和1）进行编码的，以便表示每个因子的水平。

3.进行实验：按照实验设计表格中的水平组合，进行实际的实验操作。

在实验过程中，需要记录每个水平组合下的实验结果和观察，以便后续分析和总结。

4.数据分析和解释：通过对实验结果进行统计分析，可以得出各个因子及其水平对实验结果的影响。

也可以利用统计模型来评估各个因子之间的交互作用，以进一步优化因子组合。

5.优化因子组合：在分析实验结果的基础上，可以确定最佳的因子组合，以达到实验的最优效果。

这可能需要进行进一步的实验验证和调整。

三、实例分析假设某公司要研究一个新产品的生产工艺，需要考虑三个因子：温度（高、中、低）、时间（短、中、长）、原料比例（A、B、C）。

每个因子有三个水平，因此共有3^3=27种可能的水平组合。