5.4++梁的稳定设计讲解
- 格式:pdf
- 大小:1.41 MB
- 文档页数:50
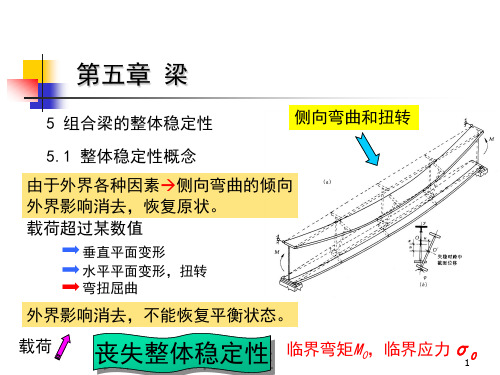

5.4 梁的整体稳定5.4.1 梁的整体失稳现象梁主要是用于承受弯距,为了提高梁的抗弯强度,节省钢材,梁的截面一般做成高而窄的形式。
如图5.18所示的工字形截面梁,荷载作用在其最大刚度平面内,当荷载较小时,梁的弯曲平衡状态是稳定的。
虽然外界各种因素会使梁产生微小的侧向弯曲和扭转变形,但外界影响消失后,梁仍能恢复原来的弯曲平衡状态。
然而,当荷载增大到某一数值后,梁在弯矩作用平面内弯曲的同时,将突然发生侧向的弯曲和扭转变形,并丧失继续承载的能力,这种现象称为梁的整体失稳或弯扭屈曲。
梁维持其稳定平衡状态所承担的最大荷载或最大弯矩,称为临界荷载或临界弯矩。
图5.18 梁的整体失稳横向荷载的临界值和它沿梁高的作用位置有关。
当荷载作用在上翼缘时,如图5-19(a)所示,在梁产生微小侧向位移和扭转的情况下,荷载F将产生绕剪力中心的附加扭矩Fe,它将对梁侧向弯曲和扭转起促进作用,会加速梁丧失整体稳定。
但当荷载F作用在梁的下翼缘时,如图5-19(b)所示,它将产生反方向的附加扭矩Fe,有利于阻止梁的侧向弯曲扭转,延缓梁丧失整体稳定。
因此,后者的临界荷载(或临界弯矩)将高于前者。
图5.19 荷载位置对整体失稳的影响5.4.2 梁的临界荷载图5-12(a)所示为一两端简支双轴对称工字形截面纯弯曲梁,梁两端均受弯矩M作用,弯矩沿梁长均分布。
这里所指的“简支”符合夹支条件,即支座处截面可自由翘曲,能绕x轴和y轴转动,但不能绕z轴转动,也不能侧向移第动。
图5-12 梁的侧向弯扭屈曲设固定坐标为x、y、z,弯矩M达到一定数值屈曲变形后,相应的移动坐标为'x、'y、'z,截面形心在x、y轴方向的位移u、v,截面扭转角为 。
在图5-12(b)和图5-12(d)中,弯矩用双箭头向量表示,其方向按向量的右手规则确定。
梁在最大刚度平面内(z y ''平面)发生弯曲(图5-12(c )),平衡方程M dzvd EI =-22x (5-20)梁在z x ''平面内发生侧向弯曲(图5-12(d )),平衡方程ϕM dzud EI =-22y (5-21)式中:y x I I ,——梁对x 轴和y 轴的毛截面惯性矩。

保证梁整体稳定的措施有在建筑和桥梁等工程项目中,梁作为承受重力和荷载的主要构件,其整体稳定性十分重要。
因此,采取一系列的措施来保证梁整体的稳定是必不可少的。
本文将就此展开探讨,并介绍几种常用的措施。
1. 确定合适的材料和截面形状当设计梁的时候,需要根据实际情况选择合适的材料和截面形状。
在选择材料的时候需要考虑材料的强度、抗压性能、抗拉性能、硬度等因素。
另外,也需要考虑截面形状对整体稳定的影响。
例如,在梁的换曲处应选用转角有弧线的截面形状,以减小应力集中,增加梁的整体稳定性。
2. 加强节点连接处梁的节点连接处是整体稳定性的薄弱点,因此加强节点连接处是保证梁整体稳定的重要措施。
其中,常用的加强措施包括增大节点的连接面积、增加锚筋数量和直径、增加连接件数量等。
另外,在节点的钢筋连接处可以使用预应力技术,通过预应力局部加固,增加节点连接处的整体稳定性。
预应力技术是通过钢筋的预拉和混凝土静力作用效应相互协作,使结构体系达到一种紧凑的力学状态,从而达到更好的稳定性。
3. 加强梁的抗震性能在地震区域,梁的抗震性能影响着其整体稳定性。
因此,在设计梁的时候需要采取一些抗震措施,如增加钢筋数量和直径,提高混凝土强度等。
除此之外,还可以采取加强节点连接处的措施来增加梁的抗震能力。
在节点的受力部位,可以加入钢板或加厚钢筋等制作抗震肋,把节点处的荷载传到梁的其他部位,增加梁的总体稳定性。
4. 控制梁的跨度梁的跨度越大,其整体稳定性就越低。
因此,在设计梁的时候需要控制梁的跨度。
如果跨度过大无法避免,那么可以采取加强节点连接处、增加钢筋数量和直径等措施来保证梁的整体稳定。
另外,在极端情况下,可以采用钢筋混凝土梁代替传统的混凝土梁,以增加整体稳定性。
5. 加强梁的安装和维护为了保证梁的整体稳定性,还需要加强其安装和维护。
在安装过程中,需要采取科学的安装施工方案,避免施工中对梁本身和周围环境造成损伤。
在维护过程中,需要定期检查梁的受力部位和节点连接处,及时对存在的问题进行处理和修复,保证梁的整体稳定性。



§5.3 梁的刚度计算——第二极限状态v v =[]v ——梁的最大挠度,按荷载标准值计算,因为相对于强度而言,刚度的重要程度差些。
[v ]——受弯构件挠度限值,按规范取。
如:手动吊车梁:500/l轻级、中级工作制(Q<50吨):006/l 重级、中级工作制(Q>50吨):007/l规范在楼(屋)盖梁或桁架和平台梁中分别规定了][T v 和][Q v 两种挠度容许值。
其中][T v 为全部荷载标准值产生的挠度(如有起拱应减去拱度),][Q v 为由可变荷载标准值产生的挠度容许值。
这是因为][T v 主要反映观感而][Q v 主要反映使用条件。
在一般情况下,当][T v 大于250/l 后将影响观瞻。
对于v 的算法可用材料力学算法解出,也可用简便算法。
如等截面简支梁:x x x x 10485EI l M EI lM l v ≈⋅=≤lv ][ 2481,3845ql M EI ql v =⋅=翼缘截面改变的简支梁:)2531(10x x x x I I I EI l M l v '-⋅+=≤lv ][ x I ——跨中毛截面抵抗矩 1I ——支座附近毛截面的抵抗矩§5.4 梁的截面选择一.型钢梁截面选择fM W x xnx γ=——查表选截面 为了节省钢材,应避免在弯矩较大的部位开栓钉孔。
二.组合截面梁截面选择 1.截面高度的确定(1)最大高度max h :由于工艺及设备等对空间的要求; (2)最小高度min h :222min 555[]484824()21.35[]31.2x x Ml Ml l v v h EI EhEW f h f ll E vσσ==⋅=≤⋅=⇒= 从中所确定的min h 为最小高度; (3)经济高度:fM W x ⋅=γxn 能达到这一目的截面可能有多种形式,可以高而窄,也可以矮而宽。
经济高度可采用如下经验公式计算:e w h t =---经验公式先假定后调整k ──系数,不变截面焊接梁为1.2,不变截面的焊接吊车梁为1.35。
结构稳定性设计要点结构稳定性是指结构在受到外部荷载或变形时仍能保持稳定,不发生失稳或倒塌的能力。
在建筑设计与施工中,结构稳定性是一个非常重要的考虑因素,直接关系到建筑的安全和可靠性。
本文将重点讨论结构稳定性设计的要点,并通过实例来进一步解释和补充说明。
在结构稳定性设计中,有几个关键要点需要特别注意。
首先是结构的形状和几何特性。
结构的形状对其稳定性有很大的影响。
例如,在建筑物中,通常会避免出现过长而且细长的构件,因为这种形状容易引起侧向位移和失稳。
而相对而言,较短、较粗的结构更容易保持稳定。
此外,结构的几何特性如平面形状、截面形状等也会对稳定性产生影响。
例如,在钢结构中,采用具有较高截面惯性矩的H形钢柱,能够提高结构的整体稳定性。
其次,荷载和力的作用也是影响结构稳定的重要因素。
结构稳定性设计需要考虑到各种静力和动力荷载,包括重力荷载、风荷载、地震荷载等。
在设计中,需要确保结构能够承受这些荷载的同时保持稳定。
例如,在高层建筑中,风荷载是一种重要的考虑因素。
设计师需要通过采用适当的结构形式和加强结构的风荷载抵抗能力,以确保建筑的稳定。
此外,材料的选择和结构连接的设计也对稳定性起着重要的作用。
不同的材料具有不同的力学性质和稳定性,并且在不同的工况下表现也不同。
因此,在结构稳定性设计中,需要根据具体情况选择合适的材料,并进行适当的连接设计。
例如,在桥梁设计中,如果使用的是钢材,就需要考虑钢的屈曲和稳定性,以及合适的螺栓连接。
最后,结构的支座和基础设计也是结构稳定性的重要方面。
结构的支座和基础要能够为结构提供足够的支撑和稳定性。
支座的选择和布置要合理,并能够均匀传递荷载。
基础的设计要满足结构的稳定性和抗倒覆要求,能够有效地将荷载传递到地基。
例如,在高层建筑和桥梁设计中,常采用深基坑和打桩的方式来增加基础的稳定性。
综上所述,结构稳定性设计要点主要包括:结构的形状和几何特性、荷载和力的作用、材料的选择和连接设计,以及支座和基础设计。
§5.6 梁的局部稳定梁在不同板段有不同的受力状态,不同的受力状态都可能使腹板丧失稳定。
梁段受力状况MM 2缘翼q222cr cr)()1(12πbt E k t N μσ-== k ——屈曲因数,与荷载种类、分布状态及边长比有关,对四边简支板,三边简支板都适用。
b ——受压边的长度,受剪时为短边长度。
考虑到钢梁受力时,并不是组成梁的所有板件同时屈曲,板件之间存在相互约束作用,引进约束系数——χ,得:222()12(1)cr E t k bπσχμ=-考虑:5220610NE mm =⨯.和03μ=.,得:24218.6()10/cr tk N mm bσχ=⨯一.受压翼缘板24218.6()10/cr t k N mm bσ=⨯tE Eη=——塑形系数 根据三边简支0.425m in =k ,和 1.0χ=,0.25η≈242118.60.425()10/cr t N mm b σ≈⨯⨯弹性阶段:0.95cr y f σ≥1b t ⇒≤ 允许发展一定的塑形:cr y f σ≥1b t ⇒≤根据四边简支(箱形截面受压翼缘中间部分b 0) 有4k =, 1.0χ=,0.25η≈ 则:cr y f σ≥0b t ⇒≤二.腹板的纯剪屈曲24218610w cr tNk mm dτχ=⋅⨯.()MPa 102.060.35⨯==E ,μ{}a h d ,m in 0= 0h a≤1时,20)(5.344h a k += 0h a≥1时,2)(45.34h a k +=105201525303540(2)矩形板的纯剪屈曲系数a/h 0(1)k对于实腹梁而言,翼缘对腹板有约束作用,通过试验研究发现,可以使稳定临界应力提高23%(比四边简支),即 1.23χ=代入前式:0h a≤1时,MPa )100]()(12393[1.232w 20cr 0at h a +==ττ 0h a≥1时,MPa )100]()(93123[1.232w 20cr 0at h a +==ττ 从曲线中可以看出,当0/h a ≤1时,随0/h a 的减小,cr τ提高。