趣味数学--图形和空间
- 格式:ppt
- 大小:2.48 MB
- 文档页数:28

数学教案图形与空间关系的理解数学教案:图形与空间关系的理解(正文开始)引言:图形与空间关系是数学中的重要概念,它涉及到几何学和代数学的基础知识。
通过理解和分析图形与空间之间的关系,学生可以培养几何思维能力,提高解决实际问题的能力。
本教案将以理论与实践相结合的方式,帮助学生深入理解图形与空间关系的概念,并通过一系列的实例来巩固所学内容。
教学目标:1. 了解图形与空间关系的基本概念;2. 掌握常见图形与二维/三维空间的关系;3. 能够运用所学概念分析和解决与图形与空间关系相关的问题。
教学内容:一、图形与二维空间关系1. 点、直线、线段的关系- 点在直线上;- 点在线段上;- 直线上的两点确定一条线段。
2. 多边形与平面的关系- 多边形位于平面上;- 多边形的内部、外部与平面的关系。
3. 圆与平面的关系- 圆在平面上;- 圆的内部、外部与平面的关系。
二、图形与三维空间关系1. 点、直线、线段的关系- 点在直线上;- 点在线段上;- 直线上的两点确定一条线段。
2. 多面体与空间的关系- 多面体位于空间中;- 多面体的内部、外部与空间的关系。
3. 球体与空间的关系- 球体在空间中;- 球体的内部、外部与空间的关系。
教学过程:一、图形与二维空间关系的理解1. 引入概念:通过展示不同几何图形与二维平面的关系,引导学生思考图形在平面上的位置和相互关系;2. 分组讨论:将学生分成小组,让他们互相交流,总结不同图形与平面的关系;3. 实例练习:给出一系列例题,让学生运用所学概念分析和解决问题;4. 小结与展示:学生汇报讨论结果,教师进行总结,并展示正确答案。
二、图形与三维空间关系的理解1. 引入概念:通过展示不同几何图形与三维空间的关系,引导学生思考图形在空间中的位置和相互关系;2. 分组讨论:将学生分成小组,让他们互相交流,总结不同图形与空间的关系;3. 实例练习:给出一系列例题,让学生运用所学概念分析和解决问题;4. 小结与展示:学生汇报讨论结果,教师进行总结,并展示正确答案。

幼儿园数学乐园:图形与空间认知培养案例在幼儿园阶段,数学教育一直被认为是非常重要的一部分,它不仅可以帮助孩子建立数学概念,还可以培养他们的逻辑思维能力和数学兴趣。
其中,图形与空间认知是数学教育中一个非常重要的环节,它不仅涉及几何形状的认知,还包括了空间方向的理解和计算能力的培养。
下面,我们将通过一个实际案例来探讨在幼儿园数学教育中,如何通过图形与空间认知来培养孩子们的数学兴趣和能力。
案例:在某幼儿园的数学教育课程中,老师们设计了一个名为“图形乐园”的活动,旨在帮助孩子们认识各种图形,并培养他们的空间认知能力。
在这个活动中,孩子们通过亲身参与各种游戏和实践活动,来感受和认识不同的图形和空间方向。
活动内容及效果:1.游戏一:图形寻宝–孩子们在幼儿园的操场上寻找各种图形的彩色卡片,比如正方形、三角形、圆形等。
通过寻找过程,孩子们能够在活动中亲身体验图形的形状特点,并且加深对不同图形的认识。
2.游戏二:图形搭配–孩子们在教室里使用纸片、积木等材料,亲手搭建各种图形。
这个游戏能够帮助孩子们培养空间想象力和手眼协调能力,同时也能够让他们更深入地理解图形的特点和构成。
3.游戏三:空间探索–孩子们在课堂上进行空间方向的认知游戏,比如前后左右、上下等。
通过这些游戏,孩子们能够更好地理解空间方向的概念,培养他们的方向感和空间计算能力。
通过这些活动,孩子们不仅能够认识各种图形和空间方向,还能够培养他们的观察力、想象力和动手能力。
这些活动也能够帮助孩子们建立数学概念,培养他们对数学的兴趣和热爱。
我的观点:我认为幼儿园数学教育中的图形与空间认知培养非常重要,它不仅可以为孩子们建立坚实的数学基础,还可以培养他们的观察力、想象力和动手能力。
通过这些活动,孩子们在快乐的氛围中学习,不知不觉中就掌握了许多数学知识,这种教育方式不仅能够激发孩子们学习的兴趣,还能够培养他们的创造力和解决问题的能力。
幼儿园数学乐园的图形与空间认知培养活动,为孩子们的数学启蒙奠定了良好的基础,让他们在快乐的氛围中爱上数学,同时也为他们未来的学习和发展打下了坚实的基础。

趣味数学数学小故事:靶上的爬虫某班战士进展打靶训练,靶上的那些圆环如下图,由间距相等的同心圆构成。
训练完毕后,战士们就地休息。
班长发现两只小虫在靶上慢悠悠地爬行,他灵机一动,向战士们说:“我们不但要学军事,而且还要学文化。
大家看,靶上的这些圆环宽度都是一样的。
假设上面这2只小虫都是匀速地爬行,并且两者速度一样。
如果1只沿最外层环的外缘爬行l周与沿内缘爬行l周所需时间的差为T1,而另1只沿最内层环的外缘、内缘各爬行1周所需时间的差为T2。
请问,T1和T2哪个大些?〞“外层的环比内层的大多了,当然T1比T2大。
〞有几个战士不假思索地答道。
他们的答复对吗?答案:我们假设最外层外缘距离靶心的距离是R1,最外层边缘距离靶心的距离是R2,那么小虫沿最外层外缘爬行一周的长度是:2πR1,沿最外层内缘爬行一周的长度是:2πR2。
内外缘爬行的距离差是2πR1-2πR2=2π〔R1-R2〕。
同样,我们再假设最内层外缘距离靶心的距离是r1,最内层边缘距离靶心的距离是r2,那么小虫沿最内层外缘爬行一周的长度是:2πr1,沿最内层内缘爬行一周的长度是:2πr2。
内外缘爬行的距离差是2πr1-2πr2=2π〔r1-r2〕。
因为小虫的爬行速度一样,比拟内、外两层的爬行时间差,只要比拟内、外层的爬行距离差就可以了。
而我们知道内层和外层的内、外缘与靶心的距离差一样,也就是R1-R2=r1-r2。
所以,战士的答复是错误的,T1和T2应该是一样大。
生活中的圆圆在日常生活中可以说是随处可见。
我们这里仅仅举两个小例子。
例一,为什么下水道的盖子是圆形的?如果留意一下,会发现街上下水道的盖子几乎都是圆的,可是,为什么要做成圆的呢?做成其他形状的,比方正方形不好吗?这个问题最早是微软公司招聘员工时的面试题,并且很可能是微软最有名的面试问题。
事实上,由于曝光率太高,微软公司在面试中已经停顿使用这一问题了。
对这个问题的最好答复是:其他形状的盖子会有一个角度让井盖掉下去,但如果井盖做成圆形的,只要直径大于井口一点,那么无论从哪个角度都不会掉下去!比方正方形,因为正方形的对角线比它的边长要长,所以如果把一个正方形盖子立起来,稍微一转,它就会很容易掉到下水道里去。

人教版五年级下册数学空间与图形知识点汇总一、轴对称与旋转1、图形的变换包括平移、旋转和对称。
2、轴对称图形:一个图形沿某一条直线对折;直线两侧的图形能够完全重合;这个图形就是轴对称图形。
这条直线叫做它的对称轴。
3、轴对称图形都有对称轴。
有一条对称轴的图形有等腰三角形;等腰梯形、线段、角。
有两条对称轴的图形有长方形、菱形。
有三条对称轴的图形有正三角形。
正方形有4条对称轴。
4、轴对称图形的特征:(1)、对应点到对称轴的距离相等;(2)、对应点连线与对称轴互相垂直。
5、轴对称图形的画法:(1)、找出已知图形的关键点。
(2)、在对称轴的另一侧画出关键点的对应点。
(3)、按顺序连接各对应点。
6、旋转:图形或物体绕着一个点或一条轴运动的现象叫做旋转。
图形旋转后只改变位置;不改变形状和大小。
一、长方体和正方体的认识【知识点1】一个长方体至少可以有两个面是正方形;最多可以有6各面是正方形;但不会存在3个、4个、5个面是正方形!1 / 17(1)判断并改正:1、长方体的六个面一定是长方形;()2、正方体的六个面面积一定相等;()3、一个长方体(非正方体)最多有四个面面积相等;()4、相交于一个顶点的三条棱相等的长方体一定是正方体。
()7、长方体的三条棱分别叫做长、宽、高。
()8、有两个面是正方形的长方体一定是正方体。
()9、有三个面是正方形的长方体一定是正方体。
()11、有两个相对的面是正方形的长方体;另外四个面的面积是相等的。
()12、长方体和正方体最多可以看到3个面。
()14、正方体不仅相对的面的面积相等;而且所有相邻的面的面积也都相等。
()15、长方体(不包括正方体)除了相对的面相等;也可能有两个相邻的面相等。
()16、一个长方体中最少有4条棱长度相等;最多有8条棱长度相等。
()(2)填空:1、一个长方体最多有()个面是正方形;最多有()条棱长度相等。
2、一个长方体的底面是一个正方形;则它的4个侧面是()形。

数学乐趣探索形和空间数学乐趣探索:形和空间数学作为一门科学,既深奥又神秘。
然而,当我们以一种探索的态度来学习数学时,它也可以带给我们无穷的乐趣和启发。
本文将以形和空间为主题,探索数学中的乐趣,带领读者走进数学的奇妙世界。
第一部分形的奥秘在日常生活中,我们经常会遇到各种各样的形状。
无论是简单的正方形、圆形,还是复杂的多面体、椭圆,每一个形状都有着自己独特的特点和性质。
通过深入了解这些形状,我们可以发现其中的美妙之处。
首先,让我们来探索正方形。
正方形是最简单的几何形状之一,它的四条边相等,四个内角都是90度。
正方形可以和其他形状组成各种各样的图案,比如著名的拼贴画。
通过拼贴各种大小的正方形,我们可以创造出千变万化的图案,展示出形的多样性。
接下来,我们来研究一下圆形。
圆形是没有边界的形状,它的每个点到中心的距离都相等。
正因为这个性质,圆形在艺术设计中常常被用来表示永恒和完美。
在建筑和雕塑中,经常可以看到圆形的运用,给人以美的享受。
除了常见的形状,我们还可以探索一些比较特殊的形状,比如椭圆和抛物线。
椭圆的形态像一个拉长的圆形,它在工程设计和天文学中有着广泛的应用。
而抛物线则是一种像开口锥形的形状,它在物理学和摄影学中起着重要的作用。
通过对形状的探索和研究,我们可以发现形与形之间的联系和变化。
不同的形状通过组合和变换,可以创造出千变万化的图案和结构。
这种美妙的联系和变化,不仅存在于数学中,也存在于我们的生活中。
第二部分空间的奇妙除了形状,空间也是数学中一个非常重要的概念。
正如我们所知,空间是一个无尽的三维世界,包含了无数的事物和相互作用。
通过数学的方法,我们可以更好地理解和探究空间的奇妙之处。
首先,我们来研究几何体。
几何体是由面、边和顶点组成的空间实体。
它们可以是简单的立方体、球体,也可以是复杂的多面体,如正十二面体和正二十面体。
每一个几何体都有着自己独特的性质和规律,通过研究几何体,我们可以揭示出空间中的许多奥秘。


小学图形与空间知识点整理小学生在学习数学的过程中,图形与空间是一个重要的知识点。
图形与空间的学习涵盖了形状、方位、位置、尺寸等内容。
通过学习图形与空间,可以帮助学生培养观察、分析和推理能力,加深对数学的理解。
以下是小学图形与空间的知识点整理。
一、平面图形1.点、线、线段、射线、角:学生需要了解这些基本概念,包括它们的定义以及区别。
2.三角形:三边相交于三个顶点,并且三个内角之和为180度,学生需要学习三角形的分类与性质。
3.四边形:四边相交于四个顶点,并且四个内角之和为360度,学生需要学习四边形的分类与性质。
4.圆:由一条曲线上的所有点与其中心点的距离相等构成,学生需要了解圆的性质,如直径、半径、弧等。
5.多边形:学生需要学习多边形的分类与性质,如正多边形、凸多边形、凹多边形等。
二、立体图形1.正方体:六个面都是正方形的立体图形,学生需要学习正方体的边、面、顶点等概念。
2.长方体:六个面都是矩形的立体图形,学生需要学习长方体的边、面、顶点等概念。
3.圆柱体:由两个平行的圆面和一个侧面组成的立体图形,学生需要学习圆柱体的边、底面、侧面等概念。
4.圆锥体:由一个圆锥面和一个顶点组成的立体图形,学生需要学习圆锥体的底面、侧面、顶点等概念。
5.圆球体:所有点到球心的距离相等的立体图形,学生需要学习圆球体的半径、表面积、体积等概念。
三、方向与位置1.方位词:学生需要学习基本的方位词,如前、后、左、右、上、下等,以便于描述位置关系。
2.平行:指两条直线在同一个平面内,永不相交,始终保持相同的距离,学生需要学习平行线的判断和性质。
3.垂直:指两条直线相交于90度,学生需要学习垂直线的判断和性质。
4.水平:指与地面平行的方向或线条,学生需要学习水平的概念及其判断。
五、尺寸与比例1.长度:学生需要学习测量长度的方法和基本单位,如米、厘米等。
2.面积:学生需要学习测量面积的方法和基本单位,如平方米、平方厘米等。
3.体积:学生需要学习测量体积的方法和基本单位,如立方米、立方厘米等。

小学数学空间与图形知识点总结:空间与图形知识点是小学学习数学时期的主要知识点之一,主要包括认识位置与方向、图形的直观认识、直线和线段、角的初步认识、长方形与正方形、平行四边形、垂线、平行线、三角形、圆、圆柱、圆锥、球、轴对称图形、作图题(操作题)、棱锥、等,以下是各具体知识点总结的理解和分析。
空间与图形全部知识点认识位置与方向:三视图位置的认识认识方向三视图:三视图是观测者从三个不同位置观察同一个空间几何体而画出的图形。
位置的认识:能正确地用上下、前后、左右等词描述物体所在的位置。
认识方向:感知东,南,西,北四个方位。
图形的直观认识:长方体正方体圆柱球长方形正方形三角形圆长方体:相邻两面的面积不同的叫长方体。
正方体:底面是正方形的直平行六面体叫正方体,即棱长都相等的六面体,又称“立方体”、“正六面体”。
圆柱:以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱。
球:在空间中到定点的距离等于或小于定长的点的集合叫做球体,简称球。
长方形:有一个角是直角的平行四边形是矩形。
正方形:在平面几何学中,正方形是具有四条相等的边和四个相等内角的多边形。
正方形是正多边形的一种,即正四边形。
三角形:由不在同一直线上的三条线段首尾顺次连接所组成的封闭图形叫做三角形。
圆:当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的轨迹叫做圆。
根据定义,通常用圆规来画圆直线和线段:直线、线段、射线测量距离数轴直线,线段,射线:直线是两端都没有端点、可以向两端无限延伸、不可测量长度的。
直线上两个点和它们之间的部分叫做线段数轴:规定了唯一的原点,唯一的正方向和唯一的单位长度的直线叫数轴。
角的初步认识:角的度量角的分类角的度量:顶点重合,一条边重合。
角的分类:平角、周角以及锐角、直角。
长方形与正方形:四棱锥的体积正方形、长方形的特征正方形、长方形的周长正方形、长方形的面积正方体、长方体的表面积正方体、长方体的体积四棱锥的体积:计算公式是底面积乘以高的三分之一。

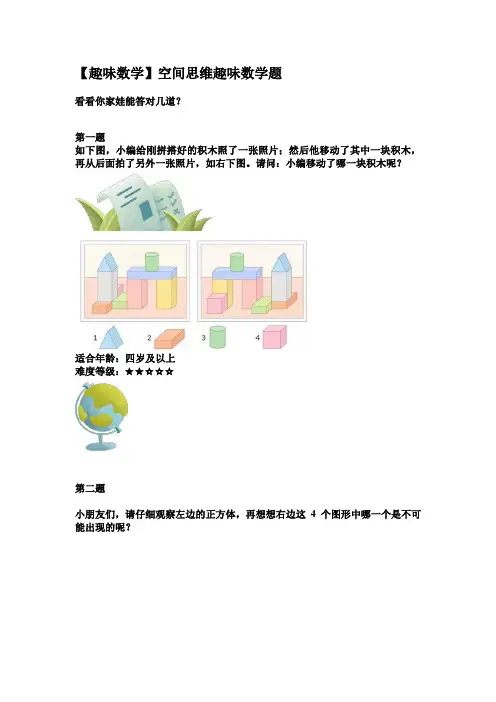
【趣味数学】空间思维趣味数学题
看看你家娃能答对几道?
第一题
如下图,小编给刚拼搭好的积木照了一张照片;然后他移动了其中一块积木,再从后面拍了另外一张照片,如右下图。
请问:小编移动了哪一块积木呢?
适合年龄:四岁及以上
难度等级:★★☆☆☆
第二题
小朋友们,请仔细观察左边的正方体,再想想右边这4个图形中哪一个是不可能出现的呢?
适合年龄:四岁及以上
难度等级:★★★☆☆
第三题
小编在房间的角落里发现了一堆箱子,箱子的大小都是一样的,如下图。
请问:这里一共有多少个箱子呢?
适合年龄:五岁及以上
难度等级:★★★★☆
揭晓答案
第一题:4(粉红色积木)
左边的照片是移动前的场景,你注意到了吗?那块灰色积木的后面是一块粉红色积木哦,但在右边的照片里,粉红色积木则被悄悄移到了黄色积木的后面。
第二题:A
如果是A中的情况,那黑色圆圈的左边应该是全白的一面哦,所以无论如何都不可能观察到A这种情况。
第三题:20个
第一层:10个;第二层:7个;
第三层:3个;总计:20个。

目录•数学之美与趣味性•数字与运算的奥秘•图形与空间的探索•数学逻辑与推理的乐趣•数学在现实生活中的应用数学之美与趣味性数学中的对称与和谐对称性的定义与性质01在数学中,对称性是指图形或数学结构在某种变换下保持不变的性质。
对称性不仅体现在几何图形中,还广泛存在于函数、方程等领域。
对称性的应用02对称性在数学中有着广泛的应用,如利用对称性简化计算、证明定理等。
同时,对称性也是自然界中一种普遍存在的现象,如雪花、蝴蝶等都具有对称性。
和谐的数学结构03数学中存在着许多和谐的结构和关系,如欧拉公式、勾股定理等。
这些结构和关系不仅具有内在的逻辑美,还能激发人们对数学的兴趣和热爱。
黄金分割与斐波那契数列黄金分割的定义与性质黄金分割是指将一条线段分割为两部分,使得较长部分与较短部分之比等于整条线段与较长部分之比。
黄金分割具有独特的美感和广泛的应用价值。
斐波那契数列的定义与性质斐波那契数列是一个著名的数列,它的每一项都是前两项的和。
斐波那契数列与黄金分割有着密切的联系,其相邻两项之比趋近于黄金分割比。
黄金分割与斐波那契数列的应用黄金分割和斐波那契数列在自然界和艺术中都有广泛的应用。
例如,许多植物的花瓣数目符合斐波那契数列的规律;在建筑和设计中,黄金分割被用来创造和谐的比例和美感。
分形几何与自然界中的美分形几何的定义与性质分形几何是一种研究不规则、破碎的几何形状的数学分支。
分形具有自相似性和无限精细的结构,能够揭示自然界中许多复杂现象背后的数学规律。
自然界中的分形现象自然界中存在着许多分形现象,如海岸线、山脉、云朵等。
这些现象的分形特征使得它们具有独特的美感和无穷的变化性。
分形几何的应用分形几何在图像处理、计算机图形学等领域有着广泛的应用。
同时,分形艺术也成为一种独特的艺术形式,通过分形算法创造出绚丽多彩的视觉效果。
趣味数学游戏与谜题数学游戏数学游戏是一种寓教于乐的方式,通过游戏的形式激发孩子们对数学的兴趣和热爱。
数学中的几何图形与空间关系数学是一门抽象而又具体的学科,其中的几何学更是让人着迷。
几何学研究的是图形和空间的关系,通过对图形的形状、大小和位置的研究,我们可以揭示出许多有趣的数学定律和规律。
在这篇文章中,我将探讨几何图形与空间关系的一些重要概念和应用。
首先,我们来谈谈点、线和面这三个基本的几何概念。
点是几何学中最基本的图形,它没有长度、宽度和高度,只有位置。
线是由无数个点组成的,它有长度但没有宽度和高度。
面是由无数个线组成的,它有长度和宽度但没有高度。
这三个概念是几何学中最基础的元素,我们可以通过它们来构建更复杂的图形和空间关系。
接下来,让我们来研究一下几何图形的形状和性质。
最简单的图形是圆形,它由一个固定点到平面上所有距离相等的点组成。
圆形具有许多有趣的性质,比如它的周长和面积都可以用数学公式来计算。
正方形是另一个常见的图形,它的四条边和四个角都是相等的。
正方形也有许多有趣的性质,比如它的对角线长度等于边长的平方根。
这些图形的形状和性质是几何学中的基础知识,它们可以帮助我们理解更复杂的几何图形和空间关系。
除了形状和性质,几何图形还有许多重要的关系和定理。
例如,平行和垂直是几何学中常见的关系。
两条直线如果在同一平面内永远不相交,就称为平行线。
垂直线是指两条相交线段的夹角为90度。
平行和垂直关系在几何学中有广泛的应用,比如在建筑设计和地图制作中,我们经常需要利用这些关系来确定位置和方向。
此外,几何学中还有一些重要的定理,例如勾股定理和相似定理。
勾股定理是指在直角三角形中,直角边的平方等于其他两条边的平方和。
这个定理在解决三角形问题时非常有用,它可以帮助我们计算三角形的边长和角度。
相似定理是指两个图形的对应边成比例,对应角相等。
相似定理在解决图形相似性问题时起着重要的作用,它可以帮助我们判断两个图形是否相似,并计算它们的比例关系。
最后,让我们来看看几何图形与空间关系在实际生活中的应用。
几何学在建筑设计、城市规划和工程建设中起着重要的作用。
中班数学活动:图形与空间一、本课核心阅历:图形与空间——图形二、活动目标:1。
情愿与同伴合作进行图形拼摆,体验拼图嬉戏带来的乐趣。
2。
尝试用各种几何图形拼合出不同的图案。
3。
通过观看各种组合图案,了解组合的方法。
三、活动预备:磁性教具(形形色色)、磁性板、各种几何图形拼版幼儿人手一份、小红人、小蓝人纸偶两个、老鼠、猫、蝴蝶、花、大卡车的几何图形图片四、活动过程:一)老师出示教具中的图形版,幼儿熟悉图形并简洁拼组。
1、出示几种图形版,带领幼儿复习几种图形的名称。
2、给每组幼儿供应若干图形板,请幼儿依据要求进行拼图。
——请幼儿任选两个图形板,尝试拼出一幢小房子。
——请幼儿说说用了哪两个外形拼出了房子?——请幼儿用更多不同的图形拼摆房子,并说出用了哪几种几何图形。
二)创设情境,叙述故事,初步观看了解各种图案的组合方法。
1。
出示小红人、小蓝人纸偶叙述故事,创设情境。
——“今日有两个小伴侣要到我们幼儿园来做客,他们是谁呢?(出示并介绍小红人、小蓝人纸偶)——“今日他们要玩一个好玩的拼图嬉戏,让我们一起来看看他们要拼什么呢?”2。
出示用不同图形组合而成的老鼠图案,提问:——“这是什么呀?是用哪几种图形拼出来的呢?”——幼儿观看、回答后,老师小结:“这是小蓝人用形、形拼出的小老鼠,拼得真好!可小红人一看,不服气了,他打算拼一只比小老鼠更厉害的小动物!会是什么呢?”3、展现用不同图形组合而成的小猫图案,提问引导幼儿猜想并观看。
——“这是谁?(小猫)小猫又是用哪几种图形拼出来的呢?”——幼儿观看、回答后,老师小结:“原来小红人用形、形拼了一只比小老鼠更厉害的小猫,真棒!”4、展现蝴蝶、花的图案,引导幼儿自主观看两个图案分别由哪几种几何图形组合而成。
——“小红与小蓝他们两个是一对好伴侣,他们打算不竞赛了,他们要合作拼出更漂亮的图案来。
”(出示蝴蝶和花的图案)——“谁来说一说蝴蝶和花是由哪几种图形组合起来的呢?”(可以考虑请两个好伴侣上来分别叙述蝴蝶和花的组合方法)5、展现大卡车的图案,设置情境并引导幼儿尝试独立拼图。
大班数学活动《趣味数学》课件.一、教学内容本节课选自大班数学教材第四章《趣味数学》,主要内容包括:认识基本的几何图形,了解图形的对称性;学习使用图形进行拼图游戏,培养空间想象力和逻辑思维能力;掌握简单的数列规律,培养推理能力。
二、教学目标1. 让学生能够识别和命名基本的几何图形,如圆形、正方形、长方形、三角形等,并了解它们的特性。
2. 培养学生观察图形的对称性,提高审美能力。
3. 通过拼图游戏,培养学生的空间想象力和逻辑思维能力,激发学生对数学的兴趣。
三、教学难点与重点教学难点:图形的对称性认识,拼图游戏中的空间想象力。
教学重点:基本几何图形的认识,数列规律的发现。
四、教具与学具准备教具:趣味数学课件,各种几何图形卡片,拼图板。
学具:学生每人一份几何图形卡片,拼图板。
五、教学过程1. 实践情景引入(5分钟)利用课件展示生活中常见的几何图形,引导学生观察并说出它们的名字。
2. 新课导入(10分钟)(1)教师通过课件讲解基本几何图形的特点,引导学生认识图形。
(2)学生跟随课件练习图形的对称性,感受图形的平衡美。
3. 例题讲解(10分钟)(1)教师出示拼图游戏,示范解题过程,引导学生观察图形之间的联系。
(2)学生跟随教师一起完成拼图,体验空间想象力。
4. 随堂练习(10分钟)学生独立完成课件中的练习题,巩固所学知识。
六、板书设计1. 基本几何图形的认识:圆形、正方形、长方形、三角形等。
2. 图形的对称性:轴对称、中心对称。
3. 拼图游戏:空间想象力与逻辑思维能力。
七、作业设计1. 作业题目:完成教材第四章课后练习题1、2、3。
2. 答案:见教材第四章课后练习题答案。
八、课后反思及拓展延伸本节课通过趣味数学课件,让学生在轻松愉快的氛围中学习数学。
课后,教师应关注学生的学习效果,针对学生的掌握情况,进行针对性的辅导。
同时,可引导学生观察生活中的几何图形,激发学生学习数学的兴趣,提高学生的数学素养。
拓展延伸方面,可以组织学生参加拼图比赛,提高学生的动手操作能力和团队协作能力。
数学教案图形和空间关系数学教案:图形和空间关系教学目标:1. 了解图形与空间的关系;2. 学习如何描述和解释图形在空间中的位置和方向;3. 掌握绘制和分析各种图形的技巧和方法。
教学内容:一、图形的基本概念1. 点、直线和平面的定义;2. 图形的分类及特点;3. 了解几何体的组成部分。
二、图形的位置关系1. 平行线与垂直线的判定;2. 角的分类及特性;3. 当两条直线相交时,角的特性与关系;4. 理解平面内的点、线和角的位置关系。
三、图形的方位关系1. 掌握方向词汇的使用;2. 学习方向的确定方法;3. 探究点、线和面的相对位置。
四、图形的运动与变换1. 平移、旋转、翻转和对称的概念;2. 学习如何进行图形的平移变换;3. 理解旋转和翻转对图形的影响;4. 掌握图形对称的判定方法。
五、图形的投影与视图1. 了解平行投影和斜投影的概念;2. 掌握绘制图形的投影方法;3. 学习视图的概念及如何绘制。
教学步骤:一、导入与引入在开始本节课的学习之前,先与学生讨论图形在日常生活中的应用,并引入本节课将要学习的内容。
二、概念讲解与示范1. 通过实际生活中的图形,引出图形的基本概念,如点、线和平面;2. 利用教具或幻灯片展示不同类型的图形,并讲解它们的分类和特点;3. 通过示例,展示图形的位置关系和方位关系;4. 运用教具或幻灯片进行图形的运动与变换的讲解;5. 引入图形的投影与视图概念,并展示实际应用。
三、练习与实践1. 让学生利用纸和铅笔进行图形的练习,如绘制平行线、垂直线和角;2. 通过小组合作,让学生设计场景,描述图形在空间中的位置关系;3. 进行图形的平移、旋转和翻转实践练习;4. 让学生观察并分析给定图形的投影和视图。
四、巩固与拓展1. 进行小组竞赛,比赛绘制图形的位置关系和方位关系;2. 让学生自主设计图形,并通过变换和投影展示其运动和视图;3. 引导学生思考图形与空间的关系在建筑、艺术等领域的应用。