平面图形的特征

平面图形的特征及分类平面图形是我们日常生活中经常遇到的一种形式。

无论是建筑物的设计、地图的绘制还是日常的几何题，平面图形都扮演着重要的角色。

本文将探讨平面图形的特征及分类，带领读者进一步了解这一领域。

一、平面图形的特征平面图形是二维的，由线段、直线和曲线组成。

它们没有厚度，只有长和宽。

平面图形可以用几何方式描述，也可以通过数学公式进行计算。

平面图形具有以下几个特征：1. 边界特征：每个平面图形都有一个边界，它是由一条或多条线段或曲线组成的。

边界确定了图形的形状和大小。

2. 角度特征：平面图形中的角度是由两条相交的线段或曲线形成的。

角度可以是锐角、直角、钝角或平角。

角度的大小和类型决定了图形的特性。

3. 对称特征：一些平面图形具有对称特征，即可以通过某种方式将图形分成两个相等的部分。

对称特征可以是轴对称或中心对称，它们赋予图形一种美感和平衡感。

4. 面积特征：平面图形的面积是指图形所占据的空间大小。

面积可以通过数学公式计算得出，不同的图形有不同的计算方法。

二、平面图形的分类平面图形可以根据不同的特征进行分类。

以下是几种常见的分类方式：1. 根据边界特征分类：平面图形可以分为封闭图形和开放图形。

封闭图形的边界形成一个闭合的曲线，例如圆、椭圆、正方形和长方形。

开放图形的边界没有闭合，例如直线、折线和曲线。

2. 根据角度特征分类：平面图形可以分为直角图形和非直角图形。

直角图形的角度是直角，例如正方形和长方形。

非直角图形的角度可以是锐角、钝角或平角，例如三角形和梯形。

3. 根据对称特征分类：平面图形可以分为对称图形和非对称图形。

对称图形具有对称轴或对称中心，例如正方形和圆。

非对称图形没有对称特征，例如折线和曲线。

4. 根据面积特征分类：平面图形可以分为有限图形和无限图形。

有限图形的面积是有限的，例如正方形和三角形。

无限图形的面积是无限的，例如直线和曲线。

总结平面图形作为几何学的重要组成部分，具有丰富的特征和分类方式。

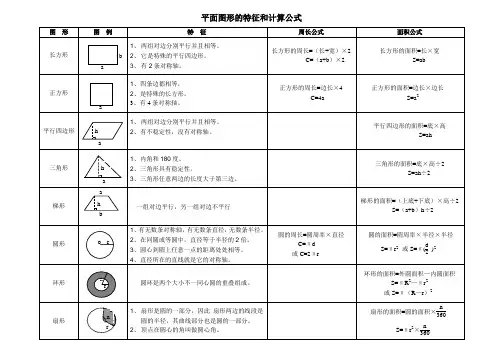
数学知识点：平面图形为大家带来平面图形，希望可以帮到您!平面图形1、长方形(1)特征对边相等，4个角都是直角的四边形。

有两条对称轴。

(2)计算公式c=2(a+b)s=ab2、正方形(1)特征：四条边都相等，四个角都是直角的四边形。

有4条对称轴。

(2)计算公式c=4as=a23、三角形(1)特征由三条线段围成的图形。

内角和是180度。

三角形具有稳定性。

三角形有三条高。

(2)计算公式s=ah/2(3)分类按角分锐角三角形：三个角都是锐角。

直角三角形：有一个角是直角。

等腰三角形的两个锐角各为45度，它有一条对称轴。

钝角三角形：有一个角是钝角。

按边分不等边三角形：三条边长度不相等。

等腰三角形：有两条边长度相等;两个底角相等;有一条对称轴。

等边三角形：三条边长度都相等;三个内角都是60度;有三条对称轴。

4、平行四边形(1)特征两组对边分别平行的四边形。

相对的边平行且相等。

对角相等，相邻的两个角的度数之和为180度。

平行四边形容易变形。

(2)计算公式s=ah5、梯形(1)特征只有一组对边平行的四边形。

中位线等于上下底和的一半。

等腰梯形有一条对称轴。

(2)公式s=(a+b)h/2=mh6、圆(1)圆的认识平面上的一种曲线图形。

圆中心的一点叫做圆心。

一般用字母o表示。

半径：连接圆心和圆上任意一点的线段叫做半径。

一般用r 表示。

在同一个圆里，有无数条半径，每条半径的长度都相等。

通过圆心并且两端都在圆上的线段叫做直径。

一般用d表示。

同一个圆里有无数条直径，所有的直径都相等。

同一个圆里，直径等于两个半径的长度，即d=2r。

圆的大小由半径决定。

圆有无数条对称轴。

(2)圆的画法把圆规的两脚分开，定好两脚间的距离(即半径);把有针尖的一只脚固定在一点(即圆心)上;把装有铅笔尖的一只脚旋转一周，就画出一个圆。

(3)圆的周长围成圆的曲线的长叫做圆的周长。

把圆的周长和直径的比值叫做圆周率。

用字母表示。

(4)圆的面积圆所占平面的大小叫做圆的面积。

几何图形的性质和分类几何图形是指由点、线、面等几何元素组成的图形。

在数学中，研究几何图形的性质和分类是非常重要的，它们为我们理解空间和解决实际问题提供了基础。

本文将介绍几何图形的主要性质和常见的分类方法。

一、点、线、面的基本性质1. 点：点是几何图形的最基本的元素。

点有无穷多个，没有大小和方向，只有位置。

2. 线：线由无数个点组成，它是一维的，无厚度，没有宽度和长度。

3. 面：面是由线围成的，它是二维的，有面积。

面的种类繁多，我们以平面和曲面为主要分类。

二、平面图形的性质和分类平面图形是在平面上展开的图形，具有许多独特的性质和分类。

下面我们将介绍几种常见的平面图形。

1. 点、线、面：以上已经提到了点、线和面的基本性质。

它们也可以被视为特殊的平面图形。

2. 矩形：矩形是一个具有四个直角的四边形，它的对边相等且平行。

矩形的特点是：四个内角均为直角，对角线相等，对边平行且相等。

3. 正方形：正方形是一种特殊的矩形，它的四边相等且内角均为直角。

正方形的特点是：四个边相等，对角线相等，对边平行且相等。

4. 三角形：三角形是由三条线段连接而成的形状。

根据三角形的边和角的关系，可以将三角形分为等边三角形、等腰三角形和一般三角形。

5. 圆：圆是由一条曲线所围成的平面图形，它的每个点到圆心的距离都相等。

圆的特点是：圆心、半径和直径。

三、立体图形的性质和分类立体图形是具有三维形状的图形，由于增加了高度的概念，所以其性质和分类与平面图形有所不同。

下面我们将介绍一些常见的立体图形。

1. 三棱锥：三棱锥是一个底面为三角形的立体图形，它的侧面由三个三角形和一个三角形的顶点组成。

2. 立方体：立方体是一个六个面均为正方形的立体图形，它的六个面都相等且平行。

立方体的特点是：六个面均为正方形，相邻面平行且相等。

3. 圆锥：圆锥是一个底面为圆的立体图形，它的侧面由直线和圆锥顶点组成。

4. 球体：球体是一个由曲线围成的立体图形，它的每个点到球心的距离都相等。

平面图形的特点
所谓平面图形是指在平面上（二维空间中）可以表示的所有形状和结构，它们只有两个维度，可以是一个图像，一个几何图形或一个图案。

平面图形的形状可以是圆形、矩形或几何图案，它们可以单独使用也可以组合使用。

而平面图形的特征主要体现在以下几个方面：首先，平面图形的颜色主要的纯色，它们使用的着色原则为“简单明了、大气有韵味”，而色彩多样的表现也丰富了图形的节奏感。

此外，平面图形的线条使用clear、simple、细腻来表现，但过于细腻的细节可能会迷失眼球，而使用保持简洁的线条，可以使设计更加平滑、简洁。

其次，平面图形的结构应该简单明了、大方洒脱，它们要表达出独特的美感。

最后，平面图形的使用范围广泛，它们可以适用于多种场景，比如宣传海报、商业标志、企业标识、产品包装等等，是绘制图形和设计师的必备技能。

总之，平面图形具有着独特的特点，它们能够表达出平滑、简洁、大气、有韵味的特性，并且使用范围也很广泛，可以说是设计行业不可缺少的重要素材。

数学教案：认识平面图形的特征和分类一、平面图形的特征和分类平面图形是我们周围常见的事物，了解和认识平面图形的特征和分类对于数学学习至关重要。

在本教案中，我们将介绍平面图形的基本特征，以及如何根据其各自的特点进行分类。

1.1 平面图形的基本特征平面图形是在二维空间中存在的图形，具有以下基本特征：（1）边：平面图形由线段组成，线段的两个端点连接起来就构成了图形的边。

（2）顶点：多边形或者折线段中相邻线段交叉所成的点称为顶点。

（3）角度：位于两条相邻边之间并以这两条边为边的角称为内角。

（4）对称性：平面图形可以具有对称轴，该轴将图形分成两个互相镜像对称的部分，每个部分都与另一个部分完全一致。

1.2 平面图形的分类根据各自不同特点，我们可以将平面图形进行分类：（1）三角形：三角形是由三条线段连接而成。

根据其内角之和等于180度来分类，可以分为锐角三角形、直角三角形和钝角三角形。

（2）四边形：四边形是由四条线段连接而成。

根据其边长和内角组成的特点，可以分为等边四边形、矩形、正方形、菱形以及一般的四边形。

（3）多边形：多边形是由多条线段连接而成。

根据其边数不同，可以分为五边形、六边形、七边形以及更多的多边形。

（4）圆：由一个固定点到平面内所有点的距离都相等的轨迹称为圆。

圆通过半径、直径和周长来进行分类。

二、认识平面图形的重要作用认识平面图形的特征和分类不仅有助于我们理解数学概念，还对我们日常生活中的应用有着重要作用。

2.1 几何建模几何建模技术在工程设计中起着至关重要的作用。

了解平面图形特征和分类，可以帮助我们更好地进行几何建模，并在设计过程中合理运用各种图案和结构。

2.2 地图制作地图是人们在导航和旅行时经常使用的工具。

通过认识不同的平面图形，我们可以更准确地理解和使用地图上的标志、符号和方向。

2.3 测量与建筑建筑师、工程师以及测量员需要准确了解和使用平面图形的特征。

他们利用几何知识进行测量、规划和构建，确保工程的稳定性和合理性。

立体图形与平面图形教案第一章：立体图形的概念与特征1.1 立方体定义：立方体是一种六个面都是正方形的立体图形。

特征：立方体有六个面，每个面都是正方形，对面的面积相等，有12条边和8个顶点。

1.2 球体定义：球体是一个所有点到球心的距离都相等的立体图形。

特征：球体只有一个面，即球面，没有边界，所有的点到球心的距离都相等。

第二章：平面图形的概念与特征2.1 矩形定义：矩形是一个有四个角都是直角的四边形。

特征：矩有两对相等的对边，对边平行，四个角都是直角。

2.2 三角形定义：三角形是一个有三个边的多边形。

特征：三角形有三条边和三个角，每个角都小于180度，任意两边之和大于第三边。

第三章：立体图形的认识与绘制3.1 立方体的绘制步骤：先画一个正方形，再在正方形的基础上画出三个相同大小的正方形，连接对面的边，形成立方体。

3.2 球体的绘制步骤：以一个中心点为圆心，画出一个圆，以同样的半径在圆的外面再画一个圆，连接圆上的点，形成球体。

第四章：平面图形的认识与绘制4.1 矩形的绘制步骤：先画一个角，画一条线段，再画一个角，再画一条线段，连接两条线段的末端，形成矩形。

4.2 三角形的绘制步骤：先画一个角，画一条线段，再画一个角，再画一条线段，连接两条线段的末端，形成三角形。

第五章：立体图形与平面图形的应用5.1 立体图形在现实生活中的应用举例：箱子、桌子、椅子等都是立体图形的应用。

5.2 平面图形在现实生活中的应用举例：门、窗户、衣物等都是平面图形的应用。

第六章：立体图形的计算与性质6.1 立方体的体积与表面积体积公式：V = a^3 （a为立方体的边长）表面积公式：S = 6a^2性质：立方体的体积和表面积与其边长的关系。

6.2 球体的体积与表面积体积公式：V = (4/3)πr^3 （r为球体的半径）表面积公式：S = 4πr^2性质：球体的体积和表面积与其半径的关系。

第七章：平面图形的计算与性质7.1 矩形的面积与周长面积公式：A = l w （l为矩形的长，w为矩形的宽）周长公式：P = 2(l + w)性质：矩形的面积和周长与其长和宽的关系。

平面图形的性质与特征一、点、线、面的基本概念及关系1.点：平面上的位置，没有长度、宽度和高度。

2.线：点的移动轨迹，有长度，没有宽度和高度。

3.面：线的移动轨迹，有长度和宽度，没有高度。

4.点、线、面的关系：点构成线，线构成面。

二、直线与射线的性质1.直线：无端点，无限长，同一平面内，直线外一点与直线上一点确定一条直线。

2.射线：有一个端点，无限长，从端点出发，沿直线方向延伸。

三、线段的性质1.线段：有两个端点，有限长。

2.线段的长度：两个端点之间的距离。

3.线段的垂直平分线：线段的中垂线，将线段平分为两个相等的部分，且与线段垂直。

四、角度的性质1.角度：由两条射线的公共端点和这两条射线的非公共部分组成的图形。

2.角度的度量：用度（°）作为单位，180°为直角，90°为锐角，小于90°为锐角，大于90°小于180°为钝角。

3.角度的补角：两个角的度数之和为180°。

4.角度的余角：两个角的度数之和为90°。

五、平行线的性质1.平行线：在同一平面内，永不相交的两条直线。

2.平行线的性质：同位角相等，内错角相等，同旁内角互补。

3.平行线的判定：同位角相等，内错角相等，同旁内角互补。

六、三角形的性质1.三角形：由三条边和三个角组成的多边形。

2.三角形的内角和：180°。

3.三角形的分类：根据边长关系，分为等边三角形、等腰三角形和普通三角形；根据角度关系，分为锐角三角形、直角三角形和钝角三角形。

4.三角形的高：从顶点到对边的垂线段。

七、四边形的性质1.四边形：由四条边和四个角组成的多边形。

2.四边形的内角和：360°。

3.四边形的分类：根据边长关系，分为矩形、正方形、平行四边形和普通四边形；根据角度关系，分为锐角四边形、直角四边形和钝角四边形。

4.四边形的角度性质：对角线互相平分，对边平行。

八、圆的性质1.圆：平面上所有到圆心距离相等的点组成的图形。

平面图形的特征平面图形是几何学中的基本概念之一，它们是由点、线和曲线所构成的。

平面图形的特征包括形状、边长、面积、角度和对称性等。

在日常生活中，我们常常遇到各种各样的平面图形，比如矩形、三角形、圆形等。

本文将从不同角度探讨平面图形的特征。

形状是平面图形最基本的特征之一。

不同的平面图形具有不同的形状，每种形状都有其独特的特点和性质。

例如，矩形具有四个直角和四条相等的边，而三角形则由三条边所构成。

形状决定了平面图形的其他特征，比如面积和角度。

边长是平面图形的另一个重要特征。

边长指的是图形的边界线的长度。

不同的图形具有不同的边长，通过测量边长可以确定图形的大小和比例关系。

例如，一个正方形的四条边边长相等，而一个长方形的两条边边长不相等。

边长也可以用来计算图形的周长，周长是图形所有边长的总和。

面积是平面图形的另一个重要特征。

面积指的是图形所占据的平面的大小。

不同的图形具有不同的面积，通过计算面积可以比较不同图形的大小。

例如，一个正方形的面积等于边长的平方，而一个长方形的面积等于两条边长的乘积。

面积也可以用来计算图形的体积，体积是图形在三维空间中所占据的大小。

角度是平面图形的另一个重要特征。

角度指的是两条线或曲线之间的夹角。

不同的图形具有不同的角度，通过测量角度可以确定图形的形状和方向。

例如，一个直角三角形的一个角度为90度，而一个等边三角形的三个角度都为60度。

角度也可以用来计算图形的旋转角度，旋转角度是图形相对于某一点或直线的旋转程度。

对称性是平面图形的另一个重要特征。

对称性指的是图形在某个轴或点对称时的性质。

不同的图形具有不同的对称性，通过观察图形的对称性可以推断出其其他特征。

例如，一个正方形具有四个对称轴，而一个圆形具有无数个对称轴。

对称性也可以用来判断图形是否相似，相似图形具有相同的形状但大小不同。

总结起来，平面图形的特征包括形状、边长、面积、角度和对称性等。

这些特征决定了图形的性质和用途。

通过研究和了解平面图形的特征，我们可以更好地理解和应用几何学的知识。