第七章 参数估计
- 格式:pdf
- 大小:190.11 KB
- 文档页数:14

第七章参数估计一、内容精要(一)点估计1.点估计的定义2.矩估计法3.最大似然估计法(二)参数的区间估计1.置信区间2.正态总体的期望和方差的区间估计求解具体步骤(三)估计量的评选标准1.无偏性2.有效性3.一致性(相合性)二、 常考题型分析(一) 点估计例1 X 设总体的概率分布为()2201232112X P θθθθθ--10,2X θθ⎛⎫<< ⎪⎝⎭其中是未知参数利用总体的如下样本值3,1,3,0,3,1,2,3.θ求的矩估计值和最大似然估计值例2 X 设总体的概率分布为()()2123211X P αβββ--1233,1,2, 1..x x x αβ===现在观察容量为的样本求和的最大似然估计值例3 ()221200,,,,,0n X X X N μσμσ> 设是总体为的简单随机样本其中已知,()221111,,,1n n i ii i X X S X X n n ====--∑∑未知记 ()22ˆ1;σσ求参数的最大似然估计量 ()22ˆˆ2.E D σσ计算和例4 12,,,n X X X X 设为总体的一个样本,总体的密度函数为()1,,,,0,,x e x f x others μθμθμθ-⎧⋅≥⎪=⎨⎪⎩0,.θθμ>其中求未知参数和的最大似然估计量例5 ()11,1,;1,0,1,x X F x xx βββ⎧->⎪=>⎨⎪≤⎩设总体的分布函数为其中未知参数 12,,,,n X X X X 是取自总体的简单随机样本求()1;β的矩估计量 ()2.β的最大似然估计量例6 X 设总体的概率密度为()01,,,,12,0,,x f x x others θθϕϕ<<⎧⎪=≤<⎨⎪⎩,()12,0,1,,,,,n X X X X N θϕθϕ<< 其中是未知参数是取自总体的简单随机样本记为12,,,,.n x x x θϕ 样本值中小于1的个数,求的最大似然估计例7 X 设总体的概率分布为221231X P θθθθ-- ()()0,1,i N X n iθ∈其中参数未知以表示来自总体的简单随机样本样本容量为中等于()312311,2,3.,,,=,i i i i a a a T a N T θ==∑的个数试求常数使为的无偏估计量并求的方差.例8 212111,,,,,,nn i i n X X X DX X X n σ===∑ 设个随机变量独立同分布()()2211,1ni i S X X n ==--∑则()A S σ是的无偏估计量 ()B S σ是的最大似然估计量 ()C S σ是的相合估计量 ()D S X 与相互独立例9 ()()(),,,,0,.x ex X f x x θθθθθ--⎧≥⎪=∈-∞+∞⎨<⎪⎩设总体的密度函数为为未知 ()121212111ˆˆ,,,,:1,min ,,,n n i ni X X X X X X X X n nθθ==-=-∑ 参数,为的一个样本证明,.θ是的两个无偏估计并确定哪个更有效例10 ()1230,,,,,X U X X X X θ 设总体是的一个样本验证1213134ˆˆmax ,4max 3i ii i X X θθ≤≤≤≤== ,θ为参数的无偏估计并比较哪个更加有效?(二) 参数的区间估计例11 ()2,0.99X N μ 设由来自正态总体容量为的简单随机样本,得样本均值5,0.95___________.X μ=则未知参数的置信度的置信区间为例12()2,,X N μσσ 假定到某地旅游的一个游客的消费额且=500元,今要对该地每一个旅客的平均消费额进行估计,为了能不小于95%的置信度,确信这估计的误差小于50元,问至少需要随机调查多少个游客.例13 (),8,,10X N X μμ设随机变量服从正态分布未知现有的个观测值10121011,,,,1500.10i i x x x x x ===∑ 已知()10.95;μ求的置信度为的置信区间()2.9n 要使05的置信区间长度不超过1,观察值个数最少应该取多少?()()3100,1,1n x x μ=-+若那么区间作为的置信区间时,置信度是多少?例14 0.50,1.25,0.80,2.00,ln X Y X =设是来自总体的简单随机样本已知(),1.N μ服从正态分布()()1EX b 求记为()2μ求的置信度为0.95的置信区间;()3,0.95.b 利用上述结果求的置信度为的置信区间。






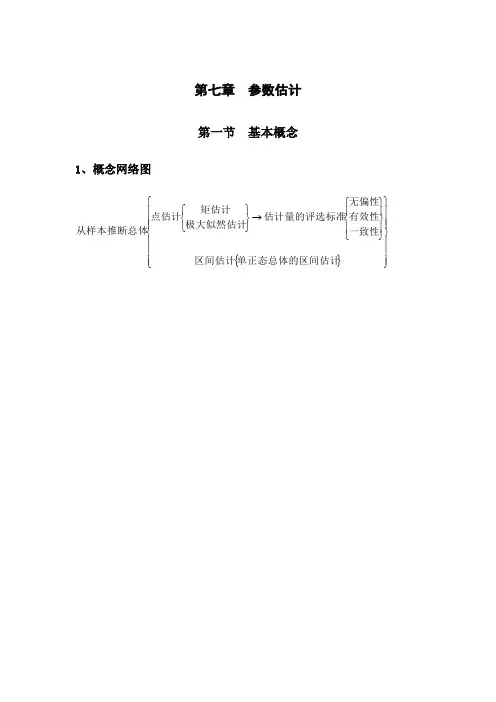
第七章 参数估计第一节 基本概念1、概念网络图{}⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧→⎭⎬⎫⎩⎨⎧单正态总体的区间估计区间估计一致性有效性无偏性估计量的评选标准极大似然估计矩估计点估计从样本推断总体2、重要公式和结论例7.1:设总体),(~b a U X ,求对a, b 的矩估计量。
例7.2:设n x x x ,,,,21 是总体的一个样本,试证(1);2110351321x x x ++=∧μ (2);12541313212x x x ++=∧μ(3).12143313213x x x -+=∧μ都是总体均值u 的无偏估计,并比较有效性。
例7.3:设n x x x ,,,,21 是取自总体),(~2σμN X 的样本,试证∑=--=ni i x x n S 122)(11 是2σ的相合估计量。
第二节 重点考核点矩估计和极大似然估计;估计量的优劣;区间估计第三节 常见题型1、矩估计和极大似然估计例7.4:设0),,0(~>θθU X ,求θ的最大似然估计量及矩估计量。
例7.5:设总体X 的密度函数为⎪⎩⎪⎨⎧≥=--.,0,1)(/)(其他μθθμx e x f x其中θ>0, θ,μ为未知参数,n X X X ,,,21 为取自X 的样本。
试求θ,μ的极大似然估计量。
2、估计量的优劣例7.6:设n 个随机变量n x x x ,,,21 独立同分布,,)(11,1,)(122121∑∑==--===n i i n i i x x n S x n x x D σ 则(A )S 是σ的无偏估计量;(B )S 是σ的最大似然估计量; (C )S 是σ的相合估计量;(D )x S 与2相互独立。
例7.7:设总体X 的密度函数为⎪⎩⎪⎨⎧<<-=,,0,0),(6)(3其他θθθx x xx fn X X X ,,,21 是取自X 的简单随机样本。
(1) 求θ的矩估计量∧θ;(2) 求∧θ的方差D (∧θ);(3) 讨论∧θ的无偏性和一致性(相合性)。

