当前位置：文档之家 › 第七章 参数估计

第七章 参数估计

  • 格式：doc
  • 大小：912.00 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

概率论与数理统计第7章参数估计PPT课件

概率论与数理统计第7章参数估计PPT课件
5
a1(1, ,k )=v1
1 f1(v1, ,vk )
假定方程组a2(1, ,k ) v2 ,则可求出2 f2(v1, ,vk )
ak (1, ,k ) vk
k fk (v1, ,vk )
则x1 xn为X的样本值时，可用样本值的j阶原点矩Aj估计vj，其中
Aj
1 n
n i1
xij ( j
L(x1, ,xn;ˆ)maxL(x1, ,xn;)，则称ˆ(x1, ,xn)为
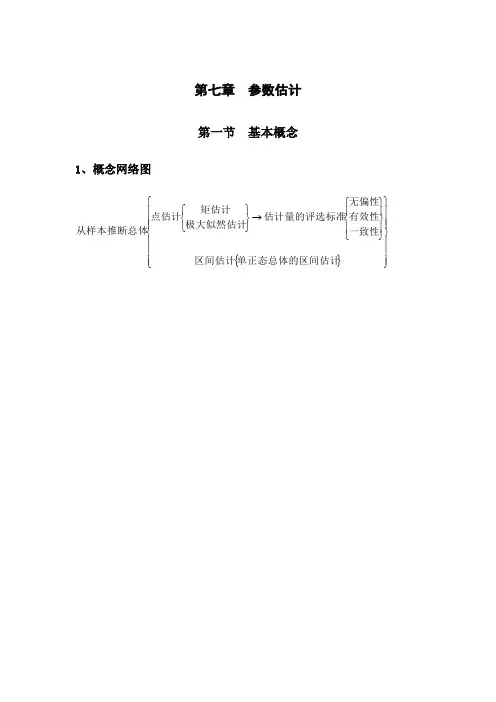
的一种参数估计方法 .
它首先是由德国数学家
高斯在1821年提出的 ,然而， 这个方法常归功于英国统
Gauss
计学家费歇（Fisher） . 费歇在1922年重新发现了
这一方法，并首先研究了这
种方法的一些性质 .
Fisher
10
极大似然估计是在已知总体分布形式的情形下的 点估计。
极大似然估计的基本思路：根据样本的具体情况
注：估计量为样本的函数，样本不同，估计量不 同。
常用估计量构造法：矩估计法、极大似然估计法。
4
7.1.1 矩估计法
矩估计法是通过参数与总体矩的关系，解出参数， 并用样本矩替代总体矩而得到的参数估计方法。 （由大数定理可知样本矩依概率收敛于总体矩， 且许多分布所含参数都是矩的函数）
下面我们考虑总体为连续型随机变量的情况：
n
它是的函数，记为L(x1, , xn; ) f (xi , ), i 1
并称其为似然函数，记为L( )。
注：似然函数的概念并不仅限于连续随机变量 ，
对于离散型随机变量，用 P {Xx}p(x,)
替代f ( x, )
即可。
14
设总体X的分布形式已知，且只含一个未知参数，

概率论 第七章 参数估计

概率论 第七章 参数估计

L( ) max L( )
称^为
的极大似然估计（MLE）.
求极大似然估计(MLE)的一般步骤是：
(1) 由总体分布导出样本的联合概率分布 (或联合密度);
(2) 把样本联合概率分布(或联合密度)中自变 量看成已知常数,而把参数 看作自变量, 得到似然函数L( );
(3) 求似然函数L( ) 的最大值点(常常转化 为求ln L( )的最大值点) ，即 的MLE;
1. 将待估参数表示为总体矩的连续函数 2. 用样本矩替代总体矩，从而得到待估参
数的估计量。
四. 最大似然估计（极大似然法）
在总体分布类型已知条件下使用的一种 参数估计方法 .
首先由德国数学家高斯在1821年提出。 英国统计学家费歇1922年重新发现此
方法，并首先研究了此方法的一些性质 .
例：某位同学与一位猎人一起外出打猎.一只 野兔从前方窜过 . 一声枪响，野兔应声倒下 .
p值 P(Y=0) P(Y=1) P( Y=2) P(Y=3) 0.7 0.027 0.189 0.441 0.343 0.3 0.343 0.441 0.189 0.027
应如何估计p?
若：只知0<p<1, 实测记录是 Y=k
(0 ≤ k≤ n), 如何估计p 呢?
注意到
P(Y k) Cnk pk (1 p)nk = f (p)
第七章 参数估计
参数估计是利用从总体抽样得到的信息 估计总体的某些参数或参数的某些函数.
仅估 计一 个或 几个 参数.
估计新生儿的体重
估计废品率
估计降雨量
估计湖中鱼数
…
…
参数估计问题的一般提法:
设总体的分布函数为 F(x, )，其中为未 知参数 (可以是向量).从该总体抽样，得样本

第七章 参数估计

第七章 参数估计

第七章 参数估计
1、正态总体、方差已知或非正态总体，大样本 当总体服从正态分布且方差已知时，或者总体不是正态分布但是大样本时，样本 均值的抽样分布均为正态分布，其数学期望为总体均值u，方差为Ϭ2/n。而样本均 值经过标准化以后的随机变量则服从标准正态分布，即 Z=(x-u)/(Ϭ/n0.5)~N(0,1) 根据上式和正态分布的性质可以得出总体均值u在1-α置信水平下的置信区间为： xα+是(-)事Z(α先/2)所(Ϭ确/n定0.5的)。而其一中个，概x率+Z值(α/2，) (Ϭ也/n称0.为5)为风置险信值上，限是，总x体-Z均(α/2值) (Ϭ不/包n0.含5)为在置置信信下区限间，的 概是率估；计1总- 体α称均为值置时信的水估平计，误Z差(α/。2) 是标准正态分布右侧面积为α/2的z值；Z(α/2) (Ϭ/n0.5) 也即是说，总体均值的置信区间由两个部分构成：点估计值和描述估计量精度的 +(-)值，这个+(-)值称为估计误差。
第七章 参数估计
在区间估计中，由样本统计量所构造的总体参数的估计区间称为置信区间。
其中，区间的最小值称为置信下限，最大值称为置信上限。
由于统计学家在某种程度上确信这个区间会包含真正的总体参数，所以给它取名 为置信区间。原因是：如果抽取了许多不同的样本，比如说抽取100个样本，根据 每一个样本构造了一个置信区间，这样，由100个样本构造的总体参数的100个置 信区间中，有95%的区间包含了总体参数的真值，而5%则没有包含，则95%这个值 称为置信水平。一般，如果将构造置信区间的步骤重复多次，置信区间中包含总 体参数真值的次数所占的比例称为置信水平，也称为置信度或置信系数。
自然使用估计效果最好的那种估计量。什么样的估计量才算一个好的估计量呢？ 统计学家给出了评价估计量的一些标准，主要包括以下几个：

第七章-参数估计

第七章-参数估计
的标准 • 1.无偏性 • 无偏估计量：用多个样本的统计量作为总体参数 的估计值，其偏差的平均数为0。
X 0
• 2.有效性
• 当总体参数的无偏估计不止一个统计量时，无偏
估计变异小者有效性高，变异大者有效性低，即 方差越小越好。
9 0.286 9 0.286 2 23.6 1.73
0.11 2 1.49
• 【例7-7】
• n=31，sn-1=5问的0.95置信区间？
• 解：先求方差的置信区间，当df=30，查χ2表，
2 0.025 47
2 0.975 16.8
2 30 52 30 5 2 47 16.8
正态分布，即Z0.05/2=1.96。
5 0.635 2 31
• 0.95的置信区间为：
5 1.96 0.635 5 1.96 0.635
3.76 6.24
• 二、方差的区间估计
• 根据χ2分布：
2
X X


2
2
2 2 n 1 sn ns 1
第七章 参数估计
思 考
• 例8-1：从某市随机抽取小学三年级学生50名，测 得平均身高为 140cm ，标准差 4 。试问该市小学 三年级学生的平均身高大约是多少？

例8-2：某教师用韦氏成人智力量表测80 名高三学生，M=105。试估计该校高三 学生智商平均数大约为多少？
什么是参数估计
当在研究中从样本获得一组数据后，如何通过 这组数据信息，对总体特征进行估计，也就是 如何从局部结果推论总体的情况，称为总体参 数估计。 • 参数估计： 样本 统计量
• 【例7-2】
• 有一个49名学生的班级，某学科历年考试成绩的

概率论与数理统计-参数估计

概率论与数理统计-参数估计

第七章 参数估计
例：
引言
设总体 X 是服从参数为 的指数分布，其中参数
未 知 ，
0 ．X1 ,,
X
是总体
n
X
的一个样本，
我们的任务是根据样本，来估计 的取值，从
而估计总体的分布．
这 是 一 个 参 数 估 计 问 题．
第七章 参数估计
§1 点估计 §2 估计量的评选标准 §3 区间估计
第七章 参数估计 §1 点估计
2
令
A1
A2
, (
2
1)
.
第七章 参数估计
例6(续）
解此方程组，得
§1 点估计
ˆ
A1 2 A2 A12
,
ˆ
A2
A1 A12
.
ˆ X 2 ,
即
B2
ˆ X .
B2
其中 B2
1 n
n i 1
Xi X
2 为样本的二阶中心矩．
第七章 参数估计（第二十二讲） 三、 极大似然法
§1 点估计
1
第七章 参数估计
例6(续）
EX 2 x 2 f
x dx x 2
x 1e x dx
0
§1 点估计
2 2 x ( e 2)1 x dx
2 0 2
2 2
1 2
1
2
因此有
EX
,
EX
2
1 .
⑵ 在不引起混淆的情况下，我们统称估计量
与估计值为未知参数 的估计．
第七章 参数估计
二、 矩估计法
§1 点估计
设X为连续型随机变量，其概率密度为
f ( x;1 ,, k ), X为离散型随机变量，其分布列为

第7章 参数估计(小结与典型例题选讲)

第7章 参数估计(小结与典型例题选讲)

估计量, 这个估计量称为矩估计 . 量
最大似然估计量
得到样本值 x1 , x2 ,, xn 时 , 选取使似然函数L( )
ˆ 取得最大值的 作为未知参数 的估计值, ˆ 即 L( x1 , x2 , , xn ; ) max L( x1 , x2 , , xn ; ).
( 其中 是 可能的取值范围)
P{ ( X 1 , X 2 ,, X n ) ( X 1 , X 2 ,, X n )} 1 ,
则称随机区间( , ) 是 的置信水平为1 的置信 区间, 和 分别称为置信水平为 的双侧置信 1 区间的置信下限和置信 上限, 1 为置信水平.
其中 Sw2
n1S12 n2 S2 2 , Sw Sw2 . n1 n2 2
1 2. 两个总体方差比 2 的置信区间 2 (1)总体均值 1 , 2 为已知的情况.
2
1 2 的一个置信水平为 1 的置信区间 2
2
m m 2 2 n ( X i 1 ) n ( X i 1 ) 1 1 i n1 . , i n1 F (m, n) F (m, n) m (Y j 2 ) 2 1 /2 m (Y j 2 ) 2 /2 j 1 j 1
ˆ Var[ p ] p(1 p) , 2 n ln f ( x; p) E p n
1 n ˆ 对于参数 p 的无偏估计量 p X X i , n i 1
1 n 1 n ˆ ] Var X i 2 Var[ X i ] Var[ p n i 1 n i 1
i 1
n
L( )称为样本似然函数 .

参数估计方法

第七章 参数估计第一节 基本概念1、概念网络图{}⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧→⎭⎬⎫⎩⎨⎧单正态总体的区间估计区间估计一致性有效性无偏性估计量的评选标准极大似然估计矩估计点估计从样本推断总体2、重要公式和结论例7．1：设总体),(~b a U X ，求对a, b 的矩估计量。

例7．2：设n x x x ,,,,21 是总体的一个样本，试证（1）;2110351321x x x ++=∧μ （2）;12541313212x x x ++=∧μ（3）.12143313213x x x -+=∧μ都是总体均值u 的无偏估计，并比较有效性。

例7．3：设n x x x ,,,,21 是取自总体),(~2σμN X 的样本，试证∑=--=ni i x x n S 122)(11 是2σ的相合估计量。

第二节 重点考核点矩估计和极大似然估计；估计量的优劣；区间估计第三节 常见题型1、矩估计和极大似然估计例7．4：设0),,0(~>θθU X ，求θ的最大似然估计量及矩估计量。

例7．5：设总体X 的密度函数为⎪⎩⎪⎨⎧≥=--.,0,1)(/)(其他μθθμx e x f x其中θ>0, θ,μ为未知参数，n X X X ,,,21 为取自X 的样本。

试求θ,μ的极大似然估计量。

2、估计量的优劣例7．6：设n 个随机变量n x x x ,,,21 独立同分布，,)(11,1,)(122121∑∑==--===n i i n i i x x n S x n x x D σ 则（A ）S 是σ的无偏估计量；（B ）S 是σ的最大似然估计量； （C ）S 是σ的相合估计量；（D ）x S 与2相互独立。

例7．7：设总体X 的密度函数为⎪⎩⎪⎨⎧<<-=,,0,0),(6)(3其他θθθx x xx fn X X X ,,,21 是取自X 的简单随机样本。

（1） 求θ的矩估计量∧θ；（2） 求∧θ的方差D （∧θ）；（3） 讨论∧θ的无偏性和一致性（相合性）。

07心理统计学-第七章 参数估计


犯错误的概率，常用α（或p）表示。则1-α为置信 度。（显著性水平越高表示的是α值越小，即犯错误的可
能性越低） α为预先设定的临界点，常用的如.05、.01、.001；p 为检验计算所得的实际（犯错误）概率。
第一节 点估计、区间估计与标准误
三、区间估计与标准误
3、区间估计的原理与标准误
转换成比率为
p

n
p, SE p

n

pq n
同理可得公式7-17。自习[例7-12、例7-13]
1、从某地区抽样调查400人，得到每月人均文化消费为 160元。已知该地区文化消费的总体标准差为40元。试 问该地区的每月人均文化消费额。（α=.05，总体呈正态
分布）
2、上题中总体方差未知，已知Sn-1=44元。 3、已知某中学一次数学考试成绩的分布为正态分布，总 体标准差为5。从总体中随机抽取16名学生，计算得平 均数为81、标准差为Sn=6。试问该次考试中全体考生成 绩平均数的95%置信区间。 4、上题中总体方差未知，样本容量改为17人。 5、假定智商服从正态分布。随机抽取10名我班学生测 得智商分别为98、102、105、105、109、111、117、 123、124、126（可计算得M=112，Sn≈9.4），试以95% 的置信区间估计我班全体的智商平均数。 返回
值表，求tα /2（df）。
5、计算置信区间CI。
σ2已知，区间为M-Zα /2 SE <μ< M+Zα /2 SE；
σ2未知，区间为M-tα /2(df)SE <μ< M+tα /2(df)SE。
6、对置信区间进行解释。
二、σ2已知，对μ的区间估计（Z分布，例7-1 & 2） 三、σ2未知，对μ的区间估计（t分布，例7-3 & 4）

统计学 第七章 参数估计


[
]
2 χα (n) （n）的α 分位数，记为k≜ n k≜
抽样分布
（3）性质 • 若X服从χ2 （n），则均值E（X）=n ，方差 D（X） =2n 。 • χ2分布具有可加性。若 X1，X2相互独立，
X1～ χ2（n1） ，X2～χ２（n2）
则（X1＋X2）～χ２（ｎ１＋n２） • 当ｎ→∞时，χ２分布渐进于正态分布
σ
2
~ χ (n −1)
2
第三节两个总体参数的区 间估计（112页）
• • • • • • • 一、两个总体均值之差的区间估计 （一）两个总体均值之差的估计：独立样本 大样本：近似于正态分布 小样本： （1）两个总体的方差均已知，近似于正态分布 （2）两个总体的方差均未知但相等，近似于ｔ分布 （3）两个服从正态分布的总体的方差均未知且不等， 但样本容量相等，近似于ｔ分布 • （4）两个总体的方差均未知且不等，样本容量也不 等，近似于ｔ分布，自由度为V
• 解：求（3）的计算步骤： • ①求样本指标：
x ＝1000小时
σ＝50 （小时）
µ x＝
σ
n
＝
50 100
＝（小时） 5
• ②根据给定的F（t）＝95%，查概率表得t＝1.96。 • ③根据∆x＝t×µx＝1.96×5＝9.8，计算总体平均耐 用时间的上、下限： x − ∆ x＝1000－9.8＝990.（小时） 2 • 下限 x ＋∆ x＝1000＋9.8＝1009 .（小时） 8 • 上限 • 所以，以95%的概率保证程度估计该批产品的平均耐 用时间在990.2～1009.8小时之间。
f (x;θ ) 其中 θ
或概率密度为
是未知参数。 是未知参数。
如何求极大似然估 计量呢？ 计量呢？

数理统计 第七章-参数估计


休息
结束
2. 最大似然法
是在总体类型已知条件下使用的一 种参数估计方法 。 它首先是由德国数学家高斯在1821 年提出的 ,费歇在1922年重新发现了这 一方法，并首先研究了这 种方法的一些 性质 。
休息 结束
最大似然法的基本思想：
已发生的事件具有最大概率。
休息
结束
先看一个简单例子： 在军训时，某位同学与一位教官同 时射击，而在靶纸上只留下一个弹孔。 如果要你推测，是谁打中的呢？ 你会如何想呢?

max f ( xi , )

i 1
n
休息
结束
X 假设X 为连续型总体： f ( x; )
( X 1 , , X n ) 为子样
( x1 , , xn ) 为子样观察值。
已发生的事件为：
x x ,X {{X 11 1x, X 1 nx1 ,n } , xn x X n xn } x

休息
结束
ˆ
1 n ( X i X )2 n i 1
1 n ˆ X ( X i X )2 n i 1
休息
结束
矩法的优点是简单易行,并不需要 事先知道总体是什么分布 。 缺点是，当总体类型已知时，没有 充分利用分布提供的信息 . 一般场合下, 矩估计量不具有唯一性 。
( 1 )x , 0 x 1 f( x) 0, 其它
1
其中 1 是未知参数,
X1,X2,…,Xn是取自X的样本,求参数 的矩估计. 解:
1 E( X ) x( 1 )x dx

0
( 1 )
从 中解得
1
0
x
1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第七章 参数估计§7.1 参数的点估计 §7.2 估计量的评选标准一、 填空题1．矩估计法是通过 参数 与 总体矩 的联系，解出参数，并用 样本矩 代替 总体矩 而得到参数估计的一种方法；2．极大似然估计法是在 总体分布形式 已知情况下的一种点估计方法；3．设n X X X 2,1是正态总体),(2σμN 的一个样本，则μ的极大似然估计为 =μˆ ∑=n i i X n 11 ；总体方差的矩估计为=σ2ˆ ∑=-n i i X X n 12)(1 ； 4.设()12ˆ,,,nX X X θ 为未知参数θ的估计量，若()ˆE θθ=，则称ˆθ为θ的无偏估计量；5．设n X X X 2,1为总体X 的一个样本，则总体均值)(X E 的无偏估计为 ∑==n i i X n X 11 ；总体方差)(X D 的无偏估计为 ∑=--=n i i X X n S 122)(11 ； 6.设总体X 服从二项分布(),,B N p N 已知，()12,,,n X X X 是来自X 的样本，则p 的极大似然估计量为XN； 解 {}()1ii iN x xx i N P x x C pp -==-，()()111111nni ii i ii i i nnx N x nN x x x x NN i i L C p p C p p ==--==∑⎛⎫∑=-=- ⎪⎝⎭∏∏， ()111ln ln ln ln 1i n n nx N i i i i i L C x p nN x p ===⎛⎫⎛⎫⎛⎫=++-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑∑∏，令11ln 110,1n ni i i i d L x nN x dp p p==⎛⎫⎛⎫=--= ⎪ ⎪-⎝⎭⎝⎭∑∑得到1ni i x X p nN N ===∑。

7.在天平上重复称量一重为a 的物品，假设各次称量结果相互独立且服从正态分布()2,0.2N a ，若以n X 表示n 次称量结果的算术平均值，则为使{}0.10.95n P X a -<≥，n 的最小值应不小于自然数16。

解 ()()220.2,n n E X a D X n n σ===，所以20.2,n X N a n ⎛⎫ ⎪⎝⎭{}0.1210.95n P X a p ⎫-<=<=Φ-≥，解得(()0.975 1.96,Φ≥=Φ所以只需 1.96≥，得到23.92n ≥。

二、 计算下列各题1. 设n X X X 2,1来自指数分布⎩⎨⎧<≥=θθ--0,00,);()(x x e x f x 的一个样本，试求θ的 矩估计。

解 ()()θθe dx xe dx x xf X E x ===⎰⎰+∞--+∞∞-0)(，令()1X E X ν==， 所以θ的矩估计为X ln ˆ=θ。

2. 设总体X 的密度函数为()()⎪⎩⎪⎨⎧<<-=其它， ,0063θθθx x xx f ，()12,,,n X X X 是取自X 的简单随机样本，（1）求θ的矩估计量ˆθ；（2）求ˆθ的方差ˆ()D θ。

解 （1）因为()()()236,2x E X xf x dx x dx θθθθ+∞-∞==-=⎰⎰令()E X X =即2X θ=，所以θ的矩估计量为ˆ2X θ=； （2）由于()()()3222363,10x E Xx f x dx x dx θθθθ+∞-∞==-=⎰⎰()()()222223,10420D X E X E X θθθ=-=-=⎡⎤⎣⎦所以()()()221ˆ244205D D X D X n nθθθ===⨯⨯=。

3. 设总体X 服从两点分布（０-１分布），{}p p x P ,1==为未知参数，10<<p 。

n X X X 2,1是来自该总体的简单随机样本，试求未知参数p 的矩估计和极大似然估计。

解 (1)∑===ν==νni i X n X p X E 1111ˆ,)( ，所以p 的矩估计X p =ˆ； ∑∑∏===----+==∑-∑===-====ni i ni i i ni x n x i xxp x n p x L x p p x X P L p p x X P ni ini i1111)1ln()(ln )(ln 1,0,)1()(,)1()(211）（∑∑∑=====---=ni i ni n i i x n X p p p x n x p dp L d 111ˆ,011)(1ln 的极大似然估计所以。

4. 设总体X 的密度函数为10,)1();(<<+α=ααx x x f ，其中1->α是未知参数，n X X X 2,1是来自该总体的一个简单随机样本，试求参数α的矩估计和极大似然估计。

解（1）矩法 21121)1()()(111+-=++=+===⎰⎰++∞∞-ααααναdx x dx x xf X E ，令()1X E X ν==，则XX X X --=--=-=+112211121αα，所以α的矩估计 XX --=α112ˆ； （2）极大似然法 ()()⎪⎩⎪⎨⎧=<<⎪⎪⎭⎫ ⎝⎛+=∏=其它，,0,,2,1,1011n i x x L i n i i n ααα ()()011,20i x i n L α<<=> 当时，，故()∑=α++α=ni i x n L 1ln 1ln ln ，并且令1ln ln 01ni i L n x αα=∂=+=∂+∑，解得∑=--=ni ixn1ln 1ˆαα的极大似然估计为。

5. 设12,,,n X X X 是来自参数为λ的泊松分布总体的一个样本，试求λ的矩估计量及极大似然估计量。

解 （1）总体X 的分布律为{},0,1,!x e P X x x x λλ-=== ，因为()()()1011!1!1!x x x x x x e e eE X x x x xλλλλλλλλ----∞∞∞====⋅===--∑∑∑，所以令()1X E X υ==，得到λ的矩估计量为ˆX λ=； （2）样本12,,,n X X X 的似然函数为()111!!niii x x n nni i ii ee L x x λλλλλ=--==∑==∏∏，则()11ln ln ln(!)nni i i i L x n x λλλ===--∑∑，令()1ln 0nii x L n λλλ=∂=-=∂∑，解得λ的极大似然估计量为11ˆn i i X X n λ===∑。

6. 设总体()2,~σμN X 其中μ未知，n X X X 2,1为其子样，试证下述统计量：3211412141ˆX X X ++=μ, 3212313131ˆX X X ++=μ,3213515351ˆX X X ++=μ 3146561ˆX X +=μ都是μ的无偏估计，并指明哪个估计“最好”。

证 )(41)(21)(41)ˆ(3211X E X E X E E ++=μμ=μ+μ+μ=412141 同理可得μμμμ===)ˆ()ˆ()ˆ(432E E E , 故均为μ的无偏估计。

又)(161)(41)(161)ˆ(3211X D X D X D D ++=μ222228316616141161σ=σ=σ+σ+σ=同理可得 2231)ˆ(σμ=D , 232511)ˆ(σμ=D , 241813)ˆ(σμ=D , 故2ˆμ最好。

7.(1)设12,,,n X X X 是来自总体X 的样本，10,1,2,,,1ni ii i n αα=>==∑ ，试证1ni ii Xα=∑是()E X μ=的无偏估计量；（2）试证在μ的一切形为110,1nni i i i i i X ααα==⎛⎫>= ⎪⎝⎭∑∑的估计中，X 为最有效的。

证 （1）因为()111()n n niiiiii i i E X E X ααμαμ======∑∑∑，所以1ni i i X α=∑是μ的无偏估计；(2)()222111n n ni i i i i i i i D X D X αασα===⎛⎫== ⎪⎝⎭∑∑∑，下面求函数()2121,,,nn i i f αααα==∑ 在条件10,1,2,,,1ni i i i n αα=>==∑ 下的极小值点。

为此令()21211,,,;1nn n i i i i F αααλαλα==⎛⎫=+- ⎪⎝⎭∑∑ ，令120,1,2,,10,i i n i i Fi n F αλααλ=∂⎧=+==⎪∂⎪⎨∂⎪=-=⎪∂⎩∑ 解得1,122n i i i n λλαα==-=-=∑，得2n λ=-，从而得1,1,2,,i i n nα== ，从而证明了X 最有效。

8. 设n X X X 2,1为正态总体()2,αμN 的一个样本，试适当选择C ，使()2111∑-=+-n i i i X X C 为2σ的无偏估计。

解 ()()()()()[]∑∑-=++-=+++-=⎥⎦⎤⎢⎣⎡+-11212111212122n i i i i i n i i i i i X E X E X E X E C X X X X C E＝()()()[]∑-=+-112222n i X E EX X E C＝()()[]()()()X D X D n C EX X E C n i =-=-∑-=1221122，()121-=n C 所以。

9.设21ˆ,ˆθθ是参数θ的两个相互独立的无偏估计，且()()21ˆ2ˆθ=θD D ，找出常数21,k k 使2211ˆˆθ+θk k 也是θ的无偏估计，并且使它在所有的这种形状的估计量中方差最小。

解 要使()()θθθθθθ=+=+=+2122112211)ˆ()ˆ(k k E k E k k k E ,只需 121=+k k 即可；()()()222212*********ˆ2)ˆ()ˆ(ˆˆθθθθθD k k D k D k k k D +=+=+，即求()22212m in k k +最小值，且121=+k k 。

设()()2121112k k k f -+= ，令()01='k f , 解得32,3121==k k 。

10.设分别来自总体()21,N μσ和()22,N μσ中抽取容量为12,n n 的两独立样本，其样本方差分别为2212,S S ，试证，对于任意常数(),1a b a b +=，2212Z aS bS =+都是2σ的无偏估计，并确定常数,a b 使()D Z 达到最小。

证 因为对于正态分布来说，样本方差为其总体方差的无偏估计，即()()222212,E S E S σσ==，而()()()()()222222221212E Z E aS bS aE S bE S a b a b σσσσ=+=+=+=+=，所以2212Z aS bS =+是2σ的无偏估计。