角动量守恒定律
- 格式:doc
- 大小:43.50 KB
- 文档页数:2

角动量守恒定律角动量守恒定律,也称转动动量守恒定律,是描述旋转系统中物体角动量守恒的物理定律。
它是在伽利略与牛顿的基础上,由欧拉和拉格朗日等人发展起来的。
它表明,在无外力矩作用下,一个封闭系统的总角动量守恒。
在物理学中,角动量是描述物体旋转运动的物理量。
一个物体的角动量等于其自转角速度和惯性矩的乘积。
考虑一个刚性物体,其围绕某个轴心旋转。
此时,物体的角动量L等于其自转惯性矩I和角速度ω的积,即L=Iω。
这个公式可以用来描述物体的旋转状态。
在没有外力矩作用的情况下,物体的角动量守恒。
也就是说,在这种情况下,刚体自身的角速度和惯性矩不会发生改变。
这个定律可以由牛顿第二定律的角动量形式推导出来。
当一个刚体受到外部力矩时,他的角动量就会发生变化。
这个变化量等于力矩与旋转时间的积。
一个封闭系统中的物体,在没有外部力矩作用时,总角动量守恒,即所有物体的角动量的代数和不变。
如果物体中有某一个物体受到外部力矩,那么这个物体的角动量就会发生变化,但是,由于总系y运中的总力矩为零,所以其他物体的角动量将以相反的方式发生变化,以保证总角动量守恒。
一个典型的例子是一个旋转跳板启动一个跳跃者,高度和角速度的变化取决于跳板和跳跃者的质量和形状。
在这个过程中,跳板和跳跃者的角动量守恒,因为在计算角速度和角动量时,两个物体的总和是不变的。
总之,角动量守恒定律是一种重要的动力学基本定律。
它说明,封闭系统中的角动量总和保持不变。
在硬物体的运动中往往非常有用,可以帮助计算速度、加速度和其他涉及运动的数值。
在工程学和物理学中,它被广泛地应用于旋转系统、制药生产,以及其他需要涉及转动的领域。



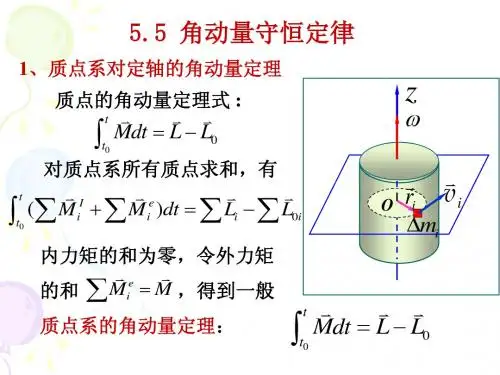


角动量守恒角动量守恒定律是指系统所受合外力矩为零时系统的角动量保持不变。
角动量守恒定律是物理和自然界的一条重要定律。
它在日常生活、天体物理、微观物理和工程中都有广泛的应用。
例如,角动量守恒定律可以很好地解释开普勒天体运行第二定律、陀螺效应等。
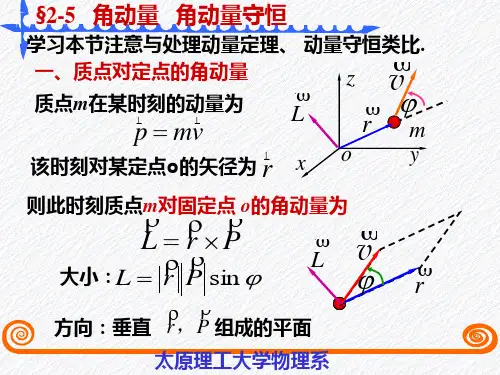
当一个质点绕原点运动时,它的角动量L=RP。
这里,R是质点相对于原点的位置向量;P是质点的线性动量;而表示矢量积。
具有一定质量的物体绕一固定轴转动,它的角动量L可表示为这个物体的惯性矩I和它的角速度向量w的乘积,即L=Iw。
角动量又称为动量矩,是一个矢量,是位矢叉乘于动量。
定理也称动量矩定理。
表述角动量与力矩之间关系的定理。
对于质点,角动量定理可表述为:质点对固定点的角动量对时间的微商,等于作用于该质点上的力对该点的力矩。
对于质点系,由于其内各质点间相互作用的内力服从牛顿第三定律,因而质点系的内力对任一点的主矩为零。
利用内力的这一特性,即可导出质点系的角动量定理:质点系对任一固定点O的角动量对时间的微商等于作用于该质点系的诸外力对O点的力矩的矢量和。
由此可见,描述质点系整体转动特性的角动量只与作用于质点系的外力有关,内力不能改变质点系的整体转动情况。
定理应用角动量守恒定律是物理和自然界的一个重要定律,它在日常生活、天体物理、微观物理和工程等许多方面都有广泛的应用。
例如:当滑冰者手臂收缩时,自我旋转滑冰者的转动速度就会加快。
用角动量守恒定律也可解析中子星有很高的转动速率等。
另外,角动量守恒定律也是陀螺效应的原因。
角动量守恒定律反映了质点和质点系围绕一点或一轴运动的普遍规律。
如一质量为 m的质点受指向固定中心O的向心力F的作用,因力F对O点的力矩为零,根据牛顿第二定律可推得质点对O点的角动量守恒,Lo=rmv=常矢量,此常矢量决定于运动的起始条件,r为质点对于O点的矢径,v为质点的速度。
如将太阳看成固定中心,行星看成质点,则角动量守恒表明行星轨道必在一平面上。
矢径在相等的时间内扫过的面积相等,这就是开普勒行星运动三定律之一—开普勒第二定律角动量守恒也是微观物理学中的重要基本规律。



角动量守恒定律的公式
1. 角动量守恒定律公式。
- 对于质点,角动量L = r× p(其中r是质点相对于某参考点的位矢,p = mv 是质点的动量,×表示矢量叉乘)。
- 在合外力矩M = 0时,角动量守恒,即L_1 = L_2。
- 对于定轴转动的刚体,角动量L = Iω(其中I是刚体对轴的转动惯量,ω是刚体的角速度)。
当合外力矩M = 0时,I_1ω_1=I_2ω_2。
2. 相关知识点(人教版教材相关内容补充)
- 转动惯量。
- 对于离散质点系,I=∑_im_ir_i^2,其中m_i是第i个质点的质量,r_i是该质点到转轴的垂直距离。
- 对于质量连续分布的刚体,I = ∫ r^2dm。
不同形状的刚体转动惯量有不同的计算公式,例如,对于质量为m、半径为R的均匀圆盘绕通过圆心且垂直于盘面的轴转动,其转动惯量I=(1)/(2)mR^2;对于质量为m、长为l的细棒绕通过中心且垂直于棒的轴转动,I=(1)/(12)ml^2。
- 角动量定理。
- 对于质点,M=(dL)/(dt)(M是合外力矩),这表明质点所受合外力矩等于它的角动量对时间的变化率。
- 对于刚体定轴转动,M = Iα(α是角加速度),结合L = Iω也可推导出
M=(dL)/(dt)。
角动量守恒定律角动量守恒定律是经典力学中的基本原理之一,它描述了封闭系统中角动量的守恒性质。
角动量是物体的旋转运动特性,它可以用来描述物体围绕某一固定点旋转时的运动状态。
本文将探讨角动量守恒定律的基本原理、重要性以及应用场景。
一、角动量角动量(angular momentum)是对物体围绕一个轴旋转运动特性的描述,它是由物体的质量、速度和旋转半径决定的。
角动量的大小与物体的质量、速度以及物体围绕轴旋转时的运动半径有关,可以用数学公式表示为L=Iω,其中L是角动量,I是物体的转动惯量,ω是物体的角速度。
二、角动量守恒定律的表达形式角动量守恒定律指出,在没有外力矩作用下,物体的角动量保持不变。
换句话说,当一个封闭系统中没有外力矩作用时,系统的总角动量保持恒定。
数学上,角动量守恒定律可以表示为:L₁ + L₂ + …… + Lₙ = 常数其中,L₁、L₂、……、Lₙ分别表示系统中各个物体的角动量。
三、角动量守恒定律的重要性角动量守恒定律在物理学中具有重要意义,它描述了自然界中许多现象的运动规律。
以下是角动量守恒定律的一些重要应用:1. 行星运动:角动量守恒定律解释了行星绕太阳运动的规律。
由于没有外力矩作用,行星绕太阳的角动量保持不变,使得行星在椭圆轨道上运动。
2. 舞蹈旋转:舞蹈演员在旋转过程中,通过改变自身的转动惯量和角速度,来保持角动量的守恒。
这就是为什么舞蹈演员在旋转时会把双臂收紧,以减小转动惯量,从而使得角速度增加,保持平衡。
3. 滑冰运动:滑冰运动员在进行旋转动作时,也是通过改变自身的转动惯量和角速度来保持角动量的守恒。
他们会把身体的质量集中在一个点上,从而减小转动惯量,并通过高速旋转来保持平衡。
四、结论角动量守恒定律是自然界中许多运动现象的基本原理之一。
它描述了封闭系统中角动量的守恒性质,是物体围绕轴旋转运动的基本规律。
角动量守恒定律在行星运动、舞蹈旋转、滑冰运动等领域具有重要应用。
通过理解和应用角动量守恒定律,我们可以更好地理解物体的旋转运动规律,提高对自然界中各种现象的理解能力。
第四节 角动量守恒定律
一、角动量
1. 质点对定点的角动量
(1)v m r p r L ⨯=⨯= (力矩:F r M ⨯=)
(2)说明:r 指质点相对于固定点O 的位置矢量;p 指质点的动量;v 指质点的速度
(3)大小:=L αsin rmv ,
(4)方向:(右手法则)v r ⨯向
(5)单位:12-s
kgm (6)量纲:12-T
ML 2. 刚体对定轴的角动量 (将刚体分解为质点组)∑∑=⋅⋅∆==⇒⋅⋅∆=⋅⋅∆=ωI w r m L L w r m v r m L i i i oz i i i i i i 22
ω I L =
此式对质点也适用
3. 角动量定理:
(1) 公式:dt
dL dt I d dt d I
I M ====)(ωωβ 或dL dt M =⋅ (2)文字表述:刚体对某一给定转轴或点的角动量对时间的变化率等于刚体所受到的对同一转轴或点的和外力矩的大小。
(3)说明:dt M ⋅称冲量矩,表示力矩的时间积累效果,单位:牛·米·秒 若何外力矩M=0,则L=IW=恒量
4. 转动定律的普遍形式 dt
dI dt d I dt L d M ωω +== 二、角动量守恒
1、角动量守恒的条件:质点所受相对于参考点的力矩的矢量和等于零;在有心
力作用下,质点相对于力心的角动量守恒。
2、应用:
例1:花样滑冰运动员的“旋”动作,当运动员旋转时伸臂时转动惯量较大,转速较慢;收臂时转动惯量减小,转速加快;再如:跳水运动员的“团身--展体”动作,当运动员跳水时团身,转动惯量较小,转速较快;在入水前展体,转动惯量增大,转速降低,垂直入水。
3、习题:
1.质点做直线运动时,其角动量( )(填一定或不一定)为零。
答案: 不一定
2.一质点做直线运动,在直线外任选一点O为参考点,若该质点做匀速直线运动,则它相对于点O的角动量( )常量;若该质点做匀加速直线运动,则它相对于点O的角动量( )常量,角动量的变化率( )常量。
(三空均填是或不是)答案: 是; 不是; 是。
3.一质点做匀速圆周运动,在运动过程中,质点的动量( ),质点相对于圆心的角动量( )。
(两空均填守恒或不守恒)
答案:不守恒;守恒。
4.一颗人造地球卫星的近地点高度为h
1 ,速率为υ
1
,远地点高度为h
2,
已知地
球半径为R.求卫星在远地点时的速率υ
2..
解:因为卫星所受地球引力的作用线通过地球中心,所以卫星对地球中心的角动量守恒。
根据角动量守恒定律得
r
1 mυ
1
= r
2
mυ
2
且r
1=R+ h
1
r
2
=R+ h
2
解得υ
2
=(R+ h
1
/R+ h
2
)υ
1。