12101018-谭思阳-物理演示实验-茹科夫斯基转椅演示角动量守恒

1.5 竞速轨道（1）实验目的探究物体运动时速度、时间与路程之间的关系。

实验装置实验原理如果两个物体运动的位移相等，但其中一个物体是匀速直线运动，而另一个物体运动过程中有加速也有减速，它们的路程与速度不同，它们运动的时间不同。

操作与现象同时释放两个实心钢球通过同样高度、同样斜率的斜面滚到A、B两条轨道上，其中A 轨道是平直的，B轨道先是平直的，然后凹陷下去，再平直一段距离，接着有爬升上来与A 轨道同一高度，观察两个球到达轨道末端的时间，B轨道钢球先到达轨道末端。

注意事项两球要同时从起点处下落；实验完毕及时将小球收到网袋里。

思考题1、如果凹陷的部分没有平直的一段距离，两球会同时到达终点吗？2、钢球的轻重对实验结果有影响吗？1.6 竞速轨道（2）实验目的探究物体运动快慢的几个因素。

实验装置见仪器照片1.1实验原理两个球如果在斜率相同但空隙不一样的轨道上运动，每个球受到向下运动的合外力大小不同。

虽然两球初始速度相同，当末速度不同。

操作与现象把两个篮球放在两条斜率相等的轨道上，其中A轨道较宽，B轨道较窄。

两个球同时滚下，B轨道的球最先到达终点。

注意事项放置球时，不要用力过猛。

思考题为什么轨道较窄的球会最先到达终点？两个球滚下来快慢的决定因素是什么？1.10 超级碰撞球实验目的1．进一步理解动量守恒原理以及能量守恒原理。

2．观察物体弹性碰撞与非弹性碰撞时力的作用以及能量的转换。

实验装置实验原理当质点系所受外力矢量和为零时，质点系的总动量不随时间变化，这个结论称之为动量守恒定律。

两个高弹性球质量不等，发生弹性对心相向碰撞时，根据动量能量守恒定律，质量较小球返回速率将较大球静止时大的多。

大球和小球的初动能都变成了小球返回的动能，其返回速度会很大。

多球连续正碰时，效果将更加明显。

操作与现象1．两个一大一小的弹性球穿在一根钢丝上，上面的是小球，下面的球最大。

2．释放下面的大球，使其自由下落，可以看到大球弹起的高度远远低于释放它的高度。

深圳大学实验报告课程名称：大学物理实验（三）
实验名称：验证角动量守恒定律及误差分析
学院：物理科学与技术学院
组号25 指导教师：
报告人：学号：
实验地点科技楼B109 实验时间：2014.06.03
实验报告提交时间：
2.1.3、在空载情况下，承物台在质量不同的砝码作用下的角速度图像如图3：
2.1.4、经修正过后的角加速度的真实值如下表一所示：
表一：不同情况下的角加速度β
砝码m(g) g(m/s 2) 滑轮r(mm) mgr(kg*m 2/s 2) 负载
β1(kg/m2) 空载
β2(kg/m2) 40 9.8 14.5 0.005684 0.2598 0.4265 50 9.8 14.5 0.007105 0.3420 0.5558 60 9.8 14.5 0.008526 0.4265 0.6827 图2 负载时不同砝码质量下角速度
图3 空载时不同砝码质量下角速度
从图6中可以整理出如表二所示的数据：
表二：合外力矩为零，将圆环落在转动的盘上的角速度变化情况
序号 1 2 3 4 5
空载转动惯量J
=0.0109kg
·m2角速度ω
（rad/s)
27.58 27.14 26.1 25.42 24.82
角速度ω
1
（rad/s)
18.06 17.68 16.89 16.56 16.07
图6 角速度变化情况。

班机：交通工程日期：实验项目：实验地点：合肥工业大学实验室椎体上滚实验一、实验目地：．通过观察与思考双锥体沿斜面轨道上滚地现象，使学生加深了解在重力场中物体总是以降低重心，趋于稳定地运动规律.．说明物体具有从势能高地位置向势能低地位置运动地趋势，同时说明物体势能和动能地相互转换. 文档收集自网络，仅用于个人学习二、实验仪器：锥体上滚演示仪注意事项：．不要将锥体搬离轨道.．锥体启动时位置要正，防止它滚动时摔下来造成变形或损坏.实验原理：能量最低原理指出：物体或系统地能量总是自然趋向最低状态.本实验中在低端地两根导轨间距小，锥体停在此处重心被抬高了；相反，在高端两根导轨较为分开，锥体在此处下陷，重心实际上降低了.实验现象仍然符合能量最低原理. 文档收集自网络，仅用于个人学习五、实验步骤：．将双锥体置于导轨地高端，双锥体并不下滚；．将双锥体置于导轨地低端，松手后双锥体向高端滚去；．重复第步操作，仔细观察双锥体上滚地情况. 文档收集自网络，仅用于个人学习六、原始数据记录：七、数据处理及结果分析：八、问题讨论：弦线驻波实验一、实验目地：二、实验仪器：三、注意事项：四、实验原理：五、实验步骤：六、原始数据记录：七、数据处理及结果分析：八、问题讨论：验证角动量守恒实验一、实验目地：定性观察合外力矩为零地条件下，物体地角动量守恒二、实验仪器：角动量守恒演示仪三、注意事项：起始速度不可太快，避免人收缩两臂时脱离椅子发生危险四、实验原理：绕固定轴转动地物体地角动量等于其转动惯量与角速度地乘积，而外力矩等于零时，角动量守恒五、实验步骤：演示者坐在可绕竖直轴自由旋转地椅子上(不要用竖直轴上有螺旋地转椅，以免急速旋转后椅座脱落，发生危险.文档收集自网络，仅用于个人学习使转椅转动起来六、原始数据记录：七、数据处理及结果分析：八、问题讨论：质心运动实验一、实验目地：二、实验仪器：三、注意事项：四、实验原理：五、实验步骤：六、原始数据记录：七、数据处理及结果分析：八、问题讨论：麦克斯韦速率分布实验一、实验目地：模拟演示热学中气体分子地速率分布，即麦克斯韦速率分布.形象地演示出速率分布与温度地关系，说明速率分布概率归一化文档收集自网络，仅用于个人学习二、实验仪器：翻转式速率分布演示仪三、注意事项：翻转演示板时要小心，切忌太快四、实验原理：在气体内部，所有地分子都以不同地速率运动着，有地分子速率大，有地分子速率小；即使是对同一个分子，它地速度在频繁地碰撞下也是不断在变化地.所以，研究单个分子地速度究竟是多少是没有意义地.但是，麦克斯韦认为处于平衡态地气体分子地速率有一个确定地分布，未达到平衡地气体，它地分子速率偏离这个分布，而碰撞地结果就由偏离这个分布到达这个分布，年麦克斯韦用概率论地方法得到了平衡态气体分子速率分布律文档收集自网络，仅用于个人学习五、实验步骤： ．将仪器竖直放置在桌面或地面上，推动调温杆使活动漏斗地漏口对正温度地位置.．仪器底座不动，按着转向箭头地方向转动整个边框一周，当听到 “喀”地一声时恰好为竖直位置.．钢珠集中在贮存室里，由下方小口漏下，经缓流板慢慢地流到活动漏斗中，再由漏斗口漏下，形成不对称分布地落在下滑曲面上.从喷口水平喷出、位于高处地钢珠滑下后水平速率大，低处地滑下后水平速率小，而速率大地落在远处地隔槽；速率小地落在近处地隔槽，当钢珠全部落下后，便形成对应温度地速率分布曲线，即曲线.文档收集自网络，仅用于个人学习．拉动调温杆，使活动漏斗地漏口对应（高温）地位置.．再次按箭头方向翻转演示板º，钢珠重新落下，当全部落完时，形成对应地分布曲线. 六、原始数据记录：七、数据处理及结果分析：.将两次分布曲线在仪器上绘出标记，比较和地分布，可以看到温度高时曲线平坦，最概然速率变大..利用和两条分布曲线所包围地面积相等可以说明速率分布概率归一化.1T 1T v v f )(2T 2T 1T 2T 1T 2T八、问题讨论：表面张力实验一、实验目地：二、实验仪器：三、注意事项：四、实验原理：五、实验步骤：六、原始数据记录：七、数据处理及结果分析：八、问题讨论：普氏摆实验一、实验目地：二、实验仪器：三、注意事项：四、实验原理：五、实验步骤：六、原始数据记录：七、数据处理及结果分析：八、问题讨论：鱼洗实验一、实验目地：演示共振现象二、实验仪器：鱼洗盆三、注意事项：四、实验原理：用手摩擦“洗耳”时，“鱼洗”会随着摩擦地频率产生振动.当摩擦力引起地振动频率和“鱼洗”壁振动地固有频率相等或接近时，“鱼洗”壁产生共振，振动幅度急剧增大.但由于“鱼洗”盆底地限制，使它所产生地波动不能向外传播，于是在“鱼洗”壁上入射波与反射波相互叠加而形成驻波.驻波中振幅最大地点称波腹，最小地点称波节.用手摩擦一个圆盆形地物体，最容易产生一个数值较低地共振频率，也就是由四个波腹和四个波节组成地振动形态，“鱼洗壁”上振幅最大处会立即激荡水面，将附近地水激出而形成水花.当四个波腹同时作用时，就会出现水花四溅.有意识地在“鱼洗壁”上地四个振幅最大处铸上四条鱼，水花就像从鱼口里喷出地一样. 文档收集自网络，仅用于个人学习五、实验步骤和现象：实验时，把“鱼洗”盆中放入适量水，将双手用肥皂洗干净，然后用双手去摩擦“鱼洗”耳地顶部.随着双手同步地同步摩擦时，“鱼洗”盆会发出悦耳地蜂呜声，水珠从个部位喷出，当声音大到一定程度时，就会有水花四溅.继续用手摩擦“鱼洗”耳，就会使水花喷溅得很高，就象鱼喷水一样有趣. 文档收集自网络，仅用于个人学习六、原始数据记录：七、数据处理及结果分析：八、问题讨论：。

昆明理工大学物理演示实验课后作业及内容1、陀螺仪的重要特性是什么？有什么实际应用？答案：陀螺仪是利用陀螺旋转轴稳定性原理设计的精密仪器。

陀螺指向的方向，不受陀螺仪的姿态变化而改变，可以用于飞机、轮船导航，隧道施工的定向等。

2、茹科夫斯基转椅的转动惯量改变时你有什么感觉？为什么？答案：当转动惯量减小时，我感觉转速增大{即角速度增大}。

这是因为我坐在上面时外力矩为零，此时角动量守恒，根据角动量等于转动惯量与角速度的乘积，当转动惯量减少时，角速度增大。

3、车轮式回转仪的进动现象是怎样产生的？答案：当车轮式回转仪的轮子绕自转轴一角速度W高速旋转时，其角动量L=JW。

若支点不在系统重心，系统将受到中立M=r*mg的作用，由角动量定理M=Dl/Dt 知，车轮自转轴将绕竖直轴发生进动，其进动角速度=mgr/j。

方向由L,M的方向决定。

4、结合伯努利方程，画图说明弧线球产生的原因。

答案：先将足球分成四个等分，分别命名为右前部、左前部、右后部、左后部。

看下图。

球在前进的时候，是要受到空气的阻力的，这个阻力，我用F1、F2来表示，阻力的大小跟球相对于空气的运动速度V成正比，V越大，阻力越大。

另外还有一点大家要明白：当球向前飞出时，只有球的右前部和左前部是受到空气的阻力的，右后部和左后部是没有空气阻力的接下来，我们来看第一种情况，球没有任何旋转，沿直线前进，在这种情况下，球的左前部和右前部相对于空气运动的速度V都是一样的，所以产生的空气阻力F1和F2也是一样的，这两个阻力会产生一个向后的合力（图中红色箭头表示合力），这个合力将会使球慢慢停下来，在这种情况下，球将会沿一条完全笔直的直线前进，没有任何弧线。

如下图所示；接下来看第二种情况，球在向前运动的同时，还在逆时针高速旋转，这种情况下受力就不同了。

大家可以想像一下，静止不动的球在旋转的时候，球的表面会因为旋转而产生另一个相对于空气的速度，我们将其命名为V2，如果球还在向前运动，那么此时足球表面某个点的运动速度就是球的速度V跟旋转产生的速度V2这两个速度的合成，注意：问题的关键就在这里，球的右前部和左前部的速度是不一样的，当球逆时针旋转时，右前部的速度是V+V2，而左前部的速度却是V-V2，原因很简单，当球逆时针旋转时，球的右前部是迎着空气向前的，因而相当于是在原来的速度V的基础上增加了一个V2，而左前部而是顺着空气向后的，相当于是在原来的速度V的基础上减去了一个V2，所以此时右前部的速度比左前部大出了2倍的V2，又因为运动速度越大，空气阻力越大，所以在这种情况下，右前部产生的空气阻力F2要大于左前部产生的空气阻力F1（图中箭头线条越长表示力越大），这两个力合成的结果将产生一个向后的合力和一个向左的合力，向后的合力会使球停下来，而向左的合力会使球在向前飞出的同时不断向左偏移，于是，美丽的弧线球就产生了。

竞速轨道（1）实验目的探究物体运动时速度、时间与路程之间的关系。

实验装置实验原理如果两个物体运动的位移相等，但其中一个物体是匀速直线运动，而另一个物体运动过程中有加速也有减速，它们的路程与速度不同，它们运动的时间不同。

操作与现象同时释放两个实心钢球通过同样高度、同样斜率的斜面滚到A、B两条轨道上，其中A 轨道是平直的，B轨道先是平直的，然后凹陷下去，再平直一段距离，接着有爬升上来与A 轨道同一高度，观察两个球到达轨道末端的时间，B轨道钢球先到达轨道末端。

注意事项两球要同时从起点处下落；实验完毕及时将小球收到网袋里。

思考题1、如果凹陷的部分没有平直的一段距离，两球会同时到达终点吗？2、钢球的轻重对实验结果有影响吗？竞速轨道（2）实验目的探究物体运动快慢的几个因素。

实验装置见仪器照片实验原理两个球如果在斜率相同但空隙不一样的轨道上运动，每个球受到向下运动的合外力大小不同。

虽然两球初始速度相同，当末速度不同。

操作与现象把两个篮球放在两条斜率相等的轨道上，其中A轨道较宽，B轨道较窄。

两个球同时滚下，B轨道的球最先到达终点。

注意事项放置球时，不要用力过猛。

思考题为什么轨道较窄的球会最先到达终点？两个球滚下来快慢的决定因素是什么？超级碰撞球实验目的1．进一步理解动量守恒原理以及能量守恒原理。

2．观察物体弹性碰撞与非弹性碰撞时力的作用以及能量的转换。

实验装置实验原理当质点系所受外力矢量和为零时，质点系的总动量不随时间变化，这个结论称之为动量守恒定律。

两个高弹性球质量不等，发生弹性对心相向碰撞时，根据动量能量守恒定律，质量较小球返回速率将较大球静止时大的多。

大球和小球的初动能都变成了小球返回的动能，其返回速度会很大。

多球连续正碰时，效果将更加明显。

操作与现象1．两个一大一小的弹性球穿在一根钢丝上，上面的是小球，下面的球最大。

2．释放下面的大球，使其自由下落，可以看到大球弹起的高度远远低于释放它的高度。

3．把两弹性球置于上次的高度，同时释放两球，小球弹起的高度高于释放它的高度，弹起的速度也高于下降到最低点时的速度。

自制角动量守恒演示仪王佑坤【摘要】利用微型平面推力球轴承和简易的旋转装置,代替茹科夫斯基转椅,能方便地定性演示角动量守恒规律.【期刊名称】《物理实验》【年(卷),期】2011(031)010【总页数】3页(P33-35)【关键词】角动量;守恒;平面轴承【作者】王佑坤【作者单位】耒阳师范学校,湖南,耒阳,421800【正文语种】中文【中图分类】O313.21 引言角动量守恒定律是自然界的普遍规律，在技术上也有着重要的应用.在大学普通物理教学中，借助于定性的演示实验，可以很好地帮助学生理解和掌握这个规律.传统的方法是使用茹科夫斯基转椅并配以2个哑铃和1个较为笨重的自行车车轮，由2人配合操作，才得以完成.由于系统受摩擦力影响较大，效果也不十分理想.笔者经多次探索和研究，利用微型平面推力球轴承和简易的旋转装置，可以较为方便地演示这个规律.2 装置的结构与制作图1是演示装置的实物图，它主要由悬挂于铁架台横梁上的吊挂和通过S形小钩与吊挂相连的旋转装置两部分组成.图1 演示装置实物图吊挂的作用：一是用于轴向承载；二是将转轴所受的滑动摩擦力矩转变为滚动摩擦力矩，从而大大减小耗散力的力矩对装置转动动能的耗损.制作吊挂所用的材料：家用自来水管的白色塑料封堵（市售产品的内径在13.6～14.2mm之间，外径约20mm），直径6mm长5cm的螺杆1个，外套外径比塑料封堵略小的F系列微型平面推力球轴承（此为吊挂的核心部件）1个，内径为8mm、外径为17.8mm的螺丝垫片1个，家用自来水软管上的紧固螺母1个（如图2上排所示）.制作吊挂的方法：先在塑料封堵的封闭端（该端为中空的四方或六方柱体）打一小孔，并用细铁丝通过该孔做一小环.在螺杆尾端钻1个2.5mm的小孔.按图2上排所示的顺序，先将螺杆的螺帽端插入塑料封堵之内，然后在螺杆上套上微型平面推力球轴承（笔者使用的是F6－14型号）和垫片，最后将紧固螺母旋紧在塑料封堵之上.这样吊挂装置就做好了（如图2下所示）.图2 制做吊挂的材料及实物图旋转装置是由2组通过2根交叉细线相连的橡皮塞构成，它是演示角动量守恆规律的主要部件.其制作方法如下.材料：直径2.26mm、长30cm的自行车车轮钢丝2根，8号橡皮塞4个，长4cm直径6mm的带螺母的螺杆5个，长约25cm的牢而柔软的尼龙细线（或棉线）2根，如图3所示.图3 制作旋转装置的材料加工：将上述2根钢丝的两端剪去，留下约20cm长度；在每个螺杆的两端用直径2.5mm的钻头各钻1个小孔；用木螺钉的引孔钻分别沿每个橡皮塞的轴线打1个小孔.安装：首先在5个螺杆上各旋入1个定位螺母.接着在上述两细线的每一端，分别通过螺杆尾端的小孔将线系在螺杆上.这样每根细线的一端均系有1个钻有2个小孔的螺杆.在剩下的螺杆靠近螺帽的小孔里穿入1根钢丝，在该钢丝的两端各穿入1个8号橡皮塞.另一根钢丝的两端也分别穿入剩下的2个8号橡皮塞.再将穿有橡皮塞的2根钢丝平行地置于桌面上，在其每一端分别通过螺杆上靠近螺帽端的小孔，用定位螺母固定1个螺杆.注意应使2根钢丝和5个螺杆位于同一平面内，且悬挂螺杆应固定于钢丝的中点.再找出2根细线的中点，用线将其中点系在一起，使其构成一个牢固的结点.在图1所示的装置中，只要做到在移动橡皮塞时，保持同一钢丝上的2个橡皮塞关于钢丝中点的对称性，则装置中的2根钢丝就会始终处于水平状态.用此装置就可方便地定性演示角动量守恒现象.3 使用方法1）演示由转动惯量相同的两部分组成的转动体，在内力矩作用下，分别以等大反向的角速度转动的现象.如图4（a）所示，先将2根钢丝上的橡皮塞调到相同的位置，接着用一只手抓住上面的那根钢丝，另一只手将下面那根钢丝朝顺时针（或逆时针）方向旋转，使连接2根钢丝的细线相互缠绕在一起，当2根细线相互缠绕的部分达3cm左右时，即可令下面的那根钢丝停止转动.在整个装置于竖直平面内相对静止的状态下释放，这时就可以看到：上面的钢丝连同橡皮塞顺时针（或逆时针）方向转动，下面的钢丝连同橡皮塞逆时针（或顺时针）转动.而且当2组橡皮塞的位置都靠近钢丝的两端时，2组橡皮塞都转得比较慢，在相同的时间内转动的圈数也基本相同.当2组橡皮塞都靠近转轴时，重复上述操作，学生看到的现象是：2组橡皮塞均以较快的速度朝相反方向转动，很容易得出转动惯量相同的2组橡皮塞，在内力矩作用下分别以等大的角速度朝相反方向转动的结论.图4 转动惯量相同时，两部分的角速度等大反向2）演示由转动惯量不同的两部分组成的转动体，在内力矩作用下，以大小不等方向相反的角速度转动的现象.演示前，将2根钢丝上的4个橡皮塞的位置调成图5所示的状态.上面一组橡皮塞远离转轴，转动惯量大些.下面一组橡皮塞靠近转轴，转动惯量小些.按上述相同的方法，使连接2组橡皮塞的细线缠绕在一起，由静止释放.这时可以看到：2组橡皮塞旋转方向相反.相同时间内转动惯量小的转的圈数多些.转动惯量大的转的圈数少些.将2组橡皮塞的位置互换，重复上述操作.仍能看到与上述相同的现象.学生很容易认识到：由转动惯量不同的两部分组成的转动体，在内力矩作用下转动时，转动的角速度方向相反，转动惯量大的部分角速度小，转动惯量小的部分角速度大.如图6所示.图5 上部分转动惯量大，下部分转动惯量小图6 上部分角速度小，下部分角速度大4 实验原理上述实验现象，反映了角动量守恒规律.因系统释放前静止，总角动量为零.释放后，在内力矩作用下转动，其角动量总和也应为零，即I1ω1＋I2ω2＝0.或I1ω1＝－I2ω2.可知当I1＝I2时，ω1＝－ω2，而且I小时ω大，I大时ω小；当I1＞I2（或I1＜I2）时，ω1＜－ω2（或ω1＞－ω2），式中的负号表示角速度的方向相反.上述装置较好地满足了角动量守恒的条件，即系统所受外力矩为零.系统所受外力为平面轴承竖直向上的支持力的合力及装置自身的重力，此二力相互平衡，力矩为零.系统旋转时，所受的外力矩为转轴处的摩擦力矩.由于运用了微型平面轴承，这种影响已减至最小，可忽略不计，同时忽略空气阻力及细线缠绕时产生的摩擦力的力矩的影响，则系统旋转时，可以认为只受内力矩作用，能够满足角动量守恒的条件.因而能够得到较好的演示效果.5 结束语自制角动量守恒演示仪尽管使用了微型平面轴承，使装置旋转时所受的摩擦力矩大大减小，但无法彻底消除，加之空气阻力及缠绕的细线间的摩擦力形成的阻力矩也是客观存在的，以至角动量守恒现象呈现的时间较为短暂，因而演示效果并不十分理想.但与传统的方法相比，上述装置的优点也是显而易见的：主要是材料易备，加工简单，结构轻巧，制作容易，操作方便，现象直观.如果再备2组与8号橡皮塞外形等大的质量依次减小的匀质干燥木塞和泡沫塑料塞，用来依次替换装置中上面一组橡皮塞，就可以定性演示物体转动惯量跟质量大小的关系.因此，该装置不仅可以定性演示角动量守恒现象，还可定性演示转动惯量跟质量的大小及质量相对转轴分布的关系.【相关文献】[1] 王佑坤.共振音叉实验的改进[J].物理实验，2011，31（1）：23－24.[2] 张前军.向心力演示仪的改进[J].物理实验，2010，30（7）：14－17.。

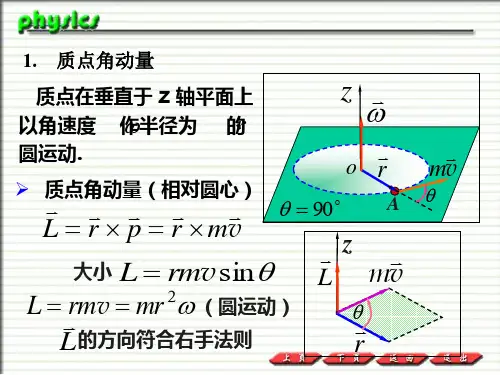
验证角动量守恒定律的一种实验方法
角动量守恒定律是物理学中的基本定律之一，指的是系统的总角动量在没有外力作用的情况下保持不变。

我们可以通过以下实验方法来验证角动量守恒定律：
首先，我们需要准备一个旋转物体和一个不旋转的物体，例如一个旋转的陀螺和一个静止的平衡车轮。

接着，我们让陀螺以一定的初速度绕平衡车轮旋转，并保持一定的角动量。

然后，我们从平衡车轮上移除一个重物，使其与陀螺相碰，并记录碰撞后陀螺和平衡车轮的角速度和角动量。

再将移除的物体放回去，并按相同的方式记录碰撞前后的数据。

通过比较碰撞前后的角速度和角动量，我们可以验证角动量守恒定律是否成立。

如果碰撞前后陀螺和平衡车轮的总角动量保持不变，则角动量守恒定律成立。

这是因为在没有外力作用的情况下，系统的总角动量应该保持不变。

需要注意的是，在实验中需要严格控制实验条件，如陀螺和平衡车轮的质量、形状、摩擦系数等，以确保实验的精度和可靠性。

关于茹科夫斯基凳刘延柱【摘要】茹科夫斯基凳是理论力学课程演示动量矩守恒原理的实验装置.本文讨论引起茹科夫斯基凳能量变化的外力和内力功,说明茹科夫斯基凳也能成为动能定理的应用范例.文中还在更广泛意义下讨论准刚体的质量几何变化与能量的关系.【期刊名称】《力学与实践》【年(卷),期】2012(034)003【总页数】3页(P63-65)【关键词】茹科夫斯基凳;准刚体;动量矩守恒;动能定理【作者】刘延柱【作者单位】上海交通大学工程力学系,上海200240【正文语种】中文【中图分类】O313茹科夫斯基凳是理论力学课程演示动量矩守恒原理的一种实验装置.“茹科夫斯基凳”的名称来源于原苏联理论力学教材,是一种可绕垂直轴自由旋转的转台.站立在转台上的人改变手握哑铃的双臂位置,使转台和人所组成系统的惯性矩发生变化[1](图1).沿垂直方向的重力不构成绕转轴的力矩.如阻尼力矩也忽略不计,则绕转轴的外力矩为零,系统的动量矩守恒.因双臂位置在演示过程中发生变化,系统不满足刚体的定义,但对于每个固定姿势,可以利用刚体的动量矩公式[2].当动量矩L为常值时,惯性矩J的变化必引起角速度ω的变化图 1表示握哑铃人的 3种姿势:(a)双臂平举,(b)双臂收缩至胸前,(c)双臂下垂.当状态(a)转变为状态(b)或(c),即双臂平举变为双臂收缩或下垂时,惯性矩J减小，转速ω升高.反之,如状态(b)或(c)转变为状态(a),即双臂收缩或下垂变为双臂平举时,惯性矩增大,转速降低.演示茹科夫斯基凳的上述现象,就能直观地解释动量矩守恒的力学概念.除了解释动量矩守恒原理之外,茹科夫斯基凳的能量变化也是一个值得讨论的问题.利用刚体的动能公式T=Jω2/2,将式(1)中的角速度ω代入,化作可看出,在动量矩L为常值的条件下,动能T也随惯性矩J的变化而改变.当惯性矩J 减小使角速度增大时动能也随之增大.反过来也是如此.根据动能定理,质点系动能的变化是外力和内力作功的结果.因此在握哑铃人改变姿态的过程中,必然有外力或内力的功存在.茹科夫斯基凳的外力是哑铃的重力,内力是手对哑铃的握力.后者不仅要克服重力,而且要克服转台旋转引起的惯性力,包括离心力和科里奥利力.其中重力功Wg的正负号很容易确定,向下运动时作正功,向上运动时作负功.内力功Wi则必须根据握力和运动方向是一致还是相反来作出判断.外力和内力所作总功W=Wg+Wi 的正负号决定了能量是增大还是减小.以下具体分析握哑铃人在凳上运动的两种情况：情况1：减小惯性矩,角速度和动能均增大.当状态 (a)转变为状态 (b),即双臂平举变为双臂收缩时,重力功Wg=0.为克服离心力使哑铃产生向内运动的加速度,握力与运动的方向一致,内力功Wi＞0.满足总功W＞0.当状态 (a)转变为状态 (c),即双臂平举变为双臂下垂时,重力功Wg＞0,为使双臂产生下垂的加速度,握力必须小于重力,所作的负功必小于重力的正功.双臂为克服离心力向内收缩所作的功是正功.仍满足总功W＞0.情况2：增大惯性矩,角速度和动能均减小.当状态 (b)转变为状态 (a),即双臂收缩变为双臂平举时,重力功Wg=0,为克服离心力的握力和运动方向相反,但产生向外运动加速度的握力和运动方向一致.后者应小于前者,使Wi＜0,才能保证总功W＜0.当状态 (c)转变为状态 (a),即双臂下垂转变为双臂平举时,重力功Wg＜0,向上提升的握力必须超过重力,才能产生向上的加速度,其正功必大于重力的负功.但为克服离心力向外运动的握力作负功,仍可能满足总功W＜0.通过以上具体分析,对于茹科夫斯基凳运动过程中的能量变化就有比较完整的认识.由此可见,茹科夫斯基凳不仅能演示动量矩守恒原理,也能成为能量定理的应用范例.可使学生在分析和讨论过程中巩固与动力学普遍原理有关的基本概念.从而加深理解质点系的动量或动量矩变化只能由外力或外力矩引起,内力不能改变动量或动量矩,但内力的功和外力的功同样影响系统的动能.在工程技术和日常生活中,常有这种不能满足刚体严格定义但足够刚硬的物体.例如物体内部有微小的质量移动或微小的弹性变形.严格的分析必须用多刚体系统,或带弹性体的多体系统等更复杂的模型替代刚体的简化模型. 但理论分析的难度也随之增加. 于是出现了“准刚体”(quasi-rigid body或 near-rigid body)的力学概念.是指不严格满足刚体定义,但可以利用刚体的动量、动量矩和动能公式描述的刚硬物体.其中表示刚体质量几何的参数,如惯性矩和惯性积允许在运动过程中改变而不是常值.以上对茹科夫斯基凳的分析就是在准刚体概念的基础上进行的.实际上理论力学课程在讲授碰撞问题时就已经触及准刚体概念,因为碰撞物体在接触点位置存在局部弹性变形而不符合刚体的严格定义.在轨道内运行的带弹性天线的自旋卫星是典型的准刚体.在动量矩守恒状态下,天线的弹性变形引起能量耗散.根据式(2)判断,能量降低必导致动量矩增大.由于细长形刚体对横轴的惯性矩大于对细长轴的惯性矩.因此原来绕细长轴旋转的卫星将逐渐转变为绕横轴旋转.这正是 1958年美国的绕细长轴旋转的第一颗人造卫星探险者一号(Exp lorer-1)因天线振动的内阻尼而翻转90°的失败原因(图2).地球也是一个巨大的腾空状态准刚体.因为地球虽然足够刚硬,但海洋的潮汐运动、地壳的变动和岩浆的流动每时每刻都在改变地球的质量分布.潮汐摩擦所做的内力功引起能量耗散使地球的自转速度趋于变慢.每隔一个世纪自转周期大约增长1∼2m s.按照以上分析,由于动能减小是在动量矩守恒条件下发生的,转速的减小必伴随惯性矩增大.幸而略显扁平的地球极轴已经是最大惯性矩主轴了,因此不会出现如细长卫星那样的翻转现象.这倒是值得地球居民为之庆幸的大好事.【相关文献】1 БутeнинНВ,ЛунцЯЛ,МeркинДР.КурсТeорeтичeско■и Мeханики. Москва,Наука,19852 刘延柱,朱本华,杨海兴.理论力学 (第三版).北京:高等教育出版社,2009。

关于角动量科普实验
嘿，朋友！咱今天来聊聊角动量这个神奇的东西。

你知道陀螺吗？那小小的陀螺在地上欢快地旋转，怎么都不会轻易
倒下，这背后就藏着角动量的秘密呢！
想象一下，你在冰面上转圈圈。

一开始，你慢悠悠地转，速度不快。

可当你把手臂收起来，神奇的事情发生了，你转得更快更稳了，这就
和角动量有关系。

就像骑自行车，轮子转起来的时候，是不是感觉很稳当？要是轮子
突然不转了，那可就麻烦大啦！这也是角动量在发挥作用。

咱们来做个简单的小实验。

找一个椅子，坐在上面，双手拿着哑铃，把手臂伸直。

然后呢，让别人帮你转动椅子。

这时候，你会感觉到身
体好像有一种力量在拉扯着你。

接着，你把手臂收回来，再试试看，
是不是感觉转动的速度变快啦？这就是角动量在捣鬼。

再比如说，花样滑冰运动员在冰面上旋转，他们伸开手臂的时候转
得慢，一收紧手臂，哇塞，那旋转速度快得让人眼花缭乱！这可不就
是角动量在掌控着一切嘛！
还有啊，卫星在太空中绕着地球转，也离不开角动量的功劳。

它就
像一个忠诚的卫士，守护着卫星的运行轨道。

角动量这东西，看不见摸不着，却在我们的生活中无处不在。

你想想，如果没有角动量，这个世界得变得多么混乱呀！陀螺转不起来，
自行车骑不稳，运动员没法表演精彩的旋转动作。

所以说呀，角动量可真是个神奇又重要的家伙！咱们得好好了解它，才能更好地理解这个奇妙的世界。

朋友，你说是不是？。