2018-2019学年度高中高一寒假作业数学试题：第十天Word版含答案

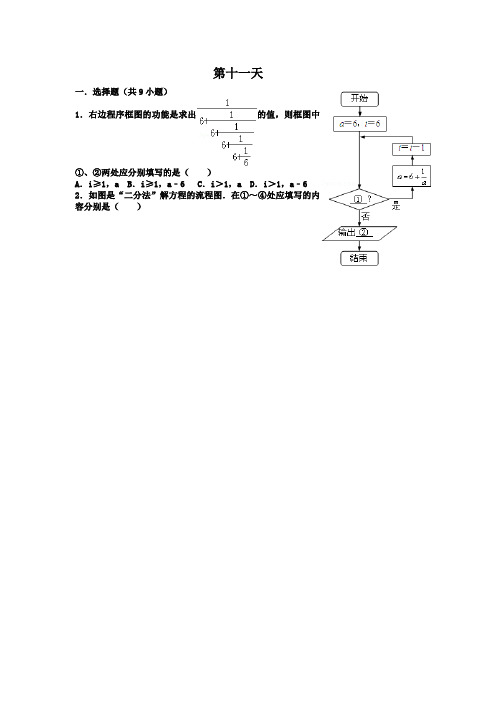
第十一天一．选择题（共9小题）1．右边程序框图的功能是求出的值，则框图中①、②两处应分别填写的是（）A．i≥1，a B．i≥1，a﹣6 C．i＞1，a D．i＞1，a﹣6 2．如图是“二分法”解方程的流程图．在①～④处应填写的内容分别是（）A ．f （a ）f （m ）＜0；a=m ；是；否B ．f （b ）f （m ）＜0；b=m ；是；否C ．f （b ）f （m ）＜0；m=b ；是；否D ．f （b ）f （m ）＜0；b=m ；否；是3．阅读如图所示程序框图，运行相应的程序，则输出的结果是（ ）A ．B ．C ．D ．4．已知实数x ∈[1，9]，执行如图所示流程图，则输出x 不小于55的概率为（ ）A ．B ．C ．D ．第2题图 第3题图第4题图第5题图5．设函数．某程序框图如图所示，若输出的结果S ＞，则判断框中可以填入的关于n 的判断条件是（ ）A ．n ≤2011B ．n ≤2012C ．n ＞2011D ．n ＞20126．在如图的程序框图，如果输入的n=9，那么输出的S=（ ）A ．81B ．53C ．45D ．417．执行如图的程序框图，如果输入p=7，则输出的S=（ ）A ．B ．C ．D ．8．下图程序框图表示的算法的功能是（ ）A ．计算小于100的奇数的连乘积B ．计算从1开始的连续奇数的连乘积C ．从1开始的连续奇数的连乘积，当乘积大于100时，计算奇数的个数D ．计算1×3×5×…×n ≥100时的最小的n 值9.中国古代有计算多项式值的秦九韶算法，如图是实现该算法 的程序框图．执行该程序框图，若输入的x=2，n=2，依次输入的a 为2，2，5，则输出的s=（ ）A ．7B ．12C ．17D ．34 第6题图 第7题图第8题图 第9题图。

高一数学寒假作业（1）集合1、设集合{|,M x R x a =∈≤=则( )A. a M ∉B. a M ∈C. {}a M ∈D. {}a M ∉2、集合{}*|32x N x ∈-<的另一种表示方法是( )A. {}0,1,2,3,4B. {}1,2,3,4C. {}0,1,2,3,4,5D. {}1,2,3,4,53、集合(){}**,|4,,x y x y x N y N +=∈∈用列举法可表示为( )A. {}1,2,3,4B. ()(){}1,3,2,2C. ()(){}3,1,2,2D. ()()(){}1,3,2,2,3,14、已知集合{}1,2,3,4,5A = ,{}(,)|,,B x y x A y A x y A =∈∈-∈,则B 中所含元素的个数为( )A.3B.6C.8D.105、已知全集{}{}|09,|1U x x A x x a =<<=<<,若非空集合A U ⊆,则实数a 的取值范围是( )B. {}|9a a ≤C. {}|19a a <<D. {}|19a a <≤6、已知集合{}2|35,Z A x x x =≤≤∈,则集合A 的真子集的个数为( )A.1B.2C.3D.47、已知集合{}{}2|320,|A x x x B x x a =-+==<,若AB ,则实数a 的取值范围是( )A. 2a ≤B. 2a <C. 2a >D. 2a ≥8、已知全集{}1,2,3,4U =,集合{}{}1,2,2,3A B ==,则()A B ⋃= ( ) A. {}1,3,4B. {}3,4C. {}3D. {}49、已知全集{}0,1,2,3,4,5U =,集合{}0,3,5M =,M ⋂{}0,3=,则满足条件的集合N 共有( )A.4个B.6个C.8个D.16个10、已知集合{}()(){}1,2,3,|120,A B x x x x Z ==+-<∈,则A B ⋃= ( )A. {}1B. {}1,2D. {1,0,1,2,3}-11、已知集合{}|13,{|0A x x B x x =≤≤<或2}x ≥,则A ⋂=__________.12、已知集合{}0,1,3M =,集合{}|3,N x x a a M ==∈,则M N ⋃=__________.13、设集合(){},|27A x y x y =+=,集合(){},|1B x y x y =-=-,则A B ⋂=__________14、已知{}(){}222||40,2110A x x x B x x a x a =+==+++-=.1.若A B B ⋃=,求a 的值.2.若A B B ⋂=,求a 的值.15、已知集合{}{}{}|37,|410,|A x x B x x C x x a =≤<=<≤=<,全集为实数集R.1.求();;R A B C A B ⋃⋂2.若,A C φ⋂≠求a 的取值范围.答案以及解析1答案及解析：答案：B解析：((2224270-=-<,∴,∴a M ∈.2答案及解析：答案：B解析：集合中的元素满足5x <且*x N ∈,所以集合的元素有1,2,3,4.3答案及解析：解析：注意题中所给集合的代表元素为(),x y .4答案及解析：答案：D解析：由x y A -∈,及{}1,2,3,4,5A =得x y >,当1y =时,x 可取2,3,4,5,有4个;当2y =时,x 可取3,4,5,有3个;当3y =时,x 可取4,5,有2个;当4y =时,x 可取5,有1个;故共有123410+++=,故选D.5答案及解析：答案：D解析：由A U ⊆知, A 是U 的子集,∴19a <≤.6答案及解析：答案：C解析：由题意知, 2x =-或2,即{}2,2A =-,故其真子集由3个.7答案及解析：答案：C解析：{}{}2|3201,2A x x x =-+==,要使A B ,只需2a >即可.8答案及解析：解析：因为{}1,2,3A B ⋃=, 所以(){}4A B ⋃=，故选D.9答案及解析：答案：C解析：∵{}0,3,5M =,{}0,3=, ∴∴0,3,5N N N ∉∉∈而全集U 中的1,2,4不能确定,故满足条件的集合N 有328= (个).10答案及解析：答案：C解析：()(){}{}{}|120,Z |12,Z 0,1B x x x x x x x =+-<∈=-<<∈=.又因为{}1,2,3A =,所以{}0,1,2,3A B ⋃=.11答案及解析：答案：{}|12x x ≤<解析：∵{|0B x x =<或2}x ≥. ∴{}|02x x ≤<∴A ⋂{}|12x x =≤<.12答案及解析：答案：{}0,1,3,9解析：{}{}|3,0,3,9N x x a a M ==∈=,所以{}0,1,3,9M N ⋃=.13答案及解析： 答案：58,33⎧⎫⎛⎫⎨⎬ ⎪⎝⎭⎩⎭解析：,x y 同时满足27x y +=和1x y -=-,则,x y 必是方程组271x y x y +=⎧⎨-=-⎩,解得5383x y ⎧=⎪⎪⎨⎪=⎪⎩ ∴58,33A B ⎧⎫⎛⎫⋂=⎨⎬ ⎪⎝⎭⎩⎭.14答案及解析：答案：1. {}4,0A =-若A B B ⋃=,则{}4,0B A ==-,解得1a =2.若A B B ⋂=,则①若B 为空集,则()()224141880a a a ∆=+--=+<,则1a <-;②若B 为单元素集合,则()()224141880a a a ∆=+--=+=,解得1a =-,将1a =-代入方程()222110x a x a +++-=,得20x =,得0x =,即{}0B =,符合要求;③若{}4,0B A ==-,则1a =.综上所述, 1a ≤-或1a =.解析：15答案及解析：答案：1.因为集合{}{}|37,|410,A x x B x x =≤<=<≤所以{}{}{}|37|410|310;?A B A x x x x x x ⋃==≤<⋃<≤=≤≤{|3R C A x x =<或7},x ≥则(){|3R C A B x x ⋂=<或{}{}7}|410|710.x x x x x ≥⋂<≤=≤≤2.由{}{}|37,|A x x C x x a =≤<=<又,A C φ⋂≠所以3a >.所以满足A C φ⋂≠的a 的取值范围是()3,.+∞解析：高一数学寒假作业（2）函数及其表示1、函数21y x =-的定义域是()[],12,5-∞⋃,则其值域是( )A. ()1,1,22⎡⎤-∞⋃⎢⎥⎣⎦B. (),2-∞C. [)1,2,2⎛⎫-∞⋃+∞ ⎪⎝⎭D. ()0,+∞2、已知函数()f x =.则m 的取值范围是()A. (]0,4B. (]0,1C. [)4,+∞D. []0,43、若()2212f x x x +=-,则()2f 的值为( )A. 34-B. 34C. 0D. 14、函数()2f x =的定义域是( ) A. 1,13⎡⎤-⎢⎥⎣⎦ B. 1,13⎛⎫- ⎪⎝⎭ C. 11,33⎛⎫- ⎪⎝⎭ D. 1,3⎛⎫-∞- ⎪⎝⎭5、函数228156x x y x x -+=--的值域是( )A. (),1-∞B. ()(),11,-∞⋃+∞C. 22,,55⎛⎫⎛⎫-∞-⋃-+∞ ⎪ ⎪⎝⎭⎝⎭ D. ()22,,11,55⎛⎫⎛⎫-∞-⋃-⋃+∞ ⎪ ⎪⎝⎭⎝⎭6下列函数中,与表示同一个函数的是() A. B. C. D.7、已知函数()f x 是一次函数,且()()()()22315,2011f f f f -=--=,则()f x =( )A. 32x +B. 32x -C. 23x +D. 23x -8、设,f g 都是由A 到B 的映射,其对应法则如下表:表1 映射f 的对应法则表2 映射g 的对应法则则()()()()()()()1,2,3f g f f f g f 的值分别为( )A. 3,3,3B. 3,1,2C. 3,3,2D.以上都不对9已知,则( )A.B.C. D.10、向高为H 的水瓶中注水,注满为止,如果注水量V 与水深h 的函数关系的图象如图所示,那么水瓶的形状可以是()A. B. C. D.11、若函数()()()()2210102232x x f x x x x +-<<⎧⎪⎪=-≤<⎨⎪⎪≥⎩,则()f x 的值域是__________.12、若()()()f a b f a f b +=⋅且()1?2f =,则()()()()()()232012...122011f f f f f f +++=__________.13、已知函数()f x 的定义域为()1,0?-,则函数()21f x +的定义域为__________.14、已知函数()214f x x x =+-. 1.若函数()f x 的定义域为[]0,3时,求()f x 的值域;2.当函数()f x 的定义域为[,1]a a +时, ()f x 的值域为11,216⎡⎤-⎢⎥⎣⎦,求a 的值.15、已知函数()3f x +的定义域是[2,4]-,求函数()23f x +的定义域.答案以及解析1答案及解析：答案：A解析：函数21y x =-的图像是由反比例函数2y x=的图像向右平移1个单位得到的,根据图像可得答案.2答案及解析：答案：D解析：由题意得, 210mx mx ++≥对一切实数恒成立.①当0m =时,不等式变为10≥.对一切实数恒成立,符合题意;②当0m ≠时,应有20,0440m m m m >⎧⇒<≤⎨∆=-≤⎩. 综上知04m ≤≤.3答案及解析：答案：A解析：令212x +=,得12x =, ∴()211322224f ⎛⎫=-⨯=- ⎪⎝⎭.4答案及解析：答案：B 解析：1101,,1131033x x x x x <⎧->⎧⎪⇒⇒-<<⎨⎨+>>-⎩⎪⎩5答案及解析：答案：D 解析：∵()()()()()2235815536322x x x x x y x x x x x x ---+-===≠---++, ∴1y ≠且25y ≠-.6答案及解析：答案： D解析： 的定义域为, 与的定义域不同,故A 不正确.与的对应关系不同,故B 不正确.的定义域为,与的定义域不同,故C 不正确.的定义域为, 与表示同一个函数,故D 正确.7答案及解析：答案：B解析：()()0f x kx b k =+≠∵()()()()22315,011f f f f -=--=,∴5{1k b k b -=+= ∴3{2k b ==- ∴()32f x x =-8答案及解析：答案：A解析：()()()()()()123,233f g f g f g ====,()()()()()()3123f g f f g f ===.故选A .9答案及解析：答案： B解析： 令, 则, 故, 即.10答案及解析：答案：B解析：若水平形状是圆柱,则2π,V r h r =不变,V 是h 的正比例函数,其图象应该是过原点的直线,与已知不符.由题图可以看出,随着高度h 的增加, V 也增加,但随h 的不断变大,每增加相同的量,体积V 的增加量变小,图象上升趋势变缓,其原因只能是瓶子平行于地面的截面的半径由底到顶逐渐变小.11答案及解析：答案：(){}1,23-⋃解析：当10x -<<时, ()()220,2f x x =+∈;当02x ≤<时, ()(]11,02f x x =-∈-;当2x ≥时, ()3f x =.故函数()f x 的值域为(){}1,23-⋃.12答案及解析：答案：4022解析：令1b =,则有()()()11f a f a f +=,∴()()()112f a f f a +==,∴()()()()()()2320122,2,...,2,122011f f f f f f ===∴()()()()()()2320122,2,...,201124022122011f f f f f f ===⨯=.13答案及解析： 答案：11,2⎛⎫-- ⎪⎝⎭解析：由1210x -<+<,得112x -<<-,所以函数()21f x +的定义域为11,2⎛⎫-- ⎪⎝⎭.14答案及解析：答案：1.∵()21122f x x ⎛⎫=+- ⎪⎝⎭,∴函数()f x 的图像的对称轴为直线12x =-.∴()f x 的值域为()()0,3f f ⎡⎤⎣⎦,即147,44⎡⎤-⎢⎥⎣⎦.2.∵()min 12f x =-∴[]1,12x a a =-∈+, ∴131212212a a a ⎧≤-⎪⎪⇒-≤≤-⎨⎪+≥-⎪⎩∵区间[,1]a a +的中点为012x a =+ ①当1122a +≥-,即112a -≤≤-时,有()()max 1116f x f a =+=,即()()21111416a a +++-=, 解得34a =-或94a =- (舍去). ②当1122a +<-,即312a -≤<-时,有()()max 116f x f a ==. 即211416a a +-=,解得54a =-或14a = (舍去).综上,知34a =-或54a =-.解析：15答案及解析：答案：已知函数()3f x +的定义域是[2,4]-,所以137x ≤+≤.在函数()23f x +中, 12x ≤≤,1237x ≤+≤解得12x -≤≤所以函数()23f x +的定义域为{}|12x x -≤≤.解析：高一数学寒假作业（3）函数的基本性质1、函数()31f x x x =--+有( )A.最大值4,最小值0B.最大值0,最小值-4C.最大值4,最小值-4D.最大值、最小值都不存在 2函数在上的最大值为( ) A. B.C.D.3、函数()245f x x x =-+在区间[]0,m 上的最大值为5,最小值为1,则m 的取值范围是( )A. [)2,+∞B. []2,4C. (,2]-∞D. []0,24、若2()2f x x ax =-+与()1a g x x =+在区间[1,2]上都是减函数,则a 的取值范围是( )A. (1,0)(0,1)-⋃B. ()(]1,00,1-⋃C. (0,1)D. (0,1]5、已知()f x 是定义在()0,+∞上的单调递增函数,若()()2f x f x >-,则x 的取值范围是( )A. ()1,+∞B. (),1-∞C. ()0,2D. ()1,26、如果()f x 是定义在R 上的奇函数,那么下列函数中,一定为偶函数的是( )A. ()y x f x =+B. ()y xf x =C. ()2y x f x =+ D. ()2y x f x = 7、函数1()f x x x=-的图像关于( ) A. y 轴对称 B.直线y x =-对称C.原点对称D.直线y x =对称8、已知()()|2|,f x g x x ==-则下列结论正确的是( )A. ()()()h x f x g x =+是偶函数B. ()()()h x f x g x =⋅是奇函数C. ()()()2f x g x h x x⋅=-是偶函数 D. ()()2()f x h x g x =-是偶函数 9、函数()f x 的定义域为,R 且满足()f x 时偶函数, (1)f x -是奇函数,若(0.5)9,f =则(8.5)f =( )A. 9-B. 9C. 3-D. 010、下列图象表示的函数具有奇偶性的是( )A.B.C. D.11、设函数()f x 在()0.2上是增函数,函数(2)f x +是偶函数,则57(1),(),()22f f f 的大小关系是__________.12、已知函数()f x 为奇函数,函数(1)f x +为偶函数, (1)1,f =则(3)f =__________.13、已知函数()[]1,1,31x f x x x -=∈+,则函数()f x 的最大值为__________,最小值为__________.14、已知函数()1f x x x=+. 1.判断()f x 在区间(]0,1和[)1,+∞上的单调性;2.求()f x 在1,52x ⎡⎤∈⎢⎥⎣⎦时的值域. 15、设函数1()f x x a x=++为定义在(,0)(0,)-∞⋃+∞上的奇函数. 1.求实数a 的值; 2.判断函数()f x 在区间()1,a ++∞上的单调性,并用定义法证明.答案以及解析1答案及解析：答案：C解析：()()()()43|3||1|221341x f x x x x x x -≥⎧⎪=--+=--≤<⎨⎪<-⎩.2答案及解析：答案： A解析： ∵, ∴ ∴函数图像的开口向下,且对称轴为轴 ∴在上,单调递减,故当时,取得最大值,最大值为9.3答案及解析：答案：B解析：二次函数()245f x x x =-+图像的对称轴为直线2x =, 且当2x =时, ()1f x =.∵当0x =时, ()5f x =∴根据二次函数图像的对称性和函数的单调性可知,满足题意的m 的取值范围为24m ≤≤.4答案及解析：答案：D解析：()()2222x ax x a a f x =-+=--+,当1a ≤时, ()f x 在区间[]1,2上是减函数, ()11g x x =+,当0a >时, ()g x 在区间[]1,2上是减函数,故a 的取值范围是01a <≤.5答案及解析：答案：D解析：由题意知210012202x xx x x x x x >->⎧⎧⎪⎪>⇒>⇒<<⎨⎨⎪⎪-><⎩⎩.6答案及解析：答案：B解析：因为()f x 是奇函数，()().f x f x ∴-=-对于A,令(),y f x =则()()()(),g x x f x x f x g x -=-+-=--=- ()y x f x ∴=+是奇函数。

第九天
一．选择题
1．已知函数f（x）=，则f（f（2））的值为（）
A．﹣ B．﹣3 C．D．3
2．设函数，则的值是（）
A．2 B．﹣2 C．D．
3．若函数f（x）满足：当x＜1时，f（x）=（）x；当x≥1时，f（x+1）=﹣f（x），则f（2017+log23）=（）A．B．C．D．
4．已知函数f（x）=，若f（f（m））≥0，则实数m的取值范围是（）A．[﹣2，2] B．[﹣2，2]∪[4，+∞）C．[﹣2，2+] D．[﹣2，2+]∪[4，+∞）5．已知函数（n＜m）的值域是[﹣1，1]，有下列结论：
①当n=0时，m∈（0，2]；
②当时，；
③当时，m∈[1，2]；
④当时，m∈（n，2]；
其中结论正确的所有的序号是（）A．①②B．③④ C．②③ D．②④
6．已知定义在R上的奇函数f（x）满足当x≥0时，f（x）=，
则关于x的函数y=f（x）﹣a，（﹣1＜a＜0）的所有零点之和为（）
A．2a﹣1 B．2﹣a﹣1 C．1﹣2﹣a D．1﹣2a
7．设函数y=f（x）在R上有定义，对于任一给定的正数p，定义函数f p（x）=，
则称函数f p（x）为f（x）的“p界函数”若给定函数f（x）=x2﹣2x﹣1，p=2，则下列结论不成立的是（）
A．f p[f（0）]=f[f p（0）] B．f p[f（1）]=f[f p（1）]
C．f p[f p（2）]=f[f（2）] D．f p[f（3）]=f[f（3）]
8．已知函数f（x）=的图象上有且仅有四个不同的点关于直线y=﹣1的
对称点在y=kx﹣1的图象上，则实数k的取值范围是（）
A． B．C． D．。

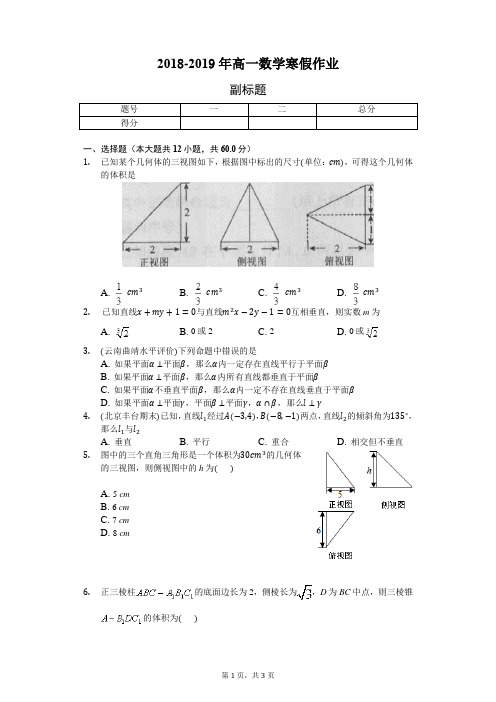
2018-2019年高一数学寒假作业副标题一、选择题（本大题共12小题，共60.0分）1.已知某个几何体的三视图如下，根据图中标出的尺寸单位：，可得这个几何体的体积是A. B. C. D.2.已知直线与直线互相垂直，则实数m为A. B. 0或2 C. 2 D. 0或3.云南曲靖水平评价下列命题中错误的是A. 如果平面平面，那么内一定存在直线平行于平面B. 如果平面平面，那么内所有直线都垂直于平面C. 如果平面不垂直平面，那么内一定不存在直线垂直于平面D. 如果平面平面，平面平面，，那么4.北京丰台期末已知，直线经过，两点，直线的倾斜角为，那么与A. 垂直B. 平行C. 重合D. 相交但不垂直5.图中的三个直角三角形是一个体积为的几何体的三视图，则侧视图中的h为A. 5 cmB. 6 cmC. 7 cmD. 8 cm6.正三棱柱的底面边长为2，侧棱长为，D为BC中点，则三棱锥的体积为A. 3B.C. 1D.7.一个正方体被一个平面截去一部分后，剩余部分的三视图如下图，则截去部分体积与剩余部分体积的比值为A.B.C.D.8.下列命题中正确的个数是若直线l上有无数个点不在平面内，则l．若直线l与平面平行，则l与平面内的任意一条直线都平行．如果两条平行直线中的一条与一个平面平行，那么另一条也与这个平面平行．若直线l与平面平行，则l与平面内的任意一条直线都没有公共点．A. 0B. 1C. 2D. 39.一个长方体的各顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为1，2，3，则此球的表面积为A. B.C. D.10.已知正方体，则直线与平面ABCD所成的角是A. B. C. D.11.已知直线在平面外，则A.B. 直线与平面至少有一个公共点C.D. 直线与平面至多有一个公共点12.若点到直线的距离是，则实数a为．A. B. 5 C. 或5 D. 或3二、填空题（本大题共1小题，共5.0分）13.长、宽、高分别为3，4，5的长方体，沿相邻面对角线截取一个三棱锥如图，剩下几何体的体积为。

2019年高中寒假作业数学参考答案2019年高中寒假作业数学参考答案
【】为大家带来2019年高中寒假作业数学参考答案，希望大家喜欢下文!
一、选择
1~5 AAACA 6~10 DCABB
(10)提示：即
在上单增，即恒成立，也就是恒成立，，故选B
二、填空
(11) (12) (13) (14) (15)
(15)提示：补充，用掉1个奇数，用掉2个奇数，依此类推，用掉m个奇数，而135是第68个奇数，则且，
三、解答
(16)解：(Ⅰ) ，，
，或 (舍)
(Ⅱ)由(Ⅰ)得，二项式系数最大项为第六项，则，(17)解：(Ⅰ)偶数个数有
(Ⅱ)被5整除的四位数有
(18)解：(Ⅰ)红球个数为
分布列为
0 1 2 3
(19)解：(Ⅰ) ，猜想
证明：①当时，，猜想成立;
②假设当时猜想成立，即
那么，，所以当时猜想也成立
由①②可知猜想对任意都成立，即
(Ⅱ)证明：即证
由均值不等式知：，则
(20)解：(Ⅰ) ，当时，
当时，，单增;当时，，单减;当时，，单增(Ⅱ)即，而在上的最大值为，，即在上恒成立，
∵ ，，恒成立
令，则，
，即在上单调递增，
(21)解：(Ⅰ)当时，，由题知，，于是，在上单减，在上单增，
又，在上的图象大致为
有两个零点即直线与函数的图象有两个交点，由图知，(Ⅱ) ，的方程为，，在点处的切线方程为，即为
由题可得，则
令，则，在上单增，在上单减
考生们只要加油努力，就一定会有一片蓝天在等着大家。

以
上就是的编辑为大家准备的2019年高中寒假作业数学参考答案。

1．设U ＝Z,A ＝{1,3,5,7, 9},B ＝{1,2,3,4,5},则图中阴影部分表示的集合是()A ．{1,3,5}B ．{1,2,3,4,5}C ．{7,9}D ．{2,4}2．已知全集U ＝{1,2,3,4,5},集合A ＝{x |x 2－3x ＋2＝0},B ＝{x |x ＝2a ,a ∈A },则集合∁U (A ∪B )中元素的个数为( ) A ．1 B ．2C ．3D ．43、f (x )满足对任意的实数a ,b 都有f (a ＋b )＝f (a )·f (b )且f (1)＝2,则f f＋f f＋f f＋…＋f f＝( ) A ．1006 B ．2014 C ．2012 D ．10074．已知集合A ＝{x |x ≤1},B ＝{x |x ≥a },且A ∪B ＝R,则实数a 的取值范围是________． 5、设U ＝{n |n 是小于9的正整数},A ＝{n ∈U |n 是奇数},B ＝{n ∈U |n 是3的倍数},则∁U (A ∪B )＝________、6、 若函数f (x )＝(x ＋a )(bx ＋2a )(常数a ,b ∈R)是偶函数,且它的值域为(－∞,4],则该函数的解析式f (x )＝________、7．设全集U ＝{2,3,x 2＋2x －3},A ＝{5},∁U A ＝(2,y ),求x ,y 的值．8．设全集为R,集合A＝{x|a≤x≤a＋3},∁R B＝{x|－1≤x≤5}．(1)若A∩B＝∅,求a的取值范围；(2)若A∩B＝A,求a的取值范围．(1)求当x<0时,f(x)的解析式；(2)作出函数f(x)的图象,并指出其单调区间．__________寒假作业（2）答案1、解析 图中阴影部分表示的集合是(∁U A )∩B ＝{2,4}．答案 D2、解析A ＝{1,2},B ＝{x |x ＝2a ,a ∈A }＝{2,4},∴A ∪B ＝{1,2,4},∴∁U (A ∪B )＝{3,5},故选B 、3、解析 因为对任意的实数a ,b 都有f (a ＋b )＝f (a )·f (b )且f (1)＝2,由f (2)＝f (1)·f (1),得f f＝f (1)＝2,由f (4)＝f (3)·f (1),得f f＝f (1)＝2,……由f (2014)＝f (2013)·f (1),得f f＝f (1)＝2,∴f f ＋f f＋f f＋…＋f f＝1007×2＝2014、答案 B4、解析 如图,要使A ∪B ＝R,只要a 不大于1,∴a ≤1、答案 a ≤15、解析 依题意得,U ＝{1,2,3,4,5,6,7,8},A ＝{1,3,5,7},B ＝{3,6}．∴A ∪B ＝{1,3,5,6,7}∴∁U (A ∪B )＝{2,4,8}．答案 {2,4,8}6、解析 f (x )＝(x ＋a )(bx ＋2a )＝bx 2＋(2a ＋ab )x ＋2a 2为偶函数,则2a ＋ab ＝0,∴a ＝0,或b ＝－2、又f (x )的值域为(－∞,4],∴a ≠0,b ＝－2,∴2a 2＝4、∴f (x )＝－2x 2＋4、答案 －2x 2＋47、解 ∵A ⊆U ,∴5∈U 、∴x 2＋2x －3＝5,即x 2＋2x －8＝0,解得x ＝－4,或x ＝2、∴U ＝{2, 3,5},∵∁U A ＝{2,y },∴y ∈U ,且y ∉A ,∴y ＝2,或y ＝3、由∁U A 中元素的互异性知,y ≠2,∴y ＝3、综上知,x ＝－4或x ＝2,y ＝3、 8、解 ∵全集为R,∁R B ＝{x |－1≤x ≤5},∴B ＝{x |x ＜－1,或x ＞5}．(1)若A ∩B ＝∅,则⎩⎪⎨⎪⎧a ≥－1，a ＋3≤5，∴－1≤a ≤2、(2)若A ∩B ＝A ,则A ⊆B ,结合数轴得a ＋3＜－1,或a ＞5,即a ＜－4,或a ＞5、 9、解 (1)当x <0时,－x >0,∴f (－x )＝(－x )2－2(－x )＝x 2＋2x 、又f (x )是定义在R 上的偶函数,∴f (－x )＝f (x )．∴当x <0时,f (x )＝x 2＋2x 、(2)由(1)知,f (x )＝⎩⎪⎨⎪⎧x 2－2xx ，x 2＋2x x作出f (x )的图象如图所示：由图得函数f(x)的递减区间是(－∞,－1],．f(x)的递增区间是,[1,＋∞)．。

河北省武邑中学2021-2021学年高一数学上学期寒假作业31．〔5分〕函数f(x)的图象是连续不断的，有如下x，f(x)的对应值表:,x123456f(x)1510－76－4－5那么函数f(x)在区间【1,6】上的零点至少有()A．2个B．3个C．4个D．5个12．〔5分〕函数f(x)＝log2x－x的零点所在区间为()A.0，1．1，1 2B2C．(1,2)D．(2,3)3．〔5分〕f(x)＝3ax＋1－2a，设在(－1,1)上存在x使f(x)00＝0，那么a的取值范围是()11A．－1<a<5B．a>51C．a>5或a<－1D．a<－14．〔5分〕把长为12cm的细铁丝截成两段，各自围成一个正三角形，那么这两个正三角形面积之和的最小值是________．5．〔5分〕假设函数f(x)＝ax＋b(a≠0)有一个零点是2，那么函数g(x)＝bx2－ax的零点是______．6．〔5分〕假设函数f(x)＝a x－x－a(a>0，且a≠1)有两个零点，那么实数a的取值范围是______．7．〔12分〕当a为何值时，函数y＝7x2－(a＋13)x＋a2－a－2的一个零点在区间(0,1)上，另一个零点在区间(1,2)上？8．〔12分〕某公司试销一种新产品，规定试销时销售单价不低于本钱单价500元/件，又不高于800元/件．经试销调查发现，销售量y(件)与销售单价x(元/件)近似满足一次函数y＝kx＋b的关系(图象如图所示)．根据图象，求一次函数y＝kx＋b的表达式；设公司获得的毛利润(毛利润＝销售总价－本钱总价)为S元，求该公司可获得的最大毛利润，并求出此时相应的销售单价．9．〔12分〕函数f(x)＝x2－3x－10的两个零点为x1，x2(x1<x2)，设A＝{x|x≤x1，或x≥x2}，B＝{x|2m－1<x<3m＋2}，且A∩B＝?，求实数m的取值范围．(1)10．〔12分〕设函数f(x)＝ax2＋(b－8)x－a－ab的两个零点分别是(2)－3和2.(3)求f(x)；当函数f(x)的定义域是【0,1】时，求函数f(x)的值域．11．〔12分〕某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t，P)，点(t，P)落在图中的两条线段上；该股票在30天内的日交易量(万股)与时间t (天)的局部数据如下表所示:,Q第t天4101622Q(万股)36302418根据提供的图象，写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式；根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关1.系式；2.用y表示该股票日交易额(万元)，写出y关于t的函数关系式，并求在这30天中第几天日交易额最大，最大值是多少？3.4.5.6.7.8.9.10.11.12.2021-2021学年高一寒假作业第3期答案解析:,根据函数零点存在性定理可判断至少有3个零点．答案:,B1 23 11解析:,因f (2)＝log 22－2＝1－2＝2>0，f (1)＝log 21－1＝－1<0，故f (x )的零点在区间(1,2)内．应选C. 答案:,C解析:,∵f (x )是x 的一次函数， 1f (－1)·f (1)<0?a >5或a <－1. 答案:,C解析:,设一个正三角形的边长为x ，12－3那么另一个正三角形的边长为x＝4－x ，33 2 3232两个正三角形的面积和为S ＝4x ＋4(4－x ) ＝2 【(x －2)＋4】(0＜x ＜4)．当x ＝2时，S min ＝23(cm 2)．答案:,2 3cm 2解析:,由2a ＋b ＝0，得b ＝－2a ，g (x )＝bx 2－ax ＝－2ax 2－ax ，令()＝0，得x ＝0或x1 ＝－，gx221∴g (x )＝bx －ax 的零点为0，－2.1答案:,0，－2解析:,函数f (x )的零点的个数就是函数y ＝a x 与函数y ＝x ＋a 的图象的交点的个数，如下列图，a >1时，两函数图象有两个交点，0<a <1时，两函数图象有唯一交点，故a>1.答案:,(1，＋∞)解:,函数对应的方程为7x2－(a＋13)x＋a2－a－2＝0，函数的大致图象如下图．根据方程的根与函数的零点的关系，方程的根一个在(0,1)上，另一个在(1,2)上，a2－a－2＞0，f(0)0那么:,f(1)0，即a2－2a－8＜0，f(2)0a2－3a＞0，a＜－1或a＞2，解得－2＜a＜4，a＜0或a＞3，∴－2＜a＜－1或3＜a＜4.8.解:,(1)由图可知所求函数图象过点(600,400)，(700,300)，400＝k×600＋b k＝－1得，解得，300＝k×700＋b b＝1000所以y＝－x＋1000(500≤x≤800)．由(1)可知S＝xy－500y＝(－x＋1000)(x－500)＝－x2＋1500x－500000＝－(x－750)2＋62500(500≤x≤800)，故当x＝750时，S max＝62500.即销售单件为750元/件时，该公司可获得最大毛利润为625009.元．10.解:,A＝{x|x≤－2，或x≥5}．要使A∩B＝?，必有2m－1≥－2，3m＋2≤5，或3m＋2≤2m－1，3m＋2>2m－1，1m≥－2，或m≤－3，解得m≤1，m>－3，1即－2≤m≤1，或m≤－3.所以m的取值范围为m－1≤m≤1或m≤－3. 210.解:,(1)∵f(x)的两个零点是－3和2，∴函数图象过点(－3,0)、(2,0)．∴有9a－3(b－8)－a－ab＝0，①4a＋2(b－8)－a－ab＝0，②①－②得b＝a＋8.③2③代入②得4a＋2a－a－a(a＋8)＝0，即a＋3a＝0.∴f(x)＝－3x2－3x＋18.(2)由(1)得f(x)＝－3x2－3x＋18123＝－3x＋＋＋18，1图象的对称轴方程是x＝－2.又0≤x≤1，f min(x)＝f(1)＝12，f max(x)＝f(0)＝18.∴函数f(x)的值域是【12,18】．解:,(1)由图象知，前20天满足的是递增的直线方程，且过两点(0,2)，(20,6)，1容易求得直线方程为P＝5t＋2；从20天到 30天满足递减的直线方程，且过两点(20,6)，(30,5)，1求得方程为P＝－10t＋8，故P(元)与时间t(天)所满足的函数关系式为:,15t＋2，0≤t≤20，t∈N，P＝1－10t＋8，20＜t≤30，t∈N.(2)由图表，易知Q与t满足一次函数关系，即Q＝－t＋40,0≤t≤30，t∈N.(3)由以上两问，可知河北省武邑中学20182019学年高一数学上学期寒假作业(含答案)31t＋2－＋，≤≤，∈N5t0t20ty＝1－10t＋8－t＋，20＜t≤30，t∈N－1t－2＋125，0≤t≤20，t∈N，＝51t－2－40，20＜t≤30，t∈N.10当0≤t≤20，t＝15时，y max＝125，当20≤t≤30，y随t的增大而减小．∴在30天中的第15天，日交易额的最大值为125万元．。

2018年高一数学寒假作业（人教A 版必修1）集合A 组 基础达标(建议用时：30分钟)一、选择题1．(2016·全国卷Ⅱ)已知集合A ＝{1,2,3}，B ＝{x |x 2＜9}，则A ∩B ＝( )A ．{－2，－1,0,1,2,3}B ．{－2，－1,0,1,2}C ．{1,2,3}D ．{1,2}2．(2015·全国卷Ⅱ)已知集合A ＝{1,2,3}，B ＝{2,3}，则( )A ．A ＝BB ．A ∩B ＝∅C ．A BD ．B A 3．(2017·潍坊模拟)已知集合A ＝{x |x 2－3x ＋2＝0，x ∈R}，B ＝{x |0＜x ＜5，x ∈N}，则满足条件A ⊆C ⊆B的集合C 的个数为( )A ．1B ．2C ．3D ．4 4．(2016·山东高考)设集合A ＝{y |y ＝2x ，x ∈R}，B ＝{x |x 2－1<0}，则A ∪B ＝( )A ．(－1,1)B ．(0,1)C ．(－1，＋∞)D ．(0，＋∞)5．(2017·衡水模拟)已知全集U ＝{1,2,3,4,5,6,7,8}，集合A ＝{2,3,5,6}，集合B ＝{1,3,4,6,7}， 则集合A ∩∁U B ＝( )A ．{2,5}B ．{3,6}C ．{2,5,6}D ．{2,3,5,6,8}6．若x ∈A ，则1x ∈A ，就称A 是伙伴关系集合，集合M ＝⎩⎨⎧⎭⎬⎫－1，0，12，2，3的所有非空子集中具有伙伴关系的集合的个数是( )A ．1B ．3C ．7D ．317．已知全集U ＝R ，A ＝{x |x ≤0}，B ＝{x |x ≥1}，则集合∁U (A ∪B )＝( )A ．{x |x ≥0}B ．{x |x ≤1}C ．{x |0≤x ≤1}D ．{x |0<x <1}二、填空题8．已知A ＝{0，m,2}，B ＝{x |x 4－4x 2＝0}，若A ＝B ，则m ＝________.9．(2016·天津高考)已知集合A＝{1,2,3,4}，B＝{y|y＝3x－2，x∈A}，则A∩B＝________.10．集合A＝{x|x＜0}，B＝{x|y＝lg[x(x＋1)]}，若A－B＝{x|x∈A，且x∉B}，则A－B＝________.B组能力提升(建议用时：15分钟)1．(2016·全国卷Ⅲ改编)设集合S＝{x|(x－2)(x－3)≥0}，T＝{x|x＞0}，则(∁R S)∩T＝( ) A．[2,3] B．(－∞，－2]∪[3，＋∞)C．(2,3) D．(0，＋∞)2．(2017·郑州调研)设全集U＝R，A＝{x|x2－2x≤0}，B＝{y|y＝cos x，x∈R}，则图1­1­2中阴影部分表示的区间是( )图1­1­2 A．[0,1]B．(－∞，－1]∪[2，＋∞)C．[－1,2]D．(－∞，－1)∪(2，＋∞)3．已知集合A＝{x|4≤2x≤16}，B＝[a，b]，若A⊆B，则实数a－b的取值范围是________.4．设集合A＝{x|x2－x－6＜0}，B＝{x|x－a≥0}．若存在实数a，使得A∩B＝{x|0≤x＜3}，则A∪B＝________.2018年高一数学寒假作业（人教A版必修1）集合答案A组基础达标(建议用时：30分钟)一、选择题1．(2016·全国卷Ⅱ)已知集合A＝{1,2,3}，B＝{x|x2＜9}，则A∩B＝( )A．{－2，－1,0,1,2,3} B．{－2，－1,0,1,2}C．{1,2,3} D．{1,2}D [∵x2＜9，∴－3＜x＜3，∴B＝{x|－3＜x＜3}．又A＝{1,2,3}，∴A∩B＝{1,2,3}∩{x|－3＜x＜3}＝{1,2}．]2．(2015·全国卷Ⅱ)已知集合A＝{1,2,3}，B＝{2,3}，则( )A．A＝B B．A∩B＝∅C．A B D．B AD [∵A＝{1,2,3}，B＝{2,3}，∴2,3∈A且2,3∈B,1∈A但1∉B，∴B A.]3．(2017·潍坊模拟)已知集合A＝{x|x2－3x＋2＝0，x∈R}，B＝{x|0＜x＜5，x∈N}，则满足条件A⊆C⊆B 的集合C的个数为( ) 【导学号：31222002】A．1 B．2C．3 D．4D [由x2－3x＋2＝0，得x＝1或x＝2，∴A＝{1,2}．由题意知B＝{1,2,3,4}，∴满足条件的C可为{1,2}，{1,2,3}，{1,2,4}，{1,2,3,4}，共4个．] 4．(2016·山东高考)设集合A＝{y|y＝2x，x∈R}，B＝{x|x2－1<0}，则A∪B＝( )A．(－1,1) B．(0,1)C．(－1，＋∞)D．(0，＋∞)C [由已知得A＝{y|y>0}，B＝{x|－1<x<1}，则A∪B＝{x|x>－1}．]5．(2017·衡水模拟)已知全集U＝{1,2,3,4,5,6,7,8}，集合A＝{2,3,5,6}，集合B＝{1,3,4,6,7}，则集合A∩∁U B＝( )A．{2,5} B．{3,6}C．{2,5,6} D．{2,3,5,6,8}A [由题意得∁U B＝{2,5,8}，∴A∩∁U B＝{2,3,5,6}∩{2,5,8}＝{2,5}．]6．若x ∈A ，则1x ∈A ，就称A 是伙伴关系集合，集合M ＝⎩⎨⎧⎭⎬⎫－1，0，12，2，3的所有非空子集中具有伙伴关系的集合的个数是( ) 【导学号：31222003】A ．1B ．3C ．7D ．31B [具有伙伴关系的元素组是－1，12，2，所以具有伙伴关系的集合有3个：{－1}，⎩⎨⎧⎭⎬⎫12，2，⎩⎨⎧⎭⎬⎫－1，12，2.] 7．已知全集U ＝R ，A ＝{x |x ≤0}，B ＝{x |x ≥1}，则集合∁U (A ∪B )＝( )A ．{x |x ≥0}B ．{x |x ≤1}C ．{x |0≤x ≤1}D ．{x |0<x <1}D [∵A ＝{x |x ≤0}，B ＝{x |x ≥1}，∴A ∪B ＝{x |x ≤0或x ≥1}，在数轴上表示如图，∴∁U (A ∪B )＝{x |0＜x ＜1}．]二、填空题8．已知A ＝{0，m,2}，B ＝{x |x 4－4x 2＝0}，若A ＝B ，则m ＝________.－2 [由题知B ＝{0，－2,2}，A ＝{0，m,2}，若A ＝B ，则m ＝－2.]9．(2016·天津高考)已知集合A ＝{1,2,3,4}，B ＝{y |y ＝3x －2，x ∈A }，则A ∩B ＝________. {1,4} [因为集合B 中，x ∈A ，所以当x ＝1时，y ＝3－2＝1；当x ＝2时，y ＝3×2－2＝4；当x ＝3时，y ＝3×3－2＝7；当x ＝4时，y ＝3×4－2＝10.即B ＝{1,4,7,10}．又因为A ＝{1,2,3,4}，所以A ∩B ＝{1,4}．]10．集合A ＝{x |x ＜0}，B ＝{x |y ＝lg[x (x ＋1)]}，若A －B ＝{x |x ∈A ，且x ∉B }，则A －B ＝________.[－1,0) [由x (x ＋1)＞0，得x ＜－1或x ＞0，∴B ＝(－∞，－1)∪(0，＋∞)，∴A －B ＝[－1,0)．]B 组 能力提升(建议用时：15分钟)1．(2016·全国卷Ⅲ改编)设集合S ＝{x |(x －2)(x －3)≥0}，T ＝{x |x ＞0}，则(∁R S )∩T ＝( )A ．[2,3]B ．(－∞，－2]∪[3，＋∞)C ．(2,3)D ．(0，＋∞) C [易知S ＝(－∞，2]∪[3，＋∞)，∴∁R S ＝(2,3)．∴(∁R S )∩T ＝(2,3)．]2．(2017·郑州调研)设全集U ＝R ，A ＝{x |x 2－2x ≤0}，B ＝{y |y ＝cos x ，x ∈R}，则图1­1­2中阴影部分表示的区间是( )图1­1­2A．[0,1]B．(－∞，－1]∪[2，＋∞)C．[－1,2]D．(－∞，－1)∪(2，＋∞)D [A＝{x|x2－2x≤0}＝[0,2]，B＝{y|y＝cos x，x∈R}＝[－1,1]．图中阴影部分表示∁U(A∪B)＝(－∞，－1)∪(2，＋∞)．]3．已知集合A＝{x|4≤2x≤16}，B＝[a，b]，若A⊆B，则实数a－b的取值范围是________. 【导学号：31222004】(－∞，－2] [由4≤2x≤16，得2≤x≤4，则A＝[2,4]，又B＝[a，b]，且A⊆B.∴a≤2，b≥4，故a－b≤2－4＝－2.因此a－b的取值范围是(－∞，－2]．]4．设集合A＝{x|x2－x－6＜0}，B＝{x|x－a≥0}．若存在实数a，使得A∩B＝{x|0≤x＜3}，则A∪B ＝________.{x|x＞－2} [A＝{x|－2＜x＜3}，B＝{x|x≥a}．如图，由A∩B＝{x|0≤x＜3}，得a＝0，A∪B＝{x|x＞－2}．]。

2019高一数学寒假作业参考答案以下是由查字典数学网为您整理提供的2019高一数学寒假作业参考答案，希望能够对您有所帮助，欢迎阅读与借鉴。

参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12答案 D D D A D D B C A C B C13. ; 14. 4 ; 15. 0.4; 16. ②③17.(1)∵A中有两个元素，关于的方程有两个不等的实数根，，且，即所求的范围是，且 ;6分(2)当时，方程为，集合A= ;当时，若关于的方程有两个相等的实数根，则A也只有一个元素，此时 ;若关于的方程没有实数根，则A没有元素，此时，综合知此时所求的范围是，或 .13分18 解：(1) ，得(2) ，得此时，所以方向相反19.解:⑴由题义整理得 ,解方程得即的不动点为-1和2. 6分⑵由 = 得如此方程有两解,则有△=把看作是关于的二次函数,则有解得即为所求. 12分20.解： (1)常数m=14分(2)当k0时，直线y=k与函数的图象无交点,即方程无解; 当k=0或k 1时, 直线y=k与函数的图象有唯一的交点，所以方程有一解;当0所以方程有两解.12分21.解：(1)设，有， 2取，则有是奇函数 4(2)设，则，由条件得在R上是减函数，在[-3，3]上也是减函数。

6当x=-3时有最大值 ;当x=3时有最小值，由，，当x=-3时有最大值6;当x=3时有最小值-6. 8(3)由，是奇函数原不等式就是 10由(2)知在[-2，2]上是减函数原不等式的解集是 1222.解：(1)由数据表知，(3)由于船的吃水深度为7米，船底与海底的距离不少于4.5米，故在船航行时水深米，令，得 .解得 .取，则 ;取，则 .故该船在1点到5点，或13点到17点能安全进出港口，而船舶要在一天之内在港口停留时间最长，就应从凌晨1点进港，下午17点离港，在港内停留的时间最长为16小时.2019高一数学寒假作业参考答案就分享到这里了，更多高一数学寒假作业尽在查字典数学网高中频道！。