自动控制原理胡寿松 第8章

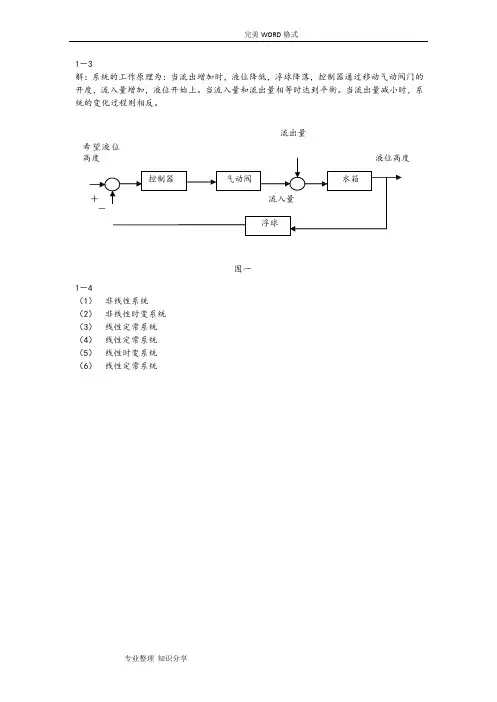
1－3解：系统的工作原理为：当流出增加时，液位降低，浮球降落，控制器通过移动气动阀门的开度，流入量增加，液位开始上。

当流入量和流出量相等时达到平衡。

当流出量减小时，系统的变化过程则相反。

流出量希望液位图一1－4（1）非线性系统（2）非线性时变系统（3）线性定常系统（4）线性定常系统（5）线性时变系统（6）线性定常系统2 2-1 解：显然，弹簧力为 kx (t ) ，根据牛顿第二运动定律有：F (t ) − kx (t ) = m移项整理，得机械系统的微分方程为：d 2x (t ) dt 2m d x (t ) + kx (t )= F (t ) dt2对上述方程中各项求拉氏变换得：ms 2 X (s ) + kX (s ) =F (s )所以，机械系统的传递函数为：G (s ) = X (s ) =F (s )1ms 2+k2-2 解一：由图易得：i 1 (t )R 1 = u 1 (t ) − u 2 (t ) u c (t ) + i 1 (t )R 2 = u 2 (t ) du c (t )i 1 (t )= Cdt 由上述方程组可得无源网络的运动方程为：C ( R + R ) du 2 (t ) u (t ) = CRdu 1 (t ) u (t )1 2 dt+ 22 + 1 dt 对上述方程中各项求拉氏变换得：C (R 1 + R 2 )sU 2 (s ) + U 2 (s ) = CR 2 sU 1 (s ) + U 1 (s )所以，无源网络的传递函数为：G (s ) = U 2 (s ) =U 1 (s )1 + sCR 21 + sC (R 1 +R 2 ) 解二（运算阻抗法或复阻抗法）：U (s ) 1 + R 2 1 + R Cs2 = Cs =2U (s ) R + 1 + R 1 + ( R + R )Cs 1 1 21Cs22-5 解：按照上述方程的顺序，从输出量开始绘制系统的结构图，其绘制结果如下图所示：依次消掉上述方程中的中间变量 X 1 , X 2 , X 3 , 可得系统传递函数为：C (s ) = R (s )G 1 (s )G 2 (s )G 3 (s )G 4(s )1 + G2 (s )G3 (s )G 6 (s ) + G 3 (s )G4 (s )G5 (s ) + G 1 (s )G 2 (s )G 3 (s )G 4(s )[G 7 (s ) − G 8 (s )]2-6 解：①将G1 (s) 与G1 (s) 组成的并联环节和G1 (s) 与G1 (s) 组成的并联环节简化，它们的等效传递函数和简化结构图为：G 12 (s) = G1(s) + G2(s)G 34 (s) = G3(s) −G4(s)②将G12 (s), G34 (s) 组成的反馈回路简化便求得系统的闭环传递函数为：2-7 解：C(s)=R(s)G12(s)1 + G12(s)G34(s)=G1(s) + G2(s)1 +[G1(s) + G2(s)][G3(s) −G4(s)]由上图可列方程组：[E(s)G1 (s) −C(s)H2(s)]G2(s) = C(s)R(s) −H1(s)C(s)G2(s)= E(s)联列上述两个方程，消掉E (s) ，得传递函数为：C(s)= R(s)G1(s)G2(s)1 + H1(s)G1(s) + H2(s)G2(s)联列上述两个方程，消掉C (s) ，得传递函数为：E(s)= R(s)1 + H2(s)G2(s)1 + H1(s)G1(s) + H2(s)G2(s)1 22 23 2-8 解：将①反馈回路简化，其等效传递函数和简化图为： 0.4G (s ) =2s + 1 =1 +0.4 * 0.5 2s + 15+ 3将②反馈回路简化，其等效传递函数和简化图为：1 G (s ) = s + 0.3s + 1 = 5s + 3 21 + 0.4 5s + 4.5s + 5.9s + 3.4(s + 0.3s + 1)(5s + 3)将③反馈回路简化便求得系统的闭环传递函数为：0.7 * (5s +3)Θo (s)= 5s 3 + 4.5s 2 + 5.9s + 3.4=3.5s + 2.1Θi (s) 1 +0.7 * Ks(5s +3)5s3+ (4.5 +3.5K )s 2+ (5.9 + 2.1K )s +3.42 5s3-3 解：该二阶系统的最大超调量：σp =e−ζπ/1−ζ2*100%当σp= 5% 时，可解上述方程得：ζ=0.69当σp= 5% 时，该二阶系统的过渡时间为：ts≈3ζwn所以，该二阶系统的无阻尼自振角频率w n 3-4 解：≈3ζts=30.69*2= 2.17由上图可得系统的传递函数：10 * (1 + Ks)C (s)= R(s)s(s + 2)1 +10 * (1 +Ks)s(s + 2)==10 * (Ks +1)s + 2 * (1 +5K )s +10所以w n =10 ，ζwn=1 +5K⑴若ζ= 0.5 时，K ≈0.116所以K ≈0.116时，ζ= 0.5⑵系统单位阶跃响应的超调量和过渡过程时间分别为：σ p = e−ζπ / 1−ζ2*100% = e−0.5*3.14 /1−0.52*100% ≈ 16.3%t s =3 ζw n= 3 0.5 *≈ 1.910⑶ 加入 (1 + Ks ) 相当于加入了一个比例微分环节，将使系统的阻尼比增大，可以有效地减小原系统的阶跃响应的超调量；同时由于微分的作用，使系统阶跃响应的速度（即变w 212p化率）提高了，从而缩短了过渡时间：总之，加入 (1 + Ks ) 后，系统响应性能得到改善。

胡寿松自动控制原理
1胡寿松自动控制原理
胡寿松自动控制原理是指一种将仪表测量仿真到自动控制仿真的理论。

这一原理最初是由中国科学家胡寿松于1963年提出的。

当时通用电器正开发其第一台自动控制产品，因此胡寿松提出了一种将仪表测量仿真到自动控制仿真的理论。

胡寿松自动控制原理的研究在控制系统研究，仿真，设计和分析中扮演了一个重要的角色。

胡寿松自动控制原理从仪表自动控制仪表来判断，从而解决了仪表控制过程中测量数据无法被准确精确转化为控制仿真的问题，使自动控制仪表变得更为稳定可靠，实现了实际的自动控制技术的发展。

胡寿松自动控制原理的理论体系包括：信息依赖机制图，胡寿松模型、状态方程、胡寿松参数、输入输出解析布局、系统方程等。

胡寿松模型可以用来定义系统中任意元素之间的固定关系，胡寿松参数可以用来描述任意元素的动态特性，而系统方程可以用来描述影响系统的其他因素，该理论的图解形式可用于实验室中的调试和使用模拟仪器时的研究。

胡寿松自动控制原理的研究和应用已广泛应用于工业和开放的系统的实践，包括机械，电子，汽车，飞行器，船舶，航空，暖通，能源，运输，医疗，以及其他服务领域。

胡寿松自动控制原理不仅能够给系统带来稳定性和准确性，还可以使计算机科学，电子学，计算机
技术，以及嵌入式微处理器等各领域的设计更方便和精准，实现与实际应用的关联，从而发挥自动控制技术的最大潜力。

自动控制原理课后答案1 请解释下列名字术语：自动控制系统、受控对象、扰动、给定值、参考输入、反馈。

解：自动控制系统：能够实现自动控制任务的系统，由控制装置与被控对象组成；受控对象：要求实现自动控制的机器、设备或生产过程扰动：扰动是一种对系统的输出产生不利影响的信号。

如果扰动产生在系统内部称为内扰；扰动产生在系统外部，则称为外扰。

外扰是系统的输入量。

给定值：受控对象的物理量在控制系统中应保持的期望值参考输入即为给定值。

反馈：将系统的输出量馈送到参考输入端，并与参考输入进行比较的过程。

2 请说明自动控制系统的基本组成部分。

解：作为一个完整的控制系统，应该由如下几个部分组成：①被控对象：所谓被控对象就是整个控制系统的控制对象；②执行部件：根据所接收到的相关信号，使得被控对象产生相应的动作；常用的执行元件有阀、电动机、液压马达等。

③给定元件：给定元件的职能就是给出与期望的被控量相对应的系统输入量（即参考量）；④比较元件：把测量元件检测到的被控量的实际值与给定元件给出的参考值进行比较，求出它们之间的偏差。

常用的比较元件有差动放大器、机械差动装置和电桥等。

⑤测量反馈元件：该元部件的职能就是测量被控制的物理量，如果这个物理量是非电量，一般需要将其转换成为电量。

常用的测量元部件有测速发电机、热电偶、各种传感器等；⑥放大元件：将比较元件给出的偏差进行放大，用来推动执行元件去控制被控对象。

如电压偏差信号，可用电子管、晶体管、集成电路、晶闸管等组成的电压放大器和功率放大级加以放大。

⑦校正元件：亦称补偿元件，它是结构或参数便于调整的元件，用串联或反馈的方式连接在系统中，用以改善系统的性能。

常用的校正元件有电阻、电容组成的无源或有源网络，它们与原系统串联或与原系统构成一个内反馈系统。

3 请说出什么是反馈控制系统，开环控制系统和闭环控制系统各有什么优缺点？解：反馈控制系统即闭环控制系统，在一个控制系统，将系统的输出量通过某测量机构对其进行实时测量，并将该测量值与输入量进行比较，形成一个反馈通道，从而形成一个封闭的控制系统；开环系统优点：结构简单，缺点：控制的精度较差；闭环控制系统优点：控制精度高，缺点：结构复杂、设计分析麻烦，制造成本高。

第六版前言第一章自动控制的一般概念1-1 自动控制的基本原理与方式1-2 自动控制系统示例1-3 自动控制系统的分类1-4 对自动控制系统的基本要求1-5 自动控制系统的分析与设计工具习题第二章控制系统的数学模型2-1 控制系统的时域数学模型2-2 控制系统的复数域数学模型2-3 控制系统的结构图与信号流图2-4 控制系统建模实例习题第三章线性系统的时域分析法3-1 系统时间响应的性能指标3-2 一阶系统的时域分析3-3 二阶系统的时域分析3-4 高阶系统的时域分析3-5 线性系统的稳定性分析3-6 线性系统的稳态误差计算3-7 控制系统时域设计习题第四章线性系统的根轨迹法4-1 根轨迹法的基本概念4-2 根轨迹绘制的基本法则4-3 广义根轨迹4-4 系统性能的分析4-5 控制系统复域设计习题第五章线性系统的频域分析法5-1 频率特性5-2 典型环节与开环系统的频率特性5-3 频率域稳定判据5-4 稳定裕度5-5 闭环系统的频域性能指标5-6 控制系统频域设计习题第六章线性系统的校正方法6-1 系统的设计与校正问题6-2 常用校正装置及其特性6-3 串联校正6-4 前馈校正6-5 复合校正6-6 控制系统校正设计习题第七章线性离散系统的分析与校正7-1 离散系统的基本概念7-2 信号的采样与保持7-3 z变换理论7-4 离散系统的数学模型7-5 离散系统的稳定性与稳态误差7-6 离散系统的动态性能分析7-7 离散系统的数字校正7-8 离散控制系统设计习题第八章非线性控制系统分析8-1 非线性控制系统概述8-2 常见非线性特性及其对系统运动的影响8-3 相平面法8-4 描述函数法8-5 非线性控制的逆系统方法8-6 非线性控制系统设计习题第九章线性系统的状态空间分析与综合9-1 线性系统的状态空间描述9-2 线性系统的可控性与可观测性9-3 线性定常系统的反馈结构及状态观测器9-4 李雅普诺夫稳定性分析9-5 控制系统状态空间设计习题第十章动态系统的最优控制方法10-1 最优控制的一般概念10-2 最优控制中的变分法10-3 极小值原理及其应用10-4 线性二次型问题的最优控制10-5 控制系统优化设计。