一元函数积分学(定积分概念性质)

一元函数积分学总结引言积分是微积分学中的重要概念之一，它与微分一样具有重要的应用价值。

一元函数积分学是微积分学的核心内容之一，其研究对象是一元函数的积分与求解。

本文将总结一元函数积分学的基本概念、性质、计算方法以及应用，旨在帮助读者更好地理解和应用一元函数的积分学知识。

一元函数积分的基本概念一元函数积分的基本概念包括不定积分和定积分。

不定积分是指对一元函数进行积分，得到的结果是一个与变量x相关的函数表达式。

定积分是指对一元函数在一个区间内进行积分，得到的结果是一个数值。

不定积分的性质不定积分具有线性性、和式性、常数倍性等性质。

这些性质使得我们可以利用不定积分的基本公式进行积分运算。

此外，不定积分还具有相应的积分表，包括多种函数的不定积分表和常见函数的不定积分表。

定积分的性质定积分具有线性性、和式性、常数倍性等性质。

这些性质使得我们可以通过分割区间，将定积分转化为多个小区间上的定积分，从而进行计算。

定积分还具有保号性、中值定理等重要性质，这些性质在实际应用中起到了重要的作用。

一元函数积分的计算方法一元函数积分的计算方法主要包括换元积分法、分部积分法、有理函数积分法等。

这些方法可以根据具体的积分问题选择合适的方法进行计算，从而简化计算过程。

换元积分法换元积分法是一种通过引入新的变量来进行积分的方法。

通过选择合适的换元公式，可以将原积分化简为简单的标准积分形式，从而进行计算。

分部积分法分部积分法是一种通过对被积函数进行分部积分来进行积分的方法。

通过选择合适的分配律，可以将原积分转化为两个函数的乘积的积分形式，从而进行计算。

有理函数积分法有理函数积分法是一种通过将有理函数进行部分分式分解来进行积分的方法。

通过分解成简单的分式形式，可以利用不定积分的基本公式进行计算。

有理函数积分法适用于有理函数的积分，可以将复杂的积分问题化简为简单的有理函数积分。

一元函数积分的应用一元函数积分在物理学、工程学、经济学等领域具有广泛的应用。

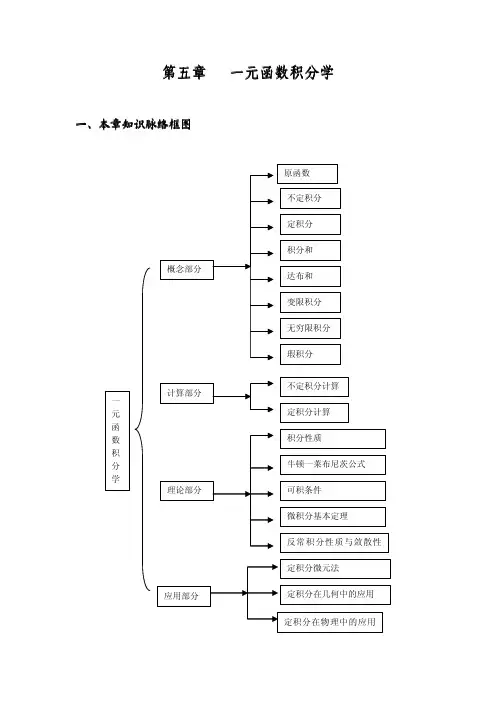
第五章一元函数积分学5.1 原函数和不定积分的概念一、原函数与不定积分的概念定义：如果在区间I内，存在可导函数F（x）使都有F＇（x）=f（x）或dF（x）=f（x）dx，那么函数F（x）就称为f（x）在区间I内原函数。

例：，sinx是cosx的原函数。

Lnx是在区间（0，+∞）内的原函数。

原函数存在定理：如果函数f（x）在区间I内连续，那么在区间I内存在可导函数F（x），使，都有F＇（x）=f（x）。

简言之：连续函数一定有原函数。

问题：（1）原函数是否唯一？（2）若不唯一它们之间有什么联系？例：（sinx）＇=cosx （sinx+C）＇=cosx（C为任意常数）关于原函数的说明：（1）若F＇（x）=f（x），则对于任意常数C，F（x）+C都是f（x）的原函数。

（2）若F（x）和G（x）都是f（x）的原函数，则F（x）-G（x）=C（C为任意常数）证∵[F（x）-G（x）] ＇=F＇（x）-G＇（x）=f（x）=f（x）=0∴F（x）-G（x）=C（C为任意常数）不定积分的定义：函数f（x）的全体原函数的集合称f（x）的不定积分，记为∫f（x）dx。

,其中∫为“积分号”，f（x）为被积函数，f（x）dx为被积表达式，C为任意常数。

例：求。

【答疑编号11050101】解：例：求。

【答疑编号11050102】解：积分曲线例设曲线通过点（1，2），且其上任一点处的切线斜率等于这点横坐标的两倍，求此曲线方程。

【答疑编号11050103】解：设曲线方程为y=f（x）,根据题意知即f（x）是2x的一个原函数。

由曲线通过点（1，2）所求曲线方程为y =x2+1。

函数f（x）的原函数的图形称为f（x）的积分曲线。

显然，求不定积分得到一积分曲线族。

不定积分的性质结论：微分运算与求不定积分的运算是互逆的。

5.2 基本积分公式实例启示能否根据求导公式得出积分公式？结论既然积分运算和微分运算是互逆的，因此可以根据求导公式得出积分公式。

一元函数积分学（1）（第十一周周三）题型•定积分概念（定积分求极限）•定积分性质及其应用（比较定积分大小，估计积分值）•变限定积分函数求导•变限积分函数极限•定积分表示变量的极限•分段求定积分•求解含定积分符号的函数方程•定积分等式与定积分不等式证明3定积分定义求极限其中极限与分点x i 的取法及x i 的取法无关.当函数f (x )在[a , b ]上连续时, 有可用于求某些通项为和式数列的极限，根据积分合式确定被积函数和积分区间→==∑⎰01()d lim ()n b i i a i f x x f x λx ()→∞=--+=∑⎰1lim ()d .n b n a i b a b a f a i f x x n n12lim 1cos 1cos 1cos n n n n n n πππ→+∞++++++11011211cos 1cos 1cos 1cos 1lim 1cos 1cos(n i n n i n i n n nn n n i x dx n nππππππ=→∞=++++++=++=+∑∑⎰()→∞=--+=∑⎰1lim ()d .n b n a i b a b a f a i f x x n n求极限).21(lim 22222nn n n n n n n ++++++∞→ 原式n n 1lim ∞→=∑=+n i ni 12)(11x x d 11102⎰+=4π=()→∞=--+=∑⎰1lim ()d .n b n a i b a b a f a i f x x n n将数列适当放大和缩小，以简化成积分和：11sin k n n k k n π=<<+∑已知11012lim sin sin d ,n n k k x x n n πππ→∞=⋅==∑⎰利用夹逼准则可知2.I π=∑=⋅+n k nn k n n 11sin 1π∑=⋅nk n n k 11sin π11lim =+∞→n n n 求()→∞=--+=∑⎰1lim ()d .n b n a i b a b a f a i f x x n n关于定积分重要性质保号性：()0,f x ≥则有()d 0.ba f x x ≥⎰若f (x )在[a ,b ]上连续, ()0,f x ≥且()0,[,]f x x a b ≡∈/则()d 0.b a f x x >⎰若f (x )在[a , b ]上连续, ≥()0,f x =⎰()d 0,b a f x x 且则()0.f x ≡积分中值定理：若f (x )在[a , b ]上连续, 则至少存在一点(,),a b x ∈使得()d ()().ba f x xb a f x =-⎰第一积分中值定理：若函数f (x ), g (x )在[a , b ]上连续, g (x )在[a , b ]上不变号,则在(a , b )内至少存在一点x , 使=⎰⎰()()d ()()d .b b a af xg x x f g x x x 估值定理：若f (x )在[a , b ]上连续，≤≤(),m f x M -≤≤-⎰()()d ()b am b a f x x M b a令,)(x e x f x-=]0,2[-∈x ,0)(>x f ,0)(02>-∴⎰-dx x e x dx e x ⎰-∴02,02dx x ⎰->于是dx e x ⎰-20.20dx x ⎰-<比较积分值dx e x ⎰-20和dx x ⎰-20的大小.比较定积分大小（积分区间相同，比较函数大小）比较定积分大小（积分区间不同）2222202220cos cos x x x x e dx e dx e xdx e xdx ππππππ---->>⎰⎰⎰⎰22222()2()200cos cos ()cos x u x u x e xdx e u dx e xdx ππππππππ--+-+=-=+=⎰⎰⎰设函数f (x )在[0, 1]上连续, 且单调减少, 试证对任意(0,1),a ∈有≥⎰⎰100()d ()d .a f x x a f x x 证明1：-⎰⎰100()d ()d a f x x a f x x =-⎰⎰00()d ()d a a f x x a f x x -⎰1()d aa f x x=-⎰0(1)()d a a f x x -⎰1()d aa f x x (0,),a α∈(1)()a af α=-(1)()a af β--(,1)a β∈()(1)()()a a f f αβ=--0.≥1100011000()()()01,01()()()()()aa f x dx x at a f at dt a f ax dx a x ax x f ax f x a f x dx a f ax dx f x dx ⇒=⇒=<<<<⇒<⇒≥≤=⎰⎰⎰⎰⎰⎰证明2：12222200sin cos d d .11x x x x x x ππ<++⎰⎰-+⎰220cos sin d 1x x x x π-=+⎰420cos sin d 1x x x x π-++⎰224cos sin d 1x x x x ππ=-+-++⎰⎰42220411(cos sin )d (cos sin )d 11x x x x x x πππx η0=--≥++2211(21)()011x η,sin 31)(3xx f +=],,0[π∈∀x ,1sin 03≤≤x ,31sin 31413≤+≤x ,31sin 31410030dx dx xdx ⎰⎰⎰πππ≤+≤.3sin 31403π≤+≤π∴⎰πdx x 估计积分dx x ⎰π+03sin 31的值. 估计积分值大小证明证:令则令得故变限积分求导2(1)2()sin ,(2)x x x f t dt t f π+==⎰22((1))(23)2(2)cos f x x x x f x xππ++-=15(2)2(2)(2)3x f f f ππ=⇒-=-⇒=-()''()(())(())()(())()g x h x d f t dt f g x g x f h x h x dx =-⎰sin '0()(sin )(),()xF x x t f t dt F x =-⎰求sin 'sin sin 00sin 0()(sin ()())(sin ())()cos ()x x x xd F x xf t tf t dt dx d d x f t tf t dt dx dx x f t dt=-=-=⎰⎰⎰⎰20cos()x d x t dt dx -=⎰2211211x x d x dt dx x t x x -+=++++⎰1x t u+=解：提示：2解：先求定积分，再求导4030sin lim xdt t x x ⎰→求极限00解：此极限为型414sin lim 330==→x x x 原式变限积分函数极限（洛必达，积分中值，等价无穷小）200cos lim x x t dt x →⎰0|sin |limx x t dt x →+∞⎰(1)00|sin ||sin |sin 2,(1)k kt dt t dt tdt x n n x n ππππππ+===∀∃≤<+⎰⎰⎰(1)000(1)0000|sin ||sin |sin |sin |2,sin 2(1)|sin |22(1)(1)|sin |2lim n x n n n x x x t dt t dt tdt t dt n tdt n t dt n n n x n t dt x πππππππ++→+∞≤<==++≤<+=⎰⎰⎰⎰⎰⎰⎰周期性.lim 222dx e x n n x n ⎰+-∞→计算)2(lim lim 22222n n e dx e x n n x n -+=-∞→+-∞→⎰x x x 22lim 2x x x e ∞→=.0=定积分表示变量的极限.01lim 10=+⎰∞→dx x x nn 证明,10n nx xx ≤+≤ dx x dx x x n n ⎰⎰≤+≤∴101010,11+=n ,011lim =+∞→n n 且.01lim 10=+⎰∞→dx x x nn 由夹逼准则可知注意:x x +=+∞→∞→⎰1lim 1lim 10nn n n dx x x (01)x ≤≤.0=错误，可用第一积分中值定理=⎰⎰()()d ()()d .bba a f x g x x f g x x x分段求定积分（含有max,min,取整符号，绝对值，被积函数含参变量）10()|()|F x t t x dt =-⎰101010()()3211()()23x x F x t t x dt x x F x t t x dt ≤⇒=-=-≥⇒=--=-⎰⎰10201()()()11323x x x F x t t x dt t t x dt x x <<⇒=--+-=-+⎰⎰=+⎰21()()1()()设连续，，求f x f x x f x dx f x 求解含定积分符号的函数方程212211()()1()(1)3122()12a f x dx f x ax f x dx ax dx a a a f x x=⇒=+⇒=+⇒=+⇒=-⇒=-⎰⎰⎰令已知函数f (x )满足方程=-⎰120()3()d ,f x x f x x 试求f (x ).解令=⎰120()d ,f x x a 则()f x =-3.x a ⎰120()d f x x a =()=-⎰1203d x a x ()=+-⎰122096d x a ax x =-+233,a a ⇒-+=2430,a a 3a ⇒=或=1,a 故=-()33f x x 或=-()31f x x定积分等式与定积分不等式证明(1) 变上限积分;(2) 积分中值定理;(3) 微分中值定理;(4) 常用不等式（柯西-施瓦茨不等式）;(5) 利用Taylor公式;(6) 利用闭区间上连续函数性质.1证明恒等式证:令则因此,)0()(2π<<=x C x f 又4π=故所证等式成立.试证使分析:要证即⎰xaxxg d)(⎰-x a xxf d)(故作辅助函数至少存在一点证明: 令⎰⎰⎰⎰-=ba x ab a x a x x g x x f x x f x x g x F d )(d )(d )(d )()(在上连续,在至少使即0d )()(d )()(=-⎰⎰b a ba x x g f x x f g x x 因在上连续且不为0 ,从而不变号,因此故所证等式成立.故由罗尔定理知,存在一点7设解法1:设且试证:t t f x F x a d )()(⎰=⎰x a t f t )(d 则=')(x F )(2a x --⎰⎢⎣⎡=x a )(t f )(t f t d 2⎥⎦⎤-t t f x f t f x f x a d )()()]()([2⎰-=故F (x ) 单调不减,即②成立.②⎰x a t t f d )(⎰x at f t )(d 2)(a x --8设函数f (x )在[0, 1]上是非负、单调减的连续函数,且0 < a < b < 1, 求证≥⎰⎰0()d ()d .a b a a f x x f x x b ⎰0()d af x x ⎰()d ba f x x 1()f a x =2()()fb a x =-1(0,)a x ∈2(,)ab x ∈(),f a a ≥()()f a b a ≤-(),bf a ≤⎰0()d af x x ()f a a ≥≥⎰()d .ba a f x xb 证明由积分中值定理, 得设f 在[0, π]上连续, 在(0, π)内内可导, 且==⎰⎰00()cos d ()sin d 0,f x x x f x x x ππ证明: 存在(0,),x π∈使得()0.f x '=证明因为在(0, π)内, sin x 0,>又=⎰0()sin d 0,f x x x π故f (x )在(0, π)内必有零点α .若在(0, π)内, f (x )恒正, 则>⎰0()sin d 0;f x x x π若在(0, π)内, f (x )恒负, 则<⎰0()sin d 0;f x x x π零点不唯一：若(0,)απ∈是f (x )的唯一零点, 则,(0,),x x απ≠∈f (x )在x = α的两侧异号. 于是sin()()x f x α-必恒正或恒负，从而-≠⎰0sin()()d 0.x f x x πα39-≠⎰0sin()()d 0.x f x x πα-⎰0sin()()d x f x x πα0()(sin cos f x x πα=⎰-cos sin )d x xα=⎰0cos ()sin d f x x x πα-⎰0sin ()cos d f x x x πα0=与上式矛盾.故f (x )在(0, π)内零点不惟一,Rolle 定理：在(0,),x π∈使得()0.f x '='11,[]()[](){(1)(2)...([])}aa x f x dx a f a f f f a >=-+++⎰证明：1'201[0,1],()()0,()()3x f x f x f x dx f ∈<≤⎰二阶可导，证明：222()[,]()cos ()sin [()]b b b a a a f x a b f x kxdx f x kxdx f x dx ∀+≤⎰⎰⎰在连续且非负,证明：k,满足：[][]sin 2'0()(),()xF x f tx dt F x =⎰222sin 2011()()x x u tx dt du xF x f u du x =⇒==⎰提示：考虑X=0？).2212(lim 12121n n n n n n n n n ++++++∞→()''()(())(())()(())()g x h x d f t dt f g x g x f h x h x dx =-⎰=-⎰()d ()().b af x x b a f x =⎰⎰()()d ()()d .bb aa f x g x x f g x x x 222[()()]()()b b b a a a f x g x dx f x dx g x dx ≤⎰⎰⎰变限积分求导公式：积分中值定理：第一积分中值定理：柯西施瓦茨积分不等式：<<a b x。

一元函数积分学的应用教案：一元函数积分学的应用引言：在高中数学中，一元函数积分学是一个重要的概念，它是微积分的核心内容之一。

积分学是研究函数积分的方法和应用的学科。

通过学习一元函数积分学，我们可以研究函数的变化趋势、面积计算、物理问题的建模和解决等一系列问题。

本教案将针对一元函数积分学的应用进行深入的探讨，帮助学生更好地理解该知识点的实际应用。

一、定积分与反常积分1.1 定积分的概念和性质- 定积分的定义与几何意义- 定积分的性质：线性性质、区间可加性、保号性1.2 反常积分的概念和性质- 反常积分存在的条件- 反常积分的判定方法二、定积分的应用2.1 函数的面积计算- 定积分与曲线下面积的关系- 利用定积分计算曲线下的面积2.2 平均值和中值定理- 平均值定理的说明和应用- 中值定理的说明和应用2.3 函数的积分学基本定理与变限积分 - 函数的积分学基本定理的说明和应用 - 变限积分的定义和计算2.4 应用题- 利用定积分求解几何问题- 利用定积分求解物理应用问题三、反常积分的应用3.1 收敛性和计算方法- 收敛性的定义和判定- 常见反常积分的计算方法3.2 物理问题的建模与解决- 利用反常积分解决物理问题- 建立数学模型求解问题结语：通过本教案的学习，学生将对一元函数积分学的应用有更深入的理解，能够掌握定积分和反常积分的基本概念、性质和应用方法，并能够将其应用于面积计算、物理问题的建模和解决等实际场景中。

同时，本教案也可激发学生对数学的兴趣和求知欲望，培养他们的数学思维和问题解决能力。

希望学生们通过学习，能够掌握一元函数积分学的应用，为今后的学习打下坚实的基础。

第五章一元函数积分学5.1 原函数和不定积分的概念一、原函数与不定积分的概念定义：如果在区间I内，存在可导函数F（x）使都有F＇（x）=f（x）或dF（x）=f（x）dx，那么函数F（x）就称为f（x）在区间I内原函数。

例：，sinx是cosx的原函数。

Lnx是在区间（0，+∞）内的原函数。

原函数存在定理：如果函数f（x）在区间I内连续，那么在区间I内存在可导函数F（x），使，都有F＇（x）=f（x）。

简言之：连续函数一定有原函数。

问题：（1）原函数是否唯一？（2）若不唯一它们之间有什么联系？例：（sinx）＇=cosx （sinx+C）＇=cosx（C为任意常数）关于原函数的说明：（1）若F＇（x）=f（x），则对于任意常数C，F（x）+C都是f（x）的原函数。

（2）若F（x）和G（x）都是f（x）的原函数，则F（x）-G（x）=C（C为任意常数）证∵[F（x）-G（x）] ＇=F＇（x）-G＇（x）=f（x）=f（x）=0∴F（x）-G（x）=C（C为任意常数）不定积分的定义：函数f（x）的全体原函数的集合称f（x）的不定积分，记为∫f（x）dx。

,其中∫为“积分号”，f（x）为被积函数，f（x）dx为被积表达式，C 为任意常数。

例：求。

【答疑编号11050101】解：例：求。

【答疑编号11050102】解：积分曲线例设曲线通过点（1，2），且其上任一点处的切线斜率等于这点横坐标的两倍，求此曲线方程。

【答疑编号11050103】解：设曲线方程为y=f（x）,根据题意知即f（x）是2x的一个原函数。

由曲线通过点（1，2）所求曲线方程为y =x2+1。

函数f（x）的原函数的图形称为f（x）的积分曲线。

显然，求不定积分得到一积分曲线族。

不定积分的性质结论：微分运算与求不定积分的运算是互逆的。

5.2 基本积分公式实例启示能否根据求导公式得出积分公式？结论既然积分运算和微分运算是互逆的，因此可以根据求导公式得出积分公式。