8.5 自旋单态和自旋三重态
- 格式:pdf
- 大小:346.07 KB
- 文档页数:9


超导体的自旋三重态超导性研究超导体的自旋三重态超导性是一个备受关注的研究领域。
自旋三重态超导性指的是在超导材料中,电子的自旋以三重态的形式结合,从而形成超导态。
这种超导性的研究对于解决能源危机和实现高效能源转化具有重要意义。
本文将对超导体的自旋三重态超导性进行综述。
一、超导体的基础知识超导体是一种在极低温下,电阻突然消失且磁场被完全排斥的物质。
超导体的研究可以追溯到1911年荷兰物理学家海克·卡末林·奥尼斯发现了水银在低温下的超导性。
迄今为止,人们已经发现了许多不同类型的超导体,包括传统超导体、低温铁基超导体和高温铜氧化物超导体等。
二、自旋三重态超导性的原理在超导材料中,电子的自旋可以以两种形式存在:自旋单态和自旋三重态。
自旋单态是指两个电子的自旋方向相反,自旋三重态是指两个电子的自旋方向相同。
在传统超导体中,电子的自旋以自旋单态的形式结合,而在自旋三重态超导体中,电子的自旋以自旋三重态的形式结合。
研究表明,自旋三重态超导体具有更高的超导转变温度和更强的磁场耐受性。
三、自旋三重态超导性的研究方法目前,研究人员主要使用实验和理论两种方法来研究自旋三重态超导性。
实验方法包括磁化率、热容、电阻率和超导体的磁场响应等测量技术。
理论方法包括利用数值计算和理论模型分析超导体的能带结构、费米面形状和电子之间的相互作用等。
四、自旋三重态超导体的应用自旋三重态超导体具有许多潜在的应用领域。
首先,自旋三重态超导体可以用于制备更高转变温度的超导体材料,从而提高能源传输的效率。
其次,自旋三重态超导体对磁场具有更好的抗干扰能力,可以用于制备高磁场强度的磁体。
此外,自旋三重态超导体还可以应用于量子计算、量子通信和量子传感等领域。
五、自旋三重态超导性的挑战和展望尽管自旋三重态超导性在理论和实验研究中取得了一些重要的进展,但仍存在一些挑战。
首先,制备高质量的自旋三重态超导体样品是一个难题。
其次,研究自旋三重态超导性的机制仍然存在许多争议。

如何理解⾃旋单态和⾃旋三重态?⾃旋单态和⾃旋三重态是研究两个1/2⾃旋耦合时得到的结果。
根据量⼦⼒学的基本理论,1/2⾃旋的粒⼦属于费⽶⼦,直接想到的例⼦就是电⼦。
当考虑两个耦合电⼦波动⽅程的解时,必须要考虑到泡利不相容原理。
泡利不相容原理说的是,在⼀个量⼦系统中,任意两个费⽶⼦不能占据相同的量⼦态。
这是费⽶⼦作为全同粒⼦的必然要求。
我们可以形式上去考虑⼀下费⽶⼦的波函数。
如果不考虑⾃旋和轨道的相互作⽤,那么电⼦波函数可以写成轨道部分和⾃旋部分的乘积。
根据费⽶⼦的定义,它的波函数必须是反对称化的。
所以可以分为两种情况:1. 轨道部分是对称化的,⾃旋部分是反对称化的;2. 轨道部分是反对称化的,⾃旋部分是对称化的。
我们考虑两个电⼦的⾃旋,可以很容易地想象出四种所有的四种状态,即↑↑,↑↓,↓↑,↓↓。
但是这四种状态不符合全同粒⼦的基本要求。
如果是全同粒⼦的话,我们将不能分辨出两个电⼦,假如是A和B,到底哪个⾃旋向上,哪个⾃旋向下。
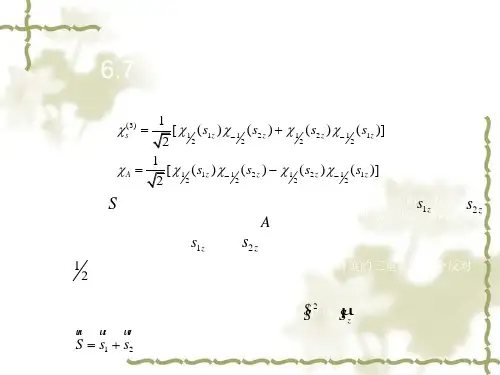
这个时候我们可以对上⾯四种状态做⼀下处理,得到四种本征⾃旋态,即↑↑,(1,1)(↑↓+↓↑)/√2 (1,0)↓↓(1,-1)(↑↓-↓↑)/√2 (0,0)其中前三种是对称化的,称为⾃旋三重态,最后⼀种是反对称化的,称为⾃旋单态。
后⾯括号中的两个数分别标出了对应⾃旋态下的总⾃旋和⾃旋z⽅向分量的值。
有些朋友可能会云⾥雾⾥。
很多⼈接下来都会想到⼀个问题就是,什么体系处于⾃旋单态,什么体系处于⾃旋三重态呢?⾸先,我们要寻找的就是多电⼦体系,因为单电⼦体系中是不存在⾃旋耦合问题的。
最简单的多电⼦体系就是氦原⼦,它有两个电⼦。
我们将处于⾃旋三重态的氦称为正氦,处于⾃旋单态的氦称为仲氦。
⾃旋三重态的氦和⾃旋单态的氦形成了两套独⽴的光谱。
可以想象,单态氦的光谱线是单线光谱,⽽三重态的氦则会有复杂的光谱结构。
事实上,⽇常⽣活中见到的⼤多数分⼦都以⾃旋单态的形式存在,有⼀个例外是氧分⼦。


分子的三重态在化学领域中,分子的三重态是指分子处于一个具有三个不同能级的电子激发态。
这些能级是由分子的电子构型和分子中的电子相互作用所决定的。
分子的三重态具有独特的性质和行为,对于理解分子的结构、反应和性质至关重要。
在三重态中,分子的电子处于高能级,激发态的状态。
这种状态与分子的基态不同,因为它具有不同的电子分布和电子自旋状况。
由于电子自旋的相互作用,分子的三重态可能具有两种不同的自旋状态,分别称为自旋三重态和自旋单态。
自旋三重态和自旋单态的能级之间存在能量差异,这使得分子在不同的电子激发态之间进行跃迁成为可能。
这些跃迁可以通过吸收或发射光的形式进行,从而产生各种各样的光谱现象。
这些光谱现象可以用于分析分子的结构和动力学行为。
分子的三重态还可以通过化学反应进行转化。
在一些反应中,分子的基态可以被激发为三重态,然后再回到基态。
这种转化可以通过光激发或化学反应来实现。
分子的三重态在这些反应中起到了重要的作用,它们可以作为反应中间体或过渡态,参与到反应的进行中。
除了在化学反应中的作用,分子的三重态还对分子的氧化还原性质和磁性质有重要影响。
分子的三重态可以影响其与其他分子或离子的相互作用,从而改变其化学性质。
此外,分子的三重态也可以影响分子的磁性,从而影响分子在外磁场中的行为。
分子的三重态是分子电子激发态的一种形式,具有重要的化学和物理性质。
通过研究分子的三重态,我们可以更好地理解分子的结构、反应和性质。
同时,分子的三重态也为开发新的材料和化学反应提供了潜在的机会。
因此,对于分子的三重态的研究具有重要的科学意义和应用价值。

半导体量子点单态和三重态
半导体量子点是一种纳米级尺寸的半导体材料,其尺寸小于其激发态的玻尔半径,因此会表现出量子力学效应。
在半导体量子点中,电子和空穴被限制在三个维度上,形成了能级结构,这种结构对于光学和电学性质具有重要影响。
单态和三重态是描述了半导体量子点中电子自旋态的两种可能性。
在单态中,电子自旋平行,总自旋为零;而在三重态中,电子自旋反平行,总自旋为一。
这两种自旋态对于半导体量子点中的能级结构和光学性质具有重要影响。
在半导体量子点中,由于空间限制和晶格势场的影响,电子和空穴之间的相互作用会导致能级的分裂。
这种分裂会导致单态和三重态的能级结构有所不同,从而影响了量子点的光学性质。
例如,单态和三重态的能级结构的差异会影响量子点的荧光发射谱,从而影响了其在光电器件中的应用。
此外,单态和三重态的存在也对于量子点中的自旋操控和量子信息处理具有重要意义。
通过外加磁场或者其他手段,可以实现对单态和三重态的控制,从而实现对量子比特的操控,为量子计算和
量子通信提供了新的可能性。
总的来说,单态和三重态是描述半导体量子点中电子自旋态的重要概念,对于量子点的能级结构、光学性质以及量子信息处理具有重要意义。
对于这些概念的深入理解,有助于我们更好地利用半导体量子点的特性,推动其在光电器件和量子技术中的应用。

低温超导材料中的自旋三重态研究低温超导材料一直以来都备受科学家们的关注,因为它们具有独特的性质和潜在的应用前景。
近年来,自旋三重态研究在低温超导材料中引起了广泛的兴趣。
自旋三重态是指自旋三个自由度之间有耦合的状态,具有非常有趣的物理特性。
首先,我们来了解一下低温超导材料的基本性质。
低温超导材料是指在接近绝对零度的温度下,电阻突然消失并且电流可以在材料中无阻碍地流动。
超导材料的超导性质由库珀对(由两个电子组成的一个复合粒子)的配对来解释。
自旋三重态的出现打破了传统上认为的库珀对的自旋为零(自旋单态)或为一(自旋三重态)的假设。
研究人员通过实验发现,在某些低温超导材料中,超导相变似乎与自旋三重态有关。
特别值得一提的是铁基超导体,其自旋三重态特性的研究一直备受关注。
铁基超导体是近年来发现的一类新型超导材料,具有较高的临界温度和复杂的电子结构。
研究表明,铁基超导体中存在着复杂的自旋状态,如自旋波和自旋密度波,这与超导性质存在耦合关系。
自旋三重态的研究不仅有助于理解低温超导材料的机制,还可能为超导材料的应用提供新的思路。
例如,自旋三重态具有比自旋单态更高的协变因子。
这意味着自旋三重态对外界磁场更加敏感,这在磁传感技术中具有重要意义。
此外,自旋三重态还具有更长的库珀对传输距离,这对于构建高性能的超导电子器件也具有一定的潜力。
然而,要深入研究低温超导材料中的自旋三重态并不容易。
首先,自旋三重态的存在常常难以直接观察到,需要借助一些精密的实验手段进行检测。
其次,自旋三重态的性质非常复杂,可能涉及到多个自由度之间的相互作用。
因此,科学家们需要运用复杂的理论模型和计算方法来解释实验数据。
最近,随着实验技术的不断发展,研究人员对低温超导材料中的自旋三重态进行了更加深入的探索。
通过应用高能分辨率的中子散射等实验技术,科学家们成功地观测到了自旋三重态的存在并研究了其性质。
此外,先进的理论模型和计算方法也为解释自旋三重态的性质提供了重要的支持。



自旋三重态解释嘿,朋友们!今天咱来聊聊自旋三重态这玩意儿。
你说这自旋三重态啊,就像是一场奇妙的舞蹈。
想象一下,粒子们就像是一群欢快的舞者,它们在微观世界里尽情地跳跃、旋转。
自旋三重态呢,就是其中一种特别带劲的舞蹈风格。
在这个微观的舞台上,粒子们有着自己独特的舞步和节奏。
自旋三重态的粒子就像是那些充满活力、激情四溢的舞者,它们以一种特别的方式展现着自己的魅力。
咱们日常生活里也有类似的情况呀。
比如说,一场热闹的派对,有些人特别活跃,能带动整个气氛,这就有点像自旋三重态的粒子。
它们充满了能量,让周围的一切都变得生动起来。
而且哦,这自旋三重态可不是随随便便就出现的,它得在特定的条件下才会闪亮登场。
这就好像一个优秀的舞者,需要在合适的舞台、合适的音乐下才能发挥出最佳水平。
你知道吗,科学家们为了研究这自旋三重态可没少下功夫!他们就像一群执着的观众,努力去理解这些粒子的“舞蹈语言”。
他们通过各种实验和观察,一点点地揭开自旋三重态的神秘面纱。
想想看,要是没有这些科学家们的努力,我们怎么能知道这么奇妙的微观世界呢?这自旋三重态可真是让我们大开眼界啊!它就像是一个隐藏在微观世界里的宝藏,等待着我们去发现、去探索。
每次想到这里,我就忍不住感叹,这世界可真是太神奇了!我们生活的这个世界,既有宏观的壮丽景象,又有微观的奇妙之处。
而自旋三重态就是微观世界里一颗璀璨的明珠。
它让我们看到了物质的另一种表现形式,让我们对世界的认识更加深入、更加全面。
这难道不令人兴奋吗?所以啊,朋友们,不要小看这小小的自旋三重态,它里面蕴含着大大的学问呢!让我们一起保持对科学的好奇心,继续去探索这个充满神奇的世界吧!总之,自旋三重态就是这么神奇、这么有趣,值得我们好好去研究和了解。
《量子力学》考试知识点第一章:绪论―经典物理学的困难考核知识点:(一)、经典物理学困难的实例(二)、微观粒子波-粒二象性考核要求:(一)、经典物理困难的实例1.识记:紫外灾难、能量子、光电效应、康普顿效应。
2.领会:微观粒子的波-粒二象性、德布罗意波。
第二章:波函数和薛定谔方程考核知识点:(一)、波函数及波函数的统计解释(二)、含时薛定谔方程(三)、不含时薛定谔方程考核要求:(一)、波函数及波函数的统计解释1.识记:波函数、波函数的自然条件、自由粒子平面波2.领会:微观粒子状态的描述、Born几率解释、几率波、态叠加原理(二)、含时薛定谔方程1.领会:薛定谔方程的建立、几率流密度,粒子数守恒定理2.简明应用:量子力学的初值问题(三)、不含时薛定谔方程1. 领会:定态、定态性质2.简明应用:定态薛定谔方程3.fdfgfdgdfg第三章:一维定态问题一、考核知识点:(一)、一维定态的一般性质(二)、实例二、考核要求:1.领会:一维定态问题的一般性质、束缚态、波函数的连续性条件、反射系数、透射系数、完全透射、势垒贯穿、共振2.简明应用:定态薛定谔方程的求解、无限深方势阱、线性谐振子第四章量子力学中的力学量一、考核知识点:(一)、表示力学量算符的性质(二)、厄密算符的本征值和本征函数(三)、连续谱本征函数“归一化”(四)、算符的共同本征函数(五)、力学量的平均值随时间的变化二、考核要求:(一)、表示力学量算符的性质1.识记:算符、力学量算符、对易关系2.领会:算符的运算规则、算符的厄密共厄、厄密算符、厄密算符的性质、基本力学量算符的对易关系(二)、厄密算符的本征值和本征函数1.识记:本征方程、本征值、本征函数、正交归一完备性2.领会:厄密算符的本征值和本征函数性质、坐标算符和动量算符的本征值问题、力学量可取值及测量几率、几率振幅。
(三)、连续谱本征函数“归一化”1.领会:连续谱的归一化、箱归一化、本征函数的封闭性关系(四)、力学量的平均值随时间的变化1.识记:好量子数、能量-时间测不准关系2.简明应用:力学量平均值随时间变化第五章态和力学量的表象一、考核知识点:(一)、表象变换,幺正变换(二)、平均值,本征方程和Schrodinger equation的矩阵形式(三)、量子态的不同描述二、考核要求:(一)、表象变换,幺正变换1.领会:幺正变换及其性质2.简明应用:表象变换(二)、平均值,本征方程和Schrodinger equation的矩阵形式1.简明应用:平均值、本征方程和Schrodinger equation的矩阵形式2.综合应用:利用算符矩阵表示求本征值和本征函数(三)、量子态的不同描述第六章:微扰理论一、考核知识点:(一)、定态微扰论(二)、变分法(三)、量子跃迁二、考核要求:(一)、定态微扰论1.识记:微扰2.领会:微扰论的思想3.简明应用:简并态能级的一级,二级修正及零级近似波函数4.综合应用:非简并定态能级的一级,二级修正、波函数的一级修正。
自旋单态的两个电子可以处于相同的空间态,而三重态不可以。
如果无外磁场,并且先不考虑电子间库伦作用,则两个电子都处于空间波函数的基态时具有最低能级,即只有自旋单态可以达到最稳定状态。
如果具有强外磁场,自旋三重态在空间态能级上将劈裂为三个能级,并且能级差随磁场增加而增加,其中有一个能级可以比空间波函数基态能级更低,在这种能级上三重态更稳定。
至于电子之间的库伦相互作用,同处于基态时的相互作用和三态时的相互作用之差似乎总是小于空间波函数激发态和基态之差(我不确定有没有哪个定理明确指出过,位力定理可能对此支持),因此考虑库伦相互作用不改变单态比三重态稳定的结果。
严格的分析涉及到多体相互作用,电子数的增加会改变空间态的能级和本征态,不过在原子这种例子中,原子核对电子的吸引总是强于电子相互作用因而能级结构改变不大,以上的简明图象是适用的。