当前位置：文档之家 › 第六章讲义异方差的性质

第六章讲义异方差的性质

  • 格式：ppt
  • 大小：398.50 KB
  • 文档页数：48

下载文档原格式

  / 48

合集下载

异方差

异方差


Econometrics 2003
9
2.随着收入的增长，人们有更多的备用收入，从而如何支配 他们的收入有更大的选择范围。因此，在做储蓄对收入的 回归时，很可能发现，由于人们对其储蓄行为有更多的选 择，2i与收入俱增。 3.随着数据采集技术的改进， 2i可能减少。 4.异方差还会因为异常值的出现而产生。一个超越正常值 范围的观测值或称异常值是指和其它观测值相比相差很多 （非常小或非常大）的观测值。 5.回归模型的设定不正确也会造成异方差。例如，在一个商 品的需求函数中，若没有把有关的互补商品和替代商品的 价格包括进来（忽略变量偏差），则回归残差就可能出现 异方差。 注：异方差在横截面数据中比时间序列数据更为常见。
2 0 0 2 var(u) E (uu) 2 I 0 0 0 0 2
Econometrics 2003
3
var( i ) 2 const ant i 1,2,...,n 2. 异方差(heterscedasticity )：是指随机扰 异方差：i的方差随的变化而变化。 动项ui随着解释变量XiX i的变化而变化，即 var( i ) i 2 f ( X i ) 古典假定之一：随机扰0 i0 动项 例如：储蓄与收入的关 的方差相同 系的模型 2 0 t 0 var() i E (u cons tan ) var(u u X ＝Vu Y 1 ) 2 i i i 1,2,...,n 0 异方差：是储蓄；0 i的变化而变化，即 其中：Yi i的方差随X 是收入 2 var( i ) i 2 f ( X i ) 例如：储蓄与收入的关 系的模型 Y 1 2 X i ui 其中：Yi 是储蓄；X i 是收入
第六章 异方差(计量经济学,南开大学)

第六章 异方差(计量经济学,南开大学)

且能确定影响随机项的解释变量。
二、格兰奇（Glejser）检验
假定 i2与某一解释变量X ik 有关。可以对以下函数形势作回归： : ˆi | 1 2 X ik vi |u ˆi | 1 2 X ik vi |u ˆi | 1 2 |u ˆi | 1 2 |u 进行回归，对和回归方程作显著性检验。若显著，则存在异方差。
2 2 f ( X 2i , X 3i , X mi )
i
以 f ( X 2i , X 3i , X mi )遍除原模型，
可得到满足CLRM假定的新模型：
Yi 1 2 f ( X 2i , X 3i , X mi ) k
X 2i f ( X 2i , X 3i , X mi ) X ki f ( X 2i , X 3i , X mi ) ui f ( X 2i , X 3i , X mi )
同 Y1 方 差 X1 异 方 Y1 差 X1
Y2
.. .
Yn Xn Yn Xn
X2
.. . X2
如果保持随机项的协方差为0，则
2 1 0 E (u' u) 0
Y Xβ u
0 0 0 2 n
的方差、协方差矩阵为：
2
1、作OLS 估计，得到ui。 2、把 ui 和X i按升序获降序赋予等级值（ 1， 2， ，n）。 3、计算斯皮尔曼等级相关系数： rs 1 6[ n( n 1)
2 2 d i
], 其中d i为第i组观测值的ui 和X i的等级差。 rs n 2 1 rs
2
4、计算统计量：
第六章 异方差
第一节 异方差的性质
一、异方差 在经典线性回归模型（CLRM）中，我们假定随即干扰项具有同方差性，即： Var(ui|Xi)=E[ui-E(ui)|Xi]2 = E(ui2|Xi]2 = 2 这实际上是假定了解释变量Yi 的值围绕其期望值的分散程度相同。实际上，对应于 解释变量的不同取值，方差可能不同，即本假定不成立。
第六章：异方差

第六章：异方差

[计量经济学讲义] 第六章：异方差§1 含义异方差是相对于同方差而言的。

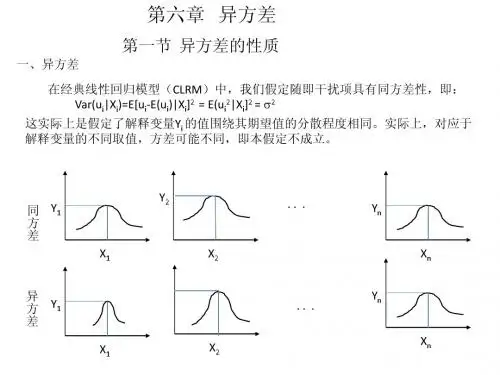
同方差：在经典线性回归模型的重要假定之一是，以解释变量的选定值为条件的每一随机扰动项u i 的方差是一个等于σ2的常数，即：var(u i )=σ2=常数，i=1,2,…,n (6.1.1)异方差：是指随机扰动项u i 随着解释变量X i 的变化而变化，即：var(i u )=2i σ=2σf(X i ) (6.1.2)§2 来源有一些理由说明为什么随机扰动项的方差有变化，其中的一些有如下述：一、按照边错边改学习模型（error-learning models ），人们在学习的过程中，其行为误差随时间而减少。

在这种情况下，预料的2i σ会减少。

例如，随着打字联系小时数的增加，不仅平均打错个数而且打错个数的方差都有所下降。

二、随着收入的增长，人们有更多的备用收入，从而如何支配他们的收入有更大的选择范围。

因此，在做储蓄对收入的回归时，很可能发现，由于人们对其储蓄行为有更多的选择，2i σ与收入俱增。

三、随着数据采集技术的改进，2i σ可能减少。

四、异方差还会因为异常值的出现而产生。

一个超越正常值范围的观测值或称异常值是指和其它观测值相比相差很多（非常小或非常大）的观测值。

五、回归模型的设定不正确也会造成异方差。

例如，在一个商品的需求函数中，若没有把有关的互补商品和替代商品的价格包括进来（忽略变量偏差），则回归残差就可能出现异方差。

注：异方差在横截面数据中比时间序列数据更为常见。

§3 影响一、参数的OLS 估计仍然是线性无偏的，但不是最小方差的估计量 以下以双变量线性回归模型为例 1、线性性∑∑=22ˆi i i x y x β=∑∑+22iii x u x β (6.2.1) 2、无偏性E(2ˆβ)=E(∑∑+22i i i x u x β)=∑∑+22)(ii i x u E x β=2β (6.2.2) 3、方差Var(2ˆβ)=Var(∑∑+22ii i x u x β)=222)()(∑∑i i i x u Var x =2222)(∑∑i ii x x σ (6.2.3) 在同方差时，Var(2ˆβ)=∑22ix σ (6.2.4) 二、t 检验失效用于参数显著性检验的统计量)ˆ(ˆ)ˆ(i i i se t βββ＝ 在同方差的假定下才被证明是服从t 分布的。

异方差

异方差

异方差异方差的性质● 经典回归的一个重要假定之一是：u i 的条件方差为常数， 即：E （2i u ）= 2σ● 异方差（heterscedasticity ）：E （2iu ）=2i σ， 不同的（heter ）分散程度（scedasticity ）● （图）消费和收入， 消费随收入的增加而增加，但变异也在增加● u i 变动的几个理由：- 按照边错边改学习模型（error-learning models ），人们在学习的过程中，其行为误差随时间而减少，如：打字出错的个数- 随着收入的增长，人们有更多的备用收入，从而如何支配他们的收入有更大的选择范围- 随着数据采集技术的改进，2iσ可能减少- 异方差性还会因为异常值的出现而产生。

包括一个异常值，尤其样本较小时，会在很大程度上改变回归分析的结果- 异方差性的另一来源来自CLRM 的假定9的破坏，即：回归模型的设定是不正确的。

● 异方差常见于横截面数据中，因为观测范围大小不一● 异方差的后果：仍然是无偏的，但不是最有效的了（1） 无偏性βββ=+==-- )](')'[(]')'[()ˆ(11U X X X X E Y X X X E E（2） 非有效性1121111)'(')'()'()'(')'(]'')'][(')'[()'ˆ)(ˆ(------Φ==--=--X X X X X X X X X UU E X X X Y X X X Y X X X E E σββββββ● 同方差性时，βˆ的协方差矩阵为: 12)'(-X X σ,会夸大或缩小真实的方差和协方差● 由此会导致β的相关检验和置信区间失效，进而引起预测失效● 以双变量模型为例：i i i u X Y ++=10ββ进行显著性检验时，构造的t 统计量)ˆ(ˆ11ββS t =)ˆ(1βS 变动，所以1ˆβ的置信区间也不稳定异方差性的侦察● 侦破异方差性并没有严明的法则，只有少数的经验规则● 因为除非我们知道对应于选定的X 值的整个Y 总体，否则2i σ是无从获知的●大多数的方法都基于对我们所能观测到的OLS残差i uˆ的分析，而不是对干扰u i的分析非正式的方法●问题的性质：-往往根据所考虑的性质就能判别是否会遇到异方差性-例如：围绕消费对收入的回归，残差的方差随收入的增加而增加●图解法：-可先在无异方差性的假定下做回归分析，然后对残差的平方2ˆi u作一事后检查，看看这些2ˆi u是否呈现任何系统性的样式-（图）-2ˆi u是对应于i Yˆ而描绘的，除此之外，还可将他们对解释变量之一描点-当我们考虑2个或多个X变量的模型时，可将2ˆi u 相对于模型中的任一个变量描点正式方法（1）帕克（park ）检验● 提出2i σ是解释变量X i 的某个函数，他建议的函数形式为：iv i ie X βσσ22=或：i i i v X ++=ln ln ln 22βσσ● 由于2iσ通常是未知的，帕克建议用2ˆi u 作为替代变量并作如下回归：ii i i v v X u++=++=i 22lnX ln ln ˆln βαβσ **● 如果β表现为统计上显著的，就表明数据中有异方差性● 帕克检验分两阶段：一是做回归，而不考虑异方差性问题，从这一回归获得i uˆ，然后在第二阶段作如** 的回归戈德菲尔德-匡特检验 （Goldfeld-Quandt test ）● 适用于异方差性方差2i σ同回归模型中的解释变量之一有正相关的情形● 步骤一：从最小X 值开始，按X 值的大小顺序将观测值排列步骤二：略去居中的C 个观测值，其中C 是预定的，并将其余的（n-c ）个观测值分成两组，每组(n-c)/2个步骤三：分别对头（n-c ）/2个观测值和末(n-c)/2 个观测值各拟合一个回归，并分别获得残差平方和RSS 1 和RSS 2步骤四：计算比值：dfRSS dfRSS //12=λ， 如果假定i uˆ是正态分布的，并且如果同方差性假定真实，则λ遵循分子和分母自由度各为（n-c-2k ）/2 的F 分布● C 个观测值是为了突出或激化小方差组（即RSS 1）与大方差组（即RSS 2 ）之间的差异● 通常当n=30 时，取c =4, 当n=60 时，取c=10为宜● 当模型中有多于1个X 变量时，在检验的步骤一中，就可按任一个X 的大小顺序将观测值排列● 例：消费支出 – 收入， 30 观测值，略去居中4 个观测值后，对开头的13个和末尾的13个观测值分别作OLS 回归：17.377RS S 6968.04094.3ˆ1=+=i i X Y 8.1536RS S 7941.00272.28ˆ2=+-=i iX Y得：07.411/17.37711/8.1536//12===df RSS df RSS λ怀特（white ）的一般异方差性检验● Goldfeld-Quandt 检验要求按照被认为是引起异方差性的X 变量把观测值重新排序● White 检验并不要求排序，而且易于付诸实施● 步骤一： 对给定的数据回归（两个解释变量），并获得残差i uˆ步骤二：再做如下（辅助）回归：ii i i i i i i v X X a X a X a X a X a a u ++++++=326235224332212ˆ从这个（辅助）回归中求得R 2步骤三：在无异方差性的虚拟假设下，2nR 渐进的遵循自由度等于辅助回归元（不包括常数项）个数的2χ分布步骤四：如果2χ值超过临界值，结论就是有异方差性，如果不超过，就没有，即：065432=====a a a a a● 例： Y= 贸易税收（进口与出口税收）与政府总收入之比，X 2 =进出口总和与GNP 之比，X 3 =人均GNP ， 假设Y 与X 2 正相关，Y 与X 3 成反比White test ：1148.0R ))(ln T rade 0.0015(ln )(ln 0491.0)(ln 4081.0 ln 6918.0ln 5629.28417.5ˆ2i 222=+--++-=i i i i i i GNP GNP Trade GNP Trade u7068.4)1148.0(41.2==R n● 如果模型有多个回归元，回归元的平方（或更高次方）项以及它们的交叉项就会耗掉许多的自由度● 遇到统计量显著的情形，原因也许不一定是异方差性异方差的修正方法 – 加权最小二乘法（广义最小二乘法）● 以消费-收入为例，消费异方差，设计一种估计方案：对来自变异较大的总体的观测值作较小的加权，而对来自较小的总体的观测值作较大的加权● OLS 方法对每一观测之同样重视或同等加权● 广义最小二乘法（generalized least square-GLS ）利用了异方差的信息，因而能产生ＢＬＵＥ估计量● 利用双变量模型：i i i i u X X Y ++=201ββ其中对每个ｉ， Ｘ０ｉ＝１● 假定相异的方差2i σ已知，用σ通除上式得：)()()(201iiiiiiiiu X X Y σσβσβσ++=为了易于阐述，将它写为：i i i i u X X Y ******201++=ββ● 转换原始模型中，转换干扰项i u *的方差，现在有了同方差性1)(1)(1)()*()*var(2222i22=====iiiiii i u E u E u E u σσσσ● ＯＬＳ应用到转换模型将产生ＢＬＵＥ估计量● ＧＬＳ是对满足标准最小二乘假定的转换变量的ＯＬＳ● 21*ˆ*ˆββ和的估计步骤是最小化： 220112)**ˆ**ˆ*(*ˆii i X X Y u ββ--=∑∑● *ˆ2β的GLS 估计量为： ∑∑∑∑∑∑∑--=222)())(())(())((*ˆi i i i i i i i i i i i i X w X w w Y w X w Y X w w β 其中2/1i i w σ=● ＯＬＳ和GLS 的差别：ＯＬＳ要求最小化：2212)ˆˆ(ˆii i X Y u ββ--=∑∑ ＧＬＳ要求最小化：2212)ˆˆ(ˆii i i i X Y w u w ββ--=∑∑● ＧＬＳ中最小化一个以2/1i i w σ=为权的加权残差平方和，而在ＯＬＳ中最小化一个无权或等权的残差平方和● 这种形式的GLS 被称为加权最小二乘法（weighted least square – WLS ）● 若i σ是已知的，异方差的问题似乎已经得到了解决，但大多数情况下，方差是未知的●加权最小二乘法至多只能用于未知方差容易被描述的那些情况●看一下课本中的例子。

第六章异方差的性质-PPT课件

第六章异方差的性质-PPT课件



（一）残差序列分析 （二）戈德菲尔德-夸特检验 （三）戈里瑟检验 （四）怀特检验



（一）残差序列分析
(a)
e
i
X k
(b)
eห้องสมุดไป่ตู้
i
X k
(c)
e
i
X k
(d)
e
i
X k
(e)
e
i
X k
(f)
e
i
X k
（二）戈德菲尔德-夸特检验


戈德菲尔德-夸特检验是最常用的异方差专门检 验方法之一。这种方法适合于检验样本容量较大 的线性回归模型的递增或递减型异方差性。 对于存在递增异方差模型，步骤：首先将样本按 X值的大小顺序将观测值排列，然后略去居中的C 个观测值，并将其余的(n-C)个观测值分成两组， 每组(n-C)/2个，分别对两个子样本进行回归， 并分别获得残差平方和，自由度都为（n-C)/2K-1。


普遍性：两类数据都有，横截面数据更多。 原因：
1.按照边错边改学习模型，人们在学习过程中，其行为误 2 差随时间而减少。在这种情形下，方差 i 会逐渐变小。 例如，随着打字练习小时数的增加，不仅平时打错的个 数而且打错的方差都有所下降。 2.随着收入的增长，人们有更多的备用收入，从而如何支 配他们的收入有更大的选择范围。因此，在作出储蓄对 收入的回归时，很可能发现，由于人们对其储蓄行为有 更多的选择， i2 与收入俱增。因此，以增长为导向的公 司比之于已发展定型的公司在红利支付方面也可能表现 更多的变异。
（二）戈德菲尔德-夸特检验
计算统计量：
F e
i2 2 i2
2 e i1 i1
计量经济学知识点整理：异方差

计量经济学知识点整理：异方差

(2)X-~e i2的散点图进行判断异方差性1、定义：如果出现即对于不同的样本点，随机误差项的方差不再是常数，而互不相同，则认为出现了异方差性。

同方差性：σi2 = 常数 ≠ f(Xi)异方差时：σi2 = f(Xi) 2、后果：参数估计量非有效OLS 估计量仍然具有无偏性，但不具有有效性 因为在有效性证明中利用了 E(μμ’)=σ2I而且，在大样本情况下，尽管参数估计量具有一致性，但仍然不具有渐近有效性。

变量的显著性检验失去意义变量的显著性检验中，构造了t 统计量如果出现了异方差性，估计的S 出现偏误则t 检验失去意义。

其他检验也是如此。

模型的预测失效一方面，由于上述后果，使得模型不具有良好的统计性质；另一方面在预测的置信区间中，同样包含参数方差的估计量。

所以，当模型出现异方差性时，参数OLS 估计值的变异程度增大，从而造成对Y 的预测误差变大，降低预测精度，预测功能失效。

3、检验：检验随机误差项的方差与解释变量观测值之间的相关性及其相关的“形式”。

图示法（1）用X-Y 的散点图进行判断，看是否存在明显的散点扩大、缩小或复杂型趋势（即不在一个固定的带型域中）看是否形成一斜率为零的直线 帕克(Park)检验与戈里瑟(Gleiser)检验偿试建立方程：i ji i X f e ε+=)(~2Var i i ()μσ=2i ji i X e εασ++=ln ln )~ln(22i e X X f jiji εασ2)(=)12,12(~)12(~)12(~2122------------=∑∑k c n k c n F k c n e k c n e F i i 选择关于变量X 的不同的函数形式，对方程进行估计并进行显著性检验，如果存在某一种函数形式，使得方程显著成立，则说明原模型存在异方差性。

如： 帕克检验常用的函数形式：若α在统计上是显著的，表明存在异方差性。

戈德菲尔德-奎恩特(Goldfeld-Quandt)检验①将n 对样本观察值(Xi,Yi)按观察值Xi 的大小排队②将序列中间的c=n/4个观察值除去，并将剩下的观察值划分为较小与较大的相同的两个子样本，每个子样样本容量均为(n-c)/2,即3n/8③对每个子样分别进行OLS 回归，并计算各自的残差平方和④在同方差性假定下，构造如下满足F 分布的统计量⑤给定显著性水平α，确定临界值F α(v1,v2)，若F> F α(v1,v2)， 则拒绝同方差性假设，表明存在异方差。

《异方差教学》课件

《异方差教学》课件

White检验
基于最小二乘法的残差，通过构造统计量检验异方差的存在 性。该方法适用于多种类型的数据，尤其适用于面板数据。
非参数检验法
Park检验
利用数据中的信息，通过比较不同阶数的自回归模型对数据的拟合效果，判断 是否存在异方差。该方法不需要预设模型形式，较为灵活。
ARCH模型
利用自回归条件异方差模型进行异方差的检验，通过比较不同滞后阶数的模型 拟合效果，判断是否存在异方差。该方法适用于波动性较大的数据。
Box-Cox变换法
总结词
Box-Cox变换法是一种通用的修正异方 差的方法，通过选择适当的λ值进行变换 ，使数据的方差变得相等。
VS
详细描述
Box-Cox变换法是一种灵活的修正异方差 的方法，适用于不同类型的异方差数据。 通过选择适当的λ值进行变换，可以使数 据的方差变得相等，从而消除异方差的影 响。Box-Cox变换法的优点在于能够自动 选择最佳的λ值进行变换，使得数据的同 方差性得到最大程度的保持。在回归模型 中，可以使用Box-Cox变换法来处理因变 量的异方差问题。
PART 03
异方差的修正
对数变换法
总结词
对数变换法是一种常用的修正异方差的方法，通过取对数将异方差转化为同方差 。
详细描述
对数变换法适用于正态分布的异方差数据，通过取自然对数或对数变换，可以使 方差变得相等，从而消除异方差的影响。在回归模型中，可以使用对数变换法来 处理因变量的异方差问题。
平方根变换法
提出相应的解决策略。
PART 06
总结与展望
异方差研究的意义
揭示数据内在规律
异方差研究有助于揭示数据分布的内在规律，为数据分析和预测 提供更准确的模型。
提高统计推断的准确性
计量经济学第六章异方差性

计量经济学第六章异方差性


构建统一的异方差 性处理框架
未来可以构建一个统一的异方 差性处理框架，整合现有的处 理方法和技巧，为实际应用提 供更为全面和系统的指导。同 时，该框架还可以为计量经济 学的教学和研究提供便利。
THANK YOU
感谢聆听
03
异方差性对假设检验 的影响
异方差性可能导致假设检验中的t统计 量和F统计量失效，从而影响假设检 验的结论。
异方差性下的模型选择和评价
异方差性检验
在进行模型选择和评价之前，需要对异方差性进行检验。常用 的异方差性检验方法有怀特检验、布雷施-帕甘检验等。
模型选择
在存在异方差性的情况下，应选择能够处理异方差性的模型， 如加权最小二乘法（WLS）、广义最小二乘法（GLS）等。
性质
异方差性违反了经典线性回归模型的同方差假设，可能导致参数 估计量的无偏性、有效性和一致性受到影响。
产生原因及影响
模型设定误差
模型遗漏了重要变量或函数形式设定错误。
数据采集问题
观测数据的误差或异常值。
产生原因及影响
• 经济现象本身：某些经济变量之间的关系可能随时间和空间的变化而变化，导致异方差性。
等级相关系数法
计算残差绝对值与解释变量之间的等 级相关系数，若显著则表明存在异方 差性。
Goldfeld-Quandt检验法
假设条件
该检验假设异方差性以解释变量的某个值为界，将样本分为两组，且两组的方差不同。
检验步骤
首先根据假设条件将样本分组，然后分别计算两组的残差平方和，最后构造F统计量进行假设检验。
05
异方差性在计量经济学模型中的应用
异方差性对模型设定的影响
01
异方差性可能导致参 数估计量的偏误
当存在异方差性时，普通最小二乘法 （OLS）的参数估计量可能不再具有无 偏性和一致性，从而导致估计结果的偏 误。
异方差课件

异方差课件

• 注意：应用加权最小二乘法要求异方差的形式是已 知的，事实上这是一个很强的假定，一般情况下模 型的异方差的形式是未知的。
4 异方差的修正方法（WLS）
（2）利用Glejser检验结果确定异方差形式，消除异方差
假设 Glejser 检验结果是
| uˆt | = aˆ0 + aˆ1 xt
说明异方差形式是 Var(ut) = ( aˆ0 + aˆ1 xt)22。用 ( aˆ0 + aˆ1 xt) 除原模型各项，
SSR2 SSR1
•
n1 n2
k k
，k为模型中被估参数个数
在H0成立条件下，F F(n2 - k, n1 - k)
④ 判别规则如下，
若 F F (n2 - k, n1 - k), 接受H0（ut 具有同方差） 若 F > F(n2 - k, n1 - k), 拒绝H0（递增型异方差） 注意：
异方差通常有三种表现形式，（1）递增型，（2）递减型，（3）条件自回
归型。 7
6
Y 6
4
DJ P Y
5
2
4
0
3
-2
2
-4
1
-6
0 20 40 60 80 100 120 140 160 180 200
-8 400 500 600 700 800 900 1000 1100 1200
2 异方差来源与后果
① 当摸型含有多个解释变量时，应以每一个解释变量为基准检验异方差。
② 此法只适用于递增型异方差。
③ 对于截面样本，计算F统计量之前，必须先把数据按解释变量的值排序。
3 异方差检验
(2) White检验
White检验由H. White 1980年提出。White检验不需要对观测值排序，也不
《异方差性》课件

《异方差性》课件


03
异方差性的后果
模型预测的准确性下降
异方差性会导致模型的预测值偏 离真实值，降低预测的准确性。
在异方差性存在的情况下，模型 的预测结果可能变得不可靠，因 为模型没有充分考虑到数据的不
确定性。
异方差性可能导致模型在预测新 数据时表现不佳，因为模型没有 充分学习到数据的内在结构和变
化规律。
模型推断的可靠性降低
详细描述
社会数据在不同群体之间的分布往往存在显著的差异，这种差异反映了不同群体之间的异方差性。这 种异方差性可能与社会经济地位、文化背景等多种因素有关，需要深入分析其产生的原因和影响。
社会数据的异方差性分析
总结词
异方差性对社会政策制定和实施具有重 要影响。
VS
详细描述
社会政策的制定和实施需要考虑不同群体 的差异和特点，而异方差性的存在为社会 政策的制定提供了重要的参考信息。通过 对异方差性的分析和研究，我们可以更好 地了解不同群体的需求和诉求，制定更为 公正和有效的社会政策。
总结词
金融数据的异方差性分析有助于提高投资策略的有效性。
详细描述
通过对金融数据的异方差性进行分析，投资者可以更好地 理解市场的波动规律和风险特征，从而制定更为有效的投 资策略。这种基于异方差性的投资策略能够更好地适应市 场的变化，提高投资的收益和风险控制能力。
社会数据的异方差性分析
总结词
社会数据在不同群体之间存在显著的异方差性。
平方根变换
当数据分布不均，特别是偏度较大时，平方根变换可以改善数 据的正态性。
Box-Cox变换
是一种通用的数据变换方法，通过选择一个适当的λ值，使数据 达到最佳的正态分布状态。
模型选择和调整
混合效应模型
异方差

异方差

Econometrics第六章异方差（教材第九章）第六章异方差6.1 异方差的涵义6.2 异方差的后果6.3 异方差的诊断6.4 补救措施学习要点异方差及其产生的后果，诊断及消除其影响的措施6.1 异方差的涵义异方差（Heteroscedasticity ）f 古典线性回归模型（CLRM ）的对u i 的假定其中，称为同方差（Homoscedasticity ）假定。

f 若，则称存在异方差（Heteroscedasticity ）。

12233i i i iY B B X B X u =+++2()0()(,)0i i i j E u Var u Cov u u σ=⎧⎪=⎨⎪=⎩2()i Var u σ=22()i i Var u σσ=≠6.1 异方差的涵义异方差（Heteroscedasticity）f例，个人储蓄的方差随个人可支配收入增加而变大。

6.1 异方差的涵义异方差（Heteroscedasticity ）f 异方差用符号表示为：（注意下标）表明u i 的方差随观察值的不同而变化。

f存在异方差问题的实际背景多存在于横截面数据（cross-sectional data）由于存在规模效应测量误差f 例如，使用横截面数据估计中国总量消费函数。

22()i iE u σ=()()2()i i i Var u E u E u =−=2i σ6.1 异方差的涵义异方差（Heteroscedasticity ）f 例，523个工人的工资：123i i i iWage B B Edu B Exper u =+++6.1 异方差的涵义异方差（Heteroscedasticity ）f 例，523个工人的工资：123i i i iWage B B Edu B Exper u =+++6.2 异方差的后果异方差的后果（证明从略）f OLS OLS6.3 异方差的诊断异方差的一些诊断工具f问题的性质：在横截面数据中常有异方差问题f帕克检验（Park test）f格莱泽检验（Glejser test）Heteroscedasticity Test）f异方差的其他检验方法6.3 异方差的诊断异方差的一些诊断工具f 残差的图形检验：用对一个或多个解释变量作图2i e6.3 异方差的诊断异方差的一些诊断工具f 残差的图形检验：多个解释变量时可用对作图2ieˆiY6.3 异方差的诊断异方差的一些诊断工具f 帕克检验（Park test ）：做对一个或多个的回归f 例如，一元模型中f 实际估计中以代替，如何获得？f 检验零假设B 2=0，即不存在异方差。

异方差知识点总结

异方差知识点总结异方差的存在可能会导致回归模型下列问题：1. 预测的不确定性增加：当异方差存在时，回归模型的预测区间可能会变得更宽，因为方差的不稳定性会使得预测更加不确定。

2. 参数估计的失真：在存在异方差的情况下，最小二乘法(OLS)回归的方法可能会导致参数估计的偏误。

3. 统计推断的失真：在存在异方差时，通常使用的标准误差可能被低估或高估，从而影响统计推断的结果。

因此，我们有必要了解异方差的特征、检验方法和处理方法。

本文将从以下几个方面对异方差进行总结。

一、异方差的特征和识别方法二、检验异方差的统计方法三、处理异方差的方法一、异方差的特征和识别方法1. 异方差的特征异方差的特征主要包括两个方面：方差的不稳定性和误差项的相关性。

首先是方差的不稳定性，即随着自变量的变化，因变量的方差也会跟着变化。

这种不稳定性可能出现在回归模型的残差中，表现为残差的离散程度随着自变量的变化而变化。

其次是误差项的相关性，即自变量与误差项之间存在相关性。

这种相关性可能是由于遗漏变量、测量误差或其他未知因素导致的，而这种相关性可能会影响到回归模型的假设前提，从而影响到参数的估计和统计推断的结果。

2. 异方差的识别方法在实际应用中，我们可以通过以下几种方法来识别是否存在异方差：（1）绘制残差图：同时绘制残差与预测值的散点图和残差与自变量的散点图，观察残差的离散程度是否与自变量相关。

（2）利用统计检验：利用统计学中的异方差检验方法，如BP检验、White检验等。

（3）利用经验判断：在经验分析中，我们也可以通过观察实际数据的特征，来判断是否存在异方差。

比如，如果数据中存在明显的带状结构或呈现出明显的异方差现象，那么可能存在异方差问题。

二、检验异方差的统计方法1. BP检验BP检验是一种常用的异方差检验方法，它的原假设是误差的方差是恒定的，备择假设是误差的方差是非恒定的。

BP检验的具体步骤为：（1）先对相关变量进行回归分析，得到残差eˆ2；（2）在残差的平方的基础上，增加自变量的平方和自变量与自变量的乘积，得到新的残差变量；（3）利用新的残差变量进行正态性检验，判断残差是否服从正态分布；（4）最后，利用新的残差变量进行F检验，检验自变量的平方及其交叉项是否显著。

异方差模型


从这，我们可以看出 ε t 是高峰和肥尾的。 估计 在 ε t = z t ht 中，若 zt 服从标准的正态分布，则伪似然估计 （Quasi-Maximum-Likelihood Estimator）的对数似然函数为：
LT = − T 1 T ln 2π − ∑ ln ht2 + zt2 2 2 t =1
2
值，即 E (rt | Ft −1 ) = μ t ，相应地可以定义 rt 的条件方差 ht ：
2
ht ≡ Var (rt | Ft −1 ) = E[(rt − μ t ) 2 | Ft −1 ] = E (ε t | Ft −1 )
2 2
(2)
式(2)是 GARCH 类波动率模型的核心部分，Engle(1982)首先提出了以 AR(q)结构 来对 ht 建模，这就是著名的自回归条件异方差模型(Auto-Regressive Conditional Heteroscedasticity,ARCH)。Engle 定义条件均值的残差序列 {ε t } 为：
无条件方差
E (ε t ) =
2
α0 1 − (α + β )
峰度 如果 1 − (α + β ) 2 − 2α 2 ，则峰度系数 E (ε t4 ) 3[1 − (α + β ) 2 ] == >3 [Var (ε t )]2 1 − (α + β ) 2 − 2α 2 从这，我们可以看出 ε t 是高峰和肥尾的。 估计 在 ε t = z t ht 中，若 zt 服从标准的正态分布，则伪似然估计 （Quasi-Maximum-Likelihood Estimator）的对数似然函数为：
可以写成为
ε t2 = α 0 + (α + β )ε t −1 2 + ε t2 − ht 2 − β (ε t2−1 − ht2−1 )

异方差

异方差§1 异方差的含义一、异方差的定义设模型为01122i i i k ki i Y X X X u ββββ=+++++如果扰动项的方差随着ji X 的变动而变动，即2()i i Var u σ=则称随机扰动项i u 存在异方差。

二、异方差的两种常见模式⒈方差随着某个解释变量的增加而增加⒉方差随着某个解释变量的增加而下降§2 异方差的产生原因和后果一、异方差的产生原因（一）设定偏误——解释变量的缺失，函数形式不正确 例：真实模型：01122i i i i Y X X u βββ=+++错误模型：011i i i Y X v ββ=++则 22i i i v X u β=+()i Var v 会随着2i X 的变化而变化（二）样本数据的观测误差随着时间的推移 () () i i Var u Var u ⎧↑⎪⎨↓⎪⎩观测误差累积观测技术提高 三、异方差的影响（以一元线性回归为例）（一）参数估计量仍然是线性无偏的（二）参数估计量不再具有最小方差性（OLS 低估真实方差）（三）解释变量显著性检验失效11111ˆˆ ()()ˆt t ˆ ()Var Se t Se ββββ⇒⇒⇒=⇒⇒低估真实方差被低估被低估检验显著性检验被高估被夸大失效 §3 异方差的判断一、直观判断――残差的图形检验222X X X i i i e e e ⎧⎪⎨⎪⎩用对作图与之间存在有规律的变化－－－异方差与之间不存在有规律的变化－－同方差二、残差分段对比――Goldfeld-Quant 检验更正：22222211(1)2[(1),(1)]22(1)2ii i i e k e n c n c F F k k e e n c k -+--==-+-+--+∑∑∑∑三、用残差绝对值或残差平方为因变量作辅助回归（一）Glejser 检验用残差绝对值对解释变量或解释变量的函数回归（二）White 检验用残差平方对解释变量的函数回归（三）ARCH 检验用残差平方对其滞后值回归2112222ˆˆˆˆˆ()()t t t p t p e e e e n p R p ααααχ---=++++-§3 异方差的修正2WLS 2.WLS i i i i e e X e X e w e e ⎧→→⎪⎪⎪⎨⎪→→⎪⎪⎩→⎫⎧→⎨⎬→⎩⎭∑i i i i i 一、异方差的修正（一）加权最小二乘法（，weighted least squares）1.OLS 法的缺陷对每个赋予相同的重要性提供的较小时应加大信息量信息量小提供的较大时应减小信息量信息量大的思路较大的权重较小的使最小化较大的较小的权重i WLS WLS （二）估计量及其性质二、为未知时的变换三、模型的对数变换。

异方差的性质

如果存在异方差性，则表明确与解释变量的某 种组合有显著的相关性，这时往往显示出有较高 的可决系数以及某一参数的t检验值较大。 缺点：在多元回归中，由于辅助回归方程中可 能有太多解释变量，从而使自由度减少。 去掉交叉项！
1-11
异方差其他检验方法
1-12
第四节 异方差的修正
观察到异方差怎么办：补救措施
W i euˆi2i2
W i [Yi ( ˆ 1 ˆ2 X 2 L
ˆ k
X
k
2
)]
在采用OLS方法时:
对较小的残差平方 uˆi2 赋予较大的权数， 对较大的残差平方 uˆi2 赋予较小的权数。
1-14
第四节 异方差的修正
第一种情况：
2 i
已知
Yi 1 2 X 2i ui
每个观测值的方差
2 i
已知
可作如下变换，等式两端各项均除以 i2:
Yi / i 1 / i 2 ( X 2i / i ) ui / i
变换后方程是否同方差呢？
E[(ui
/i )2]
E(ui2 )
/
2 i
1
1-15
第四节 异方差的修正
第二种情况：
2 i
未知
知道真实方差 信i2 息少的可怜！幸运地是，我们
可以观察残差与解释变量间的关系–诸如，线性的、 平方根、平方、双曲线; 总而言之，做残差关于解释 变量的非线性变换，使得变换后的随机项的方差为 常数！
t
ˆ2 2* se(ˆ2 )
2
var(ˆ2 )
var(ˆ2 )
1-4
其他检验也是如此。
第三节 异方差的检验方法
现实中判断异方差存在并非易事！
➢
实际观察值的方差为

计量经济学第六章 异方差-PPT精品文档


关 于 变 量 的 显 著 性 检 验 中 ， 构 造 了 统 计 量 t

( 2 . 4 . 6 ）
在该统计量中包含有随机误差项共同的方差，并且有 t统计量服从自由度为(n-k-1)的t分布。如果出现了 异方差性，t检验就失去意义。 其它检验也类似。
3、模型的预测失效
一方面，由于上述后果，使得模型不具有良好 的统计性质； 另一方面，在预测值的置信区间中也包含有随 机误差项共同的方差2。 所以，当模型出现异方差性时，参数OLS估计 值的变异程度增大，从而造成对 Y的预测误差变 大，降低预测精度，预测功能失效。
•例如，以某一行业的企业为样本建立企业生产函 数模型
Yi=Ai1 Ki2 Li3eI
产出量为被解释变量，选择资本、劳动、技术等 投入要素为解释变量，那么每个企业所处的外部 环境对产出量的影响被包含在随机误差项中。 由于每个企业所处的外部环境对产出量的影响程 度不同，造成了随机误差项的异方差性。
i = 1 , 2 , … , n i = 1 , 2 , … , n
同 方 差 性 假 设 为
如 果 出r ( ) i i
i = 1 , 2 , … , n
即对于不同的样本点，随机误差项的方差不再是 常数，则认为出现了异方差性。
2、异方差的类型 • 同方差性假定的意义是指每个i围绕其零平均
故
xi ˆ E ( ( E ( 1) E 1) i ) 1 2 x i
(2 .4 .2 )
（2）不具备最小方差性
由于
xi ˆ ) E( ˆ ) 2 E( var( x 2 i ) 2 1 1 1 i E( xi i ) ( xi2 ) 2
2
2 i
(2.4.3)

异方差的性质


预测置信区间不准确
在异方差情况下，预测的置信区间可 能不准确，导致对预测结果的信任度 降低。
对统计推断的影响
统计推断有效性下
降
在异方差情况下，常用的统计推 断方法可能不再适用，导致推断 结果的不准确。
假设检验失效
在异方差情况下，假设检验的结 果可能受到影响，导致无法准确 地做出统计决策。
置信水平降低
由于异方差的存在，统计推断的 置信水平可能会受到影响，导致 对推断结果的信任度降低。
03
CATALOGUE
异方差的检验
图示检验法
残差图检验
通过绘制残差与拟合值的图形，观察 残差是否随拟合值的变动而出现系统 性模式，如随拟合值增大而逐渐增大 或减小。
QQ图检验
将残差与标准正态分布的期望值进行 比较，观察其是否落在预期的置信区 间内，判断残差是否服从正态分布。
总结词
医学研究数据中，由于个体差异、病情 进展和治疗方法等因素，常常表现出异 方差性。
VS
详细描述
在医学研究中，由于个体之间的差异、病 情进展的不同阶段以及治疗方法的多样性 等因素，数据分布往往不均匀。例如，不 同患者的生理指标、治疗效果等可能会有 很大的差异，导致数据异方差性的出现。
实例三：社会调查数据
通过计算残差的二次项与解释变量的线性组 合，构建统计量对异方差进行检验。
04
CATALOGUE
异方差的解决方法
数据变换法
平方根变换
通过取平方根的方式减小异方差的影 响，适用于数据分布为正态分布的情 况。
对数变换
通过取对数的方式减小异方差的影响 ，适用于数据分布为偏态分布的情况 。
幂变换
通过取幂的方式减小异方差的影响， 适用于数据分布为幂律分布的情况。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Y ˆi-563.05485.3735X i (2 9 1 .5 7 7 8 ) (0 .6 4 4 2 8 4 ) t ( - 1 .9 3 1 0 6 2 )( 8 .3 4 0 2 6 5 )
R20.785456 R20.774146 F69.56003
式中 Y 表示卫生医疗机构数（个）， X 表示人口数量
一、异方差及其影响
异方差可以表示为
Vairi2
或
12
22
Байду номын сангаас
ΩVarεEεε
n2
即对于不同的样本点，随机误差项的方差不再是常
数，而互不相同，则认为出现了异方差性。
异方差产生的原因
普遍性：两类数据都有，横截面数据更多。
原因：
1.按照边错边改学习模型，人们在学习过程中，其行为误
差随时间而减少。在这种情形下，方差
但该方法的有效性还依赖于C的选择，还 有，当模型出现多于一个X变量时，就可 以按任意一个X变量的大小顺序将观测值 排列。
（三）戈里瑟检验
e
e
Xj
0
a
0
b
Xj
e
0
Xj
c
（三）戈里瑟检验
通常拟合 e 和 X j 之间的回归模型：
eXlj
根据图形中的分布选择
l 1,2,1或1 2
还可以拟合 e 2 和 X j 之间的回归模型
（万人）。
模型显示的结果和问题
●人口数量对应参数的标准误差较小； ● t统计量远大于临界值，可决系数和修正的可决系 数结果较好，F检验结果明显显著； 表明该模型的估计效果不错，可以认为人口数量 每增加1万人，平均说来医疗机构将增加5.3735人。
然而，这里得出的结论可能是不可靠的，平均说来每增加1 万人口可能并不需要增加这样多的医疗机构，所得结论并 不符合真实情况。 有什么充分的理由说明这一回归结果不可靠呢？更为接近 真实的结论又是什么呢？
第六章异方差的性质
精品jin
异方差
一、异方差及其影响 二、假性异方差 三、异方差的发现和判断 四、异方差的克服和处理
引子：更为接近真实的结论是什么？
根据四川省2000年21个地市州医疗机构数与人口数资料，分 析医疗机构与人口数量的关系，建立卫生医疗机构数与人 口数的回归模型。对模型估计的结果如下：
三、异方差的发现和判断
检验思路： 由于异方差性就是相对于不同的解释变
量观测值，随机误差项具有不同的方差。 那么：
检验异方差性，也就是检验随机误差项 的方差与解释变量观测值之间的相关性及 其相关的“形式”。
（一）残差序列分析 （二）戈德菲尔德-夸特检验 （三）戈里瑟检验 （四）怀特检验
（一）残差序列分析
V i E a i 2 r E i 0 0 1 X i 2 1 X i2
若记 A X i 0 0 1 X i 2 1 X i 则 V i a E i r A X i 2 2 A 2 X i
异方差的危害
1、参数估计量非有效 OLS估计量仍然具有无偏性，但不具有 有效性
e22f Xj e
（四）怀特检验
怀特检验是通过建立辅助回归模型的方式来判断异方差的。 不妨设回归模型为三变量线性回归模型：
Y i01 X 1 i2 X 2 ii
怀特检验的具体步骤为：
（1）估计回归模型，得到每一个残差的平方e
2 i
（2）估计辅助回归模型：
e i 2 0 1 X 1 i 2 X 2 i 3 X 1 2 i 4 X 2 2 i 5 X 1 i X 2 i i
因为在有效性证明中利用了 E(’)=2I
而且，在大样本情况下，尽管参数估 计量具有一致性，但仍然不具有渐近有效 性。
2、变量的显著性检验失去意义
变量的显著性检验中，构造了t统计量
其他检验也是如此。
3、模型的预测失效
一方面，由于上述后果，使得模型不具有良好的 统计性质；
所以，当模型出现异方差性时，参数 OLS估计值的变异程度增大，从而造成对Y 的预测误差变大，降低预测精度，预测功能 失效。
2 i
会逐渐变小。
例如，随着打字练习小时数的增加，不仅平时打错的个
数而且打错的方差都有所下降。
2.随着收入的增长，人们有更多的备用收入，从而如何支 配他们的收入有更大的选择范围。因此，在作出储蓄对
收入的回归时，很可能发现，由于人们对其储蓄行为有 更司多比的之选于择已， 发展 i2定与型收的入公俱司增在。红因利此支，付以方增面长也为可导能向表的现公 更多的变异。
异方差产生的原因
3.随着数据采集技术的改进，
2 可能减小。例如，有
i
精巧数据处理设备的银行，在他们对账户的每月或
每季收支说明书中，比之于没有这种设备的银行，
会出现更少的差错。
4.异方差还会异常值的出现而产生。
5.异方差还会因为模型的设定错误而产生。
案例分析
例：截面资料下研究居民家庭的储蓄行为
Yi=0+1Xi+i
（二）戈德菲尔德-夸特检验
计算统计量：
ei22
F i2
ei21
i1
nc K1
2
i2
ei22
nc K1
2
ei21
i1
如果 F F ，误差项存在明显的递增异方差
性；
如果1FF，误差项没有明显的异方差性。
（二）戈德菲尔德-夸特检验
对于递减异方差性模型，检验的方法相似， 只要把前面构造的F统计量的分子分母互 换，就可以用同样的程序检验模型是否存 在递减型的异方差问题。
(a)
e
i
X k
(b)
e
i
X k
(c)
e
i
X k
(d)
e
i
X k
(e)
e
i
X k
(f)
e
i
X k
（二）戈德菲尔德-夸特检验
戈德菲尔德-夸特检验是最常用的异方差专门检 验方法之一。这种方法适合于检验样本容量较大 的线性回归模型的递增或递减型异方差性。
对于存在递增异方差模型，步骤：首先将样本按 X值的大小顺序将观测值排列，然后略去居中的C 个观测值，并将其余的(n-C)个观测值分成两组， 每组(n-C)/2个，分别对两个子样本进行回归， 并分别获得残差平方和，自由度都为（n-C)/2K-1。
Yi:第i个家庭的储蓄额 Xi:第i个家庭的可支 配收入 高收入家庭：储蓄的差异较大 低收入家庭：储蓄则更有规律性，差异较 小
i的方差呈现单调递增型变化
二、假性异方差
有些定式误差也会表现出异方差的特征
例：真实关系为 Y01X2 ，其中
满足线性回归模型所有假设，包括Ei0
和 Vari2 。
如果误以为模型为Y0 1 X，那么