下载文档原格式
最优化理论与方法什么是最优化？最优化是一种以最佳结果为目标的技术。
它的主要任务是寻找最佳的解决方案，以最小的代价来实现目标。
本文将从定义、方法、应用等几个方面来探讨最优化理论与方法。
一、简介最优化是一种研究变量空间中满足限制条件下实现最大和最小化的解决问题的科学。
它是一种数学理论，用于求解多变量最优化问题的数学模型，包括线性规划、非线性规划、动态规划等。
它的思想是：希望能够将一个复杂的解决问题分解成若干简单的子问题，以便更好地求解。
最优化理论是一种科学，它涉及到多重条件下的变量求值，以实现最大化或最小化某个系统的特定性能或目标。
最优化理论可以应用于各种工程领域，如机械、航空、船舶、结构、动力、电力能源、汽车等。
二、原理最优化方法基于一组影响结果的变量，以及它们的限制条件。
主要的最优化方法可以分为精确法和近似法。
精确法求解非线性规划问题，其最终结果非常精确，但求解它的计算代价更高。
而近似法的最终结果仅大致最优，但求解计算代价较低，广泛用于工程优化设计。
最优化方法解决的问题可以分为有约束和无约束两大类。
有约束优化问题指系统内各变量受到某些限制条件的制约。
而无约束优化问题不需要考虑任何限制条件，只要达到优化目标即可。
三、应用最优化方法在工程和科学领域中有着广泛的应用，并且日益增多。
在机械设计领域，可以采用最优化方法优化设计结构的参数和性能，以更好地满足设计要求；在空间控制领域，可以采用最优化方法优化机械系统的控制参数；在机器人规划领域，可以采用最优化方法解决运动规划问题；在多异构系统优化设计领域，可以采用最优化方法综合优化系统的性能等。
最优化的应用不仅仅限于以上领域，还广泛应用于其他领域，如计算机图形学、信号处理、投资组合管理、生物学、医学、金融、科学计算等。
四、结论最优化理论与方法是一种研究变量空间中满足限制条件下实现最大和最小化的解决问题的科学，它的主要目标是寻找最佳的解决方案，以最小的代价来实现目标。
最优化原理与方法薛毅最优化原理与方法是指利用数学模型和计算方法，寻找某一目标函数的最优解的理论体系。
优化问题在实际中广泛存在，如工程设计、经济决策、生产调度等等。
最优化方法是解决这些问题的有力工具，而最优化原理是指导这些方法的理论基础。
最优化方法能够帮助我们在复杂的问题中找到最优解，提高效率和效益，因此在现代科学技术和实践应用中具有重要作用。
最优化原理主要包括两方面内容：一是最优化问题的形式化表示，二是最优化问题的解法。
最优化问题的形式化表示指的是将实际问题抽象为数学模型，确定目标函数和约束条件，并将其表示为数学公式的过程。
目标函数是指需要优化的目标，约束条件则是对目标函数的限制条件。
一般地，最优化问题可以用如下形式的数学模型来表示：\begin{aligned}\min_{x} f(x) \\\text{s.t.} \quad g_i(x) \le 0, \quad i=1,2,\ldots,m \\\;\;\;\;h_j(x) = 0, \quad j=1,2,\ldots,p\end{aligned}其中f(x) 是目标函数，g_i(x) 和h_j(x) 是约束条件。
问题的解是指满足所有约束条件的最小值\min_{x} f(x) 所对应的x 值。
最优化问题的解法可以分为解析方法和数值方法两种。
解析方法主要是利用数学分析的手段，对问题的数学模型进行推导和分析，得出最优解的解析公式。
这种方法的优点是可以直接得到最优解的解析式，比较精确和可靠；缺点是只能解决简单的问题，并且往往需要较高的数学背景和技能。
常见的解析方法有拉格朗日乘数法、KKT条件法等。
数值方法则是通过迭代算法，以数值计算的方式逐步逼近最优解。
这种方法的优点是可以解决复杂问题，适用性较广；缺点是需要选择合适的算法和参数，且结果可能只是近似解。
常见的数值方法有单纯性法、梯度下降法、牛顿法等。
最优化原理和方法的关键在于如何选择合适的数学模型和解法，以得出符合实际需要的最优解。
最优化原理与算法教学大纲第一章：优化原理
1.1优化原理概述
1.1.1优化原理的定义
1.1.2优化原理的基本思想
1.2无约束最优化原理
1.2.1无约束最优化的定义
1.2.2无约束最优化的基本原理
1.2.3无约束最优化的类型
1.3约束最优化原理
1.3.1约束最优化的定义
1.3.2约束最优化的基本原理
1.3.3约束最优化的类型
第二章：优化算法
2.1优化算法概述
2.1.1优化算法的定义
2.1.2优化算法的基本思想
2.2无约束最优化算法
2.2.1梯度下降法
2.2.2随机梯度下降法
2.2.3拟牛顿法
2.2.4动量法
2.2.5随机加权平均法
2.2.6贪心法
2.3约束最优化算法
2.3.1最小二乘法
2.3.2拉格朗日乘数法
2.3.3拉格朗日对偶形式法2.3.4快速拉格朗日方法
2.3.5牛顿法
2.3.6半牛顿法
第三章：优化算法实例分析3.1多元线性回归最小二乘法3.1.1线性拟合
3.1.2最小二乘法
3.1.3精确解求解
3.2线性规划牛顿法
3.2.1线性规划模型
3.2.2从拉格朗日函数构造出对偶形式3.2.3拉格朗日乘数法分析及牛顿法求解3.3梯度下降法
3.3.1梯度下降法概述
3.3.2单次梯度下降法分析
3.3.3批梯度下降法分析。
数学中的优化理论与最优化方法一、优化理论概述1.优化理论的定义：优化理论是研究如何从一组给定的方案中找到最优方案的数学理论。
2.优化问题的类型：–无约束优化问题–有约束优化问题3.优化问题的目标函数：–最大值问题–最小值问题二、无约束优化方法1.导数法：–单调性：函数在极值点处导数为0–凸性：二阶导数大于0表示函数在该点处为凸函数2.梯度下降法：–基本思想：沿着梯度方向逐步减小函数值–步长：选择合适的步长以保证收敛速度和避免振荡3.牛顿法（Newton’s Method）：–基本思想：利用函数的一阶导数和二阶导数信息，构造迭代公式–适用条件：函数二阶连续可导，一阶导数不间断三、有约束优化方法1.拉格朗日乘数法：–基本思想：引入拉格朗日乘数，将有约束优化问题转化为无约束优化问题–适用条件：等式约束和不等式约束2.库恩-塔克条件（KKT条件）：–基本思想：优化问题满足KKT条件时，其解为最优解–KKT条件：约束条件的斜率与拉格朗日乘数相等，等式约束的拉格朗日乘数为03.序列二次规划法（SQP法）：–基本思想：将非线性优化问题转化为序列二次规划问题求解–适用条件：问题中包含二次项和线性项四、最优化方法在实际应用中的举例1.线性规划：–应用领域：生产计划、物流、金融等–目标函数：最大化利润或最小化成本–约束条件：资源限制、产能限制等2.非线性规划：–应用领域：机器人路径规划、参数优化等–目标函数：最大化收益或最小化成本–约束条件：物理限制、技术限制等3.整数规划：–应用领域：人力资源分配、设备采购等–目标函数：最大化利润或最小化成本–约束条件：资源限制、整数限制等4.动态规划：–应用领域：最短路径问题、背包问题等–基本思想：将复杂问题分解为多个子问题，分别求解后整合得到最优解5.随机规划：–应用领域：风险管理、不确定性优化等–基本思想：考虑随机因素，求解期望值或最坏情况下的最优解数学中的优化理论与最优化方法是解决实际问题的重要工具，掌握相关理论和方法对于提高问题求解能力具有重要意义。
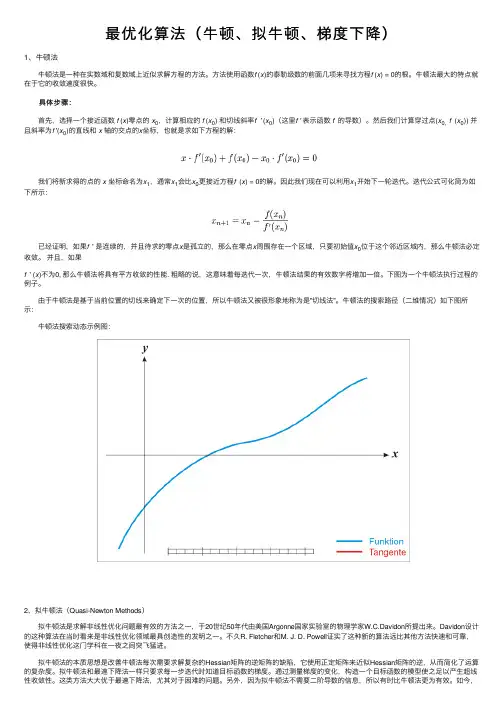
最优化算法（⽜顿、拟⽜顿、梯度下降）1、⽜顿法 ⽜顿法是⼀种在实数域和复数域上近似求解⽅程的⽅法。
⽅法使⽤函数f (x)的泰勒级数的前⾯⼏项来寻找⽅程f (x) = 0的根。
⽜顿法最⼤的特点就在于它的收敛速度很快。
具体步骤： ⾸先，选择⼀个接近函数f (x)零点的x0，计算相应的f (x0) 和切线斜率f ' (x0)（这⾥f ' 表⽰函数f 的导数）。
然后我们计算穿过点(x0, f (x0)) 并且斜率为f '(x0)的直线和x 轴的交点的x坐标，也就是求如下⽅程的解： 我们将新求得的点的x 坐标命名为x1，通常x1会⽐x0更接近⽅程f (x) = 0的解。
因此我们现在可以利⽤x1开始下⼀轮迭代。
迭代公式可化简为如下所⽰： 已经证明，如果f ' 是连续的，并且待求的零点x是孤⽴的，那么在零点x周围存在⼀个区域，只要初始值x0位于这个邻近区域内，那么⽜顿法必定收敛。
并且，如果f ' (x)不为0, 那么⽜顿法将具有平⽅收敛的性能. 粗略的说，这意味着每迭代⼀次，⽜顿法结果的有效数字将增加⼀倍。
下图为⼀个⽜顿法执⾏过程的例⼦。
由于⽜顿法是基于当前位置的切线来确定下⼀次的位置，所以⽜顿法⼜被很形象地称为是"切线法"。
⽜顿法的搜索路径（⼆维情况）如下图所⽰： ⽜顿法搜索动态⽰例图：2、拟⽜顿法（Quasi-Newton Methods） 拟⽜顿法是求解⾮线性优化问题最有效的⽅法之⼀，于20世纪50年代由美国Argonne国家实验室的物理学家W.C.Davidon所提出来。
Davidon设计的这种算法在当时看来是⾮线性优化领域最具创造性的发明之⼀。
不久R. Fletcher和M. J. D. Powell证实了这种新的算法远⽐其他⽅法快速和可靠，使得⾮线性优化这门学科在⼀夜之间突飞猛进。
拟⽜顿法的本质思想是改善⽜顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷，它使⽤正定矩阵来近似Hessian矩阵的逆，从⽽简化了运算的复杂度。
最优化原理与方法最优化原理与方法是研究如何寻找最优解的一门学科，它在数学、计算机科学、经济学、工程学等领域有着广泛的应用。
最优化问题涉及到在给定的约束条件下，如何找到使目标函数取得最值的变量取值。
最优化原理与方法的核心是通过建立数学模型，利用一些数学工具和算法来求解这些问题。
最优化问题可以分为两类：无约束优化问题和有约束优化问题。
无约束优化问题是指在没有额外限制条件的情况下，寻找目标函数的最值。
而有约束优化问题是指在满足一定限制条件的情况下，寻找目标函数的最值。
在最优化原理与方法中，常用的方法有：梯度下降法、牛顿法、拟牛顿法、线性规划、非线性规划等。
梯度下降法是一种常用的无约束优化方法，其基本思想是通过对目标函数求偏导数，得到目标函数在当前点的斜率，然后沿着负梯度的方向更新当前点的位置，以减小目标函数的值。
梯度下降法是一种迭代求解方法，每一次迭代都会向着使目标函数减小的方向前进，直到达到一定的精度要求或迭代次数。
牛顿法是一种迭代求解方法，通过利用函数的二阶导数信息来逼近函数的极值点。
牛顿法的关键是通过二阶导数的信息得到更准确的目标函数变化趋势，从而更快地找到函数的极值点。
牛顿法收敛速度快，但需要计算较为复杂的二阶导数，且对于非凸问题可能出现收敛到局部极小值点的情况。
拟牛顿法是一种在牛顿法基础上改进的方法，主要用于求解无约束优化问题。
拟牛顿法通过近似目标函数的二阶导数来逼近极值点，从而避免了计算目标函数的二阶导数的复杂性。
拟牛顿法常用的算法有DFP算法和BFGS算法，它们通过不断更新近似的Hessian矩阵来求解极值点，具有较好的收敛性能和计算效率。
线性规划是一种在约束条件为线性等式或不等式的情况下，求解线性目标函数最优解的方法。
线性规划是最优化原理与方法的重要领域之一，广泛应用于经济学、工程学、运筹学等领域。
线性规划的基本思想是将目标函数和约束条件表示为线性表达式，然后应用线性规划的算法来求解最优解。
第一章、预备知识一、考虑二次函数()2211221223f X x x x x x x =++-+1) 写出它的矩阵—向量形式: ()f X =12TTQx x xb +2) 矩阵Q 是不是奇异的? 3) 证明: f(x)是正定的 4) f(x)是凸的吗? 5) 写出f(x)在点x =()2,1T处的支撑超平面(即切平面)方程解: 1) f(x)=xx x x x x2122212132+-++=⎪⎪⎭⎫ ⎝⎛x x 2121⎪⎪⎭⎫⎝⎛6222⎪⎪⎭⎫ ⎝⎛x x 21+11T-⎛⎫ ⎪⎝⎭⎪⎪⎭⎫ ⎝⎛x x 21 其中 x=⎪⎪⎭⎫ ⎝⎛x x 21 ,Q=⎪⎪⎭⎫ ⎝⎛6222, b=⎪⎪⎭⎫⎝⎛-11 2) 因为Q=⎪⎪⎭⎫ ⎝⎛6222,所以 |Q|=6222=8>0 即可知Q 是非奇异的3) 因为|2|>0, 6222=8>0 ,所以Q 是正定的,故f(x)是正定的4) 因为2()f x ∇=⎪⎪⎭⎫ ⎝⎛6222,所以|)(2x f ∇|=8>0,故推出)(2x f ∇是正定的, 即)(2x f ∇是凸的5) 因为)(x f ∇=2121(2x 2-1,261)x x x T+++,所以)(x f ∇=(5,11)所以 ()f x 在点x 处的切线方程为5(21-x )+11(12-x )=0 二、 求下列函数的梯度问题和Hesse 矩阵 1) ()f x =2x 12+xx x x x 23923121+++x x x 2322+2) ()f x =2212()21n l x x x x ++解: 1) )(x f ∇= (,94321x xx ++ 26321+++xx x, xx 219+))(2x f ∇=⎪⎪⎪⎭⎫ ⎝⎛019161914 2) )(x f ∇=(x x x x xx 112221221+++,x x x x x x112221221+++))(2x f ∇=⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----------++++++++)()()()(2221212222212142221214222121222222121222212122221212212122x x x x x x x x x x x x x x x x x x x x xx x xx x x x x x x x 三、 设f(x)=xx x x x x x323223322122--+++,取点)1,1,1()1(Tx=.验证d )1(=(1,0,-1)是f(x)在点x )1(处的一个下降方向,并计算min >t f(x )1(+t d)1()证明: )(x f ∇=)124,123,x 2(233221-+-+x x x x T)5,4,2()(1Tx f =∇d )(1x f ∇=(1,0,-1)⎪⎪⎪⎭⎫ ⎝⎛542= -3<0所以d)1(是f(x)在x )1(处的一个下降方向f(x )1(+t d)1()=f((1+t,1,1-t))=433)1(1)1(221(222)1()1+-=----+++-+t t t t t t∇f(x )1(+t d)1()=6t-3=0 所以t=0.5>0所以0min >t f(x )1(+t d)1()=3*0.25-3*0.5+4=3.25四、设,,i i i a b c （j=1,2,….,n ）考虑问题Min f(x)=∑=nj jj xc 1s.t. b nj jjxa =∑=10≥xj(j=1,2,….,n)1) 写出其Kuhn Tuker 条件 2) 证明问题最优值是])([12112∑=nj j j b c a解：1）因),....,1(n j x j = 为目标函数的分母故0>x j所以λ*j （j=1,…,n ）都为0所以Kuhn Tuker 条件为 0)()(=∇+∇x h x f μ即 ⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---x c x c x c n n 2222211 +⎪⎪⎪⎪⎪⎭⎫ ⎝⎛a a a n 21μ=0 2）将ac xjjjμ=代入 h(x)=0 只有一点得221(nj b n j bμ==⇒=∑=故有ac ca x jj nj jjj b∑==1所以最优解是21211()n j j j b a c =⎡⎤⎢⎥⎢⎥⎣⎦∑.五、使用Kuhn Tuker 条件，求问题min f(x)=)2()1(2122--+x xs.t.,021212112≥≥=+=-x x x x x x 的Kuhn Tuker 点，并验证此点为问题的最优解 解：x=(1/2,3/2) 0≠ 故1λ*，λ*2=0 则 0)()()(2211=+∇+∇x x x f h h μμ 即0111142222121=⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛--μμx x ⇒120,1μμ==-而⎪⎪⎭⎫ ⎝⎛=∇2002)(2x f ()210g x *∇= ()220g x *∇= ()210h x *∇=()220h x *∇=,()()()()()()()22222211221122H x f x g x g x h x h x f x λλμμ***********=∇+∇+∇+∇+∇=∇(){}{}12121213|00|1020,22T T T x y h y h y y y y y y *⎧⎫⎛⎫=∇=∇==-+-=+-==⎨⎬⎪⎝⎭⎩⎭故08)(2>=∇x x f x T ,即其为最优解.第二章、无约束优化问题一、设f(x)为定义在区间[a,b]上的实值函数，x *是问题min{f(x)|a b x ≤≤}的最优解。
