(完整word版)振动力学 概念题

，即
令 引起的静变形为 ，则有：
，即
令 + 引起的静变形为 ，同理有：
得：
则系统的自由振动可表示为：
其中系统的固有频率为：
注意到 与 方向相反，得系统的自由振动为：
1.9质量为m、长为l的均质杆和弹簧k及阻尼器c构成振动系统，如图E1.9所示。以杆偏角 为广义坐标，建立系统的动力学方程，给出存在自由振动的条件。若在弹簧原长处立即释手，问杆的最大振幅是多少？发生在何时？最大角速度是多少？发生在何时？是否在过静平衡位置时？
解：
（1）保持水平位置：
（2）微幅转动：
故：
2.10求图T 2-10所示系统的固有频率，刚性杆的质量忽略不计。
图T 2-10答案图T 2-10
解：
m的位置：
， ，
，
，
2.11图T 2-11所示是一个倒置的摆。摆球质量为m，刚杆质量可忽略，每个弹簧的刚度为 。
（1）求倒摆作微幅振动时的固有频率；
（2）摆球质量m为0.9 kg时，测得频率 为1.5 Hz，m为1.8 kg时，测得频率为0.75 Hz，问摆球质量为多少千克时恰使系统处于不稳定平衡状态？
图E1.2
解：
如图，令 为柱体的转角，则系统的动能和势能分别为：
利用 和 可得：
1.3转动惯量为J的圆盘由三段抗扭刚度分别为 ， 和 的轴约束，如图E1.3所示。求系统的固有频率。
图E1.3
解：
系统的动能为：
和 相当于串联，则有：
以上两式联立可得：
系统的势能为：
利用 和 可得：
1.4在图E1.4所示的系统中，已知 ，横杆质量不计。求固有频率。
图E1.4答案图E1.4
解：
对m进行受力分析可得：

物理振动试题及答案解析1. 简谐运动的振动周期与哪些因素有关？答案：简谐运动的振动周期与振子的质量以及弹簧的劲度系数有关，与振幅无关。

2. 什么是阻尼振动？其振动周期与自由振动相比有何不同？答案：阻尼振动是指在振动过程中受到阻力作用的振动。

与自由振动相比，阻尼振动的振动周期会变长。

3. 简述单摆的周期公式。

答案：单摆的周期公式为 \( T = 2\pi \sqrt{\frac{L}{g}} \)，其中 \( T \) 是周期，\( L \) 是摆长，\( g \) 是重力加速度。

4. 什么是共振现象？请举例说明。

答案：共振现象是指当驱动力的频率接近或等于系统的固有频率时，系统振幅急剧增大的现象。

例如，当行人在桥上行走时，如果步频与桥的固有频率接近，可能会引起桥梁的共振，导致桥梁剧烈振动甚至断裂。

5. 请解释为什么在声波传播中，频率越高的声波传播距离越短？答案：频率越高的声波波长越短，波长越短的声波在传播过程中更容易受到空气分子的散射作用，因此传播距离较短。

6. 什么是多普勒效应？请用物理公式表达。

答案：多普勒效应是指当波源和观察者相对运动时，观察者接收到的波频率与波源发出的频率不同的现象。

多普勒效应的公式为 \( f'= \frac{f(u + v)}{u + v \cos \theta} \)，其中 \( f' \) 是观察者接收到的频率，\( f \) 是波源发出的频率，\( u \) 是波源的速度，\( v \) 是观察者的速度，\( \theta \) 是波源和观察者之间的夹角。

7. 请解释为什么在弹簧振子的振动过程中，振幅会逐渐减小？答案：在弹簧振子的振动过程中，振幅逐渐减小是因为存在阻力作用，如空气阻力或摩擦阻力，这些阻力会消耗振子的机械能，导致振幅减小。

8. 什么是机械波？请列举三种常见的机械波。

答案：机械波是指需要介质传播的波，其传播过程中介质的质点并不随波迁移，而是在平衡位置附近做振动。

振动力学的60对概念1 广义坐标与自由度广义坐标：能够完全确定系统在运动过程中的某一瞬时在空间所处的几何位置与形状的独立参变量。

自由度：系统独立坐标的数目。

2 线性振动与非线性振动根据系统运动微分方程的性质划分，微分方程中只包含位移、速度的一次方项称为线型振动，如果还包含位移、速度的二阶或高阶项则是非线性振动。

3 离散（集中参数)系统与连续（分布参数）系统单自由度和多自由度振动系统统称为离散系统.无限自由度系统具有连续分布的质量与连续分布的弹性，称为分布参数系统。

4角振动与扭转振动角振动：振动按位移的特征分为直线振动和角振动。

当质点只作围绕轴线的振动，就称为角振动。

扭转振动：弹性体绕其纵轴产生扭转变形的振动。

5 简谐振动与谐波分析用时间t的正弦或余弦函数表示的运动规律称为简谐振动。

一般的周期振动可以借助傅里叶级数表示成一系列简谐振动的叠加，该过程称为谐波分析.6 简谐振动的振幅与相位角振幅：振动物体离开平衡位置的最大距离叫振动的振幅.相位角：某一物理量随时间（或空间位置）作正弦或余弦变化时,决定该量在任一时刻（或位置)状态的一个数值。

7 简谐振动的周期与频率一次振动循环所需的时间T称为周期；单位时间内振动循环的次数f称为频率.8 简谐振动的旋转矢量与复指数描述方法（书P4页图1-2 公式1—6）9 幅值谱与相位谱在信号的频域描述中，以频率作为自变量,以组成信号的各个频率成分的幅值作为因变量，这样的频率函数称为幅值谱,它表征信号的幅值随频率的分布情况。

相位谱，指的是相位随频率变化的曲线，是信号的重要特征之一。

10粘性阻尼与等效粘性阻尼粘性阻尼，是振动系统的运动受大小与运动速度成正比而方向相反的阻力所引起的能量损耗。

等效粘性阻尼:11临界阻尼与阻尼比任何一个振动系统，当阻尼增加到一定程度时，物体的运动是非周期性的,物体振动连一次都不能完成，只是慢慢地回到平衡位置就停止了.当阻力使振动物体刚能不作周期性振动而又能最快地回到平衡位置的情况，称为“临界阻尼”。

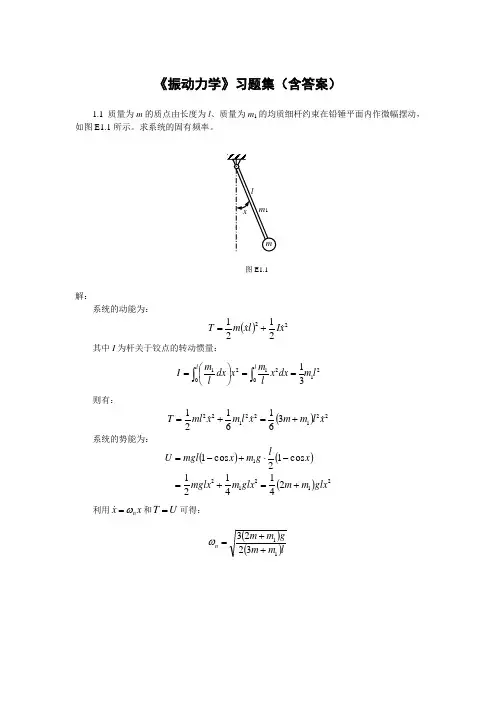
《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

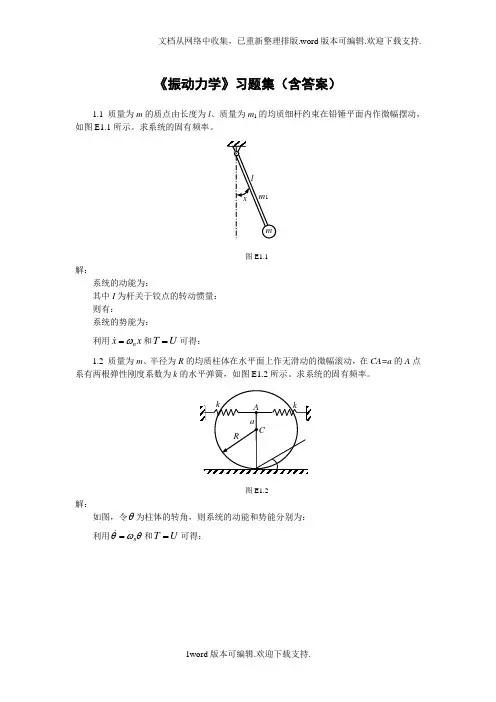
图E1.1解： 系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解： 系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得：()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得：()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

图T 2-2答案图T 2-2
解：
，
动量守恒：
，
平衡位置：
，
，
故：
故：
2.4在图E2.4所示系统中，已知m， ， ， 和 ，初始时物块静止且两弹簧均为原长。求物块运动规律。
图E2.4答案图E2.4
解：
取坐标轴 和 ，对连接点A列平衡方程：
即：
（1）
对m列运动微分方程：
即：
（2）
由（1），（2）消去 得：
图E2.7
解：
，
s=1时共振，振幅为：
（1）
远离共振点时，振幅为：
（2）
由（2）
由（1）
， ，
故：
2.7求图T 2-7中系统的固有频率，悬臂梁端点的刚度分别是 及 ，悬臂梁的质量忽略不计。
图T 2-7答案图T 2-7
解：
和 为串联，等效刚度为： 。（因为总变形为求和）
和 为并联（因为 的变形等于 的变形），则：
图E1.9答案图E1.9
解：
利用动量矩定理得：
，
，
，
，
1.12面积为S、质量为m的薄板连接于弹簧下端，在粘性流体中振动，如图E1.12所示。作用于薄板的阻尼力为 ，2S为薄板总面积，v为速度。若测得薄板无阻尼自由振动的周期为 ，在粘性流体中自由振动的周期为 。求系数 。
图E1.12
解：
平面在液体中上下振动时：
和 为串联（因为总变形为求和），故：
故：
2.9如图T 2-9所示，一质量m连接在一刚性杆上，杆的质量忽略不计，求下列情况系统作垂直振动的固有频率：
（1）振动过程中杆被约束保持水平位置；
（2）杆可以在铅锤平面内微幅转动；
（3）比较上述两种情况中哪种的固有频率较高，并说明理由。

图答案图
解：
利用动量矩定理得：
，
，
，
，
面积为S、质量为m的薄板连接于弹簧下端，在粘性流体中振动，如图所示。作用于薄板的阻尼力为 ，2S为薄板总面积，v为速度。若测得薄板无阻尼自由振动的周期为 ，在粘性流体中自由振动的周期为 。求系数 。
图
解：
平面在液体中上下振动时：
，
，
图所示系统中，已知m，c， ， ， 和 。求系统动力学方程和稳态响应。
（2）
若取下面为平衡位置，求解如下：
，
图T 2-17所示的系统中，四个弹簧均未受力，k1=k2=k3=k4=k，试问：
（1）若将支承缓慢撤去，质量块将下落多少距离？
（2）若将支承突然撤去，质量块又将下落多少距离？
图T 2-17
解：
（1） ，
（2） ，
如图T 2-19所示，质量为m2的均质圆盘在水平面上可作无滑动的滚动，鼓轮绕轴的转动惯量为I，忽略绳子的弹性、质量及各轴承间的摩擦力，求此系统的固有频率。
因此有：
图所示阶梯杆系统中已知m，ρ，S，E和k。求纵向振动的频率方程。
图
解：
模态函数的一般形式为：
题设边界条件为：
，
边界条件可化作：
，
导出C2= 0及频率方程：
，其中
长为l、密度为ρ、抗扭刚度为GIp的的等直圆轴一端有转动惯量为J的圆盘，另一端连接抗扭刚度为k的弹簧，如图所示。求系统扭振的频率方程。
《振动力学》习题集（含答案）
质量为m的质点由长度为l、质量为m1的均质细杆约束在铅锤平面内作微幅摆动，如图所示。求系统的固有频率。
图
解：
系统的动能为：
其中I为杆关于铰点的转动惯量：

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得：()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得：()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

《振动力学》习题集（含答案）质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图所示。

求系统的固有频率。

图-解： 系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l⎰⎰==⎪⎭⎫ ⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： [()()lm m g m m n 113223++=ω质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图所示。

求系统的固有频率。

图解：:如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω：转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图所示。

求系统的固有频率。

，图解： 系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：]()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω：在图所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

1、简谐运动的概念①简谐运动的定义：____________________________________________________________。

②简谐运动的物体的位移x、回复力F、加速度a、速度v、动能E K、势能E P的变化规律：A．在研究简谐运动时位移的起点都必须在处。

B．在平衡位置：位移最、回复力最、加速度最；速度最、动能最。

C．在离开平衡位置最远时：_________________________________________。

D．振动中：注意以上各量的矢量性和对称性。

③简谐运动机械能守恒，但机械能守恒的振动不一定时简谐运动。

④注意：A．回复力是效果力。

B．物体运动到平衡位置不一定处于平衡状态(如单摆，最低点有向心力)。

C．简谐运动定义式F=-K x中的K不一定是弹簧的劲度系数，是振动系数（如双弹簧）。

1.A关于回复力,下列说法正确的是( )A.回复力一定是物体受到的合外力B.回复力只能是弹簧的弹力提供C.回复力是根据力的作用效果命名的D.回复力总是指向平衡位置答案:CD2.A下列的运动属于简谐运动的是( )A.活塞在气缸中的往复运动B.拍皮球时,皮球的上下往复运动C.音叉叉股的振动D.小球在左右对称的两个斜面上来回滚动答案:C3.A一质点做简谐运动,当位移为正的最大值时,质点的( )A.速度为正的最大值,加速度为零B.速度为负的最大值,加速度为零C.速度为零,加速度为正的最大值D.速度为零,加速度为负的最大值答案:D4.A关于简谐运动的位移、加速度和速度的关系,正确的说法是( )A.位移减小时,加速度增大,速度增大B.位移方向总和加速度方向相反,和速度方向相同C.物体的速度增大时,加速度一定减小D.物体向平衡位置运动时,速度方向和位移方向相同答案:C6.B关于简谐运动中的平衡位置,下列说法正确的是( )A.平衡位置就是物体所受合外力为零的位置B.平衡位置就是加速度为零的位置C.平衡位置就是回复力为零的位置D.平衡位置就是受力平衡的位置答案:C7.B一平台沿竖直方向做简谐运动,一物体置于平台上随台一起运动,当振动平台处于什么位置时,物体对台面的压力最大( )A.振动平台在最高位置时B.振动平台向下振动经过平衡位置时C.振动平台在最低位置时D.振动平台向上运动经过平衡位置时答案:C8.B简谐运动是下列哪一种运动( )A.匀速直线运动B.匀加速运动C.匀变速运动D.变加速运动答案:D9.B做简谐运动的物体每次经过同一位置时,一定相同的物理量是( )A.速度B.位移C.回复力D.加速度答案:BCD10.B 对于弹簧振子,其回复力和位移的关系,在下图中正确的是()答案:C11.C 对简谐运动的回复力F=-kx 的理解,正确的是()A.k 只表示弹簧的劲度系数B.式中负号表示回复力总是负值C.位移x 是相对平衡位置的位移D.回复力只随位移变化,不随时间变化答案:C12.C 弹簧振子的质量是0.2kg,在水平方向做简谐运动,当它运动到平衡位置左侧x 1=2cm 的位置时,受到的回复力大小F 1=4N,则当它运动到平衡位置右侧x 2=4cm 的位置时,它的加速度是()A.20m/s 2,方向向左 B20m/s 2,方向向右C.40m/s 2,方向向左 D.40m/s 2,方向向右答案:C二、计算题(共16分)13.C 试证明:用轻弹簧悬挂一个振子,让它在竖直方向振动起来,在弹性限度内,振子是做简谐运动.(如图)答案:设振子的平衡位置为O,令向下为正方向,此时弹簧的形变为x 0,根据胡克定律及平衡条件有mg-kx 0=0.当振子向下偏离平衡位置x 时,有F=mg-k(x+x 0) 整理可得F=-kx(紧扣简谐运动特征及对称性)故重物的振动满足简谐运动的条件 2、总体上描述简谐运动的物理量①振幅A ：_ _称为振幅。

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解： 系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解： 系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

一、选择题：1．3001：把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时。

若用余弦函数表示其运动方程，则该单摆振动的初相为(A) π (B) π/2 (C) 0 (D) θ ［ ］2．3002：两个质点各自作简谐振动，它们的振幅相同、周期相同。

第一个质点的振动方程为x 1 = A cos(ωt + α)。

当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处。

则第二个质点的振动方程为：(A))π21cos(2++=αωt A x (B) )π21cos(2-+=αωt A x (C))π23cos(2-+=αωt A x (D) )cos(2π++=αωt A x ［ ］3．3007：一质量为m 的物体挂在劲度系数为k 的轻弹簧下面，振动角频率为ω。

若把此弹簧分割成二等份，将物体m 挂在分割后的一根弹簧上，则振动角频率是(A) 2 ω (B) ω2 (C) 2/ω (D) ω /2 ［ ］4．3396：一质点作简谐振动。

其运动速度与时间的曲线如图所示。

若质点的振动规律用余弦函数描述，则其初相应为 (A) π/6 (B) 5π/6 (C) -5π/6 (D) -π/6 (E) -2π/3 ［ ］5．3552：一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T 1和T 2。

将它们拿到月球上去，相应的周期分别为1T '和2T '。

则有(A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >' ［ ］ 6．5178：一质点沿x 轴作简谐振动，振动方程为)312cos(1042π+π⨯=-t x (SI)。

机械振动习题集同济大学机械设计研究所2004．91_简谐运动及其运算1-1 求下列简谐函数的单边复振幅和双边复振幅(1) x 2sin( t )(2) x 4 cos(10 t ) ( 3) x 3 cos(2 t 45 )341-2 通过简谐函数的复数表示，求下列简谐函数之和。

(1)x12sin( t 3)x23sin( t3)(2)x15sin 10 tx 24 cos(10 t4)(3) x 1 4 sin(2 t 30 ) x 2 5 sin( 2 t 60 )x 3 3cos(2 t 45 )x 47cos(2 t38 )x 5 2 cos(2 t 72 )答案：(1) x 124.359 cos( t 6.6)(2) x 12 3.566 cos(10 t 47.52 )(3) x 12345 14.776 cos(2 t9.22 )1-3试计算题 1中 x(t)的一阶对数和二阶导数对应的复振幅，并给出它们的时间历程。

1-4 设 x(t)、 f(t) 为同频简谐函数，并且满足 ax bx cx f(t) 。

试计算下列问题 (1)已知 a 1.5,b 6,c 25,x(t) 10 sin(12 37 ) ，求 f(t)(2)已知 a 3,b 7,c 30, f (t) 25 sin(7 64 )，求 x(t)1-5 简述同向异频简谐振动在不同频率和幅值下合成的不同特点。

1-6 利用“振动计算实用工具” ，通过变换频率和相位总结垂直方向振动合成的特点。

2_单自由度系统振动2-1 请解释有阻尼衰减振动时的固有圆频率d为什么总比自由振动时的固有圆频率n小？答案：因为 d 1 2 n ， <12-2 在欠阻尼自由振动中，把 改成 0.9 的时候，有人说曲线不过 X 轴了，这种说法正确么，请说明理由？答案： <1 为小阻尼的衰减振动，当然过 X 轴2-3 在单自由度自由振动时候，给定自由振动时的固有圆频率n ,阻尼系数 ,初始位移 x 0,以及初始速度 v 0 ,利用本计算工具 ,请计算有阻尼衰减振动时的固有圆频率d .答案：如n =3rad/s, =0.01, x 0 =-1, v 0=0;则 d =2.9985rad/s 2-4 如图 2-1 所示，一小车(重 P )自高 h 处沿斜面滑下，与缓冲器相撞后，随同缓冲器一 起作自由振动。

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

第九章振动复习题1. 一轻弹簧，上端固定，下端挂有质量为 m 的重物，其自由振动的周期为 T .今已知 振子离开平衡位置为 x 时，其振动速度为 v ，加速度为a .则下列计算该振子劲度系数的公 式中，错误的是： (A) k 2 . 2mvmax / xmax . (B) k mg / x . (C) k 2 24 m/T . (D) k ma/x . 2. 一长为 作成一复摆. I 的均匀细棒悬于通过其一端的光滑水平固定轴上， 1 2J -ml 2，此摆作微小振 3 已知细棒绕通过其一端的轴的转动惯量 动的周期为 (A) 2 (C) 2 fir忖(B) 2 1—()Vgrrfe .(D ) (如图所示)， 3.把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度 后由静止放手任其振动， 的初相为 从放手时开始计时.若用余弦函数表示其运动方程, O ，然 则该单摆振动 (A). (C) 0 . 4.两个质点各自作简谐振动，它们的振幅相同、周期相同.第一个质点的振动方程为 X 1 = Acos( t + ).当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个 质点正在最大正位移处.则第二个质点的振动方程为 1 2n ).2n. (B) /2. (D). (A ) (C )X 2X 2Acos( tAcos( t(B) x 2Acos((D) x 2 A cos(:6. 一质点作简谐振动.其运动速度与时间的曲线如图所 示.若质点的振动规律用余弦函数描述，则其初相应为 (A) /6 . (B) 5/6 . (C) -5/6 .(D) - /6 . (E) -2 /3 . : : 7. 一个弹簧振子和一个单摆(只考虑小幅度摆动)，在地 面上的固有振动周期分别为 T 1和T 2 .将它们拿到月球上去，有 (A) T 1 T 1 且 T 2 T2 . (C) T 1 T 1 且 T 2 T2 .(B) T 1 T 1 且 T 2(D)T 1T1 且 T21-n).F )V mh m O V(m/s) h 相应的周期分别为T i 和T 2 .则T 2 . T 2 .8. 一弹簧振子，重物的质量为 m,弹簧的劲度系数为 k,该振子作振幅为 重物通过平衡位置且向规定的正方向运动时， (A) x Acos(J k/ m t 2 ) (C) x Acos(Jm/k t 1 n开始计时.则其振动方程为： (B) x Acos(Jk/m t (D) x Acos(Jm/k t:D :A 的简谐振动.当(C)尹A 2(B) \^A 22(D)^T SA 22(E) X Acos J k / m t: B :9. 一质点在X 轴上作简谐振动，振辐A = 4 cm ，周期T = 2 s ,其平衡位置取作坐标原点. t = 0时刻质点第一次通过 处的时刻为 (A) 1 s . (C) (4⑶ s . 若 X = - 2 cm 处，且向X 轴负方向运动，则质点第二次通过 X = -2 cm (B) (2/3) s .(D) 2 s . 10. 一物体作简谐振动, 振动方程为x Acos( t1 ) •在t = T/4( T 为周期)时刻, 411. (A ) (C ) 两个同周期简谐振动曲线如图所示. 落后/2. (B)超前 落后. (D)超前.: X 1的相位比 12. 一个质点作简谐振动，振幅为 A , 1 刻质点的位移为 一A ，且向X 轴的正方向运动，代表 2 简谐振动的旋 B : 在起始时 X 2的相位(A)(C)t(D ®XX■>13. (A )(D) 2.00 s .(C ): 2.20 s . B :物体的加速度为(A)护A 215.用余弦函数描述一简谐振子的振动.若其速度〜时间( 动的初相位为(A) (C) /6. /2. (B) /3. (D) 2 /3.(E) 5 16. v17. 物的质量增为原来的四倍，则它的总能量 (A) E 1/4. (B) E 1/2. (C) 2E 1. (D) 4 E 1 . 一弹簧振子作简谐振动，总能量为 E 1，如果简谐振动振幅增加为原来的两倍，重 E2变为 18 弹簧振子在光滑水平面上作简谐振动时， 丄尿. 2 0. (A) kA 2• (B ) 弹性力在半个周期内所作的功为 (C) (1/4) kA 2. (D ) 19. 一物体作简谐振动, 振动方程为 X Acos( t 1 ).则该物体在t = 0时刻的动能与 t = T/8 (T 为振动周期)时刻的动能之比为： (A) 1:4. (B) 1:2. (C) 1:1 . (D) 2:1 . (E) 4:1. 20.图中所画的是两个简谐振动的振动曲线.若这两个简谐振动可叠加，则合成勺余弦振 动的初相为 (A) 3 . (C) 1 . 二.填空题 21.在 t = 0 时， (B) (D) 0. X 2 A/2 O X 1 -A 周期为T 、振幅为A 的单摆分别处于图(a)、(b)、 (c)三种状态.若选单摆的平衡位置为坐标的原点，坐标指向正右 方， 为 则单摆作小角度摆动的振动表达式(用余弦函数表示)分别(a) 2 X A cos(—t —) T 2 V o (a)(b ) (b ) 2X A cos(—t —)'T 2 (c ) X Acos(2—t 23. 动的周期之比为在两个相同的弹簧下各悬一物体，两物体的质量比为 2:1 . 4 : 1，则二者作简谐振24. 一质点作简谐振动，速度最大值 v m = 5 cm/s ，振幅 正最大值的那一时刻为 t = 0,则振动表达式为 A = 2 cm .若令速度具有50.02cos(—t —).2 2 —25. 一物体作余弦振动，振幅为 15 X 10-2 m ，角频率为6 s 1,初相为0.5 ，则 V 0 0I (c )振动方程为 _x 0.15cos(6 t y) (SI).27. 一简谐振动的表达式为X Acos(3t )，已知t = 0时的初位移为0.04 m ，初速度43. 一弹簧振子系统具有 1.0 J 的振动能量,为 0.09 m/s ,则振幅 A = _________________________ 0.05m . ，初相.3arcsi n- 530.已知两个简谐振动的振动曲线如图所示.两简谐振动的最大速率之比为 31. 一简谐振动用余弦函数表示，其振动曲线如图所示, 则此简谐振动的三个特征量为 A = 0.1m — rad /s 6 34.已知三个简谐振动曲线如图所示，则振动方程分别为: X 1 = 10cos X 2 = 10cos(t2) x 3 = 10cos( 37.—简谐振动的旋转矢量图如图所示，振幅矢量长 2cm ，则该简谐振动的初相为 为_x 0.02cos( t —) — 4 41. 一作简谐振动的振动系统，振子质量为 2 kg ，系统振动频率为 1000 Hz ,振幅为0.5 cm ，则其振动能量为100 2J0.10 m 的振幅和1.0 m/s 的最大速率,则弹簧的劲度系数为200N/m，振子的振动频率为 -HZ44.两个同方向的简谐振动曲线如图所示.合振动的振幅 A A i，合振动的振动方程 A 护 A 1x (A 2 A)cos(*t -) __________ . 50. 一个质点同时参与两个在同一直线上的简谐振动，其表达式分 别为 2 X 1 4 10 cos(2t1 ) , X23 10 2cos(2t I (SI )则其合成振动的振幅为 0.01m ，初相为第十章波复习题一、选择题 1.:2. (A) (B) (C) (D) C 在下面几种说法中，正确的说法是： 波源不动时，波源的振动周期与波动的周期在数值上是不同的. 波源振动的速度与波速相同. 在波传播方向上的任一质点振动相位总是比波源的相位滞后(按差值不大于 在波传播方向上的任一质点的振动相位总是比波源的相位超前. :计).(按差值不大于计) 机械波的表达式为 y = 0.03cos6 (t + 0.01X )(SI) ,_则1 (B)其周期为一 s . 3 (D)波沿X 轴正向传播. (A) 其振幅为 (C)其波速为 3. 一平面简谐波沿 s 时刻的波形图是 3 m .10 m/s . Ox 正方向传播, :B 波动表达式为y 0.10COS[2 (£ :A: X -)- 4 2 ](SI),该波在 t = 0.5横波以波速 u 沿x 轴负方向传播.t 时刻波形曲线如图•则该时刻 (A ) (C ): A 点振动速度大于零. C 点向下运动. (B) B 点静止不动. (D) D 点振动速度小于零. u 5. 振动，则 把一根十分长的绳子拉成水平，用手握其一端•维持拉力恒定，使绳端在垂直于绳子的方向上作简谐 (A)振动频率越高，波长越长. (B)振动频率越低，波长越长. (C) 振动频率越高，波速越大. 6. 一平面余弦波在t = 0时刻的波形曲线如图所示，则为： (D)振动频率越低，波速越大. O 点的振动初相 B :(B) 1 (D) 3 如图所示，有一平面简谐波沿 Acos( t 0))，则 (A)0. (C ) 7. 规律为y 1 ) : B : 2 x 轴负方向传播，坐标原点B 点的振动方程为 (或 O 的振动(A ) (B ) (C ) y Acos[ t (x/ u) Acos [t (x/u)]. Acos{ [t Acos{ [t (x/u)] 0]. (D) 8如图所示为一平面简谐波在 0}. 0}. (x/u)] t = 0时刻的波形图, 该波的波速 u =200m/s ，贝U P 处质点的振动曲线为 y (m) A 0.1...0.1y p (m)Iy p (m)A0.1&窖(m)2(A)y p (m)i\t (s) 0―xLz(B) ^-^.5t (s)0.10.2(C)y p (m)A0.1& — t (s) 0(D) t (s)9. 一平面简谐波沿x 轴正方向传播，t = 0时刻的波形图如图所示，则t =0时刻的旋转矢量图是 [A质点的振动在(A ) A S (C)A Q ，＞S(B) 0 --- ・ A A SO ，A(D)尸於(A) A 1 / A 2 = 16 .(B) A 1 / A 2 = 4 .(C) A 1 / A 2 =2 .(D) A 1 / A 2 = 1 /4 .(A)动能为零，势能最大.(B)动能为零，势能为零.10. 一平面简谐波沿 Ox 轴正方向传播，t = 0时刻的波形图如 图所示，贝U P 处介质质点的振动方程是 (A ) 0.10cos(4 (B ) y P 0.10cos(4 t(C) 0.10cos(2 3) 1) 1 (SI). (SI). (SI). (D) y P 0.10cos(2 t 6 )(SI). 图示一简谐波在t = 0时刻的波形图， 波速u (A) v 0.2 cos(2 t ) (SI). (B) v0.2 cos( t ) (SI). (C) v 0.2 cos(2 t /2) (SI). (D ) v 0.2 cos( t 3 /2) (SI).11. 0. 0.05y (m) u =20 m/s =200 m/s ，则P 处质点的振动速度表达式为 12 .在同一媒质中两列相干的平面简谐波的强度之比是4,则两列波的振幅之比是U (m)I 1 / I 2 =13. 一列机械横波在大值的媒质质元的位置是: 时刻的波形曲线如图所示，则该时刻能量为最(A) 0/, b , d , f . (C) 0/, d . 14.一平面简谐波在弹性媒质中传播，在某一瞬时，媒质中某质元 正处于平衡位置，此时它的能量是(B) a ，c ，e ，g . (D) b ， f . : B : (C)动能最大，势能最大. (D)动能最大，势能为零.15 . 一平面简谐波在弹性媒质中传播，在媒质质元从最大位移处回到平衡位置的过程中 它的势能转换成动能. 它的动能转换成势能.它从相邻的一段媒质质元获得能量，其能量逐渐增加. [C (A ) (B) (C ) 它把自己的能量传给相邻的一段媒质质元，其能量逐渐减小. [ 16 .如图所示，S 和S 2为两相干波源，它们的振动方向均垂直于图面，发出 波长为的简谐波，P 点是两列波相遇区域中的一点，已知 S 1P 2 , (D) S 2P 2.2 ，两列波在P 点发生相消干涉.若S 1的振动方程为 y i Acos(2 t 1 ),则S 2的振动方程为 2 )(A)y 2Acos(2 t(C)y 2A cos(2 t1).12 ).(B )(D )y 2 Acos(2 t y 2 2Acos(2 t 0.117.两相干波源S i 和S 2相距/4，(为波长)，S i 的相位比S 2的相位超前1一，在S i , S 2的连线上，S i 外侧各点(例如P 点)两波引起的两谐振动的相2位差是：/4 K>1 SiS2(A) 0- 1(B)—2(C) (D)-218 .&和S 2是波长均为的两个相干波的波源，相距 3 /4, S i 的相位比播时，在过S i 和S 2的直线上各点的强度相同，不随距离变化，且两波的强度都是 S i 外侧和S 2外侧各点，合成波的强度分别是(A) 4I 0，4I 0. (B) 0，0. (C) 0，4I 0 . (D) 4I 0，0.19 在驻波中，两个相邻波节间各质点的振动(A) 振幅相同，相位相同. (B)振幅不同， (C)振幅相同，相位不同.(D)振幅不同，20 在波长为的驻波中，两个相邻波腹之间的距离为1&超前一-2则在 若两波单独传I o , S i 、S 2连线上相位相同.相位不同.(A)/4.(B) /2.(C) 3 /4.(D).21.沿着相反方向传播的两列相干波，其表达式为y 1 Acos2 ( t x/ )和 y在叠加后形成的驻波中，各处简谐振动的振幅是(A) A .(B) 2A .(C) 2Acos(2 X/ ).(D)12Acos(2 x/ 二、填空题Acos2 X/)122.一个余弦横波以速度 u 沿x 轴正向传播，t 时刻波形曲线如图所示. 分别指出图中A ，B ，C 各质点在该时刻的运动方向.A _______________ ; B_____________ ； C ____________23. 一平面简谐波的表达式为y 其角频率0.025cos(125t 0.37x) (SI)，波速u =长 = ____________________ .24.频率为100 Hz 的波，其波速为250 m/s .在同一条波线上，相距为 两点的相位差为25.图为t = T / 4时一平面简谐波的波形曲线，则其波的表达式为 26、一平面简谐波沿 Ox 轴正方向传播，波长为.若如图P i 点处质点的振动方程为y rAcos(2 t )，则P 2点处质点的振动方程为 ____________________________________ ; 与卩1点处质点振动状态相同的那些点的位 0.5 m 的P i OP 2 x2I35、两相干波源 S i 和S 2的振动方程分别是y i Acos t 和1一 ).S i 距P 点3个波长，S 2距P 点2I/4个波长.两波在2位差 是如图.已知S i 的初相为丄 27、一简谐波沿x 轴正方向传播.X i 和x 2两点处的振动曲线分别如图 (a)和 (b)所示.已知X 2 .> X i 且X 2 - X i < (为波长)，则X 2点的相位比 X i 点的相位滞后28、已知某平面简谐波的波源的振动方程为 iy 0.06叫(SI)，波速为 2 m/s._KU在波传播前方离波源5 m 处质点的振动方程为(b)29、( i ) 一列波长为 的平面简谐波沿X 轴正方向传播.已知在 X振动的方程为y = Acos t ,则该平面简谐波 波疏的表达式为媒质 夕波密纟媒质h t反射面1(2)如果在上述波的波线上 X = L ( L -)处放一如图所示的反射2面，且假设反射波的振幅为 A/,则反射波的表达式为_______________________________________ (X < L).30、一平面简谐波沿 X 轴负方向传播•已知 X = -i m 处质点的振动方程为速为u 则此波的表达式为______________________________________y Acos( t )，若波相等的面积 S l 和S 2,则通过它们的平均能流之比P i /p 232、一点波源发出均匀球面波，发射功率为 4 W . 波源为2 m 处的强度是 ____________________ .不计媒质对波的吸收，则距离33、如图所示，波源 S i 和S 2发出的波在P 点相遇，P 点距波源S i 和S 的距离 分别为3和I0 3，为两列波在介质中的波长， 若P 点的合振幅总是极大 值，则两波在P 点的振动频率 _____________________________ ，波源S i 的相位比S 2的相位领 先 __________________ .S i34、如图所示，S i 和S 2为同相位的两相干波源，相距为 L ，P 点距 源S i在P 点引起的振动振幅为 A i ，波源S 2在P 点引起的振动振幅为 波 长 都 是，贝U P 点 振 幅S i 为r ；波A 2，两波i0 3L Si r PS 2y A cos( t p 点引起的两个振动的相36、 S i ，S 2为振动频率、振动方向均相同的两个点波源，振动方向垂直纸面，两者相距3-(为波长)2jM3(i)若使射线S2C上各点由两列波引起的振动均干涉相消，则S2的初相应为 .(2)若使S i S2连线的中垂线MN上各点由两列波引起的振动均干涉相消，则S2的初位相应为______________________________________________ S i j S2 CIN2I 11两列波在一根很长的弦线上传播, y i = 6.0 X 10 2cos (x - 40t) /2 y 2 = 6.0 X 10 2cos (x + 40t) /2 则合成波的表达式为 ________________ 在x = 0至x = 10.0 m 内波节的位置是 37、 其表达式为 (SI ) (SI ) ;波腹的位置是 38、设入射波的表达式为 ％ Acos2 ( t ―) •波在x = 0处发生反射,反射点 为固定端，则形成的驻波表达式为 39、 一驻波表达式为 y A cos2 x cos100 t .位于x 1 = 3 /8 m 的质元 元P 2的振动相位差为 ___________________________________ . P i 与位于X 2 = 5 /8 m 处的质 40、在弦线上有一驻波，其表达式为 y 2Acos(2 x/ )cos(2 t),两个相邻波节之间的距离是。

《振动力学》习题集(含答案)————————————————————————————————作者：————————————————————————————————日期：《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解： 系统的动能为：()222121x I l x m T &&+=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T &&&+=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω=&和U T =可得： ()()lm m gm m n 113223++=ωml m 1 x1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ&&&mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn =&和U T =可得： ()mkR a R mR a R k n 343422+=+=ωkk A Ca R θ1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解： 系统的动能为：221θ&J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn =&和U T =可得： ()()3232132k k J k k k k k n +++=ωkk 2 kJ1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

振动力学简答题1. 什么是振动力学？振动力学是研究物体在作周期性振动时的力学规律和现象的科学。

它涉及物体弹性变形、能量转换、周期性运动等方面，是力学的一个重要分支。

2. 物体振动的基本特征有哪些？物体振动的基本特征包括频率、振幅、周期和相位。

- 频率：指单位时间内振动的次数，用赫兹（Hz）表示。

- 振幅：指物体在振动过程中离开平衡位置的最大距离。

- 周期：指振动完成一个完整循环所需的时间。

- 相位：指振动物体与某一参考点的位置关系。

3. 物体振动的能量如何转化？物体在振动过程中，能量可以在不同的形式之间转化。

主要的能量转化形式包括：- 动能转化：物体振动时，动能在平衡位置和极限位置之间转化，以及在不同方向的运动中相互转化。

- 势能转化：物体由于弹性势能而产生振动，振动过程中，弹性势能在物体振动的极限位置和平衡位置之间转化。

- 损耗能转化：由于物体振动时受到摩擦力或其他非弹性力的作用，能量会以热能等形式损耗。

4. 物体的共振现象是什么？共振是指当一个物体受到与其固有振动频率相同或接近的外界激励时，会发生极大振幅的现象。

共振现象在各种实际应用中都具有重要的意义，例如乐器演奏、建筑物抗震设计等。

共振现象也需要注意，因为过大的振幅可能导致结构破坏。

5. 振动力学在工程中的应用有哪些？振动力学在工程中有广泛的应用，包括但不限于：- 结构动力学：研究建筑物、桥梁、航空器等结构物的振动特性以及抗震设计。

- 振动控制：通过引入阻尼、调节振动频率等手段，减小结构或设备的振动幅度，提高系统的稳定性和可靠性。

- 振动检测：利用振动传感器等装置，对机械设备的振动状况进行监测和诊断，以预防故障和提高设备的使用寿命。

- 振动测试：通过振动台等设备对产品进行振动测试，以评估产品的可靠性和耐久性。

以上是关于振动力学的简答题回答，希望对您有所帮助。

如需进一步了解或有其他问题，请随时提问。