梅涅劳斯定理入门篇

梅涅劳斯定理如果一条直线与ABC ∆的三边AB 、BC 、CA 或其延长线交于F 、D 、E 点， 那么1=⋅⋅EACEDC BD FB AF .等价叙述：ABC ∆的三边AB 、BC 、CA 或其延长线上有三点F 、D 、E ，则F 、D、E 三点共线的充要条件是1=⋅⋅EACEDC BD FB AF 。

三点所在直线称为三角形的梅氏线。

证法1：（平行线分线段成比例）证：如图，过A 作BC AG //交EF 延长线于G ，∵BC AG //，∴BD AG FB AF =，AGCDEA CE =， 又CDBD CD BD =则1=⋅⋅=⋅⋅CD BD AG CD BD AG CD BD EA CE FB AF ∴1=⋅⋅EACEDC BD FB AF 梅涅劳斯定理的逆定理也成立，即如果有三点F 、D 、E 分别在ABC ∆的三边AB 、BC 、CA 或其延长线上，且满足1=⋅⋅EACEDC BD FB AF ，那么F 、D 、E 三点共线。

BG利用梅涅劳斯定理的逆定理可判定三点共线。

梅涅劳斯定理的应用定理1：若ABC ∆的A ∠的外角平分线交边BC 延长线于P ，B ∠的平分线交边AC 于Q ，C ∠的平分线交边AB 于R ，则P 、Q 、R 三点共线。

证：由三角形内、外角平分线定理知，CA BA PC BP =，AB BC QA CQ =，CB CARB AR =， 则1=⋅⋅=⋅⋅ABBCCA BA CB CA QA CQ PC BP RB AR ， 故P 、Q 、R 三点共线。

例题赏析：已知：过ABC ∆顶点C 的直线，与边AB 及中线AD 分别交于点F 和E .求证：FBAFED AE 2=. 证明：直线CEF 截ABD ∆， 由梅涅劳斯定理，得：1=⋅⋅EADE CD BC FB AF又CD BC 2=，∴21=⋅EA DE FB AF ， 则FBAFED AE 2=BDBC。

第一章 梅涅劳斯定理基础知识梅涅劳斯定理：证明：梅涅劳斯定理的逆定理：证明：典型例题与基本方法例1 如图，在四边形ABCD 中，ABD ∆，BCD ∆，ABC ∆的面积比是1:4:3，点N M ,分别在AC ，CD 上，满足CD CN AC AM ::=，并且N M B ,,共线.求证：M 与N 分别是AC 和CD 的中点.例2 如图，圆1O 与圆2O 和ABC ∆的三边所在的3条直线都相切，H G F E ,,,为切点，直线EG 与FH 交于点P .求证：BC PA ⊥.例3 已知ABC ∆的重心G ，M 是BC 边的中点，过G 作BC 边的平行线交AB 边于X ，交AC 边于Y ，且XC 与GB 交于点Q ，YB 与GC 交于点P .证明：MPQ ABC DD .例4 ABC ∆是一个等腰三角形，AC AB =，M 是BC 的中点；O 是AM 的延长线上的一点，使得AB OB ⊥；Q 是线段BC 上不同于B 和C 的任意一点，E 在直线AB 上，F 在直线AC 上，使得F Q E ,,同一直线上的三个不同点.求证：（Ⅰ）若EF OQ ⊥，则QF QE =；（Ⅱ）若QF QE =，则EF OQ ⊥.例5 在凸四边形ABCD 的边AB 和BC 上取点E 和F ，使线段DE 和DF 把对角线AC 三等分，已知ABCD CDF ADE S S S 41==∆∆. 求证：ABCD 是平行四边形.例6 在ABC ∆中，1AA 为BC 边上的中线交BC 于1A ，2AA 为BAC ∠的平分线交BC 于2A ，K 为1AA 上的点，使AC KA //2. 证明：KC AA ⊥2.例7 给定锐角ABC ∆，在BC 边上取点21,A A （之间与位于C A A 12），在CA 边上取点21,B B （之间与位于A B B 12），在AB 边上取点21,C C （之间与位于B C C 12），使得122112211221C CC C CC B BB B BB A AA A AA ∠=∠=∠=∠=∠=∠，直线111,CC BB AA 与可构成一个三角形，直线222,CC BB AA 与可构成另一个三角形.证明：这两个三角形的六个顶点共圆.例8 以ABC ∆的底边BC 为直径作半圆，分别与边AB ，AC 交于点D 和E ，分别过点ED ,作BC 的垂线，垂足依次为G F ,，线段DG 和EF 交于点M .求证：BC AM ⊥.例9 已知凸四边形ABCD 的一组对边BA 与CD 的延长线交于M ，且//AD BC ，过M 作截线交另一组对边所在直线于L H ,，交对角线所在直线于','L H . 求证：'1'111ML MH ML MH +=+.例10 ABC ∆的内切圆分别切三边AB CA BC ,,于点F E D ,,，点X 是ABC ∆的一个内点，XBC ∆的内切圆在点D 处与BC 边相切，并与CX ，XB 分别相切于点Z Y ,. 证明：EFZY 是圆内接四边形.例11 如图，四边形ABCD 内接于圆，其边DC AB ,的延长线交于点P ，AD 和BC 的延长线交于点Q ，过Q 作该圆的两条切线，切点分别为F E ,.求证：F E P ,,三点共线.例12 已知ABC 的内切圆分别切AB CA BC ,,于点F E D ,,，线段CF BE 、分别与该内切圆交于点Q P 、，若直线BC FE 与交于圆外一点R . 证明：R Q P 、、三点共线.练习。

梅涅劳斯定理（入门篇）雷雨田 （广西师范大学附属外国语学校高50班 541004）梅涅劳斯定理这个定理怎么记最好呢？ 个人感觉“顶到分、分到顶、顶到分、分到顶、顶到分、分到顶”这样记忆来得非常容易不过找了很多资料，感觉仅仅是把这个定理（或者后面附一个逆定理）陈述然后证明完了之后，就直接给例题（或者直接讲赛瓦定理），看上去不怎么舒服，所以我把其他的一些东西附在这里，以供参考。

第一角元形式的梅涅劳斯定理（就是把线段比改为正弦值比）其表达式为：1=∠∠∙∠∠∙∠∠BA'B sin 'CBB sin CB 'C sin 'ACC sin AC 'A sin 'BAA sin 证明如下：如图所示，由三角形面积公式（正弦定理）可得：AC 'A sin AC 'BAA sin AB AC 'A sin AC 'AA 'BAA sin 'AA AB S S C 'A 'BA C 'AA 'ABA ∠⋅∠⋅=∠⋅⋅∠⋅⋅==∆∆2121 同理可得CB'C sin BC 'ACC sin AC B 'C 'AC ,BA 'B sin AB 'CBB sin BC A 'B 'CB ∠⋅∠⋅=∠⋅∠⋅=把这三个式子相乘，运用梅氏定理，就可得到这个式子怎么记最好呢？个人感觉根据梅涅劳斯定理中线段所对应的角来记忆最好。

第二角元形式的梅涅劳斯定理设O 是不在三角形ABC 三边所在直线上的任意一点，其他条件不变，则表达式为： 1=∠∠∙∠∠∙∠∠OA'B sin 'COB sin OB 'C sin 'AOC sin OC 'A sin 'BOA sin 现证明如下：B C A’如图，由C'A 'BA S S OC 'A 'BOA =∆∆ 可得A'B 'BA OB OC OC 'A sin 'OA B sin ⋅=∠∠同理得到另外两个对称式，相乘，运用梅氏定理即得证这个式子就这样记吧：先记住原来的梅涅劳斯定理形式，然后在每条线段表达式中间插一个O ，然后再在前面加上∠sin （比如BA'就变成'BOA sin ∠）梅氏定理的用处这个定理是平面几何的一个重要定理（好像所有竞赛书都把他与赛瓦定理放在第一节，不知是惯性还是怎么地），它大概有如下用处：可以用来证明三点共线；可以用来导出线段比例式；可以用来寻求一条线段是另一条线段的几分之几或几倍（即线段倍分）；怎么用梅氏定理知道了这个定理，还要会用才行。

补充讲义梅涅劳斯（Menelaus）定理是由古希腊数学家梅涅劳斯首先证明的。

它指出：如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点，那么(AF/FB)×(BD/DC)×(CE/EA)=1。

AFED证明：塞瓦定理ΔABC的三边BC，CA，AB上有点D，E，F.若AD，BE，CF三线交于一点O.求证：. BD/DC*CE/EA*AF/FB=1∵三角形ABC内一点O，AO，BO，CO交对边于D，E，F。

证（AF/FB）*（BD/DC）*（CE/EA）=1。

1）最简单的证法：用面积证。

2）用梅涅劳斯定理：3）用分角定理：证明：塞瓦定理的应用定理：设平行于△ABC的边BC的直线与两边AB、AC的交点分别是D、E，又设BE和CD交于S，则AS一定过边BC的中心MAD ESB M C实际运用：2010年上海中考题25．如图9，在Rt△ABC中，∠ACB＝90°.半径为1的圆A与边AB相交于点D，与边AC 相交于点E，连结DE并延长，与线段BC的延长线交于点P.（1）当∠B＝30°时，连结AP，若△AEP与△BDP相似，求CE的长；（2）若CE=2，BD=BC，求∠BPD的正切值；（3）若1tan3BPD∠=，设CE=x，△ABC的周长为y，求y关于x的函数关系式.图9 图10(备用) 图11(备DP武汉2010年中考试题24．(本题满分10分) 已知：线段OA⊥OB，点C为OB中点，D为线段OA上一点。

连结AC，BD交于点P．(1) 如图1，当OA=OB，且D为OA中点时，求APPC的值；(2) 如图2，当OA=OB，且AD1AO4时，求tan∠BPC的值．(3) 如图3，当AD∶AO∶OB=1∶n∶tan∠BPC的值．（图1）（图2）（图3）25．(本题满分12分) 如图．抛物线经过A （－1，0），C （2，）两点， 与x 轴交于另一点B ．(1) 求此地物线的解析式；(2) 若抛物线的顶点为M ，点P 为线段OB 上一动点 (不与点B 重合)，点Q 在线段MB 上 移动，且∠MPQ=45°，设线段OP=x ，MQ=，求y 2与x 的函数关系式，并直接写出 自变量x 的取值范围；(3) 在同一平面直角坐标系中，两条直线x=m ，x=n 分别与抛物线交于点E ，G ，与(2)中的 函数图象交于点F ，H ．问四边形EFHG 能否为平行四边形? 若能，求m ，n 之间的数量关 系；若不能，请说明理由．补充知识点：1、 中线定理：（巴布斯定理）设三角形ABC 的边BC 的中点为P ，则有AB 2+AC 2=2(AP 2+BP 2)AB C212y ax ax b =-+3222yP2、广勾定理：在三角形中，锐角(或钝角)所对的边的平方等于另外两边的平方和，减去(或加上)这两边中的一边与另一边在这边(或其延长线)上的射影的乘积的2倍．A AB CD C （锐角）证明：AC2=AB2+BC2-2BD*BC （钝角）证明：AC2=AB2+BC2+2BD*BC知识补充：（北京市2010年中考题第25题）1、问题：已知△ABC中，∠BAC=2∠ACB，点D是△ABC内的一点，且AD=CD，BD=BA。

梅涅劳斯定理及其应用
梅涅劳斯（Menelaus）定理（简称梅氏定理）是由古希腊数学家梅涅劳斯首先证明的。

如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点，那么(AF/FB)×(BD/DC)×(CE/EA)=1。

或：设X、Y、Z分别在△ABC的BC、CA、AB所在直线上，则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1 。

证明定理
过点A作AG∥BC交DF的延长线于G，则AF/FB=AG/BD , CE/EA=DC/AG。

三式相乘得：(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1。

定义理论：
使用梅涅劳斯定理可以进行直线形中线段长度比例的计算，其逆定理还可以用来解决三点共线、三线共点等问题的判定方法，是平面几何学以及射影几何学中的一项基本定理，具有重要的作用。

梅涅劳斯定理的对偶定理是塞瓦定理。

它的逆定理也成立：若有三点F、D、E分别在三角形的边AB、BC、CA或其延长线上，且满足AF/FB×BD/DC×CE/EA=1，则F、D、E 三点共线。

利用这个逆定理，可以判断三点共线。

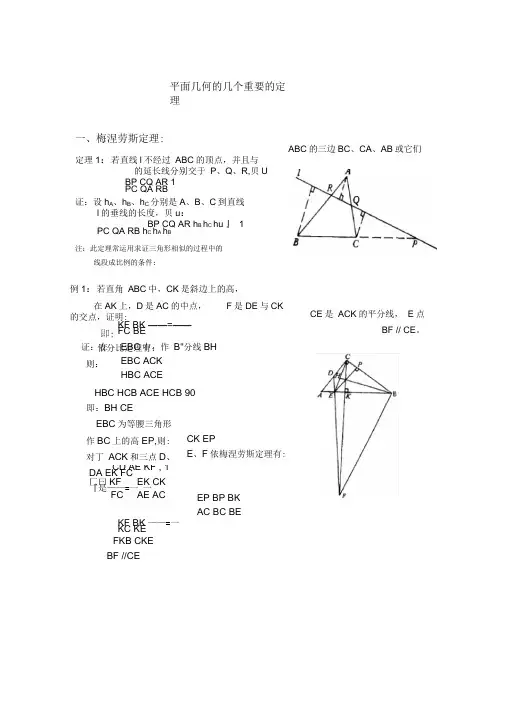
平面几何的几个重要的定理一、梅涅劳斯定理:定理1：若直线l 不经过 ABC 的顶点，并且与的延长线分别交于 P 、Q 、R,贝U BP CQ AR 1 PC QA RB证：设h A 、h B 、h C 分别是A 、B 、C 到直线l 的垂线的长度，贝u ：BP CQ AR h B h C hu 』 1PC QA RB h C h A h B注：此定理常运用求证三角形相似的过程中的线段成比例的条件;例1：若直角 ABC 中，CK 是斜边上的高， 在AK 上，D 是AC 的中点， F 是DE 与CK的交点，证明:KF BK ——=—— FC BE KF BK ——=一 KC KE FKB CKE BF //CECE 是 ACK 的平分线， E 点BF // CE 。

证：在 则：EBC 中，作 B"分线BH EBC ACK HBC ACEHBC HCB ACE HCB 90即：BH CEEBC 为等腰三角形作BC 上的高EP,则:对丁 ACK 和三点D 、 CK EPE 、F 依梅涅劳斯定理有:CD AE KF , 1 DA EK FC匚曰KF EK CK 『是——=一 一FC AE ACEP BP BK AC BC BE依分比定理有: ABC 的三边BC 、CA 、AB 或它们【练习1从点K 引四条直线，另两条直 -一 一 、…AC和 A 1、B 1、C 1、D 1,试证： ------- 1 1 1BC线分别交这四条直线丁 A 、B 、C 、DAD BD定理2：设P 、Q 、R 分别是 ABC 的三边 BC 、CA 、AB 上或它们的延长线上的 P 、Q 、R 三点中，位于 ABC 边上的点的个数为 0或2,这时若 既 PC 三点，并且 CQ AR QA RB 1, 求证：P 、Q 、R 三点共线; 证：设直线PQ 与直线AB 交丁 R ', 丁是由定理 BP CQ AR _ __ ' PC QA R B乂 BP CQ AR PC QA RB 由丁在同一直线上的 _ ' ____ AR AR1,则：^―=—— R B RB P 、Q 、R '三点中，位丁 ABC 边上的点的个数也为 0或2,因此R 与R '或者同在AB 线段上，或者同在 AB 的延长线上； 若R 与R '同在AB 线段上，则R 与R '必定重合，不然的话， 设AR AR ', AR AR BR BR 这时AB AR AB AR ',即BR BR ',丁是可得 _ ____ ' 这与AR =竺 矛盾 BR BR 类似地可证得当 R 与R '同在AB 的延长线上时,综上可得：P 、Q 、R 三点共线； 注：此定理常用于证明三点共线的问题，且常需要多次使用 R 与R '也重合再相乘;例2点P 位丁 ABC 的外接圆上；A 1、B 1、C 1是从点P 向BC 、CA 、AB 引的垂线的垂足, 证明点A 1、B 1、 BA 1BP cos PBC CA 1 CP cos PCB CB 1 CP cos PCA AB 1 AP cos PAC AC 1AP cos PABBC 1 PB cos PBAC i 共线; 证：易得: 将上面三条式子相乘， 且 PAC PBC , PAB PCB , 十曰 BA 1 CB 1 AC 1可得 一111= 1 ,CA 1 AB 1 BC 1依梅涅劳斯定理可知 A 1、B 1、C 1三点共线;PCA PBA 180A 1C 1 A 1D 1B 1C ； :BD【练习2设不等腰 ABC 的内切圆在三边 BC 、CA 、AB 上的切点分别为 D 、E 、F,则EF 与BC , FD 与CA , DE与AB 的交点 X 、Y 、Z 在同一条 直线上；【练习&已知直线 AA i, BB i, CC i 相交于O,直线AB 和A 1B 1的交点为C 2,直线 BC 与B 1C 1的交点是 A 2,直 线AC 与A i C i 的交点是B 2,试证：A 2、B 2、C 2三点共线;【练习M 在一条直线上取点 E 、C 、A,在另一条上取点 B 、F 、D,记直线AB 和ED , CD 和AF ,CD 和AF , EF 和BC 的交点依次为 L 、M 、N,证明：L 、M 、N 共线练习i 的证明练习2的证明乂 AE AF 代人上式可得：BXXC FB =—— CE CY DC AZ EA同理口」彳寸： — —YA AFZB BD将上面三条式子相乘可 得：乳CY J i XC YA ZB 乂 X 、Y 、Z 都不在 ABC 的边上，由定理 2可得X 、Y 、 证： ABC 被直线XFE 所截，由定理 Z 三点共线 证：若AD // A i D^,结论显然成立;若AD 与A i D i 相交与点 AD LD LD BD LD 〔 A i K A i D i AK BK BQ B i K LDi L,则把梅涅劳斯定理分 LC AK A 。

第一章 梅涅劳斯定理及应有习题A1．延长CB ，FE 交于H ，ADB △与截线GEH ，有13122AG DH BE DH GD HB EAHB ⋅⋅=⋅⋅=，有43DHHB=，即74CH HD =．对ACD △及截线FGH ，72141AF CH DG AF FC HD GA FC ⋅⋅=⋅⋅=，求得27AF FC=．2．设CB ，DE 的延长线交于P ，又BP BC =，32FP PB=，对AFB △与截线HEP ，CGE ，有31121AH FP BE AH GF PB EA HF ⋅⋅=⋅⋅=，即23AH HF =；11121AG FC BE AG GF CB EA GF ⋅⋅=⋅⋅=，即21AG GF =．由此求得645AH HG GF =∶∶∶∶． 3．对BDP △于截线CEA ，有1231612BC DA PE BC CD AP EA CD ⋅⋅=⋅⋅=，知BD DC =．对CDP △与截线BFA ，有22111CB DA PF PF BD AP FCFC⋅⋅=⋅⋅=，知14PFFC=．而20CF =，故15CP =． 在PBC △中，由中线长公式2PD =2BC =BD =．又22222269BP PD BD +=+==，即90BPD ∠=︒，27PBD S =△，4108ABC PBD S S ==△△．4．直线OCB 分别与DMF △和AEM △的三边延长线都相交，有1DB MO FC MB FO DC ⋅⋅=，1AB EO MCEB MO AC ⋅⋅=，即OF OE DB FC EB AC OM OM MB DC AB MC⋅⋅⋅=⋅⋅⋅．由EF AD ∥，有DB ABMB EB=，FC MCDC AC=，从而21OF OEOM ⋅=，即22OF OE OM OP ⋅==，有OFP OPE △∽△，故OPF OEP ∠=∠．5．直线截ABC △，有22133CF AD BE BE FA DB ECEC⋅⋅=⋅⋅=，即94BE EC=，故54BC CE=．直线截DBE △，有25154EF AD BC EF FD AB CEED ⋅⋅=⋅⋅=，所以21EF FD =∶∶．6．设AC BC x ==，则AB =，。

梅涅劳斯（Menelaus）定理（简称梅氏定理）是由古希腊数学家梅涅劳斯首先证明的。

它指出：如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点，那么(AF/FB)×(BD/DC)×(CE/EA)=1。

或：设X、Y、Z分别在△ABC的BC、CA、AB所在直线上，则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1 证明一：过点A作AG∥BC交DF的延长线于G,则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG。

三式相乘得：(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1证明二：过点C作CP∥DF交AB于P，则BD/DC=FB/PF，CE/EA=PF/AF所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1它的逆定理也成立：若有三点F、D、E分别在△ABC的边AB、BC、CA或其延长线上，且满足(AF/FB)×(BD/DC)×(CE/E A)=1，则F、D、E三点共线。

利用这个逆定理，可以判断三点共线。

梅涅劳斯(Menelaus)定理证明三：过ABC三点向三边引垂线AA'BB'CC'，所以AD：DB=AA'：BB'，BE：EC=BB'：CC'，CF：FA=CC'：AA'所以(AF/FB)×(BD/DC)×(CE/EA)=1证明四：连接BF。

（AD：DB）·（BE：EC）·（CF:FA)=（S△ADF：S△BDF）·（S△BEF：S△CEF）·（S△BCF：S△BAF）=（S△ADF：S△BDF）·（S△BDF：S△CDF）·（S△CDF：S△ADF）=1此外，用定比分点定义该定理可使其容易理解和记忆：在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点，又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。

第一课时： 梅涅劳斯定理1．背景：Menelaus 定理（简称梅氏定理）是由古希腊数学家梅涅劳斯首先证明的.2．定理：如果一直线顺次与三角形ABC 的三边BC 、AC 、AB 或其延长线交于D 、E 、F 三点， 则1=⋅⋅EACEDC BD FB AF3．说明：（1）不过顶点的直线与三角形3 边的关系有两种情况：①若直线与三角形的一边交于内点，则必与第二边交于内点，与第三边交于外点（延长线上的点）；②直线与三角形的三边均交于外点，因而本定理的图形有两个.（2）定理的结构是：三角形三边上6条被截线段的比，首尾相连，组成一个比值为1 的等式. （3）这个定理反映了形与数的转化，是几何位置的定量描述：“三点共线”量化为比值等于“1”；反过来，若比值等于“1”成立时，可证“三点共线”（逆定理也成立）.4．记忆：1A C C B B A =⋅⋅点分点到点到分点点分点到点到分点点分点到点到分点.5．证明：6．推广：（1）逆定理：（常用于证明三点共线）如果有三点D 、E 、F 分别在三角形ABC 的三边或其延长线，且满足：1=⋅⋅EACEDC BD FB AF ，则三点D 、E 、F 在同一直线上.7．定理的应用：例题1：已知过ABC ∆顶点C 的直线，与边AB 及中线AD 分别交于点F 和E ，求证：FBAFED AE 2=.变式练习１：在△ABC 中，AG 是角平分线，D 是BC中点，DG ⊥AG 交AB 于E ，交AC 延长线与F ，求证：BE=CF=)(21AC AB -．例题2：已知过ABC ∆重心G 的直线分别交边AB 、AC 及CB 延长线于点E 、F 、D ，求证：1=+FACFEA BE .CCF。

第一章涅劳斯定理及应用【基础知识】梅涅劳斯定理 设A '，B '，C '分别是ABC △的三边BC ，CA ，AB 或其延长线上的点，若A '，B '，C '三点共线，则1BA CB AC A B B A C B'''⋅⋅='''．① C ′B′A'A′B′C ′ADC B DCB 图1-1A证明 如图11-，过A 作直线AD C A ''∥交BC 的延长线于D ，则 CB CA B A A D ''=''，AC DA C B A B''=''，故 1BA CB AC BA CA DA A C B A C B A C A D A B''''''⋅⋅=⋅⋅=''''''． 注 此定理的证明还有如下正弦定理证法及面积证法．正弦定理证法 设BC A α''=∠，CB A β''=∠，B A B γ''=∠，在BA C ''△中，有sin sin BA C B αγ'='，同理，sin sin CB CA γβ'='，sin sin AC AB βα'='，此三式相乘即证． 面积证法 由A C B A C C S BA A C S '''''='△△，CB C CA B CB C CA B C CA B AC A AB B AC A AB AC A S S S S S CB B A S S S S S ''''''''''''''''''''+===='+△△△△△△△△△△，AC A C BA S AC C B S '''''='△△，此三式相乘即证．梅涅劳斯定理的逆定理 设A '，B '，C '分别是ABC △的三边BC ，CA ，AB 或其延长线上的点，若 1BA CB AC A C B A C B'''⋅⋅='''，② 则A '，B '，C '三点共线．证明 设直线A B ''交AB 于1C ，则由梅涅劳斯定理，得到111AC BA CB A C B A C A''⋅⋅=''．由题设，有1BA CB AC A C B A C B'''⋅⋅='''，即有11AC AC C B C B '='． 又由合比定理，知1AC AC AB AB'=，故有1AC AC '=，从而1C 与C '重合，即A '，B '，C '三点共线． 有时，也把上述两个定理合写为：设A '，B '，C '分别是ABC △的三边BC ，CA ，AB 所在直线（包括三边的延长线）上的点，则A '，B '，C '三点共线的充要条件是 1BA CB AC A C B A C B'''⋅⋅='''． 上述①与②式是针对ABC △而言的，如图11-（整个图中有4个三角形），对于C BA ''△、B CA ''△、AC B ''△也有下述形式的充要条件：1C A BC A B AB CA B C '''⋅⋅='''；1B A CB A C AC BA C B '''⋅⋅='''；1AB C A B CBC A B CA'''⋅⋅='''．③ 第一角元形式的梅涅劳斯定理 设A '，B '，C '分别是ABC △的三边BC ，CA ，AB 所在直线（包括三边的延长线）上的点，则A '，B '，C '共线的充分必要条件是 sin sin sin 1sin sin sin BAA ACC CBB A AC C CB B BA'''⋅⋅='''∠∠∠∠∠∠．④ CA′B'C '图1-2A证明 如图12-，可得 1sin 21sin 2ABA AA CAB AA BAA S BA A C S AA AC A AC ''''⋅⋅'=='''⋅⋅△△∠∠ sin sin AB BAA AC A AC'⋅='⋅∠∠．同理，sin sin CB BC CBB B A AB B BA ''⋅=''⋅∠∠，sin sin AC AC ACC C B BC C CB ''⋅=''⋅∠∠． 以上三式相乘，运用梅涅劳斯定理及其逆定理，知结论成立．第二角元形式的梅涅劳斯定理 设A '，B '，C '分别是ABC △的三边BC ，CA ，AB 所在直线上的点，点O 不在ABC △三边所在直线上，则A '，B '，C '三点共线的充要条件是 sin sin sin 1sin sin sin BOA COB AOC A OC B OA C OB'''⋅⋅='''∠∠∠∠∠∠．⑤ A′OCBB'C 'A 图1-3证明 如图13-，由BOA A OC S BA S A C'''='△△，有 sin sin BOA OC BA A OC OB A C''=⋅''∠∠． 同理，sin sin COB OA CB B OA OC B A ''=⋅''∠∠，sin sin AOC OB AC C OB OA C B''=⋅''∠∠．于是sin sin sin sin sin sin BOA COB AOC BA CB AC A OC B OA C OB A C B A C B''''''⋅⋅=⋅⋅''''''∠∠∠∠∠∠． 故由梅涅劳斯定理知A '，B '，C '共线1BA CB AC A C B A C B'''⇔⋅⋅='''．从而定理获证．注 （1）对于④、⑤式也有类似③式（整个图中有4个三角形）的结论．（2）于在上述各定理中，若采用有向线段或有向角，则①、②、③、④、⑤式中的右端均为1-，③、④、⑤式中的角也可以按①或②式中的对应线段记忆．特别要注意的是三边所在直线上的点为一点或者三点在边的延长线上． 【典型例题与基本方法】1．恰当地选择三角形及其截线（或作出截线），是应用梅涅劳斯定理的关键例1 如图14-，在四边形ABCD 中，ABD △，BCD △，△ABC 的面积比是3∶4∶1，点M ，N 分别在AC ，CD 上，满足AM ∶AC CN =∶CD ，并且B ，M ，N 共线．求证：M 与N 分别是AC 和CD 的中点． （1983年全国高中联赛题） EDCBM NA图1-4证明 设AM CNr AC CD==（01r <<），AC 交BD 于E ． Q 341ABD BCD ABC S S S =△△△∶∶∶∶， ∴17BE BD =，37AE AC =． 37371771AM AE r EM AM AE r AC AC AM MC AC AM r r AC----====----． 又因B ，M ，N 三点共线，可视BMN 为△CDE 的截线，故由梅涅劳斯定理，得1CN DB EM ND BE MC ⋅⋅=，即77311177r r r r-⋅⋅=--． 化简整理，得 2610r r --=，解得12r =，13r =-（舍去）．故M 与N 分别是AC 和CD 的中点． 例2 如图1-5，在四边形ABCD 中，对角线AC 平分BAD ∠，在CD 上取一点E ，BE 与AC 相交于F ，延长DF 交BC 于G ．求证：GAC EAC =∠∠．（1999年全国高中联赛题）G 'B'GFEDCBA图1-5证明 记BAC CAD θ==∠∠，GAC α=∠，EAC β=∠，直线GFD 与△BCE 相截，由梅涅劳斯定理，有 1ABG AEFAED ABFS S BG CD EF GC DE FB S S =⋅⋅=⋅△△△△ sin()sin sin sin sin()sin AB AC AE AC AE AB θαθβαθβθ⋅-⋅⋅=⋅⋅⋅⋅-⋅ sin()sin sin sin()θαβαθβ-⋅=⋅-．故 sin()sin sin()sin θαβθβα-⋅=-⋅．即 sin cos sin cos sin sin sin cos sin cos sin sin θαβθαβθβαθβα⋅⋅-⋅⋅=⋅⋅-⋅⋅， 亦即 sin cos sin sin sin cos sin()0πk θαβθαβαβαβ⋅⋅=⋅⋅⇔-=⇔-=，且k 只可能为0，故GAC ∠EAC =∠．例3 设E 、F 分别为四边形ABCD 的边BC 、CD 上的点，BF 与DE 交于点P ．若BAE FAD =∠∠，则BAP CAD =∠∠．证明 如图1-6，只需证得当AF 关于BAD ∠的等角线交BE 于P 时，B 、P 、F 共线即可．FED CBAP图1-6事实上，B 、P 、F 分别为△CDE 三边所在直线上的三点，且A 不在其三边所在直线上． 又FAD EAB =∠∠，DAP BAC =∠∠，PAE CAF =∠∠， 由第二角元形式的梅涅劳斯定理，有sin sin sin 1sin sin sin EAB CAF DAPBAC FAD PAE⋅⋅=∠∠∠∠∠∠．故B 、P 、F 三点共线．注 当AC 平分BAD ∠时，即为1999年全国高中联赛题．2．梅涅劳斯定理的逆用（逆定理的应用）与迭用，是灵活应用梅氏定理的一种方法例2另证 如图1-5，设B ，G 关于AC 的对称点分别为B '，G '，易知A ，D ，B '三点共线，连FB '，FG '，只须证明A ，E ，G '三点共线．设EFB α'=∠，DFE BFG B FG β''===∠∠∠，AFD GFC G FC γ'===∠∠∠，则*sin sin sin()1sin()sin sin FDA FG B FEC FB A FG C FED S S S DA B G CE FD FB FC AB G C ED S S S FB FC FD γββγαβγαγβ'''''''⋅⋅⋅+-⋅⋅=⋅⋅=⋅⋅='''⋅+-⋅⋅△△△△△△． 对△CB D '，应用梅涅劳斯定理的逆定理，知A ，E ，G '三点共线．故GAC EAC =∠∠． 注 在图1-5中，*式也可为sin(180)βγ︒--，若B '在AD 的延长上，则*式为sin()βγα++． 例4 如图1-7，1O e 与2O e 和△ABC 的三边所在的3条直线都相切，E ，F ，G ，H 为切点，直线EG 与FH 交于点P ．求证：PA BC ⊥．（1996年全国高中联赛题）P （P'）图1-7证法1 过A 作AD BC ⊥于D ，延长DA 交直线HF 于点P '．对△ABD 及截线FHP '应用梅涅劳斯定理，有1AH BF DP HB FD P A'⋅⋅='．由BF BH =，有1AH DP FD P A '⋅='．显然1O ，A ，2O 三点共线，连1O E ，1O G ，2O F ，2O H ，则由12O E AD O F ∥∥，有△1AGO ∽△2AHO ，从而12AO DE AG DF AO AH ==，即AH AGFD ED=． 又CE CG =，则1AH DP DP AG DP AG CEFD P A P A ED P A GC ED'''=⋅=⋅=⋅⋅'''． 对△ADC ，应用梅涅劳斯定理的逆定理，知P '，G ，E 三点共线，即P '为直线EG 与FH 的交点．故点P '与点P 重合，从而PA BC ⊥．证法2 延长PA 交BC 于D ，直线PHF 与△ABD 的三边延长线都相交，直线PGE 与△ADC 的三边延长线都相交，分别应用（迭用）梅涅劳斯定理，有 1AH BF DP HB FD PA ⋅⋅=，1DP AG CEPA GC ED ⋅⋅=． 上述两式相除，则有AH BF AG CEHB FD GC ED⋅=⋅． 而HB BF =，CE GC =，于是AH AG FD ED =，即AG DEAH DF=． 连1O G ，OE ，1O A ，2O A ，2O H ，2O F ，而1O ，A ，2O 共线，则OG GC ⊥，2O H BH ⊥，且△1O AG ∽△2O AH ，从而12O A AG DEO A AH DF==，于是1AD O E ∥．故AD EF ⊥，即PA BC ⊥．【解题思维策略分析】梅涅劳斯定理是三角形几何学中的一颗明珠，它蕴含着深刻的数学美，因而它在求解某些平面几何问题，特别是某些平面几何竞赛题中有着重要的应用． 1．寻求线段倍分的一座桥梁例5 已知△ABC 的重心为G ，M 是BC 边的中点，过G 作BC 边的平行线交AB 边于X ，交AC 边于Y ，且XC 与GB 交于点Q ，YB 与GC 交于点P ．证明：△MPQ ∽△ABC ．（1991年第3届亚太地区竞赛题）证明 如图1-8，延长BG 交AC 于N ，则N 为AC 的中点．由XY BC ∥，知2AX AG XB GM ==，而12NC CA =．YXGMN PQCB A图1-8对△ABN 及截线XQC ，应用梅涅劳斯定理，有1212AX BQ NC BQ XB QN CA QN ⋅⋅=⋅⋅=，故BQ QN =． 从而MQ AC ∥，且1124MQ CN AC ==．同理，MP AB ∥，且14MP AB =． 由此可知，PMQ ∠与BAC ∠的两边分别平行且方向相反，从而PMQ BAC =∠∠，且MP MQAB AC=，故MPQ ABC △∽△．例 6 △ABC 是一个等腰三角形，AB AC =，M 是BC 的中点；O 是AM 的延长线上的一点，使得OB AB ⊥；Q 是线段BC 上不同于B 和C 的任意一点，E 在直线AB 上，F 在直线AC 上，使得E ，Q ，F 是不同的和共线的，求证：（Ⅰ）若OQ EF ⊥，则QE QF =； （Ⅱ）若QE QF =，则OQ EF ⊥． （1994年第35届IMO 试题）证明 （1）如图1-9，连OE ，OF ，DC ．由OQ EF ⊥，易证O ，E ，B ，Q 四点共圆，O ，C ，F ，Q 四点共圆．则 OEQ OBQ OCQ OFQ ===∠∠∠∠，因此OE OF =．故QE QF =．QCBAEFOM 图1-9（Ⅱ）由AB AC =，EQ QF =，对△AEF 及截线BQC 运用梅涅劳斯定理，有1AB EQ EC FCBE QF CA BE=⋅⋅=，即BE CF =．于是可证Rt Rt OBE OCF △≌△，得OE OF =，故OQ EF ⊥．例7 在凸四边形ABCD 的边AB 和BC 上取点E 和F ，使线段DE 和DF 把对角线AC 三等分，已知14ADE CDF ABCD S S S ==△△，求证：ABCD 是平行四边形．（1990年第16届全俄竞赛题） 证明 如图1-10，设DE ，DF 分别交AC 于P ，Q ，两对角线交于M ．要证ABCD 是平行四边形，若证得AM MC =（或PM MQ =），且BM MD =即可．QFE DCB AP M 图1-10由ADE CDF S S =△△，ADP CDQ S S =△△（等底等高），知AEP CFQ S S =△△，而APCQ ，故有EF AC ∥，从而有BE BFEA FC=． 对△BAM 及截线EPD ，△BCM 及截线FQD ，分别应用梅涅劳斯定理，有 1BE AP MDEA PM DB ⋅⋅=， ① 1BF CQ MDFC QM DB ⋅⋅=．②由①，②两式相除得AP CQPM QM=． 而AP CQ =，故PM MQ =，即有AM MC =．此时，又有12ABD CBD ABCD S S S ==△△．又由14ADE ABCD S S =△，知BE EA =，于是①式可写为12111BE AP MD MDEA PM DB DB⋅⋅=⋅⋅=，即有2DB MD =，亦即BM MD =． 故ABCD 为平行四边形．2．导出线段比例式的重要途径例8 在△ABC 中，1AA 为BC 边上的中线，2AA 为BAC ∠的平分线，且交BC 于2A ，K 为1AA 上的点，使2KA AC ∥．证明2AA KC ⊥．（1997年第58届莫斯科竞赛题）证明 如图1-11，延长CK 交AB 于D ，只须证AD AC =．KA 2A 1DCBA图1-11由2AA 平分BAC ∠，有22BA AB AC A C=． ①由2KA AC ∥，有1122A K A A KA A C=． 注意到12BC AC =，对△1ABA 及截线DKC 运用梅涅劳斯定理，得 1121212A K A A AD BC AD DB CA KA DB A C =⋅⋅=⋅⋅．故1222=A A BD DA A C，由合比定理，有 1221211212222A A A C A A AC A A BA BD DA DA A C A C A C ++++===，即为 22BA AB AD A C=． ②由①，②式有AB ABAC AD=，故AC AD =． 例9 给定锐角△ABC ，在BC 边上取点1A ，2A （2A 位于1A 与C 之间），在CA 边上取点1B ，2B （2B 位于1B 与A 之间），在AB 边上取点1C ，2C （2C 位于1C 与B 之间），使得122112AA A AA A BB B ===∠∠∠ 211221BB B CC C CC C ==∠∠∠，直线1AA ，1BB 与1CC 可构成一个三角形，直线2AA ，2BB 与2CC 可构成另一个三角形．证明：这两个三角形的六个顶点共圆． （1995年第36届1MO 预选题） 证明 如图1-12，设题中所述两个三角形分别为△UVW 与△XYZ ．C 1C 2B 2B 12A 1UWVXYZ A图1-12由已知条件，有△1AC C ∽△2AB B ，△2BA A ∽△1BC C ，21CB B CA A △∽△，得 12AC ACAB AB=， 21BA AB BC BC =，21CB BCCA AC=，此三式相乘得1222111AC BA CB AB BC CA ⋅⋅=． ①对△1AA B 及截线1CUC ，△2AA C 及截线2BXB ，分别应用梅涅劳斯定理，得 11111AC BC AU UA CB C A ⋅⋅=， ② 22221A X AB CB XA B C BA ⋅⋅=， ③ ①，②，③三式相乘化简，得12AU AXUA XA =．故UX BC ∥． 同理，WX CA ∥．故1212AUX AA A BB B BWX ===∠∠∠∠．从而点X 在△UVW 的外接圆上．同理，可证得Y ，Z 也在△UVW 的外接圆上．证毕．例10 如图1-13，以△ABC 的底边BC 为直径作半圆，分别与边AB ，AC 交于点D 和E ，分别过点D ，E 作BC 的垂线，垂足依次为F ，G ，线段DG 和EF 交于点M ．求证：AM BC ⊥．（IMO -37中国国家队选拔赛题）H MG FEDCA图1-13证法1 设直线AM 与BC 交于H ，连BE ，CD ，则知90BEC BDC ==︒∠∠，直线FME 与△AHC 相截，直线GMD 与△ABH 相截，迭用梅涅劳斯定理，有1AM HF CE MH FC EA ⋅⋅=，1AM HG BDMH GB DA⋅⋅=． 两式相除，得 FH CF AE BDHG CE BG AD⋅⋅=⋅⋅．在Rt △DBC 与Rt △EBC 中，有2CD BC FC =⋅，2BE BC BG =⋅，即22CF CD BG BE =．将其代入①式，得 22FH CD AE BDHG BE CE AD⋅⋅=⋅⋅． 又由△ABE ∽△ACD ，有CD ADBE AE=． 将其代入②式，得 DBC EBC S FH CD BD DF DMHG BE CE S EG MG ⋅====⋅△△，从而，MH DF ∥． 而DF BE ⊥，则MH BC ⊥，故AM BC ⊥．证法 2 作高AH ，连BE ，CD ，则90BDC BEC =⋅=∠∠，于是，sin DF BD B =⋅=∠ cos sin BC B B ⋅⋅∠∠，cos sin EG BC C C =⋅⋅∠∠． ∴ cos sin cos cos sin cos GM EG C C AB CMD FD B B AC B ⋅===⋅⋅∠∠∠∠∠∠． 又cos BH AB B =⋅∠，cos HG AE C =⋅∠， ∴cos cos cos cos BH AB B AC B HG AE C AD C ⋅⋅==⋅⋅∠∠∠∠，即BH GM AB HG MD AD ⋅=，故1BH GM DAHG MD AB⋅==．对△BGD 应用梅涅劳斯定理的逆定理，知H ，M ，A 三点共线．由AH BC ⊥，知 AM BC ⊥．例11 如图1-14，设点I ，H 分别为锐角△ABC 的内心和垂心，点1B ，1C 分别为边AC ，AB 的中点．已知射线1B I 交边AB 于点2B （2B B ≠），射线1C I 交AC 的延长线于点2C ，22B C 与BC 相交于K ，1A 为△BHC 的外心．试证：A ，I ，1A 三点共线的充分必要条件是△2BKB 和△2CKC 的面积相等．（CMO -2003试题）EB 2A 1B 1C 1C 2KFHOI DCBA图1-14分析 首先证A ，I ，1A 三点共线60BAC ⇔=︒∠．设O 为△ABC 的外心，连BO ，CO ，则2BOC BAC =∠∠．又180BHC BAC =︒-∠∠，因此，60BAC =︒∠ B ⇔，H ，O ，C 四点共圆 1A ⇔在△ABC 的外接圆O e 上AI ⇔与1AA 重合A ⇔，I ，1A 三点共线．其次，再证2260BKB CKC S S BAC =⇔=︒△△∠．并在三角函数式中，用A 、B 、C 分别表示三内角． 证法 1 设△ABC 的外接圆半径为R ，CI 的延长线交AB 于D ，对△ACD 及截线12C IC ，应用梅涅劳斯定理，有12121AC CC DI C D IC C A⋅⋅=． ①注意到 112AC AB ABC D AD AC AC BC ⋅=-=-+ 22sin sin ()sin (sin sin )222()sin sin cos2C B AR AB AC BC C B A RA B AC BC B A-⋅⋅--⋅===-++，则 11sinsin22cos cos 22C B AC D C A BAC -⋅=-⋅． 而sin cos sin 22sin sin sin 22C A B B IC AC ADC C C DI AD ACD ⎛⎫-+ ⎪⎝⎭====∠∠，由①式，有2121sin2cos2B A CC CD IC C C A DI AC -=⋅=．从而 22222sincos 22cos2A BAC CC AC C AC C A⋅-==． ②又对△ACD 及截线12B IB ，应用梅涅劳斯定理，有21211AB CB DI B D IC B A⋅⋅=． 注意到11CB B A =，有22sin2cos 2C B D DI A B AB IC ==-，2222cos sin 2sin sin2222cos cos22A B C A BAB B D AD A B A B AB AB --⋅-===--，即2coscos cossin 222sin sin 2sin sin 2sin sin 2sin sin 222222A B A B A BAC B AB AD AB AB A B A B A B AC BC B A ---=⋅=⋅⋅=⋅⋅=++⋅⋅⋅cos22cos sin22B ABC A⋅⋅．从而22sincos 22cos2A C ABB AB ⋅=． ③由2222221BKB CKC ABC AB C AB AC S S S S AB AC ⋅=⇔=⇔=⋅△△△△，注意②，③24sin 12A⇔=，且A 为锐角60BAC ⇔=︒∠．证法2 如图1-14，设直线AI 交BC 于F ，直线12B B 交CB 的延长线于E ．对ACF △及截线1B IE ，应用梅涅劳斯定理，有111AB CF FIB C EF IA⋅⋅=． ④又由11AB B C =及角平分线性质，即有FI CF BF BCIA CA BA AB AC===+． 令BC a =，AC b =，AB c =，则FI aIA b c=+． 由④式，有CE b c EF a +=，即EF EF aCF CE EF b c a==-+-． 而abCF b c =+，则2()()a b EF b c a b c =+-+．又ac BF b c =+，()a a c BE EF BFbc a -=-=+-（由题设知a c >）． 从而 ()()EF abBE b c a c =+-． 对ABF △及截线2IB E ，应用梅涅劳斯定理，有221BB AI FE IF EB B A⋅⋅=． 将⑤式代入上式，得22BB IF BE a c B A AI EF b -=⋅=，∴ 2222AB B B AB a b cAB AB b++-==． ⑥同理2AC a c b AC c+-=． 由2222221BKB CKC ABC AB C AB AC S S S S AB AC ⋅=⇔=⇔=⋅△△△△，注意⑥，⑦1a b c a c bb c+-+-⇔⋅=⇔22260a b c bc BAC =+-⇔=︒∠．注 例11还有其他证法，可参见笔者另文《关于2003年中国数学奥林匹克第一题》（《中等数学》2003年第6期）．例12 如图1-15，凸四边形ABCD 的一组对边BA 与CD 的延长线交于M ，且AD BC ∥，过M 作截线交另一组对边所在直线于H ，L ，交对角线所在直线于H '，L '．求工业化：1111MH ML MH ML +=+''． H 'L'LDCAMOH图1-15证法1 如图1-15，对ML D '△及直线BLC 由梅涅劳斯定理得 1ML L B DCLL BD CM'⋅⋅='． 对DL H '△及直线BAM 由梅涅劳斯定理得 1L M HA DBMH AD BL '⋅⋅='． 对MHD △及直线CH A '由梅涅劳斯定理得1HH MC DAH M CD AH'⋅⋅='． 由①⨯②⨯③得1ML L M HH LL MH H M''⋅⋅=''， 所以HH LL MH H M ML L M ''=''⋅⋅， 所以H M MH ML ML MH H M ML L M ''--=''⋅⋅， 故1111MH ML MH HL+=+''． 证法2 设AD 与BC 的延长线相交于O ．△BML 和△CML 均被直线AO 所截，迭用梅涅劳斯定理，有 BA HL OBAM MH LO=⋅，① CD HL OCDM MH LO=⋅，② 由①LC ⋅+②BL ⋅，得 BA CD HL OB LC OC BLLC BL AM DM MH LO⋅+⋅⋅+⋅=⋅．③ 注意到 OB LC OC BL BC LO ⋅+⋅=⋅（直线上的托勒密定理），则③式变为BA CDLC BL AM DM⋅+⋅= HLDC MH⋅．④ 又由BD 截△LCM 和AC 截△LBM ，迭用梅涅劳斯定理，有LL DCBC BL L M MD'⋅=⋅'，LH ABBC LC H M AM'⋅=⋅'． 将此结果代入④式整理，即得欲证结论．注 当AD BC ∥，④式显然成立，故仍有结论成立．此题是二次曲线蝴蝶定理的推论． 3．论证点共直线的重要方法例13 如图1-16，△ABC 的内切圆分别切三边BC ，CA ，AB 于点D ，E ，F ，点X 是△ABC 的一个内点，△XBC 的内切圆也在点D 处与BC 边相切，并与CX ，XB 分别相切于点Y ，Z ．证明：EFZY 是圆内接四边形． （1995年第36届IMO 预选题） PXYZ FE D CB A图1-16证明 由切线长定理，知CE CD CY ==，Z BF BD B ==，AF AE =，XZ XY =．设BC 的延长线与FE 的延长线交于P ，对△ABC 及截线FEP ，应用梅涅劳斯定理，有1AF BP CE AF BP CEFB PC EA EA PC FB=⋅⋅=⋅⋅XZ BP CY XZ BP CYYX PC ZB ZB PC YX=⋅⋅=⋅⋅． 对△XBC 应用梅涅劳斯定理的逆定理，知Z ，Y ，P 三点共线，故由切割线定理有2PE PF PD ⋅=，2PY PZ PD ⋅=．以而PE PF PY PZ ⋅=⋅，即EFZY 是圆内接四边形．例14 如图1-17，△ABC 中，A ∠内的旁切圆切A ∠的两边于1A 和2A ，直线12A A 与BC 交于3A ；类似地定义1B ，2B ，3B 和1C ，2C ，3C ．求证：3A ，3B ，3C 三点共线．A 3图1-17证明 由切线长定理，知12AA AA =，12BB BB =，12CC CC =．对△ABC 与直线123C C C ，123A A A ，123B B B 分别应用梅涅劳斯定理，有332123213111AC AC BC CC BC C B C C C A C B C A =⋅⋅=⋅⋅，233213213111BA BA CA AA CA A C A A A B A C A B=⋅⋅=⋅⋅，332123213111CB CB AB BB AB B A B B B C B A B C=⋅⋅=⋅=． 上述三式相乘，有333111111333222222AC BA CB AC A B B C AC A B B CC B A C B A BC CA AB CA AB BC ⋅⋅=⋅⋅=⋅⋅． 设3O e 切AB 于K ，2O e 切AC 于L ，则由12BB BB =，可得21221()2BC BK B C KB ==-．同理11211()2B C CL B C LC ==-．又由两内公切线长相等，即21KB LC =，故21BC B C =．同理，21CA AC =，21AB A B =．从而3333331AC BA CB C B A C B A⋅⋅=，故对△ABC 用梅涅劳斯的逆定理，知3A ，3B ，3C 三点共直线． 例15 如图1-18，设△ABC 的三边BC ，CA ，AB 所在的直线上的点D ，E ，F 共线，并且直线AD ，BE ，CF 关于A ∠，B ∠，C ∠平分线的对称直线AD '，BE '，CF '分别与BC ，CA ，AB 所在直线交于D '，E '，F '，则D '，E '，F '也共线．D 'F'E'F EDC BA图1-18证明 对ABC ∠及截线FED 应用第一角元形式的梅涅劳斯定理，有sin sin sin 1sin sin sin BAD CBE ACFDAC EBA FCB ⋅⋅=∠∠∠∠∠∠．由题设知，CAD BAD '=∠∠，D AB DAC '=∠∠，BCF ACF '=∠∠，F CA FCB '=∠∠，ABE CBE '=∠∠，E BC EBA '=∠∠，从而有sin sin sin 1sin sin sin CAD ABE BCF D AB E BC F CA '''⋅⋅='''∠∠∠∠∠∠，即sin sin sin 1sin sin sin BAD CBE ACF D AC E BA F CB'''⋅⋅='''∠∠∠∠∠∠． 故由第一角元形式的梅涅劳斯定理，知D '，E '，F '共线．例16 在筝形ABCD 中，AB AD =，BC CD =．过BD 上的一点P 作一条直线分别交AD 、BC 于E 、F ，再过点P 作一条直线分别交AB 、CD 于G 、H ．设GF 与EH 分别与BD 交于I 、J ，求证：PI PJPB PD=． 证明 如图1-19，过B 作AD 的平行线交直线EF 于E '，再过B 作CD 的平行线交直线GH 于H '，则E BP EDP PBG '==∠∠∠，HBPHDP PBF '==∠∠∠． H 'E'PDCBAHF EG 图1-19进而H BG H BP GBP PBF PBE E BF ''''=-=-=∠∠∠∠∠∠．所以 sin sin sin sin sin sin 1sin sin sin sin sin sin PBH GBI FBE FBP GBP FBE H BG IBF E BP E BF PBF PBG'''⋅⋅=⋅⋅='''∠∠∠∠∠∠∠∠∠∠∠∠．又H '、I 、E '分别为△PGF 三边所在直线上的点，且点B 不在△PGF 三边所在的直线上．由第二角元形式的梅涅劳斯定理的逆定理知H '、I 、E '共线．于是，由PBE PDE '△∽△，PH B PHD '△∽△．有E H EH ''∥．因此，PI PE PB PJ PE PD '==．故PI PJPB PD=． 注 当PB PD =，P 为BD 中点时，即为1989年12月冬令营选拔赛试题．例17 如图1-20，四边形ABCD 内接于圆，其边AB ，DC 的延长线交于点P ，AD 和BC 的延长线交于点Q ，过Q 作该圆的两条切线，切点分别为E ，F ．求证：P ，E ，F 三点共线．（1997年CMO 试题）Q图1-20证明 设圆心为O ，连QO 交EF 于L ，连LD ，LA ，OD ，OA ，则由切割线定理和射影定理，有 2QD QA QE QL QO ⋅==⋅，从而D ，L ，O ，A 四点共圆，即有QLD DAO ODA OLA ===∠∠∠∠，亦即OL 为△LAD 的内角ALD ∠的外角平分线． 又EF OQ ⊥，则EL 平分ALD ∠． 设EF 分别交AD ，BC 于M ，N ，于是DM DL DQMA AL AQ==． 同理，CN CQBN BQ=． 于是，DM AM AM DM AD DQ AQ AQ DQ DQ AQ +===++，CN BN BCCQ BQ BQ CQ==+， 所以，211MQ DQ DQ DA AQ DM DM AD AD +=+=+=，2QN BQCN BC=． 直线PBA 与△QCD 的三边延长线相交，由梅涅劳斯定理，有1CP DA QB CP DM QNPD AQ BC PD MQ CN=⋅⋅=⋅⋅． 对△QCD 应用梅涅劳斯定理的逆定理，知P ，M ，N 三点共线．所以P ，E ，F 三点共线．注 此例的其他证法，可参见第二章例9，第九章例15等．例18 已知△ABC 的内切圆分别切BC 、CA 、AB 于点D 、E 、F ，线段BE 、CF 分别与该内切圆交于点P 、Q ，若直线FE 与BC 交于圆外一点R ．证明P 、Q 、R 三点共线．（2011年香港奥林匹克题）证明 如图1-21，由切线长定理有AE AF =．对△ABC 及截线EFR 应用梅涅劳斯定理，有1AF BR CEFB RC EA⋅⋅=，RFEDCBAPQ S 图1-21即有BR EA FB FBRC CE AF CE=⋅=． 设BE 与CF 交于点S ，由△EFC ∽△QEC ，△FEB PFB ∽△，△SEQ ∽△SFP ，有CQ CEEQ EF=，FP FE PB FB=，SP FP SQ EQ =． 又对△SBC 及所在边上的点R 、P 、Q ，有SP BR CQ SP CQ BR FP CQ FB FP CQ FBPB RC QS SQ PB RC EQ PB CE PB QE CE⋅⋅=⋅⋅=⋅⋅=⋅⋅1FE CE FBFB EF CE=⋅⋅=． 于是，由梅涅劳斯定理的逆定理，知P 、Q 、R 三点共线． 4．注意与其他著名定理配合运用例19 在Rt △ABC 中，已知90A =︒∠，B C >∠∠，D 是△ABC 处接圆的圆心，直线A l 、B l 分别切O e 于点A 、B ，BC 与直线A l 、AC 与直线B l 分别交于点S 、D ，AB 与DS 交于点E ，CE 与直线Al 交于点T ，又设P 是直线A l 上的点，且使得A EP l ⊥，Q （不同于点C ）是CP 与O e 的交点，R 是QT 与O e 的交点，令BR 与直线A l 交于点U ． 证明：22SU SP SA TU TP TA ⋅=⋅．（2005年韩国奥林匹克题）证明 如图1-22，设BA 的延长线与O e （过C 点）的切线交于点E '．由帕斯卡定理知S 、D 、E '三点共线，从而点E '与E 重合．图1-22由切割线窄弹知 2TA TR TQ =⋅，2SA SB SC =⋅．所以，22SA SB SCTA TR TQ⋅=⋅． ①设TQ 与CB 交于点X ，对△XTS 及截线RBU ，截线QCP 分别应用梅涅劳斯定理，有1XP TU SBRT US BX⋅⋅=，=1XQ TP SC QT PS CX ⋅⋅． ② 注意相交弦定理，有XP XQ XB XC ⋅=⋅．③由①、②、③，得 22SU SP XP SB XQ SC SB SC SA TU TP RT BX QT CX TR TQ TA ⋅=⋅⋅⋅=⋅=． 例20 在梯形ABCD 中，已知BC 、AD 分别为上、下底，F 为腰CD 上一点，AF 与BD 交于点E ，G 为边AB 上一点，满足EG AD ∥，CG 与BD 交于点H ，FH 与AB 交于点I ．证明：CI 、FG 、AD 三线共点． （2011年乌克兰奥林匹克题） 证明 如图1-23，设直线AB 与DC 、AF 与DG 分别交于点S 、T ．SD图1-23先证S 、H 、T 三点共线．由EG AD BC ∥∥，知△ATP ETG ∽△，△GHE CHB ∽△，△ASD ∽△BSC ．有,,AT AD EH GE BC BSTE EG HB CB AD AS ===． 上述三式相乘，有 1AT EH BS AD GE CBTE HB SA EG CB AD⋅⋅=⋅⋅=． 对△AES 应用梅涅劳斯定理的逆定理，知T 、H 、S 三点共线．考虑△AFI 和△DGC ，注意到直线IF 与CG ，FA 与GD 、AI 与DC 分别交于点H 、T 、S ，于是由戴沙格定理，知CI 、FG 、AD 三线共点．【模拟实战】习题A1．在△ABC 中，点D 在BC 上，13BD DC =，E ，G 分别在AB ，AD 上，23AE EB =，12AG GD =，EG 交AC 于点F ，求AFFC． 2．在ABCD Y中，E ，F 分别是AB ，BC 的中点，AF 与CE 相交于G ，AF 与DE 相交于H ，求AH ∶HG ∶GF ．3．P 是△ABC 内一点，引线段APD ，BPE 和CPF ，使D 在BC 上，E 在AC 上，F 在AB 上．已知6AP =，9BP =，6PD =，3PE =，20CF =，求△ABC 的面积．（第7届AIME 题） 4．设凸四边形ABCD 的对角线AC 和交于点M ，过M 作AD 的平行线分别交AB ，CD 于点E ，F ，交BC 的延长线于点O ，P 是以O 为圆心，以OM 为半径的圆上一点，求证：OPF OEP =∠∠．（1996年全国初中联赛题）5．已知D ，F 分别是△ABC 的边AB ，AC 上的点，且23AD DB CF FA ==∶∶∶，连DF 交BC 边的延长线于点E ，求EF FD ∶．6．设D 为等腰Rt △ABC （90C =︒∠）的直角边BC 的中点，E 在AB 上，且21AE EB =∶∶，求证：CE AD ⊥．7．在△ABC 中，点M 和N 顺次三等分AC ，点X 和Y 顺次三等分BC ，AY 与BM ，BN 分别交于点S ，R ，求四边形SRNM 与△ABC 的面积之比．8．E ，F ，G ，H 分别为四边形ABCD 的四条边AB ，BC ，CD ，DA 上的点，若EH ，BD ，FG 三直线共点，则EF ，AC ，HG 三直线共点或平行．9．设X ，Y ，Z 分别是△ABC 的边CB ，CA 和BA 延长线上的点，又XA ，YB 和ZC 分别是△ABC 外接圆的切线．证明：X ，Y ，Z 三点共线． （1989年新加坡竞赛题） 10．求证：三角形两角的平分线与第三角的外角平分线各与对边所在直线的交点共线．11．已知直径为AB 的圆和圆上一点X ，设A t ，B t 和X t 分别是这个圆在A ，B ，X 处的切线．设Z 是直线AX 与B t 的交点，Y 是直线BX 与A t 的交点，证明：YZ ，X t ，AB 三直线共点．（第6届加拿大竞赛题）12．P 是ABCD Y中任一点，过P 作AD 的平行线分别交AB ，CD 于E ，F ，又过P 作AB 的平行线，分别交AD ，BC 于G ，H ．求证：AH ，CE ，DP 三线共点．13．在△ABC 中，1AA 为中线，2AA 为角平分线，K 为1AA 上的点，使2KA AC ∥．证明：2AA KC ⊥． （第58届莫斯科奥林匹克题） 14．直线l 交直线OX ，OY 分别于A ，B ，点C 与D 是线段AB 两侧的直线l 上两点，且CA DB =．过C 的直线CKL 交OX 于K ，交OY 于L ；过D 的直线交OX 于M ，交OY 于N ．连结ML 和KN ，交直线l 分别于E ，F ．求证：AE BF =．15．设四边形ABCD 外切于一圆，E ，F ，G ，H 分别是AB ，BC ，CD ，DA 边上的切点，若直线HE 与DB 相交于点M ，则M ，F ，G 三点共线．16．设P 为△ABC 的内点，过点P 的直线l ，m ，n 分别垂直于AP ，BP ，CP ，若l 交BC 于Q ，m 交AC 于R ，n 交AB 于S ，证明：Q ，R ，S 共线． （IMO -28预选题） 17．已知△ABC 的BC 与它的内切圆相切于点F ．证明：该圆的圆心O 在BC 与AF 的两个中点M ，N 的连线上．18．已知凸四边形ABCD 内接于O e ，对角线AC ，BD 相交于点Q ，过Q 分别作直线AB ，BC ，CD ，DA 的垂线，垂足分别是E ，F ，G ，H ．求证：EH ，BD ，FG 三直线共点或互相平行．19．设ABCD 为圆外切四边形，又AB ，BC ，CD ，DA 与该圆的切点为E ，F ，G ，H ．求证：AC ，BD ，EG ，FH 共点．习题B1．P 是ABCD Y内一点，MN ，EF 分别过P ，MN AD ∥且分别与AB ，CD 交于点M ，N ，EF AB ∥且分别与DA ，BC 交于点E ，F ．求证：ME ，FN ，BD 三线共点． 2．在△OAB 中，AOB ∠为锐角，从AB 上任一点M 作MP OA ⊥于P ，MQ OB ⊥于Q ，点H 是△OPQ 的垂心，求当点M 在线段AB 上移动时，点H 的轨迹． （IMO -7试题） 3．在正△ABC 的边BC ，CA ，AB 上有内分点D ，E ，F 将边分成3∶(3)(6)n n ->，线段AD ，BE ，CF 相交所成的△PQR （BE 交AD 于P ，交FC 于Q ）是△ABC 的面积的449时，求n 的值． （1992年日本奥林匹克预选题）4．在△ABC 中，90A =︒∠，点D 在AC 上，点E 在BD 上，AE 的延长线交BC 于F ．若BE ∶2ED AC =∶DC ，则ADB FDC =∠∠．5．已知点E ，1D ，2D 在△ABC （AB AC >）的边BC 上，12BAD CAD =∠∠，11EF AD ∥交AB 于1F ，又与CA 的延长线交于1C ，22EF AD ∥交AB 于2F ，又与CA 的延长线交于2G ．求证：212212BF BF BE CE CG CG ⋅=⋅．（《数学通报》问题1353题）6．圆外切四边形ABCD 中，AB ，BC ，CD ，DA 边上的切点分别为P ，Q ，R ，S ．AD 与BC 的延长线交于点E ，AB 与DC 延长线相交于点F ．求证：（Ⅰ）AC ，BD ，PR ，QS 四线共点；（Ⅱ）AC ，EF ，PQ ，RS 四线共点；（Ⅲ）BD ，EF ，PS ，QR 四线共点（假定BD EF ≠）． 7．若凸四边形的对角线AC 与BD 互相垂直，且相交于E ，过E 点分别作边AB ，BC ，CD ，DA 的垂线，垂足依次为P ，Q ，R ，S ，并分别交CD ，DA ，AB ，BC 边于P '，Q '，R '，S '，再顺次连接P Q ''，Q R ''．R S ''，S P ''，则R S P Q AC ''''∥∥；R Q P S BD ''''∥∥．（IMO -22试题的推广）8．面积为1的△ABC 的边AB ，AC 上分别有点D ，E ，线段BE ，CD 相交于点P ．点D ，E 分别在AB ，AC 上移动，但满足四边形BCED 的面枳是△PBC 面积的两倍这一条件，求△PDE 面积的最大值． （1992年日本奥林匹克题） 9．ABCD 是边长为2的正方形，E 为AB 的中点，F 是BC 的中点，AF 和DE 相交于I ，BD 和AF 相交于H ．求四边形BEIH 的面积．10．P 是凸四边形ABCD 所在平面上一点，APB ∠，BPC ∠，CPD ∠，DPA ∠的平分线分别交AB ，BC ，CD ，DA 于点K ，L ，M ，N ．（Ⅰ）寻找一点P ，使KLMN 是平行四边形；（Ⅱ）求所有这样的P 点的轨迹． （1995年世界城市际联赛题） 11．△ABC 中，AB AC >，AD 为内角平分线，点E 在△ABC 的内部，且EC AD ⊥，ED AC ∥，求证：射线AE 平分BC 边． （《数学教学》问题536题） 12．设△123A A A 为非等腰三角形，内心为I ，i C （1i =，2，3）为过I 与1i i A A +和2i i A A +相切的小圆（增加的下标作模3同余），i B （1i =，2，3）为圆1i C +和2i C +的另一交点，证明：△11A B I ，△22A B I ，△33A B I 的外心共线．（IMO -38预选题）。

梅涅劳斯定理梅涅劳斯定理是元心®≠O，且三角形ABC的三个顶点都在圆周上的情况下，与元心®相互对称的三条直线（AB的对称轴、BC的对称轴和AC的对称轴）的交点M、N、P，连成一个新的三角形。

则这个三角形的垂心H，外心O和重心G一定共线，并且一个在中点上，一个在重心的两倍上。

梅涅劳斯定理由法国数学家梅涅劳斯（Menelaus）在19世纪初推导得出。

他在研究三角形性质和钻石形排列、多面体面积等问题时，发现了三角形内外接圆之间存在某种规律。

他将这种规律总结为“梅涅劳斯定理”，这让人们对三角形的研究产生了新的启示，也极大地推动了数学发展。

1.直线对称：如果直线l把一个图形分成两部分，其中一部分在直线l同侧，另一部分在直线l异侧，那么我们就称这条直线为这个图形的对称轴。

2.三角形的三条对称轴：在一个三角形中，过三个顶点分别做与对边垂直的直线，交于另一三点，这三条线分别称为这个三角形的三条对称轴。

3.外心O：一个三角形的三边的垂直平分线所交的点O就是这个三角形的外心。

梅涅劳斯定理可以用“线段长度乘积相等”来概括，即：BM/MA*CN/NP*AP/PB=1其中BM、CN、AP与MA、NP、PB分别为MN、NP、MP与BC、AC、AB的交点，再根据Euler线的性质，外心、重心、垂心三点共线，并有以下定理：1.如果三角形ABC的外接圆半径R为：R=abc/4K，其中a、b、c为三角形的三边长，K 为三角形的面积，那么重心到外心的距离等于R的三分之二。

2.如果三角形ABC的外接圆半径为R，那么垂心到外心的距离等于R。

梅涅劳斯定理是用于计算三角形各顶点到对边距离的常用方法之一。

例如，如果三角形ABC的三个顶点分别是A(-2,1)，B(0,-2)，C(3,1)，垂心的坐标为H(x,y)，那么我们可以用以下步骤来计算垂心的坐标：1.计算AB、BC、AC三边的长度。

AB=sqrt[(0-(-2))^2+(-2-1)^2]=sqrt[17]2.根据梅涅劳斯定理求出MN、NP、MP三个交点。

梅涅劳斯定理向量证明梅涅劳斯定理是欧几里得几何中一个非常重要的定理，它是描述三角形内部三条线段交点线性相关时的关系。

这个定理被广泛应用于计算三角形内心、重心、垂心等点的坐标。

在这里，我将详细介绍梅涅劳斯定理向量证明。

首先，我们需要了解几个向量的概念和符号，如向量的数量积、向量的叉积、向量之间的投影等。

假设我们有一个三角形ABC，它的三个顶点分别为A、B、C，向量AB、BC、CA分别表示从A指向B、从B 指向C、从C指向A的向量。

然后，我们需要证明两个引理：引理1：如果三角形ABC的内部有一点P，那么向量AP、BP、CP满足下列关系：$AP \times BC + BP \times AC + CP \times AB = 0$证明：我们可以将向量AP、BP、CP分别表示为向量AB、BC、CA的线性组合，即AP=kBC+lCA，BP=mCA+nAB，CP=pAB+qBC。

将这些向量代入原式，得到：$(kBC+lCA) \times BC + (mCA+nAB) \times AC + (pAB+qBC) \times AB$化简可得：$k(BC \times BC) + (l+q)(CA \times AB) + n(AB \times AC) +m(AC \times AC) + p(AB \times BC)$利用向量的叉积性质，这个式子可以进一步改写为：$-k\,{\vec{a}}^{2} + (l + q)\,{\vec{b}}\cdot{\vec{c}} +n\,{\vec{a}}\cdot{\vec{c}} + m\,{\vec{c}}^{2} +p\,{\vec{a}}\cdot{\vec{b}}=0$其中，$\vec{a}=\vec{BC}$，$\vec{b}=\vec{AB}$，$\vec{c}=\vec{CA}$，是三角形ABC的3条边，$\cdot$表示向量的数量积。

根据向量之间的投影关系，我们有$\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{c}=\vec{c}\cdot\vec{a}$和$\vec{a}+\vec{b}+\vec{c}=0$。

厦门一中2010数学竞赛讲座—平面几何平面几何定理1——梅涅劳斯定理梅涅劳斯定理：设P 、Q 、R 分别是ABC ∆三边BC ，CA 、AB 或其延长线上的点，若P 、Q 、R 三点共线，则BP 1PC CQ AR QA RB⋅⋅=。

（四种证明方法）梅涅劳斯逆定理：设P 、Q 、R 分别是ABC ∆三边BC ，CA 、AB 或其延长线上的点，若BP 1PC CQ AR QA RB⋅⋅=，则P 、Q 、R 三点共线。

第一角元形式的梅涅劳斯定理：设P 、Q 、R 分别是ABC ∆三边BC ，CA 、AB 或其延长线上的点，则P 、Q 、R 三点共线的充要条件是：sin sin sin 1sin sin sin BAP ACR CBQ PAC RCB QBA∠∠∠⋅=∠∠∠第二角元形式的梅涅劳斯定理：设P 、Q 、R 分别是ABC ∆三边BC ，CA 、AB 或其延长线上的点，点O 不在ABC ∆三遍所在直线上，则P 、Q 、R 三点共线的充要条件是： sin sin sin 1sin sin sin BOP AOR COQ POC ROB QOA∠∠∠⋅=∠∠∠例1．（笛沙格定理）如图，由O 点引出的三条射线上各有两个点：1A 和2A ，1B 和2B ，1C 和2C ，直线11B C 和22B C 交于点X ：直线11AC 和22A C 交于点Y ， 直线11A B 和22A B 交于点Z 。

求证：X 、Y 、Z 三点共线。

::练习：例2：如图，在四边形ABCD 中△ABD ，△BCD ，△ABC 的面积比是3:4:1，点M ，N 分别在AC ，CD 上，满足AM ：AC=CN ：CD ，并且Ｂ，Ｍ，Ｎ共线，求证M 与Ｎ分别是ＡＣ和ＣＤ的中点。

练习：角元形式梅氏定理例4 例5. 例3练习4.2 3 4 5。

amc 梅涅劳斯定理
【原创实用版】
目录
1.AMC 梅涅劳斯定理简介
2.梅涅劳斯定理的证明方法
3.梅涅劳斯定理的应用领域
4.梅涅劳斯定理在我国的发展和研究
正文
【1】AMC 梅涅劳斯定理简介
AMC 梅涅劳斯定理，全称为“美国数学竞赛梅涅劳斯定理”，是数学领域中的一个著名定理。

该定理的表述为：若三角形 ABC 的三边满足 a^2 + b^2 = c^2，则三角形 ABC 是一个直角三角形。

该定理在我国也被称为勾股定理，是数学竞赛中的一个重要考点。

【2】梅涅劳斯定理的证明方法
梅涅劳斯定理的证明方法有多种，其中最著名的是欧几里得证明法。

欧几里得证明法的基本思路是：以三角形 ABC 的三个顶点为圆心，以适当的半径作圆，将三个圆相交于一点 D、E、F，然后证明四边形 AFDB 是一个矩形，从而得出 AF=BD，再根据勾股定理得出结论。

【3】梅涅劳斯定理的应用领域
梅涅劳斯定理在数学领域有着广泛的应用，除了在数学竞赛中作为一个基本考点外，它还在物理、工程、计算机科学等领域有着重要的应用。

例如，在解决一些与直角三角形相关的实际问题时，梅涅劳斯定理可以提供重要的理论支持。

【4】梅涅劳斯定理在我国的发展和研究
梅涅劳斯定理在我国的发展和研究历史悠久。

在我国古代数学中，已经有了关于直角三角形的认识和研究，但是直到 20 世纪初，我国才引进了梅涅劳斯定理这个概念，并开始对其进行研究和应用。

梅涅劳斯定理（入门篇）雷雨田（广西师范大学附属外国语学校高50班 541004）梅涅劳斯定理证明2：面积法AF/FB = △ADF/△BDF ①BD/DC = △BDF/△CDF ②CE/EA = △CDF/△ADF ③式① * ② * ③可得：（AF/FB）*（BD/DC）*（CE/EA）= 1 得证。

证明3：相似法证明4：这个定理怎么记最好呢？个人感觉“顶到分、分到顶、顶到分、分到顶、顶到分、分到顶”这样记忆来得非常容易不过找了很多资料，感觉仅仅是把这个定理（或者后面附一个逆定理）陈述然后证明完了之后，就直接给例题（或者直接讲赛瓦定理），看上去不怎么舒服，所以我把其他的一些东西附在这里，以供参考。

第一角元形式的梅涅劳斯定理（就是把线段比改为正弦值比）其表达式为：1=∠∠•∠∠•∠∠BA'B sin 'CBB sin CB 'C sin 'ACC sin AC 'A sin 'BAA sin 证明如下：如图所示，由三角形面积公式（正弦定理）可得： AC 'A sin AC 'BAA sin AB AC 'A sin AC 'AA 'BAA sin 'AA AB S S C 'A 'BA C 'AA 'ABA ∠⋅∠⋅=∠⋅⋅∠⋅⋅==∆∆2121同理可得CB'C sin BC 'ACC sin AC B 'C 'AC ,BA 'B sin AB 'CBB sin BC A 'B 'CB ∠⋅∠⋅=∠⋅∠⋅= 把这三个式子相乘，运用梅氏定理，就可得到这个式子怎么记最好呢？个人感觉根据梅涅劳斯定理中线段所对应的角来记忆最好。

第二角元形式的梅涅劳斯定理设O 是不在三角形ABC 三边所在直线上的任意一点，其他条件不变，则表达式为：1=∠∠•∠∠•∠∠OA'B sin 'COB sin OB 'C sin 'AOC sin OC 'A sin 'BOA sin AB C A’ B’C’现证明如下： 如图，由C 'A 'BA S S OC 'A 'BOA =∆∆ 可得A'B 'BA OB OC OC 'A sin 'OA B sin ⋅=∠∠同理得到另外两个对称式，相乘，运用梅氏定理即得证这个式子就这样记吧：先记住原来的梅涅劳斯定理形式，然后在每条线段表达式中间插一个O ，然后再在前面加上∠sin （比如BA'就变成'B OA sin ∠）梅氏定理的用处这个定理是平面几何的一个重要定理（好像所有竞赛书都把他与赛瓦定理放在第一节，不知是惯性还是怎么地），它大概有如下用处：可以用来证明三点共线；可以用来导出线段比例式；可以用来寻求一条线段是另一条线段的几分之几或几倍（即线段倍分）；怎么用梅氏定理知道了这个定理，还要会用才行。

梅涅劳斯公式梅涅劳斯（Menelaus）公式是一个在平面几何中非常重要的定理。

这玩意儿听起来可能有点高深莫测，但其实理解起来也没那么可怕。

咱先来说说啥是梅涅劳斯公式。

它指的是如果一条直线与△ABC 的三边 AB、BC、CA 或其延长线交于 F、D、E 点，那么就有(AF/FB)×(BD/DC)×(CE/EA)=1 。

就拿我之前教过的一个学生小明来说吧。

有一次课堂上我讲到梅涅劳斯公式，这小子一脸懵，完全不知道我在说啥。

我就给他画了个三角形，标上了几个点，然后一点点给他解释。

我跟小明说：“你看啊，假设这是一个三角形 ABC，有一条直线穿过了它的三条边，分别交于 F、D、E 这三个点。

那咱们就来看看这几个线段的比例关系。

比如说 AF 和 FB 的长度比，乘以 BD 和 DC 的长度比，再乘以 CE 和 EA 的长度比，结果就会等于 1 。

”小明眨巴着眼睛，还是有点迷糊。

我就又举了个例子。

“想象一下，你在操场上跑步，从 A 点跑到 B 点，再从 B 点跑到 C 点，然后有一条线把你的路线分成了几段。

这几段的长度比例之间就存在着梅涅劳斯公式所说的那种关系。

”小明似乎有点感觉了，开始自己在本子上画图琢磨。

咱们再深入讲讲梅涅劳斯公式的证明。

证明方法有好几种，其中一种是通过面积法来证明。

把三角形 ABC 的面积看作一个整体。

因为同高的三角形面积比等于底边的比，所以我们可以通过一系列的面积比例转换，最终得出梅涅劳斯公式。

比如说，由三角形 AEF 和三角形 BEF 同高，所以它们的面积比就等于 AF 与 FB 的比。

同理，其他的几个三角形也可以这样比较。

通过巧妙的转换和运算，就能证明出这个公式啦。

在实际解题中，梅涅劳斯公式那可是相当好用的。

比如说，当我们遇到一些需要证明三点共线或者求线段比例的问题时，它就能大显身手。

记得有一次考试，有一道题给出了一个三角形和一条直线与三边的交点，让求其中两条线段的比例关系。

梅涅劳斯定理——共角三角形的三边关系
梅涅劳斯定理在初中的竞赛中是必须要掌握的知识，对于课内，没有要求。

但是需要提高的孩子，可以看看。

简单地理解，就是存在共角的两个三角形的三边关系，可以考虑梅涅劳斯定理。

注意：三个边之间的关系，有顺序的哦，不要死记硬背，换个图呢？换个顺序呢？
当然，这几道题，我们仍可以用课内方法去解答，只是比较麻烦。

如果一个三角形求两边之间的关系，常考虑的方向；
1、相似、平行线之间的比例
2、三角函数（直角三角形）
3、求长度
知识点是固定的，有限的，方法是灵活的，多思考。