奇数阶幻方
- 格式:doc
- 大小:38.00 KB
- 文档页数:4

任意奇数阶幻方的杨辉斜排法——对杨辉口诀的讨论范贤荣2016.3.8关于三阶幻方的排法,我国古代数学家杨辉给出了一个巧妙的排法:“九子斜排,上下对易,左右相更,四维挺出”。
按照这个口诀,画出“上下对易,左右相更”之后,形成图1d的图面。
因此,必定有一个“四维挺出”的步骤。
最后得到“戴九履一,左三右七,二四為肩,六八為足”的三阶幻方。
见图1。
图1 杨辉口诀的画法可见,杨辉口诀是在利用5×5的方格,斜排9个数后,按照他的步骤,仍然是画出5×5方格的3阶的幻方,如图1e。
图2 菱中取方的画法现在,我们很多人用的是“取方框”画法。
即在5×5的方阵中,取出3×3方框来,如图2b的红框。
红框外的1,是走到框内的绿方块中,红框外的9,是走到框内的蓝方块中。
因此1、9没有“对易”。
同样,3、7也没有“相更”。
因此,就没有“上下对易,左右相更”了。
所以,就不需要“四维挺出”了。
因此,现在的画法,与原来的口诀不一致了。
所以,我根据作图的次序,将杨辉的口诀,演绎成:各子斜排为菱形,中间取方当作城,城外有子城内空,四围都往城中进。
挺进多少方可止,几阶就挺几步深。
注1:“四围”就是上下左右四边。
“都往城中进”,因此是相向而行,都到城中。
注2:“几阶就挺几步深”。
如3阶进3步,5阶进5步,7阶进7步……后续亦如此类推。
见图2。
下面,我将2~13各奇数阶,由菱方阵演变成幻方的情况,列于后。
图3 5阶菱方阵与幻方图4 7阶菱方阵与幻方图5 9阶菱方阵与幻方图6 11阶菱方阵与幻方图7 11阶幻方图8 13阶菱方阵图9 13阶幻方。

奇数阶幻⽅⼝诀
⼝诀版本⼀:
先填上⾏正中央,
依次斜填莫相忘。
上格没有顶格填,
顶格没有底格放。
⼝诀版本⼆:
1居上⾏正中央,
依次斜填莫相忘。
上出框时往下填,
右出框时左边放。
排重便在下格填,
右上排重⼀个样。
⼝诀解析:
把1(或最⼩的数)放在第⼀⾏正中;按以下规律排列剩下的n*n-1个数:
(1)、每⼀个数放在前⼀个数的右上⼀格;
(2)、如果这个数所要放的格已经超出了顶⾏那么就把它放在底⾏,仍然要放在右⼀列;
(3)、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上⼀⾏;
(4)、如果这个数所要放的格已经超出了顶⾏且超出了最右列,那么就把它放在前⼀个数的下⼀⾏同⼀列的格内;
(5)、如果这个数所要放的格已经有数填⼊,处理⽅法同(4)。
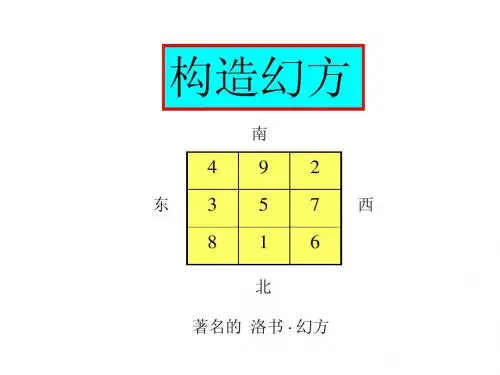

构造幻方所谓幻方,也教纵横图,就是在n×n的方阵中放入1到n2个自然数:在一定的布局下,其各行、各列和两条对角线上的数字之和正好都相等。
这个和数就叫做“幻方常数”或幻和。
幻方分为奇数阶幻方、偶数阶幻方(单偶阶幻方、双偶阶幻方),下面就这三类幻方的构造分别示范。
奇数阶幻方的经典方法-罗伯奇数阶幻方,也就是3阶、5阶、7阶……幻方,那么如何构造这样的幻方呢?我们可以采取罗伯法(也叫连续摆数法),其法则如下:把“1”放在中间一列最上边的方格中,从它开始,按对角线方向(比如说按从左下到右上的方向)顺次把由小到大的各数放入各方格中,如果碰到顶,则折向底,如果到达右侧,则转向左侧,如果进行中轮到的方格中已有数或到达右上角,则退至前一格的下方。
按照这一法则建立5阶幻方的示例如下图:罗伯法(连续摆数法)的助记口诀:1居上行正中央,依次斜填切莫忘。
上出框界往下写,右出框时左边放。
重复便在下格填,角上出格一个样。
1居上行正中央——数字1放在首行最中间的格子中依次斜填切莫忘——向右上角斜行,依次填入数字上出框界往下写——如果右上方向出了上边界,就以出框后的虚拟方格位置为基准,将数字竖直降落至底行对应的格子中右出框时左边放——同上,向右出了边界,就以出框后的虚拟方格位置为基准,将数字平移至最左列对应的格子中重复便在下格填——如果数字{N}右上的格子已被其它数字占领,就将{N +1}填写在{N}下面的格子中角上出格一个样——如果朝右上角出界,和“重复”的情况做同样处理。
偶数阶幻方的一种制作方法——双偶阶、单偶阶幻方1.双偶阶幻方(中心对称交换法)n为偶数,且能被4整除(n=4,8,12,16,20……)(n=4k,k=1,2,3,4,5……)先说明一个定义。
互补:如果两个数字的和,等于幻方最大数和最小数的和,即n×n+1,称为互补。
先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写:这个方阵的对角线,已经用颜色标出。

奇数阶幻方构造原理
奇数阶幻方是指由1到n^2 的连续整数构成的方阵,其每行、每列及两条对角线上的数字之和都相等。
以下是奇数阶幻方构造的一些原理和方法:
- 九子排列法:宋代数学家杨辉总结的“洛书”幻方的编排方法。
具体步骤为:九子排列、上下对易、左右相更、四维挺出。
- 巴舍法:以构造三阶幻方为例,假设有一个三行三列的格子,然后制造阳台、天台、地下室,再爬梯填数,最后把阳台、天台、地下室及里边的数去掉,就得到了一个三阶幻方。
- 罗伯法:可以构造出所有的奇数阶幻方。
口诀为:1居上行正中央,依次斜填切莫忘;上出框界往下写,右出框界左边放;排重便在下格填,右上出格一个样。
这些方法可以帮助构造各种奇数阶幻方,有兴趣的读者可以尝试用这些方法构造五阶幻方和七阶幻方。
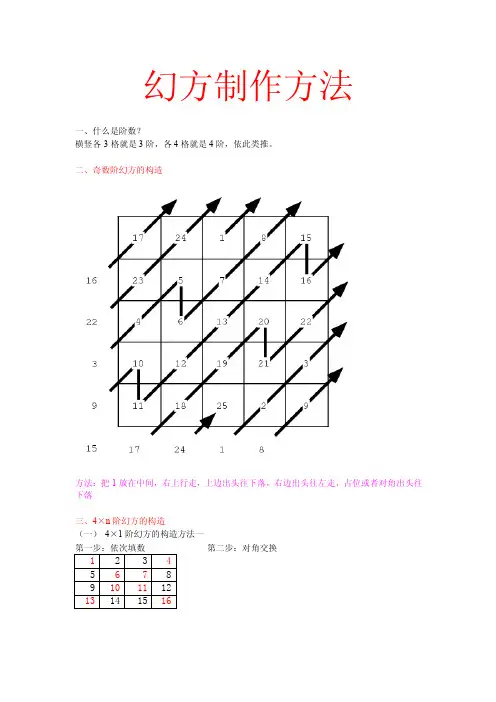
幻方制作方法一、什么是阶数?横竖各3格就是3阶,各4格就是4阶,依此类推。
二、奇数阶幻方的构造方法:把1放在中间,右上行走,上边出头往下落,右边出头往左走,占位或者对角出头往下落三、4×n阶幻方的构造(一)4×1阶幻方的构造方法一第一步:依次填数第二步:对角交换1 2 3 45 6 7 89 10 11 1213 14 15 16(二) 四阶幻方的构造方法二第一步:依次填数 第二步:不是对角的交换1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16总结:基本的四阶幻方的构造,是先依次填数,然后要么是对角的数据都交换,要么是对角的数据都不交换。
(三)4×n 阶幻方的构造我们已经知道了4×1阶幻方的构造方法:然后要么是对角的数据都交换,要么是对角的数据都不交换。
那么4×n 阶幻方的构造方法,完全与4阶幻方的构造一样,也是:要么是对角的数据都交换,要么是对角的数据都不交换。
但是,在构造4×2阶幻方时候,要把每2×2格作为一格,在构造4×3阶幻方时候,要把每3×3格作为一格,1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 5758 59 60 61 62 63 641 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 575859606162636416 2 3 13 34 5 11 10 8 34 9 7 6 12 34 4 14 15 1 34 34 34 34 341 15 14 4 34 12 6 7 9 34 8 10 11 5 34 13 3 2 16 34 34 34 34 3464 63 3 4 5 6 58 57 56 55 11 12 13 14 50 49 17 18 46 45 44 43 23 24 25 26 38 37 36 35 31 32 33 34 30 29 28 27 39 40 41 42 22 21 20 19 47 48 16 15 51 52 53 54 10 9 8 7 59 60 61 62 2 11 2 62 61 60 59 7 89 10 54 53 52 51 15 1648 47 19 20 21 22 42 4140 39 27 28 29 30 34 3332 31 35 36 37 38 26 2524 23 43 44 45 46 18 1749 50 14 13 12 11 55 5657 58 6 5 4 3 63 641 2 3 4 5 6 7 8 9 10 11 1213 14 15 16 17 18 19 20 21 22 23 2425 26 27 28 29 30 31 32 33 34 35 3637 38 39 40 41 42 43 44 45 46 47 4849 50 51 52 53 54 55 56 57 58 59 6061 62 63 64 65 66 67 68 69 70 71 7273 74 75 76 77 78 79 80 81 82 83 8485 86 87 88 89 90 91 92 93 94 95 9697 98 99 100 101 102 103 104 105 106 107 108109 110 111 112 113 114 115 116 117 118 119 120121 122 123 124 125 126 127 128 129 130 131 132133 134 135 136 137 138 139 140 141 142 143 1441 2 3 141 140 139 138 137 136 10 11 1213 14 15 129 128 127 126 125 124 22 23 2425 26 27 117 116 115 114 113 112 34 35 36108 107 106 40 41 42 43 44 45 99 98 9796 95 94 52 53 54 55 56 57 87 86 8584 83 82 64 65 66 67 68 69 75 74 7372 71 70 76 77 78 79 80 81 63 62 6160 59 58 88 89 90 91 92 93 51 50 4948 47 46 100 101 102 103 104 105 39 38 37109 110 111 33 32 31 30 29 28 118 119 120121 122 123 21 20 19 18 17 16 130 131 132133 134 135 9 8 7 6 5 4 142 143 144(三)如何在纸上快速填写4n阶幻方,参看上图1、我们假设对角不变。

任意奇数阶幻方的罗伯移步法学习心得范贤荣2016.2.25在学习幻方构成时,在网上看到了大多数幻友介绍的罗伯(loubere)法。
读后,我有心得如下:1、罗伯(loubere)法的确是最简单的任意奇数阶幻方的构成法。
它只要一步一步地填写就可以了。
2、有人称之为楼梯法。
这也非常形象,体现了一步一步斜着向上的填写规律。
因此,我觉得以罗伯楼梯法谓之,倒是一个好办法,既尊敬了罗伯的创造,又形象地体现了填写规律。
但是,楼梯太实用了,就采用了浪漫点的移步二字,编写了本文的题目。
3、罗伯法的填写步骤,非常经典。
关于“出格/出框”、“重复/遇阻”的规定,也往往还被其他方法所引用。
4、罗伯法的口诀,对“1居上行正中央”的这种幻方,是很正确且准确的。
但是,不知道这是不是罗伯老师的原话。
我现在看到的都是幻友们的介绍。
因此,就与幻友们讨论一下:这个口诀,只适用于“1居上行正中央”的这种幻方。
或者说“1居上行正中央”的这种幻方,只是罗伯幻方的一种。
罗伯幻方每一阶都有多种。
幻方数与阶数相同。
因此,我建议在这口诀下面加一个注:“1居上行正中央”只是罗伯幻方有代表性的一种。
1还可以在其他点格上。
5、1还可以在那些点格上呢?我们把方阵空格用(X,Y)即(行,列)表示。
第一行,第三列表示为(1,3)那么,各阶数方阵有几个幻方,1点在何处,可见下表:我们还可以形象地用方阵的方式,直观地看到1的位置。
5阶幻方的1点在幻和为65的格子内。
方法是:1)与阶数一样,画出阶数方阵。
例如,5阶2)将该阶幻方的幻和填在方阵的“上行正中央”。
例如5阶幻和65。
3)在斜着把幻和,逐行向左移一位,填在各行。
如下图4)再利用罗伯法则,将出格的数移回来。
就可以直观地看到1在那些点格了。
5)顺便说说方阵中的其他数据是什么?从何而来?。
这些数据都是一个不等于“幻和”的对角线之和。
我是计算出来的,计算完5阶,我就知道7阶了。
因此,就少画了许多方阵。
6)其他不等于“幻和”的对角线之和,就是将“幻和”向两边逐步加减“阶²”。

幻方”的口诀小学时,老师或者数学竞赛时经常会出现魔方的题目,记得金庸先生写的著名的武侠小说《射雕英雄传》里面的瑛姑就是被一个三阶的幻方给困住了十几年,而黄蓉不到一分钟就完成那个幻方,那么有没有什么诀窍呢?后来,在一些书上看到,对于奇数阶的幻方,有如下的口诀:居首列正中央,依次斜填左上方;左出框时向右写,上出框时往下放;遇到重合无处填,退居原数右邻行。
举例(3 阶幻方):注:*表示还没有填数字的空位置步骤(1):即“一居首列正中央”步骤(2):即“依次斜填左上方,左出框时向右写(上一行最右列)”* * *步骤(3):即“上出框时往下放(左一列最下一行)”步骤(4):即“遇到重合无处填”,(也就是左上方已经写有数字),“退居原数右邻行”,将要填写的数字放到本行靠右一列)步骤(5):步骤(6):1 * *步骤(7):注意:左上角位置的左上方位置是右下角,即6的左上方是已经填写了数据的4的位置,根据口诀“遇到重合无处填”,此时步骤(8):即“上出框时往下放(左一列最下一行)”步骤(9):即“依次斜填左上方,左出框时向右写(上一行最右列)”只要是奇数阶魔方,都可根据此“口诀”构造。
双偶阶幻方n为偶数,且能被4整除(n=4,8, 12 , 16 ,20……)(n=4k ,k=1 , 2, 3, 4 , 5……)先说明一个定义:互补:如果两个数字的和,等于幻方最大数和最小数的和,即n*n+1 ,称为互补。
先看看4 阶幻方的填法:将数字从左到右、从上到下按顺序填写:10 11 1213 14 15 16这个方阵的对角线,已经用蓝色标出。
将对角线上的数字,换成与它互补的数字。
这里,n*n+1 = 4*4+1 = 17把1 换成17-1 = 16 ;把6 换成17-6 = 11 ;把11 换成17-11=6……换完后就是一个四阶幻方对于n=4k 阶幻方,我们先把数字按顺序填写。
写好后,按4*4 把它划分成k*k 个方阵。
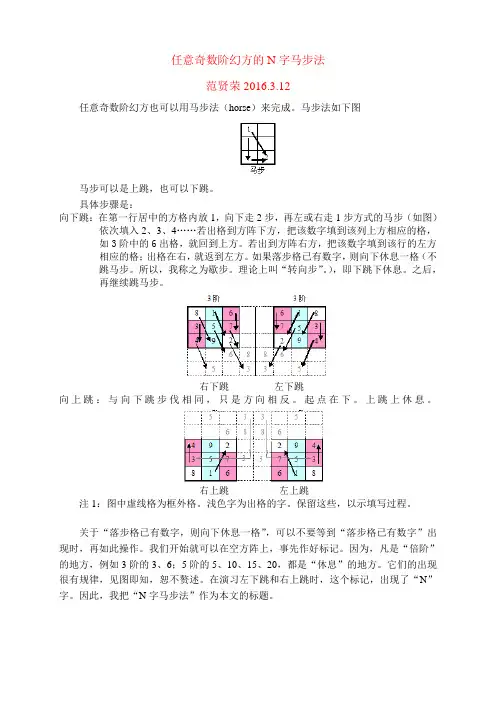
任意奇数阶幻方的N字马步法范贤荣2016.3.12任意奇数阶幻方也可以用马步法(horse)来完成。
马步法如下图马步可以是上跳,也可以下跳。
具体步骤是:向下跳:在第一行居中的方格内放1,向下走2步,再左或右走1步方式的马步(如图)依次填入2、3、4……若出格到方阵下方,把该数字填到该列上方相应的格,如3阶中的6出格,就回到上方。
若出到方阵右方,把该数字填到该行的左方相应的格;出格在右,就返到左方。
如果落步格已有数字,则向下休息一格(不跳马步。
所以,我称之为歇步。
理论上叫“转向步”。
),即下跳下休息。
之后,再继续跳马步。
右下跳左下跳向上跳:与向下跳步伐相同,只是方向相反。
起点在下。
上跳上休息。
右上跳左上跳注1:图中虚线格为框外格。
浅色字为出格的字。
保留这些,以示填写过程。
关于“落步格已有数字,则向下休息一格”,可以不要等到“落步格已有数字”出现时,再如此操作。
我们开始就可以在空方阵上,事先作好标记。
因为,凡是“倍阶”的地方,例如3阶的3、6;5阶的5、10、15、20,都是“休息”的地方。
它们的出现很有规律,见图即知,恕不赘述。
在演习左下跳和右上跳时,这个标记,出现了“N”字。
因此,我把“N字马步法”作为本文的标题。
马步法的口诀:向下跳:1居首行正中央,向下跳出马步样,遇到倍阶下一格,休息片刻再前闯。
向上跳:1居末行正中央,向上跳出马步样,遇到倍阶上一格,休息片刻再前闯。
以下展示的是下跳的3~9阶幻方。
左下跳右下跳以下展示的是上跳的3~9阶幻方。
右上跳左上跳以下还有11~17的各奇数阶幻方:。

巧填幻方一、什么叫幻方?(通俗点说)把一些有规律的数填在纵横格数都相等的正方形图内,使每一行、每一列和每一条对角线上各个数之和都相等。
这样的方阵图叫做幻方。
幻方又分为奇数阶幻方和偶数阶幻方。
奇数阶幻方是指横行、竖列都是单数(即3、5、7、9……)的方阵图。
偶数阶幻方是指横行、竖列都是双数(即4、6、8、10……)的方阵图。
二、奇数阶幻方在第一行居中的方格内放1,依次向右上方填入2、3、4…,如果右上方已有数字,则向下移一格继续填写。
(1) 将1放在第一行中间一列;(2) 从2开始直到n×n止各数依次按下列规则存放:按 45°方向向右上方行走,每一个数存放的行比前一个数的行数减1,列数加1(3) 如果行列范围超出矩阵范围,则回绕。
例如1在第1行,则2应放在最下一行,列数同样加1;(4) 如果按上面规则确定的位置上已有数,或上一个数是第1行第n列时,则把下一个数放在上一个数的下面。
例:3阶幻方例:5阶幻方三、偶阶幻方1、双偶阶幻方:四阶幻方,八阶幻方,....,4m阶幻方,采用对称元素交换法。
将幻方等分成m×m个4阶幻方,将各4阶幻方中对角线上的方格内数字与n阶(n=4×m)幻方内以中心点为对称点的对角数字进行交换。
首先把数1到n×n按从上至下,从左到右顺序填入矩阵,然后将方阵的所有4×4子方阵中的两对角线上位置的数关于方阵中心作对称交换,即a(i,j)与a(n-1-i,n-1-j)交换,所有其它位置上的数不变。
(或者将对角线不变,其它位置对称交换也可)1) 把自然数依次排成方阵2) 把幻方划成4*4的小区,每个小区划对角线,3) 把这些对角线所划到的数,保持不动,4) 把没划到的数,按幻方的中心,以中心对称的方式,进行对调。
例:4阶幻方第一步,先把1放在4阶幻方4个角的任意一个角格,按同一个方向按顺序依次填写其余数。
如下所示:第二步,进行对称交换(有两种对称交换的方法)。
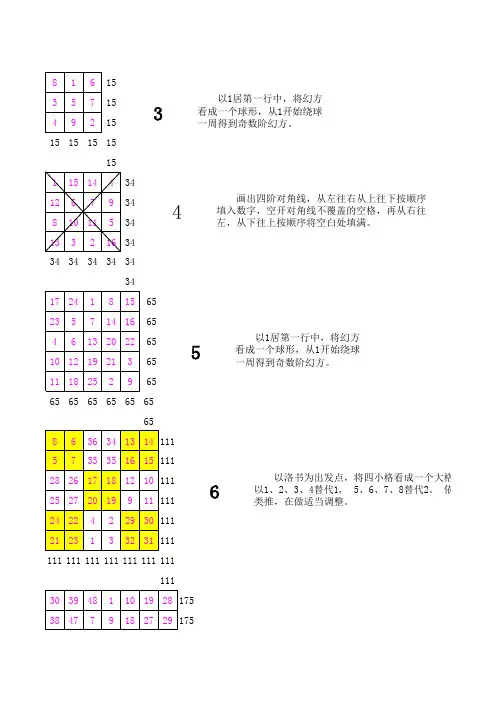
1515151515151515343434343434343434346565656565656565656565651111111111111111111111116以1居第一行中,将幻方看成一个球形,从1开始绕球一周得到奇数阶幻方。
53以1居第一行中,将幻方看成一个球形,从1开始绕球一周得到奇数阶幻方。
画出四阶对角线,从左往右从上往下按顺序填入数字,空开对角线不覆盖的空格,再从右往左,从下往上按顺序将空白处填满。
4以洛书为出发点,将四小格看成一个大格,以1、2、3、4替代1, 5、6、7、8替代2。
依次类推,在做适当调整。
1751751751751751751751751752602602602602602602602602602603693693693693693693693693693693695059以1居第一行中,将幻方看成一个球形,从1开始绕球一周得到奇数阶幻方。
87以1居第一行中,将幻方看成一个球形,从1开始绕球一周得到奇数阶幻方。
画出四阶对角线,从左往右从上往填入数字,空开对角线不覆盖的空格,再从右往左,从下往上按顺序将空白处填满。
5055055055055055055055055055055055055055055055055055055055055056716716716716716716716716716716716716716716716716716716716716716716716711011以1居第一行中,将幻成一个球形,从1开始绕球一周得到奇数阶幻方。
以五阶幻方为出发点,将成一个大格,以1、2、3、4替代1, 56、7、8替代2。
依次类推,在做适当整。
870870870870870870870 87087087087087087087087087087087087087087012 画出四阶对角线填入数字,空开对角线不覆盖左,从下往上按顺序将空白处其他幻方按上述幻方依次类推(奇数、偶数4的倍数,偶数除4于2)大格,替代2。
1)下面这些构造方法都是比较适合于编程的。
构造幻方分奇数阶幻方、4n型偶数幻方、4n+2型的偶数幻方(以下简称双偶数、单偶数)。
构造奇数阶较简单,常用的是连续摆数法。
下面的n均指阶数,在这里(y,x)表示第y横行的第x个数。
(1)在第一行的正中间(即[1,(n+1)/2])放上1 (2)若数a的位置在(y,x),则a+1的位置在:(y-1,x+1),若有这个位子且里面没数(n,x+1),若y=1且x<n (y-1,1),若x=n且y>1 (y+1,x),若x=n且y=1或(y,x)已经有数。
(y,x)已经有数的充要条件是a=n(mod n) (3)所构成的(n×n)方即为一个幻方。
我们还可以把连续摆数法推广,先定义几个概念:普通向量:正常走步的情况。
(即上面第一种情况)正常走步记作(b,a)。
中断向量:即走到(1,n)这个格子或(y,x)已经有数的情况。
记作(d,c) 下面是几个推广的情况:(1,-1)(0,1);(1,-1)(0,2);(2,1)(1,-2);(2,1)(1,-1);(2,1)(1,0);(2,1)(1,2)下面是构造双偶数阶幻方:对称法:把双偶数型的幻方分成四个正方形,在左上角正方形中每行每列各取一半打上○(实际上就是使无论从每行还是每列来看都刚好有一半有○,一半无○。
)然后向剩下的三个小方块中映象(镜像对称),于是整个方阵都布好了○。
(用电脑实行则可以选择在该布○的地方填上-1)。
接下来该填数了。
适用于电脑的方法:向所有格子内填数,(推荐x,y分别从1~n的双重计数循环):若(y,x)没有○,则填入(y-1)*n+x;若(y,x)中有○,则填入(n-y+1)*n+x+1。
适用于笔算的方法:从左上角依次1~n*n填数,遇上○则不填,这个数字还是要跳过去。
填完后,把方阵旋转180度后再从1~n*n往○里填数,没有○的地方就不填,跳过数字。
因为对称的原理,因此这回填的数刚好是上次跳过的数,这次跳过的刚好是上次填过的数。
幻方的填法幻方,亦称纵横图。
台湾称为魔术方阵。
将自然数1,2,3,……n*n排列成一个n*n方阵,使得每行、每列以及两对角线上的各个数之和都相等,等于n/2*(n*n+1),这样的方阵称为幻方。
例如:把1,2,3,4,5,6,7,8,9填入3*3的格子,使得:每行、每列、两条对角线的和是15。
n是它的阶数,比如上面的幻方是3阶。
n/2*(n*n+1)为幻方的变幻常数。
数学上已经证明,对于n>2,n阶幻方都存在。
目前填写幻方的方法,是把幻方分成了三类,每类又有各种各样的填写方法。
这里对于这三类幻方,仅举出一种方便手工填写的方法。
1、奇数阶幻方n为奇数 (n=3,5,7,9,11……) (n=2*k+1,k=1,2,3,4,5……)奇数阶幻方最经典的填法是罗伯特法(也有人称之为楼梯方)。
填写方法是这样:把1(或最小的数)放在第一行正中;按以下规律排列剩下的n*n-1个数:(1)、每一个数放在前一个数的右上一格;(2)、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;(3)、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;(4)、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内;(5)、如果这个数所要放的格已经有数填入,处理方法同(4)。
这种写法总是先向“右上”的方向,象是在爬楼梯。
2、双偶阶幻方n为偶数,且能被4整除 (n=4,8,12,16,20……) (n=4k,k=1,2,3,4,5……)先说明一个定义:互补:如果两个数字的和,等于幻方最大数和最小数的和,即 n*n+1,称为互补。
先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写:这个方阵的对角线,已经用蓝色标出。
将对角线上的数字,换成与它互补的数字。
这里,n*n+1 = 4*4+1 = 17;把1换成17-1 = 16;把6换成17-6 = 11;把11换成17-11 = 6……换完后就是一个四阶幻方。
奇数阶幻方的填充方法与步骤嘿,朋友们!今天咱来聊聊奇数阶幻方的填充方法和步骤,这可有
意思啦!
想象一下,一个正方形的格子阵,就像一个神秘的魔法阵,等着我
们去填满神奇的数字。
奇数阶幻方就是这样一个充满魅力的存在。
首先呢,咱得找个奇数阶的方格,比如说三阶、五阶啥的。
这就好
比是给魔法阵选个合适的大小。
然后,咱们把数字 1 放在第一行的正中间那个格子里。
就好像给魔
法阵种下了第一颗魔法种子。
接着,就开始有趣啦!数字 2 要放在数字 1 的右上方格子里。
哎呀,如果右上方没格子了咋办?嘿嘿,那就像绕圈圈一样,跑到最上面那
行或者最右边那列的对应格子里。
这就像在魔法阵里玩捉迷藏一样。
后面的数字就依次按照这个规则放。
你看,就这么简单,一格一格
地把数字都安排得明明白白。
这过程中,你会发现数字们就像听话的小精灵,乖乖地找到自己的
位置。
而且,等你填满整个幻方,哇塞,那可真是一种奇妙的感觉。
你说这奇数阶幻方神奇不神奇?就靠着这么简单的步骤,就能创造
出一个充满规律和美感的数字图案。
就好像是在建造一座数字的城堡,每一块石头都有它的位置,组合起来就是坚不可摧的。
咱再仔细想想,生活中不也有很多这样看似复杂,其实有简单方法的事情吗?就像解一道难题,只要找到关键的步骤,就能迎刃而解。
所以啊,朋友们,别小看这奇数阶幻方的填充方法,它可不仅仅是个数学游戏,还能让我们领悟到很多生活的道理呢!学会了这个,以后看到奇数阶幻方,咱就能轻松搞定,那感觉,多棒呀!。
奇数阶幻方填写的小窍门最近我在七年级的数学希望杯的二试辅导中碰到一题十分常见的数学题:在3×3的方格表中填入九个不同的正整数:1,2,3,4,5,6,7,8和x,使得各行、各列所填三个数的和都相等。
请确定x的值,并给出一种填数法。
这个题对于每一位数学教师来说都是再熟悉不过的,这是上学时必定做到过的九宫格,也叫“幻方”。
很容易算得x=9,并且填好方格也并非难事。
在《射雕英雄传》中黄蓉曾破解九宫格有一口诀:戴九履一,右三左七,二四为肩,六八为足。
当然填法并非只有这唯一的一种,在解这一题时,我的师傅王永生老师恰好经过我的办公桌看到这一题,他就问我这个题我是怎么填的,有没有特别的窍门,我当时的反应愣了一下,这个熟悉的不能再熟悉的九宫格,我除了知道《射雕英雄传》中的这一口诀,我还从没想过填这么一个简单的九宫格还有什么窍门。
王老师说出了他知道的一种填九宫格的窍门:先把1填在第一行的中间一格,接下来的数依次填在前一个数的右上方。
如果右上位置已经填了数字,那么下一个数字就填在前一个数字的下方。
整个过程中,如果遇到最右边,那么换到最左边继续;如果遇到最上面,那么换到最下面继续。
按照上述方法就可以得到九宫格的答案。
而且这一规律也可以用来填9×9的方格。
我之后进行了填写实践,还查了资料,发现这一规律确实存在,而且可以应用于所有奇数阶幻方的填法,不过仅限于等差数列,先将数列按从小到大的顺序排列,也按这个顺序填入格中。
将第一个数放在第一行的中间位置,依次向右上方斜填,上出幻方时就放在那一列的最下格,右出幻方时放在那一行的最左格,排重了就放在该填位置的下边一格。
还有口诀:“一居上行正中央,依次斜填切莫忘;上出框时向下放,右出框时向左放;排重便在下格填,右上排重一个样。
”一个小小的幻方中也蕴含着有趣的数学规律。
1/ 1。
没法,组合数学还考幻方构造。
这东西不看解法真不会写,虽然没见有啥用,但还是记录下,免得日后再找。
按目前填写幻方的方法,是把幻方分成了三类,即奇数阶幻方、双偶阶幻方、单偶阶幻方。
下面按这三类幻方,列出最常用解法(考试用,不求强大,只求有效!)。
奇数阶幻方(罗伯法)奇数阶幻方最经典的填法是罗伯法。
填写的方法是:把1(或最小的数)放在第一行正中;按以下规律排列剩下的(n×n-1)个数:1、每一个数放在前一个数的右上一格;2、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;4、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内;5、如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
例,用该填法获得的5阶幻方:双偶数阶幻方(对称交换法)所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方,即4K阶幻方。
在说解法之前我们先说明一个“互补数”定义:就是在 n 阶幻方中,如果两个数的和等于幻方中最大的数与 1 的和(即n×n+1),我们称它们为一对互补数。
如在三阶幻方中,每一对和为 10 的数,是一对互补数;在四阶幻方中,每一对和为 17 的数,是一对互补数。
双偶数阶幻方的对称交换解法:先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写:的四个对角上的数字对换,小正方形四个对角上的数字对换)即(1,16)(4,13)互换(6,11)(7,10)互换即可。
对于n=4k阶幻方,我们先把数字按顺序填写。
写好后,按4×4把它划分成k×k 个方阵。
因为n是4的倍数,一定能用4×4的小方阵分割。
然后把每个小方阵的对角线,象制作4阶幻方的方法一样,对角线上的数字换成互补的数字,就构成幻方。
以8阶幻方为例:(1) 先把数字按顺序填。
幻方专题王红1104班1130140223一、幻方一般地说,在n×n的方格里,既不重复也不遗漏地填上n²个连续的自然数,每个数占一格,并使每行、每列及两条对角线上n个自然数的和都相等,这样排成的数表称为n阶幻方。
这个相等的和叫幻和。
1.奇数阶幻方奇数阶幻方的方法可以简单概括为方阵斜线对换法:(1)三阶幻方(九宫幻方):具体可以概括为以下几步:第一步:将1——9九个整数如图1那样排列成方阵;第二步:如图2,画斜线;第三部:如图3,将图2中得到的正方形外四角的数字1、3、7、9,分别向斜线对面数三格,把数字填入空格内,即1和9交换,3和7交换入幻方格内。
便得到了图4的三阶幻方(九宫幻方),横排、数列,对角线上每三个数字的和都为15。
(2)五阶幻方:五阶幻方具体可以概括为以下几步:第一步:将1——25这二十五个整数如图5排列成方阵;第二步:如图6,画斜线;第三部:如图7,将图2中得到的正方形外四角的数字(1、2、6),(4、5、10);(16、21、22),和(20、24、25)分别向斜线对面数五格,把数字填入空格内,即1 和25交换,2和20交换,6 和24交换,5和21交换,4和16交换,10和22交换填入幻方格内便得到了图8的五阶幻方,横排、数列,对角线上每三个数字的和都为65。
2.偶数阶幻方偶数阶幻方的方法可以简单概括为方阵对角线数字互换和对面数字互换的方法:比如四阶幻方四阶幻方比较简单,只需要交换对角线上的数字就能使横排、竖列、对角线上的和分别都等于34。
具体步骤为:第一步:将1——16十六个整数如图9排列成方阵;第二步:如图10那样画出对角线和方框;第三步:如图10—图11,将方阵中对角线上的数字1和16,4和13,6和12,以及7和10对换,便得到了图12的四阶幻方,而六阶幻方就要复杂得多了,不仅仅需要交换对角线上的数字,还需要横排对面交换,竖列对面交换。
3.反幻方将1~9九个自然数,填在3×3正方形表格内,使其中每一横行、每一竖列及任一条对角线上的三数之和都不等,并且相邻的两个数在图中位置也相邻。
三阶幻方的解法
第一种:杨辉法:九子斜排,上下对易,左右相更,四维挺出。
1
2 4
3 5 7
6 8
9
2 9 4
7 5 3
6 1 8
第二种:九宫图也是幻方的别称,三阶幻方就是著名的洛书,他的排列是::“戴九履一,左三右七,二四为肩,六八为足,五居中央(9在上中,1在下中。
7在左中,3在右中,2在左上,4在右上,6在左下,8在右下,正中央5)
第三种:罗伯法:最小的数据上行中央,依次向右上方斜填,上出框往下写,右出框往左填,排重便在下格填,右上排重一个样
8 1 6
3 5 7
4 9 2
四阶幻方的解法
1、先把这16个数字按顺序从小到到排成一个4乘4的方阵
2、内外四个角对角上互补的数相易,(方阵分为两个正方形,外大内小,然后把大正方形的四个对角上的数字对换,小正方形四个对角上的数字对换)即(1,16)(4,13)互换
(6,11)(7,10)互换
16 2 3 13
5 11 10 8
9 7 6 12
4 14 1
5 1
另:对于n=4k阶幻方,我们先把数字按顺序填写。
写好后,按4*4把它划分成k*k个方阵。
因为n是4的倍数,一定能用4*4的小方阵分割。
然后把每个小方阵的对角线,象制作4阶幻方的方法一样,对角线上的数字换成互补的数字,就构成幻方。
五阶幻方的解法:罗伯法:最小的数据上行中央,依次向右上方斜填,上出框往下写,右出框往左填,排重便在下格填,右上排重一个样。
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
(在最上一行的中间填1,接着在1的右上方填2,由于1在最上一行,
所以1的右上方应该是第五行的第四个,
接下来在2的右上方填3,3的右上方应该是第三行第一个,所以在此填4,在4的右
上方填5,
在5的下方填6,接着按前面五个数的填法依次填7,8,9,10;
在10的下方填11,然后按上面的方法填,
每次填五个数,直到完成.
无论从上到下还是从左到右都是五排,
所以每排的五个数之和为(1+2+3+4+…+25)÷5=65,
因此,你可以验算一下是否每个和都是65.
此法适合于一切奇阶幻方.)
罗伯法
用罗伯法构造幻方:
幻方是一种广为流传的数学游戏,据说早在大禹治水时就发现过。
幻方的特点是:由自然数构成n×n正方形阵列,称为n阶幻方,每一行、每一列、两对角线上的数之和相等。
当n为奇数时,我们称幻方为奇阶幻方。
法国人罗伯总结出了构造奇数阶连续自然数幻方的简单易行的方法“罗伯法”。
下图就是一个用罗伯法排好的5阶幻方。
罗伯法的助记口诀:
(初学者可先画出一个N×N的方格阵)
1 居上行正中央——数字1 放在首行最中间的格子中
依次斜填切莫忘——向右上角斜行,依次填入数字
上出框界往下写——如果右上方向出了上边界,就以出框后的虚拟方格位置为基准,将数字竖直降落至底行对应的格子中右出框时左边放——同上,向右出了边界,就以出框后的虚拟方格位置为基准,将数字平移至最左列对应的格子中
重复便在下格填——如果数字{N} 右上的格子已被其它数字占领,就将{N+1} 填写在{N}下面的格子中
右上重复一个样——如果朝右上角出界,和“重复”的情况做同样处理
罗伯法的具体方法如下:
把1(或最小的数)放在第一行正中;
按以下规律排列剩下的n2-1个数:
1)每一个数放在前一个数的右上一格;
2)如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;
3)如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;
4)如果这个数(例如6)所要放的格已经超出了顶行且超出了最右列那么就把它放在前一个数(例如5)的下一行同一列的格内;
5)如果这个数所要放的格已经有数填入,处理方法同4)。
只要是有规律的东西,计算机很容易就可以做到。
下面我们把罗伯法翻译成计算机算法思路:
定义一个n×n数组;
把1放在第0行第n\2列;
设当前格为(i?j),设一步长变量k(k=2->n?n)
1) i减1,j加1;
2) 如果i<0那么i=n-1;
3) 如果j>n-1那么j=0;
4) 如果2)和3)同时出现那么就把j减回1,i加上2;
5) 如果a(i?j)不为空那么按照4)处理;
6) 把k的值赋给当前格a(i?j);。