探究三
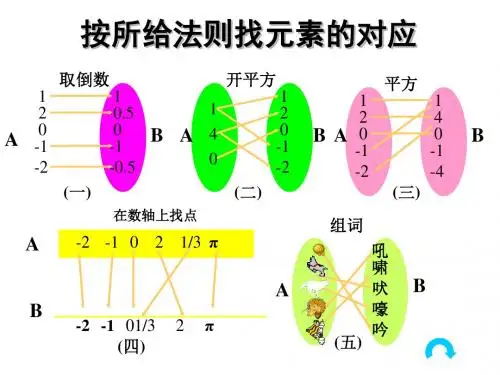
(1)解析:①②③这三个图所示的对应法则都符合映射的定义,即 A 中 每一个元素在对应法则下,在 B 中都有唯一的元素与之对应.
对于④⑤,A 的每一个元素在 B 中有 2 个元素与之对应,所以不是 A 到 B 的映射.
对于⑥,A 中的元素 a3,a4 在 B 中没有元素与之对应,所以不是 A 到 B 的 映射.
探究一
探究二
探究三
解:(1)当 x=1,y=2 时,3x-2y+1=0,4x+3y-1=9. 故 A 中元素(1,2)的象为(0,9).
(2)令 3������-2������ + 1 = 1, 得 4������ + 3������-1 = 2,
������
=
6 17
,
������
=
9 17
.
∴象为
所以不是一一映射.
探究一
探究二
探究三
求映射中的象或原象
解决象与原象问题的关键是紧扣定义,具体地说,就是若已知 A 中的元 素 a(即原象 a),求 B 中与之对应的元素 b(即象 b),这时只要将元素 a 代入对 应法则 f 求解即可;若已知 B 中的元素 b(即象 b),求 A 中与之对应的元素 a(即 原象 a),这时构造方程(组)进行求解即可,需注意解得的结果可能有多个.在 求解过程中,要注意象和原象的区别和联系.
第2课时 映射与函数
课程目标
1.了解映射的概念及表示方法. 2.会判断给出的对应法则是否是映射. 3.理解函数与映射的关系,会用映射的观点描述函 数.
学习脉络
一二
映射
映 射 设 A,B 是两个非空集合,如果按照某种对应法则 f,对 A 中的任意一个元素 及 x,在 B 中有一个且仅有一个元素 y 与 x 对应,则称 f 是集合 A 到集合 B 的 有 映射.这时,称 y 是 x 在映射 f 的作用下的象,记作 f(x).于是 y=f(x),x 称作 y 关 的原象.映射 f 也可以记为:f:A→B,x→f(x),其中 A 叫做映射 f 的定义域,由 概 所有象 f(x)构成的集合叫做映射 f 的值域,通常记作 f(A) 念 一 一 如果映射 f 是集合 A 到集合 B 的映射,并且对于集合 B 中的任意一个元素, 映 在集合 A 中都有且只有一个原象,这时我们说这两个集合的元素之间存 射 在一一对应关系,并把这个映射叫做从集合 A 到集合 B 的一一映射






![第二章第讲函数与映射的概念[可修改版ppt]](https://uimg.taocdn.com/04e48fe23968011ca20091a3.webp)

