2017-2018学年度高一数学寒假作业含答案

成都七中2018级高一数学寒假作业（带答案）
c 成都七中2，2]，解不等式
22．某港口的水深（米）是时间（，单位小时）的函数，下面是每天时间与水深的关系表
03691215182124
10139971013101710
经过长期观测，可近似的看成是函数
（1）根据以上数据，求出的解析式；
（2）若船舶航行时，水深至少要115米才是安全的，那么船舶在一天中的哪几段时间可以安全的进出该港？
成都七中3时有最大值；当x=3时有最小值，
由，，
当x=-3时有最大值6；当x=3时有最小值-6 8
(3)由，是奇函数
原不等式就是 10
由（2）知在[-2，2]上是减函数
原不等式的解集是 12
22解（1）由数据表知，
，．
．
（3）由于船的吃水深度为7米，船底与海底的距离不少于45米，故在船航行时水深米，令，得．
解得．
取，则；取，则．
故该船在1点到5点，或13点到17点能安全进出港口，而船舶要在一天之内在港口停留时间最长，就应从凌晨1点进港，下午17点离港，在港内停留的时间最长为16小时．
c。

黑龙江省牡丹江市 2017-2018学年高一数学寒假假期检测试题一、选择题（本大题共有 12个小题，每小题 5分，共 60分，在每小题给出的四选项中只有 一项是符合题目要求的。

）191、sin() 的值是（ ）6 A.1 2B.1 C.23 2D.3 252、已知cos() 121 3 ，则) sin(12的值是（ ）A ．1 3B ．2 2 1 2 C ．D ．3332 3、已知向量 a (2,3),b (x ,1), 若 ab ，则实数 x 的值为( )3 3 22 A.B.D.C.22334、为了得到函数 ysin(2x ) 的图像，只要把 ysin 2x 上所有的点（ ）3A. 向左平行移动 个单位长度B. 向左平行移动 个单位长度3 6B. 向右平行移动 个单位长度D. 向右平行移动 个单位长度365、已知 D , E , F 分别是ABC 的边 BC ,CA , AB 的中点，且 BC a ,CA b , AB c ，则1 11 1 1 1） EFc b 2） BEa b 3）CFa b 4） AD BE CF2 22 2 2中正确的等式的个数为（ ）个A. 1B. 2C. 3D.46、在边长为 4 的菱形 ABCD 中， BAD 60 ,E 为CD 的中点，则 AE BD（ ）A. 4B. 8C.6D.47、下列函数中，周期为，且在 (0, )上单调递增的是（）4A. y tan xB. y cos xC. ysin(2x ) D. y sin 2 (x) sin 2 (x )3448、已知 ( , )， a (cos )cos ，b (sin)cos ， c (cos )sin ，则（ ）4 2A ． ab c B ． a c bC ．bacD ． cab- 1 -a a9、定义 22 矩阵1 2a a34=a aa a，若1 42 3f (x )cos x sin x 3cos( 2x ) cos x sin x 2，则 f (x ) （ ）A. 图象关于,0中心对称B. 图象关于直线x对称2C.在区间[,0]上的最大值为 1D. 周期为的奇函数610、下列说法正确的是（）A. 若非零向量 AB 与CD 是共线向量，则 A,B,C,D 四点共线B. 若 O 为ABC 所在平面内一点，且OA OB OC 0，则点 O 是 ABC 的外心。

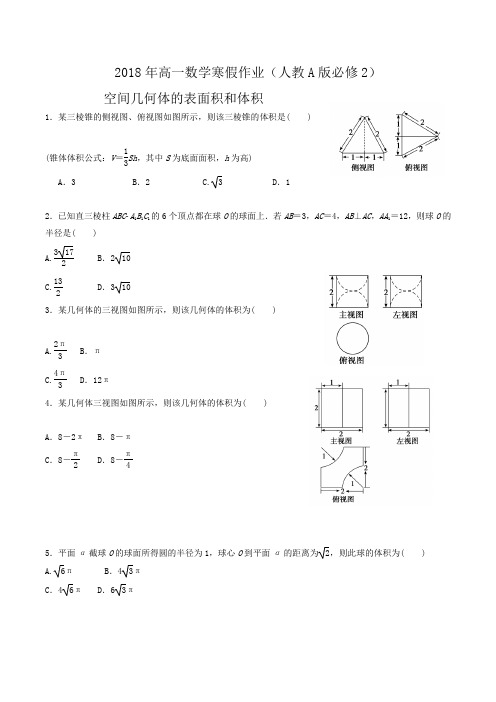
2018年高一数学寒假作业（人教A 版必修2）空间几何体的表面积和体积1．某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积是( )(锥体体积公式：V ＝13Sh ，其中S 为底面面积，h 为高) A ．3 B ．2 C. 3 D ．12．已知直三棱柱ABC ­A 1B 1C 1的6个顶点都在球O 的球面上．若AB ＝3，AC ＝4，AB ⊥AC ，AA 1＝12，则球O 的半径是( ) A.3172 B ．210C.132D ．310 3．某几何体的三视图如图所示，则该几何体的体积为( )A.2π3 B ．π C.4π3D ．12π 4．某几何体三视图如图所示，则该几何体的体积为( )A ．8－2πB ．8－πC ．8－π2D ．8－π45．平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为( )A.6π B ．43πC ．46πD ．63π6．一个四面体的三视图如图所示，则该四面体的表面积是( )A ．1＋ 3B ．1＋2 2C ．2＋ 3D ．2 27．四面体A ­BCD 的四个顶点都在球O 的球面上，AB ⊥平面BCD ，△BCD是边长为3的等边三角形．若AB ＝2，则球O 的表面积为( )A.32π3B ．12πC ．16πD ．32π8．一个多面体的三视图如图所示，则该多面体的体积为( )A.233B.476C ．6D ．79．已知某几何体的三视图如图所示，则该几何体的体积等于( )A.1603B ．160C ．64＋32 2D ．6010．某几何体的三视图如图所示，则该几何体的体积为( )A ．6π＋4B ．π＋4C.5π2D ．2π11．已知三棱锥S ­ABC 的所有顶点都在球O 的球面上，△ABC 是边长为1的正三角形，SC 为球O 的直径，且SC ＝2，则此棱锥的体积为( ) A.26 B.36 C.23 D.2212．若一个几何体的表面积和体积相同，则称这个几何体为“同积几何体”．已知某几何体为“同积几何体”，其三视图如图所示，则a＝( )A.14＋223B.8＋223C.12＋223D．8＋2 213．已知某一多面体内接于球构成一个简单组合体，如果该组合体的正视图、侧视图、俯视图均如图所示，且图中的四边形是边长为2的正方形，则该球的表面积是________．14．已知底面边长为1，侧棱长为2的正四棱柱的各顶点均在同一个球面上，则该球的体积为________．15．若一个底面是正三角形的三棱柱的主视图如图所示，其顶点都在一个球面上，则该球的表面积为________．16．一个底面直径为4的圆柱用一个不平行于底的平面截去一部分后得到一个几何体(如图)．截面上点到底面的最小距离为3.最大距离为5，则该几何体的体积为________．2018年高一数学寒假作业（人教A 版必修2）空间几何体的表面积和体积1．某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积是( )(锥体体积公式：V ＝13Sh ，其中S 为底面面积，h 为高) A ．3 B ．2 C. 3 D ．12．已知直三棱柱ABC ­A 1B 1C 1的6个顶点都在球O 的球面上．若AB ＝3，AC ＝4，AB ⊥AC ，AA 1＝12，则球O 的半径是( ) A.3172 B ．210 C.132D ．310 解析：选C.因为直三棱柱中AB ＝3，AC ＝4，AA 1＝12，AB ⊥AC ，所以BC ＝5，且BC 为过底面ABC 的截面圆的直径．取BC 中点D ，则OD ⊥底面ABC ，则O 在侧面BCC 1B 1内，矩形BCC 1B 1的对角线长即为球直径，所以2R ＝122＋52＝13，即R ＝132. 3．某几何体的三视图如图所示，则该几何体的体积为( )A.2π3 B ．π C.4π3D ．12π解析：选A.由三视图可知该几何体的直观图为一个圆柱内挖去两个与圆柱同底的半球，所以该几何体的体积V ＝V 柱－2V 半球＝π×12×2－2×12×43π×13＝23π，选A. 4．某几何体三视图如图所示，则该几何体的体积为( )A ．8－2πB ．8－πC ．8－π2D ．8－π4解析：选B.这是一个正方体切掉两个14圆柱后得到的几何体， 如图，几何体的高为2，V ＝23－14×π×12×2×2＝8－π.5．平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为( ) A.6π B ．43πC ．46πD ．63π6．一个四面体的三视图如图所示，则该四面体的表面积是( )A ．1＋ 3B ．1＋2 2C ．2＋ 3D ．2 2解析：选C.如图，该四面体有两个面为等腰直角三角形，另外两个面为正三角形．故该四面体的表面积S＝2×12×2×2＋2×12×2×2×32＝2＋ 3.7．四面体A ­BCD 的四个顶点都在球O 的球面上，AB ⊥平面BCD ，△BCD 是边长为3的等边三角形．若AB ＝2，则球O 的表面积为( )A.32π3B ．12πC ．16πD ．32π8．一个多面体的三视图如图所示，则该多面体的体积为( )A.233 B.476C ．6D ．79．已知某几何体的三视图如图所示，则该几何体的体积等于( )A.1603B ．160C ．64＋32 2D ．60解析：选A.由三视图可知，该几何体是一个直三棱柱切去一个三棱锥得到的，如图所示，故该几何体的体积为12×4×4×8－13×12×4×4×4＝64－323＝1603，故选A.10．某几何体的三视图如图所示，则该几何体的体积为( )A ．6π＋4B ．π＋4C.5π2D ．2π 11．已知三棱锥S ­ABC 的所有顶点都在球O 的球面上，△ABC 是边长为1的正三角形，SC 为球O 的直径，且SC ＝2，则此棱锥的体积为( ) A.26 B.36C.23 D.2212．若一个几何体的表面积和体积相同，则称这个几何体为“同积几何体”．已知某几何体为“同积几何体”，其三视图如图所示，则a ＝( ) A.14＋223 B.8＋223C.12＋223 D ．8＋2 2 解析：选A.根据几何体的三视图可知该几何体是一个四棱柱，如图所示，可得其体积为12(a ＋2a )·a ·a ＝32a 3，其表面积为12·(2a ＋a )·a ·2＋a 2＋a 2＋2a ·a ＋2a ·a ＝7a 2＋2a 2，所以7a 2＋2a 2＝32a 3，解得a ＝14＋223，故选A.13．已知某一多面体内接于球构成一个简单组合体，如果该组合体的正视图、侧视图、俯视图均如图所示，且图中的四边形是边长为2的正方形，则该球的表面积是________．解析：由三视图知组合体为球内接正方体，正方体的棱长为2，若球半径为R ，则2R ＝23，∴R ＝ 3.∴S 球表＝4πR 2＝4π×3＝12π.答案：12π14．已知底面边长为1，侧棱长为2的正四棱柱的各顶点均在同一个球面上，则该球的体积为________． 解析：正四棱柱外接球的球心为上下底面的中心连线的中点，所以球的半径r ＝⎝ ⎛⎭⎪⎫222＋⎝ ⎛⎭⎪⎫222＝1，球的体积V ＝4π3r 3＝4π3. 答案：4π315．若一个底面是正三角形的三棱柱的主视图如图所示，其顶点都在一个球面上，则该球的表面积为________．答案：193π 16．一个底面直径为4的圆柱用一个不平行于底的平面截去一部分后得到一个几何体(如图)．截面上点到底面的最小距离为3.最大距离为5，则该几何体的体积为________．解析：在该几何体的上方补接一个同样大小的几何体，使最小距离与最大距离相互对接，如图，则整个圆柱体积为π×22×8＝32π.所以原几何体体积为16π.答案：16π。

2018年高一数学寒假作业（人教A 版必修1）集合A 组 基础达标(建议用时：30分钟)一、选择题1．(2016·全国卷Ⅱ)已知集合A ＝{1,2,3}，B ＝{x |x 2＜9}，则A ∩B ＝( )A ．{－2，－1,0,1,2,3}B ．{－2，－1,0,1,2}C ．{1,2,3}D ．{1,2}2．(2015·全国卷Ⅱ)已知集合A ＝{1,2,3}，B ＝{2,3}，则( )A ．A ＝BB ．A ∩B ＝∅C ．A BD ．B A 3．(2017·潍坊模拟)已知集合A ＝{x |x 2－3x ＋2＝0，x ∈R}，B ＝{x |0＜x ＜5，x ∈N}，则满足条件A ⊆C ⊆B的集合C 的个数为( )A ．1B ．2C ．3D ．4 4．(2016·山东高考)设集合A ＝{y |y ＝2x ，x ∈R}，B ＝{x |x 2－1<0}，则A ∪B ＝( )A ．(－1,1)B ．(0,1)C ．(－1，＋∞)D ．(0，＋∞)5．(2017·衡水模拟)已知全集U ＝{1,2,3,4,5,6,7,8}，集合A ＝{2,3,5,6}，集合B ＝{1,3,4,6,7}， 则集合A ∩∁U B ＝( )A ．{2,5}B ．{3,6}C ．{2,5,6}D ．{2,3,5,6,8}6．若x ∈A ，则1x ∈A ，就称A 是伙伴关系集合，集合M ＝⎩⎨⎧⎭⎬⎫－1，0，12，2，3的所有非空子集中具有伙伴关系的集合的个数是( )A ．1B ．3C ．7D ．317．已知全集U ＝R ，A ＝{x |x ≤0}，B ＝{x |x ≥1}，则集合∁U (A ∪B )＝( )A ．{x |x ≥0}B ．{x |x ≤1}C ．{x |0≤x ≤1}D ．{x |0<x <1}二、填空题8．已知A ＝{0，m,2}，B ＝{x |x 4－4x 2＝0}，若A ＝B ，则m ＝________.9．(2016·天津高考)已知集合A＝{1,2,3,4}，B＝{y|y＝3x－2，x∈A}，则A∩B＝________.10．集合A＝{x|x＜0}，B＝{x|y＝lg[x(x＋1)]}，若A－B＝{x|x∈A，且x∉B}，则A－B＝________.B组能力提升(建议用时：15分钟)1．(2016·全国卷Ⅲ改编)设集合S＝{x|(x－2)(x－3)≥0}，T＝{x|x＞0}，则(∁R S)∩T＝( ) A．[2,3] B．(－∞，－2]∪[3，＋∞)C．(2,3) D．(0，＋∞)2．(2017·郑州调研)设全集U＝R，A＝{x|x2－2x≤0}，B＝{y|y＝cos x，x∈R}，则图1­1­2中阴影部分表示的区间是( )图1­1­2 A．[0,1]B．(－∞，－1]∪[2，＋∞)C．[－1,2]D．(－∞，－1)∪(2，＋∞)3．已知集合A＝{x|4≤2x≤16}，B＝[a，b]，若A⊆B，则实数a－b的取值范围是________.4．设集合A＝{x|x2－x－6＜0}，B＝{x|x－a≥0}．若存在实数a，使得A∩B＝{x|0≤x＜3}，则A∪B＝________.2018年高一数学寒假作业（人教A版必修1）集合答案A组基础达标(建议用时：30分钟)一、选择题1．(2016·全国卷Ⅱ)已知集合A＝{1,2,3}，B＝{x|x2＜9}，则A∩B＝( )A．{－2，－1,0,1,2,3} B．{－2，－1,0,1,2}C．{1,2,3} D．{1,2}D [∵x2＜9，∴－3＜x＜3，∴B＝{x|－3＜x＜3}．又A＝{1,2,3}，∴A∩B＝{1,2,3}∩{x|－3＜x＜3}＝{1,2}．]2．(2015·全国卷Ⅱ)已知集合A＝{1,2,3}，B＝{2,3}，则( )A．A＝B B．A∩B＝∅C．A B D．B AD [∵A＝{1,2,3}，B＝{2,3}，∴2,3∈A且2,3∈B,1∈A但1∉B，∴B A.]3．(2017·潍坊模拟)已知集合A＝{x|x2－3x＋2＝0，x∈R}，B＝{x|0＜x＜5，x∈N}，则满足条件A⊆C⊆B 的集合C的个数为( ) 【导学号：31222002】A．1 B．2C．3 D．4D [由x2－3x＋2＝0，得x＝1或x＝2，∴A＝{1,2}．由题意知B＝{1,2,3,4}，∴满足条件的C可为{1,2}，{1,2,3}，{1,2,4}，{1,2,3,4}，共4个．] 4．(2016·山东高考)设集合A＝{y|y＝2x，x∈R}，B＝{x|x2－1<0}，则A∪B＝( )A．(－1,1) B．(0,1)C．(－1，＋∞)D．(0，＋∞)C [由已知得A＝{y|y>0}，B＝{x|－1<x<1}，则A∪B＝{x|x>－1}．]5．(2017·衡水模拟)已知全集U＝{1,2,3,4,5,6,7,8}，集合A＝{2,3,5,6}，集合B＝{1,3,4,6,7}，则集合A∩∁U B＝( )A．{2,5} B．{3,6}C．{2,5,6} D．{2,3,5,6,8}A [由题意得∁U B＝{2,5,8}，∴A∩∁U B＝{2,3,5,6}∩{2,5,8}＝{2,5}．]6．若x ∈A ，则1x ∈A ，就称A 是伙伴关系集合，集合M ＝⎩⎨⎧⎭⎬⎫－1，0，12，2，3的所有非空子集中具有伙伴关系的集合的个数是( ) 【导学号：31222003】A ．1B ．3C ．7D ．31B [具有伙伴关系的元素组是－1，12，2，所以具有伙伴关系的集合有3个：{－1}，⎩⎨⎧⎭⎬⎫12，2，⎩⎨⎧⎭⎬⎫－1，12，2.] 7．已知全集U ＝R ，A ＝{x |x ≤0}，B ＝{x |x ≥1}，则集合∁U (A ∪B )＝( )A ．{x |x ≥0}B ．{x |x ≤1}C ．{x |0≤x ≤1}D ．{x |0<x <1}D [∵A ＝{x |x ≤0}，B ＝{x |x ≥1}，∴A ∪B ＝{x |x ≤0或x ≥1}，在数轴上表示如图，∴∁U (A ∪B )＝{x |0＜x ＜1}．]二、填空题8．已知A ＝{0，m,2}，B ＝{x |x 4－4x 2＝0}，若A ＝B ，则m ＝________.－2 [由题知B ＝{0，－2,2}，A ＝{0，m,2}，若A ＝B ，则m ＝－2.]9．(2016·天津高考)已知集合A ＝{1,2,3,4}，B ＝{y |y ＝3x －2，x ∈A }，则A ∩B ＝________. {1,4} [因为集合B 中，x ∈A ，所以当x ＝1时，y ＝3－2＝1；当x ＝2时，y ＝3×2－2＝4；当x ＝3时，y ＝3×3－2＝7；当x ＝4时，y ＝3×4－2＝10.即B ＝{1,4,7,10}．又因为A ＝{1,2,3,4}，所以A ∩B ＝{1,4}．]10．集合A ＝{x |x ＜0}，B ＝{x |y ＝lg[x (x ＋1)]}，若A －B ＝{x |x ∈A ，且x ∉B }，则A －B ＝________.[－1,0) [由x (x ＋1)＞0，得x ＜－1或x ＞0，∴B ＝(－∞，－1)∪(0，＋∞)，∴A －B ＝[－1,0)．]B 组 能力提升(建议用时：15分钟)1．(2016·全国卷Ⅲ改编)设集合S ＝{x |(x －2)(x －3)≥0}，T ＝{x |x ＞0}，则(∁R S )∩T ＝( )A ．[2,3]B ．(－∞，－2]∪[3，＋∞)C ．(2,3)D ．(0，＋∞) C [易知S ＝(－∞，2]∪[3，＋∞)，∴∁R S ＝(2,3)．∴(∁R S )∩T ＝(2,3)．]2．(2017·郑州调研)设全集U ＝R ，A ＝{x |x 2－2x ≤0}，B ＝{y |y ＝cos x ，x ∈R}，则图1­1­2中阴影部分表示的区间是( )图1­1­2A．[0,1]B．(－∞，－1]∪[2，＋∞)C．[－1,2]D．(－∞，－1)∪(2，＋∞)D [A＝{x|x2－2x≤0}＝[0,2]，B＝{y|y＝cos x，x∈R}＝[－1,1]．图中阴影部分表示∁U(A∪B)＝(－∞，－1)∪(2，＋∞)．]3．已知集合A＝{x|4≤2x≤16}，B＝[a，b]，若A⊆B，则实数a－b的取值范围是________. 【导学号：31222004】(－∞，－2] [由4≤2x≤16，得2≤x≤4，则A＝[2,4]，又B＝[a，b]，且A⊆B.∴a≤2，b≥4，故a－b≤2－4＝－2.因此a－b的取值范围是(－∞，－2]．]4．设集合A＝{x|x2－x－6＜0}，B＝{x|x－a≥0}．若存在实数a，使得A∩B＝{x|0≤x＜3}，则A∪B ＝________.{x|x＞－2} [A＝{x|－2＜x＜3}，B＝{x|x≥a}．如图，由A∩B＝{x|0≤x＜3}，得a＝0，A∪B＝{x|x＞－2}．]。

2017-2018学年高一数学寒假作业第22天圆的方程高考频度：★★★★☆难易程度：★★☆☆☆1．已知圆M与直线3x–4y=0及3x–4y+10=0都相切，圆心在直线y=–x–4上，则圆M的方程为A．（x+3）2+（y–1）2=1 B．（x–3）2+（y+1）2=1C．（x+3）2+（y+1）2=1 D．（x–3）2+（y–1）2=12．已知圆C1和C2关于直线y=–x对称，若圆C1的方程是（x+5）2+y2=4，则圆C2的方程是A．（x+5）2+y2=2 B．x2+（y+5）2=4C．（x–5）2+y2=2 D．x2+（y–5）2=43．圆心在y轴上，半径为1，且过点（1，2）的圆的方程是A．x2+（y–2）2=1 B．x2+（y+2）2=1C．x2+（y–3）2=1 D．x2+（y+3）2=14．已知圆C的圆心坐标为（2，–1），半径长是方程（x+1）（x–4）=0的解，则圆C的标准方程为A．（x+1）2+（y–2）2=4 B．（x–2）2+（y–1）2=4C．（x–2）2+（y+1）2=16 D．（x+2）2+（y–1）2=165．圆心在y轴上，半径为2，且过点（2，4）的圆的方程为A．x2+（y–1）2=4 B．x2+（y–2）2=4C．x2+（y–3）2=4 D．x2+（y–4）2=46．已知圆C1：（x+1）2+（y–1）2=4，圆C2与圆C1关于直线x–y–1=0对称，则圆C2的方程为A．（x+2）2+（y–2）2=4 B．（x–2）2+（y+2）2=4C．（x+2）2+（y+2）2=4 D．（x–2）2+（y–2）2=47．点（1，1）在圆（x–a）2+（y+a）2=4的内部，则a的取值范围是A．–1<a<1 B．0<a<1 C．a<–1或a>1 D．a=±18．点P（5a+1，12a）在圆（x–1）2+y2=1的内部，则a的取值范围是A．|a|<1 B．a<113C．|a|<15D．|a|<1139．圆x2+y2–4x+6y=0的圆心坐标是A．（2，3）B．（–2，3）C．（–2，–3）D．（2，–3）10．圆心在y轴上，且过点（3，1）的圆与x轴相切，则该圆的方程是A．x2+y2+10y=0 B．x2+y2–10y=0 C．x2+y2+10x=0 D．x2+y2–10x=011．已知圆C：x2+y2+2x–4y+1=0的圆心在直线ax–by+1=0上，则ab的取值范围是A．（–∞，14] B．（–∞，18]C．（0，14] D．（0，18]12．已知圆x2+y2–2x+4y+1=0和两坐标轴的公共点分别为A，B，C，则△ABC的面积为A．4 B．2C．D13．已知圆的一般方程为x2+y2–2x+4y=0，则该圆的半径长为AB C．3 D．5 14．圆x2+y2+2ax+4ay=0，则a等于A．5 B．–5或5 C．1 D．1或–1 15．方程x2+y2+2ax–2ay=0（a≠0）表示的圆A．关于x轴对称B．关于y轴对称C．关于直线x–y=0对称D．关于直线x+y=0对称16．已知方程x2+y2+2x–y+m=0表示圆，则实数m的取值范围是A．m>54B．m>–54C．m<54D．m<–5417．已知点P（2，1）在圆C：x2+y2+ax–2y+b=0上，点P关于直线x+y–1=0的对称点也在圆C上，则圆C的圆心坐标为A．（0，1）B．（1，0）C ．（2，1）D ．（1，2）18．经过点（1，0），（0，2）且圆心在直线y =2x 上的圆的方程是__________． 19．已知圆M 与y 轴相切，圆心在直线y =12x 上，并且在x 轴上截得的弦长为2M 的标准方程为__________．20．圆O 的方程为22(3)(4)25x y -+-=，点（2，3）到圆上的点的最大距离为__________．21．已知圆的方程22680x y x y +--=，设该圆过点（3，5）的最长弦和最短弦分别为AC 和BD ，则四边形ABCD 的面积为__________．22．如果直线l 将圆()()22125x y -+-=平分且不通过第四象限，那么l 的斜率的取值范围是__________．23．已知圆心为C 的圆经过点A （1，1）和B （2，–2），且圆心C 在直线l ：10x y -+=上，求该圆的标准方程．24．已知一个圆与y 轴相切，圆心在直线30x y -=上，且该圆经过点A （6，1），求该圆的方程．25．已知点()()()222642A B C P ----，，，，，，点在圆224x y +=上运动，求222||||||PA PB PC ++的最值．26．求经过两点A （4，2），B （−1，3），且在两坐标轴上的四个截距之和为2的圆的方程．27．已知动点M 到点A （2，0）的距离是它到点B （8，0）的距离的一半，求：（1）动点M 的轨迹方程；（2）若N 为线段AM 的中点，试求点N 的轨迹．1．【答案】C【解析】到两直线3x –4y =0及3x –4y +10=0的距离都相等的直线方程为3x –4y +5=0，联立方程组34504x y y x -+=⎧⎨=--⎩，解得31x y =-⎧⎨=-⎩．则圆心为（–3，–1）．又两平行线之间的距离为2，所以半径为1，从而圆M 的标准方程为（x +3）2+（y +1）2=1．故选C ．4．【答案】C【解析】根据圆C 的半径长是方程（x +1）（x –4）=0的解，可得半径为4，又因为圆心坐标为（2，–1），故要求的圆的标准方程为（x –2）2+（y +1）2=16，故选C ．5．【答案】D【解析】根据题意，设圆心的坐标为（0，b ），则有（0–2）2+（b –4）2=4，解得b =4，则圆的方程为 x 2+（y –4）2=4．故选D ．6．【答案】B【解析】根据题意，设圆C 2的圆心为（a ，b ），圆C 1：（x +1）2+（y –1）2=4，其圆心为（–1，1），半径为2，若圆C 2与圆C 1关于直线x –y –1=0对称，则点C 1与C 2关于直线x –y –1=0对称，且圆C 2的半径为2，则有111111022b a a b -⎧=-⎪⎪+⎨-+⎪--=⎪⎩，解可得22a b =⎧⎨=-⎩，则圆C 2的方程为：（x –2）2+（y +2）2=4，故选B ． 7．【答案】A【解析】因为点（1，1）在圆（x –a ）2+（y +a ）2=4的内部，所以表示点（1，1）到圆心（a ，–a ）的距离小于2，两边平方得：（1–a ）2+（a +1）2<4，化简得a 2<1，解得–1<a <1，故选A ．8．【答案】D【解析】由圆（x –1）2+y 2=1，得到圆心坐标为（1，0），半径r =1，点P 在圆（x –1）2+y 2=1内部⇔（5a +1–1）2+（12a ）2<1⇔|a |<113．故选D ． 9．【答案】D【解析】将圆x 2+y 2–4x +6y =0化成标准方程，得（x –2）2+（y +3）2=13，∴该圆圆心为（2，–3），故选D ．12．【答案】D【解析】令y=0，得x2–2x+1=0，解得x=1，令x=0，得y2+4y+1=0，解得y=2-±，∴圆在y轴上截得的弦长为x轴的公共点为（1，0），∴△ABC 的面积为1⨯D．1213．【答案】B【解析】由x2+y2–2x+4y=0，配方得（x–1）2+（y+2）2=5．∴y圆的圆心坐标为C（1，–2，故选B．14．【答案】D【解析】圆x2+y2+2ax+4ay=0的标准方程为（x+a）2+（y+2a）2=5a2，∵圆x2+y2+2ax+4ay=0，∴5a2=5，∴a=±1，故选D．15．【答案】D【解析】∵方程x2+y2+2ax–2ay=0表示圆，∴化成标准形式，得（x+a）2+（y–a）2=2a2，此圆的圆心为C（–a，a），半径r满足r2=2a2>0，圆心C坐标为（–a，a），满足直线方程x+y=0，∴圆心C在直线x+y=0上，可得已知圆关于直线x+y=0对称．故选D．16．【答案】C【解析】由圆的一般式方程可得D 2+E 2–4F >0，即4+1–4m >0，解得m <54，故选C ． 17．【答案】A【解析】由题意圆心C （–2a ，1）在直线x +y –1=0上，从而有–2a+1–1=0，∴a =0，∴圆C 的圆心坐标为（0，1），故选A ．19．【答案】（x –2）2+（y –1）2=4或（x +2）2+（y +1）2=4【解析】设圆M 的标准方程为（x –a ）2+（y –b ）2=r 2，由题意可得22102||3a b a r b r ⎧-=⎪⎪=⎨⎪+=⎪⎩，解得212a b r =⎧⎪=⎨⎪=⎩或212a b r =-⎧⎪=-⎨⎪=⎩，∴圆M 的标准方程为（x –2）2+（y –1）2=4或（x +2）2+（y +1）2=4．故答案为：（x –2）2+（y –1）2=4或（x +2）2+（y +1）2=4． 20．【答案】5【解析】点（2，3）与圆心连线的延长线与圆的交点到点（2，3）的距离为所求的最大距离，因为点（2，3）到圆心（3，4=再加上半径长5，即最大距离为5+．故答案为：5+． 21．【答案】【解析】22680x y x y +--=化为标准方程22(3)(4)25x y -+-=，点（3，5）在圆内，最长弦AC 即为该圆直径，∴10AC =，圆心（3，4）与点（3，5）之间的距离为1，最短弦BD ⊥AC ，由勾股定理易求得BD =412ABCD S AC BD =⋅=四边形． 22．【答案】[0，2]【解析】由题意知l 过圆心（1，2），由数形结合得02k ≤≤．23．【答案】22(3)(2)25x y +++=【解析】因为A （1，1），B （2，−2）， 所以线段AB 的中点D 的坐标为3122⎛⎫-⎪⎝⎭，， 直线AB 的斜率21321AB k --==--， 因此线段AB 的垂直平分线l '的方程为113()232y x +=-， 即330x y --=．圆心C 的坐标是方程组33010x y x y --=⎧⎨-+=⎩的解．解此方程组，得32x y =-⎧⎨=-⎩．所以圆心C 的坐标是（−3，−2）．半径长 5.r AC ===所以，该圆的标准方程是22(3)(2)25x y +++=．24．【答案】圆的方程为22(3)(1)9x y -+-=或222(111)(37)111x y -+-=．【解析】设圆的方程为222()()(x a y b r r -+-=>0），由题意得()()2223061a r a b a b r ⎧=⎪⎪-=⎨⎪-+-=⎪⎩，解得313a b r ===，，或11137111a b r ===，，．所以圆的方程为22(3)(1)9x y -+-=或222(111)(37)111x y -+-=．26．【答案】222120x y x +--=．【解析】设圆的一般方程为220x y Dx Ey F ++++=， 令0y =，得20x Dx F ++=，所以圆在x 轴上的截距之和为12x x D +=-； 令0x =，得20y Ey F ++=，所以圆在y 轴上的截距之和为12y y E +=-； 由题设，1212x x y y +++=−（D+E ）=2， 所以D+E =−2，①又A （4，2）、B （−1，3）两点在圆上，所以16+4+4D +2E +F =0，②1+9−D +3E +F =0③联立①②③解得D =−2，E =0，F =−12，故所求圆的方程为222120x y x +--=．（2）设动点N 的坐标为（x ，y ），相应的点M 的坐标是（x 1，y 1）． 由于A （2，0），且N 为线段AM 的中点，所以 112022x y x y ++==，，所以有11222x x y y =-=，① 由（1）题知，M 是圆2216x y +=上的点，所以M 的坐标（x 1，y 1）满足，221116x y +=②将①代入②整理，得()2214x y -+=． 所以点N 的轨迹是以（1，0）为圆心，以2为半径的圆．。

第十五天一．选择题1．设函数f（x）=，若从区间[﹣e，e]上任取一个实数x0，A表示事件“f（x0）≤1”，则P（A）=（）A．B．C． D．2．如图所示，在△ABC内随机选取一点P，则△PBC的面积不超过△ABC面积一半的概率是（）A．B．C．D．3．假设你家订了一份牛奶，送奶人在早上6：30～7：30之间随机地把牛奶送到你家，而你在早上7：00～8：00之间随机离家上学，则你在离家前能收到牛奶的概率是（）A．B．C．D．4．在区间[0，1]上随机取两个数，则这两个数之和小于的概率是（）A．B．C．D．5．已知函数f（x）=x2﹣x﹣2，x∈[﹣3，3]，在定义域内任取一点x0，使f（x0）≤0的概率是（）A．B．C．D．6．一个多面体的三视图和直观图如图所示，M是AB的中点，一只蜻蜓在几何体ADF﹣BCE内自由飞翔，则它飞入几何体F﹣AMCD内的概率为（）A．B．C．D．7．如图一铜钱的直径为32毫米，穿径（即铜钱内的正方形小孔边长）为8毫米，现向该铜钱内随机地投入一粒米（米的大小忽略不计），则该粒米未落在铜钱的正方形小孔内的概率为（）A． B．C． D．8．若a∈[1，6]，则函数在区间[2，+∞）内单调递增的概率是（）A．B．C．D．9．在区间[0，1]上任选两个数x和y，则的概率为（）A．B．C．D．10．从区间[﹣2，2]中随机选取一个实数a，则函数f（x）=4x﹣a•2x+1+1有零点的概率是（）A．B．C．D．二．填空题11．在区间（0，3）上随机抽取一个数a，方程表示圆的概率为．12．某人有甲、乙两只电子密码箱，欲存放三份不同的重要文件，则此人使用同一密码箱存放这三份重要文件的概率是．三．解答题13．已知袋中放有形状大小相同的小球若干，其中标号为0的小球1个，标号为1的小球1个，标号为2的小球n个，从袋中随机抽取一个小球，取到标号为2的小球的概率为，现从袋中不放回地随机取出2个小球，记第一次取出的小球标号为a，第二次取出的小球标号为b．（1）记“a+b=2”为事件A，求事件A发生的概率．（2）在区间[0，2]上任取两个实数x，y，求事件B“x2+y2＞（a﹣b）2恒成立”的概率．14．某厂家为了了解某新产品使用者的年龄情况，现随机调査100 位使用者的年龄整理后画出的频率分布直方图如图所示．（1）求100名使用者中各年龄组的人数，并利用所给的频率分布直方图估计所有使用者的平均年龄；（2）若已从年龄在[35，45），[45，55]的使用者中利用分层抽样选取了6人，再从这6人中选出2人，求这2人在不同的年龄组的概率．答案：第十五天1．解：∵函数f（x）=，x∈[﹣e，e]，解f（x0）≤1得：x0∈[﹣1，e﹣1]故P（A）==，故选：A2．解：记事件A={△PBC的面积不超过}，基本事件空间是三角形ABC的面积，（如图）事件A的几何度量为图中阴影部分的面积（DE是三角形的中位线），因为阴影部分的面积是整个三角形面积的，所以P（A）=，故选：D3．解：设送奶人到达的时间为x，此人离家的时间为y，以横坐标表示奶送到时间，以纵坐标表示此人离家时间，建立平面直角坐标系（如图）则此人离开家前能收到牛奶的事件构成区域如图示，所以所求概率P=1﹣=，故选D．4．解：设取出的两个数为x、y，则有0≤x≤1，0≤y≤1，其表示的区域为纵横坐标都在[0，1]之间的正方形区域，易得其面积为1，而x+y＜1.5表示的区域为直线x+y=1.5下方，且在0≤x≤1，0≤y≤1表示区域内部的部分，易得其面积为1﹣=，则两数之和小于1.5的概率是．故选：D．5．解：∵f（x0）≤0，∴x02﹣x0﹣2≤0，∴﹣1≤x0≤2，即x0∈[﹣1，2]，∵在定义域内任取一点x0，∴x0∈[﹣3，3]，∴使f（x0）≤0的概率P==．故选：C．6．解：因为V F﹣AMCD==，V ADF﹣BCE=，所以它飞入几何体F﹣AMCD内的概率为=，故选：D．7．解：∵S正=82=64mm2，S圆=π（）2=256πmm2，∴该粒米落在铜钱的正方形小孔内的概率为P==，∴该粒米未落在铜钱的正方形小孔内的概率为1﹣；故选B．8．解：∵函数y=在区间[2，+∞）内单调递增，∴y′=1﹣=≥0，在[2，+∞）恒成立，∴a≤x2在[2，+∞）恒成立，∴a≤4∵a∈[1，6]，∴a∈[1，4]，∴函数y=在区间[2，+∞）内单调递增的概率是=，故选C9．解：由题意可得在区间[0，1]上任选两个数x和y的区域为边长为1的正方形，面积为1，在区间[0，1]上任选两个数x和y，且的区域面积S=1﹣，∴在区间[0，1]上任取两个实数x，y，则满足的概率等于1﹣，故选D．10．解：函数f（x）=4x﹣a•2x+1+1有零点，即4x﹣a•2x+1+1=0有解，即a=，∵从区间[﹣2，2]中随机选取一个实数a，∴函数f（x）=4x﹣a•2x+1+1有零点时，1≤a≤2，区间长度为1，∴函数f（x）=4x﹣a•2x+1+1有零点的概率是=，故选：A．11．．解：若方程表示圆，则，即a2﹣4a+3＞0，解得a＜1或a＞3．∴在区间（0，3）上随机抽取一个数a，方程表示圆的概率为．故答案为：．12．．【解答】解：把三份不同放到两个不同的箱子里，分两类，第一类，一个密码箱放三件，另一个密码箱不放，共有2种方法，第二类，一个密码箱一件，另一个密码箱放两件，C31C21=6种，根据分类计数原理知有2+6=8种方法，故此人使用同一密码箱存放这三份重要文件的概率是P==，故答案为：13解：（1）根据从袋子随机抽取1个小球，取到标号为2的小球的概率是，可得=，解得n=2．从袋子中不放回地随机抽取2个球，共有基本事件12个，其中“a+b=2”为事件A的基本事件有4个，则P（A）==．（2）“x2+y2＞（a﹣b）2恒成立”为事件B，则事件B等价于“x2+y2＞4恒成立，（x，y）可以看成平面中的点，则全部结果所构成的区域为Ω={（x，y）|0≤x≤2，0≤y≤2，x，y∈R}，而事件B构成的区域B={（x，y）|x2+y2＞4，（x，y）∈Ω}，所以P（B）==1﹣．14．解：（1）由图可得，各组年龄的人数分別为：10，30，40，20．估计所有使用者的平均年龄为：0.1×20+0.3×30+0.4×40+0.2×50=37（岁）（2）由题意可知抽取的6人中，年龄在[35，45）范围内的人数为4，记为a，b，c，d；年龄在[45，55]范围内的人数为2，记为m，n．从这6人中选取2人，结果共有15种：（ab），（ac），（ad），（am），（an），（bc），（bd），（bm），（bn），（cd），（cm），（cn），（dm），（dn），（mn）．设“这2人在不同年龄组“为事件A．则事件A所包含的基本事件有8种，故，所以这2人在不同年龄组的概率为．。

2017-2018学年高一数学寒假作业 第 1天 集合高考频度：★★★★★ 难易程度：★★☆☆☆1．如果A ={}|1,x x >-那么A ．0A ⊆ B ．{} 0A ∈ C ．A ∅∈ D ．{} 0A ⊆2．已知集合}{,,2A a a a =-,若2A ∈,则实数a 的值为 A ．2- B ．2 C ．4D ．24或3．已知全集{}2,1,3,4U =--,集合{}1,3B =-,则U B =ð A ．{}1,3- B ．{}2,3- C ．{}2,4-D ．∅4．已知集合{}21,2,3,4,{|,}A B x x n n A ===∈,则A B = A ．{}1,2 B ．{}1,4 C ．{}2,3D ．{}9,165．设{},2,1,0,1,2,{|1}U A B x x ==--=≥R ,则U A B = ð A ．{}1,2 B ．{}1,0,1- C ．{}2,1,0--D ．{}2,1,0,1--6．已知集合()12{|log 5},{|2}x A x y x B y y -==-==,则A B =A ．[)0,5 B ．()0,5 C ．RD ．()0,+∞7．已知集合P =(){,|2x y x y -=3},Q =(){,|3x y x y +=2},则P Q = A ．{} 1,1-B ．(){}1,1-C ．(){}1,1- D ．(){}1,1-- 8．如图,设全集U =,M R ={|1,},x x x N ≤∈R ={|02}或x x x ≤≥,则图中阴影部分表示的集合为A ．{|12}x x ≤≤B ．{|12}x x ≤<C ．{|12}x x <≤D ．{|12}x x <<9．已知集合A ={}1,2,3,B ={}2,4,则A B = __________.10．已知集合**{|,8}且A a a a =∈-∈N N ,则A 的子集有__________个.11．已知集合A ={|x x =21,},3n n B +∈Z ={|x x =21,}3nn +∈Z ,则集合、A B 的关系为__________. 12．已知全集为R ,集合22{|120},{|50}A x x px B x x x q =++==-+= ,若(){}2A B = R ð,求p q +的值.13．已知集合A ={x |0<ax -1≤5},B ={x |﹣12<x ≤2}, (1)若a =1,求A ∪B ;(2)若A ∩B =∅且a ＞0,求实数a 的取值范围.14．已知集合A 是函数()()lg 4f x x =-的定义域,{|211},B x m x m =-≤≤+且A B A = .(1)求集合;A(2)求实数m 的取值范围.1．【答案】D【解析】因为0,A ∈所以{}0A ⊆成立.4．【答案】B【解析】∵{}{}{}21,2,3,4,|,1,4,9,16,A B x x n n A ===∈=∴{}1,4.A B =5．【答案】C【解析】因为{},2,1,0,1,2,{|1}U A B x x ==--=≥R ,所以{|1}U B x x =<ð, 则{}2,1,0U A B =-- ð.6．【答案】C【解析】因为{|5},{|0}A x x B y y =<=>,所以A B = R . 7．【答案】C【解析】解方程组2332x y x y -=⎧⎨+=⎩可得11x y =⎧⎨=-⎩，所以(){}1,1P Q =- .9．【答案】{}2【解析】∵A ={}1,2,3,B ={}2,4,∴{}2.A B = 10．【答案】128【解析】由条件可知A ={1,2,3,4,5,6,7},共7个元素,故子集个数为27=128. 11．【答案】A =B【解析】令n =k +2,则A ={|x x =21,}3k k +∈Z ,又因为B ={|x x =21,}3nn +∈Z ,所以A =B ． 12．【解析】∵(){}2A B = R ð，2,6B q ∴∈∴=,则{}2,3,3B A =∴∈,7p ∴=-, 故 1.p q +=-13．【解析】(1)若a =1,则A ={x |1<x ≤6},所以A ∪B ={x |﹣12<x ≤6}. (2)因为a ＞0,所以A ={x |1a <x 6a ≤}.由于A ∩B =∅,所以1a ≥2,即0＜a 12≤.综上所述，实数a 的取值范围为(0,12].14．【解析】(1)∵3034,40x x x +≥⎧⇒-≤<⎨->⎩∴{|34}A x x =-≤<. (2)∵A B A = ，∴B A ⊆.①当B =∅时，211,m m ->+解得2;m >②当B ≠∅时，22213112,143m m m m m m m ≤≤⎧⎧⎪⎪-≥-⇒≥-⇒-≤≤⎨⎨⎪⎪+<<⎩⎩综上所述，实数m 的取值范围为1m ≥-.。

2017-2018学年高一数学寒假作业 第 5天 奇偶性高考频度：★★★★☆ 难易程度：★★★☆☆1．下列图象表示的函数中具有奇偶性的是A BC D2．已知函数()f x 是R 上的偶函数,且()()31f f >,则下列各式一定成立的是 A ．()()06f f < B ．()()32f f > C ．()()13f f -<D ．()()20f f >3．已知函数()f x =23ax bx a b +++是定义在[]1,2a a -上的偶函数,则a b +的值为 A ．0 B ．13C ．1D ．-14．已知()f x 和()g x 分别是定义在R 上的奇函数和偶函数，且()()3223f x g x x x -=++，则()()22f g +等于A ．9-B ．7-C ．7D ．95．已知函数()f x =2211x x+-,则 A ．()f x 是奇函数且()1f f x x ⎛⎫= ⎪⎝⎭B ．()f x 是奇函数且()1f f x x ⎛⎫=-⎪⎝⎭C ．()f x 是偶函数且()1f f x x ⎛⎫= ⎪⎝⎭D ．()f x 是偶函数且()1f f x x ⎛⎫=-⎪⎝⎭6．已知()f x =222,0,0ax x x x bx x ⎧+≥⎨+<⎩是奇函数,则a b -的值为A ． 3-B ．2- C ． 1- D ．不能确定7．已知()f x 是R 上的奇函数，且当0x ≥时，()22f x x x =-+，则当0x <时，()f x 的解析式是 A ．()()2f x x x =-+ B ．()()2f x x x =- C ．()()2f x x x =--D ．()()2f x x x =+8．设函数f (x )和g (x )分别是R 上的偶函数和奇函数，则下列结论恒成立的是 A ．f (x )+|g (x )|是偶函数 B ．f (x )-|g (x )|是奇函数 C ．|f (x )|+g (x )是偶函数D ．|f (x )|-g (x )是奇函数9．已知函数3()2(,)f x ax bx a b =++∈R ，且(2)3f =，则(2)f -=____________.10．若函数()()()e e1x xf x ax -=-+为奇函数,则实数a 的值为____________.11．已知f (x )是定义在R 上的奇函数,当x ≥0时, f (x )=m+ln(e +x ),则 f (-e)= ____________. 12．判断下列函数的奇偶性:①31y x x=+；②y ③4y x x =+； ④()()()22200020x x y x x x ⎧+>⎪⎪==⎨⎪--<⎪⎩.13．已知()2121xf x =-+.(1)判断函数()y f x =的奇偶性，并进行证明；(2)解关于t 的不等式()()210f t f t t +--<.1．【答案】B【解析】选项A 中的图象关于原点或y 轴均不对称,故排除;选项C 、D 中的图象表示的函数的定义域关于原点不对称,不具有奇偶性,故排除; 选项B 中的图象关于y 轴对称,其表示的函数是偶函数.故选B ． 2．【答案】C【解析】因为函数()f x 是R 上的偶函数,且()()31f f >,所以()()13.f f -< 3．【答案】B【解析】因为函数()f x =23ax bx a b +++是定义在[]1,2a a -上的偶函数,所以b =0,且120,a a -+=则1,3a =所以13a b +=. 4．【答案】D【解析】因为()f x 和()g x 分别是定义在R 上的奇函数和偶函数,所以()()f x f x -=-,()() g x g x -=，所以()()()()()()()()32322323f x g x f x g x f x g x x x x x ⎡⎤---=--=-+=-+-+=-++⎣⎦,所以()()3223f x g x x x +=--,则()()322222239f g +=⨯--=.选D ．5．【答案】D【解析】∵函数的定义域是{}|1x x ≠±,关于原点对称,又()f x -=2211x x+-=(),f x ∴()f x 是偶函数. 1 f x ⎛⎫ ⎪⎝⎭=221111x x ⎛⎫+ ⎪⎝⎭⎛⎫- ⎪⎝⎭=2211x x +-=()f x -.8．【答案】A【解析】函数f (x )和g (x )的定义域为R ，关于原点对称,()()f x f x -=，()f x ∴为偶函数，()()()g x g x g x -=-=，()g x ∴为偶函数，由于偶函数±偶函数仍为偶函数，所以f (x )+|g (x )|是偶函数.故选A ． 9．【答案】【解析】由条件可得为奇函数,由可得,故,故10．【答案】0【解析】e e 因为x x y -=-是奇函数,所以1y ax =+是偶函数,所以0.a = 11．【答案】-ln 2【解析】由函数f (x )为R 上的奇函数可得f (0)=m+ln(e +0)=m+1=0,解得m =-1. 则当x ≥0时, f (x )=-1+ln(e +x ),故f (e)=-1+ln(e+e)=-1+ln(2e)=ln 2. 由函数f (x )为R 上的奇函数,可得f (-e)=-f (e)=-ln 2.13．【解析】(1)函数()y f x =为奇函数，∵()2121x f x =-+=2121x x -+，()f x -=2121x x ---+=1212xx-+=()f x -， ∴()f x 为奇函数． (2)()f x =2121x -+， ∵y =21x +在(),-∞+∞上单调递增且恒大于0，∴y =121x +在(),-∞+∞上单调递减， ∴y =2121x -+在(),-∞+∞上单调递增．∴()()()210f t f t t f t +--<⇔-()()2210(f t t f t f t -++<⇔<-+1)t +⇔2t t <-+1t +，即210t -<，得11t -<<. 故()1,1t ∈-．。

第十四天一．选择题1．某产品的广告费用x与销售额y的统计数据如表：用最小二乘法算得回归方程=x+中的为7，据此预测广告费用为6万元时销售额为A．58.5万元B．77.5万元C．59万元D．70万元2．给出下列四个结论：（1）如图Rt△ABC中，|AC|=2，∠B=90°，∠C=30°．D是斜边AC上的点，|CD|=|CB|．以B为起点任作一条射线BE交AC于E点，则E点落在线段CD上的概率是；（2）设某大学的女生体重y（kg）与身高x（cm）具有线性相关关系，根据一组样本数据（x i，y i）（i=1，2，…，n），用最小二乘法建立的线性回归方程为=0.85x﹣85.71，则若该大学某女生身高增加1cm，则其体重约增加0.85kg；（3）为调查中学生近视情况，测得某校男生150名中有80名近视，在140名女生中有70名近视．在检验这些学生眼睛近视是否与性别有关时，应该用独立性检验最有说服力；（4）已知随机变量ξ服从正态分布N（1，σ2），P（ξ≤4）=0.79，则P（ξ≤﹣2）=0.21；其中正确结论的个数为（）A．1 B．2 C．3 D．43．下列说法错误的是（）A．回归直线过样本点的中心（，）B．两个随机变量的线性相关性越强，则相关系数的绝对值就越接近于1C．对分类变量X与Y，随机变量K2的观测值越大，则判断“X与Y有关系”的把握程度越小D．在回归直线方程=0.2x+0.8中，当解释变量x每增加1个单位时预报变量平均增加0.2个单位4．某地区根据2008年至2014年每年的生活垃圾无害化处理量y（单位：万吨）的数据，用线性回归模型拟合y关于t的回归方程为=0.92+0.1t（t表示年份代码，自2008年起，t的取值分别为1，2，3，…），则下列的表述正确的是（）A．自2008年起，每年的生活垃圾无害化处理量与年份代码负相关B．自2008年起，每年的生活垃圾无害化处理量大约增加0.92万吨C．由此模型预测出2017年该地区的生活垃圾无害化处理量约1.92万吨D．由此模型预测出2017年该地区的生活垃圾无害化处理量约1.82万吨5．有下列关系：①学生上学的年限与知识掌握量的关系；②函数图象上的点与该点的坐标之间的关系；③葡萄的产量与气候之间的关系；④森林中的同一种树木，其横断面直径与高度之间的关系．其中有相关关系的是（）A．①②③B．①② C．②③ D．①③④6．从分别标有1，2，…，9的9张卡片中不放回地随机抽取2次，每次抽取1张，则抽到在2张卡片上的数奇偶性不同的概率是（）A．B．C．D．7．若函数f（x）=ln（x2+1）的值域为{0，1，2}，从满足条件的所有定义域集合中选出2个集合，则取出的2个集合中各有三个元素的概率是（）A．B．C．D．8．有一个正方体的玩具，六个面标注了数字1，2，3，4，5，6，甲、乙两位学生进行如下游戏：甲先抛掷一次，记下正方体朝上的数字为a，再由乙抛掷一次，朝上数字为b，若|a ﹣b|≤1就称甲、乙两人“默契配合”，则甲、乙两人“默契配合”的概率为（）A．B．C．D．9．已知函数8（a＞0，且a≠1），在集合{，，，3，4，5，6，7}中任取一个数为a，则f（3a+1）＞f（2a）＞0的概率为（）A．B．C．D．10．是由一个圆、一个三角形和一个长方形构成的图形，现用红、蓝两种颜色为其涂色，每个图形只能涂一种颜色，则相邻两个图形颜色不相同的概率为（）A．B．C．D．二．填空题11．已知x与y之间的一组数据：若y关于x的线性回归方程为=2.1x﹣1.25，则m的值为．12．把一颗骰子投掷2次，观察出现的点数，记第一次出现的点数为a，第二次出现的点数为b，则方程组只有一个解的概率为．13．有4名学生A、B、C、D平均分乘两辆车，则“A，B两人恰好在同一辆车”的概率为．14．从﹣1、1、2这三个数中，任取两个不同的数作为一次函数y=kx+b的系数k、b，则一次函数y=kx+b的图象不经过第四象限的概率是．三．解答题15．某同学在生物研究性学习中，对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究，于是他在4月份的30天中随机挑选了5天进行研究，且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数，得到如下资料：（1）从这5天中任选2天，求这2天发芽的种子数均不小于25的概率；（2）从这5天中任选2天，若选取的是4月1日与4月30日的两组数据，请根据这5天中的另三天的数据，求出y关于x的线性回归方程=x+；（3）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（2）中所得的线性回归方程是否可靠？附：=，=﹣．答案：第十四天1．解：由题意，=3.5，=41．代入回归方程可得：41=7×3.5+，∴=16.5，∴=7x+16.5，∴x=6时，=7×6+16.5=58.5万元．故选A．2．解：（1）由题意，|CD|=|CB|，∠C=30°，所以∠CBD=75°，所以E点落在线段CD上的概率是=，故不正确；（2）设某大学的女生体重y（kg）与身高x（cm）具有线性相关关系，根据一组样本数据（x i，y i）（i=1，2，…，n），用最小二乘法建立的线性回归方程为=0.85x﹣85.71，则若该大学某女生身高增加1cm，则其体重约增加0.85kg，正确；（3）为调查中学生近视情况，测得某校男生150名中有80名近视，在140名女生中有70名近视．在检验这些学生眼睛近视是否与性别有关时，应该用独立性检验最有说服力，正确；（4）已知随机变量ξ服从正态分布N（1，σ2），图象关于x=1对称，因为P（ξ≤4）=0.79，则P（ξ≤﹣2）=0.21，正确；故正确结论的个数为3，故选：C．3．解：A．回归直线过样本点的中心（，），正确；B．两个随机变量相关性越强，则相关系数的绝对值越接近1，因此正确；C．对分类变量X与Y的随机变量K2的观测值k来说，k越大，“X与Y有关系”可信程度越大，因此不正确；D．在线性回归方程=0.2x+0.8中，当x每增加1个单位时，预报量平均增加0.2个单位，正确．综上可知：只有C不正确．故选：C．4．解：对于A，0.1＞0，自2008年起，每年的生活垃圾无害化处理量和年份代码正相关，故A错误；对于B，t的系数为0.1，自2008年起，每年的生活垃圾无害化处理量大约增加0.10万吨，故B错误；对于C、D，t=10，=0.92+0.1t=1.92，由此模型可预测2017年该地区生活垃圾无害化处理量是1.92万吨，故C正确；D不正确．故选：C．5．解：根据题意，相关关系是一种不确定的关系，是非随机变量与随机变量之间的关系，依次分析所给的4个关系：①③④是相关关系，②是确定的函数关系，故选：D．6．解：从分别标有1，2，…，9的9张卡片中不放回地随机抽取2次，共有=36种不同情况，且这些情况是等可能发生的，抽到在2张卡片上的数奇偶性不同的情况有=20种，故抽到在2张卡片上的数奇偶性不同的概率P==，故选：C．7．解：令ln（x2+1）=0，得x=0，令ln（x2+1）=1，得x2+1=e，x=±，令ln（x2+1）=2，得x2+1=e2，x=．则满足值域为{0，1，2}的定义域有：{0，﹣，﹣}，{0，﹣，}，{0，，﹣}，{0，，}，{0，﹣，，﹣}，{0，﹣，，}，{0，﹣，﹣，}，{0，，﹣，}，{0，﹣，，﹣，}．则满足这样条件的函数的个数为9．从满足条件的所有定义域集合中选出2个集合，基本事件总数n=，取出的2个集合中各有三个元素的函数个数为m=，∴取出的2个集合中各有三个元素的概率是p=．故选：A．8．解：甲、乙两人抛掷玩具所有可能的事件有36种，其中“甲、乙两人‘默契配合’”所包含的基本事件有：（1，1），（1，2），（2，1），（2，2），（2，3），（3，2），（3，3），（3，4），（4，3），（4，4），（4，5），（5，4），（5，5），（5，6），（6，5），（6，6），共16种．∴甲乙两人“默契配合”的概率为P==．故选：D．9．解：∵函数8（a＞0，且a≠1），∴f（x）=log a x﹣log a8）=，∵在集合{，，，3，4，5，6，7}中任取一个数为a，∴基本事件总数n=8，∵f（3a+1）＞f（2a）＞03a+1﹣2a=a﹣1，当a＞1时，3a+1＞2a，2a＞1，即a=5，6，7时才成立；当a＜1时，3a+1＜2a，即a+1＜1，不成立．∴满足f（3a+1）＞f（2a）＞0的基本事件个数m=3，∴f（3a+1）＞f（2a）＞0的概率为p=．10．解：先涂圆，有2种方法．再涂三角形，有1种方法，最后涂长方形，有1种方法．故满足条件的涂色方法有2×1×1=2种．而所有的涂色方法有2×2×2=8种，故相邻两个图形颜色不相同的概率为=，故选C．11．0.5 ．解：由题意可得：，回归方程过样本中心点，则：，即：，解得：m=0.5．故答案为：0.5．12．．解：骰子投掷2次所有的结果有6×6=36由得（b﹣2a）y=3﹣2a当b﹣2a≠0时，方程组有唯一解当b=2a时包含的结果有：当a=1时，b=2当a=2时，b=4当a=3时，b=6共三个所以方程组只有一个解包含的基本结果有36﹣3=33由古典概型的概率公式得故答案为：13．．解：4名学生A、B、C、D平均分乘两辆车，用（XY，MN）表示X与Y同乘一车，MN同乘一车则共有（AB，CD），（AC，BD），（AD，BC），（BC，AD），（BD，AC），（CD，AB）6种情况其中（AB，CD），（CD，AB）两种情况满足“A，B两人恰好在同一辆车”故“A，B两人恰好在同一辆车”的概率P==故答案为：14．．解：列表，如图，k、b的取值共有6种等可能的结果；而一次函数y=kx+b的图象不经过第四象限，则k＞0，b≥0，∴满足条件的k、b的取值有（1，2），（2，1），∴一次函数y=kx+b的图象不经过第四象限的概率为=．故答案为：．15．解：（1）由题意，m、n的所有取值范围有：（23，25），（23，30），（23，26），（23，16），（25，30），（25，26），（25，16），（30，26），（30，16），（26，16）共有10个；设“m、n均不小于25“为事件A，则事件A包含的基本事件有（25，30），（25，26），（30，26），所有P（A）=，故事件A的概率为；（2）由数据得=12，=27，•=972，3=432；又x i y i=977，=432；==，=27﹣×12=﹣3；所有y关于x的线性回归方程为=x﹣3．（3）当x=10时，=×10﹣3=22，|22﹣23|＜2，当x=8时，=×8﹣3=17，|17﹣16|＜2．所有得到的线性回归方程是可靠的．。

2017-2018学年高一数学寒假作业第7天对数函数高考频度：★★★☆☆难易程度：★★☆☆☆1．函数=的定义域是A．B．2,3⎛⎫+∞ ⎪⎝⎭C．2,13⎛⎤⎥⎝⎦D．2,13⎛⎫⎪⎝⎭2．若,则的大小关系为A．B．C．D．3．已知函数满足当时,=12x⎛⎫⎪⎝⎭;当时,=,则=A．124B．112C．18D．384．已知则有A．B．C．D．5．函数=log(01)ax xax<<图象的大致形状是A BC D6．化简___________.7．已知函数()ln 2f x x x ax =++的图象过点()1,3,则a =___________. 8．已知函数()f x =31,,,ax bx a b -+∈R 若()ln6f =1,-则1ln 6f ⎛⎫⎪⎝⎭=___________. 9．函数y =()212log 2x x -+的单调递增区间是___________.10．已知()f x =()21log 14,x x +≤≤则函数()g x =()()22f x f x +的最大值是___________.11．已知定义在R 上的函数()f x 满足()f x -=()f x ,且对于任意[)12,0,,x x ∈+∞12x x ≠,均有()()21120f x f x x x ->-.若13f ⎛⎫- ⎪⎝⎭=181,2log 12fx ⎛⎫< ⎪⎝⎭,则x 的取值范围为__________. 12．求值:(101137)0.0273;8--⎛⎫-+- ⎪⎝⎭(23log 21)3lg163lg5lg 5++-.13．设()()222log 2log (0)f x x a x b x =-+>.当14x =时,()f x 有最小值-1. (1)求a 与b 的值;(2)求满足()0f x <的x 的取值范围.14．已知函数()f x =()()log 1,a x g x +=()log 42(0,1)a x a a ->≠且.(1)求函数y =()()f x g x -的定义域;(2)求使函数y =()()f x g x -的值为负数的x 的取值范围.15．已知函数()()()log 12log 12(0,1a a f x x x a a =--+>≠).（1）求()f x 的定义域；（2）判断()f x 的奇偶性并予以证明； （3）解不等式()0f x >.16．已知函数()g x =4(2x xn n -∈R )是奇函数,()f x =()4log 41(xmx m ++∈R )是偶函数. (1)求m n +的值;(2)设()h x =()12f x x +,若()()()4log 21g x h a >+对任意[)1,x ∈+∞恒成立,求实数a 的取值范围.1．【答案】C【解析】由题意可得,所以,则213x <≤,故选C ．4．【答案】D 【解析】因为所以且是减函数,所以=5．【答案】C 【解析】是奇函数,故排除B,D; 因为,所以令x =2,则,故排除A,故选C ． 6．【答案】11【解析】()2327lg42lg592lg2lg511++=++=. 7．【答案】1【解析】因为函数()ln 2f x x x ax =++的图象过点()1,3,所以()123f a =+=,则 1.a = 8．【答案】3【解析】∵()ln6f =()3ln6ln61a b -+=1,-∴()3ln6ln6a b -=2,-∴1ln6f ⎛⎫ ⎪⎝⎭=()3ln6ln61a b -++=21+=3.10．【答案】7【解析】∵()f x =()21log 14x x +≤≤，∴21414x x ≤≤⎧⎨≤≤⎩，∴12x ≤≤. 则20log 1.x ≤≤∴()()()22g x f x f x =+()222212log log 12log x x x =++++()2224log log 2x x =++.则()()22log 22g x x =+-， 故()max 7.g x = 11．【答案】()10,2,2⎛⎫+∞ ⎪⎝⎭【解析】函数()f x 是偶函数.由对于任意[)1212,0,,x x x x ∈+∞≠,均有()()21120f x f x x x ->-，可知函数()f x 在[)0,+∞上是减函数，所以181log 3f x f ⎛⎫⎛⎫<- ⎪ ⎪⎝⎭⎝⎭=13f ⎛⎫ ⎪⎝⎭，则118811log log 33x x ><-或, 求解可得1022x x <<>或,则x 的取值范围为()10,2,2⎛⎫+∞ ⎪⎝⎭. 12．【解析】(1)原式=101133-+=4. (2)原式=24lg23lg5lg5+++=24lg24lg5++=24+=6.14．【解析】(1)由题意可知,y =()()f x g x -=()log 1)lo 42(g a a x x +--,由10420x x +>⎧⎨->⎩,解得12x x >-⎧⎨<⎩,∴12x -<<,即函数y =()()f x g x -的定义域是()1,2-． (2)由()()0f x g x -<,得()()f x g x < , 即()()log 1log 42a a x x +<- ①,当1a >时,由①可得0142x x <+<-,解得11x -<<; 当01a <<时,由①可得1420x x +>->,解得12x <<.综上所述:当1a >时,x 的取值范围是()1,1-; 当01a <<时,x 的取值范围是()1,2．15．【解析】(1)要使函数有意义，需1201112022x x x +>⎧⇒-<<⎨->⎩， ()f x ∴的定义域为11,22⎛⎫- ⎪⎝⎭.(2) ()f x 为奇函数.证明如下： 定义域为11,22⎛⎫-⎪⎝⎭，关于原点对称， 又因为()()()()log 12log 12a a f x x x f x -=+--=-，()f x ∴为奇函数.16．【解析】(1)因为()g x 为奇函数,且定义域为R ,所以()00g =,即00402n-=,所以1n =. 因为()f x =()4log 41xmx ++,所以()f x -=()4log 41x mx -+-=()()4log 411xm x +-+.又因为()f x 是偶函数,所以()()f x f x -=恒成立,解得12m=-.所以12m n+=.。