高中数学极坐标与参数方程知识汇编及高考题型汇总

第7讲 极坐标与参数方程【基础知识】一.极坐标知识点1.极坐标系的概念：在平面内取一个定点O ，从O 引一条射线Ox ，选定一个单位长度以及计算角度的正 方向(通常取逆时针方向为正方向)，这样就建立了一个极坐标系，O 点叫做极点，射线Ox 叫做极轴①极点；②极轴；③长度单位；④角度单位和它的正方向，构成了极坐标系的四要素，缺一不可. 2.极坐标与直角坐标的互化： 二.参数方程知识点1.参数方程的概念：在平面直角坐标系中，若曲线C 上的点(,)P x y 满足()()x f t y f t =⎧⎨=⎩，该方程叫曲线C 的参数方程，变量t 是参变数，简称参数。

（在平面直角坐标系中，如果曲线上任意一点的坐标y x ,都是某个变数t 的函数⎩⎨⎧==),(),(t g y t f x 并且对于t 的每一个允许值，由这个方程所确定的点),(y x M 都在这条曲线上，那么这个方程就叫做这条曲线的参数方程，联系变数y x ,的变数t 叫做参变数，简称参数。

） 相对于参数方程而言，直接给出点的坐标间关系的方程叫做普通方程。

2．曲线的参数方程（1）圆222)()(r b y a x =-+-的参数方程可表示为)(.sin ,cos 为参数θθθ⎩⎨⎧+=+=r b y r a x .（2）椭圆12222=+b y a x )0(>>b a 的参数方程可表示为)(.sin ,cos 为参数ϕϕϕ⎩⎨⎧==b y a x .（3）抛物线px y 22=的参数方程可表示为)(.2,22为参数t pt y pt x ⎩⎨⎧==. （4）经过点),(o o O y x M ，倾斜角为α的直线l 的参数方程可表示为⎩⎨⎧+=+=.sin ,cos o o ααt y y t x x （t 为参数）.3．在建立曲线的参数方程时，要注明参数及参数的取值范围。

在参数方程与普通方程的互化中，必须使y x ,的取值范围保持一致. 规律方法指导：1.把参数方程化为普通方程，需要根据其结构特征，选取适当的消参方法.常见的消参方法有：代入消法 ；加减消参；平方和（差）消参法；乘法消参法；比值消参法；利用恒等式消参法；混合消参法等. 2.把曲线的普通方程化为参数方程的关键：一是适当选取参数；二是确保互化前后方程的等价性， 注意方程中的参数的变化范围。

极坐标与参数方程知识点一、极坐标2．直角坐标与极坐标的互化把直角坐标系的原点作为极点，x 轴正半轴作为极轴，且在两坐标系中取相同的长度单位．如图，设M 是平面内的任意一点，它的直角坐标、极坐标分别为(x ，y )和(ρ，θ)，则⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ或⎩⎪⎨⎪⎧ρ2＝x 2＋y 2，tan θ＝y x (x ≠0). 二、参数方程1．常见曲线的参数方程的一般形式(1)经过点P 0(x 0，y 0)，倾斜角为α的直线的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．设P 是直线上的任一点，则t 表示有向线段P 0P →的数量． (2)圆的参数方程⎩⎨⎧+=+=θθsin cos 00r y y r x x (θ为参数)．(3)圆锥曲线的参数方程椭圆x 2a 2＋y 2b 2＝1的参数方程为⎩⎪⎨⎪⎧x ＝a cos θ，y ＝b sin θ(θ为参数)．双曲线x 2a 2－y 2b 2＝1的参数方程为⎩⎪⎨⎪⎧x ＝a sec φ，y ＝tan φ(φ为参数)．抛物线y 2＝2px 的参数方程为⎩⎪⎨⎪⎧x ＝2pt 2，y ＝2pt (t 为参数)．2．参数方程的几何意义过定点P （x 0，y 0），倾斜角为α的直线的参数方程是 ⎩⎨⎧+=+=ααsin cos 00t y y t x x （t 为参数）．与曲线C（以抛物线px y 22=为例）相交于A 、B 两点，将直线的标准参数方程带入曲线C 中，得到关于t 的一元二次方程，由参数t 的几何意义可得如下结论：(1)||||||21t t PB PA =⋅ (2) ||||||||21t t PB PA +=+ (3)21221214)(||||t t t t t t AB -+=-=极坐标与参数方程高考题考点一、求最值（取值范围） 1.【2012高考新课标】已知曲线C 1的参数方程是⎩⎨⎧==ϕϕsin 3cos 2y x (φ为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 2的极坐标方程是ρ=2.正方形ABCD 的顶点都在C 2上，且A 、B 、C 、D 以逆时针次序排列，点A 的极坐标为(2，π3)(Ⅰ)求点A 、B 、C 、D 的直角坐标；(Ⅱ)设P 为C 1上任意一点，求|PA| 2+ |PB|2 + |PC| 2+ |PD|2的取值范围.2.（2014云南省第二次统测）已知曲线C 的参数方程为⎩⎨⎧==ααsin 3,cos 3y x （α为参数），以原点O 为极点，以x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为cos()16πρθ+=．（Ⅰ）求曲线C 的直角坐标方程；（Ⅱ）设M 是曲线C 上的点，求M 到直线l 的距离的最大值．3．[2014·全国新课标卷Ⅰ] 选修4－4：坐标系与参数方程已知曲线C ：x 24＋y 29＝1，直线l ：⎩⎪⎨⎪⎧x ＝2＋t ，y ＝2－2t (t 为参数)．(1)写出曲线C 的参数方程、直线l 的普通方程；(2)过曲线C 上任意一点P 作与l 夹角为30°的直线，交l 于点A ，求|P A |的最大值与最小值．4．(2012洛阳示范高中联考高三理) (本小题满分10分)选修4—4;坐标系与参数方程．已知直线: t t y t x (.23,211⎪⎪⎩⎪⎪⎨⎧=+=为参数), 曲线:1C cos ,sin ,x y θθ=⎧⎨=⎩ （θ为参数）. （Ⅰ）设 与1C 相交于B A ,两点,求||AB ； （Ⅱ）若把曲线1C 上各点的横坐标压缩为原来的21倍,纵坐标压缩为原来的23倍,得到曲线2C ,设点P 是曲线2C 上的一个动点,求它到直线 的距离的最小值.5 ．（云南省昆明三中2013届高三高考适应性月考（三）理科数学）在直角坐标系xoy 中，直线l 经过点P （-1，0），其倾斜角为α，以原点O 为极点，以x 轴非负半轴为极轴，与直角坐标系xoy 取相同的长度单位，建立极坐标系.设曲线C 的极坐标方程为26cos 50.ρρθ-+=（1）若直线l 与曲线C 有公共点，求α的取值范围； （2）设()y x M ,为曲线C 上任意一点，求x y +的取值范围.6.（云南省玉溪一中2013届高三第五次月考理科数学）坐标系与参数方程在平面直角坐标系xOy 中，椭圆C 方程为5cos (3sin x y ϕϕϕ=⎧⎨=⎩为参数）（1）求过椭圆的右焦点，且与直线42(3x tt y t =-⎧⎨=-⎩为参数）平行的直线l 的普通方程。

《极坐标与参数方程》高考高频题型除了简单的极坐标与直角坐标的转化、参数方程与普通方程的转化外，还涉及（一）有关圆的题型题型一：圆与直线的位置关系（圆与直线的交点个数问题）----利用圆心到直线的距离与半径比较相离，无交点；:r d > 个交点；相切，1:r d = 个交点；相交，2:r d <用圆心（x 0,y 0）到直线Ax+By+C=0的距离2200BA C By Ax d +++=，算出d ，在与半径比较。

题型二：圆上的点到直线的最值问题（不求该点坐标，如果求该点坐标请参照距离最值求法）思路：第一步：利用圆心（x 0,y 0）到直线Ax+By+C=0的距离2200BA C By Ax d +++=第二步：判断直线与圆的位置关系第三步：相离：代入公式：r d d +=max ，r d d -=min 相切、相交：r d d +=max min 0d =题型三：直线与圆的弦长问题弦长公式222d r l -=，d 是圆心到直线的距离延伸：直线与圆锥曲线（包括圆、椭圆、双曲线、抛物线）的弦长问题 （弦长：直线与曲线相交两点，这两点之间的距离就是弦长） 弦长公式21t t l -=,解法参考“直线参数方程的几何意义”（二）距离的最值： ---用“参数法”1.曲线上的点到直线距离的最值问题2.点与点的最值问题“参数法”：设点---套公式--三角辅助角①设点： 设点的坐标，点的坐标用该点在所在曲线的的参数方程来设 ①套公式：利用点到线的距离公式①辅助角：利用三角函数辅助角公式进行化一例如：【2016高考新课标3理数】在直角坐标系中，曲线的参数方程为，以坐标原点为极点，以轴的正半轴为极轴，，建立极坐标系，曲线的极坐标方程为（I ）写出的普通方程和的直角坐标方程；（II ）设点在上，点在上，求的最小值及此时的直角坐标的直角坐标方程为.这里没有加减移项省去，直接化同，那系数除到左边（①）由题意，可设点的直角坐标为 因为是直线，所以的最小值即为到的距离的最小值，xOy 1C ()sin x y ααα⎧=⎪⎨=⎪⎩为参数x 2C sin()4ρθπ+=1C 2C P 1C Q 2C PQ P 2C 40x y +-=P ,sin )αα2C ||PQ P 2C ()d α.（欧萌说：利用点到直接的距离列式子，然后就是三角函数的辅助公式进行化一）当时）（13sin =+πα即当时，，此时的直角坐标为.（三）直线参数方程的几何意义1.经过点P (x 0，y 0)，倾斜角为α的直线l 的参数方程为为参数）t t y y t x x (sin cos 00⎩⎨⎧+=+=αα若A ，B 为直线l 上两点，其对应的参数分别为t 1，t 2，线段AB 的中点为M ，点M 所对应的参数为t 0，则以下结论在解题中经常用到： (1)t 0=t 1＋t 22； (2)|PM |=|t 0|=t 1＋t 22； (3)|AB |=|t 2－t 1|； (4)|P A |·|PB |=|t 1·t 2|（5）⎪⎩⎪⎨⎧>+<-+=-=+=+0,0,4)(212121212212121t t t t t t t t t t t t t t PB PA 当当（注：记住常见的形式，P 是定点，A 、B 是直线与曲线的交点，P 、A 、B 三点在直线上） 【特别提醒】直线的参数方程中，参数t 的系数的平方和为1时，t 才有几何意义且其几何意义为：|t |是直线上任一点M (x ，y )到M 0(x 0，y 0)的距离，即|M 0M |=|t |.直线与圆锥曲线相交，交点对应的参数分别为12,t t ，则弦长12l t t =-； 2.解题思路第一步：曲线化成普通方程，直线化成参数方程()sin()2|3d παα==+-2()6k k Z παπ=+∈()d αP 31(,)22第二步：将直线的参数方程代入曲线的普通方程，整理成关于t 的一元二次方程：02=++c bt at第三步：韦达定理：a ct t a b t t =-=+2121,第四步：选择公式代入计算。

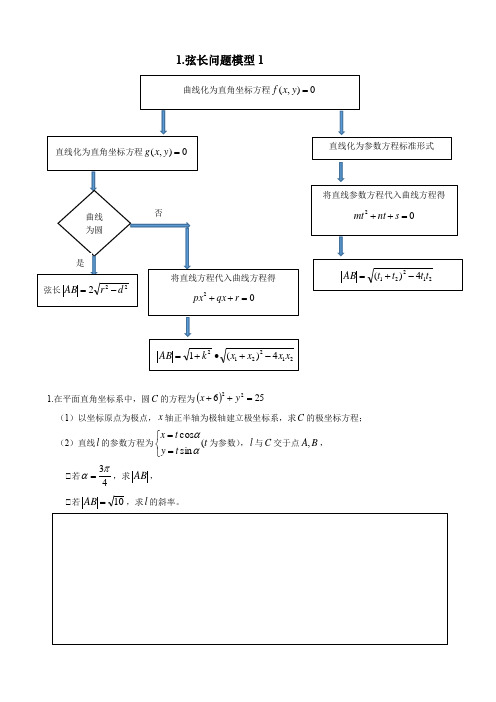
1.弦长问题模型11.在平面直角坐标系中，圆C 的方程为()25622=++y x（1）以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求C 的极坐标方程； （2）直线l 的参数方程为t t y t x (sin cos ⎩⎨⎧==αα为参数），l 与C 交于点B A ,， ①若43πα=，求AB ， ①若10=AB ，求l 的斜率。

2.已知直线t ty tx (32⎩⎨⎧=+=为参数）与曲线θθρcos 8sin 2=交于B A ,，求AB2.弦长问题模型2（只对直线过原点才可以）注意：若直线倾斜角为α且过原点，则该直线的直角坐标方程为αtan x y=，其参数方程为⎧==ααsin cos t y t x ，其极坐标方程为)(R ∈=ραθ3.在极坐标系中，以点(2,)2C π为圆心，半径为3的圆C 与直线:()3l R πθρ=∈交于,A B 两点.（1）求圆C 及直线l 的普通方程.（2）求弦长AB .3.参数方程最值问题模型4.已知曲线θθθ(sin 2cos 1:1⎩⎨⎧+=+=y x C 为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，且曲线:2C4πθ=()R ∈ρ（1）写出1C 的极坐标方程，2C 的一个参数方程；（2）设1C 与2C 交于N M ,两点，P 为1C 上一动点，求PMN ∆面积的最大值。

4.利用直线参数方程中t 的几何意义问题模型5.在极坐标系中，点M 坐标是)2,3(π，曲线C 的方程为)4sin(22πθρ+=；以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，斜率是1-的直线l 经过点M ． （1）写出直线l 的参数方程和曲线C 的直角坐标方程；（2）求证直线l 和曲线C 相交于两点A 、B ，并求||||MB MA ⋅的值．6.在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建坐标系,已知曲线()2:sin 2cos 0C a a ρθθ=>,已知过点()2,4P --的直线l 的参数方程为:2,4x y ⎧=-⎪⎪⎨⎪=-⎪⎩直线l 与曲线C 分别交于,M N(1)写出曲线C 和直线l 的普通方程; (2)若||,||,||PM MN PN 成等比数列,求a 的值.5.综合问题例题1在平面直角坐标系xoy 中，曲线13:221=+y x C ，以坐标原点为极轴，以x 轴的正半轴为极轴，建立极坐标系，曲线a C 222)4sin(:2+=+πθρ（1）写出1C 的参数方程，2C 的普通方程；（2）设点P 在1C 上，点Q 在2C ，求PQ 的最小值以及此时P 点坐标。

高中数学极坐标与参数方程知识点汇编及题型汇总【知识汇编】参数方程：直线参数方程：00cos ()sin x x t t y y t θθ=+⎧⎨=+⎩为参数 00(,)x y 为直线上的定点， t 为直线上任一点(,)x y 到定点00(,)x y 的数量；圆锥曲线参数方程：圆的参数方程：cos ()sin x a r y b r θθθ=+⎧⎨=+⎩为参数(a,b)为圆心，r 为半径； 椭圆22221x y a b +=的参数方程是cos ()sin x a y b θθθ=⎧⎨=⎩为参数； 双曲线2222-1x y a b =的参数方程是sec ()tan x a y b φθφ=⎧⎨=⎩为参数； 抛物线22y px =的参数方程是22()2x pt t y pt⎧=⎨=⎩为参数 极坐标与直角坐标互化公式：若以直角坐标系的原点为极点，x 轴正半轴为极轴建立坐标系，点P 的极坐标为(,)ρθ，直角坐标为(,)x y ，则cos x ρθ=, sin y ρθ=, 222x y ρ=+, tan yx θ=。

【题型1】参数方程和极坐标基本概念1．已知曲线C的参数方程为⎪⎩⎪⎨⎧+=+=ααsin 51cos 52y x (α为参数)，以直角坐标系原点为极点，Ox 轴正半轴为极轴建立极坐标系。

1)求曲线c 的极坐标方程2)若直线l 的极坐标方程为ρ(sinθ+cosθ)=1，求直线l 被曲线c 截得的弦长。

解：(1)∵曲线c 的参数方程为⎪⎩⎪⎨⎧+=+=ααsin 51cos 52y x (α为参数)∴曲线c 的普通方程为(x-2)2+(y-1)2=5将⎩⎨⎧==θρθρsin cos y x 代入并化简得：ρ=4cosθ+2sinθ 即曲线c 的极坐标方程为ρ=4cosθ+2sinθ (2)∵l 的直角坐标方程为x+y-1=0∴圆心c 到直线l 的距离为d=22=2∴弦长为225-=23 .2．极坐标系与直角坐标系xOy 有相同的长度单位，以原点O 为极点，以x 轴正半轴为极轴．已知曲线C 1的极坐标方程为ρ＝sin （θ＋4π），曲线C2的极坐标方程为ρsin θ＝a （a ＞0），射线θ＝ϕ，θ＝ϕ＋4π，θ＝ϕ－4π，θ＝2π＋ϕ与曲线C1分别交异于极点O 的四点A ，B ，C ，D ．（1）若曲线C1关于曲线C2对称，求a 的值，并把曲线C1和C2化成直角坐标方程； （2）求｜OA ｜·｜OC ｜＋｜OB ｜·｜OD ｜的值． 解：（1）1C ：2)1()1(22=-+-y x ， 2C ：a y =， 因为曲线1C 关于曲线2C 对称，1=a ，2C ：1=y （2）)4sin(22||πϕ+=OA ；ϕsin 22||=OC ，【题型2】直线参数方程几何意义的应用1.在平面直角坐标系xOy 中，直线l的参数方程为122x t y ⎧=-+⎪⎪⎨⎪=+⎪⎩（t为参数），直线l 与曲线C ：22(2)1y x --=交于A ，B 两点.（1）求AB的长；（2）在以O 为极点，x轴的正半轴为极轴建立的极坐标系中，设点P的极坐标为⎛⎝，求点P 到线段AB 中点M 的距离.解：（1）直线l的参数方程为1222x t y ⎧=-+⎪⎪⎨⎪=⎪⎩，，（t为参数），代入曲线C 的方程得24100t t +-=．设点A ，B 对应的参数分别为12t t ，，则124t t +=-，1210t t =-，所以12||||AB t t =-=（2）由极坐标与直角坐标互化公式得点P 的直角坐标为(22)-，， 所以点P 在直线l 上，中点M 对应参数为1222t t +=-，由参数t 的几何意义，所以点P 到线段AB 中点M 的距离||2PM =． 2．已知直线l 经过点(1,1)P ,倾斜角6πα=，（1）写出直线l 的参数方程。

极坐标与参数方程一、基础知识点梳理（一）极坐标 极坐标系的概念 (1)极坐标系如图所示,在平面内取一个定点O ,叫做极点,自极点O 引一条射线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系.(2)极坐标设M 是平面内一点,极点O 与点M 的距离|OM|叫做点M 的极径,记为ρ;以极轴Ox 为始边,射线OM 为终边的角xOM ∠叫做点M 的极角,记为θ.有序数对(,)ρθ叫做点M 的极坐标,记作(,)M ρθ.一般地,不作特殊说明时,我们认为0,ρ≥θ可取任意实数.特别地,当点M 在极点时,它的极坐标为(0, θ)(θ∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示.如果规定0,02ρθπ>≤<,那么除极点外,平面内的点可用唯一的极坐标(,)ρθ表示;同时,极坐标(,)ρθ表示的点也是唯一确定的.3、极坐标和直角坐标的互化(1)互化背景:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示:(2)互化公式:设M 是坐标平面内任意一点,它的直角坐标是(,)x y ,极坐标是(,)ρθ(0ρ≥),于是极坐标与直角坐标的互化公式如表:点M直角坐标(,)x y 极坐标(,)ρθ互化公式cos sin x y ρθρθ=⎧⎨=⎩ 222tan (0)x y yx xρθ=+=≠ 在一般情况下,由tan θ确定角时,可根据点M 所在的象限最小正角. 4、常见曲线的极坐标方程 曲线图形极坐标方程圆心在极点,半径为r 的圆(02)r ρθπ=≤<圆心为(,0)r ,半径为r 的圆2cos ()22r ππρθθ=-≤<圆心为(,)2r π,半径为r 的圆2sin (0)r ρθθπ≤<过极点,倾斜角为α的直线(1)()()R R θαρθπαρ=∈=+∈或(2)(0)(0)θαρθπαρ=≥=+≥和。

1. 极坐标及参数方程知识点1．伸缩变换：设点),(y x P 是平面直角坐标系中旳任意一点，在变换⎩⎨⎧>⋅='>⋅=').0(,y y 0),(x,x :μμλλϕ旳作用下，点),(y x P 对应到点),(y x P '''，称ϕ为平面直角坐标系中旳坐标伸缩变换，简称伸缩变换。

2.极坐标系旳概念：在平面内取一种定点O ，叫做极点；自极点O 引一条射线Ox 叫做极轴；再选定一种长度单位、一种角度单位(一般取弧度)及其正方向(一般取逆时针方向)，这样就建立了一种极坐标系。

3．点M 旳极坐标：设M 是平面内一点，极点O 与点M 旳距离||OM 叫做点M 旳极径，记为ρ；以极轴Ox 为始边，射线OM 为终边旳xOM ∠叫做点M 旳极角，记为θ。

有序数对),(θρ叫做点M 旳极坐标，记为),(θρM .极坐标),(θρ与)Z )(2,(∈+k k πθρ表达同一种点。

极点O 旳坐标为)R )(,0(∈θθ. 4.若0<ρ,则0>-ρ,规定点),(θρ-与点),(θρ有关极点对称，即),(θρ-与),(θπρ+表达同一点。

假如规定πθρ20,0≤≤>，那么除极点外，平面内旳点可用唯一旳极坐标),(θρ表达；同步，极坐标),(θρ表达旳点也是唯一确定旳。

5．极坐标与直角坐标旳互化：6。

圆旳极坐标方程：在极坐标系中，以极点为圆心，r 为半径旳圆旳极坐标方程是 r =ρ；在极坐标系中，以 )0,(a C )0(>a 为圆心， a 为半径旳圆旳极坐标方程是 θρcos 2a =； 在极坐标系中，以 )2,(πa C )0(>a 为圆心，a 为半径旳圆旳极坐标方程是θρsin 2a =；7.在极坐标系中，)0(≥=ραθ表达以极点为起点旳一条射线；)R (∈=ραθ表达过极点旳一条直线.在极坐标系中，过点)0)(0,(>a a A ，且垂直于极轴旳直线l 旳极坐标方程是a =θρcos .8．参数方程旳概念：在平面直角坐标系中，假如曲线上任意一点旳坐标y x ,都是某个变数t 旳函数⎩⎨⎧==),(),(t g y t f x 并且对于t 旳每一种容许值，由这个方程所确定旳点),(y x M 都在这条曲线上，那么这个方程就叫做这条曲线旳参数方程，联络变数y x ,旳变数t 叫做参变数，简称参数。

极坐标与参数方程知识点、题型总结一、伸缩变换：点是平面直角坐标系中的任意一点，在变换),(y x P 的作用下，点对应到点，称伸缩变换⎩⎨⎧>⋅='>⋅=').0(,y y 0),(x,x :μμλλϕ),(y x P ),(y x P '''一、1、极坐标定义：M 是平面上一点，表示OM 的长度，是，则有序实数实ρθMOx ∠数对,叫极径，叫极角；一般地，，。

，点P 的直角坐标、(,)ρθρθ[0,2)θπ∈0ρ≥极坐标分别为(x ，y )和(ρ，θ)2、直角坐标极坐标 2、极坐标直角坐标⇒cos sin x y ρθρθ=⎧⎨=⎩⇒222tan (0)x y yx xρθ⎧=+⎪⎨=≠⎪⎩3、求直线和圆的极坐标方程：方法一、先求出直角坐标方程，再把它化为极坐标方程方法二、（1）若直线过点M (ρ0，θ0)，且极轴到此直线的角为α，则它的方程为：ρsin(θ－α)＝ρ0sin(θ0－α)（2）若圆心为M (ρ0，θ0)，半径为r 的圆方程为ρ2－2ρ0ρcos(θ－θ0)＋ρ02－r 2＝0二、参数方程：（一）．参数方程的概念：在平面直角坐标系中，如果曲线上任意一点的坐标都是某个变数的函数 并且对于的每一个允许值，由这个方程所确y x ,t ⎩⎨⎧==),(),(t g y t f x t 定的点都在这条曲线上，那么这个方程就叫做这条曲线的参数方程，联系变数),(y x M 的变数叫做参变数，简称参数。

相对于参数方程而言，直接给出点的坐标间关系的y x ,t 方程叫做普通方程。

（二）．常见曲线的参数方程如下：直线的标准参数方程1、过定点（x 0，y 0），倾角为α的直线：（t 为参数）ααsin cos 00t y y t x x +=+=（1）其中参数t 的几何意义：点P （x 0，y 0），点M 对应的参数为t ，则PM =|t| (2)直线上对应的参数是。

选做题部分 极坐标系与参数方程一、极坐标系1．极坐标系与点的极坐标(1)极坐标系：如图4－4－1所示，在平面内取一个定点O ，叫做极点，自极点O 引一条射线Ox ，叫做极轴；再选定一个长度单位，一个角度单位(通常取弧度)及其正方向(通常取逆时针方向)，这样就建立了一个极坐标系．(2)极坐标：平面上任一点M 的位置可以由线段OM 的长度ρ和从Ox 到OM 的角度θ来刻画，这两个数组成的有序数对(ρ，θ)称为点M 的极坐标．其中ρ称为点M 的极径，θ称为点M 的极角． 2点M 直角坐标(x ，y )极坐标(ρ，θ)互化公式题型一 极坐标与直角坐标的互化1、已知点P 的极坐标为)4,2(π，则点P 的直角坐标为 （ ）A.（1，1）B.（1，-1）C.（-1，1）D.（-1，-1）2、设点P 的直角坐标为(3,3)-，以原点为极点，实轴正半轴为极轴建立极坐标系(02)θπ≤<，则点P 的极坐标为（ ） A ．3(32,)4π B ．5(32,)4π- C ．5(3,)4π D ．3(3,)4π-3．若曲线的极坐标方程为ρ＝2sin θ＋4cos θ，以极点为原点，极轴为x 轴正半轴建立直角坐标系，则该曲线的直角坐标方程为________．4．在极坐标系中，过点(1,0)并且与极轴垂直的直线方程是( )A ．ρ＝cos θB ．ρ＝sin θC ．ρcos θ＝1D ．ρsin θ＝15．曲线C 的直角坐标方程为x 2＋y 2－2x ＝0，以原点为极点，x 轴的正半轴为极轴建立极坐标系，则曲线C 的极坐标方程为________．6. 在极坐标系中，求圆ρ＝2cos θ与直线θ＝π4(ρ>0)所表示的图形的交点的极坐标．题型二 极坐标方程的应用由极坐标方程求曲线交点、距离等几何问题时，如果不能直接用极坐标解决，可先转化为直角坐标方程，然后求解．1.在极坐标系中，已知圆C 经过点P(2，π4)，圆心为直线ρsin ⎝ ⎛⎭⎪⎫θ－π3＝－32与极轴的交点，求圆C 的直角坐标方程．2.圆的极坐标方程为ρ＝4cos θ，圆心为C ，点P 的极坐标为⎝ ⎛⎭⎪⎫4，π3，则|CP|＝________.3.在极坐标系中，已知直线l 的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ＋π4＝1，圆C 的圆心的极坐标是C ⎝ ⎛⎭⎪⎫1，π4，圆的半径为1.(i)则圆C 的极坐标方程是________； (ii)直线l 被圆C 所截得的弦长等于________．4.在极坐标系中，已知圆C ：ρ＝4cos θ被直线l ：ρsin ⎝ ⎛⎭⎪⎫θ－π6＝a 截得的弦长为23，则实数a 的值是________．二、参数方程1．参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式．一般地，可以通过消去参数而从参数方程得到普通方程．(2)如果知道变数x ，y 中的一个与参数t 的关系，例如x ＝f (t )，把它代入普通方程，求出另一个变数与参数的关系y ＝g (t )，那么，⎩⎪⎨⎪⎧x ＝f (t )，y ＝g (t )就是曲线的参数方程．⎩⎪⎨⎪⎧x ＝x 0＋t cos αy ＝y 0＋t sin α (t 为参数)题型一 参数方程与普通方程的互化 【例1】把下列参数方程化为普通方程： (1)⎩⎨⎧x ＝3＋cos θ，y ＝2－sin θ； (2)⎩⎪⎨⎪⎧x ＝1＋12t ，y ＝5＋32t .题型二 直线与圆的参数方程的应用1、已知直线l 的参数方程为⎩⎪⎨⎪⎧ x ＝1＋t ，y ＝4－2t (参数t ∈R )，圆C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos θ＋2，y ＝2sin θ(参数θ∈[0,2π])，求直线l 被圆C 所截得的弦长．2、曲线C 的极坐标方程为：ρ=acos θ（a ＞0），直线l 的参数方程为：（1）求曲线C 与直线l 的普通方程；（2）若直线l 与曲线C 相切，求a 值．3、在直角坐标系xoy 中，曲线C 1的参数方程为，（α为参数），以原点O为极点，x 轴正半轴为极轴，建立极坐标系，曲线C 2的极坐标方程为．（Ⅰ）求曲线C 1的普通方程与曲线C 2的直角坐标方程；（Ⅱ）设P 为曲线C 1上的动点，求点P 到C 2上点的距离最小值．综合应用1、曲线25()12x tt y t =-+⎧⎨=-⎩为参数与坐标轴的交点是（ ）A 21(0,)(,0)52、B 11(0,)(,0)52、C (0,4)(8,0)-、D 5(0,)(8,0)9、3、参数方程222sin sin x y θθ⎧=+⎪⎨=⎪⎩（θ为参数）化为普通方程为（ ） A ．2y x =- B ．2y x =+ C ．2(23)y x x =-≤≤ D ．2(01)y x y =+≤≤3．判断下列结论的正误．(1)平面直角坐标系内的点与坐标能建立一一对应关系，在极坐标系中点与坐标也是一一对应关系( )(2)若点P 的直角坐标为(1，－3)，则点P 的一个极坐标是（2，－π3）( ) (3)在极坐标系中，曲线的极坐标方程不是唯一的( ) (4)极坐标方程θ＝π(ρ≥0)表示的曲线是一条直线( )4．(2013·北京高考)在极坐标系中，点⎝⎛⎭⎪⎫2，π6到直线ρsin θ＝2的距离等于________．5、平面直角坐标系中,将曲线2cos 2(sin x y ααα=+⎧⎨=⎩为参数)上的每一点横坐标不变,纵坐标变为原来的2倍得到曲线1C ,以坐标原点为极点,x 轴的非负半轴为极轴,建立的极坐标系中,曲线2C 的方程为4sin ρθ=(Ⅰ)求1C 和2C 的普通方程:(Ⅱ)求1C 和2C公共弦的垂直平分线的极坐标方程.6、已知曲线C 的极坐标方程是0sin 2cos 2=+-θθρ，以极点为平面直角坐标系的原点，极轴为x 轴的正半轴，建立平面直角坐标系，直线l 的参数方程是⎪⎪⎩⎪⎪⎨⎧=+=t y t x 222221（t 为参数）.（1）求曲线C 的直角坐标方程和直线l 的普通方程；（2）若直线l 与曲线C 交于B A ,两点，求AB 的值.7、已知圆C ：⎩⎨⎧ x ＝1＋cos θ，y ＝sin θ(θ为参数)和直线l ：⎩⎨⎧x ＝2＋t cos α，y ＝3＋t sin α(其中t 为参数，α为直线l 的倾斜角)．(1)当α＝2π3时，求圆上的点到直线l 距离的最小值；(2)当直线l与圆C有公共点时，求α的取值范围．。

极坐标与参数方程-题型归纳高考高频题型整理汇总——《极坐标与参数方程》除了简单的极坐标与直角坐标的转化、参数方程与普通方程的转化外，还涉及以下部分问题。

一）有关圆的题型题型一：圆与直线的位置关系（圆与直线的交点个数问题）----利用圆心到直线的距离与半径比较根据圆心到直线的距离公式，即可算出圆心到直线的距离d，再与半径r比较大小，得出圆与直线的位置关系。

当d>r 时，圆与直线相离，无交点；当d=r时，圆与直线相切；当d<r时，圆与直线相交，有两个交点。

题型二：圆上的点到直线的最值问题根据圆心到直线的距离公式，算出圆上任意一点到直线的距离d，再根据圆与直线的位置关系，分别代入公式dmax=d+r和dmin=d-r，得出圆上距离直线最远的点和距离直线最近的点。

题型三：直线与圆的弦长问题根据圆心到直线的距离公式，算出圆心到直线的距离d，再根据弦长公式l=2√(r^2-d^2)，得出直线与圆的弦长。

延伸：直线与圆锥曲线（包括圆、椭圆、双曲线、抛物线）的弦长问题弦长公式为l=t1-t2，其中t1和t2为直线与曲线的交点在曲线参数方程中的参数值。

二）距离的最值：用“参数法”1.曲线上的点到直线距离的最值问题2.点与点的最值问题参数法”：设点的坐标用该点在所在曲线的参数方程来表示，利用点到线的距离公式求出该点到直线的距离，再利用三角函数辅助角公式进行化简，得出距离的最值。

解：1）将圆C的参数方程化为普通方程：x = 3\cos t。

y = 3\sin t$则圆C的普通方程为：x^2 + y^2 = 9$将直线l的极坐标方程$r=2\cos\theta$化为直角坐标方程：r^2 = x^2 + y^2$r\cos\theta = x$代入$r=2\cos\theta$中得：x = 2\cos^2\theta$r\sin\theta = y$代入$r=2\cos\theta$中得：y = 2\sin\theta\cos\theta$则直线l的直角坐标方程为：x = 2y$2）在极坐标系中，圆C的半径为3，直线l的极坐标方程为$r=2\cos\theta$，则直线l与圆C的交点分别为$(\frac{4}{3},\frac{2\sqrt{2}}{3})$和$(\frac{4}{3},-\frac{2\sqrt{2}}{3})$。