弗留格尔公式的介绍(整理).pptx
- 格式:pptx
- 大小:23.09 KB
- 文档页数:2


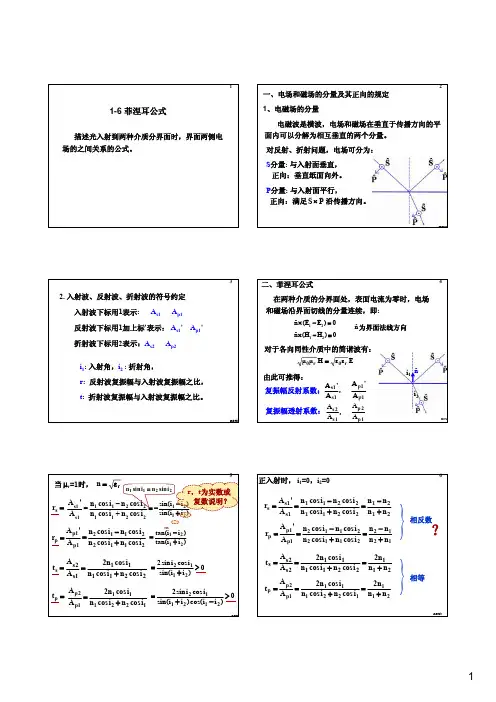

级组压力和流量的关系(弗留格尔公式)级组是由若干的相邻的,流量相同的且通流面积不变的级组合而成的。
实验表明,工况变化时,级组前后的压力p0,pz 与流量G 的关系,可用斯托拉流量锥表示级组的流量与背压的关系与喷管流量曲线相似,可用类似的方法来讨论级组的变工况。
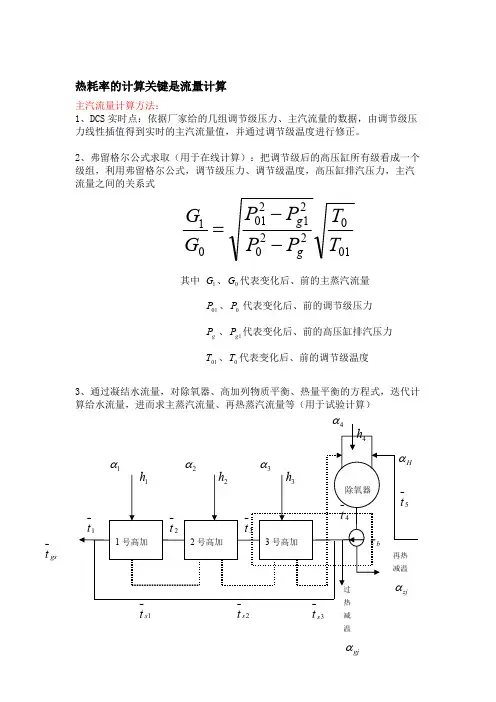
一. 级组前后压力与流量的关系1 .变工况前后级组均未达临界状态若级组中级数无限大,crg ε趋于零,且同一级内,级数不变,通流面积不变,公式简化为:22022011z zl p p p p G G --= 式称为弗留格尔公式,它表明:当变工况前后机组均未达到临界状态时,级组的流量与级组前后压力平方差的平方根成正比。
上述公示的推导是在级组前的温度保持不变的条件下求得的。
若变工况前后级组前温度变化较大时,则应考虑温度修正,即01022022011T T p p p p G G z zl--= 2. 变工况前后级组均为临界状态若级组中某一级始终处于临界状态,这种情况一般是末级首先到达临界状态。
因为末级的设计比焓降是各级中最大的。
此时,级组的流量与级组前的蒸汽压力成正比,即011p p G G = 若讨论的级组由若干级组成,则有===2210110p p p p G G 即,若级组中某一级的变工况前后均处于临界状态下工作,则通过该级组的流量与该机组中所有各级级前压力成正比。
二.弗留格尔公式的应用条件(1)级组中的级数应不小于3~4级。
严格的讲,弗留格尔公式只适用于无穷多级数的级组。
但在一定的负荷变化范围内,级组中的级数不小于3~4级时,亦可得到比较满意的结果。
(2)同一工况下,通过级组各级的流量相同。
因此,对于调整抽气的汽轮机(如供热抽气汽轮机),只能将两抽气点之间的各级取为一个级组。
(3)在不同工况下,级组中各级的通流面积应保持不变。
对于喷管调节汽轮机,其调节级的通流面积随调节阀的开启数目变化,故不能取在一个级组内。
但变工况前后,阀门开启数目相同,则可将调节级和压力级取在一个级组内。

名词解释:1、级:由一列喷嘴与同它相配合的动叶栅构成的基本作功单元。
它是与蒸汽进行能量转换的基本单元。
2、级的平均反动度:Ωm =△h b/△h t*反动度就指平均反动度。
(△h b-动叶汽道内膨胀时所降落的理想焓降;△h t*-整个级的滞止理想焓降)3、凝汽器冷却倍率:m=D W/D C称为凝汽器冷却倍率,它表示凝结一公斤蒸汽所需要的冷却水量(D W-凝汽器的冷却水量;D C-凝汽器的排汽量)4、叶片动频率:动叶片高速旋转时的自振频率称为动频率。
评价叶片振动的安全性,以其动频率为基准。
f d=f j2+Bn2,f d,f j-同一叶片相同振型的固有动频率和经温度修正后的静频率;n,B-动叶片的工作转速和动频系数。
5、频率分散度:在汽轮机同一级中所测得叶片(叶片组)的最大静频率差与其平均值之比。
△f s=[2(f max-f min)/ (f max+f min)]*100%。
6、柔性轴:一阶临界转速低于汽轮机工作转速的轴。
7、刚性轴:一阶临界转速高于汽轮机工作转速的轴。
8、节流调节:由一只或几只同时启闭的调节阀来控制进汽量的配汽方式。
9、喷嘴调节;由几只依次启闭的调节阀来控制进汽量的配汽方式。
10、速度变化率:零负荷和额定负荷对应的转速之差与额定转速的比值,称为速度变化率δ=[(n max-n min)/n0]*100%11、迟缓率:ε=[△n/n0]*100%(△n-同一负荷下最大转速变动值,n0-额定转速)综合:1、1、简要描述级的能量转换过程。
掌握典型级的最佳速比;影响级的轮周效率的主要因素;重热现象产生的原因及作用;弗留格尔公式;喷嘴调节式汽轮机各级压比、焓降的变化规律。
1)级的能量转换过程:先将蒸汽的热能在其喷嘴叶栅中转换为蒸汽所具有的动能,然后再将蒸汽的动能在动叶栅中转换为轴所出的机械功。
2)最佳速度比是指轮周效率ηu最高时,所对应的速度比称为最佳速度比。
纯冲动级的最佳速比(X1)OP=1/2COSα1;反动级的最佳速比(X1)OP=COSα1;冲动级的最佳速比(X1)OP≈COSα1/[2(1—Ωm)]3)影响级的轮周效率的主要因素:是速度系数φ、ψ以及余速损失系数ζc2,其中ζc2的影响最大,其大小取决于动叶出口绝对速度ηu=(△h t*-△h nζ-△h bζ-△h c2)/E0=1-ζn-ζb-ζc2(1-u1) ,ζn、ζb、ζc2----喷嘴能量损失系数、动叶能量损失系数、余速能量损失系数,当达到最佳速比时,ηu为最高。

格尔丰德恒等式
格尔丰德恒等式
卡特兰·格尔丰德恒等式,又被称为卡特兰·格尔弗德恒等式,是经典物理学中的重要数学公式,被称为“物理学家的本质”,是一种可以描述宇宙三大量子力学的关系的弦论方程。
这个公式也被称为“格尔弗德恒等式”。
它以18世纪德国物理学家卡特兰·格尔丰德恒的名字命名,他是物理学家、数学家和神学家、化学家和天文学家,他发现这个方程,但是没有完全弄明白它。
卡特兰·格尔弗德恒等式是物理学家们发现的最重要的基本方程,它描述的是能量的状态和分布的细节。
它描述了电磁场的生成、维持和传输的机理,以及它们对空间和时间的影响。
这是现在人们意识到的第一个物理学定律,以它作为基础,人类发现了更多的宇宙法则。
卡特兰·格尔弗德恒等式可以用来解释宇宙中广泛存在的现象,例如量子物理学、微观物理学、原子物理学和宇宙物理学。
它可以帮助我们跟踪宇宙的行为,也可以提出宇宙的相对论。
尽管卡特兰·格尔弗德恒等式是一个被认为是非常复杂的数学方程,但了解它的重要性可以帮助人们在日常生活中理解很多实际应用,比如电子和数字技术,它们都是基于卡特兰-格尔弗德恒程序。
卡特兰弗德恒等式现在被许多实验室采用来理解研究所测量的数据,这些实验结果有时是其他研究基础的一部分。

统计物理必备公式总结归纳统计物理是研究宏观系统的统计规律的分支科学,它与微观粒子的运动无关,而是通过统计方法来研究大量粒子的集体行为。
在统计物理学中,公式是理解和描述系统行为的关键工具。
本文将对统计物理中一些必备公式进行总结归纳,以帮助读者更好地理解和应用统计物理。
一、热力学量公式1. 内能U的计算公式:U = 3/2kT其中,U为内能,k为玻尔兹曼常数,T为系统温度。
2. 熵S的计算公式:S = k lnΩ其中,S为熵,k为玻尔兹曼常数,Ω为系统的微观状态数。
3. 自由能F的计算公式:F = U - TS其中,F为自由能,U为内能,T为系统温度,S为熵。
二、热力学过程公式1. 等温过程的工作公式:W = -nRT ln(V2/V1)其中,W为系统所做的功,n为物质的摩尔数,R为气体常数,T 为系统温度,V2和V1为过程中体积的变化。
2. 绝热过程的压强体积关系:P1V1^γ = P2V2^γ其中,P1和P2为过程中的初始和末态的压强,V1和V2为初始和末态的体积,γ为绝热指数。
三、碳氢化合物平均动能公式1. 一维单原子分子平均动能公式:〈E〉 = (1/2)kT其中,〈E〉为平均动能,k为玻尔兹曼常数,T为系统温度。
2. 一维双原子分子平均动能公式:〈E〉 = (1/2)kT + (1/2)kT(1 + 2/3exp(-θ/T))其中,〈E〉为平均动能,k为玻尔兹曼常数,T为系统温度,θ为势能常数。
四、费米-狄拉克分布和玻尔兹曼分布公式1. 费米-狄拉克分布公式:f(E) = 1 / (exp((E-μ)/(kT)) + 1)其中,f(E)为能级E上的费米分布函数,μ为系统的化学势,k为玻尔兹曼常数,T为系统温度。
2. 玻尔兹曼分布公式:f(E) = exp((μ-E)/(kT))其中,f(E)为能级E上的玻尔兹曼分布函数,μ为系统的化学势,k为玻尔兹曼常数,T为系统温度。
五、统计物理中的重要关系公式1. 统计物理中的状态方程:PV = NkT其中,P为系统的压强,V为系统的体积,N为系统中的粒子数,k为玻尔兹曼常数,T为系统温度。

稳定工况下超临界锅炉主蒸汽压力与其影响因素分析【摘要】本文主要通过阀门压损公式、能量守恒定律、弗留格尔公式及数学推导等基础上,从而对稳定工况下超超临界锅炉主蒸汽压力与其影响因素进行探讨分析。
通过观察主蒸汽压力变化可能受到的各类因素,从而得出各影响因素对主蒸汽压力变相对敏感度进行观察。
【关键词】超超临界锅炉;主蒸汽压力;影响因素超超临界压力锅炉能够有效提高火力发电厂的经济性,然而当蒸汽及水压力超过临界压力后,汽水混合物共存现象不可能存在,因此多采用锅筒的直流锅炉。
相较亚临界锅炉,超超临界压力锅炉具有更高的蒸汽参数,汽压控制及调节难度较大,因此对其压力影响因素进行分析有着重要的作用。
传统常采用建模仿真,然而操作不便;对某一因素进行定性分析亦是影响主汽压的常用方法,然而在对汽压具体变量进行反映等存在较大缺陷,同时亦无法对干扰最大因素进行分析,因此存在较大的缺陷。
通过模拟直流锅炉物理模型,并对主蒸汽压力及影响因素的微分关系式进行探讨,从而对主蒸汽变化的各类因素进行分析。
1 推导假设锅炉给水流量为G(kg/s),锅炉给水焓为igs(J/g),锅炉机组燃煤量为B(kg/s),锅炉输入热量为Qr(J/g),锅炉效率为ηgl,再热蒸汽流量为G(kg/s),再热器进出口蒸汽焓分别为izr、inzr(J/g)、过热器喷水流量为Gps(kg/s)、喷水焓为ips(J/g),主蒸汽焓为ingr(J/g),调阀前后蒸汽压力分别为p、p1(Pa),调阀前蒸汽比容为v(m3/kg)。
由能量守恒定律可得G(ingr—igs)+BQpsr+BQzrr=BQηgl(1),其中BQzrr为Gzr(inzr—izr)/B,BQpsr为Gps (ingr—ips)/B分别对应每kg燃料的再热蒸汽吸热量及喷水吸热量。
整理公式(1)可得G(ingr—igs)=BQingr—igs(1-rzr-rps)(2),其中rzr(Qzrr/Qrηgl)、rzr(Qpsr/Qrηgl)分别为再热蒸汽吸热份额及喷水吸热份额,由(2)得d(ingr—igs)/ingr—igs=dB/B+dQr/Qr+dηgl/ηgl—drzr/(1—rzr-rzr)—drps/(1—rzr-rps)—dG/G (3),根据阀门压损公式可得p-p1=R(G+Gps)2v(4),其中R为调阀阻力系数,由式(4)可得d(p-p1)/(p-p1)=dR/R+2d(G+Gps)/(G+Gps)+dv/v(5),由弗留格尔公式可得p1数值,p1=k(G+Gps),其中k为常数,已知:dingr=(αingr/αp)dt+(αingr/αt)dt(7)、dv=αv/αp·dp+αv/αt·dt(8),联合(3)、(5)、(7)、(8),得出结论为dp/p=[C1C2C3C4C5C6C7C8C9C10]·[dG/G·dGps/Gps·dR/R·digs/igs·dips/ips·dB/B·dQr/Qr·dηgl/ηgl·dGzr/Gzr·d(inzr—izr)/(inzr—izr)]T(9),式中dG/G、dGps/Gps、dips/ips、dQr/Qr、dηgl/ηgl、d(inzr—izr)/(inzr—izr)、dB/B、dR/R、digs/igs、dGzr/Gzr分别为给水流量、喷水流量、喷水焓、锅炉输入热量、锅炉效率、再热蒸汽比焓升、燃煤量、调阀阻力系数、给水焓、再热蒸汽流量的相对量。


1.冲动级和反动级的做功原理有何不同?在相等直径和转速的情况下,比较二者的做功能力的大小并说明原因。
答:冲动级做功原理的特点是:蒸汽只在喷嘴中膨胀,在动叶汽道中不膨胀加速,只改变流动方向,动叶中只有动能向机械能的转化。
反动级做功原理的特点是:蒸汽在动叶汽道中不仅改变流动方向而且还进行膨胀加速动叶中既有动能向机械能的转化同时有部分热能转化成动能。
在同等直径和转速的情况下,纯冲动级和反动级的最佳速比比值:上式说明反动级的理想焓降比冲动级的小一倍2.说明高压级内和低压级内主要包括哪几项损失?答:高压级内:叶高损失、喷嘴损失、动叶损失、余速损失、扇形损失、漏气损失、叶轮摩擦损失等;低压级内:湿气损失、喷嘴损失、动叶损失、余速损失,扇形损失、漏气损失、叶轮摩擦损失很小。
3.汽轮机级内有哪些损失?答:汽轮机级内的损失有:1喷嘴损失;2动叶损失3余速损失4叶高损失:又称为端部损失,产生原因:当汽流通过汽道的时候,在上下端面上,由于蒸汽的粘性形成一层很薄的附面层,附面层内粘性力损耗汽流的动能,形成了端部附面层中的摩擦损失。
5扇形损失6叶轮摩擦损失(简称摩擦损失):由两部分组成:a叶轮两侧几围带表面的粗糙度引起的摩擦损失b子午面内的涡流运动引起的损失7部分进汽损失:由鼓风损失和斥汽损失两部分组成8漏汽损失:反动级漏汽损失比冲动级大9湿气损失:过饱和损失,挟带损失,制动损失,扰流损失,工质损失4.据喷嘴斜切部分截面积变化图,请说明:(1).当喷嘴出口截面上的压力比p1/p0大于或等于临界压比时,蒸汽的膨胀特点;(2).当喷嘴出口截面上的压力比p1/p0小于临界压比时,蒸汽的膨胀特点。
答:(1)p1/p0大于或等于临界压比时,喷嘴出口截面AC上的气流速度和方向与喉部界面AB相同,斜切部分不发生膨胀,只起导向作用。
(2)当喷嘴出口截面上的压力比p1/p0小于临界压比时,气流膨胀至AB时,压力等于临界压力,速度为临界速度。
第63卷第2期2021年4月汽 轮 机 技 术TURBINE TECHNOLOGYVol. 63 No.2Apr. 2021300MW 机组高调阀流量特性曲线试验及优化黄 智S 包伟伟2,袁建丽2,李璟涛2,张小晖3(1国家电力投资集团有限公司,北京100033; 2国家电投集团中央研究院,北京102209;3国家电投集团大连发电有限公司,大连116008)摘要:通过高调阀流量特性试验,根据测量的一系列高调阀实际流量特性数据,整定并优化了高调阀流量特性曲 线。
结果表明,优化后的阀门流量特性曲线与机组实际运行特性具有更好的契合度,实现了单、顺序阀控制模式的无扰切换,优化了 AGC 和一次调频调节水平,显著提高了机组控制调节品质,并带来一定的经济性收益。
关键词:汽轮机;高压调节阀;流量特性曲线;优化;调节品质分类号:TK267文献标识码:A 文章编号:1001-5884 (2021 )02-0127-04Optimization of Flow Characteristic Curve of HP Control Valve for 300MW UnitHUANG Zhi 1, BAO Wei-wei 2, YUAN Jian-li 2, LI Jing-tao 2, ZHANG Xiao-hui 3(1 State Power Investment Corporation , Beijing 100033, China; 2 SPIC Central Research Institute ,Beijing 102209, China ; 3 SPIC Dalian Power Co. , Ltd. , Dalian 116008, China )Abstract : The flow characteristic curve of high-pressure regulating valve is set and optimized according to actual flowcharacteristic data of high-pressure regulating valve. The results show that the optimized valve flow characteristic curve has a better fit with the actual operation characteristics of the unit, realizes the undisturbed switching of single valve and sequence valve control mode , optimizes the level of AGC and primary frequency regulation , significantly improves thequality of unit control and regulation , and brings certain economic benefits.Key words : steam turbine ; HP control valve ; flow characteristic curve ; optimization ; regulating quality0 前 言汽轮机高压调节阀(以下简称高调阀)是DEH 系统的主要执行机构,高调阀管理是DEH 的主要内容。
弗汝德数公式弗汝德数公式是一种概念极其重要的数学模型,它是一种宏观的统计方法,用于表示一系列单位之间的关系。
它由18世纪的德国数学家莫里斯弗汝德发明,被应用于大量的科学和技术研究领域中。
弗汝德数公式的主要思想是,它可以用来描述多类型的相互牵连的单位间的关系,这些单位可以是质量、时间、长度、空间、力量等等。
弗汝德数是使用一种特定的方法来表示这种关系,它将指定的单位通过一系列的等式连接起来,使得这种关系可以被表达出来。
弗汝德数公式可以用来衡量不同物体之间的大小,可以帮助人们更准确地表达物体之间的关系。
它可以用来衡量物体之间的力量、时间和距离;它也可以用来测量物体之间的能源和动能以及其大小。
此外,它还可以帮助科学家更准确地描绘物体的空间结构,进行深入的物理研究。
弗汝德数公式的具体用途非常丰富,可以应用于许多不同的领域,比如计算机科学、数学、空间科学和物理学等等。
它可以用来计算数学表达式,例如求解多项式方程;它也可以用来解决物理方程,同时可以用来计算几何图形的大小和形状。
弗汝德数公式能够进行复杂的三角形计算。
弗汝德数公式也可以应用于工程领域,用于进行有关工程设计的分析,比如建筑、机械工程等等。
利用弗汝德数,可以预测材料的耐受力、结构的稳定性、结构的可行性、结构的力学特性等等。
弗汝德数也可以被应用于汽车工程、机器人工程、航空航天工程等等,可以用来衡量不同结构的大小和空间特性。
弗汝德数公式的应用也被广泛应用于生物学领域,可以用来衡量人类体内许多生物现象,如反应时间、肌肉运动控制等。
此外,它还可以用来分析基因的变化、化学反应的平衡等等,从而帮助研究生物免疫机制,更好地治疗疾病。
以上就是弗汝德数公式的最基本内容介绍,它可以应用于不同的科学和技术领域,是一个十分重要的数学模型,在很多领域都有着广泛的应用,对人们日常生活有着重要的意义。
接下来,我们将从以下几个方面进一步讨论它:弗汝德数公式的原理和特点、应用场景以及如何使用它进行分析。
2. 伏格尔法伏格尔法考虑到,一产地的产品假如不能按最小运费就近供应,就考虑次小运费, 这就有一个差额。
差额越大,说明不能按最小运费调运时, 运费增加越多。
因而对差额最大处,就应当采用最小运费调运。
例题其中到各地单位运价如下:基于此,伏格尔法的步骤是:第一步:在表3-3中分别计算出各行和各列的最小运费和次最小运费的差额, 并填入该表的最右列(R1)和最下行(C1),见表3-10。
从行(C1)或列(R1)差额中选出最大者(5), 选择它所在列(B2)中的最小元素(4)。
可确定A3 的产品先供应B2 的需要,即把B2的销量6全分配给A3B2=(4*6)。
同时将运价表中的B2 列数字划去(黄色表示已经分配)。
表3-10第二步:在表3-11中分别计算出各行和各列的最小运费和次最小运费的差额, 并填入该表的最右列(R2)和最下行(C2), 其中最大者为3,所在的列B4,而列B4中A3为最小元素,A3的总产量为9,因上面已经给B2分配了6,所以B4分配3,即A3B4=(5*3),把A3列划去。
(注意:A3的产量是9,B2只分配了6,没分完,继续分给B4的3)如下图3-11表3-11第三步:按照以上方法,找出R3和C3中的最大值(2),可知C3的B1和B4都等于2,取B1和B4中最小的元素A2B1=1,把B1的销量3全部分配给A2B1=(1*3),把A3列划去。
如下图3-12表3-12第四步:按照以上方法,找出R4和C4中的最大值(7),取B3和B4中最小的元素A1B3=3,把B3的销量5全部分配给A1B3=(3*5),把B3列划去。
如下图3-13 表3-13第五步:把A1中剩余的分配给A1B4=(10*2),把A2中剩余的分配给A2B4(8*1)第六步:把上面分配的值相加,得出最加方案。
即(4*6)+(5*3)+(1*3)+(3*5)+(10*2)+ (8*1)=85大家要特别注意:要注意每行和每的约束条件,做题时要横看销量是否完全分配完,同时也要坚看产量是否分配完,如第五步就是根据总量减去已分配得出的结果。