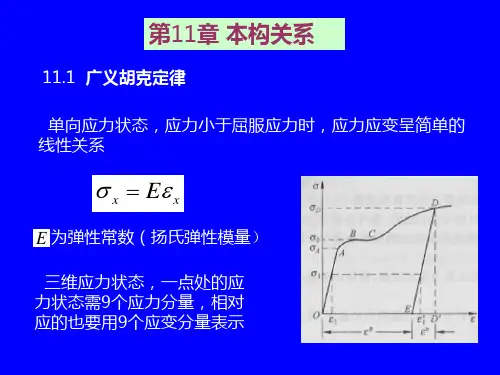
11.1 广义胡克定律 3 张量表示法
ij cijkl kl (i, j,k ,l 1,2,3)
(11-1’)
广义虎克定律或弹性本构方程 弹性系数 cmn (或cijkl ) 共有36个。对于各向同性材料,独立 的弹性常数只有2个。
附页
ij cijkl kl (i, j,k ,l 1,2,3)
个。
ij ji , ij ji
于是,对均匀的理想弹性体:
x c11 x c12 y c13 z c14 xy c15 yz c16 zx
y
c21 x
c22 y
c23 z
c24 xy
c25
yz
c26
zx
x c31 x c32 y c33 z c34 xy c35 yz c36 zx
不是独立的弹性常数。 对于各向同性弹性体,独立的弹性常数
只有两个, 即 λ和μ或 E 和ν。将式 (11-9) 稍加变换后, 可缩
2
e
2 2
3 e 23
常数λ, μ称为拉梅弹性常数。
(11-2)
通过坐标变换后, 可得任意坐标系 Oxyz 内的本构关系为
x e 2 x , xy xy
y
e
2 y , yz
yz
z
e
2 z , zx
zx
(11-3)
ij ije 2 ij
(11-3’)
以上证明了各向同性的均匀弹性体的弹性常数只有 两个。
证明:首先,在弹性状态下主应力方向与主应变方向相重合
为此,令x, y, z为主应变方向,则剪应变分量γxy,γyz, γzx应等于零。于是,由式 (4-1) 有
xy c41 x c42 y c43 z