电路分析基础习题第五章答案(史健芳)
- 格式:doc
- 大小:1.29 MB
- 文档页数:12

《电路分析基础》各章习题参考答案第1章习题参考答案1-1 (1) SOW; (2) 300 V、25V,200V、75V; (3) R=12.50, R3=1000, R4=37.5021-2 V =8.S V, V =8.S V, V =0.S V, V =-12V, V =-19V, V =21.S V U =8V, U =12.5,A mB D 'AB B CU =-27.S VDA1-3 Li=204 V, E=205 V1-4 (1) V A=lOO V ,V=99V ,V c=97V ,V0=7V ,V E=S V ,V F=l V ,U A F=99V ,U c E=92V ,U8E=94V,8U BF=98V, u cA=-3 V; (2) V c=90V, V B=92V, V A=93V, V E=-2V, V F=-6V, V G=-7V, U A F=99V, u c E=92V, U B E=94V, U BF=98V, U C A =-3 V1-5 R=806.70, 1=0.27A1-6 1=4A ,11 =llA ,l2=19A1-7 (a) U=6V, (b) U=24 V, (c) R=SO, (d) 1=23.SA1-8 (1) i6=-1A; (2) u4=10V ,u6=3 V; (3) Pl =-2W发出,P2=6W吸收,P3=16W吸收,P4=-lOW发出,PS=-7W发出,PG=-3W发出1-9 l=lA, U5=134V, R=7.801-10 S断开:UAB=-4.SV, UA0=-12V, UB0=-7.2V; S闭合:12 V, 12 V, 0 V1-12 UAB=llV / 12=0.SA / 13=4.SA / R3=2.401-13 R1 =19.88k0, R2=20 kO1-14 RPl=11.110, RP2=1000第2章习题参考答案2-1 2.40, SA2-2 (1) 4V ,2V ,1 V; (2) 40mA ,20mA ,lOmA 2-3 1.50 ,2A ,1/3A2-4 60 I 3602-5 2A, lA2-6 lA2-7 2A2-8 lOA2-9 l1=1.4A, l2=1.6A, l3=0.2A2-10 11=OA I l2=-3A I p l =OW I P2=-l8W2-11 11 =-lA, l2=-2A I E3=10V2-12 11=6A, l2=-3A I l3=3A2-13 11 =2A, l2=1A ,l3=1A ,14 =2A, l5=1A2-14 URL =30V I 11=2.SA I l2=-35A I I L =7.SA2-15 U ab=6V, 11=1.SA, 12=-lA, 13=0.SA2-16 11 =6A, l2=-3A I l3=3A2-17 1=4/SA, l2=-3/4A ,l3=2A ,14=31/20A ,l5=-11/4A12-18 1=0.SA I l2=-0.25A12-19 l=1A32-20 1=-lA52-21 (1) l=0A, U ab=O V; (2) l5=1A, U ab=llV。

第5章5.1选择题1、在关联参考方向下,R 、L 、C 三个元件的伏安关系可分别如( D )表示。
A. dt di C u d i L u u Gu i C C tL L L R R =+==⎰ ,)(1)0( ,0ττ B. dtdi C u d i L u Ri u C C t L L R R =+==⎰ ,)(1 )0(u , 0L ττ C. ⎰+===tC C C L L R R d i C u u dt di L u Gi u 0)(1)0( , ,ττ D. ⎰+===tC C C L L R R d i C u u dt di L u Ri u 0)(1)0( , ,ττ 2、一阶电路的零输入响应是指( D )。
A. 电容电压V 0)0(≠-C u 或电感电压V 0)0(≠-L u , 且电路有外加激励作用B. 电容电流A 0)0(≠-C i 或电感电压V 0)0(≠-L u , 且电路无外加激励作用C. 电容电流A 0)0(≠-C i 或电感电压A 0)0(≠-L i , 且电路有外加激励作用D. 电容电压V 0)0(≠-C u 或电感电流A 0)0(≠-L i , 且电路无外加激励作用 3、若1C 、2C 两电容并联,则其等效电容C =( A )。
A. 21C C +B.2121C C C C +C.2121C C C C +D. 21C C4、已知电路如图x5.1 所示,电路原已稳定,开关闭合后电容电压的初始值)0(+C u 等 于( A )。
A. V 2-B. V 2C. V 6D. V 8图x5.1 选择题4图5、已知V 15)(τtC e t u -=,当s 2=t 时V 6=C u ,电路的时间常数τ等于( B )。
A. s 458.0B. s 18.2C. s 2.0D. s 1.06、二阶RLC 串联电路,当C L R 2____时,电路为欠阻尼情况;当CLR 2____时, 电路为临界阻尼情况( B )。

第5章选择题1、在关联参考方向下,R 、L 、C 三个元件的伏安关系可分别如( D )表示。
A. dtdi C u d i L u u Gu i C C tL L L R R =+==⎰ ,)(1)0( ,0ττ B. dtdi C u d i L u Ri u C C tL L R R =+==⎰ ,)(1 )0(u , 0L ττC. ⎰+===tC C C L L R R d i C u u dt di L u Gi u 0)(1)0( , ,ττ D. ⎰+===tC C C L L R R d i C u u dt di Lu Ri u 0)(1)0( , ,ττ 2、一阶电路的零输入响应是指( D )。
A. 电容电压V 0)0(≠-C u 或电感电压V 0)0(≠-L u , 且电路有外加激励作用B. 电容电流A 0)0(≠-C i 或电感电压V 0)0(≠-L u , 且电路无外加激励作用C. 电容电流A 0)0(≠-C i 或电感电压A 0)0(≠-L i , 且电路有外加激励作用D. 电容电压V 0)0(≠-C u 或电感电流A 0)0(≠-L i , 且电路无外加激励作用 3、若1C 、2C 两电容并联,则其等效电容C =( A )。
A. 21C C +B.2121C C C C +C.2121C C C C +D. 21C C4、已知电路如图 所示,电路原已稳定,开关闭合后电容电压的初始值)0(+C u 等 于( A )。
A. V 2-B. V 2C. V 6D. V 85、已知V 15)(τtC e t u -=,当s 2=t 时V 6=C u ,电路的时间常数τ等于( B )。
A. s 458.0B. s 18.2C. s 2.0D. s 1.06、二阶RLC 串联电路,当C L R 2____时,电路为欠阻尼情况;当CL R 2____时, 电路为临界阻尼情况( B )。

第5章5.1解:s /rad LC 710811-⨯==ωHz LC f 571021082121⨯≈⨯⨯==-ππA .R U I 050108170-⨯==V L I U CO 2500==ω5.2解:(1)Ω61150252===max P U R H .C L 01601010250011622=⨯⨯==-ω(2)2406110102500250062=⨯⨯⨯==-R L Q ω通频带: 42102402500.Q ===ωω∆5.3解:(1)Ω3400==max I U R (2)H I U L L 1200010150300300=⨯⨯==-ω(3)F .L C μω250120==(4)15203000===S L U U Q 5.4解:(1)mH ...I U L L 05010591220100600=⨯⨯⨯==πω Ω100==I U R (2)5021000===S L U U Q(3)4010183⨯==.Qf f ∆5.5解:(1)MHz LC f 221==π (2)2402010641022660.R L Q =⨯⨯⨯⨯==-πω(3)A .R U I s 202040===(4)V .QU U S C 81600==5.6解:(1)Ωk R 51010503=⨯=- (2)F .U I C C C μω2505000501060300=⨯⨯==- (3)H ..C L 16010250500011622=⨯⨯==-ω (4)2560.CR Q ==ω5.7解:电流表读数为零,说明发生了并联谐振。
(1)F .L C μω530103002500113220=⨯⨯==-(2)︒∠=︒∠⨯==605339602555./R I U (3)︒∠==60255/I I R ︒-∠=⨯⨯︒∠==-3053010300250060533930.j .L j U I L ω ︒-∠-=-=30530.I I L C 5.8解:s/rad LC 5100010==ω 5100.CR Q ==ω s /rad Q 40010==ωω∆5.9解:(1)501020101360=⨯⨯==f f Q ∆(2)H .Q R L 183501021010630≈⨯⨯⨯==πω(3)F R Q C μπω796101010250360≈⨯⨯⨯==5.10解:(1)Ω010*********.I P R S ≈⨯==-(2)V ..R I U S 0202010=⨯==(3)nH ..I U L L 05010220002060≈⨯⨯==ω(4)mF .U I C L 510202020060≈⨯⨯==ω5.11 解:(1) 247pF 。

电路分析基础第三版课后答案【篇一:《电路分析基础》作业参考解答】txt>第一章(p26-31)1-5 试求题1-5图中各电路中电压源、电流源及电阻的功率(须说明是吸收还是发出)。
(a)(a)解:标注电压如图(a)所示。
由kvl有u?15?5?2?5v 故电压源的功率为p1??15?2??30w(发出)电流源的功率为p2?2?u?2?5?10w(吸收)电阻的功率为p3?5?22?5?4?20w(吸收)(b)解:标注电流如图(b)所示。
(b)由欧姆定律及kcl有i2?15?3a,i1?i2?2?3?2?1a5故电压源的功率为p1??15?i1??15?1??15w(发出)电流源的功率为p2??15?2??30w(发出)电阻的功率为p3?5?i2?5?32?5?9?45w(吸收)1-8 试求题1-8图中各电路的电压u,并分别讨论其功率平衡。
(b)解:标注电流如图(b)所示。
由kcl有i?6?2?4a 故u?2?i?2?4?8v2由于电流源的功率为p1??6?u??6?8??48w电阻的功率为p2?2?i2?2?42?32w外电路的功率为p3?2?u?2?8?16w且pk?13kp1p2p34832160所以电路的功率是平衡的,及电路发出的功率之和等于吸收功率之和。
(b)1-10 电路如题1-10图所示,试求:(1)图(a)中,i1与uab;解:如下图(a)所示。
因为(a)i?10?2?0.9i15所以i1?2?20?2.222a0.99uab?4(i1?i)?4??20?2??8?0.889v991-19 试求题1-19图所示电路中控制量i1及电压u0。
解:如图题1-19图所示。
由kvl及kcl有1000i1u020u0i1600i1u060005000整理得1000i1u0203000i1u00解得i1?5?10?3a?5ma,u0?15v。
题1-19图补充题:u1. 如图1所示电路,已知 i ?a , ab ? 16 v ,求电阻r。
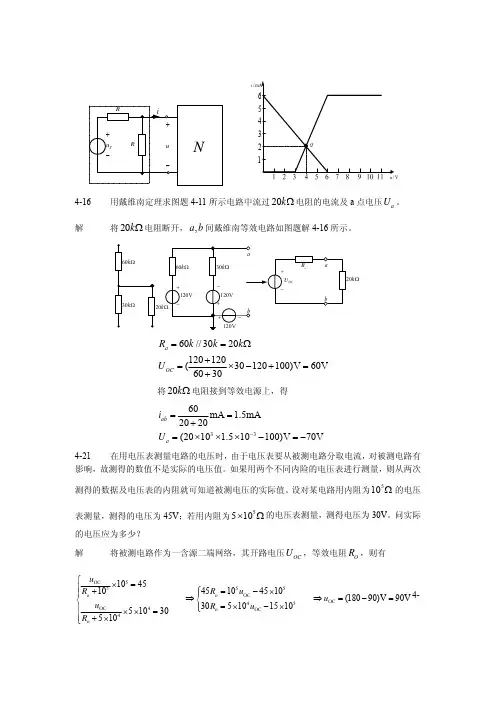
/i4-16 用戴维南定理求图题4-11所示电路中流过20k Ω电阻的电流及a 点电压。
a U 解将电阻断开,间戴维南等效电路如图题解4-16所示。
20k Ω,a bk Ω60//3020120120(30120100)V 60V6030a OCR k k k U ==Ω+=×−+=+ 将电阻接到等效电源上,得20k Ω3360mA 1.5mA2020(2010 1.510100)V 70V ab a i U −==+=×××−=− 4-21 在用电压表测量电路的电压时,由于电压表要从被测电路分取电流,对被测电路有影响,故测得的数值不是实际的电压值。
如果用两个不同内险的电压表进行测量,则从两次测得的数据及电压表的内阻就可知道被测电压的实际值。
设对某电路用内阻为的电压表测量,测得的电压为45V ;若用内阻为510Ω5510×Ω的电压表测量,测得电压为30V 。
问实际的电压应为多少? 解将被测电路作为一含源二端网络,其开路电压,等效电阻OC U O R ,则有5OC 555o o OC OC 454OCo OC 4o 10451045104510(18090)V 90V 30510151051030510u R R u u u R u R ⎧×=⎪⎧+=−×⎪⎪⇒⇒=⎨⎨=×−×⎪⎪⎩××=⎪+×⎩−=4-28 求图题4-20所示电路的诺顿等效电路。
已知:12315,5,10,R R R =Ω=Ω=Ω。
10V,1A S S u i ==解对图题4-20所示电路,画出求短路电流和等效内阻的电路,如下图所示SC i对左图,因ab 间短路,故0,0i i α==,10A 0.5A 155SC i ==+ 对右图,由外加电源法,106ab R α=Ω− 4-30 电路如图题4-22所示。


第1章试题库一、填空题(建议较易填空每空0.5分,较难填空每空1分)1、电流所经过的路径叫做,通常由、和三部分组成。
2、实际电路按功能可分为电力系统的电路和电子技术的电路两大类,其中电力系统的电路其主要功能是对发电厂发出的电能进行、和;电子技术的电路主要功能则是对电信号进行、、和。
3、实际电路元件的电特性而,理想电路元件的电特性则和。
无源二端理想电路元件包括元件、元件和元件。
4、由元件构成的、与实际电路相对应的电路称为,这类电路只适用参数元件构成的低、中频电路的分析。
5、大小和方向均不随时间变化的电压和电流称为电,大小和方向均随时间变化的电压和电流称为电,大小和方向均随时间按照正弦规律变化的电压和电流被称为电。
6、是电路中产生电流的根本原因,数值上等于电路中的差值。
7、具有相对性,其大小正负相对于电路参考点而言。
8、衡量电源力作功本领的物理量称为,它只存在于内部,其参考方向规定由电位指向电位,与的参考方向相反。
9、电流所做的功称为,其单位有和;单位时间内电流所做的功称为,其单位有和。
10、通常我们把负载上的电压、电流方向称作方向;而把电源上的电压和电流方向称为方向。
11、定律体现了线性电路元件上电压、电流的约束关系,与电路的连接方式无关;定律则是反映了电路的整体规律,其中定律体现了电路中任意结点上汇集的所有的约束关系,定律体现了电路中任意回路上所有的约束关系,具有普遍性。
12、理想电压源输出的值恒定,输出的由它本身和外电路共同决定;理想电流源输出的值恒定,输出的由它本身和外电路共同决定。
13、电阻均为9Ω的Δ形电阻网络,若等效为Y形网络,各电阻的阻值应为Ω。
I A,内阻14、实际电压源模型“20V、1Ω”等效为电流源模型时,其电流源S=i R Ω。
15、直流电桥的平衡条件是 相等;负载上获得最大功率的条件是等于 ,获得的最大功率=min P 。
16、如果受控源所在电路没有独立源存在时,它仅仅是一个 元件,而当它的控制量不为零时,它相当于一个 。

习题参考答案习题11-11-1..(1)(a )图,u 和i 参考方向是非关联参考方向;(b )图,u 和i 参考方向是关联参考方向。
参考方向。
(2)(a )图,u 的实际方向与参考方向相同,i 的实际方向与参考方向相反。
(b )图,u 的实际方向与参考方向相反,i 的实际方向与参考方向相同。
的实际方向与参考方向相同。
(3)(a )图,8=p W ,吸收功率;(b )图,24-=p W ,发出功率。
,发出功率。
1-21-2..030)24()4(24=+-+-++-=åp ,功率平衡。
,功率平衡。
1-31-3..(a )图,01R i u u s +-=;(b )图,02R i u u s -=1-41-4..022233311=+-+++-S S S U R I U R I R I U1-51-5..120W1-61-6.不能,实际电压将超过额定电压;可以。
.不能,实际电压将超过额定电压;可以。
.不能,实际电压将超过额定电压;可以。
1-71-7..(a)W =1R ;(b)W =2R1-81-8..(1)0=U V ,0=I A ;(2)3100=U V ,310=I A ;(3)25=U V ,5.2=I A (该题中已知条件中“W =10L R ”有误,应当改为“W =10R ”)1-91-9..5=aV V ,=bV 1V 1V。
1-101-10..5条支路,条支路,33个结点。
个结点。
a a 、b 两点间电流电压都等于零。
两点间电流电压都等于零。
1-111-11..=aI 11A 11A,,=bI -6A -6A,,=cI -11A -11A。
1-121-12..31-=IA 、2I =5.22A =5.22A、、3I =2.22A =2.22A。
1-131-13.开关断开时.开关断开时.开关断开时,,6=AV V ,6-=BV V 。
闭合时,8=AV V ,0=BV V 。
第4章4.1选择题1.关于叠加定理的应用,下列叙述中正确的是( D )。
A.不仅适用于线性电路,而且适用于非线性电路B.仅适用于非线性电路的电压、电流计算C.仅适用于线性电路,并能利用其计算各分电路的功率进行叠加得到原电路的功率D.仅适用于线性电路的电压、电流计算2.关于齐次定理的应用,下列叙述中错误的是( B )。
A.齐次定理仅适用于线性电路的计算B.在应用齐次定理时,电路的某个激励增大K倍,则电路的总响应将同样增大K倍C.在应用齐次定理时,所讲的激励是指独立源,不包括受控源D.用齐次定理分析线性梯形电路特别有效3.关于替代定理的应用,下列叙述中错误的是( C )。
A.替代定理不仅可以应用在线性电路,而且还可以应用在非线性电路B.用替代定理替代某支路,该支路可以是无源的,也可以是有源的C.如果已知某支路两端的电压大小和极性,可以用电流源进行替代D.如果已知某支路两端的电压大小和极性,可以用与该支路大小和方向相同的电压源进行替代4.关于戴维宁定理的应用,下列叙述中错误的是( A )。
A.戴维宁定理可将复杂的有源线性二端电路等效为一个电压源与电阻并联的电路模型B.求戴维宁等效电阻是将有源线性二端电路内部所有的独立源置零后,从端口看进去的输入电阻C.为得到无源线性二端网络,可将有源线性二端网络内部的独立电压源短路、独立电流源开路D.在化简有源线性二端网络为无源线性二端网络时,受控源应保持原样,不能置于零5.在诺顿定理的应用,下列叙述中错误的是( C )。
A.诺顿定理可将复杂的有源线性二端网络等效为一个电流源与电阻并联的电路模型B.在化简有源线性二端网络为无源线性二端网络时,受控源应保持原样,不能置于零C.诺顿等效电路中的电流源电流是有源线性二端网络端口的开路电流D .诺顿等效电路中的电阻是将有源线性二端网络内部独立源置零后,从端口看进去的等效电阻6.关于最大功率传输定理的应用,下列叙述中错误的是( C )。
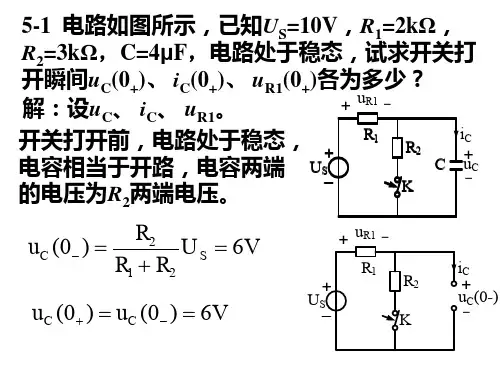
第五章5.1 如题5.1图所示电路,0<t 时已处于稳态。
当0=t 时开关S 打开,求初始值)0(+c u 和)0(+c i 。
解:V u u V u u s c 4)0()0(.4424)0(===+=-+-,所以因为电容是独立初始值。
开关断开后,,A i i u c c 8.0)0(,0)41()0()0(-==+∙+-++。
cu-cut<0,稳态c4开关断开后5.2 如题5.2图所示电路,0<t 时已处于稳态。
当0=t 时开关S 闭合,求初始值)0()0(++c L i u 、和)0(+i 。
Lu 题5.2图12V解:s 闭合,0<t ,电路处于稳态。
12VLiA i V u L c 18412)0(,812848)0(=+==⨯+=--, s 闭合后,独立初始值。
V u u c c 8)0()0(==-+,A i i L L 1)0()0(==-+.L uA i i c c 1)0(,1284==+⨯+, A i i i c 2)0(,1)0()0(=+=+++, V u u L L 4)0(,1218)0(==⨯+-+。
5.3 如题5.3图所示电路,0<t 时已处于稳态。
当0=t 时开关S 闭合求)0(+L i 和=t L dtdi 。
解:0=t 时,A i L 1)0(=-,S 闭合,A i L 1)0(=+,等效为b 图。
0442)1(4=⇒=+++i i i i ,0)0(=∴+L u ,00=+=t L dtdi ,A i L 1)0(=∴+,00=+=t L dtdi 。
iΩ题5.3图5.5 如题5.5图所示电路,0<t 时已处于稳态。
当0=t 时开关S 打开,求初始值)0(+c u 和)0(1+L i 、)0(2+L i 。
10VΩCu +-题5.5图解:0<t 时,V U c 6)0(=-,A i L 2)0(1=+,A i L 0)0(2=+; S 打开,V U c 6)0(=+,A Vi L 144)0(1=Ω=+,A i L 1)0(2=+。
5-1.已知正弦函数()()40sin31445f t t=-+,求:(1)函数的最大值,有效值,角频率,频率,周期和初相。
(2)画出波形图。
解:()()()()()40sin3144540cos314459040cos3144540cos314135f t t tt t=-+=-+-=--=+函数最大值:40mF=;函数有效值:40F==314100ωπ==(rad/s);频率:()1005022Zf Hωπππ===;周期:()110.0250T sf===;初相角:135θ=。
5-2.已知正弦信号分别是:()8cos3146u t t Vπ⎛⎫=+⎪⎝⎭,()()sin31460i t t A=--,在同一坐标系中画出其波形,计算其相位差,指出其超前、滞后关系。
解:()()()()()sin31460cos3146090cos314150cos31430cos3146i t t A t At A t A t Aπ=--=---⎛⎫=--=+=+⎪⎝⎭相位差:66u iππϕθθ=-=-=。
两个信号同相位。
5-4.(1)将下列复数表为极坐标形式:(a)87j+;(b)3241j-;(c)0.41 3.2j-+;(d)12387.5j--.解:(a)8710.6341.19j+=∠;(b)324152.0152.03j-=∠-;2πtπf t135tπ30(c )0.41 3.2 3.22697.30j -+=∠;(d )12387.5150.95144.6j --=∠-(2)将下列复数表为直角坐标形式:(a )7.925.5∠;(b )11.954.5∠-;(c )22120∠;(d )80150∠-. 解: (a )7.925.57.13 3.40j ∠=+;(b )11.954.5 6.919.69j ∠-=- (c )221201119j ∠=-+;(d )8015069.340j ∠-=--5-5.计算:(1) 615440760?∠-∠+∠-=;(2) ()()()()103456473?j j j j ++-+=;(3) 417590 2.540 2.130?j j ⎛⎫⎡⎤-++∠∠+∠-= ⎪⎣⎦⎝⎭解:(1)()()()()()6154407606cos156sin154cos 404sin 407cos607sin 606cos154cos 407cos606sin154sin 407sin 606.237.08j j j j j j j ∠-∠+∠-=+-++-=-++--=-(2)()()()()()()()()() 10345647310.4416.706.40351.347.233.697.61623.2010.44 6.4037.216.7051.3433.6923.207.61663.2011.15j j j j ++-+=∠∠∠-∠⨯⨯=∠+--=∠(3)()()(){}()()()()417590 2.540 2.1301745 2.5cos 40 2.1cos 30 2.5sin 40 2.1sin 3016 3.7340.557016903.7758.4844.23898.48j j j j j j j j ⎛⎫⎡⎤-++∠∠+∠- ⎪⎣⎦⎝⎭⎡⎤⎡⎤=--++-++-⎣⎦⎣⎦=-+=∠-∠=∠-5-8.已知元件A 的端电压:()()100030 ()u t t V =+,求流过元件A 的电流()i t 。
第5章5.1选择题1、在关联参考方向下,R 、L 、C 三个元件的伏安关系可分别如( D )表示。
A. dtdi C u d i L u u Gu i C C tL L L R R =+==⎰ ,)(1)0( ,0ττ B. dtdi C u d i L u Ri u C C tL L R R =+==⎰ ,)(1 )0(u , 0L ττ C. ⎰+===tC C C L L R R d i C u u dt di L u Gi u 0)(1)0( , ,ττD. ⎰+===tC C C L L R R d i C u u dt di Lu Ri u 0)(1)0( , ,ττ 2、一阶电路的零输入响应是指( D )。
A. 电容电压V 0)0(≠-C u 或电感电压V 0)0(≠-L u , 且电路有外加激励作用B. 电容电流A 0)0(≠-C i 或电感电压V 0)0(≠-L u , 且电路无外加激励作用C. 电容电流A 0)0(≠-C i 或电感电压A 0)0(≠-L i , 且电路有外加激励作用D. 电容电压V 0)0(≠-C u 或电感电流A 0)0(≠-L i , 且电路无外加激励作用 3、若1C 、2C 两电容并联,则其等效电容C =( A )。
A. 21C C +B.2121C C C C +C.2121C C C C +D. 21C C4、已知电路如图x5.1 所示,电路原已稳定,开关闭合后电容电压的初始值)0(+C u 等 于( A )。
A. V 2-B. V 2C. V 6D. V 8图x5.1 选择题4图5、已知V 15)(τtC e t u -=,当s 2=t 时V 6=C u ,电路的时间常数τ等于( B )。
A. s 458.0B. s 18.2C. s 2.0D. s 1.06、二阶RLC 串联电路,当C L R 2____时,电路为欠阻尼情况;当CLR 2____时, 电路为临界阻尼情况( B )。
A. >、=B. <、=C. <、>D. >、<Cu5.2 填空题1. 若L 1 、L 2两电感串联,则其等效电感L=;把这两个电感并联,则等效电感L= 。
2. 一般情况下,电感的 电流 不能跃变,电容的 电压 不能跃变。
3. 在一阶RC 电路中,若C 不变,R 越大,则换路后过渡过程越 长 。
4. 二阶RLC 串联电路,当R < 2C L /时,电路为振荡放电;当R= 0 时,电路发生等幅振荡。
5. 如图x5.2示电路中,开关闭合前电路处于稳态,()+0u = -4 V ,+0d d t u C = 2×104 V/s 。
图x5.2 填空题5图6. R =1Ω和C =1F 的并联电路与电流源I S 接通。
若已知当I S =2A ()t ≥0,电容初始电压为1V 时,u t C ()为 t - ()t ≥0,则当激励I S 增大一倍(即I S A =4),而初始电压保持原值,t ≥0时u t C ()应为V )e 34(t --。
5.3 计算题1. 电路如图x5.3所示,(1)求图(a )中ab 端的等效电容;(2)求图(b )中ab 端的等效电感。
(a)(b)图x5.3 计算题1图解:(1)ab 两端的等效电容21L L +2121L L L L +10μF10μF10μF10μFab10μF aba b 6H6H6H6HFC ab μ610)101011011()101011011(10=+++++⨯=(2)ab 两端的等效电感2. 电路图x5.4(a )所示,电压源S u 波形如图x5.4(b )所示。
(1)求电容电流,并画出波形图;(2)求电容的储能,并画出电容储能随时间变化的曲线。
解:由图可知⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤-⨯<≤-<≤+⨯-<≤<≤⨯=s t t s t s t t s t s t t t u C μμμμμ87 4010575 553 2010531 510 105)(666⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤<≤<≤-<≤<≤==s t A s t st A s t s t A dt t du c t i c C μμμμμ87 1075 053 1031 010 10)()(HL ab1066)66(6)66(=+++⨯+=S u )(t i C -+F 2μ12345678910055V /S u ust /所以电流波形图为电容储能储能变化曲线为3.如图x5.5(a )所示电路,A 00=)(L i ,电压源S u 的波形如图x5.5(b )所示。
求当t =1s 、t =2s 、t =3s 、t =4s 时的电感电流i L 。
Su i -+(a ) (b )图x5.5 计算题3图解:电感电压与电流的关系为⎰+=tt d u L t i t 0)(1)()(i 0ζζ各时段,电感电压的表达式为μsμsW C 5.2⨯⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤⨯-<≤⨯<≤⨯-⨯<≤⨯<≤⨯==--s t s t st st s t s t s t t t C W u C C μμμμμμμ87 10 )8(2575 105.253 10)4(2531 105.210 1025)(21)t (625625622⎪⎩⎪⎨⎧>≥->≥≥≥=st s t s t s t s V V t u 34,401023,002,10)( 所以,t=1s 时,有 ⎰=-⨯==+=1015.2)]01(5.2[41010410)1(|V V t dt it=2s 时,有⎰=-⨯+=+=+=2115)]12(5.25.2[4105.210415.2)2(|V V t dt i t=3s 时,有⎰=+=3250415)3(V dt it=4s 时,有V t t dt t i 75.344024105)4010(415)4(||4343432=-⨯+=-+=⎰4. 如图x5.6所示S 闭合瞬间(t=0),求初始值u C (0+),、i C (0+)。
解:t=0-时,s 断开,等效电路如图x5.6(a)。
V V V u i c c 1002080)0( ,0)0(=+==--图x5.6 计算题4图t=0+时,s 闭合,等效电路如图x5.6(b)。
V u c 100)0()0(u c ==-+A u i c c 210)0(80)0(-=-=++80V SC+20V -+-Ω2Cu Ω105. 如图x5.7所示电路的暂态过程中, 求i L 的初始值,稳态值以及电路的时间常 数τ各等于多少?如R 1增大,电路的时间 常数τ如何变化?解: 当t=0-时,s 断开, 等效电路如图如图x5.7(a) 电路中的电流恒定不变 A i L 5.22210)0(=+=-由换路定理:当t=0+时,s 闭合,等效电路如图如图x5.7(b), 电路稳定后 , 在电路放电过程中时间常数,与R 1无关所以R 1增大,τ不变。
6. 如图x5.8已知:E=6V ,R 1=5Ω,R 2=4Ω, R 3=1Ω,开关S 闭合前电路处于稳态,t=0时 闭合开关S 。
求:换路瞬间的u L (0+)、i C (0+)。
解:当t=0-时,s 断开,电路处于稳态 等效电路如图x5.8(a)。
V i c 0)0(=-V R R R E u A R R E i L 1)0( ,1)0(313c 31=+⋅==+=--由换路定理:V u u A i i C C L L 1)0()0( ,1)0()0(====-+-+当t=0+时,s 闭合等效电路如图x5.8(a)。
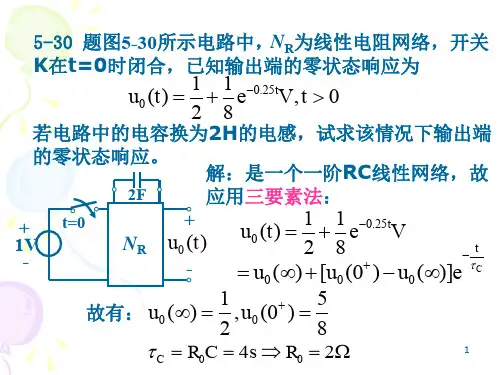
Ai i L L 5.2)0()0(==-+5.02==R LτA i L 0)(=+∞A R u E i c c 25.1)0()0(2=-=++7. 如图x5.9所示电路,t=0时开关K 闭合, 求t ≥0时的u C (t)、i C (t)和i 3(t)。
已知: I S =5A ,R 1=10Ω,R 2=10Ω,R 3=5Ω,C=250μF , 开关闭合前电路已处于稳态。
解:当t=0-时,k 断开,电路处于稳态,等效电路 如图x5.9(a)。
由换路定理:当t=0+时,k 闭合,t=+∞时,电路 达到新的稳态,等效电路如图x5.9(b)。
电容两端的等效电阻:时间常数:VR i E u L L 5)0()0(3=-=++AI i s 5)0(3==-VR i u c 25)0()0(33==--0)0(=-c i Vu u C C 25)0()0(==-+A I R R R R i S 2)(32113=++=+∞Vi R 10)()(u 33C =+∞=+∞Ω=+=4//)(321R R R R eq SC R eq 310-==τ[]Ve e e u u u t u t t tC C C C 100010001510)1025(10)()0()()(---++=-+=+∞-++∞=τ8. 如图x5.10所示电路中,t=0时试用三要素 法求出t ≥0时的i L (t)和u L (t),并画出i L (t) 的波形。
(注:在开关动作前,电路已达稳态)。
解:当t=0-时,开关S1闭合,S2打开,电路 处于稳态,等效电路如图x5.10(a)。
得 A i L 10110)0(==- 由换路定理:当t=0+时,s1断开,s2闭合,达到新的稳态,等效电路如图5.10(b )。
根据图5.10(c )求等效电阻:)(t i L 的波形为A i i L L 10)0()0(==-+Ω=+⨯=12222eq R A i L 326)(==∞s R L eq 5.0==τtLe dt di L t u 27)(--=⋅=A e e i i i t i t t L L L L )73()]()0([)()(2--+=∞-++∞=τi L /A t/s10309. 如图题x5.11所示电路在t <0已处于稳 态,在t = 0时将开关S 由1切换至2,求: (1)换路后的电容电压)(t u C ; (2)t =20ms 时的电容元件的储能。
解:当t=0-时,开关S 在位置1,电路 处于稳态,等效电路如图x5.11(a)。
t=∞时等效电路如图x5.11(b)。
V 0)(=∞c ut=20ms 时:10.电路如图x5.12所示,电路原处 于稳态。
在t = 0时将开关S 由位置1合 向位置2,试求t ﹥0时i L (t )和i (t ), 并画出它们随时间变化的曲线。
54V )0()0(V5490150010001500)0(===⨯+=-+-c c c u u u 则0t V 54)0((t)s025.010505005001500//750025.06≥===⨯⨯==Ω==--+-ttc eq eq e e u u C R R ττW 0147.026.24105021)(21Wc(t)V26.245454(0.02)2628.0025.002.0=⨯⨯⨯======---t cu e eu cc解:t=0-时,电感相当于短路,等效电路如图x5.12(a):t →∞时,电感所在支路短路。