总体均数的假设检验

格式：ppt
大小：1.46 MB
文档页数：81

下载文档原格式

总体均数的假设检验

总体均数的假设检验
$number {01}
目录
• 引言 • 假设检验的基本原理 • 总体均数的假设检验方法 • 实例分析 • 总结与展望
01 引言
目的和背景
确定样本数据是否与假设的总体均数存在显著差异，从而对总体均数进行假设检验。
在科学实验、统计学、医学研究等领域广泛应用，用于评估样本数据是否支持或拒绝关于总体均数的假设。
配对样本均数假设检验实例
总结词
配对样本均数假设检验用于比较同一组研究对象在不同条件下的均数是否存在统计学显著性差异。
详细描述
例如，为了比较同一组患者在接受两种不同治疗措施前后的改善程度，研究者收集了患者的基线数据和接受不同治疗措施后的数据，并计算出各自治疗组的平均改善程度。然后，研究者使用配对样本均数假设检验来比较同一组患者在不同治疗措施下的平均改善
概念简介
假设检验是一种统计推断方法，通过检验样本数据是否符合某个假设，从而对总体参数进行推断。
它基于概率论原理，通过计算样本数据与假设的总体参数之间的差异，评估这种差异是否具有统计学上的显著性。
02
假设检验的基本原理
假设检验的步骤
建立假设
根据研究目的，提出一个关于总体参数的假设，通常包括零假设和备择假设。
收集样本数据
从总体中随机抽取一定数量的样本，并记录样本数据。
确定检验水准
选择合适的检验水准，如α和β，以平衡第一类和第二类错误的概率。
计算统计量
根据样本数据计算适当的统计量，如t值、Z值或χ^2值。
假设检验的类型
1 2
3
单样本均数检验
比较一个样本均数与已知总体均数或正常值范围。
两样本均数比较

统计学教案习题04总体均数的估计和假设检验

第四章总体均数的估计和假设检验一、教学大纲要求（一）掌握内容1．抽样误差、可信区间的概念及计算； 2．总体均数估计的方法；3．两组资料均数比较的方法，理解并记忆应用这些方法的前提条件； 4．假设检验的基本原理、有关概念（如I 、II 类错误）及注意事项。

（二）熟悉内容两样本方差齐性检验。

（三）了解内容1． t 分布的图形与特征；2．总体方差不等时的两样本均数的比较； 3．等效检验。

二、教学内容精要（一）基本概念 1．抽样误差抽样研究中，样本统计量与总体参数间的差别称为抽样误差（sampling error ）。

统计上用标准误（standard error ，SE ）来衡量抽样误差的大小。

不同的统计量，标准误的表示方法不同，如均数的标准误用X S 表示，率的标准误用S P 表示，回归系数的标准误用S b 表示等等。

均数的标准误与标准差的区别见表4-1。

表4-1 均数的标准误与标准差的区别均数的标准误标准差意义反映的抽样误差大小反映一组数据的离散情况记法X σ（样本估计值X S ）σ（样本估计值S ）计算X σ=nσ X S =nSσ =nX 2)(∑-μS=1)(2--∑n X X控制方法增大样本含量可减小标准误。

个体差异或自然变异，不能通过统计方法来控制。

2．可信区间（1）定义、涵义：即按预先给定的概率确定的包含未知总体参数的可能范围。

该范围称为总体参数的可信区间（confidence interval ，CI ）。

它的确切含义是：CI 是随机的，总体参数是固定的，所以，CI 包含总体参数的可能性是1-α。

不能理解为CI 是固定随机的，总体参数是随机固定的，总体参数落在CI 范围内可能性为1-α。

当0.05α=时，称为95%可信区间，记作95%CI 。

当0.01α=时，称为99%可信区间，记作99%CI 。

（2）可信区间估计的优劣：一定要同时从可信度（即1-α的大小）与区间的宽度两方面来衡量。

总体均数估计与假设检验

无论做出哪一种推断结论，都面临着发生判断错误的风险。这就是假设检验的两类错误。
t 检验
t-test
三、t检验和Z检验（参数检验）
以t分布为基础的检验称为t检验。 t分布的发现使得小样本统计推断成为可能。因而，它被认为是统计学发展历史中的里程碑之一。
在医学统计学中，t检验是重要的假设检验方法之一。常用于两个均数之间差别的比较，并根据资料的分布情况及设计类型，选择不同的t检验方法。
配对样本t检验
Paired design t-test
关系：随着样本含量增加，都减小。
联系：都是表示变异度的指标，当样本量一定时，两者成正比。
标准误用途
衡量样本均数的可靠性：标准误越小，表明样本均数越可靠；
参数估计：估计总体均数的置信区间（区域）；
假设检验：用于总体均数的假设检验（比较）。
二、t分布：
标准正态分布
开创了小样本统计的新纪元，t分布主要用于总体均数的区间估计和t检验！
假设检验（Hypothesis test）
假设检验的推断原理假设检验的基本步骤 t检验和Z检验两样本总体方差齐性检验正态性检验假设检验的两类错误注意事项
一、假设检验的推断原理
上面介绍过的区间估计方法是统计推断的内容之一，假设检验是统计推断的另一重要内容。正是应用统计推断的理论和方法，人们才能顺利地通过有限的样本信息去把握总体特征，实现抽样研究的目的。
s / n 25.74 36
在H0成立的前提下，当前t值出现的概率有多大？？？
如何给出这个量的界限？
小概率事件在一次试验中基本上不会发生！
从附表2中查出在显著性水平 =0.05（双侧），自由度为35所对应的t界值=2.318，即为拒绝域与接受域的界限。如果计算

总体均数的估计和假设检验

无统计学意义，按 0.05检验水
准，不拒绝H0，尚不能认为两种
方法的检查结果不同。
成组设计的两样本均数的检验
01
完全随机设计（又称成组设计）：将受试对象完全随机地分配到各个处理组中或分别从不同总体中随机抽样进行研究。
02
01
若n1 ，n2 较小，且σ12=σ22
02
两独立样本的t检验(例3.7）；
01
方差分析法。
02
单侧检验和双侧检验（根据研究目的和专业知识选择）
假设检验（1）双侧检验：如要比较A、B两个药物的疗效，无效假设为两药疗效相同(H0：μA=μB)，备择假设是两药疗效不同(H1：μA≠μB)，可能是A药优于B药，也可能B药优于A药，这就是双侧检验。
01
02
单侧检验：若实际情况是A药的疗效不劣差于B药，则备择假设为A药优于B药(H1：μA>μB)，此时，备择假设成立时只有一种可能（另一种可能已事先被排除了），这就是单侧检验。
01
备注：单侧检验和双侧检验中计算统计量t的过程是一样的，但确定概率时的临界值是不同的。
01
统计推断应包括统计结论和专业结论两部分。统计结论只说明有统计学意义(statistical significance) 或无统计学意义，而不能说明专业上的差异大小。只有将统计结论和专业知识有机地相结合，才能得出恰如其分的专业结论。
A，B处理。
2
0.05
H0：μd =0 H1：μd ≠0
其中
式中d为每对数据的差值，为差值的样本均数， Sd为差值的标准差，为差值样本均数的标准误， n为对子数。
开机：进入统计状态：清除内存：
SHIFT
b. 近似t检验，即t＇检验（n1，n2 较小，且σ12≠σ22）

第三章总体均数的估计与假设检验

2
Sd
d
d Sd / n
2

(
d)
n
n 1
S d 0.1087 t 2.7424 0.1087/ 10 7.925
v 10 1 9
3）确定P值，作出推断结论 T0.05,9=2.262, 7.925>2.262,故P<0.05.可以认为两种方法对脂肪含量的测定结果不同。
167.41, 2.74
165.56, 6.57
168.20, 5.36 n j=10
…. 165.69, 5.09
将上述100个样本均数看成新变量值，则这个 100个样本均数构成一新分布，绘制直方图
样本均数的抽样分布具有如下特点：
1) 各样本均数未必等于总体均数
2) 各样本均数间存在差异
3) 样本均数的分布很有规律，围绕着总体均数，中间多，两边少，左右基本对称，也服从正态分布
假设检验的基本步骤：
1、建立检验假设
Ｈ0: 检验假设, 无效假设，零假设 μ=μ0
H1: 备择假设,对立假设
μ≠μ0
2、确定检验水准 α=0.05 单双侧
3、选定检验方法和计算检验统计量
4、确定P值和作出推论结论。
P值是指从H0所规定的总体进行随机抽样，获得大于（或等于及小于）现有样本获得的检验统计量值的概率。
（1012/L)
血红蛋白（g/L)
女
男女
255
360 255
4.18
134.5 117.6
0.29
7.1 10.2
4.33
140.2 124.7
*标准值：使用内科学（1976年）所载均数（转位法定单位）
1）说明女性的红细胞数与血红蛋白的变异程度何者为大？ 2）抽样误差是？ 3）试估计该地健康成年女性红细胞数的均数？ 4) 该地健康成年男女血红蛋白含量是否不同？ 5）该地男性两项血压指标是否均低于上表的标准值（若测定方法相同）？

个和两个总体平均数的假设检验

由该总体抽取量了为一 n1的个样含本，样本平均X1数，为样本方S1差 2；为
设第二个总体为的 2，平方均差数 22为，
由该总体抽取量了为 n一 2的个样含本，样本平均X2数，为样本方S2差 2；为
1，X 1
2，X 2
1 2?
X1 X2 ?
5. 2 两个总体平均数的比较
1.配对实验设计：
指先将实验单位按配对的要求两两配对，然后将每一个对子内的两个实验单位独立随机地分配到两个处理组中。
配对的要求是，配成对子的两个实验单位的初始条件应尽量一致，不同实验对子之间，实验单位的初始条件可以有差异。
每一个对子就是实验的一次重复。
我们将实验单位分为两组的方式称为配对实验设计。
3. 配对实验的检验步骤：
（1）无效假设H0 ：μd=μ1-μ2 =0 备择假设HA ：μd≠0，即μ1-μ2 ≠0
配对实验时，两组的实验单位数即两个样本的观察值数目相等，n1=n2。但是反过来，两个样本观察值相等的实验则不一定是配对实验。
判断配对实验的根据不是两个样本的观察值是否相等，而是分组的方式。
在配对实验设计中，由于实验单位是两两配对的，因此观察值也是两两配对的。
2.实验结果表示为：
处理
1 2
F
S12 S22
查F表，确定临界值，接受或者拒绝H0
如果检验结果不显著，接受零假设σ12=σ22，那么还按照前一种t检验进行检验。
如果检验结果显著，接受备择假设σ12 ≠ σ22，
那么按照下面的t检验方法进行检验。
tX1X2 X1X2 X1X2
s x1x2
s2 s2
x1
x2
s12/n1s22/n2

医学统计学总体均数的估计与假设检验

均数的抽样误差：抽样引起的样本均数与总体均数之间或样本均数之间的差别。标准误：即样本均数的标准差。表示样本均数对总体均数的离散程度。
一、均数的抽样误差与标准误（）
例4.1某市随机抽查12岁男孩100人，得身高均数139.6cm，标准差6.85cm，资料，求标准误？
第三章总体均数的估计与假设检验
添加副标题
汇报人姓名
均数的抽样误差与标准误
t分布
总体均数的估计
假设检验的一般步骤
ｔ检验
u 检验
两均数的等效检验
正态性检验
两样本方差齐性检验
假设检验时应注意的问题
利用总体均数的可信区间进行假设检验
课堂讨论
第三章总体均数的估计与假设检验
一、均数的抽样误差与标准误（）
等效检验的假设
七、两均数的等效检验
H0: | 1- 2| H1: | 1- 2|< 为等效界值，若两总体均数差值在范围内为等效，超过则为不等效。是推断两种处理效果是否相近或相等的统计方法。为什么推断两种处理效果是否相近或相等不能用前面所述的假设检验方法？
检验水准、自由度及结果判断同t检验。
＝ｎ－ 1＝25 －１＝24 查t界值表（P804），得单侧 t0.05，24 = 1.711 因: t =1.833> t0.05，24 所以：P < 0.05
结论：按照 = 0.05水准，拒绝H0 ，故可认为该山区健康成年男子脉搏高于一般人群。
1
上例如用双侧检验，查表得双侧 t0.05，24 = 2.064
样本含量一定时，增大，则减少，减少则增大，所以，的确定并不是越小越好，一般取0.05较合理。
结论时，尽可能明确相结合。
02

请简述均数假设检验的基本步骤

均数假设检验是统计学中常用的一种假设检验方法，用于检验两个总体均数是否相等。

其基本步骤如下：1. 确定假设：在进行均数假设检验之前，首先需要明确所要检验的假设。

一般来说，假设可以分为零假设（H0）和备择假设（H1）。

其中，零假设是我们要进行检验的假设，备择假设则是与零假设相对立的假设。

在均数假设检验中，零假设通常是两个总体均数相等，备择假设则是两个总体均数不相等。

2. 收集样本数据：接下来，需要收集来自两个总体的样本数据。

样本数据的选择应该是随机的，并且具有代表性，以确保检验结果的准确性和可靠性。

3. 计算样本均数和标准差：在得到样本数据之后，需要计算两个样本的均数和标准差。

均数用来衡量样本的中心位置，标准差则用来衡量样本数据的离散程度。

4. 计算检验统计量：通过样本数据的均数和标准差，可以计算出用于检验的统计量。

在均数假设检验中，常用的检验统计量包括t值和z值，具体的计算公式取决于所选择的检验方法和样本大小。

5. 确定显著性水平和自由度：在进行假设检验时，需要确定显著性水平（α）和自由度（df）。

显著性水平通常取0.05或0.01，用来衡量拒绝零假设的标准；自由度则取决于所选择的检验方法和样本大小。

6. 判断拒绝或接受零假设：通过计算得到的检验统计量，根据显著性水平和自由度进行判断，判断是否拒绝零假设。

当检验统计量落在拒绝域内时，拒绝零假设，否则接受零假设。

通过以上步骤，可以对均数假设进行严谨的检验，从而判断两个总体均数是否相等。

在实际应用中，均数假设检验被广泛应用于各个领域的数据分析和决策问题中，具有重要的理论和实践价值。

7.选择适当的检验方法：在进行均数假设检验时，需要根据样本数据的特点和总体参数的已知情况选择适当的检验方法。

如果总体标准差已知且样本容量较大，可以使用z检验；如果总体标准差未知或者样本容量较小，通常使用t 检验。

还有方差分析、秩和检验等其他检验方法可供选择，根据具体情况进行判断。

医学统计学总体均数的估计和假设检验

3.106
3.055
3.012 2.977 2.947 2.921 2.898 2.878 2.861 2.845 2.750 2.704 2.678 2.626
2.58
3.497
3.428
3.372 3.326 3.286 3.252 3.222 3.197 3.174 3.153 3.030 2.971 2.937 2.871 2.8070
t x
sX
统计量是t的分布就是t分布。
t分布的特征： ① 以0为中心，左右对称呈单峰分布； ② t分布是一簇曲线，分布参数为自由度υ。 ③ t分布的形状与样本例数n有关，高峰比正态分
布略低，两侧尾部翘得比正态分布略高。越大，曲线越近正态分布，当ν=∞时，t分布即为z分布。由于t分布是一簇曲线，为了便于应用，统计学家编制了表4-4-1 t界值表。
3）与例数的关系不同：当样本含量足够大时，标准差趋向稳定。而标准误随例数的增大而减小，甚至趋向于0。若样本含量趋向于总例数，则标准误接近于0。
联系；二者均为变异指标，如果把总体中各样本均数看成一个变量，则标准误可称为样本均数的标准差。当样本含量不变时，均数的标准误与标准差成正比。两者均可与均数结合运用，但描述的内容各不相同。
活量的95%的可信区间。
本例n=5， =4，t0.05，4=2.776
x t0.05sx =2.44±2.776×0.33/ 5 =2.03~2.85（L）
该地17岁女中学生肺活量均数的95%可信区间为2.03L~2.85L。
例4-4-3 由例4-2-1 101名30~49岁健康男子血清总胆固醇 X 4.735mmol·L-1，S=0.88 mmol·L-1，求该地健康男子血清总胆固醇值均数的95%可信区间。

第三章总体均数的估计和假设检验

本例自由度n-125-124，查附表2，得单侧t0.05（24）=1.711。
今tt0.05（24），故P0.05，无统
计学意义，按0.05水准，不
拒绝H0，根据现有样本信息，尚不能认为该山区成年男子平均每分钟脉搏数高于一般成年男子。
第一节均数的抽样误差和总体均数的估计
统计推断(statistical inference):
推断
样本
总体
(1)参数估计（2）假设检验
一、均数的抽样误差：在统计学上
把由抽样造成的样本均数与总体均数间的差异或各个样本均数间的差异统称为均数的抽样误差。
性质： (1)原分布正态
原分布偏态
新分布正态
例3.4 次/min
对一个样本均数与一个已知的或假设的总体均数0作比较，它们之间差别可能有两种原因造成：
–由于抽样误差所致，
–由环境的原因，两个总体均数间有本质差异。
一、建立检验假设和确定检验水准
（一）假设假设有两个：
–无效假设(null hypothesis)，符号为H0，又称检验假设。记为H0：μ=μ0 或μ-μ0=0
理进行区间估计）。
对上式进行变换，可得置信度为1-α
的总体均数可信区间的通式为：
习惯将上式写成：
若取1－α=0.95，则为总体均数95%可信区间，或取1－α=0.99.则为总体均数99%可信区间。
（二）σ已知（按正态分布原理）
（三）σ未知但n足够大(n>50) （按正态分布原理）
常用u值表参考范围(%)
新分布近似正态
(2)原分布 x～N(μ,σ2)
新分布～N（μ, ）
原分布 x～N(155.4,5.32)

03总体均数的估计及假设检验

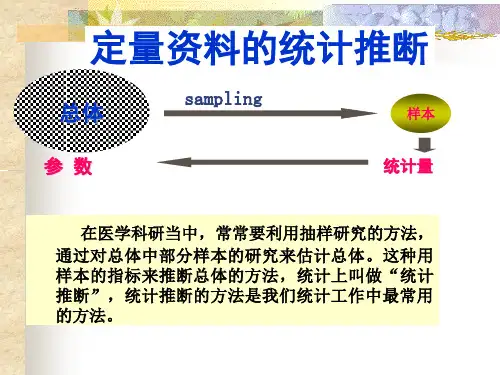
●统计推断（statistical inference）：通过样本指标来说明总体特征，这种从样本获取有关总体信息的过程称为统计推断。

●抽样误差（sampling error）：由个体变异产生的，随机抽样造成的样本统计量与总体参数的差异，称为抽样误差。

●标准误（standard error of mean，SEM ）及X s ：通常将样本统计量的标准差称为标准误。

许多样本均数的标准差X s称为均数的标准误，它反映了样本均数间的离散程度，也反映了样本均数与总体均数的差异，说明均数抽样误差的大小。

可通过增加样本含量，设计减少标准差来降低标准误。

●可信区间（confidence interval，CI）：按预先给定的概率确定的包含未知总体参数的可能范围。

该范围称为总体参数的可信区间。

它的确切含义是：可信区间包含总体参数的可能性是1- a ，而不是总体参数落在该范围的可能性为1-a 。

●参数估计：指用样本指标值（统计量）估计总体指标值（参数）。

参数估计有两种方法：点估计和区间估计。

●假设检验中P 的含义：指从H0 规定的总体随机抽得等于及大于（或等于及小于）现有样本获得的检验统计量值的概率。

●I 型和II 型错误：I 型错误（type I error ），指拒绝了实际上成立的H0，这类“弃真”的错误称为I 型错误，其概率大小用a 表示；II 型错误（type II error），指接受了实际上不成立的H0，这类“存伪”的误称为II 型错误，其概率大小用b 表示。

●检验效能：1- b 称为检验效能（power of test），它是指当两总体确有差别，按规定的检验水准a 所能发现该差异的能力。

●检验水准：是预先规定的，当假设检验结果拒绝H0，接受H1，下“有差别”的结论时犯错误的概率称为检验水准（level ofa test），记为a 。

●抽样误差：由个体变异和抽样造成的样本统计量与总体参数的差异为★标准差与标准误的区别标准差与标准误的意义、作用和使用范围均不同。

总体均数估计和假设检验

THANKS
感谢观看
检验的步骤与逻辑
步骤
提出假设、选择合适的统计量、计算P值、根据P值做出决策。
逻辑
基于样本信息推断总体特征，利用统计量进行假设检验，并根据P值判断假设是否成立。
03
常见假设检验方法
t检验
t检验是一种常用的参数检验方法，用于比较两组数据的均值是否存在显著差异。
t检验基于假设和样本数据计算t统计量，并根据临界值判断假设是否成立。通常用于小样本数据或已知总体分布的情况。
当实际无差异时，由于误差率较高或检验效能不足，错误地判断出差异，导致得出阳性结论。
多重比较与校正
多重比较问题
在多个样本或组别的比较中，如果没有采取适当的校正措施，会导致假阳性结论增多。
校正方法
为控制多重比较导致的假阳性风险，可以采用Bonferroni校正、Holm-Bonferroni校正等校正方法，对显著性水平进行调整。
卡方检验
卡方检验是一种非参数检验方法，用于比较实际观测频数与期望频数之间的差异。
卡方检验基于卡方统计量，通过比较实际观测频数与期望频数，评估分类变量之间是否存在显著关联。
04
假设检验中的问题与注意事项
样本选择与偏差
样本选择偏差
在选择样本时，如果未能遵循随机抽样的原则，或者存在选择偏见，会导致样本不能代表总体，从而影响估计的准确性。
Z检验
Z检验是用来检验比例或比率是否显著不同于预期值。
Z检验基于正态分布理论，通过计算Z 统计量来评估样本比例或比率与预期值之间的差异程度。
方差分析
方差分析（ANOVA）用于比较两个或多个组间的均值是否存在显著差异。
方差分析通过比较组间和组内方差，评估各组均值是否存在显著差异，适用于多组数据的比较。

均数假设检验的基本步骤

均数假设检验的基本步骤
均数假设检验是数据分析中一种常用的统计检验方法，它可以用来检验某一总体数据的均值是否与预先根据实际情况所建立的一个均值假设进行比较。

均数假设检验的基本步骤如下：
1. 确定总体参数：首先，确定检验的总体参数，其中可包括总体的均数μ、总体的方差σ、总体的规模n等多种参数；
2. 建立假设：其次，将以上总体参数转化为假设，如均数假设，即μ0=μ，μ0为假设的均数，μ为实际的总体均数；
3. 检验统计量：然后，根据检验的假设类型，选取相应的检验统计量，通常采用Z统计量
来检验均数假设；
4. 计算临界值：接着，根据所采用的检验统计量，根据拒绝域理论计算出相应的临界值；
5. 检验：最后，结合样本数据，运用检验统计量及临界值，做出检验结论，即根据检验统计量的值与临界值的比较，得出是拒绝原假设还是不拒绝原假设。

以上是均数假设检验的基本步骤，必要时还需要根据假设的类型，重复上述步骤，进行进
一步的检验；也可以根据样本数据特点，采用其它更契合的统计检验方法，以得出精准有
效的检验结论。

统计学--第三章总体均数的估计与假设检验

第三章
总体均数的估计与假设检验
课件
1
统计推断的目的：
用样本的信息去推论总体。
医学研究中大多数是无限总体，即使是有限总体，但也经常受各种条件的限制，不可能直接获得总体的信息。
课件本科生卫生学（5)
2
第一节均数的抽样误差与标准误
• 抽样误差（sampling
error）:因各样本包含的个体不同，所得的各个样本统计量（如均数）往往不相等，这种由于个体差异和抽样造成的样本统计量与总体参数的差异，称为抽样误差。
均数的95%可信区间为3.47~ 3.81（mmol / L） 95%参考值范围为1.29~ 5.99（mmol / L）
S 1.20 X u / 2 S X X 1.96 3.64 1.96 n 200 (3.47, 3.81)
X 1.96S 3.64 1.961.20 (1.29, 5.99) 32 课件本科生卫生学（5)
t分布的应用：总体均数的区间估计 t检验
课件本科生卫生学（5) 18
第三节总体均数的置信区间估计 confidence interval
可信区间的概念总体均数可信区间的计算均数可信区间与参考值范围的区别
课件本科生卫生学（5)
19
一、可信区间的概念
统计推断：参数估计与假设检验。参数估计: parametric estimation，用样本统计量估计总体参数的方法。点（值）估计:point estimation，直接用样本统计量作为总体参数的估计值。方法简单但未考虑抽样误差大小。区间估计:interval estimation，按预先给定的概率95%，或(1-)，确定的包含未知总体参数的可能范围。考虑了抽样误差。

医学统计学--第三章总体均数的估计与假设检验

的 95%可信区间。
32
本例 n=10，按公式(3-2)算得样本均数的标准误为
S1=101=9,双尾 =0.05，
查附表 2 的 t 界值表得 t0.05 2,9 2.262 。按公式(3-5) (166.95 2.262 1.1511) 即(164.35, 169.55)cm 故该地 18 岁男生身高均数的 95%可信区间为(164.35, 169.55)cm。
X
2 X
、
) ,则通
过同样方式的 u 变换( X
2
)也可将其转换为
标准正态分布 N (0 , 1 )，即 u 分布。
17
3．实际工作中，由于 X 未知，用S X 代替，
则(X
) / SX
不再服从标准正态分布，而
服从t 分布。
t X SX X S n , n 1
2
第一节均数的抽样误差与标准误
3
统计推断：由样本信息推断总体特征。
样本统计指标（统计量）
总体统计指标（参数）
2
正态（分布）总体：N 说明！
~ ( , )
推断！
为说明抽样误差规律，先用一个实例，后引出理论。
4
例 3-1 若某市 1999 年 18 岁男生身高服从均数μ =167.7cm、标准差 =5.3cm 的正态分布。对该总体进行随机抽样，每次抽 10 人， n =10）（，共抽得 100 个样本（ g =100），计算得每个样本均数 X 及标准差 S 如图 3-1 和表 3-1 所示。

1 2 3 4 5 6 7 8 9 10 21 22 23 24 25
单侧双侧

研究生统计学讲义第3讲总体均数估计和假设检验

19
所谓小概率原理，就是“在一次试验中，概率很小 (接近于零)的事件认为是实际上不可能发生的事件” 。例如，假设在1000支复方大青叶注射液针剂中只有一支是失效的，现在从中随机抽取一支，则取得“失效的那支”概率为1/1000，这个概率是很小的，因此，可以认为在一次抽取中是不会发生的，若从中任取一支恰好为“失效的那支”，我们就有理由怀疑“失效概率为1/1000”的假设不成立，而认为失效率不是 1/1000，从而否定假设。否定假设的依据就是小概率原例理4.3。已知正常成年男子脉博平均为72次/分，现随机检查20名慢性胃炎所致脾虚男病人，其脉博均数为75次/分，标准差为6.4次/分，能否认为此类脾虚男病人的脉博快于健康成年男子的脉博？
13
4.单个总体均数的估计样本均数是总体均数μ的一个点估计。σ已知时，按（式4-3）计算的统计量服从标准正态分布，根据标准正态分布的规律
P（-uα/2< u <uα/2） =1-α ，有
σ已知时，正态总体均数μ的双侧（1－α）可信区间计算公式为（4-7）
而σ往往未知
σ未知时，按（式4-4）计算的统计量服从 t 分布，由t 分布的规律 P（-tα/2<t<tα/2） =1-α
14
有了抽样分布，对任何样本，在预先不知道总体特性
的任何知识时，利用抽样分布可以产生总体均数的置
信区间．
C
t
0
X
s/ n
t0
1
t0=tα/2
解这个不等式，把关心的参数μ从中间分离出来，就
得到置信度为1－α的总体均数的置信区间为：
X t0 s X t0 s （4-8）
n
n
S
注意－t 0和t 0由自由度n－1和置信水平确定，X 和 n

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

n 1 n 2 2 1 2 1 2 2 2 2
(3) 确定P值,作出统计推断
查附表3 , t界值表,
0.002<P<0.005，按=0.05水准拒绝H0，接受H1，差异有统计学意
义，可认为…..
方差齐性检验
F
S12(较大) S22(较小)
1 n1 1 2 n2 1
总体方差不等时处理方式
H0
160 样本均值
P (t≥4.841)
0 t＝4.841 t分布
若只考虑单侧，P值就是统计量t≥4.841的概率
QUESTION
如果考虑双侧，即回答例7.3的问题， P是什么？
结论
➢若P≤，表示在H0成立的条件下，出现等
于及大于(或等于及小于)现有统计量的概率是小概率，按小概率事件原理现有样本
P93例8.3
某医生研究血清白介素-6(IL-6)与银屑病的关系，收集了12例处于进行期的银屑病患者及12例正常人的血清标本进行IL-6检测，得到表8.2结果，问银屑病患者与正常人的血清IL-6均数是否不同？
未知总体 1 ？
(银屑病患者)
未知总体 2 (正常人)
样本1
X1 182.4
样本2
I 型错误与II 型错误(p85)
拒绝了实际上成立的H0，这类“弃真” 的错误为I 型错误(type I error)；
不拒绝实际上不成立的H0，这类“存伪” 的错误为II 型错误(type II error)。
0.08
0.06 0.04
=0
0.02 0 40
,
60
X80
100
120
0.07 0.06 0.05 0.04 0.03 0.02 0.01
0 20
>0
40
60
X 8 0
100
120
140
160
检验效能
II 型错误概率大小用表示，但值的大小很难确切估计，只有在已知样本含量n、两总体参数差值以及所规定的检验水准的条件下,才能估算出大小。
检验效能
1-称为检验效能或把握度(power of a
test) 统计学意义是：若两总体确有差别，
按水准能检出其差别的能力。
客观实际拒绝H0
H0成立 I 型错误() H0不成立推断正确(1-)
不拒绝H0
推断正确(1-) II 型错误()
，的关系
通常当n固定时，愈小，愈大；反之，愈大，愈小。
增大n，可同时减小，。
作业(P403)
四. 综合分析题 ✓1 ✓ 2(检验甲药是否有效) ✓3
X2 149.7
统计量t
均数之差的标准误
t X 1 X 2X X 2
X 1 X 2
s X 1 X 2
s c 2 (n 1 1 n 1 2 )
s 1 2 (n 1 1 ) s 2 2 (n 2 1 )(1 1 ) n 1 n 2 2 n 1 n 2
合并方差
n 1 n 2 2 1 2 1 2 2 2 2
配对设计
同源配对：来源相同，予不同处理
如同一窝别同性别的小鼠来自同一家庭的姐妹、双胞胎同性别，同病情和年龄相近的病人配成一对…..
按
雌
雄
符合实验要求
、
的大白鼠
体
重
配
对
随机
T
对子 1
C
随机
T
对子 2
C
随机
T
对子 3
C
配对设计
✓ 自身配对 a. 同一对象给予两种不同处理 b. 同一对象处理前后
✓ 再如：天下乌鸦一般黑。如果能够找到另外一种颜色的乌鸦，则原来的假设就被推翻。
假设检验中的小概率原理
什么是小概率？ 1. 在一次试验中，一个几乎不可能发生
的事件发生的概率。 2. 在一次试验中小概率事件一旦发生，
我们就有理由拒绝原假设。 3. 小概率由研究者事先确定。
例7.3 一般正常成年男子血红蛋白的平均值为 140g/L，某研究者随机抽取60名高原地区健康成年男性进行检查，测得血红蛋白均数为 155g/L，标准差为24g/L。可否认为高原地区成年男性居民的血红蛋白平均水平不同于一般正常成年男子？
已知： 0 1 4 0 X 1 5 5 s 2 4 n 6 0
从统计学角度考虑，高原成年男子与一般人群有差别有两种可能： 1）差别是由于抽样误差引起的，即二者来自同一总体。统计学上称为差异无统计学意义。 2）差异是本质上的差异，即二者来自不同总体。统计学上称为差异有统计学意义。
s X1X2
s2 s2
X1
X2
s12s2 2
n1 n2
t X 1 X 2X 1 X 2
X 1 X 2
s X 1 X 2
s c 2 (n 1 1 n 1 2 )
s 1 2 (n 1 1 ) s 2 2 (n 2 1 )(1 1 ) n 1 n 2 2 n 1 n 2
z检验为t检验在样本含量较大时的近似计算法
品中出现2个、3个甚至4个坏鸡蛋。
于是P值就是坏鸡蛋数目≥1的概率。
什么是P值？
例7.3 H0： 0 140
t 4.841
基本思想 Basic Idea
抽样分布
总体均值
t ＝ 4.841
= 140 155 样本均值
H0
基本思想 Basic Idea
抽样分布
总体均值
t ＝ 6.455
= 140
P92 例8.2
(1) 建立假设检验,确定检验水准
H0：儿童皮肤对不同结核菌素的反应性无差别，即d=0 H1：儿童皮肤对不同结核菌素的反应性有差别，即d0
=0.05
(2) 计算统计量
t d 0d 3 .2 5 4 .5 2 0
s d
sd/ n2 .4 9 1 /1 2
=n-1=12-1=11
假设检验
LOGO
假设检验
统计分析
统计推断
参数估计假设检验
统计描述
假设检验是统计推断的另一个重要方面
什么是假设检验？
1、概念事先对总体参数(总体分布)作出某种假设然后利用样本信息来判断原假设是否成立
2、特点采用逻辑上的反证法依据统计上的小概率事件原理
什么是反证法？
✓ 例如：根据经验我们可以说成都的6月天不会下雪，假如有一年的6月份下了一场雪，则原来的结论就被推翻。这样的推理方法就是反证法。
*
PPT模板下载：/moban/ 节日PPT模板：/jieri/ PPT背景图片：/beijing/ 优秀PPT下载：/xiazai/ Word教程： /word/ 资料下载：/ziliao/ 范文下载：/fanwen/ 教案下载：/jiaoan/
信息不支持H0，因而拒绝H0。
➢因此，当P≤时，按所取检验水准，拒
绝H0，接受H1。
若P>时，表示在H0成立的条件
下，出现等于及大于(或等于及小于)现有统计量的概率不是小
概率，现有样本信息还不足以拒绝H0。
结论
➢若P≤，拒绝H0，可以认为……差
异有统计学意义。
➢若P>时，不拒绝H0，尚不能认
tXX3.273.361.294
s X
s/ n 0.44/ 40
(3) 确定P值,作出统计推断
查附表3，t界值表，t0.20,39=1.304，t0.40,39=0.851，得0.40>P>0.20，
按=0.05水准不拒绝H0，尚不能认为该地农村新生儿体重与该
地新生儿平均出生体重不同。。
2.配对设计的均数比较
两样本均数的比较
(1) 建立假设检验,确定检验水准
H0:1=2 , 即两总体均数相等 H1:12 , 即两总体均数不相等双侧=0.05
(2) 计算统计量
t X 1 X 2X 1 X 2
X 1 X 2
s X 1 X 2
s c 2 (n 1 1 n 1 2 )
s 1 2 (n 1 1 ) s 2 2 (n 2 1 )(1 1 ) n 1 n 2 2 n 1 n 2
✓根据样本数据计算相应的统计量。
计算统计量
例7.3应计算t检验的检验统计量t：
tXX1551404.8412
s X
s/ n 24/ 60
=n-1=60-1=59
假设检验的基本步骤
建立检验假设，确定检验水准选定检验方法，计算检验统计量确定P值，作出统计推断
什么是P值？
P值是指在H0所规定的总体中随机抽样，获得等于及大于(或等于及小于)现有样本统计量的概率。
➢ 其分析目的是推断样本所代
表的未知总体均数与已知总体均数0有无差别。
已知总体 0 ？
3.36kg
未知总体
样本
X 3.27
(1) 建立检验假设，确定检验水准
H0：=0该地农村新生儿体重与该地新生儿平均出生体重相同
H1：0该地农村新生儿体重与该地新生儿平均出生体重不同
=0.05
(2) 计算统计量
什么是P值？
如果总体状况跟H0一致，统计量获得现有数值以及更不利于H0的数值的可能性(概率)有多大。
example
某商家宣称他的一大批鸡蛋都是新鲜鸡蛋——H0
为了对鸡蛋质量做出判断，顾客与商家约定，从中随机抽取5个做检验，结果有4个好的，一个坏的。
那么更不利于广告词(H0)的可能是5个鸡蛋样
(3) 确定P值,作出统计推断
查附表3，t界值表，得P<0.001，按=0.05水准拒
绝H0 ，可认为两种不同结核菌素对儿童皮肤反应性有差别。
成组设计的两样本均数的比较
什么是成组设计？

总体均数的假设检验

合集下载