培优 易错 难题综合题辅导专题训练及答案解析

一、中考初中化学综合题1．央视《是真的吗？》栏目中有一段视频：将“锡纸”剪成一段两头宽中间窄的纸条，然后两头分别连接电池的正负极，观察到“锡纸”立即燃烧。

据此，某实验小组同学取某种“锡纸”进行了以下探究。

（1）“锡纸”燃烧的原因：“锡纸”两端接入电池两极后造成短路致使“锡纸”燃烧，从燃烧的条件分析：开始“锡纸”不燃烧，但短路后却能燃烧的原因是。

（2）探究“锡纸”中金属的成分：“锡纸”中的金属是锡吗？（查阅资料）①“锡纸”是锡箔或铝箔和纸粘合而成；②锌粉是一种深灰色固体；③ 锡（Sn）与酸或盐溶液反应生成+2价的锡盐。

（提出猜想）猜想Ⅰ：“锡纸”中的金属是锡；猜想Ⅱ：“锡纸”中的金属是铝。

（进行实验）设计方案并进行实验。

（交流讨论）①实验中打磨“锡纸”的目的是；②下列物质的溶液不可以替代氯化锌溶液完成上述实验的是（填序号）。

A．氯化铜 B．硝酸银 C．硫酸钠 D．硫酸亚铁（反思应用）电器短路会引起火灾，我们要严加防范。

如果电器着火应该采取的灭火方法是：。

（探究拓展）该小组为了测定镁铜合金中镁的质量分数，取出3g合金样品，将60g稀硫酸分为6等份依次加入样品中，充分反应后过滤、洗涤、干燥、称重，得到的实验数据如下：（3）表格中，m= 。

（4）合金样品中镁的质量= 。

（5）计算所用稀硫酸中H2SO4的质量分数。

（要求写出计算过程，下同）（6）计算当加入第4份硫酸溶液且充分反应后所得溶液中溶质的质量分数。

【答案】（1）温度达到了着火点；（2）Ⅱ；2Al+3ZnCl2=3Zn+2AlCl3；除去表面的氧化物；ABC；先切断电源，然后用干粉灭火器扑灭或者用沙土盖灭；（3）2.5g；（4）2.4g；（5）20.4% ；（6）23.9%【解析】探究一：“锡纸”与氧气接触，但是开始“锡纸”不燃烧而短路后却能燃烧的原因是短路时，温度升高，温度达到了“锡纸”的着火点；探究二：【进行实验】铝比锌活泼，而锡不如锌活泼，所以打磨后的“锡纸”片放入试管中，滴加氯化锌溶液．若有深灰色固体析出则为铝，若没有深灰色固体析出则为锡；铝与氯化锌反应生成锌和氯化铝；故答案为Ⅱ成立；反应的化学方程式为2Al+3ZnCl2=3Zn+2AlCl3；【交流讨论】(1)实验中打磨“锡纸”的目的是除去表面的氧化物；(2)选择的盐溶液中的金属元素应介于铝和锡之间，铜和银均排在锡的后面，钠排在铝的前面，而铁介于二者之间，硫酸亚铁满足条件，故答案为ABC；【反思应用】因水能导电，则如果电器着火应采取的灭火方法是先切断电源，然后用干粉灭火器扑灭或者用沙土盖灭；【探究拓展】(3)第2和3实验对比中可知，每10g稀硫酸能与0.5g镁反应，可知第一次剩余固体为3g-0.5g=2.5g；(4)由最后剩余0.6g固体可知，镁的质量为3g-0.6g=2.4g；(5)根据每10g稀硫酸能与0.5g镁反应，设10g硫酸中溶质的质量为x，Mg+H2SO4=MgSO4+H2↑24 980.5g x240.5 98gx=，解得：x=2.04g则稀硫酸中溶质的质量分数为2.0410gg×100%=20.4%；(6)设加入第四份硫酸后生成的MgSO4质量为y、生成的氢气为z，Mg+H2SO4=MgSO4+H2↑24 120 22g y z2412022g y z==，解得：y=10g、z=0.17g；充分反应后所得溶液中溶质的质量分数为10402g0.17gg+-×100%=23.9%。

一、中考初中化学综合题1．数型图象是研究化学问题的一种常见描述方法，根据下列图象进行回答：.向盐酸（1）图一是用盐酸和氢氧化钠进行中和反应时，反应过程中溶液的pH变化曲线中加入的氢氧化钠溶液质量为mg时，所得溶液中含有的离子为 ______ (填离子符号)；（2）图二是20℃时，取10mL10%的NaOH溶液于烧杯中，逐滴加入10%的盐酸，随着盐酸的加入，烧杯中溶液温度与加入盐酸体积的变化关系．①由图可知中和反应是放热反应，你的依据为 ______ ；②甲同学用氢氧化钠固体与稀盐酸反应也能得到相同结论，乙同学认为不严密，因为______ ；③图三是a、b、c三种物质的溶解度曲线a与c的溶解度相交于P点，据图回答：①t1℃时，接近饱和的c物质溶液，在不改变溶液质量的条件下，可用 ______ 的方法达到饱和状态；②将t2℃时，150ga物质的饱和溶液降温到t1℃时，可以析出____g a物质．【答案】Na+、Cl﹣、H+开始随着反应的进行，溶液温度逐渐升高氢氧化钠固体溶于水放热升温 30【解析】本题考查了中和反应及其应用和溶解度曲线的应用。

（1）根据图一，向盐酸中加入的氢氧化钠溶液质量为mg时，所得溶液中含有的离子为反应生成的氯化钠中的钠离子和氯离子及其过量的稀盐酸中的氢离子和氯离子，故答案为Na+、Cl-、H+；（2）①由图2可知随着反应的进行，溶液温度逐渐升高，所以中和反应是放热反应；②用氢氧化钠固体与稀盐酸反应不能得到相同结论，这是因为氢氧化钠固体溶于水放热，无法判断溶液温度升高是由于哪种原因导致的；（3）①t1℃时，接近饱和的c物质溶液，在不改变溶液质量的条件下，由于c的溶解度随着温度升高而减小，因此可用升温的方法达到饱和状态；②将t2℃时，a的溶解度是50g，150ga物质的饱和溶液中溶质质量是50g，水的质量为100g，降温到t1℃时a的溶解度是20g，因此可以析出(50g-20g)=30ga物质。

一、一元二次方程真题与模拟题分类汇编（难题易错题）1.随着经济收入的不断提高以及汽车业的快速发展，家用汽车已越来越多地进入普通家庭，汽车消费成为新亮点.抽样调查显示，截止2008年底全市汽车拥有量为14.4万辆.已知2006年底全市汽车拥有量为10万辆.（1）求2006年底至2008年底我市汽车拥有量的年平均增长率：（2）为保护城市环境，要求我市到2010年底汽车拥有量不超过15.464万辆，据估计从2008年底起，此后每年报废的汽车数量是上年底汽车拥有量的10%,那么每年新增汽车数量最多不超过多少辆？（假定每年新增汽车数量相同）【答案】详见解析【解析】试题分析：（1）主要考查增长率问题，一般用增长后的量=增长前的量x （1+增长率）解决问题；（2）参照增长率问题的一般规律，表示出2010年的汽车拥有量，然后根据关键语列出不等式来判断正确的解.试题解析：（1）设年平均增长率为x,根据题意得：10 （1+x） 2=144解得x=-2.2 （不合题意舍去）x=0.2,答：年平均增长率为20%：（2）设每年新增汽车数量最多不超过y万辆，根据题意得：2009年底汽车数量为14.4x90%+y,2010 年底汽车数量为（14.4x90%+y） x90%+y,/. （14.4x90%+y） x90%+y<15,464,y<2.答：每年新增汽车数量最多不超过2万辆.考点：一元二次方程一增长率的问题2.关于x的方程必-2 （k-1） x+k2 = 0有两个实数根X】、X2.（1）求k的取值范围；（2 ）若X1+X2=l - XPQ,求k的值.【答案】（1）〃［：（2）k=3【解析】试题分析：（1）方程有两个实数根，可得△ = 〃-4acN0,代入可解出k的取值范围：（2）由韦达定理可知，%+9=2（4—1）,百马=上列出等式，可得出k的值.试题解析：⑴..W = 4（k—1产-4k2?0, -8k+420, .•.人!；2(2)二・xi+xz=2(k-1), xixz=k\ ：. 2(k—l)=l—k2.「・匕=1, kz=—3.1•/ k<-,.」=—3. 23.解方程：（x+l）（x-3）=-l.【答案】Xl=l+ y/3 , x2=l - yf3【解析】试题分析：根据方程的特点，先化为一般式，然后利用配方法求解即可.试题解析：整理得：x2 - 2x=2,配方得：x2 - 2x+l=3,即（X-1） 2=3, 解得：X1=1+ y/3 , X2=l - y/3 .4.“父母恩深重，恩怜无歇时”，每年5月的第二个星期日即为母亲节，节日前夕巴蜀中学学生会计划采购一批鲜花礼盒赠送给妈妈们.（1）经过和花店卖家议价，可在原标价的基础上打八折购进，若在花店购买80个礼盒最多花费7680元，请求出每个礼盒在花店的最高标价：（用不等式解答）（2）后来学生会了解到通过“大众点评"或“美团〃同城配送会在（1）中花店最高售价的基础上降价25%,学生会计划在这两个网站上分别购买相同数量的礼盒，但实际购买过程中，'‘大众点评”网上的购买价格比原有价格上涨2 m%，购买数量和原计划一样：“美团〃网29上的购买价格比原有价格下降了一m元，购买数量在原计划基础上增加15m%,最终，在20两个网站的实际消费总额比原计划的预算总额增加了—m%,求出m的值.2【答案】（1） 120；（2） 20.【解析】试题分析：（1）本题介绍两种解法：解法一：设标价为x元，列不等式为0.8x・8047680,解出即可：解法二：根据单价=总价+数量先求出1个礼盒最多花费，再除以折扣可求出每个礼盒在花店的最高标价：（2）先假设学生会计划在这两个网站上分别购买的礼盒数为a个礼盒，表示在“大众点评" 网上的购买实际消费总额：120a （1-25%）（l+^m%）,在“美团〃网上的购买实际消费29总额：a[120（1 - 25%）- —m]（l+15m%）:根据“在两个网站的实际消费总额比原计划的预算总额增加了"列方程解出即可.2试题解析：（1）解：解法一：设标价为X元，列不等式为0.8x・80W7680, x<120；解法二：76804-80^0.8=964-0.8=120 （元）.答：每个礼盒在花店的最高标价是120元；(2)解：假设学生会计划在这两个网站上分别购买的礼盒数为a个礼盒，由题意得：5 9120x0.8a (1 - 25%) (l+-m%) +a[120x0.8 (1 - 25%) - —m]=120x0.8。

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，⊙O是△ABC的外接圆，点E为△ABC内切圆的圆心，连接AE的延长线交BC于点F，交⊙O于点D；连接BD，过点D作直线DM，使∠BDM=∠DAC．（1）求证：直线DM是⊙O的切线；（2）若DF=2，且AF=4，求BD和DE的长．【答案】（1）证明见解析（2）23【解析】【分析】（1）根据垂径定理的推论即可得到OD⊥BC，再根据∠BDM=∠DBC，即可判定BC∥DM，进而得到OD⊥DM，据此可得直线DM是⊙O的切线；（2）根据三角形内心的定义以及圆周角定理，得到∠BED=∠EBD，即可得出DB=DE，再判定△DBF∽△DAB，即可得到DB2=DF•DA，据此解答即可．【详解】（1）如图所示，连接OD．∵点E是△ABC的内心，∴∠BAD=∠CAD，∴BD CD=，∴OD⊥BC．又∵∠BDM=∠DAC，∠DAC=∠DBC，∴∠BDM=∠DBC，∴BC∥DM，∴OD⊥DM．又∵OD为⊙O半径，∴直线DM是⊙O的切线．（2）连接BE．∵E为内心，∴∠ABE=∠CBE．∵∠BAD=∠CAD，∠DBC=∠CAD，∴∠BAD=∠DBC，∴∠BAE+∠ABE=∠CBE+∠DBC，即∠BED=∠DBE，∴BD=DE．又∵∠BDF=∠ADB（公共角），∴△DBF∽△DAB，∴DF DBDB DA=，即DB2=DF•DA．∵DF=2，AF=4，∴DA=DF+AF=6，∴DB2=DF•DA=12，∴DB=DE=23．【点睛】本题主要考查了三角形的内心与外心，圆周角定理以及垂径定理的综合应用，解题时注意：平分弦所对一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧；三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．2．在平面直角坐标系xOy中，点M的坐标为（x1，y1），点N的坐标为（x2，y2），且x1≠x2，y1≠y2，以MN为边构造菱形，若该菱形的两条对角线分别平行于x轴，y轴，则称该菱形为边的“坐标菱形”．（1）已知点A（2，0），B（0，23），则以AB为边的“坐标菱形”的最小内角为；（2）若点C（1，2），点D在直线y=5上，以CD为边的“坐标菱形”为正方形，求直线CD 表达式；（3）⊙O的半径为2，点P的坐标为（3，m）．若在⊙O上存在一点Q，使得以QP为边的“坐标菱形”为正方形，求m的取值范围．【答案】（1）60°；（2）y=x+1或y=﹣x+3；（3）1≤m≤5或﹣5≤m≤﹣1【解析】分析：（1）根据定义建立以AB为边的“坐标菱形”，由勾股定理求边长AB=4，可得30度角，从而得最小内角为60°；（2）先确定直线CD与直线y=5的夹角是45°，得D（4，5）或（﹣2，5），易得直线CD的表达式为：y=x+1或y=﹣x+3；（3）分两种情况：①先作直线y=x，再作圆的两条切线，且平行于直线y=x，如图3，根据等腰直角三角形的性质分别求P'B=BD=1，PB=5，写出对应P的坐标；②先作直线y=﹣x，再作圆的两条切线，且平行于直线y=﹣x，如图4，同理可得结论．详解：（1）∵点A（2，0），B（0，3∴OA=2，OB3．在Rt△AOB中，由勾股定理得：AB22（），∴∠ABO=30°．223∵四边形ABCD是菱形，∴∠ABC=2∠ABO=60°．∵AB∥CD，∴∠DCB=180°﹣60°=120°，∴以AB为边的“坐标菱形”的最小内角为60°．故答案为：60°；（2）如图2．∵以CD为边的“坐标菱形”为正方形，∴直线CD与直线y=5的夹角是45°．过点C作CE⊥DE于E，∴D（4，5）或（﹣2，5），∴直线CD的表达式为：y=x+1或y=﹣x+3；（3）分两种情况：①先作直线y=x，再作圆的两条切线，且平行于直线y=x，如图3．∵⊙O的半径为2，且△OQ'D是等腰直角三角形，∴OD=2OQ'=2，∴P'D=3﹣2=1．∵△P'DB是等腰直角三角形，∴P'B=BD=1，∴P'（0，1），同理可得：OA=2，∴AB=3+2=5．∵△ABP是等腰直角三角形，∴PB=5，∴P（0，5），∴当1≤m≤5时，以QP为边的“坐标菱形”为正方形；②先作直线y=﹣x，再作圆的两条切线，且平行于直线y=﹣x，如图4．∵⊙O的半径为2，且△OQ'D是等腰直角三角形，∴OD=2OQ'=2，∴BD=3﹣2=1．∵△P'DB是等腰直角三角形，∴P'B=BD=1，∴P'（0，﹣1），同理可得：OA=2，∴AB=3+2=5．∵△ABP是等腰直角三角形，∴PB=5，∴P（0，﹣5），∴当﹣5≤m≤﹣1时，以QP为边的“坐标菱形”为正方形；综上所述：m的取值范围是1≤m≤5或﹣5≤m≤﹣1．点睛：本题是一次函数和圆的综合题，考查了菱形的性质、正方形的性质、点P ，Q 的“坐标菱形”的定义等知识，解题的关键是理解题意，学会利用图象解决问题，学会用分类讨论的思想思考问题，注意一题多解，属于中考创新题目．3．如图1，等边△ABC 的边长为3，分别以顶点B 、A 、C 为圆心，BA 长为半径作AC 、CB 、BA ，我们把这三条弧所组成的图形称作莱洛三角形，显然莱洛三角形仍然是轴对称图形，设点l 为对称轴的交点．（1）如图2，将这个图形的顶点A 与线段MN 作无滑动的滚动，当它滚动一周后点A 与端点N 重合，则线段MN 的长为 ；（2）如图3，将这个图形的顶点A 与等边△DEF 的顶点D 重合，且AB ⊥DE ，DE =2π，将它沿等边△DEF 的边作无滑动的滚动当它第一次回到起始位置时，求这个图形在运动过程中所扫过的区域的面积；（3）如图4，将这个图形的顶点B 与⊙O 的圆心O 重合，⊙O 的半径为3，将它沿⊙O 的圆周作无滑动的滚动，当它第n 次回到起始位置时，点I 所经过的路径长为 （请用含n 的式子表示）【答案】（1）3π；（2）27π；（3）3． 【解析】试题分析：（1）先求出AC 的弧长，继而得出莱洛三角形的周长为3π，即可得出结论； （2）先判断出莱洛三角形等边△DEF 绕一周扫过的面积如图所示，利用矩形的面积和扇形的面积之和即可；（3）先判断出莱洛三角形的一个顶点和O 重合旋转一周点I 的路径，再用圆的周长公式即可得出．试题解析：解：（1）∵等边△ABC 的边长为3，∴∠ABC =∠ACB =∠BAC =60°，AC BC AB ==，∴AC BC l l ==AB l =603180π⨯=π，∴线段MN 的长为AC BC AB l l l ++=3π．故答案为3π；（2）如图1．∵等边△DEF 的边长为2π，等边△ABC 的边长为3，∴S 矩形AGHF =2π×3=6π，由题意知，AB ⊥DE ，AG ⊥AF ，∴∠BAG =120°，∴S 扇形BAG =21203360π⨯=3π，∴图形在运动过程中所扫过的区域的面积为3（S矩形AGHF+S扇形BAG）=3（6π+3π）=27π；（3）如图2，连接BI并延长交AC于D．∵I是△ABC的重心也是内心，∴∠DAI=30°，AD=12AC=32，∴OI=AI=3230ADcos DAI cos∠=︒=3，∴当它第1次回到起始位置时，点I所经过的路径是以O为圆心，OI为半径的圆周，∴当它第n次回到起始位置时，点I所经过的路径长为n•2π•3=23nπ．故答案为23nπ．点睛：本题是圆的综合题，主要考查了弧长公式，莱洛三角形的周长，矩形，扇形面积公式，解（1）的关键是求出AC的弧长，解（2）的关键是判断出莱洛三角形绕等边△DEF 扫过的图形，解（3）的关键是得出点I第一次回到起点时，I的路径，是一道中等难度的题目．4．在平面直角坐标系中，已知点A（2，0），点B（0，），点O（0，0）．△AOB绕着O顺时针旋转，得△A'OB'，点A、B旋转后的对应点为A'，B'，记旋转角为α．（Ⅰ）如图1，A'B'恰好经过点A时，求此时旋转角α的度数，并求出点B'的坐标；（Ⅱ）如图2，若0°＜α＜90°，设直线AA'和直线BB'交于点P，求证：AA'⊥BB'；（Ⅲ）若0°＜α＜360°，求（Ⅱ）中的点P纵坐标的最小值（直接写出结果即可）．【答案】（Ⅰ）α＝60°，B'（3，）；（Ⅱ）见解析；（Ⅲ）点P纵坐标的最小值为﹣2．【解析】【分析】（Ⅰ）作辅助线,先根据点A（2,0）,点B（0,）,确定∠ABO＝30°,证明△AOA'是等边三角形,得旋转角α＝60°,证明△COB'是30°的直角三角形,可得B'的坐标;（Ⅱ）依据旋转的性质可得∠BOB'＝∠AOA'＝α,OB＝OB',OA＝OA',即可得出∠OBB'＝∠OA'A＝（180°﹣α）,再根据∠BOA'＝90°+α,四边形OBPA'的内角和为360°,即可得到∠BPA'＝90°,即AA'⊥BB';（Ⅲ）作AB的中点M（1,）,连接MP,依据点P的轨迹为以点M为圆心,以MP＝AB＝2为半径的圆,即可得到当PM∥y轴时,点P纵坐标的最小值为﹣2.【详解】解：（Ⅰ）如图1，过B'作B'C⊥x轴于C,∵OA＝2,OB＝2,∠AOB＝90°,∴∠ABO＝30°,∠BAO＝60°,由旋转得：OA＝OA',∠A'＝∠BAO＝60°,∴△OAA'是等边三角形,∴α＝∠AOA'＝60°,∵OB＝OB'＝2,∠COB'＝90°﹣60°＝30°,∴B'C＝OB’＝,∴OC＝3,∴B'（3,）,（Ⅱ）证明：如图2,∵∠BOB'＝∠AOA'＝α,OB＝OB',OA＝OA',∴∠OBB'＝∠OA'A＝（180°﹣α）,∵∠BOA'＝90°+α,四边形OBPA'的内角和为360°,∴∠BPA'＝360°﹣（180°﹣α）﹣（90°+α）＝90°,即AA'⊥BB';（Ⅲ）点P纵坐标的最小值为-2．理由是：如图，作AB的中点M（1,）,连接MP,∵∠APB＝90°,∴点P的轨迹为以点M为圆心,以MP＝AB＝2为半径的圆,除去点（2,2）,∴当PM⊥x轴时,点P纵坐标的最小值为﹣2．【点睛】本题属于几何变换综合题,主要考查了旋转的性质,含30°角的直角三角形的性质,四边形内角和以及圆周角定理的综合运用,解决问题的关键是判断点P的轨迹为以点M为圆心,以MP 为半径的圆．5．.如图，△ABC中，∠ACB＝90°，∠A＝30°，AB＝6．D是线段AC上一个动点（不与点A 重合），⊙D与AB相切，切点为E，⊙D交射线．．BC于．．DC于点F，过F作FG⊥EF交直线点G，设⊙D的半径为r．（1）求证AE＝EF；（2）当⊙D与直线BC相切时，求r的值；（3）当点G落在⊙D内部时，直接写出r的取值范围．【答案】(1)见解析,(2)r=3,(3)63 3r<<【解析】【分析】（1）连接DE，则∠ADE=60°=∠DEF+∠DFE，而∠DEF=∠DFE，则∠DEF=∠DFE=30°=∠A，即可求解；（2）如图2所示，连接DE，当圆与BC相切时，切点为F，∠A=30°，AB=6，则BF=3，AD=2r，由勾股定理，即可求解；（3）分点F在线段AC上、点F在线段AC的延长线上两种情况，分别求解即可．【详解】解：设圆的半径为r；（1）连接DE，则∠ADE=60°=∠DEF+∠DFE，而∠DEF=∠DFE，则∠DEF=∠DFE=30°=∠A，∴AE=EF；（2）如图2所示，连接DE，当圆与BC相切时，切点为F∠A=30°，AB=6，则BF=3，AD=2r，由勾股定理得：（3r）2+9=36，解得：3（3）①当点F 在线段AC 上时，如图3所示，连接DE 、DG ，333,3933FC r GC FC r =-==-②当点F 在线段AC 的延长线上时，如图4所示，连接DE 、DG ，333,3339FC r GC FC r ===-两种情况下GC 符号相反，GC 2相同， 由勾股定理得：DG 2=CD 2+CG 2， 点G 在圆的内部，故：DG2＜r2， 即：22(332)(339)2r r r +-< 整理得：25113180r r -+< 6335r << 【点睛】本题考查了圆的综合题：圆的切线垂直于过切点的半径；利用勾股定理计算线段的长．6．如图，在△ABC 中，AB ＝AC ，以AB 为直径的⊙O 与边BC 交于点D ，DE ⊥AC ，垂足为E ，交AB 的延长线于点F ． (1)求证：EF 是⊙O 的切线；(2)若∠C ＝60°，AC ＝12，求BD 的长． (3)若tan C ＝2，AE ＝8，求BF 的长．【答案】(1)见解析;(2) 2π；(3)103. 【解析】分析：（1）连接OD ，根据等腰三角形的性质：等边对等角，得∠ABC=∠C ，∠ABC=∠ODB ，从而得到∠C=∠ODB ，根据同位角相等，两直线平行，得到OD ∥AC ，从而得证OD ⊥EF ，即 EF 是⊙O 的切线；（2） 根据中点的性质，由AB=AC=12 ，求得OB=OD=12AB =6，进而根据等边三角形的判定得到△OBD 是等边三角形，即∠BOD=600，从而根据弧长公式七届即可；（3）连接AD ，根据直角三角形的性质，由在Rt △DEC 中, tan 2DEC CE== 设CE=x,则DE=2x ，然后由Rt △ADE 中, tan 2AEADE DE∠== ，求得DE 、CE 的长，然后根据相似三角形的判定与性质求解即可.详解：（1）连接OD ∵AB=AC ∴∠ABC=∠C ∵OD=OB ∴∠ABC=∠ODB ∴∠C=∠ODB ∴OD ∥AC又∵DE ⊥AC ∴OD ⊥DE ，即OD ⊥EF ∴EF 是⊙O 的切线 （2） ∵AB=AC=12 ∴OB=OD=12AB =6 由（1）得：∠C=∠ODB=600 ∴△OBD 是等边三角形 ∴∠BOD=600∴BD =6062180ππ⨯= 即BD 的长2π （3）连接AD ∵DE ⊥AC ∠DEC=∠DEA=900在Rt △DEC 中, tan 2DEC CE== 设CE=x,则DE=2x ∵AB 是直径 ∴∠ADB=∠ADC=900∴∠ADE+∠CDE=900 在Rt △DEC 中,∠C+∠CDE=900 ∴∠C=∠ADE 在Rt △ADE 中, tan 2AEADE DE∠== ∵ AE=8，∴DE=4 则CE=2∴AC=AE+CE=10 即直径AB=AC=10 则OD=OB=5 ∵OD//AE ∴△ODF ∽△AEF ∴OF OD AF AE = 即：55108BF BF +=+ 解得：BF=103 即BF 的长为103. 点睛：此题考查了切线的性质与判定、圆周角定理、等腰三角形的性质、直角三角形以及相似三角形的判定与性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．7．如图，AB 为⊙O 的直径，且AB ＝m （m 为常数），点C 为AB 的中点，点D 为圆上一动点，过A 点作⊙O 的切线交BD 的延长线于点P ，弦CD 交AB 于点E ． （1）当DC ⊥AB 时，则DA DBDC+＝ ； （2）①当点D 在AB 上移动时，试探究线段DA ，DB ，DC 之间的数量关系；并说明理由；②设CD 长为t ，求△ADB 的面积S 与t 的函数关系式； （3）当9220PD AC =时，求DE OA 的值．【答案】（12；（2）①DA+DB 2DC ，②S ＝12t 2﹣14m 2 ；（3）24235DE OA =. 【解析】 【分析】（1）首先证明当DC ⊥AB 时，DC 也为圆的直径，且△ADB 为等腰直角三角形，即可求出结果；（2）①分别过点A ，B 作CD 的垂线，连接AC ，BC ，分别构造△ADM 和△BDN 两个等腰直角三形及△NBC 和△MCA 两个全等的三角形，容易证出线段DA ，DB ，DC 之间的数量关系；②通过完全平方公式（DA+DB ）2＝DA 2+DB 2+2DA•DB 的变形及将已知条件AB ＝m 代入即可求出结果；（3）通过设特殊值法，设出PD 的长度，再通过相似及面积法求出相关线段的长度，即可求出结果． 【详解】解：（1）如图1，∵AB 为⊙O 的直径， ∴∠ADB ＝90°， ∵C 为AB 的中点， ∴AC BC =， ∴∠ADC ＝∠BDC ＝45°， ∵DC ⊥AB ，∴∠DEA ＝∠DEB ＝90°， ∴∠DAE ＝∠DBE ＝45°， ∴AE ＝BE ， ∴点E 与点O 重合， ∴DC 为⊙O 的直径， ∴DC ＝AB ，在等腰直角三角形DAB 中， DA ＝DB ＝2AB ， ∴DA+DB ＝2AB ＝2CD ， ∴DA DBDC+＝2；（2）①如图2，过点A 作AM ⊥DC 于M ，过点B 作BN ⊥CD 于N ，连接AC ，BC ， 由（1）知AC BC =， ∴AC ＝BC ， ∵AB 为⊙O 的直径，∴∠ACB ＝∠BNC ＝∠CMA ＝90°，∴∠NBC+∠BCN ＝90°，∠BCN+∠MCA ＝90°，∴∠NBC ＝∠MCA ， 在△NBC 和△MCA 中，BNC CMA NBC MCA BC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△NBC ≌△MCA （AAS ）， ∴CN ＝AM ，由（1）知∠DAE ＝∠DBE ＝45°， AM ＝2DA ，DN＝2DB ， ∴DC ＝DN+NC ＝22DB+22DA ＝22（DB+DA ）， 即DA+DB ＝2DC ；②在Rt △DAB 中， DA 2+DB 2＝AB 2＝m 2，∵（DA+DB ）2＝DA 2+DB 2+2DA•DB ， 且由①知DA+DB 2DC 2t ， ∴2t ）2＝m 2+2DA•DB ， ∴DA•DB ＝t 2﹣12m 2， ∴S △ADB ＝12DA•DB ＝12t 2﹣14m 2， ∴△ADB 的面积S 与t 的函数关系式S ＝12t 2﹣14m 2； （3）如图3，过点E 作EH ⊥AD 于H ，EG ⊥DB 于G ， 则NE ＝ME ，四边形DHEG 为正方形，由（1）知AC BC =， ∴AC ＝BC ，∴△ACB 为等腰直角三角形， ∴AB 2AC ， ∵92PD AC =， 设PD ＝2，则AC ＝20，AB ＝2，∵∠DBA ＝∠DBA ，∠PAB ＝∠ADB ， ∴△ABD ∽△PBA ， ∴AB BD ADPB AB PA==， ∴20292202DB =+， ∴DB ＝162， ∴AD ＝22AB DB -＝122，设NE ＝ME ＝x ， ∵S △ABD ＝12AD•BD ＝12AD•NE+12BD•ME ， ∴12×122×162＝12×122•x+12×162•x ， ∴x ＝482， ∴DE ＝2HE ＝2x ＝967， 又∵AO ＝12AB ＝102， ∴962427102DE OA =⨯=．【点睛】本题考查了圆的相关性质，等腰直三角形的性质，相似的性质等，还考查了面积法及特殊值法的运用，解题的关键是认清图形，抽象出各几何图形的特殊位置关系．8．在平面直角坐标系xOy 中，对于点P 和图形W ，如果以P 为端点的任意一条射线与图形W 最多只有一个公共点，那么称点P 独立于图形W ．（1）如图1，已知点A（-2，0），以原点O为圆心，OA长为半径画弧交x轴正半轴于点 B．在P1（0，4），P2（0，1），P3（0，-3），P4（4，0）这四个点中，独立于AB的点是；（2）如图2，已知点C（-3，0），D（0，3），E（3，0），点P是直线l：y=2x+8上的一个动点．若点P独立于折线CD-DE，求点P的横坐标x p的取值范围；（3）如图3，⊙H是以点H（0，4）为圆心，半径为1的圆．点T（0，t）在y轴上且t＞-3，以点T为中心的正方形KLMN的顶点K的坐标为（0，t+3），将正方形KLMN在x轴及x轴上方的部分记为图形W．若⊙H上的所有点都独立于图形W，直接写出t的取值范围．【答案】（1）P2，P3；（2）x P＜-5或x P＞-53．（3）-3＜t＜2或2＜t＜2【解析】【分析】（1）根据点P独立于图形W的定义即可判断；（2）求出直线DE，直线CD与直线y=2x+8的交点坐标即可判断；（3）求出三种特殊位置时t的值，结合图象即可解决问题.【详解】（1）由题意可知：在P1（0，4），P2（0，1），P3（0，-3），P4（4，0）这四个点中，独立于AB的点是P2，P3．（2）∵C（-3，0），D（0，3），E（3，0），∴直线CD的解析式为y=x+3，直线DE的解析式为y=-x+3，由283y xy x+⎧⎨+⎩＝＝，解得52xy-⎧⎨-⎩＝＝，可得直线l与直线CD的交点的横坐标为-5，由283y xy x+⎧⎨-+⎩＝＝，解得53143xy⎧-⎪⎪⎨⎪⎪⎩＝＝，可得直线l与直线DE的交点的横坐标为-53，∴满足条件的点P的横坐标x p的取值范围为：x P＜-5或x P＞-5．3（3）如图3-1中，当直线KN与⊙H相切于点E时，连接EH，则EH=EK=1，HK=2，∴OT=KT+HK-OH=3+2-4=2-1，∴T（0，1-2），此时t=1-2，∴当-3＜t＜1-2时，⊙H上的所有点都独立于图形W．如图3-2中，当线段KN与⊙H相切于点E时，连接EH．22∴T（0，22如图3-3中，当线段MN与⊙H相切于点E时，连接EH．OT=OM+TM=4-2+3=7-2，∴T（0，7-2），此时t=7-2，∴当1+2＜t＜7-2时，⊙H上的所有点都独立于图形W．综上所述，满足条件的t的值为-3＜t＜1-2或1+2＜t＜7-2．【点睛】本题属于圆综合题，考查了切线的性质，一次函数的应用，点P独立于图形W的定义等知识，解题的关键是理解题意，灵活运用所学知识解决问题，学会利用特殊位置解决实际问题.9．如图，在△ABC中，以AC为直径作⊙O交BC于点D，交AB于点G，且D是BC中点，DE⊥AB，垂足为E，交AC的延长线于点F．（1）求证：直线EF是⊙O的切线；（2）若CF=3，cosA=25，求出⊙O的半径和BE的长；（3）连接CG，在（2）的条件下，求CGEF的值．【答案】(1)见解析；（2）2，65（3）CG:EF＝4：7【解析】试题分析：（1）连结OD．先证明OD是△ABC的中位线，根据中位线的性质得到OD∥AB，再由DE⊥AB，得出OD⊥EF，根据切线的判定即可得出直线EF是⊙O的切线；（2）先由OD∥AB，得出∠COD=∠A，再解Rt△DOF，根据余弦函数的定义得到cos∠FOD==，设⊙O的半径为R，解方程=，求出R=，那么AB=2OD=，解Rt△AEF，根据余弦函数的定义得到cosA==，求出AE=，然后由BE=AB﹣AE即可求解．试题解析：（1）证明：如图，连结OD．∵CD=DB，CO=OA，∴OD是△ABC的中位线，∴OD∥AB，AB=2OD，∵DE⊥AB，∴DE⊥OD，即OD⊥EF，∴直线EF是⊙O的切线；（2）解：∵OD∥AB，∴∠COD=∠A．在Rt△DOF中，∵∠ODF=90°，∴cos∠FOD==，设⊙O的半径为R，则=，解得R=，∴AB=2OD=．在Rt△AEF中，∵∠AEF=90°，∴cosA===，∴AE=，∴BE=AB﹣AE=﹣=2．【点睛】本题考查了切线的判定，解直角三角形，三角形中位线的性质知识点．要证某线是圆的切线，已知此线过圆上某点，连结圆心与这点（即为半径），再证垂直即可．10．如图，已知在△ABC中，AB=15，AC=20，tanA=12，点P在AB边上，⊙P的半径为定长.当点P与点B重合时，⊙P恰好与AC边相切；当点P与点B不重合时，⊙P与AC边相交于点M和点N．（1）求⊙P的半径；（2）当AP=65时，试探究△APM与△PCN是否相似，并说明理由．【答案】（1）半径为35；（2）相似，理由见解析.【解析】【分析】（1）如图，作BD⊥AC，垂足为点D，⊙P与边AC相切，则BD就是⊙P的半径，利用解直角三角形得出BD与AD的关系，再利用勾股定理可求得BD的长；（2）如图，过点P作PH⊥AC于点H，作BD⊥AC，垂足为点D，根据垂径定理得出MN=2MH，PM=PN，再利用勾股定理求出PH、AH、MH、MN的长，从而求出AM、NC的长，然后求出AMMP、PNNC的值，得出AMMP=PNNC，利用两边对应成比例且夹角相等的两三角形相似即可证明.【详解】（1）如图，作BD⊥AC，垂足为点D，∵⊙P 与边AC 相切， ∴BD 就是⊙P 的半径， 在Rt △ABD 中，tanA= 1BD 2AD=， 设BD=x ，则AD=2x ， ∴x 2+(2x)2=152， 解得：x=35， ∴半径为35； （2）相似，理由见解析，如图，过点P 作PH ⊥AC 于点H ，作BD ⊥AC ，垂足为点D ， ∴PH 垂直平分MN ， ∴PM=PN ， 在Rt △AHP 中，tanA=12PH AH=， 设PH=y ，AH=2y ， y 2+（2y ）2=（65）2 解得：y=6（取正数）， ∴PH=6，AH=12， 在Rt △MPH 中， MH=()22356-=3，∴MN=2MH=6， ∴AM=AH-MH=12-3=9， NC=AC-MN-AM=20-6-9=5， ∴3535AM MP ==，35PN NC =， ∴AM MP =PNNC ， 又∵PM=PN ，∴∠PMN=∠PNM ， ∴∠AMP=∠PNC ， ∴△AMP ∽△PNC.【点睛】本题考查了解直角三角形、垂径定理、相似三角形的判定与性质等，综合性较强，有一定的难度，正确添加辅助线、灵活应用相关的性质与定理是解题的关键.。

一、中考初中化学综合题1．通过海水晾晒可得粗盐，粗盐除NaCl外，还含有MgCl2、CaCl2、Na2SO4以及泥沙等杂质，以下是制备精盐的实验方案，各步操作流程如下：（1）在第①步粗盐溶解操作中要用玻璃棒搅拌，作用是_____。

（2）第⑤步“过滤”操作中得到沉淀的成分有：泥沙、BaSO4、Mg（OH）2、_____（填化学式）。

（3）在第③步操作中，选择的除杂的试剂不能用KOH代替NaOH，理由是_____。

（4）在利用粗盐制备精盐过程的第⑥步操作中，加入适量盐酸的目的是_____。

（5）实验所得精盐的质量大于粗盐中NaCl的质量，原因是_____。

（6）某品牌纯碱中含有杂质NaCl，化学兴趣小组的同学进行了如下实验研究：称取12g 样品放入烧杯中，加入稀盐酸至不再产生气泡为止，并绘制出加入稀盐酸的质量与放出气体质量的关系如图。

①纯碱恰好完全反应时，生成CO2的质量为_____g②计算当盐酸与纯碱恰好完全反应时，所得溶液的溶质质量分数是多少？____【答案】加速溶解CaCO3 BaCO3引入了新的杂质KCl除去溶液中过量的氢氧化钠和碳酸钠反应生成了氯化钠 4.4g16.3%【解析】本题考查了氯化钠与粗盐提纯，酸、碱、盐的化学性质，根据化学反应方程式的计算和有关溶质质量分数计算，综合性较强，认真审题，理清反应过程是解题的关键。

（1）在第①步粗盐溶解操作中要用玻璃棒搅拌，作用是加快溶解速率；（2）第②步中氯化钡与硫酸钠反应生成硫酸钡沉淀和氯化钠，第③步中氢氧化钠与氯化镁反应生成氢氧化镁沉淀和氯化钠，第④步中碳酸钠与过量的氯化钡反应生成碳酸钡沉淀和氯化钠，碳酸钠与氯化钙反应生成碳酸钙和氯化钠。

第⑤步“过滤”操作中得到沉淀的成分有：泥沙、BaSO4、Mg（OH）2、CaCO3、BaCO3；（3）氢氧化钾会与氯化镁反应生成氢氧化镁沉淀和氯化钾，氯化钾对氯化钠来说就是杂质。

在第③步操作中，选择的除杂的试剂不能用KOH代替NaOH，理由是会带入新的杂质氯化钾；（4）在第④、⑤步中加入过量的氢氧化钠和碳酸钠。

培优易错难题易错题选择题辅导专题训练附答案解析一、选择题1．仅用下列各组试剂无法完成验证Zn，Cu，Ag三种金属活动性顺序的是（）A．Zn、Ag、CuSO4溶液B．Cu、ZnSO4溶液、AgNO3溶液C．Zn、Ag、稀硫酸、ZnSO4溶液D．Zn、Cu、稀硫酸、AgNO3溶液答案：C解析：C【解析】试题分析：依据金属活动性顺序表，锌在氢前，铜在氢后，铜在银前；A. 锌与硫酸铜溶液析出红色金属，银与硫酸铜溶液无明显现象，选项说法正确；B.铜与硫酸锌溶液无明显现象，使硝酸银溶液变蓝色，析出银白色的金属，选项说法正确；C.没有涉及铜及其化合物，故无法测定铜与锌和银的金属活动性顺序，选项说法错误；D.锌与稀硫酸有气泡产生，铜与稀硫酸没有明显现象，铜使硝酸银溶液变蓝色，析出银白色的金属，，选项说法正确；故选C考点：金属活动性顺序表的应用2．下列关于金属材料的说法不．正确的是A．硬铝(铝合金)的硬度大于纯铝B．铁在干燥的空气中容易生锈C．常温下，铝能与空气中的氧气反应，在其表面生成致密的氧化铝薄膜D．金属资源的回收利用既保护了环境，又节约了矿石资源答案：B解析：B【解析】A、合金的硬度比组成它的纯金属的硬度大，硬铝（铝合金）的硬度大于纯铝，正确；B、铁在空气中锈蚀，实际上是铁跟空气中的氧气和水共同作用的结果，铁在干燥的空气中不易生锈，错误；C、常温下，铝能与空气中的氧气反应，在其表面生成致密的氧化铝薄膜，正确；D、金属资源的回收利用，节约了金属资源，减少的冶炼金属产生的污染，保护了环境，正确。

故选B。

3．X、Y、Z三种金属中，只有Z能和稀硫酸反应；将Y放人X的盐溶液中，Y表面有X析出。

则X、Y、Z三种金属的活动性顺序为A．X > Z > Y B．Y > X > Z C．Y ＞ Z ＞ X D．Z ＞ Y ＞ X答案：D解析：D【解析】试题分析：X、Y、Z三种金属中，只有Z能和稀硫酸反应，说明Z的活动性最强，将Y放人X的盐溶液中，Y表面有X析出，说明Y的活动性比X强，所以X、Y、Z三种金属的活动性顺序为Z ＞ Y ＞ X ，故选D考点：金属的活动性顺序4．向m克Zn和Fe的混合物中加入一定质量的溶液，充分反应后过滤，将滤渣洗涤、干燥后称量，质量仍为m g。

一、初中物理电路类问题1．用毛皮摩擦过的橡胶棒A带负电。

如图甲，用橡胶棒A接触不带电的验电器的金属球B时，验电器的金属箔张开；如图乙，让橡胶棒A靠近（不接触）不带电的验电器的金属球B，验电器的金属箔也会张开。

下列说法正确的是（）A．毛皮与橡胶棒相比，毛皮的原子核对电子的束缚能力强B．图甲中，金属箔张开是因为异种电荷相互排斥C．图乙中，橡胶棒靠近金属球B时，橡胶棒A所带电荷量减小D．图乙中，金属球B上的一部分电子转移到金属箔上【答案】D【解析】【分析】【详解】A．摩擦起电的实质是电子的转移，原子核对电子的束缚能力强，物体得到电子带负电。

橡胶棒A带负电，说明橡胶棒得到电子，即橡胶棒的原子核对电子的束缚能力强，故A错误；B．验电器的工作原理是同种电荷相互排斥，故B错误；C．橡胶棒A没有接触验电器的金属球B，所以橡胶棒A所带电荷量不变，故C错误；D．橡胶棒A带负电，接近金属球B上，B上的自由电子被排斥而远离，转移到金属箔上，故D正确。

故选D。

2．受新型冠状病毒的影响，一“罩”难求。

一般医用口罩至少要有三层，外层需要阻挡外界空气中的灰层、细菌、唾沫等飞溅物，中间层经过静电处理，可以阻挡细菌等微小颗粒（潮湿环境中会失去静电），内层要吸收佩戴者呼出的水汽、飞沫等。

某口罩的构造如图所示。

下列说法正确的是（）A．口罩潮湿后防护能力降低B．佩戴口罩时应该使白色吸水无纺布朝外C．口罩的中间层静电熔喷布能吸引小磁针D．佩戴口罩后内层潮湿是呼出的水蒸气升华形成【答案】A【解析】【分析】【详解】A．潮湿环境中会失去静电，口罩潮湿后，会失去静电，中间层不可以阻挡细菌等微小颗粒, 口罩防护能力降低，A正确；B．由题意可知，内层要吸收佩戴者呼出的水汽、飞沫等，那么白色吸水无纺布应该是内层，有吸水能力，佩戴口罩时应该使白色吸水无纺布朝内，B错误；C．带电体能吸引轻小物体，所以中间层静电熔喷布能吸引细菌等微小颗粒，但它不是磁体，不能吸引小磁针，C错误；D．佩戴口罩后内层潮湿是呼出的水蒸气液化形成的，D错误。

一、圆的综合 真题与模拟题分类汇编（难题易错题）1．如图，AB 为⊙O 的直径，AC 为⊙O 的弦，AD 平分∠BAC ，交⊙O 于点D ，DE ⊥AC ，交AC 的延长线于点E ．（1）判断直线DE 与⊙O 的位置关系，并说明理由；（2）若AE ＝8，⊙O 的半径为5，求DE 的长．【答案】（1）直线DE 与⊙O 相切（2）4【解析】试题分析：（1）连接OD ，∵AD 平分∠BAC ，∴EAD OAD ∠∠＝，∵OA OD ＝，∴ODA OAD ∠∠＝，∴ODA EAD ∠∠＝，∴EA ∥OD ，∵DE ⊥EA ，∴DE ⊥OD ，又∵点D 在⊙O 上，∴直线DE 与⊙O 相切（2）如图1，作DF ⊥AB ，垂足为F ，∴DFA DEA 90∠∠︒＝＝，∵EAD FAD ∠∠＝，AD AD ＝，∴△EAD ≌△FAD ，∴AF AE 8＝＝，DF DE ＝，∵OA OD 5＝＝，∴OF 3＝，在Rt △DOF 中，22DF 4OD OF -＝＝，∴AF AE 8＝＝ 考点：切线的证明，弦心距和半径、弦长的关系点评：本题难度不大，第一小题通过内错角相等相等证明两直线平行，再由两直线平行推出同旁内角相等．第二小题通过求出两个三角形全等，从而推出对应边相等，接着用弦心距和弦长、半径的计算公式，求出半弦长．2．如图，AB 为O 的直径，弦//CD AB ，E 是AB 延长线上一点，CDB ADE ∠=∠． ()1DE 是O 的切线吗？请说明理由；()2求证：2AC CD BE =⋅．【答案】（1）结论：DE 是O 的切线，理由见解析；（2）证明见解析.【解析】【分析】 （1）连接OD ，只要证明OD DE ⊥即可；（2）只要证明：AC BD =，CDB DBE ∽即可解决问题.【详解】()1解：结论：DE 是O 的切线．理由：连接OD ．CDB ADE ∠=∠，ADC EDB ∴∠=∠，//CD AB ，CDA DAB ∴∠=∠，OA OD =，OAD ODA ∴∠=∠，ADO EDB ∴∠=∠， AB 是直径，90ADB ∴∠=，90ADB ODE ∴∠=∠=，DE OD ∴⊥，DE ∴是O 的切线．()2//CD AB ，ADC DAB ∴∠=∠，CDB DBE ∠=∠，AC BD ∴=，AC BD ∴=，DCB DAB ∠=∠，EDB DAB ∠=∠，EDB DCB∴∠=∠，CDB∴∽DBE，CD DBBD BE∴=，2BD CD BE∴=⋅，2AC CD BE∴=⋅．【点睛】本题考查相似三角形的判定和性质、圆周角定理、切线的判定等知识，解题的关键是学会添加常用辅助线，准确寻找相似三角形解决问题，属于中考常考题型.3．如图，在RtΔABC中，∠ABC=90°，AB=CB，以AB为直径的⊙O交AC于点D，点E是AB边上一点（点E不与点A、B重合），DE的延长线交⊙O于点G，DF⊥DG，且交BC于点F.（1）求证：AE=BF；（2）连接EF，求证：∠FEB=∠GDA；（3）连接GF,若AE=2，EB=4，求ΔGFD的面积.【答案】（1）（2）见解析；（3）9【解析】分析：（1）连接BD，由三角形ABC为等腰直角三角形，求出∠A与∠C的度数，根据AB 为圆的直径，利用圆周角定理得到∠ADB为直角，即BD垂直于AC，利用直角三角形斜边上的中线等于斜边的一半，得到AD=DC=BD=12AC，进而确定出∠A=∠FBD，再利用同角的余角相等得到一对角相等，利用ASA得到三角形AED与三角形BFD全等，利用全等三角形对应边相等即可得证；（2）连接EF，BG，由三角形AED与三角形BFD全等，得到ED=FD，进而得到三角形DEF为等腰直角三角形，利用圆周角定理及等腰直角三角形性质得到一对同位角相等，利用同位角相等两直线平行，再根据平行线的性质和同弧所对的圆周角相等，即可得出结论；（3）由全等三角形对应边相等得到AE=BF=1，在直角三角形BEF中，利用勾股定理求出EF的长，利用锐角三角形函数定义求出DE的长，利用两对角相等的三角形相似得到三角形AED与三角形GEB相似，由相似得比例，求出GE的长，由GE+ED求出GD的长，根据三角形的面积公式计算即可．详解：（1）连接BD．在Rt△ABC中，∠ABC=90°，AB=BC，∴∠A=∠C=45°．∵AB为圆O的直径，∴∠ADB=90°，即BD⊥AC，∴AD=DC=BD=12AC，∠CBD=∠C=45°，∴∠A=∠FBD．∵DF⊥DG，∴∠FDG=90°，∴∠FDB+∠BDG=90°．∵∠EDA+∠BDG=90°，∴∠EDA=∠FDB．在△AED和△BFD中，A FBDAD BDEDA FDB∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AED≌△BFD（ASA），∴AE=BF；（2）连接EF，BG．∵△AED≌△BFD，∴DE=DF．∵∠EDF=90°，∴△EDF是等腰直角三角形，∴∠DEF=45°．∵∠G=∠A=45°，∴∠G=∠DEF，∴GB∥EF，∴∠FEB=∠GBA．∵∠GBA=∠GDA，∴∠FEB=∠GDA；（3）∵AE=BF，AE=2，∴BF=2．在Rt△EBF中，∠EBF=90°，∴根据勾股定理得：EF2=EB2+BF2．∵EB=4，BF=2，∴EF=2242+=25．∵△DEF为等腰直角三角形，∠EDF=90°，∴cos∠DEF=DEEF．∵EF=25，∴DE=25×22=10．∵∠G=∠A，∠GEB=∠AED，∴△GEB∽△AED，∴GEAE=EBED，即GE•ED=AE•EB，∴10•GE=8，即GE=410，则GD=GE+ED=910．∴119101109222S GD DF GD DE=⨯⨯=⨯⨯=⨯⨯=．点睛：本题属于圆综合题，涉及的知识有：全等三角形的判定与性质，相似三角形的判定与性质，勾股定理，圆周角定理，以及平行线的判定与性质，熟练掌握判定与性质是解答本题的关键．4．如图，△ABC内接于⊙O，∠BAC的平分线交⊙O于点D，交BC于点E（BE＞EC），且BD＝23．过点D作DF∥BC，交AB的延长线于点F．（1）求证：DF为⊙O的切线；（2）若∠BAC＝60°，DE＝7，求图中阴影部分的面积．【答案】（1）详见解析；（2）93﹣2π．【解析】【分析】（1）连结OD，根据垂径定理得到OD⊥BC，根据平行线的性质得到OD⊥DF，根据切线的判定定理证明；（2）连结OB，连结OD交BC于P，作BH⊥DF于H，证明△OBD为等边三角形，得到∠ODB=60°，OB=BD=23，根据勾股定理求出PE，证明△ABE∽△AFD，根据相似三角形的性质求出AE，根据阴影部分的面积=△BDF的面积-弓形BD的面积计算．【详解】证明：（1）连结OD，∵AD平分∠BAC交⊙O于D，∴∠BAD=∠CAD，∴BD CD，∴OD⊥BC，∵BC∥DF，∴OD⊥DF，∴DF为⊙O的切线；（2）连结OB，连结OD交BC于P，作BH⊥DF于H，∵∠BAC=60°，AD平分∠BAC，∴∠BAD=30°，∴∠BOD=2∠BAD=60°，∴△OBD为等边三角形，∴∠ODB=60°，，∴∠BDF=30°，∵BC ∥DF ，∴∠DBP=30°，在Rt △DBP 中，PD=12，， 在Rt △DEP 中，∵∴=2，∵OP ⊥BC ，∴BP=CP=3，∴CE=3﹣2=1，∵∠DBE=∠CAE ，∠BED=∠AEC ，∴△BDE ∽△ACE ，∴AE ：BE=CE ：DE ，即AE ：5=1，∴AE=7∵BE ∥DF ，∴△ABE ∽△AFD ， ∴BE AE DF AD=，即5DF = ， 解得DF=12，在Rt △BDH 中，BH=12， ∴阴影部分的面积=△BDF 的面积﹣弓形BD 的面积=△BDF 的面积﹣（扇形BOD 的面积﹣△BOD 的面积）=221601223604π⨯⨯-﹣2π． 【点睛】考查的是切线的判定，扇形面积计算，相似三角形的判定和性质，圆周角定理的应用，等边三角形的判定和性质，掌握切线的判定定理，扇形面积公式是解题的关键．5．已知：如图，在四边形ABCD 中，AD ∥BC ．点E 为CD 边上一点，AE 与BE 分别为∠DAB 和∠CBA 的平分线．（1）请你添加一个适当的条件 ，使得四边形ABCD 是平行四边形，并证明你的结论；（2）作线段AB 的垂直平分线交AB 于点O ，并以AB 为直径作⊙O （要求：尺规作图，保留作图痕迹，不写作法）；（3）在（2）的条件下，⊙O交边AD于点F，连接BF，交AE于点G，若AE=4，sin∠AGF=45，求⊙O的半径．【答案】（1）当AD=BC时，四边形ABCD是平行四边形，理由见解析；（2）作出相应的图形见解析；（3）圆O的半径为2.5．【解析】分析：（1）添加条件AD=BC，利用一组对边平行且相等的四边形为平行四边形验证即可；（2）作出相应的图形，如图所示；（3）由平行四边形的对边平行得到AD与BC平行，可得同旁内角互补，再由AE与BE为角平分线，可得出AE与BE垂直，利用直径所对的圆周角为直角，得到AF与FB垂直，可得出两锐角互余，根据角平分线性质及等量代换得到∠AGF=∠AEB，根据sin∠AGF的值，确定出sin∠AEB的值，求出AB的长，即可确定出圆的半径．详解：（1）当AD=BC时，四边形ABCD是平行四边形，理由为：证明：∵AD∥BC，AD=BC，∴四边形ABCD为平行四边形；故答案为：AD=BC；（2）作出相应的图形，如图所示；（3）∵AD∥BC，∴∠DAB+∠CBA=180°，∵AE与BE分别为∠DAB与∠CBA的平分线，∴∠EAB+∠EBA=90°，∴∠AEB=90°，∵AB为圆O的直径，点F在圆O上，∴∠AFB=90°，∴∠FAG+∠FGA=90°，∵AE平分∠DAB，∴∠FAG=∠EAB，∴∠AGF=∠ABE，∴sin∠ABE=sin∠AGF=45AE AB ，∵AE=4，∴AB=5，则圆O的半径为2.5．点睛：此题属于圆综合题，涉及的知识有：圆周角定理，平行四边形的判定与性质，角平分线性质，以及锐角三角函数定义，熟练掌握各自的性质及定理是解本题的关键．6．如图1，四边形ABCD是正方形，点E是边BC上一点，点F在射线CM上,∠AEF=90°，AE=EF，过点F作射线BC的垂线，垂足为H，连接AC．(1) 试判断BE与FH的数量关系，并说明理由；(2) 求证：∠ACF=90°；(3) 连接AF，过A，E，F三点作圆，如图2. 若EC=4，∠CEF=15°，求的长.图1 图2【答案】（1）BE="FH" ；理由见解析（2）证明见解析（3）=2π【解析】试题分析：（1）由△ABE≌△EHF（SAS）即可得到BE=FH（2）由（1）可知AB=EH，而BC=AB，FH=EB，从而可知△FHC是等腰直角三角形，∠FCH 为45°，而∠ACB也为45°，从而可证明（3)由已知可知∠EAC=30°，AF是直径，设圆心为O，连接EO，过点E作EN⊥AC于点N，则可得△ECN为等腰直角三角形，从而可得EN的长，进而可得AE的长，得到半径，得到所对圆心角的度数，从而求得弧长试题解析：（1）BE=FH．理由如下：∵四边形ABCD是正方形∴∠B=90°，∵FH⊥BC ∴∠FHE=90°又∵∠AEF=90°∴∠AEB+∠HEF="90°" 且∠BAE+∠AEB=90°∴∠HEF=∠BAE ∴∠AEB=∠EFH 又∵AE=EF∴△ABE≌△EHF（SAS）∴BE=FH(2)∵△ABE≌△EHF∴BC=EH，BE=FH 又∵BE+EC=EC+CH ∴BE="CH"∴CH=FH∴∠FCH=45°，∴∠FCM=45°∵AC 是正方形对角线，∴ ∠ACD=45°∴∠ACF=∠FCM +∠ACD =90°（3）∵AE=EF ，∴△AEF 是等腰直角三角形△AEF 外接圆的圆心在斜边AF 的中点上．设该中点为O ．连结EO 得∠AOE=90°过E 作EN ⊥AC 于点NRt △ENC 中，EC=4，∠ECA=45°，∴EN=NC=Rt △ENA 中，EN =又∵∠EAF=45° ∠CAF=∠CEF=15°（等弧对等角） ∴∠EAC=30°∴AE=Rt △AFE 中，AE== EF ，∴AF=8 AE 所在的圆O 半径为4，其所对的圆心角为∠AOE=90°=2π·4·（90°÷360°）=2π考点：1、正方形；2、等腰直角三角形；3、圆周角定理；4、三角函数7．如图，AB 为O 的直径，C 、D 为O 上异于A 、B 的两点，连接CD ，过点C 作CE DB ⊥，交CD 的延长线于点E ，垂足为点E ，直径AB 与CE 的延长线相交于点F .（1）连接AC 、AD ，求证：180DAC ACF ∠+∠=︒.（2）若2ABD BDC ∠=∠.①求证：CF 是O 的切线.②当6BD =，3tan 4F =时，求CF 的长. 【答案】（1）详见解析；（2）①详见解析；② 203CF =. 【解析】【分析】（1）根据圆周角定理证得∠ADB=90°，即AD⊥BD，由CE⊥DB证得AD∥CF，根据平行线的性质即可证得结论；（2）①连接OC．先根据等边对等角及三角形外角的性质得出∠3=2∠1，由已知∠4=2∠1，得到∠4=∠3，则OC∥DB，再由CE⊥DB，得到OC⊥CF，根据切线的判定即可证明CF为⊙O的切线；②由CF∥AD，证出∠BAD=∠F，得出tan∠BAD=tan∠F=BDAD=34，求出AD=43BD=8，利用勾股定理求得AB=10，得出OB=OC=，5，再由tanF=OCCF=34，即可求出CF．【详解】解：（1）AB是O的直径，且D为O上一点，90ADB∴∠=︒，CE DB⊥，90DEC∴∠=︒，//CF AD∴，180DAC ACF∴∠+∠=︒.（2）①如图，连接OC.OA OC=，12∴∠=∠.312∠=∠+∠，321∴∠=∠.42BDC∠=∠，1BDC∠=∠，421∴∠=∠，43∴∠=∠，//OC DB∴.CE DB⊥，OC CF∴⊥.又OC为O的半径，CF∴为O的切线.②由（1）知//CF AD，BAD F∴∠=∠，3tan tan 4BAD F ∴∠==， 34BD AD ∴=. 6BD =483AD BD ∴==， 226810AB ∴=+=，5OB OC ==.OC CF ⊥，90OCF ∴∠=︒，3tan 4OC F CF ∴==， 解得203CF =. 【点睛】本题考查了切线的判定、解直角三角形、圆周角定理等知识；本题综合性强，有一定难度，特别是（2）中，需要运用三角函数、勾股定理和由平行线得出比例式才能得出结果．8．如图所示，ABC ∆内接于圆O ，CD AB ⊥于D ；（1）如图1，当AB 为直径，求证：OBC ACD ∠=∠；（2）如图2，当AB 为非直径的弦，连接OB ，则（1）的结论是否成立？若成立请证明，不成立说明由；（3）如图3，在（2）的条件下，作AE BC ⊥于E ，交CD 于点F ，连接ED ，且2AD BD ED =+，若3DE =，5OB =，求CF 的长度．【答案】（1）见解析；（2）成立；（3）145【解析】【分析】 （1）根据圆周角定理求出∠ACB=90°，求出∠ADC=90°，再根据三角形内角和定理求出即可；（2）根据圆周角定理求出∠BOC=2∠A ，求出∠OBC=90°-∠A 和∠ACD=90°-∠A 即可；（3）分别延长AE 、CD 交⊙O 于H 、K ，连接HK 、CH 、AK ，在AD 上取DG=BD ，延长CG 交AK 于M ，延长KO 交⊙O 于N ，连接CN 、AN ，求出关于a 的方程，再求出a 即可．【详解】（1）证明：∵AB 为直径，∴ACB 90∠=︒， ∵CD AB ⊥于D ， ∴ADC 90∠=︒，∴OBC A 90∠∠+=︒，A ACD 90∠∠+=︒，∴OBC ACD ∠∠=；（2）成立，证明：连接OC ，由圆周角定理得：BOC 2A ∠∠=，∵OC OB =， ∴()()11OBC 180BOC 1802A 90A 22∠∠∠∠=︒-=︒-=︒-， ∵ADC 90∠=︒，∴ACD 90A ∠∠=︒-，∴OBC ACD ∠∠=；（3）分别延长AE 、CD 交⊙O 于H 、K ，连接HK 、CH 、AK ，∵AE BC ⊥，CD BA ⊥，∴AEC ADC 90∠∠==︒，∴BCD CFE 90∠∠+=︒，BAH DFA 90∠∠+=︒，∵CFE DFA ∠∠=，∴BCD BAH ∠∠=，∵根据圆周角定理得：BAH BCH ∠∠=，∴BCD BAH BCH ∠∠∠==，∴由三角形内角和定理得：CHE CFE ∠∠=， ∴CH CF =，∴EH EF =，同理DF DK =，∵DE 3=，∴HK 2DE 6==，在AD 上取DG BD =，延长CG 交AK 于M ，则AG AD BD 2DE 6=-==，BC GC =，∴MCK BCK BAK ∠∠∠==，∴CMK 90∠=︒，延长KO 交⊙O 于N ，连接CN 、AN ，则NAK 90CMK ∠∠=︒=，∴CM //AN ，∵NCK ADK 90∠∠==︒，∴CN //AG ，∴四边形CGAN 是平行四边形，∴AG CN 6==，作OT CK ⊥于T ，则T 为CK 的中点，∵O 为KN 的中点， ∴1OT CN 32==， ∵OTC 90∠=︒，OC 5=，∴由勾股定理得：CT 4=，∴CK 2CT 8==，作直径HS ，连接KS ，∵HK 6=，HS 10=，∴由勾股定理得：KS 8=， ∴3tan HSK tan HAK 4∠∠==， ∴1tan EAB tan BCD 3∠∠==， 设BD a =，CD 3a =， ∴AD BD 2ED a 6=+=+，11DK AD a 233==+， ∵CD DK CK +=，∴13a a 283++=， 解得：9a 5=， ∴113DK a 235=+=， ∴2614CF CK 2DK 855=-=-=． 【点睛】本题考查了垂径定理、解直角三角形、等腰三角形的性质、圆周角定理、勾股定理等知识点，能综合运用知识点进行推理是解此题的关键，综合性比较强，难度偏大．9．如图，已知,,BAC AB AC O ∆=为ABC ∆外心，D 为O 上一点，BD 与AC 的交点为E ，且2·BC AC CE =．①求证：CD CB =；②若030A ∠=，且O 的半径为33+，I 为BCD ∆内心，求OI 的长．【答案】①证明见解析； ②3【解析】【分析】①先求出BC CE AC BC=，然后求出△BCE 和△ACB 相似，根据相似三角形对应角相等可得∠A =∠CBE ，再根据在同圆或等圆中，同弧所对的圆周角相等可得∠A =∠D ，然后求出∠D =∠CBE ，然后根据等角对等边即可得证；②连接OB 、OC ，根据在同圆或等圆中，同弧所对的圆心角等于圆周角的2倍求出∠BOC =60°，然后判定△OBC 是等边三角形，再根据等腰三角形三线合一的性质以及三角形的内心的性质可得OC 经过点I ，设OC 与BD 相交于点F ，然后求出CF ，再根据I 是三角形的内心，利用三角形的面积求出IF ，然后求出CI ，最后根据OI =OC ﹣CI 计算即可得解．【详解】①∵BC 2=AC •CE ，∴BC CE AC BC=．∵∠BCE=∠ECB，∴△BCE∽△ACB，∴∠CBE=∠A．∵∠A=∠D，∴∠D=∠CBE，∴CD=CB；②连接OB、OC．∵∠A=30°，∴∠BOC=2∠A=2×30°=60°．∵OB=OC，∴△OBC是等边三角形．∵CD=CB，I是△BCD的内心，∴OC经过点I，设OC与BD相交于点F，则CF=BC×sin30°12=BC，BF=BC•cos30°3=BC，所以，BD=2BF=23⨯BC3=BC，设△BCD内切圆的半径为r，则S△BCD12=BD•CF12=（BD+CD+BC）•r，即12•3BC•12BC12=（3BC+BC+BC）•r，解得：r3223=+（）BC2332-=BC，即IF2332-=BC，所以，CI=CF﹣IF12=BC233--BC=（23-）BC，OI=OC﹣CI=BC﹣（23-）BC=（3-1）BC．∵⊙O的半径为33+，∴BC=33+，∴OI=（3-1）（33+）=33+3﹣3323-=．【点睛】本题是圆的综合题，主要考查了相似三角形的判定与性质，等腰三角形的判定与性质，圆周角定理，等边三角形的判定与性质，三角形的内心的性质，（2）作辅助线构造出等边三角形并证明得到OC经过△BCD的内心I是解题的关键．10．已知：如图，以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E，过点D作DF⊥BC，垂足为F．（1）求证：DF为⊙O的切线；（2）若等边三角形ABC 的边长为4，求图中阴影部分的面积．【答案】（1）见解析（2）332 23π-【解析】试题分析：（1）连接DO，要证明DF为⊙O的切线只要证明∠FDP=90°即可；（2）首先由已知可得到CD，CF的长，从而利用勾股定理可求得DF的长；再连接OE，求得CF，EF的长，从而利用S直角梯形FDOE﹣S扇形OED求得阴影部分的面积．试题解析：（1）证明：连接DO．∵△ABC是等边三角形，∴∠A=∠C=60°．∵OA=OD，∴△OAD是等边三角形．∴∠ADO=60°，∵DF⊥BC，∴∠CDF=90°﹣∠C=30°，∴∠FDO=180°﹣∠ADO﹣∠CDF=90°，∴DF为⊙O的切线；（2）∵△OAD是等边三角形，∴AD=AO=AB=2．∴CD=AC﹣AD=2．Rt△CDF中，∵∠CDF=30°，∴CF=CD=1．∴DF=，连接OE，则CE=2．∴CF=1，∴EF=1．∴S直角梯形FDOE=（EF+OD）•DF=，∴S扇形OED==，∴S阴影=S直角梯形FDOE﹣S扇形OED=﹣．【点睛】此题考查学生对切线的判定及扇形的面积等知识点的掌握情况，当已知条件中明确指出直线与圆有公共点时，常连接过该公共点的半径，证明该半径垂直于这条直线．也考查了等边三角形的性质和利用割补法计算补规则图形的面积．。

一、中考初中化学综合题1．化学兴趣小组对某工业废水(含有H 2SO 4、Na 2SO 4)中H 2SO 4的含量进行测定．甲、乙两同学各提出不同的测定方法，请回答有关问题：(1)甲同学：取50g 废水于烧杯中，逐渐滴入溶质质量分数为20%的NaOH 溶液，反应过程溶液pH 变化如图．①当加入 30gNaOH 溶液时，烧杯中的溶质为______(填化学式)。

②50g 废水中 H 2SO 4的质量分数是_______？(写出计算过程)。

(2)乙同学：改用BaCl 2溶液代替NaOH 溶液测定废水中的H 2SO 4的含量，结果可能会_____(填“偏高”、“偏低”、“不变”)，理由是_______。

【答案】NaOH 、Na 2SO 4 19.6% 偏高 Na 2SO 4与BaCl 2反应【解析】【分析】【详解】(1)①当加入 30gNaOH 溶液时，氢氧化钠过量，烧杯中的溶质为过量的NaOH 、生成的Na 2SO 4；②设50g 废水中 H 2SO 4的质量为x242422NaOH+ H SO Na SO 2H O2=+809820g x0%⨯ 2080%98=20g x⨯ x=4.9g50g 废水中 H 2SO 4的质量分数是4.9g ÷50g ×100%=9.8%(2)硫酸、硫酸钠都和氯化钡反应生成白色沉淀，改用BaCl 2溶液代替NaOH 溶液测定废水中的H 2SO 4的含量，结果可能会偏高。

2．酸、碱、盐是几类重要的化合物，他们之间能发生复分解反应。

（1）复分解反应发生的条件是有沉淀析出，或有气体放出，或有____________生成。

（2）某化学小组进行“酸和碱的中和反应”实验：将盐酸滴入一定量的澄清石灰水中，实验无明显现象。

取反应后的部分溶液加热、蒸干、得到白色固体。

以下是探究白色固体成分的实验，已知CaCl2溶液呈中性。

请填写下表：实验反思：无明显现象的中和反应可借助酸碱指示剂判断反应终点。

一、中考初中化学综合题1．生活离不开水。

某化学兴趣小组对学校附近河流水质的状况进行调查研究。

（1）要除去水样中的不溶物，可采取的操作是_____。

（2）完成（1）中的操作后，可用_____检验所得水样属于硬水还是软水。

（3）完成（2）中的操作后，测定水样为硬水。

日常生活中，当水的硬度大并且担心病菌过多时，可以采取_____的方法降低水的硬度和杀灭病菌。

（4）ClO2是一种安全的饮用水消毒剂，生产ClO2的化学反应方程式为2NaClO2+X==2ClO2+2NaCl,方程式中X的化学式为_____。

（5）爱护水资源是公民的责任和义务。

下列行为不属于节约用水的是_____。

A用未经处理的工业废水浇地 B洗衣机洗衣服时不间断地边注水边冲洗、排水C洗过菜的水用来浇花 D农业和园林浇灌改大水浸灌为喷灌、滴灌【答案】过滤肥皂水加热 Cl2 C 、D【解析】(1)要除去水样中的不溶物，可采取的操作是过滤；(2)检验所得水样属于硬水还是软水，可用的物质是肥皂水，遇肥皂水产生的泡沫少的是硬水，遇肥皂水产生的泡沫多的是软水；(3)在日常生活中将硬水转化为软水的方法是煮沸；(4)根据X+2NaClO2=2ClO2+2NaCl可知生成物中有2个钠原子、4个氯原子、4个氧原子、在反应物中有2个钠原子、4个氧原子、2个氯原子所以还少2个氯原子，所以化学式是Cl2；(5)A、用工业废水浇地，会造成减产甚至绝产和水体的污染等，不属于节约用水；B、洗衣机洗衣服时不间断地边注水边冲洗、排水，会造成水的浪费；C、洗菜的水用来浇花，一水多用，能节约用水；D、农业和园林浇灌改大水浸灌为喷灌、滴灌，能节约用水。

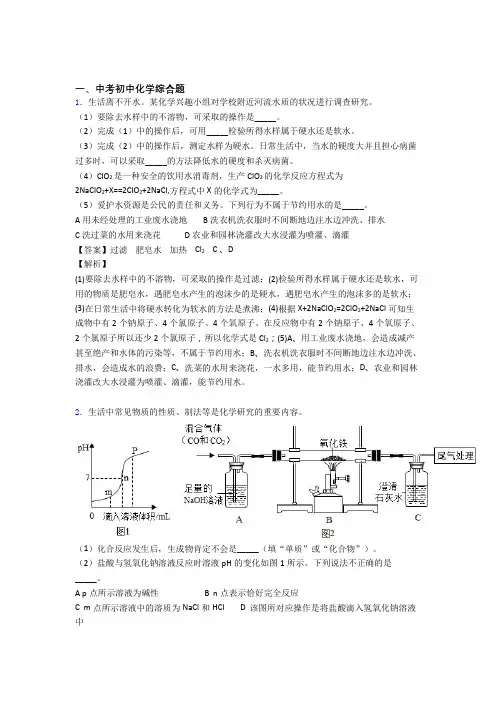
2．生活中常见物质的性质、制法等是化学研究的重要内容。

（1）化合反应发生后，生成物肯定不会是_____（填“单质”或“化合物”）。

（2）盐酸与氢氧化钠溶液反应时溶液pH的变化如图1所示。

下列说法不正确的是_____。

A p点所示溶液为碱性B n点表示恰好完全反应C m点所示溶液中的溶质为NaCl和HClD 该图所对应操作是将盐酸滴入氢氧化钠溶液中（3）沾有浓氨水的棉棒放在浓盐酸瓶口为什么有白烟生成：_____。

一、中考初中化学综合题1．化学兴趣小组同学进行如下实验与探究活动，请你参与。

Ⅰ．制取气体并验证气体性质。

（1）写出仪器a的名称：______。

（2）用A装置制取氧气，反应的化学方程式为______，装置C可以收集氧气，这是因为氧气具有______的性质。

（3）装置B与D组合制取并验证CO2的某些性质。

①检查装置B的气密性的方法：______。

②若装置D中盛放滴有紫色石蕊试液的水，可以观察到的现象是______；若盛放氢氧化钠溶液，则没有明显现象产生。

Ⅱ．在老师的指导下，兴趣小组同学多角度探究二氧化碳与氢氧化钠确实能发生反应。

（4）小明进行如下实验：将收集满CO2的两支试管（相同规格）分别倒立在水和NaOH溶液中，轻轻晃动试管，产生了如下图所示现象。

①小明根据______，判断CO2和NaOH发生了反应，反应的化学方程式为______。

②甲实验的目的是______。

（5）小菁同学取氢氧化钠溶液于烧杯中，用pH计测定溶液的pH为13.5，通入二氧化碳一会儿，测得溶液的pH为11.2，继续通入二氧化碳，再测得溶液的pH为9.2，溶液的pH 降低的原因是______，该实验可以说明CO2和NaOH发生了反应。

（6）小菁根据化学变化的本质特征，设计了另一个实验方案。

实验步骤实验现象实验结论____________CO2与NaOH发生了反应。

【答案】长颈漏斗2KClO32KCl+ 3O2↑（或其他合理答案）氧气的密度比空气大关闭止水夹，往长颈漏斗注入一定量的水，如果长颈漏斗与锥形瓶中的液面形成稳定的水位差说明装置气密（或其他合理答案） 紫色石蕊试液变红 乙试管内液体高度比甲试管内的液体高得多（或其他合理答案） 2NaOH + CO 2 == Na 2CO 3 + H 2O 对比实验（或其他合理答案） 溶液中 NaOH 减少，溶液碱性减弱 取少量 NaOH 溶液于试管中，通入一定量二氧化碳后，再往溶液中滴加稀盐酸 有大量的气泡冒出 【解析】(1)通过分析题中所指仪器的作用可知，a 是长颈漏斗；(2)A 装置制取氧气的反应物是固体，反应条件是加热，氯酸钾在二氧化锰的催化作用下加热生成氯化钾和氧气，化学方程式为：32KClO 22KCl+3O ，C 装置收集氧气的方法是向上排空气法，原因是：氧气的密度比空气大；(3)①检查装置B 的气密性的方法是：关闭止水夹，向长颈漏斗注入一定量的水，如果长颈漏斗与锥形瓶中的液面形成稳定的水位差说明装置气密，说明装置气密性良好；②二氧化碳和水反应生成碳酸，碳酸能使紫色石蕊变红色，所以装置D 中若盛放滴有紫色石蕊试液的水，可以观察到的现象是：紫色石蕊溶液变红色；若盛放氢氧化钠溶液，则没有明显现象产生；(4)①氢氧化钠和二氧化碳反应生成碳酸钠和水，所以小明根据乙试管内的液体比甲试管内的液体高得多，判断二氧化碳和氢氧化钠发生了反应，化学方程式为：22322NaOH+CO ==Na CO +H O ；②甲实验中液面的高度对比乙实验中液面的高度得出结论，所以甲实验的目的是对比实验；(5)溶液的碱性强弱与溶液中的氢氧根离子浓度有关，所以小菁取氢氧化钠溶液于烧杯中，用pH 计测定溶液的pH 为13.5。

一、中考初中化学综合题1．下列A→D的实验装置进行合理组合，即可制取二氧化碳气体也可制取氧气。

（1）写出标注①的仪器名称：__________。

（2）实验室用A装置制取氧气时，在分液漏斗中添加的药品是_________（填化学式），用排水法收集氧气，观察到_______时，再将注满水的集气瓶倒扣住导气管，收集氧气。

若用加热分解高锰酸钾的方法制取氧气，则选用的发生装置为______（填标号），该反应的化学方程式为_____________。

（3）用A、D装置制取并收集二氧化碳，仪器接口的连接顺序是a→___（填“b”或“c”）。

若在D中装半瓶氢氧化钠溶液，将A中生成的二氧化碳气体通入其中一会儿，肉眼观察不到什么可见现象。

实验小组将进行如下三个实验探究活动。

用实验的方法证明二氧化碳与氢氧化钠发生了反应，并验证产物碳酸钠。

实验一：取反应后的D中溶液，滴加酚酞试剂，溶液变红。

实验二：取反应后的D中溶液，加几滴稀盐酸，未观察到气泡的产生。

实验三：取反应后的D中溶液，滴加澄清石灰水，出现浑浊。

（4）研究表明，实验一不能证明化学反应是否进行，理由是___________________。

（5）请判断实验二能否证明变化中无碳酸钠生成并说明理由___________________。

（6）写出实验三发生变化的化学反应方程式_________________________________。

查资料：常温下，氢氧化钠易溶于酒精溶剂形成溶液，而碳酸钠难溶于酒精溶剂。

（7）请你根据“资料”信息，设计一个实验方案，证明二氧化碳与氢氧化钠发生了化学的反应：____________________________________________________________。

（8）若以上方案有人用75%的医用酒精来配制氢氧化钠溶液进行实验，结果达不到预期效果，原因是________________________________________________________。

初三培优 易错 难题平行四边形辅导专题训练附详细答案一、平行四边形1．在四边形ABCD 中，180B D ∠+∠=︒，对角线AC 平分BAD ∠.（1）如图1，若120DAB ∠=︒，且90B ∠=︒，试探究边AD 、AB 与对角线AC 的数量关系并说明理由.（2）如图2，若将（1）中的条件“90B ∠=︒”去掉，（1）中的结论是否成立？请说明理由.（3）如图3，若90DAB ∠=︒，探究边AD 、AB 与对角线AC 的数量关系并说明理由.【答案】（1）AC AD AB =+.证明见解析；（2）成立；（3）2AD AB AC +=.理由见解析.【解析】试题分析：（1）结论：AC=AD+AB ，只要证明AD=12AC ，AB=12AC 即可解决问题； （2）（1）中的结论成立．以C 为顶点，AC 为一边作∠ACE=60°，∠ACE 的另一边交AB 延长线于点E ，只要证明△DAC ≌△BEC 即可解决问题；（3）结论：AD +AB ＝2AC ．过点C 作CE ⊥AC 交AB 的延长线于点E ，只要证明△ACE 是等腰直角三角形，△DAC ≌△BEC 即可解决问题；试题解析：解：（1）AC=AD+AB ．理由如下：如图1中，在四边形ABCD 中，∠D+∠B=180°，∠B=90°，∴∠D=90°，∵∠DAB=120°，AC 平分∠DAB ，∴∠DAC=∠BAC=60°，∵∠B=90°，∴AB＝12AC，同理AD＝12AC．∴AC=AD+AB．（2）（1）中的结论成立，理由如下：以C为顶点，AC为一边作∠ACE=60°，∠ACE的另一边交AB延长线于点E，∵∠BAC=60°，∴△AEC为等边三角形，∴AC=AE=CE，∵∠D+∠ABC=180°，∠DAB=120°，∴∠DCB=60°，∴∠DCA=∠BCE，∵∠D+∠ABC=180°，∠ABC+∠EBC=180°，∴∠D=∠CBE，∵CA=CE，∴△DAC≌△BEC，∴AD=BE，∴AC=AD+AB．（3）结论：AD+AB＝2AC．理由如下：过点C作CE⊥AC交AB的延长线于点E，∵∠D+∠B=180°，∠DAB=90°，∴DCB=90°，∵∠ACE=90°，∴∠DCA=∠BCE，又∵AC平分∠DAB，∴∠CAB=45°，∴∠E=45°．∴AC=CE．又∵∠D+∠ABC=180°，∠D=∠CBE，∴△CDA ≌△CBE ，∴AD=BE ，∴AD+AB=AE ．在Rt △ACE 中，∠CAB=45°，∴AE ＝245AC AC cos ︒＝ ∴2AD AB AC +＝.2．如图①，在等腰Rt ABC 中，90BAC ∠=，点E 在AC 上(且不与点A 、C 重合)，在ABC △的外部作等腰Rt CED △，使90CED ∠=，连接AD ，分别以AB ，AD 为邻边作平行四边形ABFD ，连接AF ．()1请直接写出线段AF ，AE 的数量关系；()2①将CED 绕点C 逆时针旋转，当点E 在线段BC 上时，如图②，连接AE ，请判断线段AF ，AE 的数量关系，并证明你的结论；②若25AB =，2CE =，在图②的基础上将CED 绕点C 继续逆时针旋转一周的过程中，当平行四边形ABFD 为菱形时，直接写出线段AE 的长度．【答案】（1）证明见解析；（2）①AF 2AE =②4222【解析】【分析】 ()1如图①中，结论：AF 2AE =，只要证明AEF 是等腰直角三角形即可； ()2①如图②中，结论：AF 2AE =，连接EF ，DF 交BC 于K ，先证明EKF ≌EDA 再证明AEF 是等腰直角三角形即可；②分两种情形a 、如图③中，当AD AC =时，四边形ABFD 是菱形.b 、如图④中当AD AC =时，四边形ABFD 是菱形.分别求解即可.【详解】()1如图①中，结论：AF 2AE =．理由：四边形ABFD 是平行四边形，AB DF ∴=，AB AC =，AC DF ∴=，DE EC =，AE EF ∴=，DEC AEF 90∠∠==，AEF ∴是等腰直角三角形，AF 2AE ∴=．故答案为AF 2AE =．()2①如图②中，结论：AF 2AE =．理由：连接EF ，DF 交BC 于K ．四边形ABFD 是平行四边形，AB //DF ∴，DKE ABC 45∠∠∴==，EKF 180DKE 135∠∠∴=-=，EK ED =，ADE 180EDC 18045135∠∠=-=-=，EKF ADE ∠∠∴=，DKC C ∠∠=，DK DC ∴=，DF AB AC ==，KF AD ∴=，在EKF 和EDA 中，EK ED EKF ADE KF AD =⎧⎪∠=∠⎨⎪=⎩，EKF ∴≌EDA ，EF EA ∴=，KEF AED ∠∠=，FEA BED 90∠∠∴==，AEF ∴是等腰直角三角形，AF 2AE ∴=． ②如图③中，当AD AC =时，四边形ABFD 是菱形，设AE 交CD 于H ，易知EH DH CH 2===，22AH (25)(2)32=-=，AE AH EH 42=+=，如图④中当AD AC =时，四边形ABFD 是菱形，易知AE AH EH 32222=-=-=，综上所述，满足条件的AE 的长为4222【点睛】本题考查四边形综合题、全等三角形的判定和性质、等腰直角三角形的判定和性质、平行四边形的性质、勾股定理等知识，解题的关键是熟练掌握全等三角形的判定和性质，寻找全等的条件是解题的难点，属于中考常考题型．3．已知：如图，在平行四边形ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．（1）求证：△DOE≌△BOF．（2）当∠DOE等于多少度时，四边形BFDE为菱形？请说明理由．【答案】（1）证明见解析；（2）当∠DOE=90°时，四边形BFED为菱形，理由见解析.【解析】试题分析：（1）利用平行四边形的性质以及全等三角形的判定方法得出△DOE≌△BOF （ASA）；（2）首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD是平行四边形，进而利用垂直平分线的性质得出BE=ED，即可得出答案．试题解析：（1）∵在▱ABCD中，O为对角线BD的中点，∴BO=DO，∠EDB=∠FBO，在△EOD和△FOB中，∴△DOE≌△BOF（ASA）；（2）当∠DOE=90°时，四边形BFDE为菱形，理由：∵△DOE≌△BOF，∴OE=OF，又∵OB=OD，∴四边形EBFD是平行四边形，∵∠EOD=90°，∴EF⊥BD，∴四边形BFDE为菱形．考点：平行四边形的性质；全等三角形的判定与性质；菱形的判定．4．如图，四边形ABCD中，AD∥BC，∠A=90°，BD=BC，点E为CD的中点，射线BE交AD 的延长线于点F，连接CF．（1）求证：四边形BCFD是菱形；（2）若AD=1，BC=2，求BF的长．【答案】（1）证明见解析（2）23【解析】（1）∵AF∥BC，∴∠DCB=∠CDF，∠FBC=∠BFD，∵点E为CD的中点，∴DE=EC，在△BCE与△FDE中，FBC BFDDCB CDFDE EC∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BCE≌△FDE，∴DF=BC，又∵DF∥BC，∴四边形BCDF为平行四边形，∵BD=BC，∴四边形BCFD是菱形；（2）∵四边形BCFD是菱形，∴BD=DF=BC=2，在Rt△BAD中，AB=223BD AD-=，∵AF=AD+DF=1+2=3，在Rt△BAF中，BF=22AB AF+=23．5．如图，ABCD是正方形，点G是BC上的任意一点，DE⊥AG于E，BF∥DE，交AG于F．求证：AF=BF+EF．【答案】详见解析.【解析】【分析】由四边形ABCD为正方形，可得出∠BAD为90°，AB=AD，进而得到∠BAG与∠EAD互余，又DE垂直于AG，得到∠EAD与∠ADE互余，根据同角的余角相等可得出∠ADE=∠BAF，利用AAS可得出△ABF≌△DAE；利用全等三角的对应边相等可得出BF=AE，由AF-AE=EF，等量代换可得证.【详解】∵ABCD是正方形，∴AD=AB，∠BAD=90°∵DE ⊥AG ，∴∠DEG=∠AED=90°∴∠ADE+∠DAE=90°又∵∠BAF+∠DAE=∠BAD=90°，∴∠ADE=∠BAF ．∵BF ∥DE ，∴∠AFB=∠DEG=∠AED ．在△ABF 与△DAE 中，AFB AED ADE BAF AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△ABF ≌△DAE （AAS ）．∴BF=AE ．∵AF=AE+EF ，∴AF=BF+EF ．点睛：此题考查了正方形的性质，全等三角形的判定与性质，矩形的判定与性质，熟练掌握判定与性质是解本题的关键．6．如图，在△ABC 中，∠ACB=90°，∠CAB=30°，以线段AB 为边向外作等边△ABD ，点E 是线段AB 的中点，连接CE 并延长交线段AD 于点F ．（1）求证：四边形BCFD 为平行四边形；（2）若AB=6，求平行四边形ADBC 的面积．【答案】（1）见解析；（2）S 平行四边形ADBC 273 【解析】【分析】（1）在Rt △ABC 中，E 为AB 的中点，则CE=12AB ，BE=12AB ，得到∠BCE=∠EBC=60°.由△AEF ≌△BEC ，得∠AFE=∠BCE=60°.又∠D=60°，得∠AFE=∠D=60度.所以FC ∥BD ，又因为∠BAD=∠ABC=60°，所以AD ∥BC ，即FD//BC ，则四边形BCFD 是平行四边形.（2）在Rt △ABC 中，求出BC ，AC 即可解决问题；【详解】解：（1）证明：在△ABC 中，∠ACB=90°，∠CAB=30°，∴∠ABC=60°，在等边△ABD 中，∠BAD=60°，∴∠BAD=∠ABC=60°，∵E 为AB 的中点，∴AE=BE ，又∵∠AEF=∠BEC ，∴△AEF ≌△BEC ，在△ABC 中，∠ACB=90°，E 为AB 的中点，∴CE=12AB ，BE=12AB ，∴CE=AE ，∴∠EAC=∠ECA=30°，∴∠BCE=∠EBC=60°，又∵△AEF ≌△BEC ，∴∠AFE=∠BCE=60°，又∵∠D=60°，∴∠AFE=∠D=60°，∴FC ∥BD ，又∵∠BAD=∠ABC=60°，∴AD ∥BC ，即FD ∥BC ，∴四边形BCFD 是平行四边形；（2）解：在Rt △ABC 中，∵∠BAC=30°，AB=6，∴BC=AF=3，AC=∴S 平行四边形BCFD =3×，S △ACF =12×3×，S 平行四边形ADBC ． 【点睛】本题考查平行四边形的判定和性质、直角三角形斜边中线定理、等边三角形的性质、解直角三角形、勾股定理等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型.7．（问题情境）在△ABC 中，AB ＝AC ，点P 为BC 所在直线上的任一点，过点P 作PD ⊥AB ，PE ⊥AC ，垂足分别为D 、E ，过点C 作CF ⊥AB ，垂足为F ．当P 在BC 边上时（如图1），求证：PD+PE ＝CF ．证明思路是：如图2，连接AP ，由△ABP 与△ACP 面积之和等于△ABC 的面积可以证得：PD+PE ＝CF ．（不要证明）（变式探究）（1）当点P 在CB 延长线上时，其余条件不变（如图3），试探索PD 、PE 、CF 之间的数量关系并说明理由；请运用上述解答中所积累的经验和方法完成下列两题：（结论运用）（2）如图4，将长方形ABCD 沿EF 折叠，使点D 落在点B 上，点C 落在点C′处，点P 为折痕EF 上的任一点，过点P 作PG ⊥BE 、PH ⊥BC ，垂足分别为G 、H ，若AD ＝16，CF ＝6，求PG+PH 的值．（迁移拓展）（3）在直角坐标系中，直线l 1：y ＝-43x+8与直线l 2：y ＝﹣2x+8相交于点A ，直线l 1、l 2与x 轴分别交于点B 、点C ．点P 是直线l 2上一个动点，若点P 到直线l 1的距离为2．求点P 的坐标．【答案】【变式探究】证明见解析【结论运用】8【迁移拓展】（﹣1，6），（1，10）【解析】【变式探究】连接AP，同理利用△ABP与△ACP面积之差等于△ABC的面积可以证得；【结论运用】过点E作EQ⊥BC，垂足为Q，根据勾股定理和矩形的性质解答即可；【迁移拓展】分两种情况，利用结论，求得点P到x轴的距离，再利用待定系数法可求出P的坐标．【详解】变式探究:连接AP，如图3：∵PD⊥AB，PE⊥AC，CF⊥AB，且S△ABC＝S△ACP﹣S△ABP，∴12AB•CF＝12AC•PE﹣12AB•PD．∵AB＝AC，∴CF＝PD﹣PE；结论运用:过点E作EQ⊥BC，垂足为Q，如图④，∵四边形ABCD是长方形，∴AD＝BC，∠C＝∠ADC＝90°．∵AD＝16，CF＝6，∴BF＝BC﹣CF＝AD﹣CF＝5，由折叠可得：DF＝BF，∠BEF＝∠DEF．∴DF＝5．∵∠C＝90°，∴DC2222-=-8．106DF CF∵EQ⊥BC，∠C＝∠ADC＝90°，∴∠EQC＝90°＝∠C＝∠ADC．∴四边形EQCD是长方形．∴EQ＝DC＝4．∵AD∥BC，∴∠DEF＝∠EFB．∵∠BEF＝∠DEF，∴∠BEF＝∠EFB．∴BE＝BF，由问题情境中的结论可得：PG+PH＝EQ．∴PG+PH＝8．∴PG+PH的值为8；迁移拓展:如图，由题意得：A（0，8），B（6，0），C（﹣4，0）∴AB2210，BC＝10．68∴AB＝BC，（1）由结论得：P1D1+P1E1＝OA＝8∵P1D1＝1＝2，∴P1E1＝6 即点P1的纵坐标为6又点P1在直线l2上，∴y＝2x+8＝6，∴x＝﹣1，即点P1的坐标为（﹣1，6）；（2）由结论得：P2E2﹣P2D2＝OA＝8∵P2D2＝2，∴P2E2＝10 即点P1的纵坐标为10又点P1在直线l2上，∴y＝2x+8＝10，∴x＝1，即点P1的坐标为（1，10）【点睛】本题考查了矩形的性质与判定、等腰三角形的性质与判定及勾股定理等知识点，利用面积法列出等式是解决问题的关键．8．如图所示，矩形ABCD中，点E在CB的延长线上，使CE＝AC，连接AE，点F是AE的中点，连接BF、DF，求证：BF⊥DF．【答案】见解析.【解析】【分析】延长BF，交DA的延长线于点M，连接BD，进而求证△AFM≌△EFB，得AM=BE，FB=FM，即可求得BC+BE=AD+AM，进而求得BD=BM，根据等腰三角形三线合一的性质即可求证BF⊥DF．【详解】延长BF，交DA的延长线于点M，连接BD．∵四边形ABCD是矩形，∴MD∥BC，∴∠AMF=∠EBF，∠E=∠MAF，又FA=FE，∴△AFM≌△EFB，∴AM=BE，FB=FM．∵矩形ABCD中，∴AC=BD，AD=BC，∴BC+BE=AD+AM，即CE=MD．∵CE=AC，∴AC=CE= BD =DM．∵FB=FM，∴BF⊥DF．【点睛】本题考查了矩形的性质，全等三角形的判定和对应边相等的性质，等腰三角形三线合一的性质，本题中求证DB=DM是解题的关键．9．现有一张矩形纸片ABCD（如图），其中AB＝4cm，BC＝6cm，点E是BC的中点．将纸片沿直线AE折叠，点B落在四边形AECD内，记为点B′，过E作EF垂直B′C，交B′C于F．（1）求AE、EF的位置关系；（2）求线段B′C的长，并求△B′EC的面积．【答案】（1）见解析；（2）S△B′EC＝108 25．【解析】【分析】（1）由折线法及点E 是BC 的中点，可证得△B'EC 是等腰三角形，再有条件证明∠AEF=90°即可得到AE ⊥EF ；（2）连接BB′，通过折叠，可知∠EBB′=∠EB′B ，由E 是BC 的中点，可得EB′=EC ，∠ECB′=∠EB′C ，从而可证△BB′C 为直角三角形，在Rt △AOB 和Rt △BOE 中，可将OB ，BB′的长求出，在Rt △BB′C 中，根据勾股定理可将B′C 的值求出.【详解】（1）由折线法及点E 是BC 的中点，∴EB ＝EB ′＝EC ，∠AEB ＝∠AEB ′，∴△B 'EC 是等腰三角形，又∵EF ⊥B ′C∴EF 为∠B 'EC 的角平分线，即∠B ′EF ＝∠FEC ，∴∠AEF ＝180°﹣（∠AEB +∠CEF ）＝90°，即∠AEF ＝90°，即AE ⊥EF ；（2）连接BB '交AE 于点O ，由折线法及点E 是BC 的中点，∴EB ＝EB ′＝EC ，∴∠EBB ′＝∠EB ′B ，∠ECB ′＝∠EB ′C ；又∵△BB 'C 三内角之和为180°，∴∠BB 'C ＝90°；∵点B ′是点B 关于直线AE 的对称点，∴AE 垂直平分BB ′；在Rt △AOB 和Rt △BOE 中，BO 2＝AB 2﹣AO 2＝BE 2﹣（AE ﹣AO ）2将AB ＝4cm ，BE ＝3cm ，AE ＝5cm ，∴AO ＝165 cm ，∴BO ＝125cm ， ∴BB ′＝2BO ＝245cm ，∴在Rt △BB 'C 中，B ′C 518cm ， 由题意可知四边形OEFB ′是矩形，∴EF ＝OB ′＝125， ∴S △B ′EC ＝*111812108225525B C EF '⨯=⨯⨯=．【点睛】考查图形的折叠变化及三角形的内角和定理勾股定理的和矩形的性质综合运用．关键是要理解折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，只是位置变化．10．在ABC 中，AD BC ⊥于点D ，点E 为AC 边的中点，过点A 作//AF BC ，交DE 的延长线于点F ，连接CF ．()1如图1，求证：四边形ADCF 是矩形；()2如图2，当AB AC =时，取AB 的中点G ，连接DG 、EG ，在不添加任何辅助线和字母的条件下，请直接写出图中所有的平行四边形（不包括矩形ADCF ）．【答案】(1) 证明见解析；（2）四边形ABDF 、四边形AGEF 、四边形GBDE 、四边形AGDE 、四边形GDCE 都是平行四边形．【解析】【分析】（1）由△AEF ≌△CED ，推出EF=DE ，又AE=EC ，推出四边形ADCF 是平行四边形，只要证明∠ADC=90°，即可推出四边形ADCF 是矩形．（2）四边形ABDF 、四边形AGEF 、四边形GBDE 、四边形AGDE 、四边形GDCE 都是平行四边形．【详解】()1证明：∵//AF BC ，∴AFE EDC ∠=∠，∵E 是AC 中点，∴AE EC =，在AEF 和CED 中，AFE CDE AEF CED AE EC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴AEF CED ≅，∴EF DE =，∵AE EC =，∴四边形ADCF 是平行四边形，∵AD BC ⊥，∴90ADC ∠=，∴四边形ADCF 是矩形．()2∵线段DG 、线段GE 、线段DE 都是ABC 的中位线，又//AF BC ，∴//AB DE ，//DG AC ，//EG BC ， ∴四边形ABDF 、四边形AGEF 、四边形GBDE 、四边形AGDE 、四边形GDCE 都是平行四边形．【点睛】考查平行四边形的判定、矩形的判定、三角形的中位线定理、全等三角形的判定和性质等知识，正确寻找全等三角形解决问题是解题的关键.11．猜想与证明：如图1，摆放矩形纸片ABCD 与矩形纸片ECGF ，使B 、C 、G 三点在一条直线上，CE 在边CD 上，连接AF ，若M 为AF 的中点，连接DM 、ME ，试猜想DM 与ME 的关系，并证明你的结论．拓展与延伸：（1）若将”猜想与证明“中的纸片换成正方形纸片ABCD 与正方形纸片ECGF ，其他条件不变，则DM 和ME 的关系为 ．（2）如图2摆放正方形纸片ABCD 与正方形纸片ECGF ，使点F 在边CD 上，点M 仍为AF 的中点，试证明（1）中的结论仍然成立．【答案】猜想：DM=ME ，证明见解析；（2）成立，证明见解析.【解析】试题分析：延长EM交AD于点H，根据ABCD和CEFG为矩形得到AD∥EF，得到△FME和△AMH全等，得到HM=EM，根据Rt△HDE得到HM=DE，则可以得到答案；（1）、延长EM交AD于点H，根据ABCD和CEFG为矩形得到AD∥EF，得到△FME和△AMH全等，得到HM=EM，根据Rt△HDE得到HM=DE，则可以得到答案；（2）、连接AE，根据正方形的性质得出∠FCE=45°，∠FCA=45°，根据RT△ADF中AM=MF得出DM=AM=MF，根据RT△AEF中AM=MF得出AM=MF=ME，从而说明DM=ME.试题解析：如图1，延长EM交AD于点H，∵四边形ABCD和CEFG是矩形，∴AD∥EF，∴∠EFM=∠HAM，又∵∠FME=∠AMH，FM=AM，在△FME和△AMH中，∴△FME≌△AMH（ASA）∴HM=EM，在RT△HDE中，HM=DE，∴DM=HM=ME，∴DM=ME．（1）、如图1，延长EM交AD于点H，∵四边形ABCD和CEFG是矩形，∴AD∥EF，∴∠EFM=∠HAM，又∵∠FME=∠AMH，FM=AM，在△FME和△AMH中，∴△FME≌△AMH（ASA）∴HM=EM，在RT△HDE中，HM=EM∴DM=HM=ME，∴DM=ME，（2）、如图2，连接AE，∵四边形ABCD和ECGF是正方形，∴∠FCE=45°，∠FCA=45°，∴AE和EC在同一条直线上，在RT△ADF中，AM=MF，∴DM=AM=MF，在RT△AEF中，AM=MF，∴AM=MF=ME，∴DM=ME．考点：（1）、三角形全等的性质；（2）、矩形的性质.12．如图，在正方形ABCD中，点E在CD上，AF⊥AE交CB的延长线于F．求证：AE=AF．【答案】见解析【解析】【分析】根据同角的余角相等证得∠BAF=∠DAE，再利用正方形的性质可得AB=AD，∠ABF=∠ADE=90°，根据ASA判定△ABF≌△ADE，根据全等三角形的性质即可证得AF=AE．【详解】∵AF⊥AE，∴∠BAF+∠BAE=90°，又∵∠DAE+∠BAE=90°，∴∠BAF=∠DAE，∵四边形ABCD是正方形，∴AB=AD，∠ABF=∠ADE=90°，在△ABF和△ADE中，，∴△ABF≌△ADE（ASA），∴AF=AE．【点睛】本题主要考查了正方形的性质、全等三角形的判定和性质等知识点，证明△ABF≌△ADE是解决本题的关键．13．小明在矩形纸片上画正三角形，他的做法是：①对折矩形纸片ABCD(AB>BC)，使AB 与DC重合，得到折痕EF，把纸片展平；②沿折痕BG折叠纸片，使点C落在EF上的点P 处，再折出PB、PC，最后用笔画出△PBC(图1)．（1）求证：图1中的PBC是正三角形：（2）如图2，小明在矩形纸片HIJK上又画了一个正三角形IMN，其中IJ=6cm，且HM=JN．①求证：IH=IJ②请求出NJ的长；（3）小明发现：在矩形纸片中，若一边长为6cm，当另一边的长度a变化时，在矩形纸片上总能画出最大的正三角形，但位置会有所不同．请根据小明的发现，画出不同情形的示意图(作图工具不限，能说明问题即可)，并直接写出对应的a的取值范围．【答案】（1）证明见解析；（2）①证明见解析；②1233）3a＜3a＞3【解析】分析：（1）由折叠的性质和垂直平分线的性质得出PB=PC，PB=CB，得出PB=PC=CB即可；（2）①利用“HL”证Rt△IHM≌Rt△IJN即可得；②IJ上取一点Q，使QI=QN，由Rt△IHM≌Rt△IJN知∠HIM=∠JIN=15°，继而可得∠NQJ=30°，设NJ=x，则IQ=QN=2x、3，根据IJ=IQ+QJ求出x即可得；（3）由等边三角形的性质、直角三角形的性质、勾股定理进行计算，画出图形即可．（1）证明：∵①对折矩形纸片ABCD(AB>BC)，使AB与DC重合，得到折痕EF∴PB=PC∵沿折痕BG 折叠纸片，使点C 落在EF 上的点P 处 ∴PB=BC∴PB=PC=BC∴△PBC 是正三角形：（2）证明：①如图∵矩形AHIJ∴∠H=∠J=90°∵△MNJ 是等边三角形∴MI=NI在Rt △MHI 和Rt △JNI 中MI NI MH NJ =⎧⎨=⎩∴Rt △MHI ≌Rt △JNI （HL ）∴HI=IJ②在线段IJ 上取点Q ，使IQ=NQ∵Rt △IHM ≌Rt △IJN ，∴∠HIM=∠JIN ，∵∠HIJ=90°、∠MIN=60°，∴∠HIM=∠JIN=15°，由QI=QN 知∠JIN=∠QNI=15°，∴∠NQJ=30°，设NJ=x ，则IQ=QN=2x ，22=3QN NJ -x ， ∵IJ=6cm ，∴3，∴33cm ）． （3）分三种情况：①如图：设等边三角形的边长为b ，则0＜b≤6，则tan60°=3=2a b ，∴a=32b ， ∴0＜b≤632=33； ②如图当DF 与DC 重合时，DF=DE=6，∴a=sin60°×DE=632=33， 当DE 与DA 重合时，a=6643sin6032==︒， ∴33＜a ＜43；③如图∵△DEF 是等边三角形∴∠FDC=30°∴DF=6643 cos3032==︒∴a＞43点睛：本题是四边形的综合题目，考查了折叠的性质、等边三角形的判定与性质、旋转的性质、直角三角形的性质、正方形的性质、全等三角形的判定与性质等知识；本题综合性强，难度较大．14．如图①，在△ABC中，AB=7，tanA=，∠B=45°．点P从点A出发，沿AB方向以每秒1个单位长度的速度向终点B运动（不与点A、B重合），过点P作PQ⊥AB．交折线AC-CB于点Q，以PQ为边向右作正方形PQMN，设点P的运动时间为t（秒），正方形PQMN 与△ABC重叠部分图形的面积为S（平方单位）．（1）直接写出正方形PQMN的边PQ的长（用含t的代数式表示）．（2）当点M落在边BC上时，求t的值．（3）求S与t之间的函数关系式．（4）如图②，点P运动的同时，点H从点B出发，沿B-A-B的方向做一次往返运动，在B-A 上的速度为每秒2个单位长度，在A-B上的速度为每秒4个单位长度，当点H停止运动时，点P也随之停止，连结MH ．设MH将正方形PQMN分成的两部分图形面积分别为S 1、S 2（平方单位）（0＜S1＜S 2），直接写出当S2≥3S1时t 的取值范围．【答案】(1) PQ=7-t．(2) t=．(3) 当0＜t≤时，S=．当＜t≤4，．当4＜t＜7时，．（4）或或．【解析】试题分析：（1）分两种情况讨论：当点Q 在线段AC 上时，当点Q在线段BC上时．（2）根据AP+PN+NB=AB，列出关于t的方程即可解答；（3）当0＜t≤时，当＜t≤4，当4＜t＜7时；（4）或或．试题解析：（1）当点Q在线段AC上时，PQ=tanAAP=t．当点Q在线段BC上时，PQ=7-t．（2）当点M落在边BC上时，如图③，由题意得：t+t+t=7，解得：t=．∴当点M落在边BC上时，求t的值为．（3）当0＜t≤时，如图④，S=．当＜t≤4，如图⑤，．当4＜t＜7时，如图⑥，．（4）或或．．考点：四边形综合题.15．如图，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点（不与点A、点D重合），将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH．（1）求证：∠APB=∠BPH；（2）当点P在边AD上移动时，求证：△PDH的周长是定值；（3）当BE+CF的长取最小值时，求AP的长．【答案】（1）证明见解析．（2）证明见解析．（3）2．【解析】试题分析：（1）根据翻折变换的性质得出∠PBC=∠BPH，进而利用平行线的性质得出∠APB=∠PBC即可得出答案；（2）首先证明△ABP≌△QBP，进而得出△BCH≌△BQH，即可得出PD+DH+PH=AP+PD+DH+HC=AD+CD=8；（3）过F作FM⊥AB，垂足为M，则FM=BC=AB，证明△EFM≌△BPA，设AP=x，利用折叠的性质和勾股定理的知识用x表示出BE和CF，结合二次函数的性质求出最值．试题解析：（1）解：如图1，∵PE=BE，∴∠EBP=∠EPB．又∵∠EPH=∠EBC=90°，∴∠EPH-∠EPB=∠EBC-∠EBP．即∠PBC=∠BPH．又∵AD∥BC，∴∠APB=∠PBC．∴∠APB=∠BPH．（2）证明：如图2，过B作BQ⊥PH，垂足为Q．由（1）知∠APB=∠BPH，又∵∠A=∠BQP=90°，BP=BP，在△ABP和△QBP中，，∴△ABP≌△QBP（AAS），∴AP=QP，AB=BQ，又∵AB=BC，∴BC=BQ．又∠C=∠BQH=90°，BH=BH，在△BCH和△BQH中，，∴△BCH≌△BQH（SAS），∴CH=QH．∴△PHD的周长为：PD+DH+PH=AP+PD+DH+HC=AD+CD=8．∴△PDH的周长是定值．（3）解：如图3，过F作FM⊥AB，垂足为M，则FM=BC=AB．又∵EF为折痕，∴EF⊥BP．∴∠EFM+∠MEF=∠ABP+∠BEF=90°，∴∠EFM=∠ABP．又∵∠A=∠EMF=90°，在△EFM和△BPA中，，∴△EFM≌△BPA（AAS）．∴EM=AP．设AP=x在Rt△APE中，（4-BE）2+x2=BE2．解得BE=2+，∴CF=BE-EM=2+-x，∴BE+CF=-x+4=（x-2）2+3．当x=2时，BE+CF取最小值，∴AP=2．考点：几何变换综合题．。

一、初中物理电路类问题1．如图所示，两盏相同的电灯在闭合开关后都能发光．过了一会儿，两盏电灯突然同时都不亮了，且电压表和电流表的示数均变为零．如果电路中只有一处故障，则故障可能是 ( )A．电灯L1断路B．电灯L2断路C．电灯L1短路D．电灯L2短路【答案】A【解析】【分析】电路故障分为短路和断路．如图灯L1和灯L2串联，电压表测灯L2两端电压．在闭合开关后两盏电灯突然同时都不亮了，且电压表和电流表的示数均变为零．如果是电路短路，电路中还有电流．则电路为断路，电路中无电流．【详解】A．电灯L1断路，则整个电路中都没有电流，灯都不亮，电表无示数．符合题意；B．电灯L2断路．则电压表会与灯L1串联，电压表分担电源电压有示数，灯不亮，电流表无示数．不合题意；C．电灯L1短路，灯L2会分担电源电压，会变亮，电表有示数．不合题意；D．电灯L2短路，电压表也短路无示数．但灯L1会分担电源电压，会变亮，电流表有示数．不合题意；故选A。

2．关于如图所示电路的判断，正确的是（）A．只闭合开关1S时，灯泡1L、3L并联B．只闭合开关2S时，灯泡2L、3L并联C．只闭合开关2S、3S时，灯泡2L、3L串联D ．闭合所有开关时灯泡1L 、2L 并联，3L 短路【答案】D【解析】【分析】【详解】A ．从图中可以看到，只闭合开关1S 时，电流从电源正极流出，流过灯泡3L ，流过开关1S ，再流过灯泡1L ，最后回负极，这时灯泡1L 、3L 是串联的，A 错误；B ．从图中可以看到，只闭合开关2S 时，电流从电源正极流出，流过灯泡3L ，流过开关2S ，再流过灯泡2L ，最后回负极，这时灯泡2L 、3L 是串联的，B 错误；C ．从图中可以看到，只闭合开关2S 、3S 时，电流从电源正极流出，不会流过灯泡3L ，会流过开关3S ，接着电流不会流过开关2S ，因为开关1S 是断开的，电流会流过灯泡2L ，最后回负极，这情况下只有灯泡2L 接在电路中，C 错误；D ．从图中可以看到，闭合所有开关时，电流从电源正极流出，不会流过灯泡3L ，会流过开关3S ，然后分为两部分电流，一部分电流往上流，流过开关2S 、1S 、灯泡1L ，最后回负极，另一部分电流流过灯泡2L ，最后回负极，由上述可知，灯泡1L 、2L 并联，3L 被短路了，D 正确。

一、初中物理家庭电路故障的分析问题1．小明家火线上的熔丝熔断,小明检查时，断开所有的开关，将一只完好的白炽灯L接到图示位置；下列说法正确的是（）A．只闭合S、S1，若灯L正常发光，说明L1支路无故障B．只闭合S、S2，若灯L正常发光，说明L2支路短路C．只闭合S、S1，若灯L发光较暗，说明L1支路断路D．只闭合S、S2，若灯L不发光，说明L2支路短路【答案】B【解析】【分析】【详解】A．只闭合S、S1，若灯L正常发光，灯泡两端的电压为电源电压，说明L1支路短路，故A 错误；B．只闭合S、S2，若灯L正常发光，灯泡两端的电压为电源电压，说明L2支路短路，故B 正确；C．只闭合S、S1，若灯L发光较暗，表示检验灯泡与另一灯泡串联接在火线与零线之间，这是一正常现象，故C错误；D．只闭合S、S2，若灯L不发光，表示该电路中有断路现象，说明L2支路断路，故D错误。

故选B。

2．下列关于生活用电常识，正确的是（）A．发现有人触电时，应立即用手将触电者拉开B．控制电灯的开关应该接在火线和灯泡之间C．空气开关跳闸，一定是电路中用电器的总功率过大D．正常使用测电笔检测线路时，没有电流通过人体【答案】B【解析】【分析】【详解】A．发现有人触电应该先切断电源，不能直接用手拉开，否则施救者也会触电。

故A错误；B．为了安全，开关要接在火线上，这样在断开开关之后，接触灯泡就不会有触电危险了。

故B正确；C．家庭电路空气开关跳闸，可能是发生的短路，也可能是总功率过大。

故C错误；D．在正确使用试电笔辨别火线时，试电笔的氖管发光，电流需要经过人体形成回路，所以有电流经过人体，故D错误。

故选B。

3．在如图所示的家庭电路中，将充电插头插入插座后，插座不能给手机充电；闭合开关，灯泡不亮；拔出充电插头，将测电笔分别插入插座的两孔，氖管均发光。

若电路中只有一处故障，则故障可能是（）A．零线ab段断路B．火线上的保险丝烧断C．灯泡灯丝烧断D．插座短路【答案】A【解析】【分析】【详解】闭合开关，灯泡不亮，说明电路中存在断路故障；若灯丝烧断，则插座能给手机充电，故不可能是灯丝烧断。

一、初中物理电路类问题1．下列电路正确的是（）A．B．C．D．【答案】C【解析】【分析】【详解】选项A中电压表的正负接线柱接反；B中电流表的正负接线柱接反；C中两灯并联，正确；D中若开关闭合会造成短路．故选C．2．如实物图所示，以下判断正确的是( )A．灯L1与灯L2并联，电压表测灯L1两端的电压B．灯L1与灯L2并联，电压表测灯L2两端的电压C．灯L1与灯L2串联，电压表测灯L1两端的电压D．灯L1与灯L2串联，电压表测灯L2两端的电压【答案】C【解析】【分析】【详解】由实物图可知,电流从正极出发经开关、电流表、灯泡L2、L1回负极,电压表并联在L1两端，则灯L1与灯L2串联，电压表与灯L1并联，所以电压表测灯L1两端的电压，故C正确，ABD错误．故选C.3．在如图所示的电路中，电源电压保持不变，闭合开关S，电路正常工作，一段时间后，发现两个电表的示数都变大，则出现这种故障的可能原因是（）A．R1短路B．R1断路C．R2短路D．R2断路【答案】C【解析】【分析】判断电路故障问题，是中考题中常见的题型，在不能直接确定故障原因时，将选项逐一代入题干，检查是否符合题意。

【详解】A．如果R1发生了短路，电压表示数变为零，故A错误；B．如果R1发生了断路，电流表示数变为零，故B错误；C．如果R2出现短路，电压表测量电源电压，示数变大；电路总电阻减小，电路电流增大，电流表示数增大，故C正确；D．如果R2出现断路，电流表示数变为零，故D错误。

故选C。

4．如图所示，电源电压为6V，闭合开关后，电压表的示数为4V，下列描述不正确的是（）A ．L 1两端电压为2VB ．L 1两端电压为4VC ．L 2两端电压为4VD ．L 1和L 2两端电压之和为6V【答案】B【解析】【分析】【详解】 由图可知，L 1、L 2串联，电源电压为6 V ，故开关闭合后，两个灯泡的总电压是6 V ， 电压表测L 2两端的电压，则L 2两端的电压：24V U =.因为两灯串联，根据串联电路电压关系，则L 1两端的电压：126?V 4?V 2?V U U U =-=-=．所以B 错误，ACD 正确． 故选ACD5．如图所示，电源电压不变，R 1、R 2为定值电阻，R 为滑动变阻器，a 、b 是电流表或电压表。

一、中考初中化学计算题1．在我国青海湖地区有一种说法，冬天捞碱，夏天晒盐。

这里的碱是指Na2CO3，盐是指NaCl。

人们从盐湖中捞得的碱会含有少量的NaCl。

某研究性学习小组称取含NaCl的Na2CO3固体25.0g，将其配制成溶液，再向其中逐滴加入足量的溶质质量分数为7.3%的稀盐酸，使气体完全放出，共收集到8.8gCO2气体。

试计算：（1）原固体中Na2CO3的质量分数________。

（2）反应中消耗盐酸的总质量______。

【答案】（1）84.8%．（2）200g．【解析】解：（1）设碳酸钠的质量为x，盐酸溶液中溶质的质量为yNa2CO3+2HCl=2NaCl+H2O+CO2↑106 73 44x y 8.8gx=21.2g，y=14.6g所以原固体中碳酸钠的质量分数为 ×100% =84.8%（2）反应中消耗盐酸的总质量为： =200g答：（1）原固体中Na2CO3的质量分数为84.8%；（2）反应中消耗盐酸总质量为200g。

2．向一定质量的5%的氢氧化钠溶液中加入66.9g硫酸铜溶液，恰好完全反应，得到4.9g 蓝色沉淀。

请计算:（1）所用氢氧化钠溶液的质量________。

（2）反应后所得溶液的溶质质量分数__________。

【答案】80g5%【解析】设参加反应的氢氧化钠的质量为x，反应生成硫酸钠的质量为y；2NaOH + CuSO4 = Cu(OH)2↓+ Na2SO480 98 142x 4.9g y80/98=x/4.9g x= 4g142/98=y/4.9g y=7.1g氢氧化钠溶液的质量为：4g÷5%=80g反应后所得溶液中溶质的质量分数是：答：所用氢氧化钠溶液的质量80g；反应后所得溶液的溶质质量分数为5%。

3．现有Fe和Fe2O3的固体混合物，东东同学为了分析混合物中Fe和Fe2O3的含量，设计了如下实验方案：（注意：100g是Fe与Fe2O3两种物质的总质量）（实验数据）实验共记录了两组实验数据：第①组，完全吸收气体后，NaOH溶液质量增加了66g；第②组，完全反应，冷却后称量剩余固体的质量为Wg。