2014高教社杯全国大学生数学建模竞赛
- 格式:doc
- 大小:519.89 KB
- 文档页数:20

碎纸片的拼接复原摘要本文利用Manhattan距离,聚类分析,图像处理等方法解决了碎纸片的拼接复原问题。
由于碎纸机产生的碎纸片是边缘规则且等大的矩形,此时碎纸片拼接方法就不能利用碎片边缘的尖角特征等基于边界几何特征的拼接方法,而要利用碎片内的字迹断线或碎片内的文字位置搜索与之匹配的相邻碎纸片。
拼接碎片前利用数学软件MATLAB软件对碎片图像进行数据化处理,得到对应的像素矩阵,后设置阈值对像素矩阵进行二值化处理,得到相应的0-1矩阵。
下面分别对三个问题的解决方法和算法实现做简单的阐述:问题一,分别对附件1和附件2的碎片数据进行处理得到相应的0-1矩阵,依次计算某个0-1矩阵最右边一列组成向量与其他所有0-1矩阵的最左边向量的Manhattan距离,可以得到某个最小距离值、说明最小距离值对应的碎片是可与基准碎片拼接的,最终得到碎片拼接完整的图像。
问题二,同样对于附件3和附件4中的碎片数据进行处理得到相应的数值矩阵,并计算得到每个碎片顶部空白高度和文字高度,即指每行像素点都为255的行数、一行中存在像素点为非255的行数,根据空白高度和文字高度对碎片进行聚类分类,聚类阀值取3像素,得到11组像素矩阵,进而得到11类可能在同一行的碎片类。
其中对附件4中的英文的处理中,我们还采用水平像素投影累积的方法,进一步分类出可能在同一行的碎片类。
用问题一的方法,计算Manhattan 距离可以对每一类碎片按次序排列好,得到11行已经排列好的碎片,再应用曼哈顿距离在竖直方向上进行聚合得到完整的图像。
问题三,首先,对于附件5中的碎片数据我们采用正反相接,本文将b面最左边的一列像素拼接到a面最右边的一列像素的下面,构成360×1的向量,再把其他的碎片采用相同的办法得到360×1的向量,再用问题一的方法,计算出各碎片之间的Manhattan距离。
其次,根据每个碎片顶部的空白高度或者文字高度对碎片进行区间分类,得到22组矩阵,然后应用曼哈顿距离将得到的22组矩阵聚成两类,每类各包含两面的11组矩阵,最后利用Manhattan距离在竖直方向上进行聚合得到完整的图像。

2014高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名):1.2.指导教师或指导教师组负责人(打印并签名):(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)赛区评阅编号(由赛区组委会评阅前进行编号):2014高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):创意平板折叠桌摘要折叠与伸展也已成为家具设计行业普遍应用的一个基本设计理念,占用空间面积小而且家具的功能又更加多样化自然会受到人们的欢迎,着看创意桌子把一整块板分成若干木条,组合在一起,也可以变成很有创意的桌子,就像是变魔术一样,真的是创意无法想象。

2014高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A题嫦娥三号软着陆轨道设计与控制策略嫦娥三号于2013年12月2日1时30分成功发射,12月6日抵达月球轨道。
嫦娥三号在着陆准备轨道上的运行质量为 2.4t,其安装在下部的主减速发动机能够产生1500N到7500N的可调节推力,其比冲(即单位质量的推进剂产生的推力)为2940m/s,可以满足调整速度的控制要求。
在四周安装有姿态调整发动机,在给定主减速发动机的推力方向后,能够自动通过多个发动机的脉冲组合实现各种姿态的调整控制。
嫦娥三号的预定着陆点为19.51W,44.12N,海拔为-2641m(见附件1)。
嫦娥三号在高速飞行的情况下,要保证准确地在月球预定区域内实现软着陆,关键问题是着陆轨道与控制策略的设计。
其着陆轨道设计的基本要求:着陆准备轨道为近月点15km,远月点100km的椭圆形轨道;着陆轨道为从近月点至着陆点,其软着陆过程共分为6个阶段(见附件2),要求满足每个阶段在关键点所处的状态;尽量减少软着陆过程的燃料消耗。
根据上述的基本要求,请你们建立数学模型解决下面的问题:(1)确定着陆准备轨道近月点和远月点的位置,以及嫦娥三号相应速度的大小与方向。
(2)确定嫦娥三号的着陆轨道和在6个阶段的最优控制策略。
(3)对于你们设计的着陆轨道和控制策略做相应的误差分析和敏感性分析。
附件1:问题的背景与参考资料;附件2:嫦娥三号着陆过程的六个阶段及其状态要求;附件3:距月面2400m处的数字高程图;附件4:距月面100m处的数字高程图。
附件1:问题A的背景与参考资料1.中新网12月12日电(记者姚培硕)根据计划,嫦娥三号将在北京时间12月14号在月球表面实施软着陆。
嫦娥三号如何实现软着陆以及能否成功成为外界关注焦点。
目前,全球仅有美国、前苏联成功实施了13次无人月球表面软着陆。
北京时间12月10日晚,嫦娥三号已经成功降轨进入预定的月面着陆准备轨道,这是嫦娥三号“落月”前最后一次轨道调整。
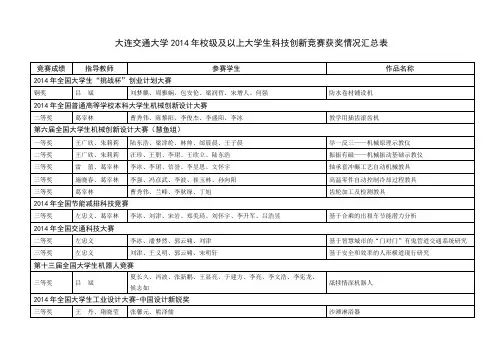
大连交通大学2014年校级及以上大学生科技创新竞赛获奖情况汇总表竞赛成绩指导教师参赛学生作品名称2014年全国大学生“挑战杯”创业计划大赛铜奖吕斌刘梦麒、周雅娴、包安伦、梁润哲、宋增人、何强防水卷材铺设机2014年全国普通高等学校本科大学生机械创新设计大赛二等奖葛宰林曹秀伟、陈黎阳、李俊杰、李盛阳、李冰教学用插齿滚齿机第六届全国大学生机械创新设计大赛(慧鱼组)一等奖王广欣、朱莉莉陆东浩、梁津纶、林帅、邰晨晨、王子晨举一反三——机械原理示教仪二等奖王广欣、朱莉莉汪珍、王朋、李珺、王欣立、陆东浩振振有磁——机械振动基础示教仪三等奖雷蕾、葛宰林李冰、李珺、信誉、李昱思、文怀宇轴承套冲碾工艺自动机械教具三等奖施晓春、葛宰林李强、冯彦武、李波、崔玉林、孙向阳高温零件自动控制冷却过程教具三等奖葛宰林曹秀伟、兰峰、李秋缘、丁旭齿轮加工及检测教具2014年全国节能减排科技竞赛三等奖左忠义、葛宰林李冰、刘津、宋岩、郑美琦、刘怀宇、李升军、吕浩昱基于合乘的出租车节能潜力分析2014年全国交通科技大赛二等奖左忠义李冰、潘梦然、郭云啸、刘津基于智慧城市的“门对门”有鬼管道交通系统研究三等奖左忠义刘津、王义明、郭云啸、宋明轩基于安全和效率的人形横道现行研究第十三届全国大学生机器人竞赛三等奖吕斌夏长久、冯波、张新鹏、王显亮、于建方、李亮、李文浩、李宪龙、候志如舐犊情深机器人2014年全国大学生工业设计大赛-中国设计新锐奖三等奖王丹、隋晓莹张馨元、熊泽儒沙滩淋浴器三等奖赵劲杨恩光、高嘉义、黄静静、赵琪、刘冬冬、肖磊、卢兴旺、张金鑫、蔡秀洁、马明赫智能高空停车位系统三等奖王孝坤李晓旭、苗春艳、赵翎希、卢艳丽、李博韬“快来电”移动设备充电站三等奖孙晓园焦智博、盛兴顺、兰东玉、顾家铭、宋颖、陈冠宇sunny未成年人素质培训中心三等奖张德南李尧坤、王懿、李斯加追求心灵的原生态三等奖王晗李青、秦立强、黄金桥、赵蓓、张碧芮、黄可、任建树、尹一伊、林晓薇、司广旭易途箱包有限责任公司创业策划书三等奖赵劲孙杨、戴祥祥、吕引红、邢丽、洪成文、唐博凯、张雅霖考拉电脑支架创意计划书三等奖李磊张喆、严广琪、郝珏“泰刻细”手机打车软件三等奖赵劲邢丽、李忠源、吕引洪、刘青林卡法咖啡屋三等奖靳长青马英石、严广骐、郑勇成协同学习平台三等奖李磊周乐安、刘子麟、尹建、王梦莹、张天睿、吴振、张彧明德筑梦公益创业计划书三等奖靳长青隆宏斌、严广骐、王擎天、李经纬同城快递手机软件服务平台三等奖陈少华王雷、陈硕、戴鹏程、康君妍、李强、苏辉亮校园电子DIY制作及电子服务工坊三等奖陈少华戴鹏程、李岳枫、陈硕、庄子艾、沈朝海、何江涛、朱思鹏商用厨房油烟及余热利用系统三等奖陈少华李哲、张永生、肖思雨、蔡宇、孔乾坤、黎万里北京盛大科技有限责任公司——指纹车票三等奖吕斌李亮、熊泽儒、李文浩、李宪龙、王亮、袁子豪、黄显梦、储劲大连天地人和环保科技有限公司三等奖刘薇吴可、李造璐、任相宇、刘楠、孙誉支“创新工场”摄影工作室三等奖吕斌潘浩、孙琪、赵荣彪、陆倩囡荣御家电产品开发有限公司三等奖赵劲李望博、聂磊、张兴浩、何思宏、夏中羽、林胜男、李绍震、张向捷、蔡垚、朱国源大连绘玩世界股份有限公司2014年辽宁省普通高等学校本科大学生机器人竞赛一等奖吕斌、卢琦孙宇航、李昂、李宪龙、王浩棣竞技机器人一等奖吕斌、葛宰林夏常玖、王显亮、刘云朔、王瑞东、于建方、刘全利、陈黎阳竞技机器人二等奖吕斌李亮、李文浩、王亮、岳翊杨、于俊洋、敬仙波竞技机器人2014年辽宁省普通高等学校本科大学生机械创新设计大赛一等奖雷蕾、金路葛宰林曹秀伟、陈黎阳、李俊杰、李盛阳、李冰教学用插齿滚齿机二等奖武力、金路葛宰林孙伟奇、徐乙涵、贾贵宇、王显亮、杨蕙铭小型拉伸冲击试验一体机二等奖李荣华、李新峰陈百强、李闯、张琦、苗天雨、查海恩卧式圆规二等奖李永华、金路葛宰林信誉、李想、程仲奎、文怀宇、王瑞东锻压工艺自动机三等奖施晓春、温爱玲葛宰林李想、信誉、赵赛、夏常玖、李亮机械振动分析模拟装置三等奖葛宰林、吕斌李宪龙、杜立晗、李文浩、于建方、王显亮教学用直线发电机模型2014年辽宁省普通高等学校本科大学生结构设计竞赛一等奖王生武赵宁、陈冬冬、韩萌萌INFINITE一等奖张蓬勃于双杰、尹建、耿鹏师生塔二等奖王生武覃国辉、刘小雷、马原破军逐梦2014年辽宁省普通高等学校本科大学生工业设计大赛一等奖邹雅琢、张齐绮赵晓君、张茜、佟瑶、林立、赵久鹏Z-Digger小型挖掘机一等奖陶然、王丹郭志勇BLUE忆一等奖马笑玲、王丹肖芸芸、潘强、张茜“成长的礼物”多功能婴儿床一等奖王丹、隋晓莹张馨元、熊泽儒沙滩淋浴器二等奖姚善良殷释然、王轩宇、徐萌、李玉倩、张蓓佳提词麦克二等奖邹雅琢、张齐绮张庆泉、张茜、佟瑶、林立、赵久鹏搅拌车设计二等奖陶然、葛宰林赵峰、邵文汐、赵可心剪纸流韵—餐具设计二等奖高勇、张琪夏雨、李晨歌、郭慧敏、张超凡观-中式家具设计二等奖王强郭高峰、邵文汐、田嘉珩、王冲霄城市移动餐车设计——兰蒂帕克二等奖隋晓莹、胡俊于静瑶、司广旭、赵可心墨▪道人二等奖胡俊、隋晓莹林立、杨易东、周荣辉DIGITAC投影笔二等奖陶然、张生芳郭玥彤、王帅沙漠地型混合动力概念汽车设计二等奖王丹、胡俊马丽莎、马梁毓、张茜盲人导航拐杖三等奖马笑玲、张琪赵峰、赵可心、邵文汐JANE LOVE挤牙膏器三等奖丛琳琳史婉瑛、郭帅HomeBox——折叠家具设计三等奖胡俊、张生芳马笑玲王晓璇、邵文汐、马君晖EM电动·机械两用榨汁机三等奖姚善良聂鑫、司光旭、赵雨芊、朱艳芳、苗萌萌根本停不下来三等奖张琪、明珠赵赫、黄思宇Oscar三等奖张生芳、万壮邵文汐、熊泽儒、赵晓君乘风破浪——轨道车设计三等奖王强成元凌、田嘉珩、王冲霄、邵文汐FAT MAN LIKE保健趣味性多功能餐具设计三等奖门书洋李玲、张向捷家用急救箱设计三等奖邹雅琢、张齐绮郭志勇、张茜、佟瑶、林立、赵久鹏Sun Flowers2014年辽宁省普通高等学校本科大学生计算机设计竞赛二等奖丁立佳李昊、张钊、宋睿树·心·家二等奖马海波曹乾、王通、唐周益丹街景校园三等奖丁立佳熊钟铭、王思达、李帅生命的绽放三等奖丁立佳王维玺、辛士超、李昊挣脱三等奖丁立佳王建国、李洋、熊钟铭我爱我家大连市大学生为老服务创新设计竞赛三等奖左忠义刘晶、陈洪顺、韩志轩老年人交通安全指示灯三等奖王强宋佳遇生命体征监测仪三等奖吕斌谢铖、范长江、唐飞老年人智能提醒药箱。
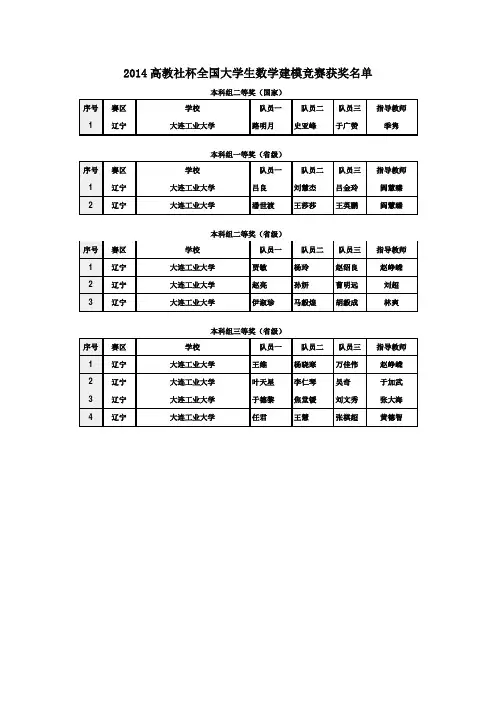
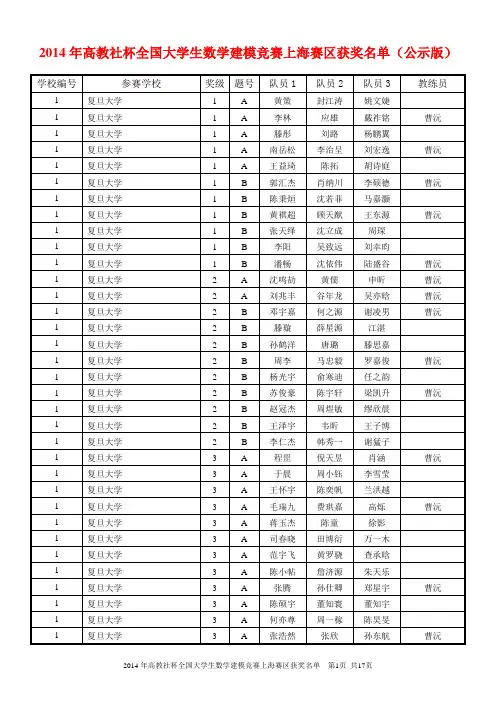
2014高教社杯全国大学生数学建模竞赛获奖名单
本科组二等奖(国家)
序号赛区学校队员一队员二队员三指导教师1 辽宁大连工业大学路明月史亚峰于广赞季隽
本科组一等奖(省级)
序号赛区学校队员一队员二队员三指导教师
1 辽宁大连工业大学吕良刘慧杰吕金玲阎慧臻
2 辽宁大连工业大学潘世渡王莎莎王英鹏阎慧臻
本科组二等奖(省级)
序号赛区学校队员一队员二队员三指导教师
1 辽宁大连工业大学贾敏杨玲赵绍良赵峥嵘
2 辽宁大连工业大学赵亮孙妍曹明远刘超
3 辽宁大连工业大学伊淑珍马毅煌胡毅成林爽
本科组三等奖(省级)
序号赛区学校队员一队员二队员三指导教师
1 辽宁大连工业大学王维杨晓寒万佳伟赵峥嵘
2 辽宁大连工业大学叶天星李仁琴吴奇于加武
3 辽宁大连工业大学于德黎焦堂锾刘文秀张大海
4 辽宁大连工业大学任君王慧张棋超黄德智
本科组一等奖(校级)
队员一队员二指导教师队员一队员二指导教师刘国庆吕睿张玉杰蒋乾坤王晶刘燕王晗吴爽张凤荣吕涛钱思源于加武吴文兵黄冰杨开兵甘耀王军强邵慧燕何超琪刘文涛王玮莉
孙悦戴紫茵薛晓东
刘亚伟胡晓情毕秀国
本科组二等奖(校级)
队员一队员二指导教师队员一队员二指导教师王珂李玉莹张玉杰黄哲伦葛玉鑫张玉杰郭莲东赵如雪张凤荣魏明海范志勇毕秀国于辛瑶谢龙杨开兵戴浩王凯丽康健佟佳钰李宗昕张玉杰魏迎辉王树棋刘燕王琛陈曦泽王玮莉范中磊史恒波邵慧燕刘晓琳姜珊薛晓东刘豹付彬高超
本科组三等奖(校级)
队员一队员二指导教师队员一队员二指导教师罗瑞申政毕秀国王左涛刘莹莹赵峥嵘袁麟段国栋高超全超杨子扬于加武张颖薛豪鹏张大海王英宇林琳董晓梅宣昂韦茂成阎慧臻金阳张阳鹏高超梁王荣赵馨雅刘超石品汪志奇于加武徐鹏孙浩季隽费舒杰吴滟帮林爽。
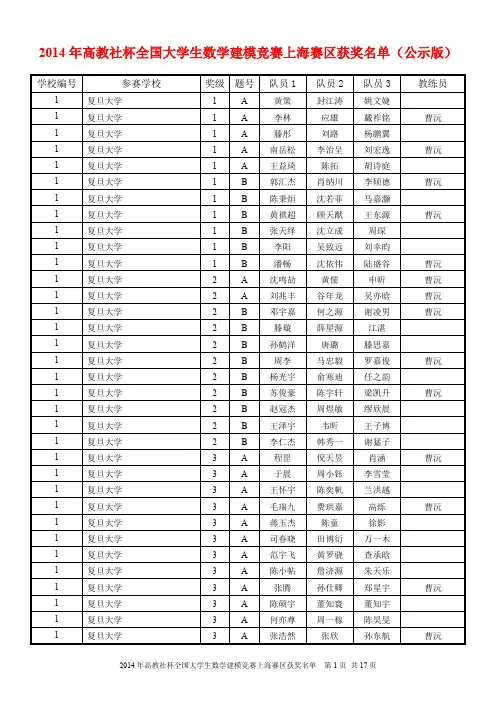

高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)B 题 穿越沙漠考虑如下的小游戏:玩家凭借一张地图,利用初始资金购买一定数量的水和食物(包括食品和其他日常用品),从起点出发,在沙漠中行走。
途中会遇到不同的天气,也可在矿山、村庄补充资金或资源,目标是在规定时间内到达终点,并保留尽可能多的资金。
游戏的基本规则如下:(1)以天为基本时间单位,游戏的开始时间为第0天,玩家位于起点。
玩家必须在截止日期或之前到达终点,到达终点后该玩家的游戏结束。
(2)穿越沙漠需水和食物两种资源,它们的最小计量单位均为箱。
每天玩家拥有的水和食物质量之和不能超过负重上限。
若未到达终点而水或食物已耗尽,视为游戏失败。
(3)每天的天气为“晴朗”、“高温”、“沙暴”三种状况之一,沙漠中所有区域的天气相同。
(4)每天玩家可从地图中的某个区域到达与之相邻的另一个区域,也可在原地停留。
沙暴日必须在原地停留。
(5)玩家在原地停留一天消耗的资源数量称为基础消耗量,行走一天消耗的资源数量为基础消耗量的2倍。
(6)玩家第0天可在起点处用初始资金以基准价格购买水和食物。
玩家可在起点停留或回到起点,但不能多次在起点购买资源。
玩家到达终点后可退回剩余的水和食物,每箱退回价格为基准价格的一半。
(7)玩家在矿山停留时,可通过挖矿获得资金,挖矿一天获得的资金量称为基础收益。
如果挖矿,消耗的资源数量为基础消耗量的3倍;如果不挖矿,消耗的资源数量为基础消耗量。
到达矿山当天不能挖矿。
沙暴日也可挖矿。
(8)玩家经过或在村庄停留时可用剩余的初始资金或挖矿获得的资金随时购买水和食物,每箱价格为基准价格的2倍。
请根据游戏的不同设定,建立数学模型,解决以下问题。
1. 假设只有一名玩家,在整个游戏时段内每天天气状况事先全部已知,试给出一般情况下玩家的最优策略。
求解附件中的“第一关”和“第二关”,并将相应结果分别填入Result.xlsx 。

2012高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): C我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):(隐去论文作者相关信息等)日期: 2012 年 9 月 10 日赛区评阅编号(由赛区组委会评阅前进行编号):2012高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国评阅编号(由全国组委会评阅前进行编号):脑卒中发病环境因素分析及干预摘 要:脑卒中逐渐威胁人们的生活,本文主要针对脑卒中发病病例信息和受病环境因素进行统计分析,从实际数据结果加深对脑卒中的认识,旨在对脑卒中加以预防。
针对问题一,先主要借助于EXCEL 编程及筛选功能、MATLAB 辅助编程对附件数据进行错误修复及标准化处理,得到2007~2010年期间有效数据的发病年、月、日,然后在EXCEL 中分别按性别、年龄、职业、时间(包括年、月、日)四个字段对发病人数进行统计,并以图、表的形式予以展示,最后总结出脑卒中患者男女性别比为1.17:1、集中患病年龄段为71~80岁、高危职业为农民、存在一定季节性等结论,该问属于一般的数据统计分析模型。

承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的报名参赛队号为(8位数字组成的编号):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期: 2014 年 9 月 15日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):创意平板折叠桌摘要目前住宅空间的紧张导致越来越多的折叠家具的出现。
某公司设计制作了一款折叠桌以满足市场需要。
以此折叠桌为背景提出了三个问题,本文运用几何知识、非线性约束优化模型等方法成功解决了这三个问题,得到了折叠桌动态过程的描述方程以及在给定条件下怎样选择最优设计加工参数,并针对任意形状的桌面边缘线等给出了我们的设计。
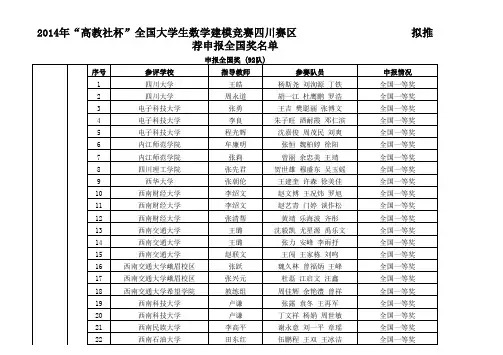
2014 年高教社杯全国大学生数学建模竞赛上海赛区获奖名 单(公示版)学校编 号1 1 1 1 1 1 1 1 1 1 1 1 1参赛学校奖 级1 1 1 1 1 1 1 1 1 1 1 2 2题 号A A A A A B B B B B B A A队员 1队员 2队员 3教练员复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学黄策 李林 滕彤 南岳松 王益琦 郭汇杰 陈秉烜 黄祺超 张天绎 李阳 潘畅 沈鸣劼 刘兆丰封江涛 应雄 刘路 李治呈 陈拓 肖纳川 沈若菲 顾天猷 沈立成 吴致远 沈依伟 黄儒 谷年龙姚文婕 戴祚铭 杨鹏翼 刘宏逸 胡诗庭 李硕德 马嘉灏 王东源 周琛 刘幸昀 陆盛谷 申昕 吴亦晗 曹沅 曹沅 曹沅 曹沅 曹沅 曹沅 曹沅1 / 39学校编 号1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1参赛学校奖 级2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3题 号B B B B B B B B B A A A A A A A A队员 1队员 2队员 3教练员复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学邓宇嘉 滕璇 孙鹤洋 周李 杨光宇 苏俊豪 赵冠杰 王泽宇 李仁杰 程罡 于晨 王怀宇 毛瑞九 蒋玉杰 司春晓 范宇飞 陈小帖何之源 薛星源 唐璐 马忠毅 俞寒迪 陈宇轩 周煜敏 韦昕 韩秀一 倪天昱 周小钰 陈奕帆 费珙嘉 陈童 田博衍 黄罗骁 詹济源谢凌男 江湛 滕思嘉 罗嘉俊 任之韵 梁凯升 缪欣晨 王子博 谢猛子 肖涵 李雪莹 兰洪越 高烁 徐影 万一木 查承晗 朱天乐曹沅曹沅曹沅曹沅曹沅2 / 39学校编 号1 1 1 1 1 1 1 1参赛学校奖 级3 3 3 3 3 3 3 3题 号A A A A A A A A队员 1队员 2队员 3教练员复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学张腾 陈硕宇 何亦尊 张浩然 刘小满 袁超宇 徐嘉灿 李凯莅 周苏田 介 陈力 陈品翰 何雨宸 邹晨 黄明媚 李涓涓 余若凡 王佳俊孙仕卿 董知寰 周一稼 张欣 杨诗颖 吴艺娴 吴皓琪 陈思佳郑星宇 董知宇 陈昊旻 孙东航 赵旭 高月洁 李根 刘晓洋曹沅曹沅 曹沅 曹沅曹沅1复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学 复旦大学3 3 3 3 3 3 3 3 3A B B B B B B B B吴金鑫 王耀辉 马扬清 许夏杰 周士强 舒静 王德泉 蒲秋实 项思远杨心铭 陈天奇 何天成 冀渤匀 许昊天 葛启阳 吕智 丁岱宗 谈福嘉 曹沅 曹沅 曹沅1 1 1 1 1 1 1 13 / 39学校编 号1 2 2 2 2 2 2参赛学校奖 级3 1 1 1 1 1 1题 号B A A A A A A队员 1队员 2队员 3教练员复旦大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学吕赫 江河 施浅 贾冬雨 李纬尘 贺甜甜 郑博艺 叶迪卓 然 刘一鸣 王凡 刘曦阳 许哲宇 高天 何俊贤 彭瑾龙 谭昊 赵紫荆李有方 罗盛杰 谢异 杨蕊 唐梓峻 房悦竹 邓舒文李拱乾 李翰正 金耀楠 谢延平 楼畅 蔡佳铭 杨姝颖曹沅 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组2上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学1 1 1 1 1 1 1 1 1 1A A A A A A A A B B王依宁 郭振乾 阎谨 高策 梁玉鼎 罗嘉婧 韩璐岭 胡麒 刘梦云 游杰李梦源 刘晓桐 乔梁 马诗韬 章佐铭 施怡昀 周新杰 刘飞扬 姚浙威 李文新数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组2 2 2 2 2 2 2 2 24 / 39学校编 号2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2参赛学校奖 级1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2题 号B B B B B B B B B B B B B A A A A队员 1队员 2队员 3教练员上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学邓志鹏 陈宗晨 宋振宇 朱旭 傅嘉豪 杨佳涛 俞敏浩 魏祯 郭运奇 黄超 朱冠东 陆雷 戴世刚 殷柯 邓宇宸 黎幸东 宋艾伦万强 刘文青 杨泽 沈少波 陈若冰 李健达 曹逸夫 吴可奕 乔思远 侯春一 杨启哲 林天威 姚垚 胡航 李菁 谈兆炜 吴思远孙一新 许文 马寅桐 陈晓 胡春嘉 娄炯 陈靖远 吴秉鸿 胡泾莓 周文韬 马睿 石乾乾 陈丽霞 杨慧军 罗莹 沈嘉明 史璟晨数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组5 / 39学校编 号2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2参赛学校奖 级2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3题 号A A A A B B B B B B B B B B B B A队员 1队员 2队员 3教练员上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学李尔玉 曾俊 朱昊越 林泽冰 胡子希 赵鹤宁 张宇锋 劳迪 张文烨 潘司晨 李晓波 陈祥玉 李倩茹 池海 王昊天 黄奇杰 郑煌杰王迪 陈旻侃 王子冠 杜辛亚 高岩松 刘炳元 陈之钦 张肇桓 黄晨 申若斐 宋宇博 张晓斌 李浩楠 冯哲 王泽鹏 夏振宇 陈颀万思宇 王一帆 毛乾康 毕书瑶 陈皓 陈龙 孙照印 刘筱 张丹 邱帆 李文博 李成伟 吴学阳 王力功 张宁 沈佳华 竺烨数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组6 / 39学校编 号2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2参赛学校奖 级3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3题 号A A A A A A A A A A A A A A A A A队员 1队员 2队员 3教练员上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学余一宽 周凌锋 周弘宽 庄子骏 蔚馨 李佳荣 张布衣 魏笑 倪恺翔 张智峰 张昳亭 廖铭鼎 曾一鸣 李东 王澍 孙佳硕 戚文韬陆泽超 谌建权 陆玉晨 刘家玺 朱文晓 孔博源 张翔 马力天 陆栋梁 曾亚东 刘俊诚 琚毓琪 王欣 李泽凡 唐琦 顾章轩 闫盛凯李思轩 陈冠宏 陈正煦 葛宇韬 陆炯炯 王俊 罗逸夫 高梦宇 杨宇森 陈冬 陶泓成 王平 邱宇贤 刘儒峰 周伟涛 马文铧 杨靖数模指导组 数模指导组 王晓敏 数模指导组 数模指导组 数模指导组 蒋启芬 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组7 / 39学校编 号2 2 2 2 2 2 2 2 2 2参赛学校奖 级3 3 3 3 3 3 3 3 3 3题 号A A A A B B B B B B队员 1队员 2队员 3教练员上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学聂希 申炳宇 王敏思 韓瑞晞 陈家明 李沛珂 陈子豪 戴领 郑戈迪 陈洁锋张宇初 杨照雄 刘雨哲 刘泽洲 冯榆晨 武宇 邵俊儒 付豪 丁佳晨 范博宇 陈家 WEI 毛一曼 郭沣 洪毅恺 龚芷以 林利 何正贤邱晓云 唐浩 孙云涛 孙亦磊 侯晟乾 李睿明 陈迪 左楠 李泽源 施宇数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组2上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学3 3 3 3 3 3 3B B B B B B B孟浩然 张宇韬 程然 李昊辰 张俊 刘璐 万成城张泽宇 李宝林 马杰 杨逸伦 潘灏 龙雨珺 温洪林数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组2 2 2 2 2 28 / 39学校编 号2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3参赛学校奖 级3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 1 1题 号B B B B B B B B B B B B B B B A A队员 1队员 2队员 3教练员上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学 同济大学 同济大学罗梓萌 王佳怡 刘学成 刘凯文 冯姝绮 苏鹏 颜鹏 钟秋辰 吴耀骏 刘培元 崔文韬 李佳骏 卢思佳 焦点 张霆钧 吴育蔚 朱升发杨秋洁 徐巡 李莎 褚天逸 吴慧迪 李陶然 范帆 吕秋怡 陆晓彤 华鑫宇 唐颀伟 白志豪 钱雨欣 刘燚 张舒翼 汤富超 万克阳丁磊 赵传凯 刘君毅 邵伟钊 费文媛 吴威辰 田兴龙 李叶辰 张浩铭 赵性雅 董子玥 马豪君 吴海潮 梁志栋 朱仁杰 刘杰 刘宇鹏数模指导组 数模指导组 数模指导组 王晓敏 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 数模指导组 金建刚 唐炎林 陈雄达9 / 39学校编 号3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3参赛学校奖 级1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2题 号A A A A A B B B B B B A A A A A A队员 1队员 2队员 3教练员同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学冯禹 章程 徐清悦 王川 易正翔 赵鹏 张天宇 金猛 董利宽 王天益 贾启新 权晨嘉 史沛瑶 马东发 韩俊强 石莜迪 林宜葳郭亚南 程怀磊 熊星 吴景天 邓宇洁 王宇江 胡月 叶常青 薛炳晟 苏炎 王昕 吉卓然 傅卓 冯正 关天一 史东辉 方志晗汤一嘉 姚佳蓉 周昭豪 姜秀财 邱爽 赵亦峰 祁玥 邓泽恒 梁思寒 王昊 王梦真 李一鸣 储鑫 高述琪 张锐陈雄达 尚培培 陈雄达 靳全勤 项家梁 无 陈雄达 陈雄达 无 卞永明 陈雄达 陈雄达 陆洪文 殷俊锋 尚培培 无施逸文无10 / 392014年高教社杯全国大学生数学建模竞赛上海赛区组委会,2014.10.22。
高教社杯全国大学生数学建模竞赛获奖名单
本科组高教社杯获得者:程双泽、李君昌、陈凌勤(信阳师范学院)
专科组高教社杯获得者:丁晓彤、回荣洲、段君宜(海军航空工程学院青岛校区)本科组MATLAB创新奖获得者:陈超、唐梦珏、杨克宇(浙江工业大学)
专科组MATLAB创新奖获得者:王磊、蒋国辉、蔡姗姗(四川建筑职业技术学院)[注]以下每一获奖等级内,按赛区顺序排列(同一赛区内,按学校笔画顺序排列)。
本科组一等奖(共293名)
本科组二等奖(共1256名)
专科组一等奖(共47名)
专科组二等奖(共197名)。
2014高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A 我们的报名参赛队号为(8位数字组成的编号):25001113所属学校(请填写完整的全名):云南大学参赛队员(打印并签名) :1. 林博文2. 张竞文3. 方春晖指导教师或指导教师组负责人(打印并签名):李海燕(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期:2014年9月15日赛区评阅编号(由赛区组委会评阅前进行编号):2014高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):嫦娥三号软着陆轨道设计与控制策略优化摘 要 嫦娥三号是中国国家航天局嫦娥工程第二阶段的登月探测器,包括着陆器和玉兔号月球车。
嫦娥三号在高速飞行的情况下,要保证准确地在月球预定区域内实现软着陆,关键问题是着陆轨道与控制策略的设计。
学生宿舍设计方案的评价摘 要本题是一个典型的对于多指标(或多因素)的对象进行综合测评问题,就是要通过建立合适的综合测评数学模型将多个评价指标综合成为一个整体的综合评价指标作为一个恶综合评价的依据,从而得到相应的评价结果。
针对本题,,我们进行研究并做了以下工作:1.由于在评价过程中,涉及到一些定性和定量的指标,使决策具有明显的模糊性和不确定性,因此我们应用模糊决策法和层次分析法进行综合评价。
2.经过对平面设计图的分析和整理,我们选择建设成本1P 、运行成本2P 、收费标准3P 、人均面积4P 、使用方便5P 、互不干扰6P 、采光和通风7P 、人员疏散8P 和防盗9P 作为评价要素。
3.对于定性的指标我们采用线性隶属度来确定指标评语集合特征值;对于定量的指标我们采用最大最优min max minij i ij i i x x y x x -=-和最小最优max max mini ij ij i i x x y x x -=-的原则确定指标的特征值。
4.利用层次分析求出评价因素指标的权重向量,在层次分析方法求权重的过程中,我们建立目标层、准则层和指标层三个层次,通过同一层目标之间的重要性的两两比较,得到判断矩阵,求出判断矩阵的特征向量,用方根法求出它们的最大特征根()max 1nii iPw nw λ==∑和特征向量()ij n nP p ⨯=,作为各指标相对上层指标的权重()121......T j n Q q q q ⨯=。
5.确定评价指标的特征值矩阵和评价指标的相对优属度矩阵,最后计算系统的综合评价判值。
6.结合模糊决策方法,我们将与宿舍有关的主要因素及其相对重要性进行量化,得到模糊关系矩阵Y ,从而得到宿舍设计方案的综合评价模型:121(,,)()()T m ij m n j n Z z z z Y Q y q ⨯⨯==⨯=⨯L 根据四种设计方案给出的数据,利用Matlab 对上述模型和算法进行实践求 解得到()0.21500.10750.10750.16770.16770.06450.03010.09380.0462Q = Z ()0.37430.40110.49400.5799T=。
2014高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):上海建桥学院参赛队员(打印并签名) :1. 张训一2. 刘雅静3. 赵明明指导教师或指导教师组负责人(打印并签名):陈苏婷(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):2014高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):关于嫦娥三号的着陆轨道及最优控制策略问题的研究摘要我国嫦娥三号成功着陆月球,引发了我们对其着陆轨道和最优控制策略的关注和探讨。
首先,我们由开普勒第一、二定律及机械能守恒,确定着陆准备轨道近月点和远月点的位置分别在月球北极正上方15km和南极上方100km,在建立的中的坐模型中标分别为 A(0,1794.513),B(0,–1794.513);以及嫦娥三号相应速v A 1.74km/s (垂直于纵轴沿横轴正方向),度的大小与方向,=v B1,701km/s (垂直于纵轴沿横轴负方向)。
=其次,在确定飞船从运行轨道转入着陆轨道时,根据各项指标的限制,建立制动火箭并在相应的变轨阶段使用,即给嫦娥三号一个与运行轨道方向相反的附加速度,使嫦娥三号由运行轨道转入椭圆形的着陆轨道。
其中:(1)在第一阶段着陆准备轨道的着陆点,制动火箭得到附加速度而进入着陆轨道;(2)第二主减速阶段采用非线性变结构控制与状态反馈相结合的控制方法,使软着陆过程的燃料消耗变化率达到最低;(3)在第三阶段快速调整阶段中,根据第二阶段过程中所建立的模型,计算嫦娥三号的发动机的实时推力大小;(4)在第四阶段粗避障阶段,于四次多项式制导律的基础上,提出一个改进的多项式制导算法,通过设计每个方向的约束条件,将安全着陆点置为制导目标中的着陆点,通过姿态机动实现推力指向变化,进而实现并完成粗避障;(5)在第五阶段细避障阶段中,将悬停段选取的安全着陆点置为制导目标点,利用外环加内环制导方式及避障下降过程中实时跟踪目标指令的操作,控制避障段的终端状态,最后增加了速度机动逻辑,保证了避障平移速度来节省推进剂的消耗;(7)在第六阶段缓速下降阶段中,缓速下降也采用外环加内环制导方式,水平方向速度控制目标为零,位置控制目标为进入缓速下降段时的着陆器位置;利用伽马敏感器和触地敏感器测量信号的关机策略,另外基于加速度测量信息的关机备份策略,以确保着陆后主发动机的关闭。
最后,我们利用敏感性系数来分析着陆轨道和控制策略相应的敏感性分析,并分析了其误差。
关键词:制动火箭非线性变结构控制四次多项式制导律外环加内环导速度机动逻辑敏感性系数一问题重述2013年12月6日嫦娥三号已经成功降轨进入预定的月面着陆准备轨道,嫦娥三号在着陆准备轨道上的运行质量为 2.4t,其安装在下部的主减速发动机能够产生1500N到7500N的可调节推力,其比冲(即单位质量的推进剂产生的推力)为2940m/s,可以满足调整速度的控制要求。
嫦娥三号在高速飞行的情况下,要保证准确地在月球预定区域内实现软着陆。
在实施软着陆之前,嫦娥三号还将在为着陆准备的一条近月点高度约15公里、远月点高度约100公里的椭圆轨道运行。
着陆轨道从近月点至着陆点,其软着陆过程共分为6个阶段。
嫦娥三号将在近月点15公里处以抛物线下降,相对速度从每秒1.7公里逐渐降为零。
嫦娥三号的预定着陆点为19.51W,44.12N,海拔为-2641m。
嫦娥三号在高速飞行的情况下,要保证准确地在月球预定区域内实现软着陆,关键问题是着陆轨道与控制策略的设计。
要求满足每个阶段在关键点所处的状态;尽量减少软着陆过程的燃料消耗。
由此,引出建立数学模型来解决下面的问题:(1)确定着陆准备轨道近月点和远月点的位置,以及嫦娥三号相应速度的大小与方向。
(2)确定嫦娥三号的着陆轨道和在6个阶段的最优控制策略。
(3)对于你们设计的着陆轨道和控制策略做相应的误差分析和敏感性分析。
二问题分析2.1问题一的分析嫦娥三号的运动遵循开普勒三定律,在远月点和近月点之间嫦娥三号运动的轨迹是一个椭圆,且在远月点和近月点上嫦娥三号只受到月球对其的万有引力。
由开普勒第一定律,月球的地心位于椭圆轨道的焦点上,远月点和近月点之间的连线是椭圆的一条长轴。
以长轴的中点为原点,长轴为纵轴建立直角坐标系,由已知数据,求出远月点和近月点在坐标系中的坐标。
根据开普勒第二定律和机械能守恒定律,得到嫦娥三号在远月点和近月点的速度,由万有引力定律,在远月点和近月点的速度方向是其轨道点的切线方向,与椭圆轨道的的长轴垂直且方向相反。
2.2问题二的分析要确定嫦娥三号的着陆轨道,首先要知道嫦娥三号近月点时的位置,即在距离月球北极15km处的位置,而嫦娥三号的预定着陆点为19.51W,44.12N,海拔为-2641m(如下图所示);飞船从运行轨道即在大于15km处转入着陆轨道15km 处,可以采用这种方法是:嫦娥三号附加速度的方向与原来的轨道速度方向相反。
因此将运用机械能守恒定律和开普勒定律进行分析和讨论。
如图2所示,由于制动火箭的起动,使宇宙飞船获得一个附加速度乙v,飞船由运行轨道转入椭圆形的着陆轨道。
若选择的着陆点为A,则该点应为椭圆轨道的近地点,由开普勒第一定律可知,月球中心应是椭圆轨道的一个焦点。
对于嫦娥三号在6个阶段的最优控制策略,这6个阶段分别包括着陆准备轨道段,主减速段,快速调整段,粗避障段,精避障段和缓速下降阶段。
要使嫦娥三号达到最优控制,必须要保证它能够实现在6个阶段中实现燃料消耗的变化率最小,从而能够达到最优。
理想情况下的最优控制方案流程可简单描述为开始时,让探测器自由下落,当下落到某个状态时启动发动机,以最大推力对火箭减速。
当速度减小到零时正好到达地面。
然而,这种控制方案对切换时机的准确程度要求极高,同时不允许存在任何形式的干扰,而这在实际环境中是不可能实现的。
因此,我们需要对这6个阶段逐一突破。
2.3 问题三的分析解决问题三的方法主要是根据敏感性系数来判断敏感度,不确定因素在-20%~ 20%之间波动时,说明轨道设计的模型与实际情况相似,模型抗干扰能力强。
而敏感性系数大于0的情况下,说明这个模型是可行的,根据提出的这条思路分析模型的敏感性。
同时,嫦娥三号的实施也依赖于对着陆过程中误差源的详细分析,其核心思想是将飞行器发动机的各项技术指标的误差作为待考察的随机误差源,通过计算这些误差随轨道运动的传播进而评估它们对飞行轨道的影响。
利用协方差来分析向月飞行轨道误差。
三模型假设(1)嫦娥三号做椭圆轨迹运动时,假设月球是一个质点。
(2)假设嫦娥三号在近月点和远月点只受万有引力的作用。
(3)起动制动火箭,其提供的附加速度大小保持不变。
(4)在嫦娥三号软着陆过程中,无其它能源的损耗,只有行进过程中燃料的消耗。
四定义和符号的说明v A:嫦娥三号在近月点A的速度大小;v B:嫦娥三号在远月点B的速度大小;m: 嫦娥三号的质量;M:月球的质量;:制动火箭提供的附加速度;:嫦娥三号沿原运行轨道运行时的速度;:嫦娥三号在近地点A时的速度;R:地球半径,即近地点A到地心的距离;K:偏二甲肼燃料燃烧后喷出气体相对于嫦娥三号的速度;r tGz,v Gz和a tGz:制导系的航向位置、速度和加速度制导目标;r Gz和v Gz:制导系的航向位置和速度;t go:制导剩余时间。
五模型的建立和求解5.1问题一模型的建立和求解如图1 所示, 嫦娥三号的运动的轨道为椭圆, 月球位其中的一个焦点F 上, 椭圆的半长轴为a , 半短轴为b , 半焦距为c, 月球质量为M .嫦娥三号质量为m , A ,B 分别其运动的近月点和远月点, 以v A 和v B 分别表示经这两点的速度, 由于速度沿轨迹的切线方向,可知v A 和 v B 的方向均与椭圆的长轴垂直,且A ,B 两点距月球球心的距离分别为L A =a-c 与L B =a+c, 在A ,B 两点分别取极短的相等时间t,则嫦娥三号与月球连线在这两段时间内扫过的面积分别为S A =21v A *t*L A ,S B =21v B *t*L B 。
根据开普勒第二定律:嫦娥三号与月球连线在相等的时间内扫过相等的面积,故有S A =S B ,代入得:v B =c a ca +-v A (1)嫦娥三号的总机械能等于其动能和引力势能之和, 故当嫦娥三号分别经过A ,B 两点时的机械能为: L v L v E A A A A A GMm m GMm m -=-+=2221)(21 , (2) L v L v E B B B B B GMm m GMm m +=-+=2221)(21 , (3)由于嫦娥三号在运动过程中受万有引力作用, 所以遵循机械能守恒定律, 故有: E A =E B (4)将( 1) - (4) 式联立解得: ,)()(,)()(ac a GM c a a c a GM c a v v B A +-=-+= 经分母有理化并结合椭圆中c b a 222+=可得: ,a GM c a b v A ∙-= aGM c a b v B += 由题意知:2a=15+100+2R (单位Km )c=a-R-15 (单位Km )R 为月球平均半径:1737.013km ,M 为月球质量:7.3477×1022kg ,G 为万有引力常量:G=6.67x 1011- N ·m2 /kg2 。
因此:近月点和远月点的坐标分别为A (0,1794.513),B (0,–1794.513)则代入数据得:=v A 1.74km/s (垂直于纵轴沿横轴正方向)=v B 1,701km/s (垂直于纵轴沿横轴负方向)5.2问题二 模型的建立和求解5.2.1 着陆轨道的研究确定嫦娥三号的着陆轨道,建立一个制动火箭,使嫦娥三号获得一个附加速度彻以改变运行轨道的形状使着陆轨道与月球表面相切,以达到安全着陆的目的。