常微分方程 §3.3 解过初值的连续性和可微性

第三章一阶微分方程解的存在定理[教学目标]1.理解解的存在唯一性定理的条件、结论及证明思路，掌握逐次逼近法，熟练近似解的误差估计式。

2.了解解的延拓定理及延拓条件。

3.理解解对初值的连续性、可微性定理的条件和结论。

[教学重难点] 解的存在唯一性定理的证明，解对初值的连续性、可微性定理的证明。

[教学方法] 讲授，实践。

[教学时间] 12学时[教学内容] 解的存在唯一性定理的条件、结论及证明思路，解的延拓概念及延拓条件，解对初值的连续性、可微性定理及其证明。

[考核目标]1.理解解的存在唯一性定理的条件、结论，能用逐次逼近法解简单的问题。

2.熟练近似解的误差估计式，解对初值的连续性及可微性公式。

3.利用解的存在唯一性定理、解的延拓定理及延拓条件能证明有关方程的某些性质。

§1 解的存在性唯一性定理和逐步逼近法微分方程来源于生产实践际，研究微分方程的目的就在于掌握它所反映的客观规律，能动解释所出现的各种现象并预测未来的可能情况。

在第二章介绍了一阶微分方程初等解法的几种类型，但是，大量的一阶方程一般是不能用初等解法求出其通解。

而实际问题中所需要的往往是要求满足某种初始条件的解。

因此初值问题的研究就显得十分重要，从前面我们也了解到初值问题的解不一定是唯一的。

他必须满足一定的条件才能保证初值问题解的存在性与唯一性，而讨论初值问题解的存在性与唯一性在常微分方程占有很重要的地位，是近代常微分方程定性理论，稳定性理论以及其他理论的基础。

例如方程dydx=过点(0,0)的解就是不唯一，易知0y =是方程过(0,0)的解，此外，容易验证，2y x =或更一般地，函数20 0() c<1x cy x c x ≤≤⎧=⎨-≤⎩ 都是方程过点(0,0)而且定义在区间01x ≤≤上的解，其中c 是满足01c <<的任一数。

解的存在唯一性定理能够很好地解释上述问题，它明确地肯定了方程的解在一定条件下的存在性和唯一性。

常微分方程课程总结第一章 绪论§1.2微分方程的基本概念（1）常微分方程偏微分方程微分方程：凡含有未知函数的导数或微分的方程叫微分方程。

常微分方程：未知函数为一元函数的微分方程。

()(),dyaxy a dxdy p x y Q x dx=+=为常数 偏微分方程：未知函数为多元函数，从而出现偏导数的微分方程。

()22,22242u uf x y x y u u y x ∂∂+=∂∂∂∂=∂∂（2）线性与非线性一般n 阶线性微分方程具有形式：（等式左面全是一次有理整式）()(1)11()()()().n n n n y a x y a x y a x y f x --'++++=（3）解和隐式解微分方程的解：代入微分方程能使方程成为恒等式的函数. 隐式解：Φ（x,y ）=0 （4）通解和特解通解：微分方程的解中含有任意常数,且任意常数的个数与微分方程的阶数同.） 特解： 确定了通解中任意常数以后的解. 初始条件：用来确定任意常数的条件.初值问题: 求微分方程满足初始条件的解的问题.（5）积分曲线：微分方程任一特解的图形都是一条曲线,称为微分方程的积曲线。

第二章 一阶微分方程的初等解法§2.1 变量分离方程与变量变换2.1.1、变量分离方程)()(y x f dxdyϕ= ⎰⎰+=c dx x f y dy )()(ϕ 2.1.2、可化为变量分离方程的类型1.形如)(x y g dx dy =，称为齐次微分方程，令u ＝xy ,即y ＝ux ，于是dx dy ＝x dx du ＋u ，代入原方程，变形为x dx du ＋u ＝g （u ），整理得dx du ＝xuu g -)(2.形如222111c x b x a c x b x a dx dy ++++= 的方程也可经变量变换化为变量分离方程（1）常数）(212121k c c b b a a ===，方程化为dxdy ＝k ，有通解c kx y += （2）≠==k b b a a 212121c c 情形，令u ＝y b x a 21+，这时有dx du ＝dx dy b a 22+＝2122c u c ku b a +++是分离变量方程 （3）2121b b a a ≠情形，若21c c 、不全为零，方程右端分子、分母都是x 、y 的一次多项式，因此111c x b x a ++＝0，222c y b x a ++＝0，交点（),βα，令X ＝x －α，Y ＝y －β，化为011=+Y b X a ， 022=+Y b X a 。

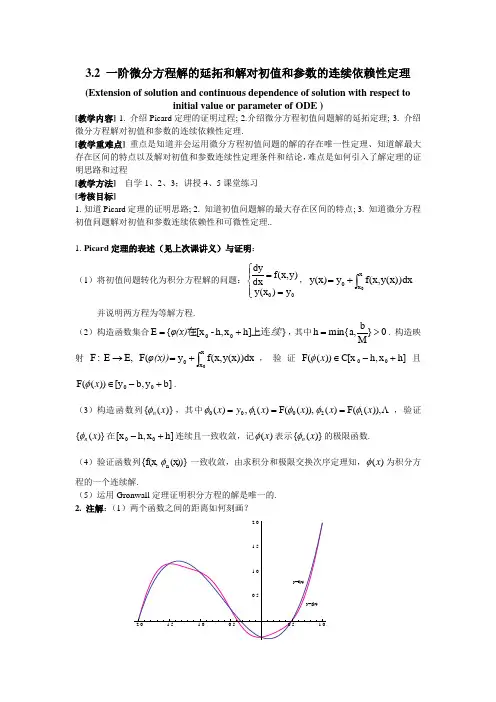
3.2 一阶微分方程解的延拓和解对初值和参数的连续依赖性定理(Extension of solution and continuous dependence of solution with respect toinitial value or parameter of ODE )[教学内容] 1. 介绍Picard 定理的证明过程; 2.介绍微分方程初值问题解的延拓定理; 3. 介绍微分方程解对初值和参数的连续依赖性定理.[教学重难点] 重点是知道并会运用微分方程初值问题的解的存在唯一性定理、知道解最大存在区间的特点以及解对初值和参数连续性定理条件和结论，难点是如何引入了解定理的证明思路和过程[教学方法] 自学1、2、3；讲授4、5课堂练习 [考核目标]1. 知道Picard 定理的证明思路;2. 知道初值问题解的最大存在区间的特点;3. 知道微分方程初值问题解对初值和参数连续依赖性和可微性定理..1. Picard 定理的表述（见上次课讲义）与证明：（1）将初值问题转化为积分方程解的问题：⎪⎩⎪⎨⎧==00y )y(x y)f(x,dx dy ，⎰+=x x 00y(x ))dx f(x ,y y(x )并说明两方程为等解方程.（2）构造函数集合}上连h]x h,-[x 在{E 00续φ(x)+=，其中0}Mbmin{a,h >=. 构造映射⎰+=→xx 00y(x ))dx f(x ,y F( E,E :F φ(x))，验证h]x h,C[x ))((F 00+-∈x φ且]b y b,[y ))((F 00+-∈x φ.（3）构造函数列)}({x n φ，其中 )),((F )()),((F )(,)(120100x x x x y x φφφφφ===，验证)}({x n φ在h]x h,[x 00+-连续且一致收敛，记)(x φ表示)}({x n φ的极限函数.（4）验证函数列(x ))}{f(x ,n φ一致收敛，由求积分和极限交换次序定理知，)(x φ为积分方程的一个连续解.（5）运用Gronwall 定理证明积分方程的解是唯一的. 2. 注解：（1）两个函数之间的距离如何刻画？y=f(x)y=g (x )2.0 1.5 1.00.50.5 1.00.51.01.52.0定义|g(x)f(x)|max g(x)f(x)h]x h,[x x 00-=-+-∈，从图像来看这样刻画是合理的！（2）Picard 函数列与精确解的误差估计：h]x h,[x x ,h 1)!(n ML )()(001n n +-∈+≤-+x x n φφ.（3）柯西定理及其特殊情形，线性方程解的存在唯一性的条件. （4）一阶隐方程解的存在唯一性定理（参见教材P86定理2） 3. 微分方程初值问题的Picard 近似解计算和误差估计 例42. 方程22y x dxdy+=定义在矩形域1] 1,[1] 1,[D -⨯-=，试利用解的存在唯一性定理确定经过(0, 0)的解的存在区间，并求出在此区间上与精确解误差不超过0.05的近似解的表达式.（参见教材P87例题1）作业35. 教材P88，习题3，习题10.3. 解的延拓定理（1）问题表述： 由解的存在性定理知，⎪⎩⎪⎨⎧==00y )y (x y)f(x,dx dy的解为φ(x )y =至少在h]x h,[x 00+-上存在，那么上述解函数最大的存在区间是什么呢？（2）理解教材P90，图(3.2)，知道饱和解. （3）解的延拓定理及其参见教材P91和P92.考察初值问题⎪⎩⎪⎨⎧==00y )y(x y)f(x,dx dy，其中y)f(x ,在开区域内连续，且在G 内对y 满足局部的Lipschitz 条件，设位于G 内一点)y ,(x 00出发的解φ(x )y =的最大存在区间为),(βα，则),(βα具有如下特征：当+→αx ，))(,(x x ϕ趋于G 的边界；当-→βx ，))(,(x x ϕ趋于G 的边界. 特别地，若G=2R ，且方程的任一解都有界，则方程任一解的最大存在区间为),(∞+-∞.例43. （1）讨论方程21y dx dy 2-=分别通过点3)2,(ln (0,0),-的解的最大存在区间. （2）讨论方程1t 2dt dx 2-=分别通过点1) (2, 1), (0,的解的最大存在区间.（3）讨论方程y 2dxdy-=过点1) (0,的解最大存在区间. 解：（1）参见教材P92例题1. (2) 两个解分别为1t 1-1,|1t 1t |ln x <<++-=和1t 3,ln 1|1t 1t |ln x >+++-=. (3) 右端函数y 2y)f(x,-=的存在域为0}y |y){(x ,≥. 方程的通解为0y ,x )(c y 2=-=过点1) (0,的解为2x)(1y -=，该解向左可以延伸到∞-，向右延伸到0y 1,x →→；但注意到∞<<∞-=x 0,y ，因此，该解向右可以延伸到∞+.作业36. （1）考察⎪⎩⎪⎨⎧==00x )x(t x)f(t,dt dx，若x )f(t,在整个Otx 平面上有定义，连续且有界，同时对变量x 存在一阶连续偏导数，则方程的任一解的最大存在区间为) ,(∞+-∞.（2）讨论方程22y x 1dx dy +=和方程2y 1dxdy +=解的最大存在区间.4. 微分方程解对初值的连续性和可微性定理（1）问题表述：由解的存在性定理知，⎪⎩⎪⎨⎧==00y )y(x λ)y,f(x,dx dy的解为φ(x )y =至少在h]x h,[x 00+-上存在，为了表示解与初值和参数λ相关，将上述解函数记为),y ,x φ(x ,y 00λ=. 问解函数),y ,x φ(x ,00λ是否对变量λ ,y ,x 00连续，是否可导，以及导函数例如y ∂∂ϕ的表达式？ 考察一个具体的例子：⎪⎩⎪⎨⎧==00y )y(x y λdx dy 的解为)x λ(x 00e y y -=，这就是一个关于变量λ) ,y , x (x ,00的多元函数λ),y ,x (x ,y 00ϕ=. （2）回答：教材P95 定理，P99定理，P100定理. （3）形式推导出0x ∂∂ϕ，0y ∂∂ϕ，λ∂∂ϕ满足的方程和表达式.（一）、⎪⎩⎪⎨⎧==00y )(x )f(x,dx d ϕϕϕ，对上面两式两边关于0y 求导得到，⎪⎪⎩⎪⎪⎨⎧=∂∂∂∂⋅∂∂=⎪⎪⎭⎫ ⎝⎛∂∂1)(x y y )f(x,y dx d 0000y ϕϕϕϕ，求解上述方程初值问题得到，⎰=∂∂∂∂x0x dx y)f(x,0e y ϕϕ.（二）、⎪⎩⎪⎨⎧==00y )(x )f(x,dx d ϕϕϕ，对上面两式两边关于0x 求导得到，⎪⎪⎩⎪⎪⎨⎧-=∂∂∂∂⋅∂∂=⎪⎪⎭⎫ ⎝⎛∂∂=)y ,f(x x x y )f(x,x dx d 00000x x ϕϕϕϕ，说明第二式：0000y λ),y ,x ,(x =ϕ， 关于0x 求导得到)y ,f(x xx 0,x x00x x 00x x 0-=∂∂-=∂∂=∂∂+∂∂==ϕϕϕϕ.求解上述方程初值问题得到，⎰-=∂∂∂∂x0x dx y)f(x,000e )y ,f(x x ϕϕ.例44. 假设函数Q(x ) P(x ),为区间b] [a,上连续函数，)y ,x (x ,y 00ϕ=为线性方程Q(x )y P(x )dxdy +=的解，)y ,x ,(x y 0000ϕ=. 试求(1)00y ,x ,x ∂∂∂∂∂∂ϕϕϕ; (2) 用常数变易公式求出方程的解函数再通过直接求导法来求出00y ,x ,x ∂∂∂∂∂∂ϕϕϕ. 解：（1）由公式有 ,))eQ(x )y P(x ())eQ(x )P(x (xx0x xx 0P(x)dx000P(x)dx0x x 00⎰+-=⎰+-=∂∂=ϕϕ,e y x0x P(x)dx 0⎰=∂∂ϕQ(x )y P(x )x+=∂∂ϕ. （2）由常数变易公式得到，C)Q(t)dt e(e(x)x x P(s)dsP(t)dtt0x x0x +⎰⎰=⎰-ϕ.再由初值条件确定出0y C =. 因此，)y Q(t)dt e(e)y ,x (x,0xx P(s)dsP(t)dt000t0x x0x +⎰⎰=⎰-ϕ.Q(t)dt )P(x e )Q(x e y Q(t)dt e )P(x (e x x x 0P(s)ds0P(t)dt 0x x P(s)ds 0P(t)dt0tx x 0x 0t 0x xx ⎪⎪⎭⎫ ⎝⎛⎰+-⎰+⎪⎪⎭⎫ ⎝⎛+⎰-⎰=∂∂⎰⎰--ϕ⎰+-=∂∂x0x P(x)dx0000))e Q(x y )P(x (x ϕ； ⎰=∂∂x0x P(x)dxe y ϕ ； Q(x)e e y Q(t)dt e P(x) e x x0x x0x 0t0x x0x P(s)ds P(t)dt 0x x P(s)ds P(t)dt⎰⎰+⎪⎪⎭⎫ ⎝⎛+⎰⎰=∂∂--⎰ϕ；Q(x ) P(x )x+=∂∂ϕϕ.作业37. 给定方程⎪⎭⎫⎝⎛=x y sin dx dy ，试求00000),,(,),,(y y x x y x y x x y ∂∂∂∂在0,100==y x 时的表达式.附录：。

常微分方程初值问题数值解法初值问题：即满足初值条件的常微分方程的解y′=f(x,y),x∈[x0,b]y(x0)=y0.定理1（利普希茨条件）若存在正数L，使得对任意，y1，y2，有|f(x,y1)−f(x,y2)|≤L|(y1−y2)|定理2（解存在性）①若函数f在方区域x∈[a,b],y∈R连续，②函数f关于y 满足利普希茨条件，则对任意x∈[a,b]，常微分方程存在唯一的连续可微数值解.两类问题：①单步法---计算下一个点的值yn+1只需要用到前面一个点的值yn②多步法---计算下一个点的值yn+1需要用到前面l个点的值yl1、欧拉法---下一个点的计算值等于前一个点的计算值加上步长乘以前一个点的函数值•具体过程一些批注：显式欧拉方程指下一步要计算的值，不在迭代方程中；隐式欧拉方程指下一步要计算的值，在迭代方程中。

怎么计算隐式欧拉方程----要借助显示欧拉迭代计算---一般用迭代法-----迭代---将微分方程在区间[xn,xn+1]进行积分，然后函数f进行近似，即可得到迭代方程-----迭代方程收敛性？由函数关于y满足利普希茨条件，可以推出迭代公式收敛。

•局部截断误差：假设前n步误差为0，我们计算第n+1步的误差，将次误差称为局部截断误差，且局部误差为O(hp+1)•p阶精度：由理论证明：若局部误差阶的时间复杂度为O(hp+1)，则整体误差阶为O(hp)我们称公式精度为p。

•显示欧拉法与隐式欧拉法•梯形方法----将显式欧拉迭代方程与隐式欧拉迭代方程做一下加权平均，构造的计算公式.•改进的欧拉方法---思想：因为梯形公式是隐式公式，将显式欧拉公式对下一步的计算值进行预估，用梯形公式对下一步的计算值进行校正.2、龙格-库塔方法思想：根据Lagrange中值定理，下一次的计算值可以用前一次的计算值加上h乘以前一个点的斜率；而这个斜率用该区间上的多个点的斜率的算数平均来逼近。

注意：怎么计算任意斜率Ki？第i个点的斜率Ki有微分方程可以算出f′=f(xn,yn)所以要算的f(xn,yn)值，由欧拉法即可算出, yn+1=yn+hf′•2阶-龙格-库塔方法----类似改进的欧拉法根据Lagrange中值定理，下一次的计算值可以用前一次的计算值加上h乘以斜率；而这个斜率用区间上的端点和中点的斜率的算数平均来逼近。

§3.3 解对初值的连续性和可微性定理在初值问题中我们都是把初值看成是固定的数值，然后再去讨论方程⎪⎩⎪⎨⎧==)(),(00x y y y x f dx dy),(00y x 经过点的解.但是假如变动，则相应初值问题的解也随之变动，也就是),(y x f dxdy=),(00y x 00(,)x y 说初值问题的解不仅依赖于自变量,还依赖于初值.例如：时,方程的解x 00(,)x y y y x f =),(y y ='是,将初始条件带入,可得.很显然它是自变量和初始条件的xce y =00)(y x y =00x x ey y -=x 00(,)x y 函数.因此将对初值问题的解记为,它满足.⎪⎩⎪⎨⎧==)(),(00x y y y x f dx dy),,(00y x x y ϕ=0000(,,)y x x y ϕ=当初值发生变化时，对应的解是如何变化的？当初始值微小变动时，方程解的变化是否也很小呢？为此就要讨论解对初值的一些性质.1、解关于初值的对称性设方程(3.1)满足初始条件的解是唯一的,记为,则在此关系式中,00()y x y =),,(00y x x y ϕ=与可以调换其相对位置.即在解的存在范围内成立关系式(,)x y 00(,)x y 00(,,)y x x y ϕ=证明在方程(3.1)满足初始条件的解的存在区间内任取一点,显然00()y x y =1x ,则由解的唯一性知,过点的解与过点的解是同一条积分曲线,即此解1100(,,)y x x y ϕ=11(,)x y 00(,)x y 也可写为11(,,)y x x y ϕ=并且,有.又由是积分曲线上的任一点,因此关系式对该积分0011(,,)y x x y ϕ=11(,)x y 00(,,)y x x y ϕ=曲线上的任意点均成立.2、 解对初值的连续依赖性由于实际问题中初始条件一般是由实验 测量得到的，肯定存在误差. 有的时候误差比较大，有的时候误差比较小，在实际应用中我们当然希望误差较小，也就是说当变动很小的时候，相00(,)x y 应的方程的解也只有微小的变动，这就是解对初值的连续依赖性所要研究的问题：在讨论这个问题之前，我们先来看一个引理：引理：如果函数于某域内连续，且关于满足Lipschtiz 条件（Lipschtiz 常数为），(,)f x y D y L 则对方程（3.1）的任意两个解及，在它们公共存在的区间内成立着不等式()x ϕ()x ψ0||00|()()||()()|L x x x x x x eϕψϕψ--≤-（3.17）其中为所考虑区域内的某一值.0x 证明 设, 于区间上均有定义,令()x ϕ()x ψa x b ≤≤ 2()[()()],V x x x a x bϕψ=-≤≤则()2[()()][(,)(,)]V x x x f x f x ϕψϕψ'=--于是 ()|()|2|()()||(,)(,)|2()V x V x x x f x f x LV x ϕψϕψ''≤=--≤ 22()2()0LxLx V x eLV x e --'-≤从而2(())0Lx dV x e dx-≤所以,对,有0[,]x a b ∀∈ 02()00()(),L x x V x V x ex x b-≤≤≤对于区间,令,并记,则方程(3.1)变为0a x x ≤≤x t -≤00x t -≤(,)dyf t y dx=--而且已知它有解和.()y t ϕ=-()y t ψ=-类似可得02()00()(),L x x V x V x ea x x -≤≤≤因此, 02||00()(),,L x x V x V x ea xb a x b-≤≤≤≤≤两边开平方即得(3.17).利用此引理我们可以证明解对初值的连续依赖性： 解对初值的连续依赖定理假设在区域内连续，且关于满足局部李普希兹条件，如果，初值问题),(y x f G y 00(,)x y G ∈有解，它于区间上有定义(),则对任意， ⎪⎩⎪⎨⎧==)(),(00x y y y x f dxdy00(,,)y x x y ϕ=b x a ≤≤0a x b ≤≤0>ε，使得当时,方程(3.1)满足条件的解(,,)0a b δδε∃=>2220000()()x x y y δ-+-≤00()y x y =在区间上也有定义，并且有00(,,)y x x y ϕ=b x a ≤≤.0000(,,)(,,),x x y x x y a x b ϕϕε-<≤≤证明 记积分曲线段是平面上一个有界闭集.00:(,,)(),S y x x y x a x b ϕϕ=≡≤≤xy 第一步:找区域,使,而且在上关于满足Lipschitz 条件.D S D ⊂(,)f x y D y 由已知条件,对,存在以它为中心的开圆,使在其内关于满足(,)x y S ∀∈,C C G ⊂(,)f x y y Lipschitz 条件.因此,根据有限覆盖定理,可以找到有限个具有这种性质的圆(不同的(1,2,,)i C i N = ,其半径和Lipschitz 常数的大小可能不同),它们的全体覆盖了整个积分曲线段,令,则i C i r i L S 1Nii G C == S G G ⊂⊂ 对,记,则以上的点为中心,以为半径0ε∀>1(,),min(,2),max(,)Nd G S L L L ρηερ=∂== S η的圆的全体及其边界构成包含的有界闭域,且在上关于满足Lipschitz 条件, S D GG ⊂⊂ (,)f x y D y Lipschitz 常数为.L 第二步:证明，使得当时,解(,,)0()a b δδεδη∃=><2220000()()x x y y δ-+-≤在区间上也有定义.00()(,,)y x x x y ψϕ==a x b ≤≤由于是一个有界闭域,且在其内关于满足Lipschitz 条件,由解的延拓定理可知,解D (,)f x y y 必能延拓到区域的边界上.设它在的边界上的点为和,00()(,,)y x x x y ψϕ==D D (,())c c ψ(,())d d ψ,这时必有.否则设,由引理有c d <,c a d b ≤≥,c a d b >< 0||00|()()||()()|,L x x x x x x ec x dϕψϕψ--≤-≤≤利用的连续性,对,必有存在,使当时有,()x ϕ()112L b a e δ--=20δ>02||x x δ-≤01|()()|x x ϕϕδ-<取,则当时就有12min(,)δδδ=2220000()()x x y y δ-+-≤ (3.18)0002||22002||200002||2200002101|()()||()()|2(|()()||()()|) 2(|()()||()()|) 2(|L x x L x x L x x x x x x e x x x x e x x x x ey ϕψϕψϕϕϕψϕϕϕψδ----≤-≤-+-≤-+-<+-22()022()21|) 4 ()L b a L b a y e e c x d δη--≤=≤≤于是对一切成立,特别地有[,],|()()|x c d x x ϕψη∈-< ,|()()|c c ϕψη-<|()()|d d ϕψη-<即点和均落在域的内部,这与假设矛盾,故解在区间上有定义.(,())c c ψ(,())d d ψD ()y x ψ=[,]a b 第三步 证明.|()()|,x x a x b ϕψε-<≤≤在不等式（3.18）中将区间换成，可知当[,]c d [,]a b 时，就有2220000()()x x y y δ-+-≤ .0000(,,)(,,),x x y x x y a x b ϕϕηε-<≤≤≤根据方程解对初值的连续依赖定理及解对自变量的连续性有3、解对初值的连续性定理若函数在区域内连续，且关于满足局部李普希兹条件,则方程(3.1)的解),(y x f G y 作为的函数在它的存在范围内是连续的.00(,,)y x x y ϕ=00,,x x y 证明对,方程(3.1)过的饱和解定义于00(,)x y G ∀∈00(,)x y 00(,,)y x x y ϕ=上,令0000(,)(,)x y x x y αβ≤≤ 00000000{(,,)|(,)(,),(,)}V x x y x y x x y x y G αβ=≤≤∈下证在上连续.00(,,)y x x y ϕ=V 对,,使解在上有定义,其中.00(,,)x x y V ∀∈[,]a b ∃00(,,)y x x y ϕ=[,]a b 0,[,]x x a b ∈对,使得当时,10,0εδ∀>∃>22200001()()x x y y δ-+-≤ 0000(,,)(,,),2x x y x x y a x bεϕϕ-<≤≤又在上对连续,故,使得当时有00(,,)y x x y ϕ=[,]x a b ∈x 20δ∃>2||x x δ-≤ 0000(,)(,,),[,]2x x y x x y x x a b εϕϕ-<∈取,则只要就有12min(,)δδδ=22220000()()()x x x x y y δ-+-+-≤ 000000000000(,,)(,,)|(,,)(,,)||(,,)(,,)|22x x y x x y x x y x x y x x y x x y ϕϕϕϕϕϕεεε-≤-+-<+=从而得知在上连续.00(,,)y x x y ϕ=V 4、解对初值和参数的连续依赖定理讨论含有参数的微分方程λ(3.19) (,,)dyf x y dxλ:(,),G x y G λαλβ∈<<如果对，都存在以为中心的球，使得对任何(,,)x y G λλ∀∈(,,)x y λC G λ⊂，成立不等式12(,,),(,,)x y x y C λλ∈ 1212|(,,)(,,)|||f x y f x y L y y λλ-≤-其中是与无关的正数，称函数在内关于一致地满足局部的李普希兹条件.由L λ(,,)f x y λG λy 解的唯一性，对每一，方程（3.19）通过点的解是唯一确定的，记这个解为0(,)λαβ∈00(,)x y G ∈.000(,,,)y x x y ϕλ=设在内连续,且在内关于一致地满足局部的李普希兹条件, (,,)f x y λG λG λy 是方程(3.19)通过的解,在区间上有定义,其中000000(,,),(,,,)x y G y x x y λλϕλ∈=00(,)x y a x b ≤≤,则对,使得当0a x b ≤≤0,(,,)0a b εδδε∀>∃=> 222200000()()()x x y y λλδ-+-+-≤时,方程(3.19)通过点的解在区间上也有定义,并且00(,)x y 00(,,,)y x x y ϕλ=a x b ≤≤ 00000(,,,)(,,,),[,]x x y x x y x a b ϕλϕλε-<∈5、解对初值和参数的连续性定理设函数在区域内连续，且在关于一致地满足局部李普希兹条件,则方程(3.19)(,,)f x y λG λG λy 的解作为的函数在它的存在范围内是连续的.00(,,,)y x x y ϕλ=00,,,x x y λ6、 解对初值的可微性定理如果函数以及都在区域内连续，则对初值问题的解),(y x f y y x f ∂∂),(G ⎪⎩⎪⎨⎧==)(),(00x y y y x f dx dy作为 的函数，在它有定义的范围内有连续可微的.),,(00y x x y ϕ=00,,x x y 证明 由在区域内连续，可知在内关于满足局部Lipschitz 条件，根据yy x f ∂∂),(G ),(y x f G y 解对初值的连续性定理，在它的存在范围内关于是连续的.),,(00y x x y ϕ=00,,x x y 下面证明函数在它的存在范围内的任一点偏导数.00(,,)y x x y ϕ=00,,xx y ϕϕϕ∂∂∂∂∂∂存在且连续.(,),f x xϕϕ∂=∂显然存在且连续.0x ϕ∂∂先证存在且连续00000(,)(,)x y x x y +∆由初值和所确定的解分别为00(,,),y x x y ϕϕ=≡000(,,),y x x x y ϕψ=+∆≡即 00(,),xx y f x dx ϕϕ≡+⎰000(,),xx x y f x dx ψψ+∆≡+⎰于是 00(,)(,)xx x x x f x dx f x dxψϕψϕ+∆-≡-⎰⎰ 000(,)x x x f x dx ψ+∆=-⎰(,())()xx f x dxyϕθψϕψϕ∂+-+-∂⎰01,,,fyθϕψ∂<<∂其中注意到及的连续性有(,())f x y ϕθψϕ∂+-=∂1(,)f x r yϕ∂+∂类似有010100,00.x r x r ∆→→∆==这里当时,且时, 000021(,)(,)x x x f x dx f x y r x ψ+∆-=-+∆⎰120,0r r x ∆≠其中与具有相同性质因此对有00210(,)()[(,)][]xx f x f x y r r dx x y x ψϕϕψϕ-∂-≡-+++∆∂∆⎰ 即 是初值问题z x ψϕ-=∆100020(,)[]()(,)dz f x r z dx y z x f x y r zϕ∂⎧=+⎪∂⎨⎪=-+≡⎩的解，.根据解对初值和参数的连续性定理00,x ∆=显然当时上述初值问题仍然有解000,,,,z x x z x x ψϕ-=∆∆知是的连续函数从而存在 00limx x x ψϕϕ∆→-∂≡∆∂x ϕ∂∂而是初值问题 000(,)()(,)dz f x z dxy z x f x y ϕ∂⎧=⎪∂⎨⎪=-⎩的解,容易得到0000(,)(,)exp()x x f x f x y dx x yϕϕ∂∂=-∂∂⎰.00,,x x y 显然它是的连续函数.y ϕ∂∂同样可证存在且连续00000(,)(,)x y x y y +∆设由初值和所确定的解分别为00(,,),y x x y ϕϕ=≡000(,,),y x x y y ϕψ=+∆≡类似上述方法可证是初值问题z y ψϕ-=∆ 30(,)[]()1dz f x r z dxy z x ϕ∂⎧=+⎪∂⎨⎪=⎩的解.因而30(,)exp([])xx f x r dx y yψϕϕ-∂=+∆∂⎰其中具有性质:所以有3r 030300,0.y r y r ∆→→∆==当时,且时,0000(,)lim exp()x x y f x dx y y yϕψϕϕ∆→∂-∂==∂∆∂⎰.00,,x x y 显然它是的连续函数故00(,(,,))f x x x y xϕϕ∂=∂000(,)(,)exp()x x f x f x y dx x yϕϕ∂∂=-∂∂⎰0(,)exp()x x f x dx y yϕϕ∂∂=∂∂⎰例1已知方程为试求，.)sin(xy dx dy =00000==∂∂y x y ϕ0000==∂∂y x x ϕ解：方程右端函数在平面内连续，且也在平面内连续，(,)sin()f x y xy =xy )cos('xy x f y =xy 且其满足的解为.0)0(=y 0y =于是，.20210cos 000),,(x ds s e e y y x x y x=⎰=∂∂00sin ),,(00cos 000=⎰-=∂∂xds s e x y x x y。