第二章题库和习题解答

第二章习题及解答2-1 如题图2-1所示为一小型冲床，试绘制其机构运动简图，并计算机构自由度。

（a）（b）题图2-1解：1)分析该小型冲床由菱形构件1、滑块2、拨叉3和圆盘4、连杆5、冲头6等构件组成，其中菱形构件1为原动件，绕固定点A作定轴转动，通过铰链B与滑块2联接，滑块2与拨叉3构成移动副，拨叉3与圆盘4固定在一起为同一个构件且绕C轴转动，圆盘通过铰链与连杆5联接，连杆带动冲头6做往复运动实现冲裁运动。

2)绘制机构运动简图选定比例尺后绘制机构运动简图如图（b）所示。

3)自由度计算其中n=5，P L=7, P H=0,F=3n-2P L-P H=3×5-2×7=1故该机构具有确定的运动。

2-2 如题图2-2所示为一齿轮齿条式活塞泵，试绘制其机构运动简图，并计算机构自由度。

（a）（b）题图2-2解：1)分析该活塞泵由飞轮曲柄1、连杆2、扇形齿轮3、齿条活塞4等构件组成，其中飞轮曲柄1为原动件，绕固定点A作定轴转动，通过铰链B与连杆2联接，连杆2通过铰链与扇形齿轮3联接，扇形齿轮3通过高副接触驱动齿条活塞4作往复运动，活塞与机架之间构成移动副。

2) 绘制机构运动简图选定比例尺后绘制机构运动简图如图（b）所示。

3)自由度计算其中n=4，P L=5, P H=1F=3n-2P L-P H=3×4-2×5-1=1故该机构具有确定的运动。

2-3 如图2-3所示为一简易冲床的初步设计方案，设计者的意图是电动机通过一级齿轮1和2减速后带动凸轮3旋转，然后通过摆杆4带动冲头实现上下往复冲压运动。

试根据机构自由度分析该方案的合理性，并提出修改后的新方案。

题图2-3解：1)分析2)绘制其机构运动简图(图2-3 b)选定比例尺后绘制机构运动简图如图（b ）所示。

3)计算机构自由度并分析其是否能实现设计意图由图b 可知，45200l h n p p p F ''===== 故3(2)34(2520)00l h F n p p p F ''=-+--=⨯-⨯+--=因此，此简易冲床根本不能运动，需增加机构的自由度。

第二章补充习题及答案普通化学概念、习题与解答化学反应基本原理——判断题1、指定单质的fGm、fHm、Sm皆为零。

(错：指定单质S不为零，)θmθθθ(错：升高温度正逆反应速率都增大，不会减小)10、反应活化能越大，反应速率也越大。

(错：相同温度下，活化能越大，速率常数越小，一般讲速率也越小)11、若反应速率方程式中浓度的指数等于反应方程式中反应物的系数，则该反应使基元反2、ΔrSm>0的反应都能自发进行。

(错：该条件只能判断对应温度孤立系统、标准状态下自发)3、rGm<0的反应必能自发进行。

(错：该条件只能判断对应温度标准状态4、若生成物的分子数比反应物的分子数多，则该反应的ΔrSm>0(错：主要看气体分子数)5、CaCO3在高温下可以发生分解反应，故该反应为吸热熵增。

(对：)6、根据能量最低原理，放热反应是自发进行的。

(错：影响自发性因素还有混乱度)7、冰在室温下自动融化成水，是熵增起了重要作用的结果。

(对：)8、化学反应的熵变与温度有关，但随温度变化不明显。

(对：温度变化没有引起状态变化的前提下)9、对于可逆反应C()+H2O(g)=CO(g)+H2(g),rHm0,升高温度使正增大，逆减小，故平衡向右移动。

应。

(错：例如H2（g）+I2(g)=2HI的反应就不是基元反应)12、反应级数取决于反应方程式中反应物的计量系数。

(错：非基元反应必须以试验为依据)13、根据分子碰撞理论，具有一定能量的分子在一定方位上发生有效碰撞，才可能生成产物。

(对)14、根据质量作用定律，反应物浓度增大，则反应速率加快，所以反应速率常数增大。

(错：速率常数与浓度无关)15、反应速率常数与温度有关，而与反应物浓度无关。

(对)二、选择题1热力学函数的定义与性质1-1下列各热力学函数中，哪一个为零：（B）(A)fGm(I2,g.298K)(B)fHm(Br2,l.298K)概念、习题与解答(C)Sm(H2,g.298K)(D)fGm(O3,g.298K)(E)fHm(CO2,g.298K)(C)对孤立体系而言，rSm>0的反应总是自发进行的。

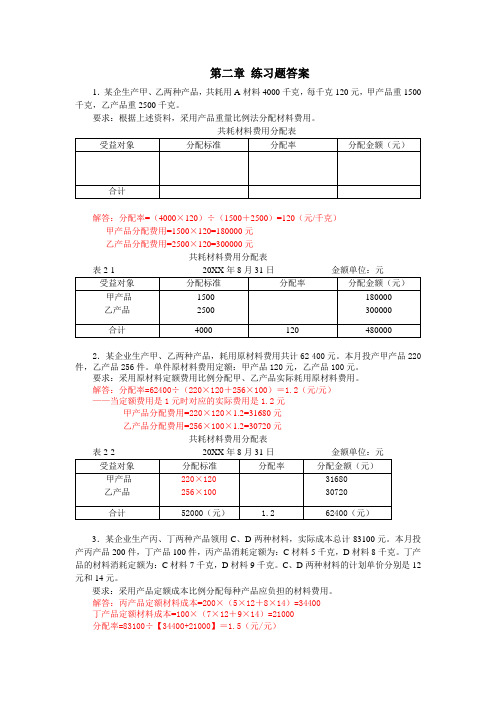
共耗材料费用分配表件，乙产品256件。

单件原材料费用定额：甲产品120元，乙产品100元。

要求：采用原材料定额费用比例分配甲、乙产品实际耗用原材料费用。

解答：分配率=62400÷（220×120＋256×100）＝1.2（元/元）——当定额费用是1元时对应的实际费用是1.2元甲产品分配费用=220×120×1.2=31680元乙产品分配费用=256×100×1.2=30720元共耗材料费用分配表表2-2 20XX年8月31日金额单位：元丁产品定额材料成本=100×（7×12＋9×14）=21000分配率=83100÷【34400+21000】＝1.5（元/元）——每一元定额成本对应的实际成本为1.5元。

丙产品分配费用=34400×1.5=34400×1.5=51600元丁产品分配费用=21000×1.5=21000×1.5=31500元或=83100-51600=315004.某企业本月共耗费原材料7200千克，每千克1.5元，共计10800元。

其中，基本车间生产甲、乙产品共领用6000千克；辅助生产车间消耗600千克；行政管理机构消耗600千克。

当月生产甲、乙产品分别为1200件和800件，单件甲、乙产品原材料消耗定额分别为3千克、1.5千克。

要求：（1）对甲、乙产品共同耗用的原材料费用按定额耗用量比例法进行分配；解答：分配率=（6000×1.5）÷（1200×3＋800×1.5）＝1.875（元/千克）甲产品分配费用=（1200×3）×1.875=6750元乙产品分配费用=6000×1.5-6750=2250元（2）将计算结果填入下表2-3；（3）编制原材料费用分配的会计分录。

02牛顿运动定律习题解答第二章牛顿运动定律一选择题1．下列四种说法中，正确的为：（）A.物体在恒力作用下，不可能作曲线运动；B.物体在变力作用下，不可能作曲线运动；C.物体在垂直于速度方向，且大小不变的力作用下作匀速圆周运动；D.物体在不垂直于速度方向的力作用下，不可能作圆周运动；解：答案是C。

2．关于惯性有下面四种说法，正确的为：（）A.物体静止或作匀速运动时才具有惯性；B.物体受力作变速运动时才具有惯性；C.物体受力作变速运动时才没有惯性；D.惯性是物体的一种固有属性，在任何情况下物体均有惯性。

解：答案是D3．在足够长的管中装有粘滞液体，放入钢球由静止开始向下运动，下列说法中正确的是：（）A.钢球运动越来越慢，最后静止不动；B.钢球运动越来越慢，最后达到稳定的速度；C.钢球运动越来越快，一直无限制地增加；D.钢球运动越来越快，最后达到稳定的速度。

解：答案是D4．一人肩扛一重量为P的米袋从高台上往下跳，当其在空中运动时，米袋作用在他肩上的力应为：（）A.0B.P/4C.PD.P/2解：答案是A。

简要提示：米袋和人具有相同的加速度，因此米袋作用在他肩上的力应为0。

5．有两辆构造相同的汽车在相同的水平面上行驶，其中甲车满载，乙车空载，当两车速度相等时，均关掉发动机，使其滑行，若从开始滑行到静止，甲车需时t1，乙车为t2，则有：（）A.t1=t2B.t1>t2C.t1<t2D.无法确定谁长谁短解：答案是A。

简要提示：两车滑动时的加速度大小均为g，又因v0at1=v0at2=0，所以t1=t26.若你在赤道地区用弹簧秤自已的体重，当地球突然停止自转，则你的体重将：（）A.增加；B.减小；C.不变；D.变为0解：答案是A简要提示：重力是万有引力与惯性离心力的矢量和，在赤道上两者的方向相反，当地球突然停止自转，惯性离心力变为0，因此体重将增加。

7.质量为m的物体最初位于某0处，在力F=k/某2作用下由静止开始沿直线运动，k为一常数，则物体在任一位置某处的速度应为（）A.k112k113k11k11()B.()C.()D.()m某某0m某某0m某某0m某某0解：答案是B。

第二章 需求、供给与均衡价格(题目及习题解答)一、判断题1.需求曲线描述了:其它条件不变，市场需求量与价格之间的关系。

解答:√。

知识点：课本第14页倒数第3行。

2.以纵轴代表价格，横轴代表数量，如果两条需求曲线通过同一点，则在那一点处，较陡的那条的弹性更大。

解答：×。

知识点：(考察弹性的几何意义)课本21页公式2.6和22页6-15行。

应该是“较陡的那条的弹性更小”。

理由：图中，直线AC 、BD 分别为需求曲线1和需求曲线2,AC 比BD 陡峭。

AC 之上的E 点弹性等于|AE|/|CE|,而BD 之上的E 点弹性等于|BE|/|DE|。

不难判定，|BE|>|AE|,而|DE|<|CE|，所以|AE|/|CE|<|BE|/|DE|，即“在那一点处，较陡的那条的弹性更小”。

3.如果需求是一条倾斜的直线，则价格水平越高，需求的价格弹性（绝对值）越大。

解答：√。

知识点：两种解法。

第一种是利用弹性的几何意义，课本22页6-7行。

如左下图所示：D 点价格大于B 点，D 点弹性=|AD|/|CD|>B 点弹性=|AB| /|BC|；第二种利用21页公式2.6。

因为B 点和D 点都在同一条直线上，所以dQ/dP 都相同，而P2<P 1，Q 2>Q1。

2121E E B D P P dQ dQ dP Q dP Q =⋅<=⋅ 4.如供给是一条直线，则供给的价格弹性为常数。

解答：×。

26页2.10b 。

“供给的价格弹性不确定”。

设供给函数为P=a+b ·Q s ，则dQ s /dP=-1/b 2,5.需求曲线越陡峭，则供给的变化对价格的影响越大。

P=a 1+b 1·Q s ，需求曲线P=a 2-b 2·Q d 。

令Q *=Q s =Q d ，得P *=(a 1b 2+b 1a 2)/(b 1+b 2)。

需求曲线a 1变化而b 1不变（平行移动）。

第二章习题解答参考习 题 2-11．设()=8f x x ，试按定义求(1)f '． 解 ()()()0011818(1)=limlim 8x x f x f x f x x∆→∆→+∆-+∆-'==∆∆． 2．设2()=f x ax bx c ++，其中,,a b c 为常数.按定义求()f x '． 解 ()()()0=limx f x x f x f x x∆→+∆-'∆()()()220limx a x x b x x c ax bx c x∆→+∆++∆+-++=∆()202lim 2x ax x a x b x ax b x∆→∆+∆+∆==+∆． 3．证明 (sin )=cos x x '． 证 设()sin f x x =，则()()()sin sin 2cos sin 22x x f x x f x x x x x ∆∆⎛⎫+∆-=+∆-=+ ⎪⎝⎭ ()()()002cos sin 22lim lim x x x x x f x x f x f x x x∆→∆→∆∆⎛⎫+ ⎪+∆-⎝⎭'==∆∆0sin2lim cos cos 22x xx x x x ∆→∆∆⎛⎫=+⋅= ⎪∆⎝⎭， 所以 (sin )=cos x x '．4．下列说法可否作为()f x 在0x 可导的定义 （1）000()()limh f x h f x h h→+--存在；解 不能．因为从极限式中不能判断()0f x 存在，也不能判断000()()limh f x h f x h→+-存在．例如()f x x =在0x =点不可导，但00(0)(0)limlim 0h h h h f h f h h h→→--+--==却存在．（2）000()()lim h f x h f x h +→+-和000()()lim h f x h f x h+→---存在且相等；解 可以．因为()0000()()lim h f x h f x f x h++→+-'=，()0000000()()()()lim lim h h f x h f x f x h f x f x h h+--→-→----'==--，根据导数存在的充要条件，可知()0f x '存在．5．求下列函数的导数：（1）5y x =； （2）y =； （3）y x =； （4）13log y x = ； （5）y =（6）lg y x =．解 （1）51455y x x -'==；（2）132212y x x --'⎛⎫'==-= ⎪⎝⎭（3）221577222277y x x x '⎛⎫'=== ⎪⎝⎭（4）111ln 3ln3y x x '==-； （5）25152326616y x x x +--''⎛⎫⎛⎫'==== ⎪ ⎪⎝⎭⎝⎭；（6）1ln10y x '=． 6．已知物体的运动规律为3s t =(米)，求这物体在2t =(秒)时的速度． 解 因为3s t =，23dsv t dt==，所以2t =时，()223212v =⨯=． 7．如果()f x 为偶函数，且(0)f '存在，证明(0)=0f '．证 因为()()0(0)=lim x f x f f x∆→∆-'∆，而()f x 为偶函数，故()()f x f x -∆=∆，所以()()()()000(0)limlim (0)x x f x f f x f f f x x∆→∆→-∆--∆-''==-=-∆-∆， 所以(0)=0f '．8．抛物线2y x =在哪一点的切线平行于直线45y x =-在哪一点的切线垂直于直线2650x y -+=解 由2y x =，可得2y x '=，若切点为()200,x x ，则依题设024x =，即02x =时，切线平行于直线45y x =-；01213x ⋅=-，即032x =-时，切线垂直于直线2650x y -+=；所以抛物线2y x =在点()2,4的切线平行于直线45y x =-在点39,24⎛⎫- ⎪⎝⎭的切线垂直于直线2650x y -+=．9．在抛物线2y x =上取横坐标为11x =及23x =的两点，作过这两点的割线，问该抛物线上哪一点的切线平行于这条割线解 由题设可知2y x '=，所取的两点为()1,1，()3,9，连接两点的直线斜率为4k =，依题设，应有24x =，即2x =，所以所求点为()2,4．10.如果()y f x =在点()4,3处的切线过点()0,2，求()4f '． 解 依题设，曲线在点()4,3处的切线为()()344y f x '-=-，满足()()23404f '-=-，从而()144f '=．11．讨论下列函数在0x =处的连续性与可导性：（1）y = （2）21sin ,0,0,0.x x y xx ⎧≠⎪=⎨⎪=⎩ 解（1）因为()000x y →==，所以y =0x =点连续，而20031lim x x x →→==+∞，所以y =0x =点不可导；（2）因为()201lim sin 00x x y x →==，所以21sin ,0,0,0.x x y x x ⎧≠⎪=⎨⎪=⎩在0x =点连续， 又 2001sin1limlim sin 0x x x x x x x →→==，所以21sin ,0,0,0.x x y x x ⎧≠⎪=⎨⎪=⎩在0x =点可导． 12．设sin ,0()=,0x x f x ax b x <⎧⎨+≥⎩在0x =处可导，求,a b 的值．解 因为sin ,0()=,0x x f x ax b x <⎧⎨+≥⎩在0x =处可导，所以()0lim ()0x f x f →=，且()()00f f -+''=，又0lim ()0x f x -→=，0lim ()x f x b +→=，()0f b =，故0b =，()00f =， 从而()()()000sin 0lim lim 1x x f x f xf x x---→→-'===， ()()()0000lim lim x x f x f ax f a xx +++→→-'===，所以1a =． 13．已知2,0(),0x x f x x x ⎧≥=⎨-<⎩，求(0)f +'，(0)f -'和(0)f '．解 因为2,0(),0x x f x x x ⎧≥=⎨-<⎩，所以()200()0(0)lim lim 0x x f x f x f x x +++→→-'===， ()00()0(0)lim lim 1x x f x f xf x x---→→--'===-，所以(0)f '不存在． 14．设函数33,0()=,0x x f x x x ⎧≥⎨-<⎩，求()f x '．解 当0x >时，2()3f x x '=，当0x <时，2()3f x x '=-，当0x =时，()()3000(0)limlim 0x x f x f x f xx +++→→-'===， ()()3000(0)lim lim 0x x f x f x f xx ---→→--'===，所以(0)0f '=，所以 223,0()=3,0x x f x x x ⎧≥'⎨-<⎩．15．设所给的函数可导，证明：（1）奇函数的导函数是偶函数；偶函数的导函数是奇函数； （2）周期函数的导函数仍是周期函数． 证 （1）设()f x 为奇函数，则()()f x f x -=-， 而()()()limh f x h f x f x h→+-'=，()()()()()0limlim h h f x h f x f x h f x f x h h→→-+----+'-== ()()0lim h f x h f x h →--=-()()()0lim h f x h f x f x h→--'==-，所以()f x '为偶函数；相似地，若()f x 为偶函数，则()()f x f x -=，于是()()()()()0limlim h h f x h f x f x h f x f x h h→→-+----'-== ()()()0limh f x h f x f x h→--'=-=--，所以()f x '为奇函数．（2）设()f x 为周期函数，则存在T ，使()()f x T f x +=，则()()()0limh f x T h f x T f x T h →++-+'+=()()()0lim h f x h f x f x h→+-'==， 所以()f x '也是以T 为周期的周期函数．16．设有一根细棒，取棒的一端作为原点，棒上任意点的坐标为x ．于是分布在区间[0,]x 上细棒的质量m 是x 的函数()m m x =．应怎样确定细棒在点0x 处的线密度（对于均匀细棒来说，单位长度细棒的质量叫这细棒的线密度）解 设在0x 处的线密度为()0x ρ，给0x 以x ∆的增量， 则在区间00[,]x x x +∆上细棒的平均线密度为()()00m x x m x x+∆-∆，故()()()()00000limx m x x m x x m x xρ∆→+∆-'==∆．17．证明：双曲线2xy a =上任一点处的切线与两坐标轴构成的三角形的面积都等于22a ．证 由2xy a =可得2,0a y x x =≠，于是22,0a y x x '=-≠，若切点为200,a x x ⎛⎫ ⎪⎝⎭，则该点处的切线为()220200a a y x x x x -=--，它与两坐标轴的交点分别为()02,0x ，2020,a x ⎛⎫ ⎪⎝⎭，所以所求三角形的面积为220012222a S x a x =⨯⨯=． 18．设函数()f x 在0x =处可导，试讨论函数|()|f x 在0x =处的可导性． 解 因为函数()f x 在0x =处可导，所以()()0()0lim0x f x f f x→-'=存在， 而()()()0limx x f x f f x x=→-'=，故（1）若(0)0f =，由()()0()0lim 0x f x f f x →-'=可知：()()0f x f xα'=+，其中lim 0x α→=，从而()()0f x x f α'=+⎡⎤⎣⎦，此时()()()000limlim 0x x x x f xf x f xxαα=→→'+⎡⎤⎣⎦''==⋅+， 因此|()|f x 在0x =点的左导数为()0f '-，右导数为()0f '， 所以|()|f x 在0x =处可导的充要条件是()00f '=；（2）若(0)0f ≠，设(0)0f >，则()0lim ()00x f x f →=>，由保号性定理，0δ∃>，当()0,x U δ∈时，()0f x >， 此时有()()()()0()0()0limlim0x x x f x f f x f f x f xx=→→--''===，相似地， 若(0)0f <，则()0lim ()00x f x f →=<，由保号性定理，0δ∃>，当()0,x U δ∈时，()0f x <，此时有()()()()00()0()0limlim 0x x x f x f f x f f x f x x=→→---⎡⎤⎣⎦''===-； 总之，若()f x 在0x =处可导，则当(0)0f ≠时，|()|f x 在0x =处可导；当(0)0f =时，|()|f x 在0x =处可导的充要条件是()00f '=．习 题 2-21．求下列函数的导数： （1）3cos2y x =；（2）4sin(31)y t =-；（3）32e 4cos2x y x =+； （4）5(1)y x =+；（5）43e 1x y -=+； （6）y =（7）1ln y x x=； （8）23(1)(1)y x x x =++-；（9）3e sin xy x x =；（10）322ln 3ln x x y x x +=+．解（1）()()()()3sin 223sin 226sin 2y x x x x ''=⋅-=-⋅=-； （2）()4cos(31)3112cos(31)y t t t ''=-⋅-=-；（3）()()()()332e 34sin 226e 8sin 2x x y x x x x '''=+-=-； （4）()445(1)15(1)y x x x ''=++=+； （5）()443e 4012e x x y x --''=-+=-；（6）y '==（7）()()()()2221ln ln ln 1ln ln ln x x x x x x y x x x x x x +⋅'+'=-=-=-； （8）()()3222221(1)(1)3(1)(1)522y x x x x x x x x '=+-+++⋅-=-++； （9）()23323e sin e sin e cos e 3sin sin cos x x x x y x x x x x x x x x x x x '=++=++；（10）()()()()()2234222222333ln 2ln 294ln 323ln 3ln x x x x x x x x x x x xx x y x x x x ⎛⎫⎛⎫++-++ ⎪ ⎪-+-+⎝⎭⎝⎭'==++2．证明：（1）2(cot )csc x x '=-； （2） (csc )csc cot x x x '=- ．证 （1）22cos sin sin cos cos (cot )csc sin sin x x x x x x x x x '-⋅-⋅⎛⎫'===- ⎪⎝⎭； （2）21cos 1cos (csc )csc cot sin sin sin sin x x x x x x x x x '⎛⎫'==-=-⋅=- ⎪⎝⎭． 3．证明：（1）(arccos )x '= （2）21(arccot )1x x '=-+． 证 （1）设arccos y x =，则其反函数为cos x y =，,22y ππ⎡⎤∈-⎢⎥⎣⎦，由于sin x y '=-，由反函数求导法则，()1arccos sin x y '=-== （2）设arccot y x =，则其反函数为cot x y =，()0,y π∈， 由于2csc x y '=-，由反函数求导法则，()222111arccos csc 1cot 1x y y x'=-=-=-++． 4．求下列函数在给定点处的导数：（1）2cos 3sin y x x =-，求π4x y ='； （2）2233x y x =+-，求(2)f '． 解 （1）因为2sin 3cos y x x '=--，所以π4ππ2sin3cos 442x y ='=--=-； （2）因为()()()22212223333x xy x x ⋅-'=-+=+--，所以()22222103332x y =⋅'=+=-．5．写出曲线122y x x=-与x 轴交点处的切线方程． 解 令0y =，得曲线122y x x =-与x 轴交点为1,02⎛⎫ ⎪⎝⎭和1,02⎛⎫- ⎪⎝⎭， 而2122y x '=+，所以142y ⎛⎫'±= ⎪⎝⎭， 所以所求切线有两条，方程分别为42y x =+，42y x =-．6．求下列函数的导数： （1）25(23)y x =+；（2）2sin (52)y x =-；（3）2321e xx y -++=；（4）2sin ()y x =； （5）2cos y x =；（6）y =（7）()arctan x y e =； （8）2(arccos )y x =； （9）lnsin y x =；（10）3log (1)a y x =+．解 （1）242245(23)(23)20(23)y x x x x ''=⋅+⋅+=+； （2）222cos(52)(52)4cos(52)y x x x x ''=-⋅-=--； （3）()()223212321e 32162e xx x x y x x x -++-++''=⋅-++=-+；（4）222cos()()2cos()y x x x x ''=⋅=；（5）()()2cos cos 2cos sin sin 2y x x x x x ''==-=-； （6）()22y a x ''=-==（7）()()221e e 1e 1e xxxx y ''==++； （8）2(arccos )(arccos )2(arccos )y x x x ⎛⎫''=== ⎝ （9）()1cos sin cot sin sin xy x x x x''===； （10）233313(1)(1)ln (1)ln x y x x a x a''=+=++．7．求下列函数的导数：（1）arccos(12)y x =-； （2）1arcsin y x=；（3）1ln 1ln xy x-=+；（4）ln (y x =；（5）sin cos n y x nx =⋅； （6）y =（7）e y =；（8）[]ln ln(ln )y x =；（9）y =（10）1arccot tan 22x y ⎛⎫= ⎪⎝⎭．解 （1）2)y x ''=-==；（2）211y x x '⎫⎫'==-=⎪⎪⎭⎭； （3）()()()()22111ln 1ln 21ln 1ln x x x x y x x x -+--'==-++； （4）y x ''=+==；（5）()()()1sin sin cos sin sin n n y n x x nx x nx nx -'''=⋅+-()1sin cos cos sin sin n n x x nx x nx -=⋅-()1sin cos 1n n x n x -=+⎡⎤⎣⎦；（6）1sin 21sin 2x y x '-⎛⎫'=⎪+⎝⎭()()()22cos 21sin 21sin 22cos 21sin 2x x x x x -+--=+2cos 21sin 2xx-=+()2cos 2cos 21sin 2x x x =-+；（7）(1ee1y x'''===+ （8）()()()1111ln (ln )ln ln (ln )ln (ln )ln ln ln (ln )y x x x x x x x x '''==⋅=； （9）y'====；（10）211tan 2211tan 22x y x '⎛⎫'=- ⎪⎝⎭⎛⎫+ ⎪⎝⎭2241sec 2224tan 2x x x '⎛⎫=- ⎪⎝⎭⎛⎫+ ⎪⎝⎭ 222sec 1213cos 4tan 22xx x =-=-⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭． 8．设1cos ,0()ln (1)cos ,0x x f x x x x x -<⎧=⎨+-≥⎩，求()f x '．解 当0x ≠时，sin ,0()1cos sin ,01x x f x x x x x x<⎧⎪'=⎨-+>⎪+⎩，当0x =时，20002sin sin1cos 022(0)lim limlim sin 022x x x x xx x f xxx ----→→→--'===⋅=，()()100ln 1cos 0(0)lim lim ln 1cos ln 10x x x x x x f x x e x +++→→+--⎡⎤'==+-=-=⎢⎥⎣⎦， 所以()00f '=，从而sin ,0()1cos sin ,01x x f x x x x x x <⎧⎪'=⎨-+≥⎪+⎩．9．求函数cos (sin )x y x =的导函数． 解法1 因为cos cos lnsin (sin )x x x y x e ==，所以()()cos cos lnsin cos cos ln sin sin sin ln sin cos sin x x x x y e x x x x x x x ⎛⎫''=⋅=-+ ⎪⎝⎭()2cos cos sin sin ln sin sin xx x x x x ⎛⎫=-+ ⎪⎝⎭．解法2 对数求导法，由cos (sin )x y x =，得ln cos ln (sin )y x x =， 两边同时对x 求导，得cos sin ln sin cos sin y x x x x y x'=-+， 所以()2cos cos sin sin ln sin sin xx y x x x x ⎛⎫'=-+ ⎪⎝⎭．10．设()sin f x x =，3()x x ϕ=，求[()]f x ϕ'，[()]f x ϕ'，{[()]}f x ϕ'．解 因为()sin f x x =，3()x x ϕ=，所以()cos f x x '=，2()3x x ϕ'=， 所以()()22[()]3sin 3f x f x x ϕ'==，[]()3[()]cos ()cos f x x x ϕϕ'==，()()()()33323{[()]}sin cos 3cos f x x x x x x ϕ''⎡⎤'===⎣⎦. 11．设()f x '存在，求下列函数的导数： （1）(cos )n f x ； （2）cos [()]n f x ．解 （1）[]()11(cos )(cos )(cos )(cos )(cos )cos nn n f x nf x f x nf x f x x --''''⎡⎤==⎣⎦1sin (cos )(cos )n n xf x f x -'=-；（2）{}{}{}()11cos [()]cos [()]cos[()]cos [()]sin[()]n n n f x n f x f x n f x f x f x --'''==-()1sin[()]cos [()]n n f x f x f x -'=-⋅⋅．12. 求曲线()22sin sin f x x x =+所有具有水平切线的点． 解 因为()2cos 2sin cos f x x x x '=+，令()0f x '=，得()cos 1sin 0x x +=，于是cos 0x =，或sin 1x =-， 推得 ,2x k k Z ππ=+∈，或32,2x k k Z ππ=+∈， 所以所求的点为2,32k ππ⎛⎫+ ⎪⎝⎭，32,12k ππ⎛⎫+- ⎪⎝⎭，其中k Z ∈． 习 题 2-31．求下列函数的二阶导数： （1）35e x y -= ；（2）e sin t y t -= ； （3）2sin ln y x x = ；（4）tan y x = ；（5）ln(y x = ； （6）2(1)arctan y x x =+ ． 解 （1）353e x y -'=，359e x y -''=；（2）()e sin e cos e cos sin t t t y t t t t ---'=-+=- ，()()e cos sin e sin cos 2e cos t t t y t t t t t ---''=--+--=-；（3）()221sin 2sin cos ln sin ln sin 2xy x x x x x x x x'=+⋅=⋅+，()()22sin 22sin cos sin ln 2cos 2x x x x xy x x x x ⋅-''=+⋅+ ()()222sin 2sin 2cos 2ln x xx x x x=+⋅-；（4）2sec y x '=，22sec sec tan 2sec tan y x x x x x ''=⋅⋅=⋅；（5）1y ⎛⎫'=+= ⎝ ()3221422y x x -''=-+⋅=；（6）2arctan 1y x x '=+，22arctan 1x y x x ⎛⎫''=+ ⎪+⎝⎭． 2．3e x y x = ，求(5)(0)y ． 解 设3u x =，x v e =，则23u x '=，6u x ''=，6u '''=，()0,4n u n =∀≥；(),nx v e n N +=∀∈， 代入莱布尼兹公式，得 ()()()()5445(5)510105y u v u v u v u v u v uv ''''''''''''=+++++2310610653x x x x e xe x e x e =⋅+⋅+⋅+，所以 (5)(0)60y =．3．22e x y x =，求(20)y ． 解 设2u x =，2x v e =，则2u x '=，2u ''=，()0,3n u n =∀≥；()22,nn x v e n N +=∀∈，代入莱布尼兹公式，得 ()()20(20)200n k k k k yC u v -==∑()()()181920210202020C u v C u v C uv '''=++ 182119202202202019022222x x x e C x e C x e =⋅⋅+⋅+⋅()202229520x e x x =++．4．试从d 1d x y y='导出：（1）223d d ()x y y y ''=-'；（2）3235d 3()d ()x y y y y y ''''''-='．解 因为d 1d x y y ='，所以()()2232d 111d x d d dx y y y dy y dx y dy y y y ''''⎛⎫⎛⎫==⋅=-⋅=- ⎪ ⎪'''''⎝⎭⎝⎭， ()()3333d d x d y d y dx y dy dx dyy y ⎛⎫⎛⎫''''=-=-⋅ ⎪ ⎪ ⎪ ⎪''⎝⎭⎝⎭ ()()()()()32265331y y y y y y y y y y y '''''''''''''''-⋅-=-⋅='''． 5．证明：函数12e e x x y C C λλ-=+（12,,C C λ是常数）满足关系式20y y λ''-=． 解 因为12e e x x y C C λλ-=+，所以()1212e e e e x x x x y C C C C λλλλλλλλ--'=+-=-，2212e e x x y C C λλλλ-''=+， 所以()22221212e e e e 0x x x x y y C C C C λλλλλλλλ--''-=+-+=． 6. 求常数λ的值，使得函数x y e λ=满足方程560y y y '''+-=．解 因为x y e λ=，所以x y e λλ'=，2x y e λλ''=，代入方程560y y y '''+-=， 得()2560x e λλλ+-=，因为0,x e x R λ≠∀∈，所以2560λλ+-=， 解得16λ=-，21λ=．7. 设()()sin f x x a =+，()sin cos g x b x c x =+，求常数,b c 的值，使得()()00f g =，且()()00f g ''=.解 因为()()sin f x x a =+，()sin cos g x b x c x =+， 所以()()cos f x x a '=+，()cos sin g x b x c x '=-,所以由()()00f g =，()()00f g ''=，可得sin c a =，且cos b a =． 8．求下列函数的n 阶导数．（1）12121n n n n n y x a x a x a x a ---=+++++L （12,,n a a a L 是常数）； （2）e x y x =； （3）2sin y x =； （4）2156y x x =-+．解 （1）()()12312112n n n n y nx n a x n a x a ----'=+-+-++L ，()()()()()23412211223n n n n y n n x n n a x n n a x a ----''=-+--+--++L ，根据幂函数的导数公式特点：每求导一次，幂函数降一次幂，故()!ny n =．（2）()e e e 1x x x y x x '=+=+，()()e 1e e 2x x x y x x ''=++=+，()()e 2e e 3x x x y x x '''=++=+，由此可见，每求一次导数，增加一个e x ， 所以()()e n x y x n =+，n N +∀∈； （3）()()21cos 211sin cos 2222x y x x -===-， ()2sin cos sin 2cos 22y x x x x π⎛⎫'===-+ ⎪⎝⎭，()2cos 22cos 222y x x π⎛⎫''==-+⋅ ⎪⎝⎭，()222sin 22cos 232y x x π⎛⎫'''=-=-+⋅⎡⎤ ⎪⎣⎦⎝⎭， ()()4332cos 22cos 242y x x π⎛⎫=-=-+⋅⎡⎤ ⎪⎣⎦⎝⎭， 所以()12cos 22nn y x n π-⎛⎫=-+⋅ ⎪⎝⎭，n N +∀∈．（4）因为 21115632y x x x x ==--+--， 而()2133x x -'⎛⎫=-- ⎪-⎝⎭，()()()311233x x -''⎛⎫=--- ⎪-⎝⎭， ()()()()4112333x x -'''⎛⎫=---- ⎪-⎝⎭， 可见，()()()()()()1112333n n n x x --⎛⎫=----- ⎪-⎝⎭L ()()11!3n n n x --=--，同理，()()()()()()()()11112321!22n n nn n x n x x ----⎛⎫=-----=-- ⎪-⎝⎭L ，所以()()()()()()()1111111!321!32nn n nn n n y n x x n x x ----++⎛⎫⎡⎤=----=-- ⎪⎣⎦ ⎪--⎝⎭．习 题 2-41．求由下列方程所确定的隐函数的导数d d y x： （1）e 0xy x y +-=；（2）22320x y xy y -+=；（3）e ln sin 2xy y x x +=；（4= （0a >的常数）．解 （1）将方程两边同时对x 求导，得1e 0xy dy dy y x dx dx ⎛⎫+-+= ⎪⎝⎭，变形得：e 11e xy xydy y dx x -=-；（2）将方程两边同时对x 求导，得22222230dy dy dy xy x y x y y dx dx dx ⎛⎫⎛⎫+-+⋅+= ⎪ ⎪⎝⎭⎝⎭，变形整理得：2224223dy xy y dx x xy y -+=-+； （3）将方程两边同时对x 求导，得 e ln 2cos 2xy dy dy y y x x x dx dx x ⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭，变形整理得：22cos 2e ln exyxy dy x x y xy dx x x x --=+；（4）将方程两边同时对x 求导，得0+=，变形整理得：()0dy x dx =>． 2．求曲线2520x y xy +-=在点(1,1)处的切线方程． 解 将方程两边同时对x 求导，得：42520dy dy x y y x dx dx ⎛⎫+-+= ⎪⎝⎭， 将1x =，1y =代入，解得：()1,10dydx=，所以曲线在点(1,1)处的切线方程为：1y =．3．已知sin cos()0y x x y -+=，求隐函数()y y x =在点π0,2⎛⎫⎪⎝⎭的导数值．解 将方程两边同时对x 求导，得：sin cos sin()10dy dy x y x x y dx dx ⎛⎫⎛⎫++++= ⎪ ⎪⎝⎭⎝⎭，将0x =，2y π=代入，解得：0,212dydxππ⎛⎫ ⎪⎝⎭=--．4．求下列方程所确定的隐函数的二阶导数22d d yx．（1）tan()y x y =+； （2）1e y y x =+；（3）ln y y x y =+； （4）arctan yx=. 解 （1）将方程两边同时对x 求导，得：2sec ()1dy dy x y dx dx ⎛⎫=++ ⎪⎝⎭， 解得2csc ()dyx y dx=-+， 再求导，得：()222csc()csc()cot 1d y dy x y x y x y dx dx ⎛⎫=-+-+++⎡⎤ ⎪⎣⎦⎝⎭， 将2csc ()dy x y dx=-+代入，整理得：()22322csc ()cot d y x y x y dx =-++；（2）将方程两边同时对x 求导，得：e e y ydy dyx dx dx=+， 解得：e 1e y y dy dx x =-，再求导，得：()()222e 1e e e e 1e yy y y y y dy dy x x dx dx d ydxx ⎡⎤⎛⎫---+ ⎪⎢⎥⎝⎭⎣⎦=-，将e 1e y y dy dx x =-代入，整理化简得：()()()()222332e 2e e 321e yyyy x y d y dx y x --==--； （3）将方程两边同时对x 求导，得：ln 1dy dy dyy dx dx dx+=+， 解得：1ln dy dx y =，再求导，得：()2221ln dyd yy dxdx y =-， 将1ln dy dx y =代入，整理化简得：()2321ln d y dx y y =-；（4）将方程两边同时对x 求导，得：2222221121dy dy x y x ydx dx x x y y x -+⋅=⋅+⎛⎫+ ⎪⎝⎭， 解得：dy x y dx x y +=-，再求导，得：()()()22211dy dy x y x y d y dx dx dx x y ⎛⎫⎛⎫+--+- ⎪ ⎪⎝⎭⎝⎭=-， 将dy x ydx x y +=-代入，整理化简得：()()222322x y d y dx x y +=-. 5．用对数求导法求下列函数的导数： （1）cos (sin )x y x =；（2）(tan 2)x y x =；（3）1xx y x ⎛⎫= ⎪+⎝⎭；（4）(2y x =-解 （1）两边取自然对数，得：ln cos ln(sin )y x x =， 两边同时对x 求导，得：()1cos sin ln sin cos sin dy xx x x y dx x=-+⋅, 整理化简得：()cos (sin )sin ln sin cos cot x dyx x x x x dx=-+⋅⎡⎤⎣⎦； （2）两边取自然对数，得：ln ln(tan 2)y x x =，两边同时对x 求导，得：()2sec 221ln(tan 2)tan 2x dyx x y dx x ⋅=+⋅， 整理化简得：4(tan 2)ln(tan 2)sin 4x dy x x x dx x ⎡⎤=+⎢⎥⎣⎦； （3）两边取自然对数，得：()ln ln ln ln 11x y x x x x x ⎛⎫==-+⎡⎤ ⎪⎣⎦+⎝⎭， 两边同时对x 求导，得：()111ln ln 11dy x x x y dx x x ⎛⎫=-++-⎡⎤ ⎪⎣⎦+⎝⎭整理化简得：1ln 111xdy x x dx x x x ⎛⎫⎡⎤=+ ⎪⎢⎥+++⎝⎭⎣⎦； （4）两边取自然对数，得：()111ln ln(21)ln ln(31)ln 1248y x x x x =-++++-，两边同时对x 求导，得：()121312124(31)81dy y dx x x x x =+++-+-，整理化简得：()2131(22124(31)81dy x dx x x x x ⎤=-+++⎢⎥-+-⎦6．求下列参数方程所确定的函数的导数d d yx： （1）cos sin sin cos x a bt b at y a bt b at =+⎧⎨=-⎩（,a b 为常数）； （2）22221(1)1at x t a t y t ⎧=⎪⎪+⎨-⎪=⎪+⎩（a 为常数）． 解 （1）因为()()sin cos dx ab bt ab at dt =-+，()()cos sin dyab bt ab at dt=+， 所以()()()()()()()()cos sin cos sin d d sin cos sin cos ab bt ab at bt at y x ab bt ab at bt at ++==-+-+； （2）因为()()()()22222221222111a t at t a t dx dt t t +-⋅-==++， ()()()22222221(1)2411at t a t t dy atdt t t -+--⋅-==++ 所以22d 22d 11y t tx t t =-=--． 7．求曲线2e 1(2)ettx t y t t --⎧=+⎪⎨=-⎪⎩在0t =处的切线方程与法线方程． 解 因为e e t t dx t dt --=-，()222e (2)e t t dy t t t dt--=---， 所以221dy t dx t +=-，02t dy dx==，又01,0t t xy====故所求切线为：()21y x =-，法线为：()112y x =--． 8．已知曲线2e 2e tx t mt n y p ⎧=++⎪⎨=-⎪⎩在0t =时过原点，且在该点处的切线与2350x y +-=平行，求常数,,m n p ．解 因为2dx t m dt =+，e tdy p dt=，故e 2t dy p dx t m =+，由题设可知：00t xn ===，02e 0t yp ==-=，23t dy p dxm ===-， 所以所求常数为：0n =，2e p =，3e m =-． 注：此题的书后答案有误．9．求下列参数方程所确定的函数的二阶导数22d d yx：（1）231x t y t t⎧=-⎪⎨=-⎪⎩； （2）e cos e sin t t x t y t ⎧=⎨=⎩； （3）()2ln 1arctan x t y t t⎧=+⎪⎨=-⎪⎩； （4）()()()x f t y tf t f t '=⎧⎨'=-⎩（()f t ''存在且不为零）．解 （1）因为2dx t dt =-，213dy t dt=-，所以21313222dy t t dx t t -==-+-， 于是 22223131313222224d y d t dt t t dx dt t dx t t ++⎛⎫=-+⋅==- ⎪-⎝⎭；（2）因为e cos e sin t t dx t t dt =-，e sin e cos t t dyt t dt=+， 所以e sin e cos sin cos e cos e sin cos sin t t t tdy t t t t dx t t t t++==--，于是 ()()()22222cos sin sin cos sin cos 1cos sin e cos e sin cos sin t tt t t t d y d t t dt dx dt t t dx t t t t -+++⎛⎫==⋅ ⎪--⎝⎭- ()32e cos sin tt t =-；（3）因为221dx t dt t =+，2111dy dt t =-+，所以22111221dy t t t dx t -+==+， 于是2222112241d y t t dx t t+==+； （4）因为()dx f t dt ''=，()()()()dy f t tf t f t tf t dt ''''''=+-=，所以dy t dx=，于是221()d y dx f t =''．10．将水注入深8米、上顶直径8米的正圆锥形容器中，注水速率为4吨/分钟．当水深为5米时，其表面上升的速率为多少解 如图所示，设在t 时刻容器中水面的高度为()h t （米），此时水面的半径为()r t （米），则依题意应有()()2143r t h t t π=，而()()84h t r t =， 所以()31412h t t π=，两边同时对时间t 求导， 可得()2144dh h t dt π=，当()5h t =时，可求得1625dh dt π=， 所以当水深为5米时，其表面上升的速率为16min 25m π． 11．汽车A 以50公里/小时的速度向西行驶，汽车B 以60公里/小时的速度向北行驶，两辆车都朝着两条路的交叉口行驶．当汽车A 距离交叉路口0.3公里，汽车B 距离交叉路口0.4公里时，两辆车以什么速率接近解 如图所示，设在t 时刻，汽车A 距离交叉路口()x t ，汽车B 距离交叉路口()y t ，则两车之间的直线距离为()()()22s t x t y t =+t 求导，可得()()()()22dx dy x t y t ds dt dt dtx t y t +=+50dx dt =，60dy dt =，故当()0.3x t =，()0.4y t =时，22780.30.4ds dt ==+，即当汽车A 距离交叉路口0.3公里，汽车B 距离交叉路口0.4公里时，两辆车以78/km h 的速率接近．12．一个路灯安装在15英尺高的柱子上，一个身高为6英尺的人从柱子下以5英尺/秒的速度沿直线走离柱子，当他距离柱子40英尺时，他身影的顶端以多快的速率移动解 如图所示，设在t 时刻，此人离灯柱的水平距离为()x t ，身影的顶端离灯柱的水平距离为()y t ，则依题意有：5dx dt =，()()()615y t x t y t -=，可见()()53y t x t =， 两边同时对时间t 求导，得52533dy dx dt dt ==， 所以他身影的顶端以25feet /3s 的速率移动，与他离灯柱的水平 距离无关，只与他的前进速度、身高、灯柱高有关．习 题 2-51．函数2y x =，求当1x =，而0.1x ∆=，0.01时，y ∆与d y 之差是多少 解 当1x =，0.1x ∆=时，21.110.21y ∆=-=，d 20.2y x x =∆=， 所以 0.01y dy ∆-=；当1x =，0.01x ∆=时，21.0110.0201y ∆=-=，d 20.02y x x =∆=， 所以 0.0001y dy ∆-=；2．求函数2y x x =+在3x =处，x ∆等于0.1，0.01时的增量与微分． 解 因为2y x x =+，所以()21dy x x =+∆，当3x =，0.1x ∆=时，223.1 3.1330.71y ∆=+--=，0.7dy =； 当3x =，0.01x ∆=时，223.01 3.01330.0701y ∆=+--=，0.07dy =．3．函数3y x x =-，求自变量x 由2变到1.99时在2x =处的微分． 解 因为3y x x =-，所以()231dy x x =-∆，当2x =，0.01x ∆=-时，()()23210.010.11dy =⨯-⨯-=-．4．求下列函数的微分（1）234123y x x x x =+-+；（2）2e x y x -=； （3）21xy x =- ； （4）22tan (1)y x =+； （5）ln cos 3x y = ；（6）e sin ax y bx =．解 （1）()23144dy x x x dx =+-+；（2）()()()2222222e e e e 2e 12x x x x x dy dx x d x dx x x dx x dx -----=+-=+-=-；（3）()()()()()()()222222222211121111x dx xd x x dx x x dx xdy dx x x x ------+===---；（4）2222222tan(1)tan(1)2tan(1)sec (1)(1)dy x d x x x d x =++=+++2224tan(1)sec (1)x x x dx =++；（5）()()ln cos ln cos 13ln 3ln cos 3ln 3cos cos x x dy d x d x x==⋅lncos 3ln 3tan x xdx =-⋅；（6）()()()()()()e sin e cos e sin cos ax ax ax dy d ax bx bx d bx a bx b bx dx =+=+⎡⎤⎣⎦． 5．将适当的函数填入下列括号内，使等式成立： （1）d()sin d t t ω=； （2）2d()sec 3d x x =； （3）d()x =；（4）22d d()xx a =+； （5）2d()e d x x x =；（6）ln d()d xx x=. 解 （1）()1cos t ωω-； （2）()1tan 33x ； （3； （4）1arctan x a a ； （5）21e 2x ； （6）21ln 2x ．6．某扩音器的插头为圆柱形，其截面半径r 为0.15厘米，长度L 为4厘米，为了提高它的导电性能，要在圆柱的侧面镀一层厚度为0.001厘米的铜，问每个插头约需要多少克纯铜（铜的密度为8.9克/立方厘米， 3.1416π≈）解 因为圆柱形的扩音器插头的体积为2V r L π=，侧面镀层的体积约为2V dV rL r π∆≈=∆，当0.15r =，0.001r ∆=，4L =时，32 3.14160.1540.001 3.7699210V -∆≈⨯⨯⨯⨯≈⨯， 故所需铜的重量约为33.76992108.90.03355m -≈⨯⨯≈克．7．设有一凸透镜，镜面是半径为R 的球面，镜面的口径为2h ，若h 比R 小得多，试证明透镜的厚度22h D R≈．解 如下图所示，镜面半径R 、镜面口径2h 、透镜厚度D 之间有关系：()222h R D R +-=，化简得：2220h RD D -+=，得：22222441R R h h D R R --==--若h 比R 小得多，则2222112h h R R-≈-，故222221122h h h D R R R R R R R⎛⎫=--≈--= ⎪⎝⎭．8．利用微分求下列函数值的近似值（1）cos59o ；（2）tan 46o ；（3）lg11； （4） 1.01e ；（526；（63996解 （1）()00cos59cos 601cos cos sin 318033180πππππ⎛⎫⎛⎫⎛⎫⎛⎫=-=-≈-- ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭o130.51512180π⎫=-≈⎪⎝⎭； （2）()002tan 46tan 451tan tan sec 418044180πππππ⎛⎫⎛⎫⎛⎫=+=+≈+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭o 12 1.0349180π=+⨯≈；（3）()1lg11lg 101lg101 1.043410ln10=+≈+⨯≈；（4） 1.0110.010.01 2.7455e e e e +=≈+⨯≈； （526251251 5.1225=+≈=； （6()233331996100041000100049.98673-=-≈⨯⨯-≈．9．当||x 较小时，证明下列近似公式： （1）sin x x ≈；（2）(1)1x x αα+≈+；（3）ln(1)x x +≈．解 （1）设()sin f x x =，则()cos f x x '=，当||x 较小时，()sin sin0cos0f x x x x =≈+⋅=，所以sin x x ≈；（2）设()(1)f x x α=+，则()1(1)f x x αα-'=+图2-11当||x 较小时，()()()(1)111f x x f f x x αα'=+≈+=+，所以(1)1x x αα+≈+；（3）设()ln(1)f x x =+，则()11f x x'=+， 当||x 较小时，()()()ln(1)11f x x f f x x '=+≈+=，所以ln(1)x x +≈．习 题 2-61.一飞机在离地面2000米的高度，以200公里/小时的速度飞临某目标之上空，以便进行航空摄影．试求飞机飞至该目标上方时摄影机转动的速度．解 如右图示意，A 为摄影目标，B 为其正上方的点，设t 时刻飞机离B 点的水平距离为()x t ，摄影机镜头C 与A 点连线与飞机的水平飞行方向成θ夹角，则()cot 2000x t θ=，()()20000003600x t x t =-，两边同时对时间t求导，可得()211csc 200036dx t d dt dt θθ-==-，即21sin 36d dt θθ=，当飞机飞至该目标上方时，2πθ=， 代入解得：()13605/362d rad s dt θππ=⨯=． 2.一架飞机着陆的路径如图2-11所示，并且满足下列条件： （ⅰ）降落点为原点，飞机开始降落时水平距离为l ，飞行高度为h ．（ⅱ）在整个降落过程中，飞行员必须使飞机保持恒定的水平速度v ．（ⅲ）垂直方向的加速度的绝对值不能超过常数k （必须比重力加速度小很多）．（1） 求一个三次多项式()32P x ax bx cx d =+++，通过在开始降落和着陆的点对()P x 和()P x '施加一定的条件限制，使它满足条件（ⅰ）；（2） 根据条件（ⅱ）和（ⅲ），试证明：226hv k l≤；（3） 假设一条航线不允许飞机的垂直加速度超过2860k =哩小时．如果 一架飞机的飞行高度为35000呎，速度为300哩小时，飞机应从距离飞机场多远处开始降落（4） 画出满足问题（3）中条件的航线图．解 假设从飞机开始着陆时计时，飞行时间为t ，飞机位置为(),x y ． （1）如要满足条件（ⅰ），应有0t =时，,x l y h ==，0t dy dt==；t T =（T 为着陆时刻）时，0x y ==，0t Tdydt==，因为()32y P x ax bx cx d ==+++，于是()()232dy dx dxP x ax bx c dt dt dt'==++， 所以应有 32h al bl cl d =+++，2320al bl c ++=，0d =，0c =， 解得3223,,0h h a b c d l l =-===，所以()323223h h P x x x l l=-+； （2）由条件（ⅱ）和（ⅲ）可知：dxv dt =，22d y k dt ≤，由()323223h h y P x x x l l==-+，可得：23266dy h h dx x x dt l l dt ⎛⎫=-+ ⎪⎝⎭， 222223232212666d y h h dx h h d xx x x dt ll dt l l dt ⎛⎫⎛⎫⎛⎫=-++-+ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭， 所以[]0,x l ∀∈，应有232126hh x v k ll ⎛⎫-+≤ ⎪⎝⎭， 故226hv k l ≤；（3）当2860k =哩，0.62135000350000.305 6.62921000h ==⨯⨯≈呎哩，300v =哩小时，由226hv k l ≤，可解得64.52l ≥≈（哩），即飞机应从距离飞机场约64.52哩的水平距离处开始降落．（4）满足条件（3）的航线为()3232322350003350000.260625.223264.5264.52P x x x x x ⨯⨯=-+≈-+（呎）（注：式中x 的单位哩，图略）．本章复习题A1、填空题（1）()f x 在点0x 可导是()f x 在点0x 连续的_____条件，()f x 在点0x 连续是()f x 在点0x 可导的______条件．解 因为()f x 在点0x 可导，则()f x 在点0x 连续，故第一个空应填“充分”，第二个空应填“必要”．（2）()f x 在点0x 可导是()f x 在点0x 可微的______条件． 解 应填“充分必要”． （3）若假定0()f x '存在，则000()()limh f x h f x h h→+--=______．解 因为()()00000000()()()()limlim h h f x h f x f x f x h f x h f x h h h→→+-+--+--= ()()00000()()lim h f x h f x f x h f x h h →+---⎡⎤=+⎢⎥-⎣⎦()02f x '=， 所以应填“()02f x '”．（4）若()(1)(2)f x x x x =++，则(0)_______f '=．解 因为()(1)(2)(2)(1)f x x x x x x x '=++++++，故(0)2f '=，应填“2”．（5）曲线231x t y t⎧=+⎨=⎩在2t =处的切线方程为________． 解 因为23322t t y dy t t dx x t '==='，所以2t =时，23t dy dx ==，5x =，8y =，切线方程为()835y x -=-，即370x y --=，所以应填“370x y --=”．2、选择题（1）()f x 在点0x 的左导数0()f x -'及右导数0()f x +'都存在且相等是()f x 在点0x 可导的（ ）．A ．充分条件B ．充分必要条件C ．必要条件D ．既非充分条件也非必要条件 解 选B ．（2）设101()n n n f x a x a x a -=+++L ，则()(0)n f =（ ）．A ．n aB ．0aC ．0!n aD ．0 解 选C ．因为()0()!n f x n a =．（3）设函数()y f x =二阶可导，(ln )y f x =，则22d d yx等于（ ）．A ．1(ln )f x x 'B ．21[(ln )(ln )]f x f x x '''- C ．21[(ln )(ln )]xf x f x x '''- D ．21(ln )f x x' 解 选B ．因为1(ln )(ln )f x y f x x x'''=⋅=， 则221(ln )(ln )(ln )(ln )f x x f x f x f x x y x x '''⋅⋅-'''-''==． （4）若函数()y f x =有01()2f x '=，则当0x ∆→时，该函数在0x x =处的微分d y 是（ ）．A ．与x ∆等价的无穷小B ．与x ∆同阶的无穷小C ．比x ∆低阶的无穷小D ．比x ∆高阶的无穷小 解 选B ．因为()0012x x dyy x x x ='=∆=∆，所以001lim 2x x x dy x =∆→=∆．（5）已知方程222x y R +=确定了函数()y y x =，则22d d yx 等于（ ）．A ．xy- B ．23R y C ．33R y - D ．23R y -解 选D ．由222x y R +=可得220x y y '+⋅=，。

第二章：电力电子习题解答第二章 整流电路习题及思考题１．单相半波可控整流电路对电阻负载供电，R ＝20Ω，U ＝100V ，求当α＝0°和60°时的负载电流Id ，并画出u d 与i d 波形。

解：当α＝0°时： ）（V .U .U d 451004504502=⨯==）（A ./RU I dd 2522045===当α＝60°时： ）（A ..U .U d 753325014502=+⨯=）（A ..RU I dd 691207533===u d 与i d 的波形见：教材43页图2－1。

２．图2－9为具有变压器中心抽头的单相全波可控整流电路。

问该变压器还有直流磁化问题吗？试说明：① 晶闸管承受的最大正反向电压为222U ；② 当负载为电阻或电感时其输出电压和电流的波形与单相全控桥时相同。

解：由图2－9图可以看出，在2U 正半周1VT 导通，负载电流由变压器次级上端流出，由中心抽头流入，当2U 负半周时2VT 导通，负载电流由B 次级下端流出由中心抽头流入，正负半周电流相等，但在铁芯中产生的磁势方向大小相等且方向相反，故变压器无直流磁化问题。

① 当1VT 导通时，在2u ＝22U 时，2VT 的阴极为22U ，而其阳极为－22U ，所以VT 承受的最大反压为222U 。

如果是阻感负载且电感是足够大时，当90=α，1VT 导通，2VT 的阴极电压为－22U 而其阳极电压为22，故其承受的最大正向电压为－222U 。

② 正半周1VT 导通，2U ud=，负半周2VT 导通2U u d =。

所以输出电压和电流的波形与单相全控桥时相同。

３．单相桥式全控整流电路，V U 1002＝，负载中Ｒ＝Ω2，Ｌ值极大，当30时，要求：① 作出du ，di 和2i 的波形；② 求整流输出平均电压dU 、电流dI ，变压器二次电流有效值2I ；③ 考虑安全裕量，确定晶闸管的额定电压和额定电流。

第二章心理辅导的理论基础一、理论测试题（一）单项选择题1．（）是根据操作性条件反射原理，强调行为的改变是依据行为后果而定的。

A •强化法B •系统脱敏法C.代币法D •来访者中心疗法2•在对学生进行心理辅导时，常使用的“强化法”属于（）。

A •行为改变技术B •认知改变法C.运动改变法D •精神分析法3•在心理辅导的行为演练中，系统脱敏法是由（）首创。

A .皮亚杰B •沃尔帕C艾利斯D •罗杰斯4•心理辅导老师帮李晓明建立焦虑等级，让他想象引起焦虑的情境，然后逐渐减少焦虑等级，直至完全放松，以缓解其考试焦虑，这种方法是（）。

A •强化法B •系统脱敏法C.理性一情绪疗法D •来访者中心疗法5 •行为塑造法是根据（）的操作条件反射研究结果而设计的培育和养成新反应或行为模式的一项行为治疗技术，是操作条件作用法强化原则的有力应用之一。

A .皮亚杰B •斯金纳C.艾利斯D .奥苏贝尔6．（）就是运用代币并编制一套相应的激励系统来对符合要求的目标行为的表现进行肯定和奖励。

A .强化法B .理性一情绪疗法C.代币法D .来访者中心疗法7.李老师通过奖励小红花来表扬学生的行为，这种心理辅导方法属于（）。

A .系统脱敏法B •代币法C.行为塑造法D .来访者中心疗法8.晓红是韩老师班上的学生，她孤僻、羞涩，当她主动与同学交谈或请教老师时，韩老师就给予肯定或激励。

这种心理辅导方法是（）。

A .强化法B •系统脱敏法C.来访者中心法D .理性一情绪疗法9.（）不是行为改变的基本方法。

A .强化法B .代币法C.自我控制法D .演练法10.小伟过分害怕狗，通过让他看狗的照片，谈论狗，远看狗到近看狗、摸狗、抱狗，消除对狗的惧怕反应，这是行为训练的（）。

A .全身松弛训练B .系统脱敏法C.行为塑造法D .肯定性训练11.当一位胆小的学生敢于主动向教师提问时，教师教师耐心解答并给予表扬和鼓励。

的这种做法属于行为改变方法中的（）。

高中物理教材第二章练习题及答案
本文档提供了高中物理教材第二章的练题及答案，旨在帮助高中物理学生巩固和复相关知识。

1. 第一节练题
1.1. 问题：描述牛顿第一定律的内容是什么？
答案：牛顿第一定律又称惯性定律，它指出一个物体如果没有外力作用，将保持匀速运动或静止状态。

1.2. 问题：如何判断一个物体是否处于平衡状态？
答案：一个物体处于平衡状态时，所有作用在它上面的力的合力为零。

1.3. 问题：什么是质量和重量？
答案：质量是一个物体所固有的特性，衡量了物体对于改变其运动状态所需要的力。

重量是物体受地球引力作用的结果，由质量乘以重力加速度计算得出。

...
2. 第二节练题
2.1. 问题：什么是力的合成？
答案：力的合成是将两个或多个力的作用效果用一个等效的单一力表示的方法。

2.2. 问题：如何计算力的合成？
答案：力的合成可以通过将各个力的大小和方向相加来计算。

2.3. 问题：什么是力的分解？
答案：力的分解是将一个力分解成多个分力的过程。

...
以上所列为部分练题及其答案，希望对学生们的物理研究有所帮助。

更多练题和答案请参考教材第二章。

第 二 章 热力学第一定律一、思考题1. 判断下列说法是否正确，并简述判断的依据（1）状态给定后,状态函数就有定值,状态函数固定后，状态也就固定了。

答：是对的。

因为状态函数是状态的单值函数。

(2）状态改变后,状态函数一定都改变.答：是错的。

因为只要有一个状态函数变了，状态也就变了，但并不是所有的状态函数都得变.（3）因为ΔU=Q V ，ΔH=Q p ，所以Q V ,Q p 是特定条件下的状态函数？ 这种说法对吗？答：是错的.∆U ，∆H 本身不是状态函数，仅是状态函数的变量，只有在特定条件下与Q V ，Q p 的数值相等，所以Q V ，Q p 不是状态函数。

(4）根据热力学第一定律，因为能量不会无中生有,所以一个系统如要对外做功，必须从外界吸收热量.答:是错的。

根据热力学第一定律U Q W ∆=+，它不仅说明热力学能（ΔU ）、热（Q ）和功（W ）之间可以转化,有表述了它们转化是的定量关系，即能量守恒定律。

所以功的转化形式不仅有热，也可转化为热力学能系.（5）在等压下,用机械搅拌某绝热容器中的液体,是液体的温度上升，这时ΔH=Q p =0答：是错的。

这虽然是一个等压过程，而此过程存在机械功，即W f ≠0，所以ΔH≠Q p 。

（6)某一化学反应在烧杯中进行，热效应为Q 1，焓变为ΔH 1.如将化学反应安排成反应相同的可逆电池,使化学反应和电池反应的始态和终态形同，这时热效应为Q 2，焓变为ΔH 2，则ΔH 1=ΔH 2。

答：是对的。

Q 是非状态函数，由于经过的途径不同，则Q 值不同，焓(H ）是状态函数，只要始终态相同，不考虑所经过的过程，则两焓变值∆H 1和∆H 2相等。

2 . 回答下列问题,并说明原因(1)可逆热机的效率最高,在其它条件相同的前提下，用可逆热机去牵引货车，能否使火车的速度加快？答？不能.热机效率hQ W -=η是指从高温热源所吸收的热最大的转换成对环境所做的功。

但可逆热机循环一周是一个缓慢的过程，所需时间是无限长.又由v F tW P ⨯==可推出v 无限小。

--一、填空题1. 进程是一个程序对某个数据集的一次执行过程。

进程从结构上讲，包括程序、数据和PCB三部分。

2. 进程是一个动态的概念，程序是一个静态的概念。

3. 操作系统中，可以并行工作的基本单位是进程，它是由程序、数据集和PCB组成。

4. 进程存在的唯一标志是PCB的存在。

当系统创建一个进程时，系统为其建立一个PCB，当进程被撤销时系统就将其收回。

5. 进程有三种基本状态，即运行状态、就绪状态、阻塞状态。

当进程由(1)变换到(2)或(3)时，就会立即引起重新调度。

6. 在操作系统中，不可中断执行的操作称为原语。

7. 并发进程之间的基本关系是同步或互斥。

其中互斥是指进程之间的一种间接关系。

8. 临界资源是指一段时间只允许一个进程使用的资源，而临界区是指进程中访问临界资源的程序代码。

9. P，V操作原语是在信号量上操作的。

10. 信号量的物理意义是：当信号量的值大于零时，表示可用资源的数量；当信号量值小于零时，其绝对值为等待使用信号量所代表资源的进程的数量。

11. 有n个进程共享同一个临界区，若使用信号量机制实现对临界资源的互斥访问，则信号量值的变化范围是1~-（n-1）。

12.如果系统中有n个进程，则在等待(阻塞)队列中进程的个数最多可为个n。

13. 如果信号量的当前值为－5，则表示系统中在该信号量上有5 个等待进程。

14.某程序运行时经常需打印中间结果。

计算时，该进程处于用户态，打印时处于系统态，打印结束时进程处于用户态。

（指系统状态）、15. 在操作系统中引入线程的主要目的是减少程序并发执行时的时空开销，使OS更具有并发性。

16. 如果一个程序能为多个进程同时共享执行，那么它应该以纯码形式编写，即该程序是可重人码程序，这种程序的特点是：在它执行过程中自身不可修改。

17. 中断优先级是由硬件规定的，若要调整中断的响应次序可通过系统调用。

18. 进程初建时处于就绪态，运行时因为时钟中断而处于就绪态，因等待事件或资源而处于阻塞态。

第二章练习题参考解答练习题资料来源:《深圳统计年鉴2002》，中国统计出版社(1)建立深圳地方预算内财政收入对GDP的回归模型；(2)估计所建立模型的参数，解释斜率系数的经济意义；（3）对回归结果进行检验；(4)若是2005年年的国内生产总值为3600亿元，确定2005年财政收入的预测值和预测区间(0.05α=)。

2.2某企业研究与发展经费与利润的数据(单位:万元)列于下表:1995 1996 1997 1998 1999 2000 2001 2002 2003 2004研究与发展经费 10 10 8 8 8 12 12 12 11 11利润额 100 150 200 180 250 300 280 310 320 300 分析企业”研究与发展经费与利润额的相关关系，并作回归分析。

2.3为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系，分析表中1990年—2001年中国货币供应量（M2）和国内生产总值（GDP）的有关数据:年份货币供应量(亿元)M2国内生产总值(亿元)GDP1990 1529.31 8598.41991 19349.92 1662.51992 25402.2 26651.91993 34879.8 34560.51994 46923.5 46670.01995 60750.5 57494.91996 76094.9 66850.51997 90995.3 73142.71998 104498.5 76967.21999 119897.9 80579.42000 134610.3 88228.12001158301.994346.4资料来源:《中国统计年鉴2002》，第51页、第662页，中国统计出版社对货币供应量与国内生产总值作相关分析，并说明分析结果的经济意义。

2.4表中是16支公益股票某年的每股帐面价值和当年红利：根据上表资料：（1）建立每股帐面价值和当年红利的回归方程； （2）解释回归系数的经济意义；（3）若序号为6的公司的股票每股帐面价值增加1元，估计当年红利可能为多少？2.5美国各航空公司业绩的统计数据公布在《华尔街日报1999年年鉴》（The Wall Street Journal 1。

第二章解析函数习题及解答2.1 研究下列函数在任一点处的可导性、解析性，若可导求其导数值．1）； 2）； 3）； 4）. 2.2 证明 如果在区域内解析且满足下列条件之一，则必为一常数.1）在内为实值. 2）在内解析.3）在内为常数.4）在内为一常数.5）在内有，其中，，是不全为0的实常数.6）或在内为常数.7）在内有.2.3 证明在极坐标系下的柯西－黎曼条件为【提示：另一证明方法，可利用，然后根据复合函数求导证明】2.4 设在内解析．证明.2.5 证明解析函数的实、虚部所确定的曲线族与在的点处是正交的.（，为任意实数）2.6 已知下列调和函数求复势表达式．并写成关于的表达式.1）， 2），2.7设，求之值，使为一调和函数，并求一解析函数.2.8 计算下列复数1） 2），其中； 3）； 4）； 5）; 6)Ln(1+i) 2.9 求解方程 2.10 解下列方程1） 2）2.11 证明，对任何数（复数、实数），方程均有解. 2.12 求，使对任意，有.2.13 若某解析函数的实部等于虚部的平方，证明该解析函数必为常数.(提示：参考例2.6.1即可证明，这是该例的一个特殊情况)本章计算机编程实践与思考()33i y x z f -=()z z f =()z z f =()y y z f x x sin ie cos e +=()()()y x v y x u z f ,i ,+=D ()z f ()z f D ()z f D ()z f D ()z f arg D D ()()c y x bv y x au =+,,a b c ()()z f Re ()()z f Im D D ()0='z f 11, u u r ρϕρρϕ∂∂∂∂==-∂∂∂∂v v cos ,sin x y ρϕρϕ==()()()y x v y x u z f ,i ,+=D ()()2222224z f z f y x '=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂()()()y x v y x u z f ,i ,+=()C y x u =,()B y x v =,()0≠'z f C B ()()()y x v y x u z f ,i ,+=z ()()12,-=x y y x u ()i 2-=f ()x yy x v arctan,=0>x ()y y x v pxsin e ,=p v ()()()y x v y x u z f ,i ,+=()ii 1+z 1y x z i +=()i ln -i 1i +()2ln -sin cos 0z z +=0sin =z 0e 1=+zωω=z cos ωz ()zz sin sin =+ω(说明：读者可参考第五部分 计算机仿真编程实践)2.14 计算机编程计算2.15 计算机编程计算2.16 计算机编程解方程 2.17 计算机编程计算2.18 计算机求解方程2.19 计算机仿真（Matlab,Mathcad,Mathmatic ）绘出 的图形. 2.20 对于下列解析函数，分别用计算机仿真方法（Matlab,Mathcad,Mathmatic ）绘出其实部和虚部的等值曲线图．（如等势线、电力线）本章习题解答2.1 研究下列函数在任一点处的可导性、解析性．1）； 2）； 3）； 4）．解 1）故，；，，，显见，，在全平面有连续一阶偏导，故，全平面处处可微，又令得，即即，当且仅当时，C-R 方程成立．所以仅在处可导，其他任何点不可导．由解析的定义可知，于全平面处处不解析．注 由此结果可见，复变函数可存在孤立的甚至唯一的可导点，而无孤立的解析点．2），对任一，考虑极限即对任一，上述极限不存在，由可导定义知，于任一点处不可导．故全平面不解析．3）其中，．所以，当时，有π1i i i1234, (1i), i z ez z z -===+=12Ln(34i), ln(i 1)z z =-+=-sin 2z =tan(1i)Arc +10ze +=sin , cos , tan , ctan z z z z23(1)(); (2)()f z z f z z ==()33i y x z f -=()z z f =()z z f =()y y z f x x sin ie cos e +=()()()y x v y x u y x z f ,i ,i 33+=-= ()3,x y x u =()3,y y x v -=23x x u =∂∂0≡∂∂y u 0≡∂∂x v 23y y v -=∂∂u v()y x u ,()y x v ,⎪⎪⎩⎪⎪⎨⎧∂∂-=∂∂∂∂=∂∂y u xv y vx u 2233y x -=0022==⇔=+y x y x 0==y x ()z f 0=z ()z f ()y x z z f i -==0z ()()⎩⎨⎧≠∆=∆-=∆≠∆=∆+∆∆-∆=∆-∆+→∆→∆0,0,10,0,1i i lim lim0000y x y x y x y x z z f z z f z z0z ()z z f =0z ()()()y x v y x u y x z z f ,i ,22+=+==()22,y x y x u +=()0,≡y x v ()()0,0,≠y x，，因此，对，C-R 方程不成立．而当时，由于不存在，即不存在，同理，不存在，故在处不可导．于是，于全平面处处不可导，不解析．注 在本题讨论中，仍然采用检验可导充要条件的方法，由于时，，，，均连续，故，可微，但C-R 方程处处不成立．对，从偏导定义出发，得知与不存在，从而在处不可微，故对平面任一点，可导的充要条件不满足．4），，，且，于全平面连续，故于全平面处处可导，全平面处处解析．又，因此有注 1.这里用区域解析的充分条件得到结论； 2.本题中的是一性质极好的函数：不仅全平面解析，且具有特性，它正是实指数函数在复平面的推广，即．但应注意这一推广产生的新性质：1） 由于与以为周期，使得以的整数倍为周期．2） 可取到除0以外的任意复值，包括负值．这两点是值得注意的．2.2 证明 如果在区域内解析且满足下列条件之一，则必为一常数．1）在内为实值． 2）在内解析．3）在内为常数．4）在内为一常数．22y x x xu +=∂∂22y x yyu +=∂∂0≡∂∂=∂∂yu x v ()()0,0,≠∀y x ()()0,0,=y x ()()x x x x x u x u x x x 0200limlim 0,00,lim →→→=-=-()x u ∂∂0,0()y u ∂∂0,0()z z f =0=z ()zz f =()()0,0,≠y x x u∂∂y u ∂∂x v ∂∂y v∂∂u v ()()0,0,=y x x u ∂∂y u∂∂()y x u ,()0,0()()()y x v y x u y y z f xx ,i ,sin ie cos e +=+=()y y x u x cos e ,=()y y x v x sin e ,=y v y x u x ∂∂==∂∂cos e x v y y u x ∂∂-=-=∂∂sin e x u ∂∂y u ∂∂()z f ()x vx u z f ∂∂+∂∂='i ()()z f y y z f xx =+='sin ie cos e ()f z ()()z f z f ='x e ()ecos ie sin exp e xx zf z y y z '=+==ycos y sin πk 2z e i 2πz e ()()()y x v y x u z f ,i ,+=D ()z f ()z f D ()z f D ()z f D ()z f arg D5）在内有，其中，，是不全为0的实常数．6）或在内为常数．7）在内有．证 首先，由条件在内解析a ），均在内可微，且b ）在内处处成立．1）因为在内取实值，即，．于是，．将此结果代入C-R 方程b ），得，．所以．．即（为一常数）2）于在内解析．因而除条件a ），b ）成立之外，条件c ）成立．联立b ），c ）得，即，．又由b ）或c ）得．所以在内，恒有，．即为常数．3）由于，．若，则，，．若，则由，两端分别关于，求偏导得：e ）将b ）代入e ）得D ()()c y x bv y x au =+,,a b c ()()z f Re ()()z f Im D D ()0='z f ()()()y x v y x u z f ,i ,+=D ⇔u v D ⎪⎪⎩⎪⎪⎨⎧∂∂-=∂∂∂∂=∂∂x v yu y v x u D ()z f D ()0,≡y x v ()D y x ∈,0≡∂∂=∂∂y v x v ()D y x ∈,0≡∂∂=∂∂y u x u ()D y x ∈,()A y x u =,()D y x ∈,()A z f =D z ∈A ()()()()()[]y x v y x u y x v y x u z f ,i ,,i ,-+=-=D ()()⎪⎪⎩⎪⎪⎨⎧∂∂=∂-∂-=∂∂∂∂-=∂-∂=∂∂x v x v yu y v y v x u y v y v ∂∂-=∂∂x vx v ∂∂-=∂∂0=∂∂=∂∂y v x u ()D y x ∈,0=∂∂=∂∂y ux u D ()A y x u =,()B y x v =,()B A z f i +=()()()Cy x v y x u z f ≡+=,,22()D y x ∈, 10=C ()0≡z f ()0≡⇔∈z f D z D z ∈ 20≠C ()()0,,222≠≡+C y x v y x u x y ⎪⎪⎩⎪⎪⎨⎧=∂∂+∂∂=∂∂+∂∂00y v v y u u x v v xuu ()D y x ∈,由得 ，代入b ）得，于是， 即， （，为任意实常数）3）因为常数，，由主值支的表达式得f ）常数，及， 若，则 归为1）的情形，得证．若，对c ）两端分别关于，求偏导得 即将b ）代入得，再由b ）即得 ，从而得，（，为任意实常数）5），，且，，是不全为0的实常数．所以有．于是对上式两端分别关于，求偏导得⎪⎪⎩⎪⎪⎨⎧=∂∂+∂∂=∂∂-∂∂00y u u xu v y u v x uu ()D y x ∈,()()0,,222≠≡+C y x v y x u 0≡∂∂=∂∂y u x u ()D y x ∈,0≡∂∂=∂∂y vx v ()D y x ∈,()A y x u ≡,()B y x v ≡,()B A z f i +=D z ∈A B ()≡z f arg D z ∈ωarg ()()≡y x u y x v ,,arctan C =()()0,,222≠≡+C y x v y x u ()D y x ∈, 10=C ()()⎩⎨⎧>≡0,0,y x u y x v ()D y x ∈, 20≠C x y ⎪⎪⎪⎩⎪⎪⎪⎨⎧=+∂∂-∂∂=+∂∂-∂∂002222v u y u v y v u v u x u v x vu ()022≠+v u ⎪⎪⎩⎪⎪⎨⎧=∂∂-∂∂=∂∂-∂∂00y u v yvu x u v x v u ⎪⎪⎩⎪⎪⎨⎧=∂∂-∂∂=∂∂-∂∂00x u u xv v x u v x vu ()D y x ∈,()()0,,22≠+y x v y x u 0=∂∂=∂∂∴x vx u 0=∂∂y v 0=∂∂y u ()B A z f i +=D z ∈A B ()()c y x bv y x u =+,,a ()D y x ∈,a b c 022≠+b a x y将b ）代入得因为，故得 再由条件b ）即得，．于是得，（，为任意实常数）6）若，则在内取实值．即1）所证．若即，则，，，代入b ），即得，．，， （，为任意实常数） 若，即，则，，则由b ）知，，即，7）由于．所以若在内有，则，， 由条件b ）即得，． 所以， （，为任意实常数）．注 以上各命题的论证均是在于区域上解析的前提下进行的，否则结论不一定成立．例如，为一实值函数，满足条件1）．但它于全平面不解析（见1-26题，3）．显然在任何区域上不可能取常数值，即无题中的结论． 2.3 证明在极坐标系下的柯西－黎曼条件为【提示：另一证明方法，可利用，然后根据复合函数求导证明】⎪⎪⎩⎪⎪⎨⎧=∂∂+∂∂=∂∂+∂∂00y v b yu a x v b x ua ⎪⎪⎩⎪⎪⎨⎧=∂∂-∂∂=∂∂+∂∂00x v a x u b x v b x ua 022≠+b a ⎪⎪⎩⎪⎪⎨⎧=∂∂=∂∂00xv x u()D y x ∈,0=∂∂y v 0=∂∂y u ()B A z f i +≡D z ∈A B1()()0Im =≡C z f ()z f D ()()0Im ≠≡C z f ()C y x v ≡,()D y x ∈,0≡∂∂x v0≡∂∂y v ()D y x ∈,0≡∂∂x u0≡∂∂y u ()D y x ∈,()B A z f i +=∴ D z ∈A B 2()()C z f ≡Re ()C y x u ≡,()D y x ∈,0≡∂∂x u 0≡∂∂x u 0≡∂∂x v0≡∂∂y v ()B A z f i += D z ∈()x v x u z f ∂∂+∂∂='i D ()0='z f 0=∂∂x u 0=∂∂x v()D y x ∈,0=∂∂y u 0=∂∂y v()D y x ∈,()B A z f i +=D z ∈A B ()z f D ()zz f =()zz f =D 11, u u r ρϕρρϕ∂∂∂∂==-∂∂∂∂v v cos ,sin x y ρϕρϕ==2.4 设在内解析．证明．证 令则（1） 同理得（2） 并注意在内解析．所以有即且，均为调和函数，即．于是（1）+（2）得注 本题证明中用到解析函数三条性质：（1）实、虚部满足C-R 方程．（2）．（3）实部、虚部均为调和函数．即，．2.5 证明解析函数的实、虚部所确定的曲线族与在的点处是正交的．（，为任意实数）证 因为在的点，曲线族在该点处的切线斜率为．曲线族在该点处的切线斜率为．所以．即曲线族与曲线族正交．（2）对使得，的点，曲线族在该点处的切线为铅直线（∵），而曲线族在该点处的切线为水平线（∵），故二者正交，同理，当，时，二者也正交．注 1.本题证明中用到曲线与曲线正交即为二者在交点处切线的正交这一概念； 2.本题的结论是解析函数在处的又一性质．2.6 已知下列调和函数求复势表达式．并写成关于的表达式．()()()y x v y x u z f ,i ,+=D ()()2222224z f z f y x '=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂()()()()y x G y x v y x u z f ,,,222=+=⎥⎥⎦⎤⎢⎢⎣⎡∂∂+∂∂+⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=∂∂222222222x v v x u u x v x u x G ⎥⎥⎦⎤⎢⎢⎣⎡∂∂+∂∂+⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂=∂∂222222222y v v y u u y v y u y G ()z f D ()y u y v x v x u z f ∂∂-∂∂=∂∂+∂∂='i i ()22222⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂='y v y u x v x u z f u v 0=∆=∆v u ()222224zf y G x G '=∂∂+∂∂()y u y v x v x u z f ∂∂-∂∂=∂∂+∂∂='i i 0=∆u 0=∆v ()()()y x v y x u z f ,i ,+=()C y x u =,()B y x v =,()0≠'z f C B ()0≠'z f ()y x ,()C y x u =,x v x u y u x u x y k ∂∂∂∂=∂∂∂∂-==d d 1()B y x v =,x uxvy v xvx y k ∂∂∂∂-=∂∂∂∂-==d d 2121-=k k ()C y x u =,()B y x v =,0≠∂∂x u 0=∂∂x v ()y x ,()C y x u =,0d d =y x ()B y x v =,0d d =x y0≠∂∂x v 0=∂∂x u ()0≠'z f ()()()y x v y x u z f ,i ,+=z1）， 2）， 解 由于解析，所以，满足C-R 方程．1），故．由此得，这里为的任一可导函数．又由得所以，为任一实常数． 于是． 令，即得 ∴ 于是，满足条件的解析函数为所以2）在极坐标系下，C-R 方程为形式． 令（则由得），有，，所以得，即解得 为的任一可导函数． 又由得．为任一实常数． 所以注意，得2.7设，求之值，使为一调和函数，并求一解析函数．解 因为，所以 ，，，()()12,-=x y y x u ()i 2-=f ()x yy x v arctan,=0>x ()()()y x v y x u z f ,i ,+=()y x u ,()y x v ,()()12,-=x y y x u yx u y v 2=∂∂=∂∂()()x C y y x v +=2,()x C x y ux v ∂∂-=∂∂()()12--='x x C ()122C x x x C ++-=1C ()1222,C x x y y x v ++-=2=z ⎩⎨⎧==02y x ()i i 21-==C f 11-=C ()()()12i 1222-+-+-=x x y x y z f ()()21i --=z z f ⎪⎪⎩⎪⎪⎨⎧∂∂=∂∂∂∂-=∂∂r u r v r v r uθθθ==x y v arctan 0>x ⎪⎭⎫ ⎝⎛-∈2,2ππθ1=∂∂θv 0=∂∂r v 1=∂∂r u r r r u 1=∂∂()()θθC r r u +=ln ,()θC θ()0=∂∂-='=∂∂r v r C u θθ()1C C =θ1C ()1ln ,C r r u +=θ()()()θθθi ln ,i ,1++=+=C r r v r u z f z r =()0arg arctan >==x z x yθ()1arg i ln C z z z f ++=()y y x v pxsin e,=p v ()()()y x v y x u z f ,i ,+=()y y x v pxsin e ,=y p x v px sin e =∂∂y p x v px sin e 222=∂∂y y v px cos e =∂∂y y v px sin e -=∂∂由，得． （1）当时，．由1-32题的方法易求出调和函数，则为所求解析函数，其中为任意实常数．（2）当时，．可求得调和函数．（为任一实常数）．于是所求的解析函数为(全平面解析)2.8 计算下列复数1） 2），其中； 3）； 4）；5）解 1）（为整数）2）当时得3）4）；5） 注 （i ）.以上各题均由定义求得；(ii). 值得注意的是，1只是无穷多个值中的一个值（对应于），这与实变量函数中的概念不同．2.9 求解方程【解】2.10 解下列方程1） 2）解2） ∵∴ ，即由对数函数定义得∴ ，为任意整数． 3）由得由对数函数定义得为任意整数[]1sin e 22222=-=∂∂+∂∂=∆p y y vx v v px 1±=p 1=p ()y y x v xsin e ,=()c y y x u x +=cos e ,()C y C y z f z x x +=++=e sin ie cos e C 1-=p ()y y x v x sin e ,-=()1cos e ,C y y x u x +-=-1C ()()()[]111e sin i cos e sin ie cos e C C y y y C y z f x z x x +-=+-+--=++-=----()ii 1+z 1y x z i +=()i ln -i 1i +()2ln -()()2iln 2412i 4i 2ln i i 1iln i ee e i 1+⎪⎭⎫⎝⎛+-⎥⎦⎤⎢⎣⎡+++===+πππk k k ()()()x k x k yk y y x z ππππ2sin i 2cos e e 11k 22i i x i +===-++() ,2,1,0±±=k 0=k 11=z()()πππk k 2i 2i2i i iarg i ln i ln +-=+-+-=-() ,2,1,0±±=k ()() ,2,1,0ie k 22/1±±=+k π()() ,2,1,012i 2ln ±±=++k k πz10=k sin cos 0z z +=(2)2sin cos 0(1)(1)2211/4, (0,1,2,)iz iz iz iziz iz i n iz e e e e z z e i e i i i e i eiz n n ππππ-----++=+=∴-=-++=-=-=-∴=-=±±0sin =z 0e 1=+zi 2e e sin i i =-=-zz z z z i i e e -=1e 2i =zπk z 2i 1ln 2i ==πk z k=k 01e =+z 1e -=z()()π12i 1ln +=-=k z k k主值为2.11 证明，对任何数（复数、实数），方程均有解．证 在中，令，则，且，所以．且可取到任意非0值．于是，原方程即为，即．所以．（这里有两个根）故，由对数函数定义得所以．故右端对任意均有意义，得证． 注 这里的结果说明两点：（1）复变量余弦函数可取到任意值（复、实值），而不象实余弦函数取值区间仅为；（2）所得结果改变与的位置，即得）．这正是的反函数．可对进行同样讨论，此略． 2.12 求，使对任意，有．解 由的定义，即求满足方程的一切值．整理化简即得 ，对任意成立．且因． 故得，即．为任意整数． 所以注 由此题结果可见，复变量正、余弦函数为周期函数，且周期与实变量正、余弦的相同． 2.13 若某解析函数的实部等于虚部的平方，证明该解析函数必为常数． 【提示，参考例2.6.1即可证明，这是该例的一个特殊情况】i0π=z ωω=z cos 2e e cos i i zz z -+=zt i e =⎪⎭⎫ ⎝⎛+=t t z 121cos ()x x t y z sin i cos e e i +==-0≠t t ω=⎪⎭⎫ ⎝⎛+t t 1210122=+-t t ω12-+=ωωt 12-ω01e 2i ≠-+=ωωz ()()1iln 1ln i 122-+-=-+=ωωωωz 012≠-+ωωω[]1,1-z ω()1iln 2-+-=z z ωz cos =ωz sin ωz ()z z sin sin =+ωz sin ()()zz z z i i i i e e e e -+-+-=-ωωω()()ωωωi i i 2i e 1e 1e e ----=-⋅z z 0e e i 2i ≠⋅ωz 0e1i =--ωπωk 2i 1ln i ==-k πωm 2=(),2,1,0±±=m。

第二章知识表示习题参考解答2.3 练习题2.1 什么是知识?它有哪些特性?有哪几种分类方法?2.2 何谓知识表示? 陈述性知识表示法与过程性知识表示法的区别是什么?2.3 在选择知识的表示方法时，应该考虑哪些主要因素?2.4 一阶谓词逻辑表示法适合于表示哪种类型的知识?它有哪些特点?2.5 请写出用一阶谓词逻辑表示法表示知识的步骤。

2.6 设有下列语句，请用相应的谓词公式把它们表示出来：（1）有的人喜欢梅花，有的人喜欢菊花，有的人既喜欢梅花又喜欢菊花。

（2）他每天下午都去玩足球。

（3）太原市的夏天既干燥又炎热。

（4）所有人都有饭吃。

（5）喜欢玩篮球的人必喜欢玩排球。

（6）要想出国留学，必须通过外语考试。

2.7 房内有一只猴子、一个箱子，天花板上挂了一串香蕉，其位置关系如图2. 11所示，猴子为了拿到香蕉，它必须把箱子推到香蕉下面，然后再爬到箱子上。

请定义必要的谓词，写出问题的初始状态（即图2.16 所示的状态）、目标状态（猴子拿到了香蕉，站在箱子上，箱子位于位置b）。

图2.11 猴子摘香蕉问题2.8 对习题2.7 中的猴子摘香蕉问题，利用一阶谓词逻辑表述一个行动规划，使问题从初始状态变化到目标状态。

2.9 产生式的基本形式是什么？它与谓词逻辑中的蕴含式有什么共同处及不同处？2.10 何谓产生式系统？它由哪几部分组成？2.11 产生式系统中，推理机的推理方式有哪几种？在产生式推理过程中，如果发生策略冲突，如何解决？2.12 设有下列八数码难题：在一个3× 3的方框内放有8 个编号的小方块，紧邻空位的小方块可以移入到空位上，通过平移小方块可将某一布局变换为另一布局（如图2.12 所示）。

请用产生式规则表示移动小方块的操作。

图2.12 习题2.12 的图图2.13 习题2.13 的图2.13 推销员旅行问题：设有五个相互可直达且距离已知的城市A、B、C、D、E，如图2.13 所示，推销员从城市A 出发，去其它四城市各旅行一次，最后再回到城市A ，请找出一条最短的旅行路线。

高等数学习题集及解答第二章一、 填空题1、设()f x 在x a =可导，则0()()lim x f a x f a x x →+--=。

2、设(3)2f '=，则0______________(3)(3)lim 2h f h f h →--=。

3、设1()xf x e -=，则0_____________(2)(2)limh f h f h→--=。

4、已知00cos (),()2,(0)1sin 2x f x f x x x π'==<<-，则0_______________________()f x =。

5、已知2220x y y x +-=，则当经x ＝1、y ＝1时，_______________dydx =。

6、()x f x xe =，则_______________(ln 2)f '''=。

7、如果(0)y ax a =>是21y x =+的切线，则__________a =。

8、若()f x 为奇函数，0()1f x '=且，则0_________________()f x '-=。

9、()(1)(2)()f x x x x x n =+++，则_________________(0)f '=。

10、ln(13)x y -=+，则____________________y '=。

11、设0()1f x '=-，则0___________00lim(2)()x xf x x f x x →=---。

12、设tan x y y +=，则_________________________dy =。

13、设lny =_______________(0)y '''=。

14、设函数()y f x =由方程42ln xy x y +=所确定，则曲线()y f x =在点（1，1）处的切线方程是______________________。