例1用分枝定界法求解下面的整数规划

《运筹学》样卷参考答案（48课时）一、判断题（对的记√，错的记×，共10分，每小题2分）1.线性规划模型中增加一个约束条件，可行域的范围一般将缩小，减少一个约束条件，可行域的范围一般将扩大；（）y 说明在最优生产计划中第i种资源2.已知*y为线性规划的对偶问题的最优解，若*0i已完全耗尽；( ) 3.运输问题是一种特殊的线性规划模型，因而求解结果也可能出现下列四种情况之一：有惟一最优解、有无穷多最优解、无界解和无可行解；（）4.求解整数规划是可以先不考虑变量的整数约束，而是先求解相应的线性规划问题，然后对求解结果中的非整数的变量凑整即得最优解。

（）5.11个公司之间可能只有4个公司与偶数个公司有业务联系；（）答案：1. T； 2. T； 3. F； 4. F； 5. F二、选择题（共15分，每小题3分）1.在利用图解法求解最大利润问题中中，通过各极点作与目标函数直线斜率相同的平行线，这些平行线称之为。

( )A.可行解B.可行域C.等利润线D.等成本线2.用单纯形法求解线性规划问题时引入的松弛变量在目标函数中的系数为。

( )A.0B.很大的正数C.很大的负数D.13.以下关系中，不是线性规划与其对偶问题的对应关系的是。

( )A．约束条件组的系数矩阵互为转置矩阵B．一个约束条件组的常数列为另一个目标函数的系数行向量C．两个约束条件组中的方程个数相等D．约束条件组的不等式反向4.需求量大于供应量的运输问题需要做的是。

( )A.虚设一个需求点B.删去一个供应点C.虚设一个供应点，取虚设供应量为恰当值D.令供应点到虚设的需求点的单位运费为05.对一个求目标函数最大的混合整数规划问题，以下命题中不正确的是。

（）A.其线性规划松弛问题的最优解可能是该整数规划问题的最优解。

B.该问题可行解的个数一定是有限的；C.任一可行解的目标函数值不可能大于其线性规划松弛问题的目标函数值；D.该问题可行解中可能存在不取整数值的变量。

分支定界法和割平面法分支定界法和割平面法在上学期课程中学习的线性规划问题中，有些最优解可能是分数或消失，但现实中某些具体的问题，常要求最优解必须是整数，这样就有了对于整数规划的研究。

整数规划有以下几种分类：（1）如果整数规划中所有的变量都限制为（非负）整数，就称为纯整数规划或全整数规划；（2）如果仅一部分变量限制为整数，则称为混合整数规划；（3）整数规划还有一种特殊情形是0-1规划，他的变量取值仅限于0或1。

本文就适用于纯整数线性规划和混合整数线性规划求解的分支定界法和割平面法，做相应的介绍。

一、分支定界法在求解整数规划是，如果可行域是有界的，首先容易想到的方法就是穷举变量的所有可行的整数组合，然后比较它们的目标函数值以定出最优解。

对于小型问题，变量数量很少，可行的整数组合数也是很小时，这个方法是可行的，也是有效的。

而对于大型的问题，可行的整数组合数很大时，这种方法就不可取了。

所以我们的方法一般是仅检查可行的整数组合的一部分，就能定出最有的整数解。

分支定界法就是其中一个。

分枝定界法可用于解纯整数或混合的整数规划问题。

在二十世纪六十年代初由Land Doig和Dakin等人提出。

由于这方法灵活且便于用计算机求解，所以现在它已是解整数规划的重要方法。

目前已成功地应用于求解生产进度问题、旅行推销员问题、工厂选址问题、背包问题及分配问题等。

设有最大化的整数规划问题A，与它相应的线性规划为问题B，从解问题B开始，若其最优解不符合A的整数条件，那么B的最优目标函数必是A的最优目标函数z*的上界，记作z；而A的任意可行解的目标函数值将是z*的一个下界z。

分枝定界法就是将B的可行域分成子区域再求其最大值的方法。

逐步减小z和增大z，最终求到z*。

现用下例来说明：例1 求解下述整数规划 Maxz?40x1?90x2?9x1?7x2?56? ?7x1?20x2?70?x,x?0且为整数?12解（1）先不考虑整数限制，即解相应的线性规划B，得最优解为：x1?4.81,x2?1.82,z?356可见它不符合整数条件。

第五章 整数规划主要内容：1、分枝定界法； 2、割平面法； 3、0－1型整数规划； 4、指派问题。

重点与难点：分枝定界法和割平面法的原理、求解方法，0－1型规划模型的建立及求解步骤，用匈牙利法求解指派问题的方法和技巧。

要 求：理解本章内容，熟练掌握求解整数规划的方法和步骤，能够运用这些方法解决实际问题。

§1 问题的提出要求变量取为整数的线性规划问题，称为整数规则问题（简称IP ）。

如果所有的变量都要求为（非负）整数，称之为纯整数规划或全整数规划；如果仅一部分变量要求为整数，称为混合整数规划。

例1 求解下列整数规划问题211020m ax x x z +=⎪⎪⎩⎪⎪⎨⎧≥≤+≤+为整数21212121,0,13522445x x x x x x x x 如果不考虑整数约束，就是一个线性规划问题（称这样的问题为原问题相应的线性规划问题），很容易求得最优解为：96m ax ,0,8.421===z x x 。

用图解法将结果表示于图中画“+”号的点都是可行的整数解，为满足要求，将等值线向原点方向移动，当第一次遇到“+”号点（1,421==x x ）时得最优解为1,421==x x ，最优值为z=90。

由上例可看出，用枚举法是容易想到的，但常常得到最优解比较困难，尤其是遇到变量的取值更多时，就更困难了。

下面介绍几种常用解法。

§2 分枝定界法分枝定界法可用于解纯整数或混合的整数规划问题。

基本思路：设有最大化的整数规划问题A ，与之相应的线性规划问题B ，从解B 开始，若其最优解不符合A 的整数条件，那么B 的最优值必是A 的最优值*z的上界，记为z ；而A 的任意可行解的目标函数值是*z的一个下界z ，采取将B 的可行域分枝的方法，逐步减少z 和增大z ，最终求得*z 。

现举例说明： 例2 求解A219040m ax x x z +=⎪⎪⎩⎪⎪⎨⎧≥≤+≤+为整数21212121,0,702075679x x x x x x x x 解：先不考虑条件⑤，即解相应的线性规划B （①--④），得最优解=1x 4.81, =2x 1.82,①② ③ ④ ⑤=0z 356（见下图）。

故最优解为：X
0010
1 0
0 1
0 0
0 0
，最优值为 14。
0001
6103 0211 1030 5300
5、在今后三年内有五项工程考虑施工，每项工程的期望收入和年度费用（千元）如表所示。假定 每一项已批准的工程要在三年内完成，目标是要选出使总收入达到最大的那些工程。
工程
第1年
费用（千元） 第2年
2 3 14 s. t. 4 2 18
, 0 且为整数
B：X=（3.25,2.5）z=14.75
x2<=3
x2>=4
B1：X=（3,2.67）z=14.33
B2：X=（4,1）z=14
x2<=2
x2>=3
B11：X=（3,2）z=13
B12：X=（2.5,3）z=13.5
所以，最优解为：X=（4,1），最优值为 14。
人
A
B
C
D
E
甲
25
29
31
42
37
乙
39
38
26
20
33
丙
34
27
28
40
32
丁
24
42
36
23
45
解：（1）由于任务数多于人数，所以需要一名假想的人，设为戊。因为工作 E 必须完成，故设戊完
成 E 的时间为 M，其余的假象为 0，建立如下的效率矩阵。
任务
人
A
B
C
D
E
甲
25
29
31
42
37
乙
39
38
解：变换目标函数 max Z=16‐（2 3 5 6 ）

-x1+x2≤1 3x1+x2≤4 x1,x2≥0
用图解法求得可行域D及最优解点A，见下图：
x2
A（3/4，7/4） 由标准化的约束方程组可得
-x1+x2=1
1
D B（1，1）
x3 =1+x1-x2 x4=4 -3x1-x2 代入切割方程 得
-1 0
3x1+x2=4
3（1+x1-x2）+（4-3x1-x2）≥3
下面以实例来说明算法的步骤。
例2 求解下面整数规划
x2
maxZ=40x1+90x2
⑴8
9x1+ 7x2≤56 7x1+20x2≤70 xx11,,xx22≥0整数
⑵
⑶ ⑷
4
⑸
解：先不考虑条件⑸，求解相 0
应的线性规划问题L，得最优解
x1=4.81，x2=1.82，Z0=356（见图） 该解不是整数解。选择其中一个
整个分枝定界过程如下图所示：
问题L
Z0=356 x1=4.81x2=1.82
Z 0,Z 356
x1≤4
问题L1 Z1=349 x1=4.00，x2=2.10
x2≤2 问题L3 Z3=340 x1=4.00 x2=2.00
Z※=340
x2≥3
问题L4 Z4=327 x1=1.42 x2=3.00
×
x1≥5
运筹学
整数线性规划
§1 整数规划问题
在前面的线性规划问题中，它的解都假设为可以取连续数值。 但是在许多实际问题中，决策变量仅仅取整数值时才有意义，比如 变量表示的是工人的人数、机器的台数、货物的箱数、装货的车皮 数等等。为了满足整数解的要求，比较自然的简便方法似乎就是把 用线性规划方法所求得的非整数解进行“四舍五入”取整或“舍尾 取整”处理。当然，这样做有时确实也是有效的，可以取得与整数 最优解相近的可行整数解，因此它是实际工作中经常采用的方法。 但是实际问题中并不都是如此，有时这样处理得到的解可能不是原 问题的可行解，有的虽是原问题的可行解，但却不是整数最优解。 （详见后面例1）。因而有必要专门研究只取整数解的线性规划的 解法问题。

约束条件组
n aij xj b i My i j1 st. p (i 1 ,2,...,p) yi pq i1
在约束条件中保证了在P个0-1 变量中有p-q个1,q个0;凡取值 =0的yi对应的约束条件为原约束 条件,凡取值=1的yi对应的约束 条件将自然满足,因而为多余.
,先加工某种产品 0 yj （ j 1 ,2 ,3 ,4 ） 1 ，先加工另外产品 机床1:x11+a11≤x21+My1 ; x21+a21≤x11+M(1-y1) 机床2:x22+a22≤x32+My2 ; x32+a32≤x22+M(1-y2) 机床3:x13+a13≤x33 +My3 ; x33+a33≤x13+M(1-y3) 机床4:x14+a14≤x24 +My4 ; x24+a24≤x14+M(1-y4) 当y1=0,表示机床1先加工产品1,后加工产品2;当y1=1,表示机床1先 加工产品2,后加工产品1.
不同的搜索策略会导致不同的搜索树，一般 情况下，同一层的两个子问题，先搜索目标 函数比较大的较有利（如果是极小问题，则 应先搜索目标函数值小的较为有利）。这样 可能得到数值比较大的下界，下界越大被剪 去的分支越多。 分支定界算法对于混合整数规划特别有效， 对没有整数要求的变量就不必分支，这将大 大减少分支的数量。
Max Z = X1 + X2 14X1 + 9X2 ≤ 51 - 6X1 + 3X2 ≤ 1 X1 ≥2 X2 ≤ 2 X1 ， X2 ≥ 0 Max Z = X1 + X2 14X1 + 9X2 ≤ 51 - 6X1 + 3X2 ≤ 1 X1 ≥3 X2 ≤ 2 X1 ， X2 ≥ 0 Max Z = X1 + X2 14X1 + 9X2 ≤ 51 - 6X1 + 3X2 ≤ 1 2≤ X1 ≤2 X2 ≤ 2 X1 ， X2 ≥ 0

习 题 11 用图解法求解下列线性规划问题，并指出问题具有唯一最优解、无穷最优解、无界解还是无可行解。

⎪⎩⎪⎨⎧≥≥+≥++=0x x 42x 4x 66x 4x 3x 2x minz )a (21212121， ⎪⎩⎪⎨⎧≥≥+≤++=0x ,x 124x 3x 2x 2x 2x 3x maxz )b (21212121⎪⎩⎪⎨⎧≤≤≤≤≤++=8x 310x 512010x 6x x x maxz )c (212121⎪⎩⎪⎨⎧≥≤+-≥-+=0x ,x 23x 2x 2x 2x 6x 5x maxz )d (21212121 答案： (a)唯一解3*,)5.0,75.0(*==z X T); (b)无可行解;(c)唯一解16*,)6,10(*==z X T); (d)无界解）2 用单纯形法求解下列线性规划问题。

⎪⎩⎪⎨⎧≥≤+≤++=0x ,x 82x 5x 94x 3x 5x 10x maxz )a (21212121 ⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+=0x ,x 5x x 242x 6x 155x x 2x maxz )b (212121221 答案：(a)唯一解5.17*,)5.1,1(*==z X T)，对偶问题5.17*,)786.1,357.0(*==w Y T; (b)唯一解5.8*,)5.1,5.3(*==z X T），5.8*,)5.0,25.0,0(*==w Y T3 用大M 法和两阶段法求解下列线性规划问题，并指出属于哪一类解。

⎪⎪⎩⎪⎪⎨⎧≥≥-≥+-≥+++-=0x x x 0x 2x 2x 2x 6x x x 2x x 2x maxz )a (3,2,13231321321 ⎪⎩⎪⎨⎧≥≥+≥++++=0x ,x ,x 62x 3x 82x 4x x x 3x 2x minz )b (32121321321 答案：(a)无界解；(b)唯一解8*,)0,8.1,8.0(*==z X T)，对偶问题8*,)0,1(*==w Y T4已知线性规划问题的初始单纯形表（如表1-54所示）和用单纯形法迭代后得到的表（如表1-55所示）如下，试求括弧中未知数a ～l 的值。

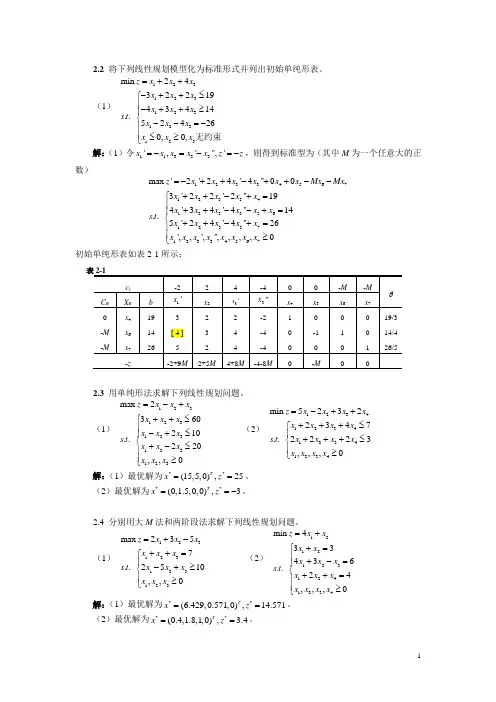
2.2 将下列线性规划模型化为标准形式并列出初始单纯形表。

（1）123123123123123min 243221943414..524260,0,z x x x x x x x x x s t x x x x x x =++-++≤⎧⎪-++≥⎪⎨--=-⎪⎪≤≥⎩无约束 解：（1）令11333','",'x x x x x z z =-=-=-，则得到标准型为（其中M 为一个任意大的正数）12334567123341233561233712334567max '2'24'4''003'22'2''194'34'4''14..5'24'4''26',,','',,,,0z x x x x x x Mx Mx x x x x x x x x x x x s t x x x x x x x x x x x x x =-++-++--++-+=⎧⎪++--+=⎪⎨++-+=⎪⎪≥⎩初始单纯形表如表2-1所示：表2-1c j-22 4-4 0 0 -M -M θC B X B b 1'xx 2 3'x3''xx 4 x 5 x 6 x 7 0 x 4 19 3 2 2 -2 1 0 0 0 19/3 -M x 6 14 [ 4 ] 3 4 -4 0 -1 1 0 14/4 -Mx 7 265 2 4-40 0 0 1 26/5 -z-2+9M2+5M4+8M -4-8M-M2.3 用单纯形法求解下列线性规划问题。

（1）123123123123123max 2360210..220,,0z x x x x x x x x x s t x x x x x x =-+++≤⎧⎪-+≤⎪⎨+-≤⎪⎪≥⎩ （2） 1234123412341234min 52322347..2223,,,0z x x x x x x x x s t x x x x x x x x =-+++++≤⎧⎪+++≤⎨⎪≥⎩解：（1）最优解为**(15,5,0),25T x z ==。

7
二、固定成本问题 例2．高压容器公司制造小、中、大三种尺寸的金属容器， 所用资源为金属板、劳动力和机器设备，制造一个容器所需 的各种资源的数量如表所示。不考虑固定费用，每种容器 售出一只所得的利润分别为 4万元、5万元、6万元，可使用的 金属板有500吨，劳动力有300人/月，机器有100台/月，此外 不管每种容器制造的数量是多少，都要支付一笔固定的费用： 小号是l00万元，中号为 150 万元，大号为200万元。现在要制 定一个生产计划，使获得的利润为最大。
=0。
这样我们可建立如下的数学模型： Max z = 4x1 + 5x2 + 6x3 - 100y1 - 150y2 - 200y3 s.t. 2x1 + 4x2 + 8x3 ≤ 500 2x1 + 3x2 + 4x3 ≤ 300 x1 + 2x2 + 3x3 ≤ 100 xi ≤ M yi ，i =1，2，3，M充分大 xj ≥ 0 yj 为0--1变量，i = 1,2,3
线性规划的最优解为x1=2.44, x2=3.26,目标函数值为14.66。由图表
可看出，整数规划的最优解为x1=4, x2=2,目标函数值为14。 一般求整数解的线性规划问题，不可用四舍五入法或去尾法对线性规
划的非整数解加以处理来解决整数规划。
在整数规划中，如果所有的变量都为非负整数，则称为纯整数规划问 题；如果有一部分变量为负整数，则称之为混合整数规划问题。在整 数规划中，如果变量的取值只限于0和1，这样的变量我们称之为0-1 变量。在纯整数规划和混合整数规划问题中，如果所有的变量都为01变量，则称之为0-1规划。
9
三、分布系统设计 例3．某企业在 A1 地已有一个工厂，其产品的生产能力为 30 千箱，为了 扩大生产，打算在 A2，A3，A4，A5地中再选择几个地方建厂。已知在 A2 ， A3，A4，A5地建厂的固定成本分别为175千元、300千元、375千 元、500千元，另外， A1产量及A2，A3，A4，A5建成厂的产量，那时 销地的销量以及产地到销地的单位运价(每千箱运费)如下表所示。

剪枝 x 3 再分枝： 2
不是问题A解 而z (12 ) z
B1 : x1 4.00 x2 2.10 z (1) 349 z
z (12 ) 327
4
x2 2
B11 : x1 4.00 x2 2.00 z (11) 340
定界： z 340 z 341
z 340 z 341
分支定界的全过程： B2 : x1 5.00 B1 : x1 4.0 0
x 2 2 .1 0
x2 1.57
x2 2
z
(1)
B11 : x1 4.00 x2 2.00 z
(11)
xx 34 2 最优解： 1
3 49
z ( 2 ) 341
（3）求解
点
求解过程如表4－6所示。
过滤条件 约束 ④ × √ √ √ 4x1＋3x2＋2x3≥5 × √ × √ √ √ √ × √ √ 5 √ 2 ① ② ③ z值
4x1＋3x2＋2x3≥2
（0，0，0）T （0，0，1）T （0，1，0）T （0，1，1）T （1，0，0）T （1，0，1）T
§4 分枝定界法
第二步:定界
记A的目标函数最优值为z*,以z(0)作为z* 的上界,记为 z =z(0).再用观察法找的一个整数可 行解X′,并以其相应的目标函数值z′作为z*的下 界,记为z＝z′,也可以令z＝－∞,则有: *
zz z
§3 分枝定界法
第三步:分枝
在以上界 z 所对应的解 X (b1,, br ,, bm ,0,,0)T 中,任选一个不符合整数条件的变量,例如 br(不 为整数),以 [br ]表示不超过 br 的最大整数.构造 两个约束条件

B1 B 2 c11 c12 c 21 c 22
cm1 cm 2 b1 b 2
生产 建设
Bn 能力 费用 c1n a1 f1 c2n a2 f2
c mn a m f m bn
设： xij 表示从工厂运往销地的运量(i=1.2…m、
j=1.2…n), 1 在Ai建厂
又设 Yi＝
（i=1.2…m）
⑵ ⑴
A
(18/11,40/11)
BCD
E
F
⑶
求（LP6），如图所示。 1
此时 F在点取得最优解。
x1＝3, x2 =2.5,
1
3
x1
Z(6)＝－31/2≈－15.5 > Z(5)
如对 Z(6) 继续分解，其最小值也不会低于－15.5 ，问 题探明,剪枝。
至此，原问题 （IP）的最优解 为：
x1=2， x2 =3, Z* = Z(5)
x1≥3
LP4 无可 行解
＃
LP5 x1=2, x2=3 Z(5) ＝－17
＃
LP6 x1=3, x2=5/2 Z(6) ＝－15.5
＃
三、0－1 整数规划
0－1 整数规划是一种特殊形式的整数规划，这时的 决策变量xi 只取两个值0或1，一般的解法为隐枚举法。
例一、求解下列0－1 规划问题
max Z 3 x 1 2 x 2 5 x 3
4、修改上、下界：按照以下两点规则进行。 ⑴.在各分枝问题中，找出目标函数值最大者作为新 的上界； ⑵.从已符合整数条件的分枝中，找出目标函数值最 大者作为新的下界。
5、比较与剪枝 ：
各分枝的目标函数值中，若有小于Z 者，则剪掉此 枝，表明此子问题已经探清，不必再分枝了;否则继续 分枝。

运筹学习题库一、线性规划1．某工厂生产甲、乙、丙三种产品，单位产品所需工时分别为2、3、1个工时；单位产品所需原材料分别为3、1、5公斤；单位产品利润分别为2元、3元、5元。

工厂每天可利用的工时为12个，可供应的原材料为15公斤。

1）试确定使总利润为最大的日生产计划和最大利润。

2）若由于原材料涨价，使得产品丙的单位利润比原来减少了2元，问原来的最优生产计划变否？若不变，说明为什么；若变，请求出新的最优生产计划和最优利润。

3）在保持现行最优基不变的情况下，若要增加一种资源量，应首先考虑增加哪种资源？为什么？单位资源增量所支付的费用是多少才合算？为什么？2．给出一线性规划问题如下：max z = 3x1 + x2x1 + x2≤4－x1 + x2≤26x1 + 2x2≤18x１，x2≥0试用对偶理论判断该问题是否存在以x１、x2和x3为基变量的最优解？3．用单纯形法求解某个目标函数为max，约束为≤形式，x4、x5为松弛变量的线性规划问题的最终表如下：试用改进单纯形法原理求该问题的数学模型。

4．给出一个线性规划问题如下：max z = x1 +2 x2 +3 x3x1 + 2x2 + 3x3≤84x1+ 5x3≤12x1，x2 ，x3 ≥0已知其对偶问题的最优解为Y* = (1，0 )，试用对偶理论求上述问题的最优解和最优值。

5．试用大M法求下述线性规划问题的最优解和最优值（不能用图解法）：max z = 3x 1 – 3 x 2x1 + x2 ≥1 2x 1 + 3x 2 ≤6x 1，x 2 ≥06．已知一线性规划问题如下：max z = 5x 1 + 2 x 2 + 4 x 3 3 x 1 + x 2 + 2 x 3 ≤ 46 x 1 + 3 x 2 + 5 x 3 ≤ 10 x 1，x 2，x 3 ≥ 0试用松紧定理判断X = ( 0，0，2 )T 是否是该问题的最优解，若不是，说明为什么；若是， 请求出相应的目标函数值。

整数规划习题4-1某厂拟在A 、B 、C 、D 、E 五个城市中建立若干个配送中心，各处设配送中心都需要资金、人力、设备等，而这样的需求量及能提供的利润各处不同，有些点可能亏本，但却能得到贷款和人力等资源。

设数据已知，由下表所示。

厂方应作出4-2用分支定界法求解下列整数规划问题⎪⎩⎪⎨⎧≥≥+≤+⎪⎩⎪⎨⎧≥≥+≤+-+=+=且为整数且为整数）（）（0,5427230,5021010m 2min 12121212121212121x x x x x x x x x x x x x x z ax x x z4-3用割平面法求解下列整数规划问题⎪⎩⎪⎨⎧≥≤+≤+⎪⎩⎪⎨⎧≥≥+≥++=+=且为整数且为整数）（）（0,102920,1029232m 232min 12121212121212121x x x x x x x x x x x x x x z ax x x z 4-4用隐枚举法求解下列0-1规划问题⎪⎪⎪⎩⎪⎪⎪⎨⎧=≤+≤+≤++≤-++-=1,0,,162444233max 3212232321321321x x x x x x x x x x x x x x x x z4-5安排4个人做4项不同的工作，每个人完成工作所需要的时间如下表所示，（1）应如何指派，可使总的时间最少？（2）如果表中的数据为创造的效益，应如何指派，使总效益最大？（3）如果在表中增加一个人（一行），完成A、B、C、D工作的时间分别为16、17、20、21天，这时应如何指派，使总时间最少？4-6对每题结论进行判断，如果结论错误请改正。

（1）整数规划的最优解是先求相应的线性规划的最优解然后取整得到。

（2）求最大值整数规划问题的目标函数值是各分支函数值的上界。

（3）求最小值整数规划问题的目标函数值是各分支函数值的上界。

（4）整数规划的可行解集合是离散型集合。

（5）0一1规划的变量有n个，则有2n个可行解。

（6）割平面约束是将可行域中一部分非整数解切割掉。

xj 0 j 1,2,3,4
(5.2.6) (5.2.7) (5.2.8) (5.2.9)

18
二、求解线性规划问题(1)
用单纯形法的表格形式求解，得最终表，见表5.2.1。 由表5.2.1及式max Z =一[min(一Z)]可知，问题(0)的
最优解A1点为
求解过程参见图5.3.1

30
2.判断无约束下最优解(0，0，0)T即节点1是否 是可行解?
显然，(0，0，0) T是无约束下的最优解，若它能使各 约束式得到满足，则它必是0-1规划原问题的最优解。
本例中把(0，0，0) T代入各约束式。得. Q1 = 4≥0 Q2 = －3 Q3 = －1
第五章
整数规划

1
线性规划问题中，最优解可能是整数，也可能不 是整数，而实际中有相当多的问题要求解答必须 是整数。
对于线性规划问题，如果增加部分变量或全部变 量为整数的要求，就构成了整数线性规划问题。 其中，要求全部变量为整数的问题称为纯整数规 划问题，要求部分变量为整数的问题称为混合整 数规划问题。

32
4.欲分枝，必须从某个不满足的约束的系数为 正值的变量中，选择一个自由变量Xj作非自由 变量。
求解问题(2)时，可以利用3.4节灵敏度分析中介 绍的增加一个新的约束条件的做法，尽快地得 到新的最优解。

21
五、例题的图解法结果
上述例题的 图解法结果示于 图 5.2.1中 。 图5.2.1中，各点的坐标及最优点的目标函数值列于
表5.2.3。


12
五、修改原来的上、下界
1．修改下界Z ：
– 从分支中，找出目标函数最大者为新的下界。

x1 3.25;
x2 2.5
分枝定界法思路
第二步：分枝与定界 在x1=3.25；x2=2.5 中，任选一变量的解X2=2.5 ， 可将其分为 x2≤2；x2≥3（去掉小数部分），则有：
max Z 3x1 2 x2 2 x1 3x2 14 x 0.5 x 4.5 1 2 s.t. x2 2 x1 , x2 0
(3.5, 2); z 14.5
X1可分为x1≤3；x1≥4，则有：
max Z 3x1 2 x2 2 x1 3x2 14 x 0.5 x 4.5 1 2 s.t. x2 2 x 3 1 x1 , x2 0 (3, 2); z 13
逻辑变量在建立数学模型中的作用
y1 y2 ... ym
中m-k不起作用
（2）割平面法思路
max Z 3 x1 2 x2 2 x1 3 x2 14 s.t. x1 0.5 x2 4.5 x , x 0 且取整数 1 2
第一步：将约束条件决策变量的系数化为整数，用单纯形法求 解出最终单纯形表 找一个分数部
（3）分支定界法
max Z 3 x1 2 x2 2 x1 3 x2 14 s.t. x1 0.5 x2 4.5 x , x 0束，求解。
max Z 3x1 2 x2 2 x1 3x2 14 s.t. x1 0.5 x2 4.5 x , x 0 1 2
max Z 3x1 2 x2 2 x1 3x2 14 x 0.5 x 4.5 1 2 s.t. x2 2 x 4 1 x1 , x2 0
(4, 1);

j 1
n
s.t
i1
xij
1,
j V
(2)
xij S 1,
S V , 2 S n 1
(3)
iS jS
xij 0, 1
二、典型整数规划问题建模方法
3、指派问题
混合游泳接力接力队的选拔
甲
乙
丙
蝶泳 仰泳 蛙泳 自由泳
1’06”8 1’15”6 1’27” 58”6
57”2 1’06” 1’06”4 53”
14
二、典型整数规划问题建模方法
Page 15
• 记为赋权图G=(V,E)，V为顶点集，E为边集，各顶点间的距 离dij已知。设
xij
1 , 0,
若i, j 在回路路径上
其他
则经典的TSP可写为如下的数学规划模型：
nn
min Z
dij xij
i 1 j 1
n
xij 1,
i V
(1)
5
应用统计 微积分；线性代数
6
计算机模拟
计算机编程
7
计算机编程
8
预测理论
应用统计
9
数学实验 微积分；线性代数
模型求解:
最优解： x1 = x2 = x3 = x6 = x7 = x9 =1, 其它为0；6门 课程，总学分21（注意：最优解可能不唯一！）
约束条件：先修课程要求 x3=1必有x1 = x2 =1
Page 3
max z 20x1 10x2
5x1 4x2 24 2x1 5x2 13 x1, x2 0, x1, x2整数
• 用单纯形法解得：x1 4.8, x2 0, z 96
一、概述
Page 4

第五章
概念
整数规划
（整数线性规划）
分枝定界解法
0-1型整数规划 指派问题 应用
第一节 概念
整数规划是一类要求变量取 整数值的数学规划，可分成线性 和非线性两类。
根据变量的取值性质，又可 以分为纯整数规划，混合整数规 划，0-1整数规划等。
整数规划是数学规划中一 个较弱的分支，目前只能解中 等规模的线性整数规划问题， 而非线性整数规划问题，还没 有好的办法。
第三节

0-1型整数规划
0-1变量的引入 1 采取方案j Xj＝
0
不采取方案j
例1：相互排斥的决策参量
某公司要建立门市部，有七个备选地点： 东区：A1A2A3中至多选两个； 西区：A4A5中至少选一个 南区：A6A7中至少选一个 若选用Aj，投资费为bj，年获利为cj，投资总额不超 过B。如何定夺方案？
车运 5 4
船运 7 3 45
利润 20 10
乙
托运限制 24
0
y＝
采用车运
采用船运
1
5X1+4X2≤24+yM (1’) 7X1+3X2 ≤ 45+(1-y)M (2’) y＝0或1
当y＝0采用车运，(1’)＝ (1)；(2’)显然成立，是多余条件。 当y＝1采用船运，(2’)＝ (2)；(1’)显然成立，是多余条件。
例2 背包问题( Knapsack
Problem)
一个旅行者,为了准备旅行的必须用品,要 在背包内装一些最有用的东西,但有个限 制,最多只能装b公斤的物品,而每件物品 只能整个携带,这样旅行者给每件物品规 定了一个“价值”以表示其有用的程度, 如果共有n件物品,第j件物品aj公斤,其价 值为cj.问题变成:在携带的物品总重量不 超过b公斤条件下,携带哪些物品,可使总 价值最大?