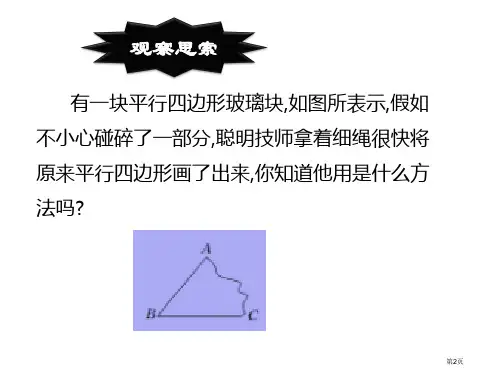
第8页
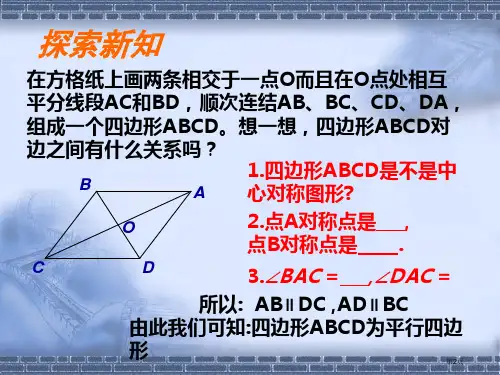
平行四边形判定方法: 对角线相互平分四边形是平行四边形.
数学语言表述这个定理: ∵OA=OC,OB=OD, ∴四边形ABCD是平行四边形.
第9页
提问:经过以上证实,我们得到了平行四边形 判定定理.这些定理与平行四边形性质定理有何 关系?
平行四边形判定定理与平行四边形性质定理互
为逆定理.
①平行四边形定义. ②两组对边分别相等四边形是
第15页
检测反馈
1.如图所表示,在四边形ABCD中,AC,BD相交于点
O.(1)若AD=8 cm,AB=4 cm,那么当BC8=
cm,
CD= 4 cm时,四边形ABCD为平行四边形;
解析: 此题主要考查了平行四边形判定定理应用.依据两组对边 分别相等四边形是平行四边形,即可确定BC,CD长.
第16页
平行四边形. ③两组对角分别相等四边形是平行四
边形. ④对角线相互平分四边形是平行四边形.
第10页
例:(教材例3)如图所表示, □ABCD对角线AC,BD相交于点
O,E,F是AC上两点,而且AE=CF.求证四边形BFDE是平行四边形.
〔解析〕由已知条件可知:=OD,OA=OC,因为AE=CF,所以 OE=OF,依据平行四边形判定定理:对角线相互平分四边形是平行 四边形,即可证实四边形BFDE是平行四边形.
证实:连接BD交AC于点O,如图所表示, ∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.∵AE=CF,
∴OA-AE=OC-CF,即OE=OF. ∴四边形BEDF是平行四边形, ∴∠EBF=∠FDE.
第20页
第11页
【变式训练】如图所表示, □ABCD中,E,F分别是
AC上两点,且BE⊥AC于E,DF⊥AC于F.求证四边形BEDF 是平行四边形. 〔解析〕利用条件证实△ABE≌△CDF, 得AE=CF,连接BD交AC于O,证实四边形 BEDF对角线EF,BD相互平分即可.