线性代数—矩阵的秩

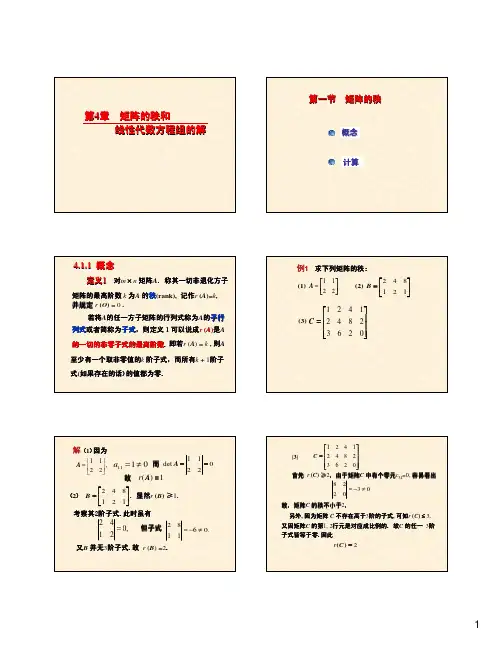
一、 矩阵的秩定义1 在一个n m ⨯矩阵A 中，任意选定k 行和k 列（{}n m k ,min ≤），位于这些选定的行和列的交点上的2k 个元素按原来的次序所组成的k k ⨯矩阵的行列式，称为A 的一个k 阶子式。

例1 在矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=0000500041201311A 中，选第3,1行和第4,3列，它们交点上的元素所成的2阶行列式155013=就是一个2阶子式。

又如选第3,2,1行和第4,2,1列，相应的3阶子式就是.10500420111=定义2 非零矩阵的不为零的子式的最高阶数称为该矩阵的秩，零矩阵的秩规定为0。

矩阵A 的秩记为()A rank 。

例2 证明：矩阵A 与其转置矩阵T A 有相同的秩。

例3 证明：阶梯形矩阵的秩等于它的非零行的个数。

证 设A 是一个阶梯形矩阵，不为零的行数是r 。

选取这r 个非零行以及各非零行第一个非零元素所在的列，由这些行和列交点上的元素所成的r 阶子式是一个上三角行列式，并且主对角线上的元素都不为零，因此它不等于零。

而A 的所有阶数大于r 的子式都至少有一行的元素全为零，因而子式为零。

所以()r A r a n k =。

由于矩阵的子式的阶数不超过矩阵的行数及列数，所以n m ⨯矩阵A 的秩()()n m A rank ,min ≤。

而如果()m A rank =，就称A 是行满秩的；如果()n A rank =，就称A 是列满秩的。

此外，如果A 的所有1+r 阶子式全为零，由行列式的定义可知，A 的2+r 阶子式也一定为零，从而A 的所有阶数大于r 的子式全都为零。

因此秩有下面等价的定义：定理1 n m ⨯矩阵A 的秩为r 充分必要条件是：在A 中存在一个r 阶子式不为零，且在()()n m A rank ,min <时，矩阵A 的所有1+r 子阶式都为零。

定理2 初等变换不改变矩阵的秩。

换句话说，等价的矩阵具有相同的秩。

证 设n m A ⨯经初等行变换变为n m B ⨯，且()()21,r B r a n k r A r a n k ==。

矩阵的秩小结
矩阵的秩是线性代数中一个重要的概念，它可以帮助我们理解矩阵的性质和解决一些实际问题。

本文将对矩阵的秩进行总结，包括定义、计算方法以及应用。

矩阵的秩是指矩阵中非零行的最大个数，或者说矩阵中不可被其他行线性表示的行的个数。

换句话说，矩阵的秩是指矩阵所包含的最大线性无关行的个数。

矩阵的秩可以通过多种方式进行计算，其中常见的有高斯消元法。

高斯消元法通过进行初等行变换将矩阵转化为行最简形，然后数非零行的个数即为矩阵的秩。

另一种常见的方法是使用特征值和特征向量来计算矩阵的秩。

具体而言，矩阵的秩等于其非零特征值的个数。

矩阵的秩在实际应用中有很多重要的作用。

首先，矩阵的秩可以帮助我们判断一个线性方程组是否有解以及解的唯一性。

如果线性方程组的系数矩阵的秩等于增广矩阵的秩，那么该线性方程组有解；如果系数矩阵的秩小于增广矩阵的秩，那么线性方程组无解。

其次，矩阵的秩可以用于判断矩阵是否可逆。

如果矩阵的秩等于其阶数，那么矩阵是可逆的；如果矩阵的秩小于其阶数，那么矩阵不可逆。

此外，矩阵的秩还可以用于判断线性相关性。

如果矩阵的秩小于列数，那么矩阵的列向量线性相关；如果矩阵的秩等于列数，那么矩阵的列向量线性无关。

总结起来，矩阵的秩是一个重要的概念，在线性代数中具有广泛的应用。

我们可以通过高斯消元法或者特征值和特征向量来
计算矩阵的秩。

矩阵的秩可以帮助我们判断线性方程组的解的情况、矩阵是否可逆以及向量的线性相关性。

矩阵的秩8个公式及证明
矩阵的秩是线性代数中的一个重要概念，它描述了矩阵中线性无关的列（或行）的最大数量。

下面我将列举并证明矩阵的秩的八个公式。

1. 零矩阵的秩为0，证明很简单，因为零矩阵中没有非零的行或列。

2. 对角矩阵的秩等于非零对角元素的个数，证明也比较简单，因为对角矩阵中只有对角线上的元素可能非零，所以秩等于非零对角元素的个数。

3. 初等变换不改变矩阵的秩，初等变换包括交换矩阵的两行（列），用非零常数乘以矩阵的某一行（列），以及用一个非零常数乘以矩阵的某一行（列）加到另一行（列）上。

这些操作不改变矩阵的秩。

4. 行（列）等价的矩阵具有相同的秩，行等价指的是通过一系列的初等行变换可以相互转化的矩阵，列等价类似。

由于初等变换不改变矩阵的秩，所以行（列）等价的矩阵具有相同的秩。

5. 矩阵的秩不超过它的行数和列数中的较小值，这是因为矩阵
的秩描述的是矩阵中线性无关的列（或行）的最大数量，而这个数
量不可能超过矩阵的行数或列数。

6. 对于任意的矩阵A和B，秩(A + B) ≤ 秩(A) + 秩(B)，证
明过程比较复杂，可以使用矩阵的行列式性质和秩的定义进行证明。

7. 对于任意的矩阵A和B，秩(AB) ≤ min(秩(A), 秩(B))，
证明过程比较复杂，可以使用矩阵的行列式性质和秩的定义进行证明。

8. 对于任意的矩阵A，秩(A) = 秩(A^T)，这个公式的证明比
较简单，可以通过矩阵的转置操作和秩的定义进行证明。

综上所述，这是矩阵的秩的八个公式及其证明。

这些公式在线
性代数中具有重要的应用和意义。