设计中心对称图案

3.3 设计中心对称图案——整合教学设计概述设计中心对称图案是一种常见的美学形式，它通过在垂直或水平方向上复制和镜像图案元素来创造对称效果。

在教学中，引入设计中心对称图案的概念可以帮助学生培养审美意识和创造力，并提高他们的几何思维能力。

本文将介绍如何整合教学设计，以帮助学生理解和应用设计中心对称图案。

1. 教学目标设计中心对称图案的教学设计的目标是帮助学生： - 理解什么是中心对称图案；- 辨别中心对称图案中的对称轴； - 了解中心对称图案的特点和应用； - 运用中心对称图案进行创作和设计。

2. 教学内容和活动2.1 概念介绍在引入中心对称图案之前，可以通过一些例子和图像来展示中心对称图案的基本概念和特征。

可以使用黑板或投影仪展示一些中心对称图案的示例，并让学生观察和分析这些图案。

2.2 辨识中心对称图案让学生观察一些具有中心对称性质的物体，如风车、雪花等，并引导他们辨认出对称轴和复制的图案元素。

2.3 制作中心对称图案让学生使用纸和彩色铅笔或蜡笔，设计和制作自己的中心对称图案。

可以提供一些模板供学生参考，然后他们可以在模板的基础上进行创作。

2.4 分享和展示学生可以互相交换他们设计的中心对称图案，并进行分享和讨论。

教师可以鼓励学生讲解他们的设计灵感和创作过程，并提出建议和反馈。

3. 教学评估为了评估学生对设计中心对称图案的理解和应用能力，可以采用以下方法： -学生展示和讲解自己设计的中心对称图案，教师评估他们对批评和建议的接受程度；- 给学生提供一些中心对称图案，让他们标出对称轴； - 给学生一些中心对称图案的未完成版本，让他们进行创作并补全对称的部分。

4. 教学资源在教学过程中，可以使用以下资源来辅助教学： - 中心对称图案的示例和图片；- 制作中心对称图案的纸和彩色铅笔/蜡笔； - 中心对称图案的模板； - 展示学生设计作品的展板或墙面。

5. 教学拓展在掌握了设计中心对称图案的基本概念和技巧后，可以进一步引导学生进行更复杂的设计活动。

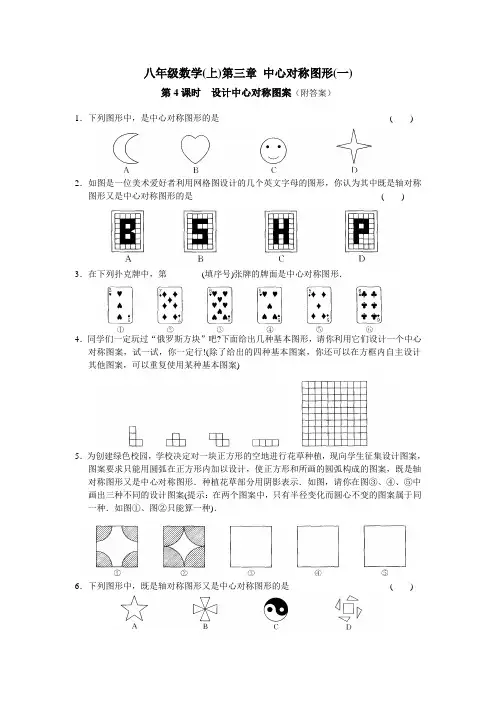
八年级数学(上)第三章中心对称图形(一)第4课时设计中心对称图案（附答案）1．下列图形中，是中心对称图形的是( )2．如图是一位美术爱好者利用网格图设计的几个英文字母的图形，你认为其中既是轴对称图形又是中心对称图形的是( )3．在下列扑克牌中，第________(填序号)张牌的牌面是中心对称图形．4．同学们一定玩过“俄罗斯方块”吧?下面给出几种基本图形，请你利用它们设计一个中心对称图案，试一试，你一定行!(除了给出的四种基本图案，你还可以在方框内自主设计其他图案，可以重复使用某种基本图案)5．为创建绿色校园，学校决定对一块正方形的空地进行花草种植，现向学生征集设计图案，图案要求只能用圆弧在正方形内加以设计，使正方形和所画的圆弧构成的图案，既是轴对称图形又是中心对称图形．种植花草部分用阴影表示．如图，请你在图③、④、⑤中画出三种不同的设计图案(提示：在两个图案中，只有半径变化而圆心不变的图案属于同一种．如图①、图②只能算一种)．6．下列图形中，既是轴对称图形又是中心对称图形的是( )7．如图①，三张扑克牌放在桌子上，小敏把其中一张牌旋转180°后，如图②所示，则她所旋转的牌从左数起是( )A．第一张B．第二张C．第三张D．无法确定8．如图，方格纸中左边图形到右边图形的变换是( )A．向右平移7格B．以AB的垂直平分线为对称轴作轴对称，再以AB为对称轴作轴对称C．绕AB的中点旋转180°，再以AB为对称轴作轴对称D．以AB为对称轴作轴对称，再向右平移7格9．如图是一个中心对称图形的一半，请补出图形的另一半．10．下列网格中，各个小正方形的边长都为1，请你将最左边网格中的图形按以下要求进行分割后重新拼接，并分别画在从左至右的网格中．(1)拼得的图形是轴对称图形而不是中心对称图形．(2)拼得的图形是中心对称图形而不是轴对称图形．(3)拼得的图形既是轴对称图形又是中心对称图形．11．认真观察图①的四个图形中阴影部分构成的图案，回答下列问题：(1)请写出这四个图案都具有的两个共同特征．特征1：__________________________________________．特征2：__________________________________________．(2)请在图②中设计出你心中最美丽的图案，使它也具备你所写出的上述特征．参考答案1．D 2．C 3．⑤4．略5．略6．B 7．A 8．D 9．略10．略11．略。

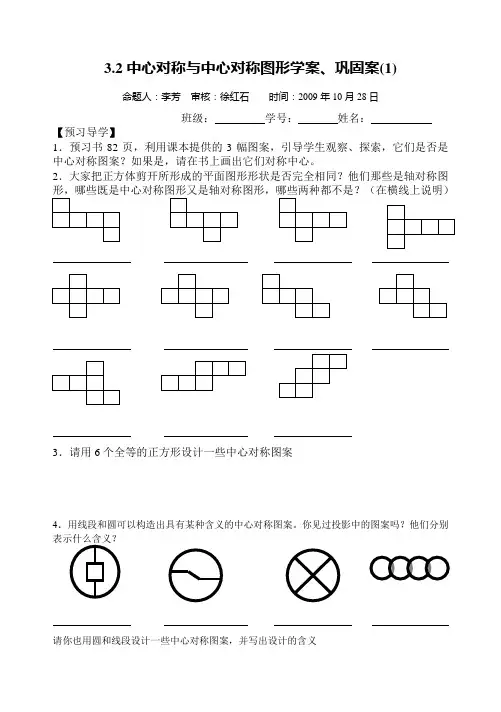
3.2中心对称与中心对称图形学案、巩固案(1)命题人：李芳审核：徐红石时间：2009年10月28日班级：学号：姓名：【预习导学】1．预习书82页，利用课本提供的3幅图案，引导学生观察、探索，它们是否是中心对称图案？如果是，请在书上画出它们对称中心。

2．大家把正方体剪开所形成的平面图形形状是否完全相同？他们那些是轴对称图3．请用6个全等的正方形设计一些中心对称图案4．用线段和圆可以构造出具有某种含义的中心对称图案。

你见过投影中的图案吗？他们分别表示什么含义？请你也用圆和线段设计一些中心对称图案，并写出设计的含义【精讲点拨】例12、利用图形“、”（两个平行线段、两个圆、两个三角形）为还能构思其他满足已知条件的图形吗？并写出一两句贴切、诙谐的解说词。

（奖牌）例2：为了美化校园，学校准备在一块圆形空地上建花坛，现征集设计方案。

要求设计的图案由圆和等边三角形组成（圆和等边三角形的大小、个数不限），并且使整个圆形场地是一个中心对称图形。

请画出你的设计方案。

（画图必须用尺规作图）【反馈矫正】练习：课本P82，练习1、2随堂练⒈下列图形中，是轴对称图形但不是中心对称图形的是 （ ）A 圆B 正方形C 等边三角形D 平行四边形2．在计算器上按出两位数“”，这个电子数字可以看成一个中心对称图案。

你还能写出多少个组成中心对称图案的两位数、三位数？3．把如下的26个英文大写字母看成图案，哪些英文大写字母是中心对称图案？A B C D E F G H I J K L M N O P Q R S T U V WX Y Z4. 如图，由4个全等的正方形组成的L 形图案，请按下列要求画图：⑴在图案①中添加1个正方形，使它成轴对称图案；⑵在图案②中添画1个正方形，使它成中心对称图案；⑶在图案中改变1个正方形的位置，画成图案③，使它既成中心对称图形，又成轴对称图形5.用9根火柴拼出如图所示的图形，你能移动若干根火柴棒，使它们搭成的图形是中心对称图形吗？至少移动几根？画出移动后的图形。

汇报人：日期:目录•中心对称图形的定义•中心对称图形的性质•中心对称图形的应用•中心对称图形的证明方法•中心对称图形的作图方法•中心对称图形的拓展思考中心对称图形的定义特性中心对称图形是轴对称图形的一种特例，其特点是图形以对称中心为旋转轴，旋转180度后能与自身重合。

定义如果一个图形绕某一点旋转180度后，能与自身重合，那么这个图形就叫做中心对称图形。

这个点叫做对称中心。

中心对称图形的定义及特性在中心对称图形中，过对称中心的任意一条直线，都将图形分成两个全等形。

在中心对称图形中，过对称中心的任意一条直线，若该直线与对称中心垂直，则这条直线将图形分成两个全等形。

中心对称图形的几何意义平行线性质垂直平分线性质01直线型以一条直线为对称轴的图形，如正弦函数图像等。

02圆型以圆为对称轴的图形，如圆形、椭圆形等。

03多边形型以多边形为对称轴的图形，如正多边形等。

中心对称图形的分类中心对称图形的性质旋转性质旋转中心01中心对称图形有一个明显的旋转中心，图形围绕这个中心旋转能够完全重合。

旋转角度02对于中心对称图形，旋转角度可以是任意角度，但旋转后图形不会改变形状和大小。

旋转对称性03中心对称图形在旋转后保持对称性，即旋转前后的图形是全等的。

在中心对称图形中，过图形旋转中心的平行线段长度相等且互相平行。

平行线段平行四边形平行性质的应用平行四边形是中心对称图形的一种，其两条对角线互相平分且相等。

利用中心对称图形的平行性质，可以方便地解决一些几何问题。

030201中心对称图形有一条经过图形旋转中心的对称轴，该轴将图形分为两个完全相同的部分。

对称轴对于中心对称图形，沿对称轴进行对称变换可以得到新的图形，这个新的图形与原图形是全等的。

对称变换利用中心对称图形的对称性质，可以找到解决几何问题的捷径。

对称性质的应用中心对称图形的应用中心对称图形在绘画和雕塑中有着广泛的应用，如旋转对称的图案、对称的花纹等，能够带来视觉上的舒适感和美感。

第十二讲中心对称与图形设计【知识要点】一．轴对称与轴对称图形（复习巩固）：1.轴对称：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，两个图形中的对应点叫做对称点，对应线段叫做对称线段。

2.轴对称图形：如果一个图形沿着一条直线折叠，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线就是它的对称轴。

注意：对称轴是直线而不是线段。

3.轴对称的性质：（1）关于某条直线对称的两个图形是全等形；（2）如果两个图形关于某条直线对称，那么对称轴是对应点连线的垂直平分线；（3）两个图形关于某条直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上；（4）如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称。

二.中心对称与中心对称图形：1.中心对称：把一个图形绕着某一个点旋转180°，如果它能够和另外一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做对称中心，这两个图形中的对应点叫做关于中心的对称点。

2.中心对称图形：在平面内，一个图形绕某个点旋转180°，如果旋转前后的图形互相重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心。

3.中心对称的性质：（1）关于中心对称的两个图形是全等形；（2）在成中心对称的两个图形中，连接对称点的线段都经过对称中心，并且被对称中心平分；（3）成中心对称的两个图形，对应线段平行（或在同一直线上）且相等。

三.轴对称与中心对称的区别与联系：轴对称中心对称有一条对称轴——直线有一个对称中心——点图形沿对称轴对折(翻折180º)后重合图形绕对称中心旋转180 º后重合对称点的连线被对称轴垂直平分对称点连线经过对称中心，且被对称中心平分三.几种常见的轴对称图形和中心对称图形：1.轴对称图形：线段、角、等腰三角形、等边三角形、菱形、矩形、正方形、等腰梯形、圆2.对称轴的条数：角有一条对称轴，即该角的角平分线；等腰三角形有一条对称轴，是底边的垂直平分线；等边三角形有三条对称轴，分别是三边上的垂直平分线；菱形有两条对称轴，分别是两条对角线所在的直线；矩形有两条对称轴分别是两组对边中点的直线；3.中心对称图形：线段、平行四边形、菱形、矩形、正方形、圆4.对称中心：线段的对称中心是线段的中点；平行四边形、菱形、矩形、正方形的对称中心是对角线的交点；圆的对称中心是圆心。

3.3设计中心对称图形导学稿班级姓名一、教学目标：1经历对生活中中心对称图案的欣赏、观察、分析等过程，发展空间观念，增强审美意识。

2、认识中心对称图案在生活中的应用，会设计一些中心对称图案。

二重点：1、在观察、欣赏图案的基础上，会用所学知识分析它们的形成过程。

2、设计中心对称图案。

三难点：分析图案形成过程，设计中心对称图案。

四、教学过程1.用6个全等的正方形可以拼成如下的一些中心对称图案，请用这6个正方形再设计一些中心对称图案2 你能用6个全等的正方形设计既是中心对称，又是轴对称的图案吗？3、由5个全等的正方形组成L形图案，请按照下列要求画图：（1）在图案中添画1个正方形，使它成轴对称图形（2）在图案中添画1个正方形，使它成中心对称图形（3）在图形中改变1个正方形的位置，使它既成中心对称图案又成轴对称图案。

4. 在计算器上按出两位数“69”，这个电子数字可以组成一个中心对称图案。

你还能写出几个能组成中心对称图案的两位数或三位数？5.如图，在正方形ABCD 的中间有一个圆，其圆心是正方形对角线的交点O ，E 是圆上任意一点，请在圆上按逆时针顺次再取三点F 、G 、H ，连结AG 、BH 、CE 、DF ，把正方形中圆外的部分分成形状和大小都相同的四块6. 用四块如图（1）所示的黑白两色正方形瓷砖拼成一个新的正方形，使拼成对称图案，请至少给出三种不同的拼法：①设计既是中心对称图形又是轴对称的图案；②设计是中心对称图形但不是轴对称的图案；③设计不是中心对称图形但是轴对称的图案。

（四）课堂小结 ：通过这节课的学习活动你你对中心对称有哪些认识?3.3设计中心对称图形作业 姓名1．如图，学校的圆形花坛中放有24盆花，构成圆内的正三角形，且三角形的三个顶点都在A(1)圆上，则该花坛构成的图形 ( )A．是轴对称图形，又是中心对称图形B．是轴对称图形，但不是中心对称图形C．是中心对称图形，但不是轴对称图形D．既不是轴对称图形，也不是中心对称图形2．如图，魔术师把4张扑克牌放在桌子上，然后蒙住眼睛，请一位观众上台，把一张牌旋转了180º，魔术师解除蒙具后，看到4张扑克牌如图所示，那么旋转了（）A.方块5B.梅花6C.黑桃7D.红桃9(变化前) (变化后)3.如图，在4×3的网格上，由个数相同的白色方块与黑色方块组成一幅图案，请仿照此图案，在下列网格中分别设计出符合要求的图案（注：①不得与原图案相同；②黑、白方块的个数要相同），（1）设计一个图形，使它既是轴对称图形，又是中心对称图形，请把你所设计的图案在图（1）中表示出来；（2）设计一个图形，使它是轴对称图形，但不是中心对称图形，请把你所设计的图案在图（2）中表示出来；（3）设计一个图形，使它是中心对称图形，但不是轴对称图形，，请把你所设计的图案在图（3）中表示出来M 4.如图,在梯形ABCD 中,AD//BC,E 是CD 的中点,连接AE 并延长交BC 的延长线于点F(1) 图中哪两个图形成中心对称?(2) 梯形ABCD 的面积与图中哪个三角形的面积相等?(3) 若AB=AD+BC,∠B=70°,求∠DAF 的度数5．如图，点O 是边长为2的正方形ABCD 的对称中心，过O 作OM ⊥ON ，交正方形的边于M 、N ，求四边形OMCN 的面积.。