下载文档原格式
隐马尔可夫模型三个基本问题以及相应的算法1. 背景介绍隐马尔可夫模型（Hidden Markov Model, HMM）是一种统计模型，用于描述具有隐藏状态的序列数据。
HMM在很多领域中得到广泛应用，如语音识别、自然语言处理、机器翻译等。
在HMM中，我们关心三个基本问题：评估问题、解码问题和学习问题。
2. 评估问题评估问题是指给定一个HMM模型和观测序列，如何计算观测序列出现的概率。
具体而言，给定一个HMM模型λ=(A,B,π)和一个观测序列O=(o1,o2,...,o T)，我们需要计算P(O|λ)。
前向算法（Forward Algorithm）前向算法是解决评估问题的一种经典方法。
它通过动态规划的方式逐步计算前向概率αt(i)，表示在时刻t处于状态i且观测到o1,o2,...,o t的概率。
具体而言，前向概率可以通过以下递推公式计算：N(i)⋅a ij)⋅b j(o t+1)αt+1(j)=(∑αti=1其中，a ij是从状态i转移到状态j的概率，b j(o t+1)是在状态j观测到o t+1的概率。
最终，观测序列出现的概率可以通过累加最后一个时刻的前向概率得到：N(i)P(O|λ)=∑αTi=1后向算法（Backward Algorithm）后向算法也是解决评估问题的一种常用方法。
它通过动态规划的方式逐步计算后向概率βt(i)，表示在时刻t处于状态i且观测到o t+1,o t+2,...,o T的概率。
具体而言，后向概率可以通过以下递推公式计算：Nβt(i)=∑a ij⋅b j(o t+1)⋅βt+1(j)j=1其中，βT(i)=1。
观测序列出现的概率可以通过将初始时刻的后向概率与初始状态分布相乘得到：P (O|λ)=∑πi Ni=1⋅b i (o 1)⋅β1(i )3. 解码问题解码问题是指给定一个HMM 模型和观测序列，如何确定最可能的隐藏状态序列。
具体而言，给定一个HMM 模型λ=(A,B,π)和一个观测序列O =(o 1,o 2,...,o T )，我们需要找到一个隐藏状态序列I =(i 1,i 2,...,i T )，使得P (I|O,λ)最大。
隐马尔可夫模型维基百科，自由的百科全书跳转到：导航, 搜索隐马尔可夫模型状态变迁图（例子）x—隐含状态y—可观察的输出a—转换概率（transition probabilities）b—输出概率（output probabilities）隐马尔可夫模型（Hidden Markov Model，HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。
其难点是从可观察的参数中确定该过程的隐含参数。
然后利用这些参数来作进一步的分析，例如模式识别。
在正常的马尔可夫模型中，状态对于观察者来说是直接可见的。
这样状态的转换概率便是全部的参数。
而在隐马尔可夫模型中,状态并不是直接可见的，但受状态影响的某些变量则是可见的。
每一个状态在可能输出的符号上都有一概率分布。
因此输出符号的序列能够透露出状态序列的一些信息。
目录[隐藏]∙ 1 马尔可夫模型的演化∙ 2 使用隐马尔可夫模型o 2.1 具体实例o 2.2 隐马尔可夫模型的应用∙ 3 历史∙ 4 参见∙ 5 注解∙ 6 参考书目∙7 外部连接[编辑]马尔可夫模型的演化上边的图示强调了HMM的状态变迁。
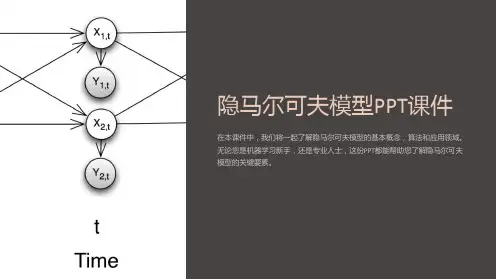
有时，明确的表示出模型的演化也是有用的,我们用x（t1）与x（t2）来表达不同时刻t1和t2的状态。
在这个图中,每一个时间块（x(t), y(t)）都可以向前或向后延伸。
通常，时间的起点被设置为t=0 或t=1.另外,最近的一些方法使用Junction tree算法来解决这三个问题。
[编辑]具体实例假设你有一个住得很远的朋友,他每天跟你打电话告诉你他那天作了什么.你的朋友仅仅对三种活动感兴趣:公园散步,购物以及清理房间.他选择做什么事情只凭天气.你对于他所住的地方的天气情况并不了解,但是你知道总的趋势.在他告诉你每天所做的事情基础上,你想要猜测他所在地的天气情况.你认为天气的运行就像一个马尔可夫链.其有两个状态 "雨"和"晴",但是你无法直接观察它们,也就是说,它们对于你是隐藏的.每天,你的朋友有一定的概率进行下列活动:"散步", "购物", 或 "清理".因为你朋友告诉你他的活动,所以这些活动就是你的观察数据.这整个系统就是一个隐马尔可夫模型HMM.你知道这个地区的总的天气趋势,并且平时知道你朋友会做的事情.也就是说这个隐马尔可夫模型的参数是已知的.你可以用程序语言(Python)写下来:states = ('Rainy', 'Sunny')observations = ('walk', 'shop', 'clean')start_probability = {'Rainy': 0.6, 'Sunny': 0.4}transition_probability = {'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},}emission_probability = {'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},}在这些代码中,start_probability代表了你对于你朋友第一次给你打电话时的天气情况的不确定性(你知道的只是那个地方平均起来下雨多些).在这里,这个特定的概率分布并非平衡的,平衡概率应该接近（在给定变迁概率的情况下）{'Rainy': 0.571, 'Sunny': 0.429}< transition_probability表示基于马尔可夫链模型的天气变迁,在这个例子中,如果今天下雨,那么明天天晴的概率只有30%.代码emission_probability表示了你朋友每天作某件事的概率.如果下雨,有 50% 的概率他在清理房间;如果天晴,则有60%的概率他在外头散步.这个例子在Viterbi算法页上有更多的解释。
隐马尔可夫模型在自然语言处理中的应用在自然语言处理领域，隐马尔可夫模型（Hidden Markov Model）是一种常用的统计模型，它被广泛应用于诸多任务，如语音识别、机器翻译、自动文本分类等。
本文将探讨隐马尔可夫模型在自然语言处理中的应用，并讨论其优势和局限性。
一、隐马尔可夫模型的基本原理隐马尔可夫模型描述了一个由观测序列和状态序列组成的系统。
观测序列是我们可以观察到的现象，而状态序列则是隐藏在观测序列背后的真实状态。
隐马尔可夫模型基于两个基本假设：状态转移和观测独立。
状态转移假设：系统中的状态只与其前一个状态有关，与之前的状态无关。
换句话说，每个状态仅依赖于前一个状态的转移概率。
观测独立假设：观测序列中的每个观测值只依赖于相应状态的概率分布，与其他观测值无关。
通过这两个假设，隐马尔可夫模型可以根据已知观测序列来估计系统中的状态序列，从而进行各种语言处理任务。
二、语音识别中的应用隐马尔可夫模型在语音识别任务中扮演着重要的角色。
语音识别的目标是将连续语音信号转化为文字内容。
隐马尔可夫模型能够帮助解决语音中的特征提取和声学模型训练问题。
在特征提取方面，隐马尔可夫模型可以通过训练一个声学模型，将连续语音信号划分为多个帧。
每个帧通过提取一些声学特征（如梅尔频率倒谱系数）来描述。
然后，通过隐马尔可夫模型来建模每个帧的观测值和相应的语音状态。
在声学模型训练方面，隐马尔可夫模型可以通过使用已有的语音数据集来学习状态转移概率和观测独立概率。
通过最大似然估计等统计方法，可以得到在给定观测序列下状态序列的最优估计。
这个估计可以用于建模不同语音状态之间的转换和观测概率。
三、机器翻译中的应用隐马尔可夫模型在机器翻译任务中也有广泛应用。
机器翻译的目标是将一种语言中的文本转化为另一种语言中的对应文本。
而隐马尔可夫模型可以帮助解决翻译模型训练和解码问题。
在翻译模型训练方面，隐马尔可夫模型可以通过使用双语平行语料库来学习源语言和目标语言之间的状态转移和观测概率。
隐马尔可夫模型(HMM)是一种统计模型，常用于语音识别、自然语言处理等领域。
它主要用来描述隐藏的马尔可夫链，即一种具有未知状态的马尔可夫链。
在语音识别中，HMM被广泛应用于对语音信号进行建模和识别。
下面我将从HMM的基本概念、参数迭代和语音识别应用等方面展开阐述。
1. HMM的基本概念在隐马尔可夫模型中，有三种基本要素：状态、观测值和状态转移概率及观测概率。
状态表示未知的系统状态，它是隐藏的，无法直接观测到。
观测值则是我们可以观测到的数据，比如语音信号中的频谱特征等。
状态转移概率描述了在不同状态之间转移的概率，而观测概率则表示在每个状态下观测到不同观测值的概率分布。
2. HMM参数迭代HMM的参数包括初始状态概率、状态转移概率和观测概率。
在实际应用中，这些参数通常是未知的，需要通过观测数据进行估计。
参数迭代是指通过一定的算法不断更新参数的过程，以使模型更好地拟合观测数据。
常见的参数迭代算法包括Baum-Welch算法和Viterbi算法。
其中，Baum-Welch算法通过最大化似然函数来估计模型的参数，Viterbi算法则用于解码和预测。
3. HMM在语音识别中的应用在语音识别中，HMM被广泛用于建模和识别语音信号。
语音信号被转换成一系列的特征向量，比如MFCC（Mel-Frequency Cepstral Coefficients）特征。
这些特征向量被用来训练HMM模型，学习模型的参数。
在识别阶段，通过Viterbi算法对输入语音进行解码，得到最可能的文本输出。
4. 个人观点和理解从个人角度看，HMM作为一种强大的统计模型，在语音识别领域有着重要的应用。
通过不断迭代参数，HMM能够更好地建模语音信号，提高语音识别的准确性和鲁棒性。
然而，HMM也面临着状态空间爆炸、参数收敛速度慢等问题，需要结合其他模型和算法进行改进和优化。
总结回顾通过本文对隐马尔可夫模型(HMM)的介绍，我们从基本概念、参数迭代和语音识别应用等方面对HMM有了更深入的了解。
