第3章电容式传感器.
- 格式:doc
- 大小:40.00 KB
- 文档页数:18
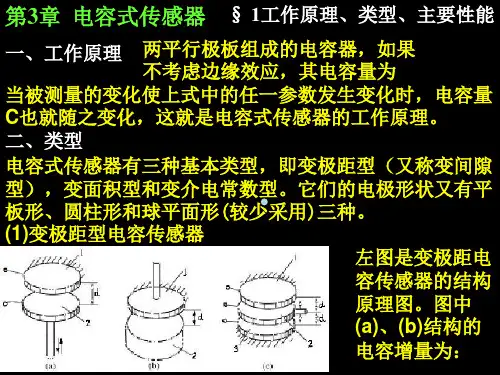


实验八 电容式传感器的位移特性实验一、实验目的:了解电容式传感器结构及其特点。
二、基本原理:利用平板电容C =εS /d 和其它结构的关系式通过相应的结构和测量电路可以选择ε、S 、d 中三个参数中,保持两个参数不变,而只改变其中一个参数,则可以有测谷物干燥度(ε变)测微小位移(变d )和测量液位(变S )等多种电容传感器。
变面积型电容传感器中,平板结构对极距特别敏感,测量精度受到影响,而圆柱形结构受极板径向变化的影响很小,且理论上具有很好的线性关系,(但实际由于边缘效应的影响,会引起极板间的电场分布不均,导致非线性问题仍然存在,且灵敏度下降,但比变极距型好得多。
)成为实际中最常用的结构,其中线位移单组式的电容量C 在忽略边缘效应时为: ()12ln 2r r l C πε= (1) 式中 l ——外圆筒与内圆柱覆盖部分的长度;12r r 、——外圆筒内半径和内圆柱外半径。
当两圆筒相对移动l ∆时,电容变化量C ∆为 ()()()()ll C l l l l C r r r r r r ∆=∆=∆--=∆0121212ln 2ln 2ln 2πεπεπε (2) 于是,可得其静态灵敏度为: ()()()()()121212ln 4/ln 2ln 2r r r r r r g l l l l l l C k πεπεπε=∆⎥⎦⎤⎢⎣⎡∆--∆+=∆∆= (3) 可见灵敏度与,12r r 有关,12r r 与越接近,灵敏度越高,虽然内外极筒原始覆盖长度l 与灵敏度无关,但l 不可太小,否则边缘效应将影响到传感器的线性。
本实验为变面积式电容传感器,采用差动式圆柱形结构,因此可以很好的消除极距变化对测量精度的影响,并且可以减小非线性误差和增加传感器的灵敏度。
三、需用器件与单元:电容传感器、电容传感器实验模板、测微头、数显单元、直流稳压源。
四、实验步骤:1、将电容式传感器装于电容传感器实验模板上,将传感器引线插头插入实验模板的插座中。

第3章 电容式传感器习题1、 简述电容式传感器的工作原理。
2、简述电容式传感器的优点。
3、试计算习题4—2图所示各电容传感元件的总电容表达式。
习题图4-2解:由习题图4-2可见(1) 三个电容串联111d SC ε=, 222d SC ε=, 333d SC ε=则 Sd d d S d S d S d C C C C 3212133123213322113211111εεεεεεεεεεεε++=++=++=串故332211213312321321///εεεεεεεεεεεεd d d Sd d d S C ++=++=串(2)两个电容器并联d SC C C C dSC C C εε222121==+====并(3)柱形电容器()12/ln 2d d L C πε=4、在压力比指示系统中采用差动式变间隙电容传感器和电桥测量电路,如习题图4-3所示。
已知:δ0=0.25mm ;D=38.2mm ;R=Ω;U sr =60V(交流),频率f=400Hz 。
试求: (1)该电容传感器的电压灵敏度K u (V/µm);(2)当电容传感器的动极板位移△δ=10µm 时,输出电压U sc 值。
习题图4-3解:由传感器结构及其测量电路可知 (1)初始电容20214δπεD C C C ===()()pF F 6.40106.401025.04102.381085.81232312=⨯=⨯⨯⨯⨯⨯⨯=----π由于 1200106.4040021211-⨯⨯⨯===ππωfC C X c())k .(R .Ω=>>Ω⨯=1510896则00022δdU C C U U i i ∆=∆=从而得 mV mm V U d U K i u μδ/12.0/12025.0260200==⨯==∆=(2) U 0 = K u Δd=m×10m=5、有一台变间隙非接触式电容测微仪,其传感器的极板半径r=4mm ,假设与被测工件的初始间隙d 0=0.3mm 。



第三章 电容式传感器电容测量技术近几年来有了很大进展,它不但广泛用于位移、振动、角度、加速度等机械量的精密测量,而且,还逐步扩大应用于压力、差压、液面、料面、成分含量等方面的测量。
由于电容式传感器具有一系列突出的优点:如结构简单,体积小,分辨率高,可非接触测量等。
这些优点,随着电子技术的迅速发展,特别是集成电路的出现,将得到进一步的体现。
而它存在的分布电容、非线性等缺点又将不断地得到克服,因此电容式传感器在非电测量和自动检测中得到了广泛的应用。
第一节 电容式传感器的工作原理和结构 一、基本工作原理电容式传感器是一种具有可变参数的电容器。
多数场合下,电容是由两个金属平行板组成并且以空气为介质,如图3—1所示。
由两个平行板组成的电容器的电容量为dAC ε=(3—1)式中ε——电容极板介质的介电常数。
A ——两平行板所覆盖面积; d ——两平行板之间的距离; C ——电容量当被测参数使得式(3—1)中的d 、A 和r ε发生变化时,电容量C 也随之变化。
如果保持其中两个参数不变而仅改变另一个参数,就可把该参数的变化转换为电容量的变化。
因此。
电容量变化的大小与被测参数的大小成比例。
在实际使用中,电容式传感器常以改变平行板间距d 来进行测量,因为这样获得的测量灵敏度高于改变其他参数的电容传感器的灵敏度。
改变平行板间距d 的传感器可以测量微米数量级的位移,而改变面积A 的传感器只适用于测量厘米数量级的位移。
二、变极距型电容式传感器由式(3—1)可知,电容量c 与极板距离d 不是线性关系,而是如图3—2所示的双曲线关系。
若电容器极板距离由初始值do 缩小d ∆,极板距离分别为do 和do-d ∆,其电容量分别为C0和C1,即0d AC ε=(3—2)⎪⎪⎭⎫⎝⎛∆-⎪⎪⎭⎫ ⎝⎛∆+=⎪⎪⎭⎫ ⎝⎛∆-=∆-=2020********d d d d d A d d d Add AC εεε(3—3)当Ad 《Ju 时,1…菩*1,则式(3—3)可以简化为 一W一一这时c1与AJ 近似呈线性关系,所以改变极板距离的电容式传感器注注是设计成Ad 在极小的范围内变化。

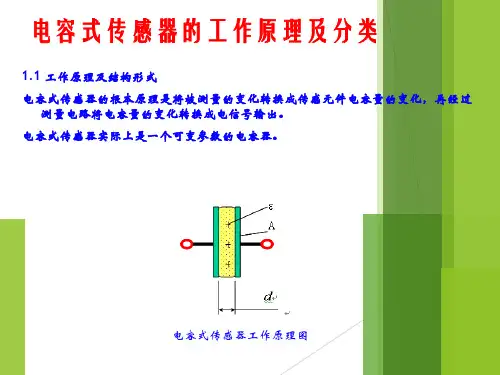


第 3章电容式传感器
3.1 电容式传感器的工作原理
1. 基本工作原理平行板电容器δ
εεδ
εS S C r 0=
=
0ε--真空的介电常数; ((cm
PF
cm F /6. 31/10
94111
0π
πε=
⨯⨯=
;
ε--电容极板间介质的介电常数;
r ε-- 介质的相对介电常数,对于空气, 1=r ε
单位:1法拉(F =106微法(µF =1012皮法(PF 或微微法(µµF 2. 变面积型电容式传感器
δ
εδ
εab S C ==0
(x b C b
x a S C ∆⋅-
=∆-=
=
δ
εδεδ
ε0
x
b C C C ∆⋅=
-=∆δ
ε0
灵敏度:↓
↑=
∆∆↑=
δεb x
C K (与 a 的大小无关
问题:极板间距δ能否很小?不能 3. 变介质介电常数型电容式传感器 (1电容式液面计(液位传感器
h 1—待测液面高度
⎪⎭
⎫⎝⎛=
r R h C ln 2111επ ⎪⎭
⎫⎝⎛-=
⎪⎭
⎫⎝⎛=
r R h h r R h C ln (2ln 22
1222επεπ
(
(ln 2ln 2ln (2ln 2111
2122
11121h f Kh A h r R r R h r R h h r R h C C C =+=⋅⎪⎭⎫⎝⎛-+
⎪⎭
⎫⎝⎛=
⎪⎭
⎫⎝⎛-+
⎪⎭
⎫⎝⎛=
+=εεπεπεπεπ
结论:传感器的电容量 C 与液位高度 h 成正比。
(2测湿(测厚传感器
d S C -=
δε11
d
S
C 22ε=
2
1
21212
121εεδεδεεεd
d S
d
S
d
S d
S
d S
C C C C C +
-=
+
-⋅-=
+=
结论:①若 d 不变, (2εg C =,为介电常数ε的测试传感器,如湿度传感器(粮食、纺织品,木材等 ;
②若2ε不变, (d h C =,可用来测量纸张、绝缘薄膜等厚度的测
厚传感器。
4. 变极板间距型电容式传感器初始电容:δ
εS
C =
假若动极板上移δ∆ δ
δ
δδ
δ
εδ
δε∆-
=∆-
⋅=
∆-=
11110
C S S C
若
1<<∆δ
δ
,上式可按级数展开
⎥⎥
⎦
⎤⎢⎢⎣⎡⋅⋅⋅+⎪⎭⎫
⎝⎛∆+⎪⎭⎫⎝⎛∆+∆+=3
201δδδδδδC C
电容增量为⎥⎥
⎦⎤⎢⎢⎣⎡⋅⋅⋅+⎪⎭⎫⎝⎛∆+⎪⎭⎫⎝⎛∆+∆=-=∆3 200
δδδδδδC C C C
电容量的相对变化⎥⎥⎦⎤⎢⎢⎣⎡⋅⋅⋅+⎪⎭⎫⎝⎛∆+∆+∆=∆2
1δδδδδδC C
同理:若动极板下移δ∆δ
δ
δδ
δ
εδ
δε∆+
=∆+
⋅=
∆+=
11110
C S S C
⎥⎥⎦
⎤⎢⎢⎣⎡⋅⋅⋅-⎪⎭⎫
⎝⎛∆+∆-∆=∆2
1δδδδδδC C
略去高次项
δ
δ
∆≈∆0
C C (近似线性关系灵敏度为
↓
=
∆∆↑=
2
δ
εδ
S C K
非线性误差为
%100%1002
00
⨯∆=
⨯∆⎪⎭⎫⎝⎛∆≈
⎪⎪⎭⎫⎝⎛∆⎪⎪⎭⎫⎝⎛∆-⎪⎪⎭⎫⎝⎛∆=δ
δ
δ
δ
δδ理想
理想
实际 C C C C C C r
结论:
①欲提高灵敏度,应减少起始间隙δ,但受电容器击穿电压的限制; ②为了保证一定的线性度, 即减小非线性误差, 应限制动极板的相对位量。
③为了改善非线性,应采用差动式结构。
5.差动式电容传感器
假若动极板上移:
⎥⎥
⎦
⎤⎢⎢⎣⎡⋅⋅⋅+⎪⎭⎫
⎝⎛∆+⎪⎭⎫⎝⎛∆+∆+=3
2011δδδδδδC C
⎥⎥
⎦
⎤⎢⎢⎣⎡⋅⋅⋅+⎪⎭⎫⎝⎛∆-⎪⎭⎫⎝⎛∆+∆-=3 202
1δδδδδδC C
⎥⎥
⎦
⎤⎢⎢⎣⎡⋅⋅⋅+⎪⎭⎫⎝⎛∆+⎪⎭⎫⎝⎛∆+∆=-=∆5 302
1222δδδδδδC C C C
⎥⎥⎦
⎤⎢⎢⎣⎡⋅⋅⋅+⎪⎭⎫
⎝⎛∆+⎪⎭⎫
⎝⎛∆+∆=∆4
20
12δδδδδδC C 忽略高次项,则δδ
∆≈∆2
0C C
灵敏度为 2
2δ
εδ
S
C K =
∆∆=
非线性误差为
%100%100222
3
00
⨯⎪⎭
⎫
⎝⎛∆=⨯∆⎪⎭⎫⎝⎛∆≈
⎪⎪⎭⎫⎝⎛∆⎪⎪⎭⎫⎝⎛∆-⎪⎪⎭⎫⎝⎛∆=
δδδ
δ
δδ理想
理想
实际 C C C C C C r
结论:差动式电容传感器比单一电容传感器灵敏度提高一倍, 而且非线性误差大大降低。
3.2 电容式传感器的等效电路
1. 等效电路
Rp —并联损耗电阻
包括了电极间直流漏电阻和气隙中介质损耗; Rs —串联损耗电阻
包括引线电阻、金属接线柱电阻和电容极板电阻; L —表示传感器各连线端间总电感。
⎪
⎪⎭
⎫⎝⎛-+-⎪⎪⎭
⎫
⎝
⎛++=L C R C R j C R R R Z p p
p p S C
ωωωω22222221
1
因为 Rp 很大,
E
S S S C C j R LC
C j
R C
LC
j
R Z ωωωωω111
12
2
+
=-+
=--≈
等效电容: 2
02
11⎪⎪⎭
⎫
⎝⎛-=
-=
f f C LC
C C E ω
LC
f π
210=
为电路谐振频率,应选择电源频率 0f f <。
2. 高阻抗、小功率
由于电容式传感器的几何尺寸较小,一般电容量 C 很小,容抗C
X
C
ω1
=
很大,视在功率(C U UI P C ω2==很小。
3.3 电容式传感器的测量电路
1. 电桥测量线路
(1交流不平衡电桥
变压器桥路框图如图所示
Z f 为放大器的输入阻抗
∞
→f
Z
E E E ==2
1
感测技术讲义(2)交流平衡电桥以飞机上一种电容式油量表为例(自动平衡电桥电路)已知:油箱中无油时,起始电容,电刷位于 a 点,即
R=0,E=0,此时电桥平衡,电桥输出电压为 0,电机不转动,
0 ,仪表指针指在零位上。
初始电桥平衡条件:当油量
液位升高 h,电桥平衡被破坏,电桥产生输出电压,电机转动,带动电刷、仪表指针移动,使电桥重新恢复平衡,此时,电刷、仪表指针停止移动。
已知: E 所以:
1K 2h 2. 差动脉冲宽度调制电路研究输出方波脉冲宽度与 C1 和 C2 的关系 - 26 -
感测技术讲义工作原理:设电源接通时,(高电平)(低电平)A 点经过 R1 对 C1 ,充电,至,A1 产生一脉冲,使触发器翻转,,,此时,M 点通过 D1 迅速放电至 0;同时,B 点经过 R2 对C2 充电,至,A2 产生一脉冲,使触发器翻转,,
(1)若则:
A、B 点的平均输出电压:
(2)若,,、B 点的平均输出电压: - 27 -
感测技术讲义
同理:
电容式传感器应用举例(P51) 1. 2. 3. 4. 5. 运算型电容测厚传感器频率变换型电容测厚传感器电容传感器在真空注油机自动控制中的作用电容式压力传感器高分子电容式湿度传感器 - 28 -。