当前位置：文档之家 › 单项式与多项式相乘PPT

单项式与多项式相乘PPT

  • 格式：pptx
  • 大小：434.63 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

单项式与多项式相乘课件(共17张PPT)

单项式与多项式相乘课件(共17张PPT)

上面的等式提供了单项式与多项式相 乘的方法.
p pa
pb
pc
a
b
c
14.1.4.2 单项式与多项式相乘 根据乘法的分配律
p (a + b+ c)
归纳总结
pa + pb + pc
单项式乘多项式的乘法法则 单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得 的积相加.
14.1.4.2 单项式与多项式相乘
解：(-2x)2·(3x2 - mx - 6) - 3x3 + x2 = 4x2·(3x2 - mx - 6) - 3x3 + x2 ＝12x4－4mx3－24x2 - 3x3 + x2 ＝12x4 - (4m + 3)x3 - 23x2.
∵原式不含x3项，所以4m + 3 = 0. ∴m = 3 .
随堂练习
1. 如果一个三角形的底边长为 2x2y + xy - y2，高为 6xy，则这个三角形 的面积是 ( A ) A. 6x3y2 + 3x2y2 - 3xy3 B. 6x3y2 + 3xy - 3xy3 C. 6x3y2 + 3x2y2 - y2 D. 6x3y + 3x2y2
14.1.4.2 单项式与多项式相乘
14.1.4.2 单项式与多项式相乘
例3 如图，一块长方形基地用来种植A、B、C 3种不同的蔬菜，求这块
地的面积. 解：由图得，
3a+2b
2a-b
4a[(3a+2b)+(2a-b)]
＝4a(5a+b) ＝4a·5a+4a·b =20a2+4ab.
B
4a

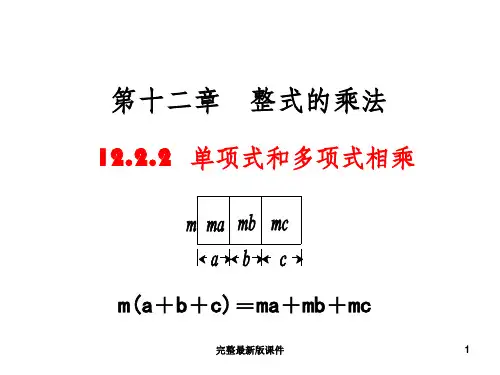
6.整式的乘法——单项式与多项式相乘PPT课件(北京课改版)

6.整式的乘法——单项式与多项式相乘PPT课件(北京课改版)

面积可表示为___m__(_a_+_b_)___.
面积可表示为___m__a_+__m__b___.
m(a+b) ＝ ma + mb
n
x
y
z
(1) 如果把它看成一个大长方形，
(2) 如果把它看成三个大长方形，
那么它的边长为__x_+__y_+_z_和__n___,
那么它的每个面积为_n__x__n__y___n_z__,
面积可表示为__n_(_x_+_y_+_z_)___.
面积可表示为___n_x_+_n_y_+_n__z__.
n(x+y+z) ＝ nx + ny + nz
1.本节课我们学到了哪些知识？ 2.在运用这些知识进行计算时，需要注意什么？ 3.在得出法则过程中，我们采用了什么思想和方法？
1、如何进行单项式与单项式的乘法运算？ （系数×系数）×（同字母幂相乘）×单独的幂
2、抢答：
（1） 2a 5a3 =10a4
（3）1 x (4x2 y) =-2x3y 2
（2）2a2 ab4 3a =6a4b4 （4）(2107 ) (3103) =6×1010
m(a+b)= ma + mb
n(x+y+z)= nx + ny + nz
单项式与多项式相乘的法则:
单项式与多项式相乘,就是用单项式分别去乘多项式 的每一项，再把所得的积相加.把它看成一个大长方形，
(2) 如果把它看成两个大长方形，
那么它的长和宽为___a__+_b_和__m____, 那么它的每个面积为__m__a___m__b____,

1.4.2单项式与多项式相乘 课件

1.4.2单项式与多项式相乘 课件

x米
方法1：先表示出画面的长与宽，再去求画面的面积.
长：nx - 1 x
4
宽： x 面积: （nx - 1 x) xm2
4
方法2：用纸的面积减去空白处的面积，再去求画面的面积.
纸的面积： nx2m2
空白处的面积：
1 4
x2m2
画面的面积:（nx2 - 1 x2 )m2
4
【思考】通过观察上面表示面积的两个式子，你发现了什么？
相乘,其余字母 连同它的指数不变，作为积的因式 .
2、多项式：若干个单项式的和组成的式子. 多项式的项：多项式中的每个单项式.
3、指出多项式
新知讲解
合作学习
才艺展示中，小颖也作了一幅画，所用纸的大小如
图所示，她在纸的左、右两边各留了 1 xm 的空白，这
8
幅画的画面面积是多少？
1 xm 8
1 xm 8
结果是多少？
解：设这个多项式为A，则
A＋(－3x2)＝x2－2x＋1， A＝4x2－2x＋1. 所以A·(－3x2)＝(4x2－2x＋1)(－3x2)
＝－12x4＋6x3－3x2.
综合拓展题
3. 一条防洪堤坝，其横断面是梯形，上底宽a米， 下底宽(a＋2b)米，坝高 1 a米．
2
(1)求防洪堤坝的横断面面积；
原式＝－20×4－9×2＝－98.
方法总结：在做乘法计算时，一定要注意单项式 的符号和多项式中每一项的符号，不要搞错．
归纳概念
注意： （1）计算时，要注意符号问题； （2）不要出现漏乘现象； （3）运算顺序：先乘方，再乘除，最后加减； （4）对于混合运算，注意最后应合并同类项.
课堂练习
必做题
1.计算(－3xy2)·(2y2－xyz＋1)的结果是( B ) A．－3xy4＋3x2y3＋3xy2 B．－6xy4＋3x2y3z－3xy2 C．－6xy4－3x2y3z－3xy2 D．－6xy4＋3x2y2z

单项式与多项式相乘通用课件

单项式与多项式相乘通用课件
ONE
KEEP VIEW
单项式与多项式相乘 通用课件目 录PART源自01单项式与多项式相乘的定 义
单项式的定义
定义
单项式是只包含一个项的代数式，可以表示为数字、字母或数字与字母的积。
示例
a、3x、4xy^2等都是单项式。
多项式的定义
定义
多项式是由有限个单项式通过加 法或减法连接而成的代数式。
PART 04
单项式与多项式相乘的注 意事项
幂次相加时需要注意的问题
01
幂次相加时，需要注意同底数的 幂次相加时，底数不变，指数相加。
02
例如， $2x^3 times 5x^4 = 10x^{3+4} = 10x^7$。
系数相乘时需要注意的问题
系数相乘时，需要注意将两个单项式 的系数相乘，即 $2x^3 times 5x^4 = 10x^7$。
多个单项式与单一多项式相乘
总结词：逐项相乘
详细描述：当有多个单项式需要与一个多项式相乘时，可以分别将每个单项式的系数与多项式的每一项相乘，然后合并同类项。
单一单项式与多个多项式相乘
总结词：连续相乘
详细描述：当一个单项式需要与多个多项式相乘时，可以先将单项式与第一个多项式的每一项相乘， 然后再将结果与第二个多项式的每一项相乘，以此类推，直到所有多项式都被乘完，最后合并同类项。
01
02
03
力学分析
在分析力学问题时，单项 式与多项式相乘可以用来 表示物体的运动状态和受 力情况。
电磁学
在电磁学中，单项式与多 项式相乘可以用来表示电 磁场的变化规律和分布情 况。
光学
在光学中，单项式与多项 式相乘可以用来表示光的 波动性质和传播规律。
在工程中的实际应用

《单项式乘多项式》课件

《单项式乘多项式》课件
《单项式乘多项式》ppt课件
• 引言 • 单项式乘多项式的定义与性质 • 单项式乘多项式的计算方法 • 单项式乘多项式的应用 • 练习与巩固 • 总结与回顾
01
引言
主题介绍
01
02
03
单项式乘多项式
理解单项式与多项式相乘 的规则和步骤。
数学表达式的简化
掌握如何将单项式与多项 式相乘后的结果进行简化 。
。
计算步骤与示例
列出多项式中的每一项，并确定单项 式的系数、字母因数和常数因数。
将相乘的结果按多项式的排列顺序组 合，得到最终的乘积。
将单项式的系数、字母因数和常数因 数分别与多项式的每一项相乘。
示例：计算2x^2y(x+3y)，首先将 2x^2y分别与x和3y相乘，得到 2x^3y和6x^2y^2，然后将两项相加 得到2x^3y + 6x^2y^2。
实际应用
了解单项式乘多项式在日 常生活和科学计算中的应 用。
学习目标
01
02
03
04
掌握单项式与多项式相乘的基 本规则。
能够正确计算单项式与多项式 相乘的结果。
理解简化数学表达式的意义和 方法。
能够在实际问题中运用单项式 乘多项式的知识。
02
单项式乘多项式的定义与性质
单项式的定义与性质
定义
单项式是只包含一个项的代数式 ，通常表示为字母、数字和字母 的积。
ห้องสมุดไป่ตู้
通过练习和巩固，提 高了自己的计算能力 和数学思维能力。
理解了单项式乘多项 式的实际应用，如代 数式求值、解方程等 。
下节课预告
主题
《多项式乘多项式》
内容提要
掌握多项式乘多项式的计算方法，理解其实际应 用，如代数式求值、解方程等。

单项式与多项式相乘公开课课件

单项式与多项式相乘公开课课件

乘法分配律的运用
乘法分配律是数学中的一个基本定律，它指出一个数乘以 两个数的和等于这个数分别乘以这两个数再求和。在单项 式与多项式相乘时，乘法分配律是非常重要的。
例如，单项式$a^3$与多项式$b + c$相乘时，可以运用 乘法分配律进行计算：$(a^3)(b+c) = a^3b + a^3c$。 这样可以简化计算过程，提高计算效率。
单项式与多项式相乘公开课课件
contents
目录
• 单项式与多项式简介 • 单项式与多项式相乘的法则 • 单项式与多项式相乘的运算实例 • 单项式与多项式相乘的注意事项 • 习题与解答
01
单项式与多项式简介
单项式的定义与性质
定义
单项式是只包含一个项的代数式 ，通常表示为数字、字母的积。
性质
单项式具有加法封闭性、乘法交 换律和结合律等基本性质。
单项式的几何意义
在数轴上，单项式可以表示一个点或一个单位长度。例如，$3x$表示在x轴上， 每移动一个单位长度，坐标增加3。
多项式的几何意义
多项式可以表示一条曲线或曲面。例如，$y = x^2$表示一个开口向上的抛物线 。
02
单项式与多项式相乘的法则
单项式乘以多项式的法则
单项式乘以多项式的运算法则，是将单项式中的每一个因子 与多项式中的每一个项分别相乘，然后将所得的积相加。
多项式的定义与性质
定义
多项式是由有限个单项式通过加法运 算组成的代数式，表示为$P(x) = a_n x^n + a_{n-1} x^{n-1} + cdots + a_1换律 和结合律等基本性质，还具有分配律 和幂的运算法则等特殊性质。
单项式与多项式的几何意义

单项式乘以多项式课件


乘法运算的顺序
单项式乘以多 项式的计算方
法
乘法运算的顺 序：从左到右，
先乘后加
计算示例： 3x^2 * 2x + 1 = 6x^3 + 3x^2 + 3x +
1
注意事项：注 意符号和系数 的变化，以及
幂次的变化
计算步骤的演示
确定单项式和多项式的系数和次数 将单项式的系数与多项式的每一项的系数相乘 将单项式的次数与多项式的每一项的次数相加 合并同类项，得到结果
基础题：单项 式乘以多项式
的基本运算
中等题：涉及 单项式乘以多 项式的变形和
化简
提高题：涉及 单项式乘以多 项式的综合应
用和拓展
挑战题：涉及 单项式乘以多 项式的创新思 维和解题技巧
练习题的答案及解析
● 单项式乘以多项式：x^2y+xy^2=x^2y+xy^2 ● 单项式乘以多项式：2x^2y+3xy^2=2x^2y+3xy^2 ● 单项式乘以多项式：-x^2y-xy^2=-x^2y-xy^2 ● 单项式乘以多项式：2x^2y-3xy^2=2x^2y-3xy^2 ● 单项式乘以多项式：-2x^2y+3xy^2=-2x^2y+3xy^2 ● 单项式乘以多项式：-2x^2y-3xy^2=-2x^2y-3xy^2 ● 单项式乘以多项式：2x^2y+3xy^2=2x^2y+3xy^2 ● 单项式乘以多项式：-2x^2y-3xy^2=-2x^2y-3xy^2 ● 单项式乘以多项式：-2x^2y+3xy^2=-2x^2y+3xy^2 ● 单项式乘以多项式：2x^2y-3xy^2=2x^2y-3xy^2
单项式乘以多项式：(x + 1) * (x^2 - 2x + 1) =?

单项式乘以多项式(课件)PPT

③再把所得的积相加.
四点注意：
1. 计算时,要注意符号问题,多项式中每一项都包括它前 面的符号,单项式分别与多项式的每一项相乘时，同号相 乘得正，异号相乘得负。 2.不要出现漏乘现象。 3.运算要有顺序：先乘方，再乘除，最后加减。 4.对于混合运算，注意最后应合并同类项。
2.解：原式=
x
2
x 2 x 2 x 6 x 15x
2
2
2
3 x 16x
课时小结：
1、单项式与多项式相乘的实质是利用分配律把单项式 乘以多项式转化为单项式乘法 2.单项式与多项式相乘时，分三个阶段： ①按分配律把乘积写成单项式与单项式乘积的代数和的形式；
②按照单项式的乘法法则运算。
单项式乘以多项式法则：
单项式与多项式相乘,就是用单项 式去乘多项式的每一项,再把所得 的积相加.
m(a+b+c) =ma+mb+mc
例5
(1)
计算:
4 x 3x 12源自2 2 1 (2) a b 2ab ab 3 2
解：（1）原式= 4 x 3 x 4 x 1
2 2
4 3x x 4 x
2 2

12 x 4 x
3
2
2 1 2 1 （2）原式= 3 a b 2 ab 2ab 2 ab
1 2 3 2 2 3a b a b
巩固练习： １.计算：(1)3a(5a-2b) (2)(x-3y)·(-6x) 2.化简 x(x-1)+2x(x+1)-3x(2x-5) 解 (1)３a(5a-2b) (2)(x-3y)·(-6x) =3a·5a+3a·(-2b) =x·(-6x)+(-3y)·(-6x) =15a-6ab =-6x+18xy

单项式乘以多项式课件


02
单项式乘以多项式的运算规则
乘法分配律的应用
乘法分配律
a(b+c) = ab + ac
举例
2(x+y) = 2x + 2y
应用
将单项式与多项式的每一项分别相乘，再将结果 相加。
乘法结合律的应用
乘法结合律
(ab)c = a(bc)
举例
(2x)(3y) = 6xy
应用
改变乘法运算的顺序，不影响结果。
工程设计
在物理和工程中，线性代数方程组经 常出现，单项式乘以多项式可以用于 求解这些方程组。
在工程设计中，单项式乘以多项式可 以用于计算和分析各种参数，如结构 强度、流体动力学等。
控制系统分析
在控制系统分析中，单项式乘以多项 式可以用于描述和分析系统的动态行 为。
05
单项式乘以多项式的注意事项 与易错点
数学建模中的应用
建立数学模型
在数学建模过程中，单项 式乘以多项式可以用于构 建和表示复杂的数学模型 。
参数估计
在模型中，单项式乘以多 项式可以用于估计未知参 数，从而更好地拟合数据 。
对模型进行预测和优 化，从而更好地解决实际 问题。
物理和工程中的应用
线性代数方程组
运算次序的注意事项
01
运算次序是先乘除后加减，单项 式乘以多项式时，应先进行单项 式与多项式中每一项的乘法运算 ，再将结果相加。
02
运算次序的错误可能导致结果不 正确，因此需要特别注意。
乘法分配律的易错点
乘法分配律是单项式乘以多项式的关 键，但也是易错点。学生需要理解并 掌握乘法分配律的运用，避免在计算 过程中出现错误。
乘法交换律的应用
乘法交换律

单项式与多项式相乘ppt

单 项 式 与 多 项 式 相 乘
3、练一练： (1)

5x(3x 4)
(2)
(5a2-4a+1) (- 3a)
1 (3) (a)( 2ab) 3a(ab b 1) 3
(4)
x(x2+3)+x2 ( x-3)-3x(x2-x-1)
单 项 3、长方体长为a+1,宽为a，高为3, 式 与 这个长方体的体积是多少？表面积 多 呢？ 项 a （单位：m） 式 3 相 乘
n(a+b+c) ？ 猜一猜 n(a+b+c)=
探究验证
单 项 问题： 一个施工队修筑一条路面宽为n米的公路， 式 与 第一天修筑a米长，第二天修筑b米长,第三天 多 修筑c米长，三天共修筑路面的面积是多少？ 项 式 相 乘
单n 项 式 a c b 与 n(a+b+c) 算法一： 从整体上看 多 项 算法二：从部分上看 na+nb+nc 式 相 因此，有 乘 n(a+b+c) =na+nb+nc
a+1
学以致用
单 课堂小结 项 这节课你有什么收获？ 式 与 多 项 式 相 乘
单 项 式 作业布置： 与 习题8.2 第4，5题 多 同步练习 项 式 相 乘
单项式与多项式相乘
程辛贤
类比引入
计算： 1：原式＝
1 1 1 (12) (12) (12) ( ) 2 3 4 6 (4) 3 7
类比引入
1 1 1 12 ( ) 2 3 4
如果我把上式中的数字全部换成字母呢？
第一天
第二天
第三天
单 项 式 与 多 项 式 相 乘
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

随堂测试
1 x4 y2 21x4 y3 2 1 x4 y2 21x4 y3 2
随堂测试
随堂测试
40
LOGO
第十四章 整式的乘法与因式分解
感谢各位的仔细聆听
人教版 数学（初中） （八年级 上）
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
运算结果
18x5-3x2y
8x2y132xx3yy3-9x4y2
12a3b-4a2bc8a2bd
6x2y39a24xb42y-43a4b4c2
观察运算结果你发现了什么？
单项式乘以多项式的结果是多项式，积的项数与原多项式的项数相同
单项式乘以多项式注意事项 1.单项式乘多项式的结果是多项式，积的项数与原多解
14.1.4 单项式与多项式相乘
人教版 数学（初中） （八年级 上）
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
主讲人：XXXX
时间：2020.4.4
前言
学习目标
1、探索并了解单项式乘以多项式的法则。 2、灵活运用单项式乘以多项式的法则进行运算。
重点难点
重点：单项式乘以多项式的法则运用。 难点：单项式乘以多项式法则的推导。
单项式知识点回顾
单项式概念：由数字与字母、字母与字母的乘积组成的式子。 单项式系数：单项式中的数字因数。 单项式次数：单项式中所有字母的指数的和。
10
方法二：两次加宽之后现有绿地变为由三个长方形组成
的区域
5
8
3
S=S1+S2+S3=10×5+10×8+10×3 =50+80+30=160 ㎡ ②
16
情景思考
为了扩大绿地面积，要把街心花园的一块长为p米，宽为a米的长方形绿地，向两边分 别加宽b米和c米，求扩大后的绿地面积？
p
a
b
c
a+b+c
方法一：加宽之后的原宽变为（a+b+c）米 即现有绿地变成一个长为（a+b+c）米，宽p为米的长方形 S=p×(a+b+c)=p(a+b+c)㎡ ①
方法二：两次加宽之后现有绿地变为由三个长方形组成 的区域
S=S1+S2+S3=pa+pb+pc ㎡ ②
情景思考
为了扩大绿地面积，要把街心花园的一块长为p米，宽为a米的长方形绿地，向两边分 别加宽b米和c米，求扩大后的绿地面积？
p
a
b
c
a+b+c
由于① ②表示同一个数量，所以 p(a+b+c)= pa+pb+pc
主讲人：XXXX
时间：2020.4.4
2.单项式分别与多项式的每一项相乘时，要注意积的各项符号。 （同号相乘得正，异号相乘得负）
3.不要出现漏乘现象，运算要有顺序。
随堂测试
1．若ab2=-6，则-ab(a2b5-ab3-b)的值为__2_4_6_____．
【详解】 原式=-a3b6+a2b4+ab2=-（ab2）3+（ab2） 2+ab2， 当ab2=-6时， 原式=-（-6）3+（-6）2-6=216+36-6=246
多项式概念：由几个单项式的和组成的式子。 多项式的项：每个单项式。 多项式的常数项：不含字母的项。 多项式次数：多项式里次数最高项的次数。
情景思考
为了扩大绿地面积，要把街心花园的一块长为10米，宽为5米的长方形绿地，向两边分 别加宽8米和3米，求扩大后的绿地面积？
方法一：加宽之后的原宽变为（5+8+3）=16米 即现有绿地变成一个长为16米，宽为10米的长方形 S=10×(5+8+3)=160㎡ ①
根据乘法分配律也可得到上述结果
p(a+b+c)= pa+pb+pc
单项式乘以多项式法则
单项式与多项式相乘，就是用单项式乘多项式的每一项，再把所得 的积相加。
思路： 单 × 多 分配律
单×单+单×单+….
练一练
练一练
试一试
单项式×多项式
3x2·(6x3 -y) 4y·(2x2-3xy2) (-3x2y) ·(-x+3x2y) (-4a2b) ·(-3a+c+2d) (3y-x2y2)·2x2y2 (3a3b)·(3ab-ab3c2)