调节变量和中介变量模型举例

调节变量和中介变量

调节变量和中介变量
自变量自变量
中介变量调节变量
因变量因变量
280 articles
76 (27%) tested for mediation
99 (35%) 19 tested for
moderation
mentioned the moderator implied a mediator
. Incidence of tests of mediation and moderation in the Journal of Applied Psychology (volumes 84-86).
Job
Job
Sat
SatSalຫໍສະໝຸດ rySalary调节变量亦即交互作用
在模型中有特殊的表达方法 Mod
X1
Y
如何检验调节效应：
取决于变量的类型如果自变量是二分变量，调节变量也是二分
变量
2x2 ANOVA
二分变量的调节效应
例:奖励食物数量影响动物的作业水平,内驱力是调节变量
依次检验方法的局限
1. 总体作用显著并不是中介作用显著的必要条件；我们只要直接检验间接作用即可发现是否有中介作用。研究者按照Baron和Kenny因果步骤，会因为总体作用c不显著而停止余下的检验，可能错失发现间接作用显著的机会
2. Baron和Kenny的方法需要a和b都要显著，而直接检验间接作用的中介分析（比如Sobel检验）却只需a和 b的乘积显著即可。显然，拒绝两个虚无假设要比拒绝一个要困难。
测量间接效应
间接效应即中介作用的大小
完全中介或部分中介间接效应=(c - c') 理论上, c - c' = a*b

调节变量和中介变量模型举例

调节变量和中介变量模型举例
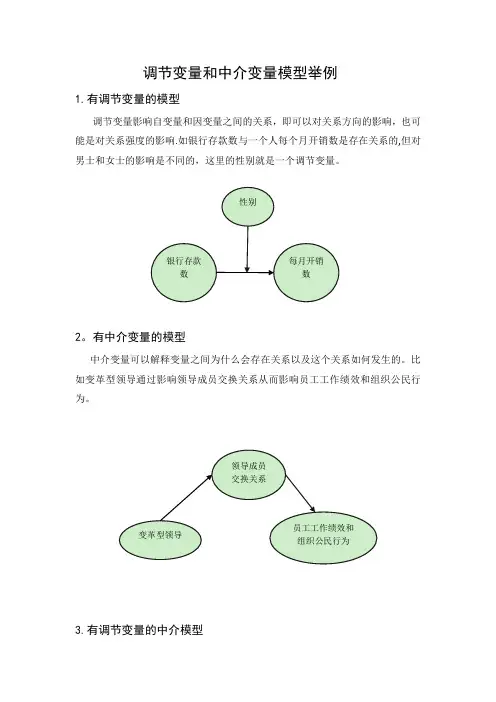
1.有调节变量的模型
调节变量影响自变量和因变量之间的关系，即可以对关系方向的影响，也可能是对关系强度的影响.如银行存款数与一个人每个月开销数是存在关系的,但对男士和女士的影响是不同的，这里的性别就是一个调节变量。

2。

有中介变量的模型
中介变量可以解释变量之间为什么会存在关系以及这个关系如何发生的。

比如变革型领导通过影响领导成员交换关系从而影响员工工作绩效和组织公民行为。

3.有调节变量的中介模型
在很多的模型中，可能既有中介变量又有调节变量，如良好的校园氛围会影响一个人的学业成就，但是校园氛围是通过学校依恋这一中介变量对学业成就进行影响，在这个过程中，学生自控能力的差别会影响这种关系，所以学生自控能力是这个模型里的调节变量.。

Mplus：中介模型与调节模型

中介调节模型基础
常见模型示例（二）
e1
1
X1
Y1
1
e1
X1
X2
1
e1
X2
Y2
非递归模型一
1
e2
X4
非递归模型二
X3
1
e1
中介调节模型基础
常见模型示例（三）
Y1
Y2 自回归模型
Y3
Y4
MODEL：y2 on y1； y3 on y4； x4 on y3 ； MODEL：y2 on y1 w1； y3 on y2 w2； y4 on y3 w3； w2 on y1 w1； w3 on y2 w2； w4 on y3 w3； w1 with y1；

如果变量Y与变量X的关系是变量M的函数，称M为调节变量。就是说，Y与X 的关系收到第三个变量M的影响，这种有调节变量的模型一般可以用下图表示： M
X

Y
e
Y=f(X，M)+e

调节变量可以是定性的（如性别、种族、学校所在地等），也可以是定量的（如年龄、受教育年限、刺激次数等），它影响自变量和因变量之间关系的方向（正或负）和强弱。例如：
c`=0.05*
张晓等 (2009) 《家庭收入与儿童早期的社会能力：中介效应与调节效应》
中介调节模型基础

考虑自变量X对因变量Y的影响，如果X通过影响变量M来影响Y，则称M为中介变量。例如：
−
上司的归因研究：下属的表现→上司对下属表现的归因→上司对下属表现的反应，其中，“上司对下属表现的归因”为中介变量。 X
中介调节模型基础

最简单常用的调节模型，即假设Y与X之间有如下关系： Y=aX+bM+cXM+e

有调节的中介效应模型方程

有调节的中介效应模型方程有调节的中介效应模型是社会科学研究中常用的方法，用于分析一个变量对两个其他变量之间关系的调节作用。

该模型可以帮助研究者深入理解变量之间的复杂关系，并揭示其背后的机制。

本文将介绍有调节的中介效应模型的基本原理和应用，并通过一个具体案例来解释该模型的使用方法和结果解读。

有调节的中介效应模型的基本方程可以表示为：Y = a + b1*X + b2*M + b3*X*M + e其中，Y代表因变量，X代表自变量，M代表中介变量，a代表常数项，b1、b2、b3代表回归系数，e代表误差项。

该模型通过回归分析来估计各个变量之间的关系，并通过系数b2和b3来判断中介和调节效应的存在与程度。

在实际应用中，有调节的中介效应模型可以帮助研究者回答以下问题：自变量对因变量的影响是否通过中介变量实现？中介变量是否受到调节变量的影响？调节变量对自变量与中介变量之间关系的影响程度如何？通过分析这些问题，研究者可以深入了解变量之间的关系，并为实际问题的解决提供有力支持。

为了更好地理解有调节的中介效应模型，我们以一个假设情境为例进行解释。

假设我们研究了某公司员工的工作满意度（Y）、工作压力（X）、以及工作支持（M）之间的关系。

我们想要探究工作支持在工作满意度和工作压力之间的中介作用，并考察工作压力对这一中介效应的调节作用。

我们进行回归分析，将工作满意度作为因变量，工作压力作为自变量，工作支持作为中介变量。

通过回归分析，我们可以得到自变量对因变量的直接效应系数b1，以及中介变量对因变量的效应系数b2。

如果b1的显著性检验结果为正且显著，说明工作压力对工作满意度存在直接影响；如果b2的显著性检验结果为正且显著，说明工作支持对工作满意度存在中介效应。

接下来，我们引入调节变量工作压力对中介变量工作支持的影响进行分析。

我们将工作压力和工作支持作为自变量，工作满意度作为因变量，进行回归分析。

通过回归分析，我们可以得到工作压力对工作支持的直接效应系数b3。

中介变量和调节变量

例如：
父亲的社会经济地位——儿子的教育程度——儿子的社会经济地位（Duncan, Featherman & Duncan, 1972）
中介变量：儿子的教育程度
下属的表现——上司对下属表现的归因——上司对下属表现的反应（James & Brett，1984）
中介变量：上司对下属表现的归因
效应之间的关系：c=c’+ab
2. 广义乘积指标（GAPI）方法（ Wall & Amemiya, 2001) 3. 无约束方法（Marsh, Wen & Hau, 2004)
拟极大似然估计（QML）方法(Klein & Muthen, 2002)
2 中介变量和中介效应
2.1 中介变量的定义考虑自变量X对因变量Y的影响，如果X通过影响变量M来影响Y，则称M为中介变量。（Judd & Kenny，1981； Baron & Kenny, 1986)
第三者：老师的管教方式（U）老师对学生的喜欢程度（W）
5.1 教师喜欢程度是调节变量还是中介变量
调节效应分析
5.1 教师喜欢程度是调节变量还是中介变量
中介效应分析
5.2 管教方式是调节变量还是中介变量
调节效应分析
5.2 管教方式是调节变量还是中介变量
中介效应分析
Sobel 检验
化潜为显（均值或因子得分）两步最小二乘回归（Bollen & Paxton, 1998) 分组线性结构方程分析（如Bagozzi & Yi ，
1989 ； Joreskog, 1971）
带潜变量乘积项的结构方程分析
1. 参数非线性约束方法（Kenny & Judd, 1984; Joreskog & Yang , 1996; Algina & Moulder, 2001)

中介变量,调节变量

中介效应检验2：sobel检验

在显著性水平为0.05下对应的Z的临界值为 0.97。பைடு நூலகம்明只要Z>0.97，则在P<0.05的显著性水平下，中介效应显著。
调节变量

变量X与变量Y有关系，但是X与Y的关系受到第三个变量Z的影响，那么Z就是调节变量。
调节作用检验
中介变量调节变量
中介变量

X影响Y，并且X通过一个中间的变量M对Y 产生影响，M就是中介变量。检验中介变量的方法（Baron ，Kenny1986）

自变量影响因变量自变量影响中介变量控制中介变量后，自变量对因变量的作用消失了，或者明显地减小了
检验中介效应

第一种方法：( i ) 系数 c 显著 ( 即 H0 : c = 0 的假设被拒绝) ; (ii) 系数 a 显著 ( 即H0 : a = 0 被拒绝) , 且系数 b 显著 ( 即 H0 : b = 0 被拒绝) 。完全中介过程还要加上 : ( iii ) 系数 c’不显著第二种方法：检验经过中介变量的路径上的回归系数的乘积 ab 是否显著 , 即检验 H0 : ab = 0 , 如果拒绝原假设 , 中介效应显著, 这种做法其实是将 ab 作为中介效应第三种做法：检验 c’ 与 c 的差异是否显著 ,即检验 H0 : c - c’ = 0 , 如果拒绝原假设 , 中介效应显著

有中介的调节变量和有调节的中介变量

收稿日期 : 2005 - 06- 29
[ 1]
1 有中介的调节变量
如果一个模型除了自变量和因变量外, 涉及的第三变量不止一个 , 可能会同时包含调节变量和中介变量。这些变量出现在模型中的位置不同会产生不同的模型, 联系着不同的统计背景和意义。设要研究学生行为 ( X ) 对同伴关系 ( Y ) 的影响。以往的研究发现 , 老师的管教方式 ( U ) 是调节变量 , 老师对学生的喜欢程度 ( W ) 是中介变量。据此可以建立如图 1 所示的模型。我们知道 , UX 是调节效应项, 如果它影响 W, 而 W 影响 Y, 说明调节效应 ( 至少部分地 )通过中介变量 W 而起作用 , 称这样的调节变量是有中介的调节变量 ( m ed iated m od erato r) 。 Baron 和 Kenny 提到过这一概念, 但没有讨论如何分析这种模型。可以仿照文 [ 2] 中的中介效应检验程序检验有中介的调节效应是否显著。以依次检验为例, 有中介的调节效应显著意味着 : ( 1) 做 Y 对 X 、 U 和 UX 的回归, UX 的系数显著; ( 这一步说明 U 对 Y 与 X 关系的调节效应显著。 ) ( 2) 做 W 对 X 、 U 和 UX 的回归 , UX 的系数显著 ;
- 9. 78 - 2. 20 0. 63 0. 48 0. 09 0. 04
中介效应也低。
表 2 中介效应分析
预测变量对 Y 的直接效应对 W 的直接效应经过 W 对 Y 的中介效应中介效应与直接效应之比 W X U UX 0 . 144 UW 1 . 308
5. 52 - 0. 55 0. 00 0. 00
[ 3] [ 1]

调节变量和中介变量(温忠麟)

面的影响机制远端关系（distal）的前提与研究目的 X与Y的相关因为是远端关系而不显著，但关系敏感 (subtle) ，研究中介变量的每一段效应（Shrout & Bolger, 2002, Psych. Methods )
6.1 遮掩效应
检验步骤和中介效应检验相同，但可以忽略第一步
例如 X—居民区每月人均购物消费 Y—居民区每月人均便利店购物消费 M—居民区每月人均超市购物消费
拟极大似然估计（QML）方法(Klein & Muthen, 2002) 贝叶斯（Bayesian)方法
2 中介变量和中介效应
2.1 中介变量的定义考虑自变量X对因变量Y的影响，如果X通过影响变量M来影响Y，则称M为中介变量。（Judd & Kenny，1981； Baron & Kenny, 1986)
愿人间凝聚的能量激荡每一个人的智场 —— 等概率
敬请批评指正
谢谢各位
1. 做Y对X、U和UX的回归， UX的系数显著； 2. 做W对X、U 和UX的回归， UX的系数显著； 3. 做Y对X、U 、UX和W的回归， W的系数显著。
如果在第（3）步中，UX的系数不显著，则U的调节效应完全通过中介变量W而起作用。
4.2 有调节的中介模型
有调节的中介效应显著意味着：
1.做Y对X和U的回归，X的系数显著； 2.做W对X和U的回归，X的系数显著； 3.做Y对X、U和W的回归，W的系数显著；
带潜变量乘积项的结构方程分析
1. 参数非线性约束方法（Kenny & Judd, 1984; Joreskog & Yang , 1996; Algina & Moulder, 2001)
2. 广义乘积指标（GAPI）方法（ Wall & Amemiya, 2001) 3. 无约束方法（Marsh, Wen & Hau, 2004, 2006, 2007)

中介变量与调节变量

• 中介效应的大小c- c’= a b，即0.300.17=0.13=ab.则部分中介效果显著。 • a=0.26 b=0.49 ab=0.13 • 中介效应与总效应之比( ^a^b/ ( ^c’+ ^a^b) )，即（0.26×0.49）/ （0.17+0.26×0.49）=42.8%
调节变量
调节效应
调节变量和自变量都是类别变量时：做方差分析当两者的交互效应显著时,则说明调节变量产生了调节效应。之后,可以通过简单效应分析进一步了解调节变量的具体作用。
当调节变量是连续变量时,无论自变量是何种变量,均可采用层次回归技术来进行检验。即先分别考察自变量和调节变量对因变量的主效应大小,然后将“自变量×调节变量” 乘积项纳入回归方程,若该项系数显著,则表明调节效应显著。
调节变量（moderator）：如果因变量Y与自变量X的关系是变量M的函数，称M为调节变量。就是说，Y与X的关系受到第三个变量M的影响，这种有调节变量的模型一般地可以用图示意。
• 在做调节效应分析时, 通常要将自变量和调节变量做中心化变换(即变量减去其均值)。本文主要考虑最简单常用的调节模型, 即假设Y与X有如下关系 • Y= aX + bM+ cXM+ e (1) 可以把上式重新写成 • Y= bM + ( a + cM)X+ e c衡量了调节效应 (moderating effect)的大小
调节变量可以是定性的(如性别、种族、学校类型等) ,也可以是定量的(如年龄、受教育年限、刺激次数等) ,它影响因变量和自变量之间关系的方向(正或负)和强弱。在调节效应中,哪个是自变量,哪个是调节变量是很明确的,在一个确定的模型中两者不能互换。

以调节的方式检验中介作用的例子

以调节的方式检验中介作用的例子调节的方式是指通过改变某个变量来观察中介变量和因变量之间的关系。

下面将列举10个例子来说明调节方式在检验中介作用中的应用。

1. 例子一：研究人员想要探究社交支持对个体健康的影响，并且怀疑这种影响可能受到性别的调节。

研究人员首先通过调查问卷收集个体的社交支持水平和身体健康状况，然后将样本按性别分组进行分析。

通过比较不同性别组内社交支持与身体健康之间的关系，可以验证性别是否对社交支持和身体健康之间的中介关系产生调节作用。

2. 例子二：假设研究人员想要研究教育对收入的影响，并且认为这种影响可能受到家庭背景的调节。

研究人员首先收集样本的教育水平和收入水平，然后将样本按家庭背景（如父母教育水平）分组进行分析。

通过比较不同家庭背景组内教育与收入之间的关系，可以检验家庭背景是否对教育和收入之间的中介关系产生调节作用。

3. 例子三：研究人员想要研究工作满意度对员工绩效的影响，并且认为这种影响可能受到工作环境的调节。

研究人员首先收集样本的工作满意度和绩效指标，然后将样本按工作环境（如工作压力水平）分组进行分析。

通过比较不同工作环境组内工作满意度与绩效之间的关系，可以验证工作环境是否对工作满意度和绩效之间的中介关系产生调节作用。

4. 例子四：研究人员想要研究环境意识对环保行为的影响，并且怀疑这种影响可能受到个人价值观的调节。

研究人员首先通过调查问卷收集个体的环境意识水平和环保行为水平，然后将样本按个人价值观（如环保意识）分组进行分析。

通过比较不同个人价值观组内环境意识与环保行为之间的关系，可以验证个人价值观是否对环境意识和环保行为之间的中介关系产生调节作用。

5. 例子五：研究人员想要研究父母监管对青少年犯罪行为的影响，并且认为这种影响可能受到同伴压力的调节。

研究人员首先收集样本的父母监管水平和犯罪行为水平，然后将样本按同伴压力（如朋友圈子）分组进行分析。

通过比较不同同伴压力组内父母监管与犯罪行为之间的关系，可以验证同伴压力是否对父母监管和犯罪行为之间的中介关系产生调节作用。

有中介的调节变量和有调节的中介变量

有中介的调节变量和有调节的中介变量一、本文概述在社会科学和心理学研究中，变量之间的关系常常是复杂而多元的。

中介变量和调节变量是理解这种复杂关系的重要工具。

然而，当这两者同时存在时，它们之间的互动和影响就变得更加复杂。

本文将深入探讨有中介的调节变量和有调节的中介变量这两种特殊情况，旨在帮助读者更好地理解和应用这些概念。

我们将概述中介变量和调节变量的基本概念和作用。

中介变量通常用于解释自变量和因变量之间的内在机制，它揭示了一个过程或路径，通过这个过程，自变量的变化影响了因变量。

而调节变量则用于描述一个变量如何影响自变量和因变量之间的关系强度或方向，它揭示了在何种条件下，这种关系会发生变化。

接下来，我们将详细讨论有中介的调节变量。

这种情况指的是，调节变量不仅直接影响自变量和因变量之间的关系，而且还通过中介变量间接影响这种关系。

我们将通过具体案例和数学模型来解释这种复杂的相互作用，并讨论如何识别和分析这种关系。

我们还将探讨有调节的中介变量。

在这种情况下，中介变量的作用受到调节变量的影响。

这意味着，在不同的调节变量水平下，中介变量可能发挥不同的作用，从而影响自变量和因变量之间的关系。

我们将探讨这种关系的特点和识别方法，并通过实例进行说明。

我们将总结这两种特殊情况在理论和实践中的应用。

通过本文的阐述，读者将能够更好地理解和分析复杂变量之间的关系，从而在研究中做出更准确的推断和更有力的解释。

二、有中介的调节变量在统计分析中，中介变量和调节变量各自扮演着不同的角色，然而在某些复杂的情况下，它们可能会共同出现，形成“有中介的调节变量”这一概念。

这意味着一个变量既在自变量和因变量之间起中介作用，又受到另一个调节变量的影响。

理解这一概念对于深入研究变量间的关系，揭示现象背后的复杂机制具有重要意义。

有中介的调节变量模型通常涉及四个主要变量：自变量（）、调节变量（M）、中介变量（W）和因变量（Y）。

在这个模型中，自变量通过中介变量W影响因变量Y，同时调节变量M也影响中介变量W。

调节效应与中介效应

调节效应与中介效应调节效应与中介效应1调节效应1.1 调节变量的定义如果变量Y与变量X的关系是变量M 的函数,称M 为调节变量。

就是说, Y与X 的关系受到第三个变量M 的影响,这种有调节变量的模型一般地可以用图1 示意。

调节变量可以是定性的(如性别、种族、学校类型等) ,也可以是定量的(如年龄、受教育年限、刺激次数等) ,它影响因变量和自变量之间关系的方向(正或负)和强弱。

图1调节变量模型在做调节效应分析时,通常要将自变量和调节变量做中心化变换(即变量减去其均值,参见文献) 。

本文主要考虑最简单常用的调节模型,即假设Y与X 有如下关系Y = aX + bM + cXM + e (1)可以把上式重新写成Y = bM + ( a + cM ) X + e对于固定的M ,这是Y对X 的直线回归。

Y与X 的关系由回归系数a + cM 来刻画,它是M 的线性函数, c衡量了调节效应(moderating effect)的大小。

1.2 调节效应分析方法调节效应分析和交互效应分析大同小异。

这里分两大类进行讨论。

一类是所涉及的变量(因变量、自变量和调节变量)都是可以直接观测的显变量(observable variable) ,另一类是所涉及的变量中至少有一个是潜变量( latent variable) 。

1.2.1 显变量的调节效应分析方法调节效应分析方法根据自变量和调节变量的测量级别而定。

变量可分为两类, 一类是类别变量( categorical variable) ,包括定类和定序变量,另一类是连续变量( continuous variable) ,包括定距和定比变量。

定序变量的取值比较多且间隔比较均匀时,也可以近似作为连续变量处理。

表1分类列出了显变量调节效应分析方法。

当自变量和调节变量都是类别变量时做方差分析。

当自变量和调节变量都是连续变量时,用带有乘积项的回归模型,做层次回归分析: ( 1)做Y对X和M 的回归,得测定系数R21。

中介变量和调节变量的例子

中介变量和调节变量的例子中介变量和调节变量是社会科学研究中常用的概念，它们可以帮助研究者深入探索变量之间的关系。

本文将通过一个具体的例子来说明中介变量和调节变量的作用。

一、研究背景假设我们想研究人们对于环境问题的态度与其行为之间的关系。

我们可以通过问卷调查等方式来收集数据，然后进行分析。

在这个过程中，我们需要考虑到可能存在的中介变量和调节变量。

二、自我效能感是一个中介变量自我效能感是指个体对于自己能否完成某项任务的信心程度。

在这个例子中，我们可以将自我效能感作为一个中介变量，来探讨人们对于环境问题的态度与其行为之间的关系。

具体来说，我们可以假设人们对于环境问题持有积极态度时，他们更有可能采取实际行动去保护环境。

而人们是否采取实际行动又可能受到自我效能感的影响。

也就是说，如果一个人认为自己有能力保护环境，那么他更有可能采取实际行动去做。

为了验证这个假设，我们可以进行如下的研究设计：1. 收集数据，包括人们对于环境问题的态度、其自我效能感以及是否采取实际行动等信息。

2. 进行数据分析，探讨人们对于环境问题的态度与其是否采取实际行动之间的关系。

3. 探讨自我效能感在这个关系中的作用。

具体来说，我们可以将自我效能感作为一个中介变量，并检验其是否能够解释人们对于环境问题的态度与其是否采取实际行动之间的关系。

4. 如果自我效能感确实起到了中介作用，那么我们还可以进一步探讨什么因素影响了人们的自我效能感。

这些因素可能包括教育程度、社会支持等等。

三、性别是一个调节变量除了中介变量，调节变量也是社会科学研究中常用的概念。

调节变量指那些可以影响两个变量之间关系强度或方向的因素。

在这个例子中，我们可以将性别作为一个调节变量来探讨人们对于环境问题的态度与其行为之间的关系。

具体来说，我们可以假设男性和女性在对待环境问题上有所不同。

也就是说，男性和女性可能会有不同的环保意识和行为。

因此，性别可能会影响人们对于环境问题的态度与其行为之间的关系。

【最新精选】调节效应与中介效应

调节效应与中介效应1调节效应1.1 调节变量的定义如果变量Y与变量X的关系是变量M 的函数,称M 为调节变量。

就是说, Y与X 的关系受到第三个变量M 的影响,这种有调节变量的模型一般地可以用图1 示意。

调节变量可以是定性的(如性别、种族、学校类型等) ,也可以是定量的(如年龄、受教育年限、刺激次数等) ,它影响因变量和自变量之间关系的方向(正或负)和强弱。

图1调节变量模型在做调节效应分析时,通常要将自变量和调节变量做中心化变换(即变量减去其均值,参见文献) 。

本文主要考虑最简单常用的调节模型,即假设Y与X 有如下关系Y = aX + bM + cXM + e (1)可以把上式重新写成Y = bM + ( a + cM ) X + e对于固定的M ,这是Y对X 的直线回归。

Y与X 的关系由回归系数a + cM 来刻画,它是M 的线性函数, c衡量了调节效应(moderating effect)的大小。

1.2 调节效应分析方法调节效应分析和交互效应分析大同小异。

这里分两大类进行讨论。

一类是所涉及的变量(因变量、自变量和调节变量)都是可以直接观测的显变量(observable variable) ,另一类是所涉及的变量中至少有一个是潜变量( latent variable) 。

1.2.1 显变量的调节效应分析方法调节效应分析方法根据自变量和调节变量的测量级别而定。

变量可分为两类, 一类是类别变量( categorical variable) ,包括定类和定序变量,另一类是连续变量( continuous variable) ,包括定距和定比变量。

定序变量的取值比较多且间隔比较均匀时,也可以近似作为连续变量处理。

表1分类列出了显变量调节效应分析方法。

当自变量和调节变量都是类别变量时做方差分析。

当自变量和调节变量都是连续变量时,用带有乘积项的回归模型,做层次回归分析: ( 1)做Y对X和M 的回归,得测定系数R21。

Mplus：中介模型与调节模型

Y1
Y2
Y3
Y4
W1
W2
W3
W4
自回归交叉滞后模型
中介调节模型基础
X1 Y1
1
e1
中介变量
路径系数估计与效应分解

一个因变量：最小二乘法多个因变量：极大似然估计
X2
Y2
1
e2
参数估计完成后，需要对变量间关系进行分解，即效应分解，包
括直接效应和间接效应

当模型中一个变量既是自变量又是因变量时，通常在两个变量间

将多个中介变量都放进模型中，可以降低由于遗漏变量导致的参数估计偏差；
在此模型下，可以判断某个变量所引致的特定中介效应的相对大小，从而可以进行不同理论之间的比较。

基于结构方程模型的多重中介效应
单步多重中介模型

M1 X M2
单步多重中介模型 single－step multiple mediator model
有9个题目（如班主任愿意听我们的意见等）。老师对学生的喜欢程度由班主任对被试打分（从
“一点都不喜欢”到“非常喜欢”，共5点计分），
−
问题一：喜欢程度是调节变量还是中介变量？
−
问题二：管教方式是调节变量还是中介变量？
中介调节模型基础

中介效应与调节效应的比较
如果一个变量与自变量或因变量相关不大，它不可能成为中介变量，但有可能成为
自变量是潜变量；二是调节变量和自变量都是潜变量。
−
当调节变量是类别变量时，做分组结构方程分析。
−
当调节变量和自变量都是潜变量时，可采用Algina和Moulder的中心化乘积指标方法(适用于正态
分布情形)；Wall和Amemiya的广义乘积指标( GAP I)方法(非正态分布情形也适用)；这两种方法都需要用到非线性参数约束( constraint) ，使用起来很麻烦且容易出错。Marsh，Wen和Hau提出的无

调节效应和中介效应

调节变量(Moderator) vs 中介变量(Mediator)1、调节变量的定义变量Y与变量X 的关系受到第三个变量M 的影响,就称M为调节变量。

调节变量可以是定性的，也可以是定量的。

在做调节效应分析时,通常要将自变量和调节变量做中心化变换。

简要模型：Y = aX + bM + cXM + e 。

Y与X 的关系由回归系数a + cM 来刻画,它是M 的线性函数, c衡量了调节效应(moderating effect)的大小。

如果c显著，说明M 的调节效应显著。

2、调节效应的分析方法显变量的调节效应分析方法：分为四种情况讨论。

当自变量是类别变量，调节变量也是类别变量时，用两因素交互效应的方差分析，交互效应即调节效应；调节变量是连续变量时，自变量使用伪变量,将自变量和调节变量中心化,做Y=aX+bM+cXM+e 的层次回归分析：1、做Y对X和M的回归,得测定系数R12。

2、做Y对X、M和XM的回归得R22，若R22显著高于R12，则调节效应显著。

或者,作XM的回归系数检验,若显著,则调节效应显著；当自变量是连续变量时，调节变量是类别变量，分组回归:按M的取值分组,做Y对X的回归。

若回归系数的差异显著,则调节效应显著，调节变量是连续变量时，同上做Y=aX +bM +cXM +e的层次回归分析。

潜变量的调节效应分析方法：分两种情形：一是调节变量是类别变量,自变量是潜变量；二是调节变量和自变量都是潜变量。

当调节变量是类别变量时,做分组结构方程分析。

做法是,先将两组的结构方程回归系数限制为相等,得到一个χ2值和相应的自由度。

然后去掉这个限制,重新估计模型,又得到一个χ2值和相应的自由度。

前面的χ2减去后面的χ2得到一个新的χ2,其自由度就是两个模型的自由度之差。

如果χ2检验结果是统计显著的,则调节效应显著；当调节变量和自变量都是潜变量时，有许多不同的分析方法，最方便的是Marsh,Wen和Hau 提出的无约束的模型。

控制变量调节变量中介变量

M
X
Y
e Y=fX;M+e
例如;学生的学习效果和指导方案的关系;往往受到学生个性的影响:一种指导方案对某类学生很有效;对另一类学生却没有效;从而学生个性是调节变量又如;学生一般自我概念与某项自我概念如外貌体能等的关系;受到学生对该项自我概念重视程度的影响:很重视外貌的人;长相不好会大大降低其一般自我概念;不重视外貌的人;长相不好对其一般自我概念影响不大;从而对该项自我概念的重视程度是调节变量在做调节效应分析时;通常要将自变量和调节变量做中心化变换本次主要考虑最简单常用的调节模型;即假设Y与X 有如下关系 Y = aX + bM + cXM + e 1 可以把上式重新写成 Y = bM + a + cM X + e 对于固定的M ;这是Y对X 的直线回归 Y与X 的关系由回归系数a + cM 来刻画;它是M 的线性函数; c衡量了调节效应moderating effect的大小
将自变量和调节变量中心化;做
Y=aX+bM+cXM+e 的层次回归分析同左除了考虑交互效应项XM外;还可以考虑高阶效应项如XM2;表示非线性调节效应；MX2;表示曲线回归得调节
2 3 2潜变量的调节效应分析方法
有关潜变量的分析需要用到结构方程模型;潜变量的测量
会带来测量误差;所以考虑潜变量时都认为是连续变量有
方法：采用层级Logistic分析;第一层纳入控制变量
2 调节变量
2 1 调节变量的定义如果变量Y与变量X的关系是变量M 的函数;称M 为调节变量就是说; Y与X 的关系受到第三个变量M 的影响;这种有调节变量的模型一般地可以用图示意调节变量可以是定性的如性别种族学校类型等 ;也可以是定量的如年龄受教育年限刺激次数等 ;它影响因变量和自变量之间关系的方向正或负和强弱

有中介的调节变量和有调节的中介变量

有中介的调节变量和有调节的中介变量有中介的调节变量（Mediated Mod erator）有中介的调节效应的检验程序：1）、做Y对X、U和UX的回归，UX的系数显著；（这一步说明U对Y与X关系的调节效应显著。

）2）、做W对X、U和UX的回归，UX的系数显著；3）、做Y对X、U、UX和W的回归，W的系数显著。

如果在第3）步中，UX的系数不显著，则U的调节效应完全通过中介变量W而起作用。

有调节的中介变量（Mod erated Mediator）有中介的调节效应的检验程序：1）、做Y对X和U的回归，X的系数显著；2）、做W对X和U的回归，X的系数显著；3）、做Y对X、U和W的回归，W的系数显著；（到此为止说明W的中介效应显著。

）4）、做Y对X、U、W和UW的回归，UW的系数显著。

从上面分析步骤可知，检验有调节的中介效应时，先要检验中介效应，然后检验调节效应。

混合模型（Mixed Mod el）1）、U的直接调节效应显著，即UX→Y的系数显著；2）、W的中介效应显著，即X→W，W→Y的系数显著；3）、由UX→W的系数显著和W→Y的系数显著，可知U是有中介的调节变量，即除了直接调节效应外，U通过W还对Y有间接调节效应。

4）、由UX→Y的系数显著，U是X→W的调节变量，再由UW→Y的系数显著，U是W→Y的调节变量，从而X→W和W→Y的中介过程受到U的影响，所以从这个角度看W是有调节的中介变量。

Notes：在通常的调节模型中，Y对X的回归系数是调节变量U的线性函数，而在混合模型中，调节不是通常的线性调节，而是二次调节，即Y对X的回归系数是调节变量U的二次函数。

当U在一定区域内，X对Y的效应不显著。

（可通过方程推导该区域）。

调节变量和中介变量模型举例

合集下载