【全国百强校】陕西省西安碑林区西铁一中学2017-2018学年七年级10月月考语文试题(含答案)

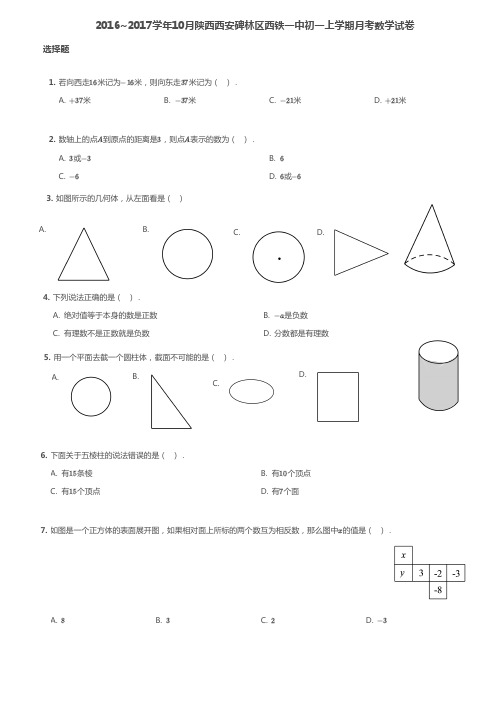
2016~2017学年10月陕西西安碑林区西铁一中初一上学期月考数学试卷选择题1.A.米 B.米 C.米 D.米若向西走米记为米，则向东走米记为（ ）．16−1637+37−37−21+212.A.或 B.C. D.或数轴上的点到原点的距离是，则点表示的数为（ ）．A 3A 3−36−66−63.A. B.C.D.如图所示的几何体，从左面看是（）4.A.绝对值等于本身的数是正数B.是负数C.有理数不是正数就是负数D.分数都是有理数 下列说法正确的是（ ）．−a 5.用一个平面去截一个圆柱体，截面不可能的是（ ）．A. B. C. D.6.A.有条棱B.有个顶点C.有个顶点D.有个面下面关于五棱柱的说法错误的是（ ）．15101577.A. B. C. D.如图是一个正方体的表面展开图，如果相对面上所标的两个数互为相反数，那么图中的值是（ ）．x 832−3填空题8.A. B. C. D.用小正方体搭一个几何体，使它的主视图和俯视图如图所示，这样的几何体最少需要正方体个数为（ ）．56789.A.， B.，C.， D.，如图，矩形中，，，，以边为轴将矩形绕其旋转一周形成圆柱体甲，再以边为轴将矩形绕其旋转一周形成圆柱体乙，记两个圆柱体的体积分别为、【注意有文字】，侧面积分别为、，则下列式子正确的是（ ）．ABCD AB =a BC =b a >b AB BC V 甲V 乙S S >V V 甲=S S 乙<V V 甲=S S 乙=V V 甲=S S 乙>V V 甲<S S 乙10.A.个 B.个 C.个 D.个有理数，在数轴上的对应点如图所示，则下列式子中：①．②．③．④，正确的有（ ）．a b −b >a |b |<|a |a −b >a +b |a |+|b |>|a −b |1234。

绝密★启用前 陕西省西安市碑林区铁一中学2017-2018学年八年级上期期中考试数学试卷 试卷副标题 注意事项： 1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上 第I 卷（选择题) 请点击修改第I 卷的文字说明 一、单选题 1．16的算术平方根是 A.4 B.±4 C.±2 D.2 2．点P （﹣1 ） A.第一象限 B.第二象限 C.第三象限 D.第四象限 3．下列条件中，不能判断一个三角形是直角三角形的是（ ） A ．三个角的比为1：2：3 B ．三条边满足关系a 2=b 2﹣c 2 C ．三条边的比为1：2：3 D ．三个角满足关系∠B+∠C=∠A 4．如图,矩形OABC 的边OA 长为2,边AB 长为1,OA 在数轴上,以原点O 为圆心,以对角线OB 的长为半径画弧,交正半轴于一点,则这个点表示的实数是( ) A ．2.5 B ．C D 5．在平面直角坐标系中，点P （－20，a ）与点Q （b ，13）关于原点对称，则a+b 的值为（） A ．33 B ．－33 C ．－7 D ．7 6．若正比例函数的图象经过点（1-，2），则这个图象必经过点（ ）． A.（1，2） B.（1-，2-） C.（2，1-） D.（1，2-）7．已知正比例函数y=kx 的图象经过第一、三象限，则一次函数y=kx ﹣k 的图象可能是下图中的（ ） A. B. C. D.8a ，小数部分为b ，则a ﹣b 的值为（ ）A ．B ．6C ．8D 6 9．如图所示，在Rt △ABC 中，斜边OB 在x 轴的正半轴上，直角顶点A 在第四象限内，S △OAB =20，OA ：AB=1：2，则点B 的坐标为（ ）A.（，0）B.（12，0）C.（10，0）D.（，0） 10．在平面直角坐标系中，将直线平移后，得到直线，则下列平移作法正确的是（ ）A ．将向右平移3个单位长度B ．将向右平移6个单位长度C ．将向上平移2个单位长度D ．将向上平移4个单位长度第II 卷（非选择题) 请点击修改第II 卷的文字说明 二、填空题 110，π，3.1415，﹣3，2.1010010001…（相邻两个1之间0的个数逐次加1）中，无理数有______个． 12．已知点（﹣2，y 1），（1，y 2）在直线y=13x b -+上，则y 1_____y 2（填“＞”、“＜”或“=”）． 13．已知点A 在x 轴的下方，且到x 轴的距离为5，到y 轴的距离为3，则点A 的坐标为_____. 14．小颖在画一次函数y ＝ax +b （a ，b 为常数，且a ≠0）的图象时，求得x 与y 的部分对应值如表，则方程ax +b ＝0的解是_____． 15．如图，在一个长为20m ，宽为16m 的矩形草地上放着一根长方体木块，已知该木块的较长边和场地宽AD 平行，横截面是边长为2m 的正方形，一只蚂蚁从点A 处爬过木块到达点C 处需要走的最短路程是__m ． 16．如图，在平面直角坐标系中，直线l ：1+ 交x 轴于点A ，交y 轴于点B ，点A 1、A 2、A 3，…在x 轴上，点B 1、B 2、B 3，…在直线l 上．若△OB 1A ，△A 1B 2A 2，△A 2B 3A 3，…均为等边三角形，则△A 5B 6A 6的面积是__．三、解答题 17．计算下列各式 （1； （2； （3）（π﹣1）0+（﹣12）﹣1+|5|-（4）（2﹣（2）（.18．如图，一个小正方形网格的边长表示50米．A 同学上学时从家中出发，先向东走250米，再向北走50米就到达学校．（1）以学校为坐标原点，向东为x 轴正方向，向北为y 轴正方向，在图中建立平面直角坐标系：（2）B 同学家的坐标是 ；（3）在你所建的直角坐标系中，如果C 同学家的坐标为（﹣150，100），请你在图中描出表示C 同学家的点．193﹣27|=0，求（a ﹣b ）b ﹣1的值．20．已知一次函数y=（m+3）x ﹣（2n ﹣4），当m ，n 满足什么条件时．（1）该函数图象经过一、二、四象限．（2）该函数图象经过原点．21．一次函数y=kx+b 的图象经过M （0，2），N （1，3）两点，（1）求k ，b 的值；（2）求一次函数y=kx+b 与两坐标轴围成的三角形的面积．22．如图，在△ABC 中，AB=8，BC=6，AC=10，将△ABC 折叠，使A 点与BC 的中点D 重合，折痕为MN ，求线段BN 的长．23．甲、乙两人利用不同的交通工具，沿同一路线从A 地出发前往B 地，甲出发1h 后，乙出发．设甲与A 地相距y 甲（km ），乙与A 地相距y 乙（km ），甲离开A 地时间为x （h ），y 甲、y 乙与x 之间的函数图象如图所示． （1）甲的速度是 km/h ．（2）请分别求出y 甲、y 乙与x 之间的函数关系式． （3）当乙与A 地相距240km 时，甲与B 地相距多少千米？ 24．（1）发现 如图1，点A 为线段BC 外一动点，且BC=a ，AB=b.当点A 位于 时，线段AC 的长取得最大，最大值为 （用含a ，b 的式子表示）； （2）应用 点A 为线段BC 外一动点，且BC=3，AB=1.如图2所示，分别以AB ，AC 为边，作等边△ABD 和等边△ACE,连接CD ，BE. ①请找出图中与BE 相等的线段，并说明理由； ②直接写出BE 长的最大值. （3）拓展 如图3，在平面直角坐标系中，点A 的坐标为（2，0）点B 的坐标（5，0），点P 为线段AB 外一动点，且PA=2，PM=PB ，∠BPM=90°.请直接写出线段AM 长的最大值及此时点P 的坐标.参考答案1．A【解析】【分析】根据算术平方根的定义即可求出结果．【详解】∵42=16=4．故选A．【点睛】本题主要考查了算术平方根的定义．一个正数的算术平方根就是其正的平方根．2．B【解析】【分析】直接利用坐标系中点的坐标特点进而得出答案．【详解】点P（﹣1故选B．【点睛】本题主要考查了点的坐标，正确掌握各象限内点的坐标符号是解题的关键．3．C【解析】试题分析：选项A，三个角的比为1：2：3，设最小的角为x，则x+2x+3x=180°，x=30°，3x=90°，选项A正确；选项B，三条边满足关系a2=b2-c2，根据勾股定理的逆定理可得选项B正确；选项C，三条边的比为1：2：3，12+22≠32，选项C错误；选项D，三个角满足关系∠B+∠C=∠A，则∠A为90°，选项D正确．故答案选C．考点：三角形的内角和定理；勾股定理的逆定理．4．D【解析】在Rt△OAB中，∵OA＝2，AB＝1，由勾股定理知OB 5．D【解析】试题分析：关于原点对称的两个点，横坐标和纵坐标分别互为相反数．根据性质可得：a=－13，b=20，则a+b=－13+20=7．考点：原点对称6．D【解析】设正比例函数的解析式为y=kx （k≠0），因为正比例函数y=kx 的图象经过点（-1，2），所以2=-k ，解得：k=-2，所以y=-2x ，把这四个选项中的点的坐标分别代入y=-2x 中，等号成立的点就在正比例函数y=-2x 的图象上，所以这个图象必经过点（1，-2）．故选D ．7．D【解析】【分析】根据正比例函数y kx =的图象经过第一,三象限可得: 0k >, 因此在一次函数y kx k =-中0k >, 0b k =-<,根据0k >直线倾斜方向向右上方, 0b <直线与y 轴的交点在y 轴负半轴,画出图象即可求解.【详解】根据正比例函数y kx =的图象经过第一,三象限可得:所以0k >,所以一次函数y kx k =-中0k >, 0b k =-<,所以一次函数图象经过一,三,四象限,【点睛】本题主要考查一次函数图象象限分布性质,解决本题的关键是要熟练掌握一次函数图象图象的象限分布性质.8．B【解析】【分析】a 、b 的值，最后代入求出即可．【详解】∵34，∴a =3，b 3，∴a ﹣b =33）=6故选B ．【点睛】9．C【解析】【分析】设OA 为x ，则AB 为2x ，利用三角形的面积公式列出方程求出x ，根据勾股定理可得OB 为，进一步确定B 点的坐标．【详解】OA 为x ，则AB 为2x ．∵S △OAB =20，∴12×x ×2x =20，解得：x =±，由勾股定理得：OB x ，，则点B 的坐标为（10，0）． 故选C ．【点睛】本题考查的是勾股定理和坐标与图形的性质，运用勾股定理求出有关的边的长度是解题的关键．【解析】试题分析：根据函数平移的规则：上加下减，左加右减．A．向右平移3个单位长度得到的直线是：=，正确；B．向右平移6个单位长度得到的直线是：=，不正确；C．将向上平移2个单位长度得到的直线是：，不正确；D．将向上平移4个单位长度得到的直线是：=，不正确；故选A．考点：函数的平移．11．3【解析】【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．【详解】π，2.1010010001…（相邻两个1之间0的个数逐次加1）共有3个．故答案为：3．【点睛】本题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．12．＞【解析】【分析】利用一次函数图象上点的坐标特征可求出y1、y2的值，比较后即可得出结论（利用一次函数的性质解决亦可，y随x的增大而减小）．【详解】∵点（﹣2，y1），（1，y2）在直线y=13x b-+上，∴y1=23+b，y2=﹣13+b．∵23+b＞﹣13+b，∴y1＞y2．故答案为：＞．【点睛】本题考查了一次函数图象上点的坐标特征，利用一次函数图象上点的坐标特征求出y1、y2的值是解题的关键．13．（3，﹣5）或（﹣3，﹣5）【解析】【分析】直接利用点A在x轴下方再结合到坐标轴的距离进而得出答案．【详解】∵点A在x轴的下方，且到x轴的距离为5，到y轴的距离为3，∴点A的纵坐标为：﹣5，横坐标为：±3，故点A的坐标为：（3，﹣5）或（﹣3，﹣5）．故答案为：（3，﹣5）或（﹣3，﹣5）．【点睛】本题主要考查了点的坐标，正确分类讨论是解题的关键．14．x=1【解析】【分析】方程ax+b=0的解为y=0时函数y=ax+b的x的值，根据图表即可得出此方程的解．【详解】根据图表可得：当x=1时，y=0；因而方程ax+b=0的解是x=1．故答案为：x=1．【点睛】本题主要考查了一次函数与一元一次方程之间的关系：方程ax+b=0的解为函数值y=0时函数y=ax+b自变量x的取值．15．【解析】【分析】解答此题要将木块展开，然后根据两点之间线段最短解答．【详解】由题意可知，将木块展开，相当于是AB+2个正方形的宽，∴长为20+2×2=24米；宽为16米．故答案为：【点睛】本题主要考查平面展开﹣最短路径问题，两点之间线段最短，有一定的难度，要注意培养空间想象能力．16．【解析】【分析】首先求得点A与B的坐标，即可求得∠OAB的度数，又由△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形，易求得OB1=OA A1B1=A1A，A2B2=A2A，则可得规律：OA n=（2n﹣1）A5A6=OA6﹣OA5求得△A5B6A6的边长，进而求得【详解】∵点A0），点B（0，1），∴OA OB=1，∴tan∠OAB，∴∠OAB=30°．∵△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形，∴∠A1OB1=∠A2A1B2=∠A3A2B3=60°，∴∠OB1A=∠A1B2A=∠A2B3A=∠OAB=30°，∴OB1=OA，A1B2=A1A，A2B3=A2A，∴OA1=OB1OA2=OA1+A1A2=OA1+A1B2，同理：OA3，OA4，OA5OA6A5A6=OA6﹣OA5则△A5B6A6的面积是故答案为：．【点睛】本题考查了一次函数的性质、等边三角形的性质、等腰三角形的判定与性质以及三角函数的知识．此题难度较大，注意掌握数形结合思想的应用．17．（1）；（2）﹣1；（3）﹣4）．【解析】【分析】（1）直接利用二次根式的混合运算法则化简求出答案；（2）直接利用二次根式的性质化简求出答案；（3）直接利用负指数幂的性质以及零指数幂的性质和绝对值的性质、二次根式的性质分别化简即可求出答案；（4）直接利用乘法公式结合二次根式的性质化简求出答案．【详解】（1）原式=4+=4；﹣2（2）原式=1﹣2=﹣1；（3）原式=1﹣2+5﹣=﹣6；（4）原式=9+2+﹣（4﹣3）=10+．【点睛】本题主要考查了实数运算，熟练掌握实数的运算法则是解题的关键．18．见解析.【分析】（1）由于A同学上学时从家中出发，先向东走250米，再向北走50米就到达学校，则可确定A点位置，然后画出直角坐标系；（2）利用第一象限点的坐标特征写出B点坐标；（3）根据坐标的意义描出点C．【详解】（1）如图；（2）B同学家的坐标是（200，150）；（3）如图：故答案为：（200，150）．【点睛】本题考查了坐标确定位置：平面内的点与有序实数对一一对应；记住平面内特殊位置的点的坐标特征．19．121【解析】【分析】根据非负数的性质即可求出a与b的值．【详解】由题意可知：a2﹣64=0，b3﹣27=0，∴a=±8，b=3．当a=8，b=3时，原式=（8﹣3）2=25；当a=﹣8，b=3时，原式=（﹣8﹣3）2=121．综上所述：（a﹣b）b﹣1的值为25或121．【点睛】本题考查了非负数的性质，解题的关键是运用非负数的性质求出a与b的值，本题属于基础20．（1）m＜﹣3，n＜2；（2）m≠﹣3，n=2．【解析】【分析】（1）利用一次函数图象与系数的关系得到m+3＜0，﹣（2n﹣4）＞0，然后解两个不等式即可；（2）利用一次函数图象与系数的关系得m+3≠0，﹣（2n﹣4）=0，然后解不等式和方程即可．【详解】（1）∵函数图象经过一、二、四象限，∴30240mn+⎧⎨--⎩＜（）＞，∴m＜﹣3，n＜2；（2）∵该函数图象经过原点，∴m+3≠0，﹣（2n﹣4）=0，即m≠﹣3，n=2．【点睛】本题考查了一次函数与系数的关系：直线y=kx+b与y轴交于（0，b），当b＞0时，（0，b）在y轴的正半轴上，直线与y轴交于正半轴；当b＜0时，（0，b）在y轴的负半轴，直线与y轴交于负半轴．k＞0，b＞0⇔y=kx+b的图象在一、二、三象限；k＞0，b＜0⇔y=kx+b的图象在一、三、四象限；k＜0，b＞0⇔y=kx+b的图象在一、二、四象限；k＜0，b＜0⇔y=kx+b 的图象在二、三、四象限．21．（1）k，b的值分别是1和2；（2）2.【解析】【分析】（1）根据待定系数法求出一次函数解析式即可；（2）根据直线与坐标轴的交点坐标求得围成的直角三角形的两直角边，然后根据直角三角形的面积公式求得即可．【详解】（1）由题意得：23bk b=⎧⎨+=⎩，解得：12kb=⎧⎨=⎩，∴k，b的值分别是1和2；（2）由（1）可知一次函数解析式为y=x+2，则与坐标轴的交点是（﹣2，0），（0，2），所以，图象与两坐标轴围成的三角形面积为12×2×2=2．本题考查了待定系数法求一次函数的解析式，直线与x轴的交点坐标以及三角形的面积等，熟练掌握待定系数法是解题的关键．22．55 16【解析】试题分析：设BN=x，则由折叠的性质可得DN=AN=9-x，根据中点的定义可得BD=3，在Rt△ABC中，根据勾股定理可得关于x的方程，解方程即可求解．试题解析：设BN=x，由折叠的性质可得DN=AN=9-x，∵D是BC的中点，∴BD=3，在Rt△ABC中，x2+32=（9-x）2，解得x=4．故线段BN的长为4．考点：翻折变换（折叠问题）．23．（1）60．（2）y乙=90x﹣90；y甲=60x．（）220km【解析】【分析】（1）根据图象确定出甲的路程与时间，即可求出速度；（2）利用待定系数法即可解决问题；（3）求出乙距A地240km时的时间，加上1，再乘以甲的速度即可得到结果．【详解】（1）根据图象得：360÷6=60km/h．故答案为：60．（2）当1≤x≤5时，设y乙=kx+b，把（1，0）与（5，360）代入得：5360k bk b+=⎧⎨+=⎩，解得：k=90，b=﹣90，则y乙=90x﹣90；当0＜x≤6时，设y甲=mx，把（6，360）代入得到m=60，∴y甲=60x．（3）∵乙与A地相距240km，且乙的速度为360÷（5﹣1）=90km/h，∴乙用的时间是240÷90=8 3h，则甲与A地相距60×（83+1）=220km．本题考查了一次函数的应用，弄清图象中的数据是解答本题的关键．24．（1）CB的延长线上，a+b；（2）①CD=BE，理由见解析；② 4；（3）最大值为2+3；P（2﹣，）．【解析】试题分析：（1）根据点A位于CB的延长线上时，线段AC的长取得最大值，即可得到结论；（2）①根据等边三角形的性质得到AD=AB，AC=AE，∠BAD=∠CAE=60°，推出△CAD≌△EAB，根据全等三角形的性质得到CD=BE；②由于线段BE长的最大值=线段CD的最大值，根据（1）中的结论即可得到结果；（3）连接BM，将△APM绕着点P顺时针旋转90°得到△PBN，连接AN，得到△APN是等腰直角三角形，根据全等三角形的性质得到PN=PA=2，BN=AM，根据当N在线段BA的延长线时，线段BN取得最大值，即可得到最大值为2+3；过P作PE⊥x轴于E，根据等腰直角三角形的性质，即可得到结论．试题解析：（1）∵点A为线段BC外一动点，且BC=a，AB=b，∴当点A位于CB的延长线上时，线段AC的长取得最大值，且最大值为BC+AB=a+b，（2）①CD=BE，理由：∵△ABD与△ACE是等边三角形，∴AD=AB，AC=AE，∠BAD=∠CAE=60°，∴∠BAD+∠BAC=∠CAE+∠BAC，即∠CAD=∠EAB，在△CAD与△EAB中，，∴△CAD≌△EAB（SAS），∴CD=BE；②∵线段BE长的最大值=线段CD的最大值，∴由（1）知，当线段CD的长取得最大值时，点D在CB的延长线上，∴最大值为BD+BC=AB+BC=4；（3）如图1，连接BM，∵将△APM绕着点P顺时针旋转90°得到△PBN，连接AN，则△APN是等腰直角三角形，∴PN=PA=2，BN=AM，∵A的坐标为（2，0），点B的坐标为（5，0），∴OA=2，OB=5，∴AB=3，∴线段AM长的最大值=线段BN长的最大值，∴当N在线段BA的延长线时，线段BN取得最大值，最大值=AB+AN，∵AN=AP=2，∴最大值为2+3；如图2，过P作PE⊥x轴于E，∵△APN是等腰直角三角形，∴PE=AE=，∴OE=BO﹣AB﹣AE=5﹣3﹣=2﹣，∴P（2﹣，）．考点：三角形综合题；全等三角形的判定与性质；等腰直角三角形；旋转的性质．。

西安铁一中2016-2017 学年七年级放学期期末考试数学试题一、选择题 .1. 数字用科学记数法表示为（）．A. B. C. D.【答案】 B【分析】解：绝对值小于的正数也能够利用科学记数法表示，一般形式为，与较大数的科学记数法不一样的是其所使用的是负指数幂，指数由原数左侧起第一个不为零的数字前面的的个数所决定．从左侧起第一个不为零的数是，其前面有个零，所以，应选．点睛：本题考察用科学记数法表示较小的数，一般形式为，此中，为由原数左侧起第一个不为零的数字前面的的个数所决定．2. 以下运算正确的选项是（）．A. B. C. D.【答案】 C【分析】解： A ．，故本选项错误；B ．，故本选项错误；C．，正确；D ．，故本选项错误．应选．3.以下五种图形中：（）线段；（）角；（）等腰三角形；（）平行四边形；（）长方形，是轴对称图形的有（）．A. 个B.个C.个D.个【答案】 C【分析】解：（ 1）线段；（ 2）直角；（ 3）等腰三角形；（ 5）长方形是轴对称图形，共 4 个；只有（ 4）平行四边形，不是轴对称图形，应选．4. 如图，在和中，，若增添条件后使得≌，则在以下条件中，不可以添加的是（）．A. ，B. ，C. ，D. ，【答案】 D【分析】解： A ．增添，可用判断两个三角形全等，故本选项正确；B．增添，可用判断两个三角形全等，故本选项正确；C．由有可得，；再加上可用判断两个三角形全等，故本选项正确；D．增添，后是，没法判断两个三角形全等，故本选项错误；应选．点睛：本题考察全等三角形的判断方法，要娴熟掌握、、、、五种判断方法．5. 有长度分别为，，，的四条线段，从中任取三条线段能够构成三角形的概率是（）．A. B. C. D.【答案】 D【分析】解：由条线段中随意取条，共有，，；，，；，，；，，四种可能，每种可能出现的时机同样，而此中知足两边之和大于第三边构成三角形的有，，；，，；，，三个结果，所以从中任取三条线段能够构成三角形的概率是，应选．点睛：本题考察概率的求法，假如一个事件有种可能，且这些事件的可能性同样，此中事件出现中结果，那么事件的概率为．在本题中事件为构成三角形，要求为两边之和大于第三边．6. 如图，，，则、、的关系为（）．A. B.C. D.不存在【答案】 D【分析】解：方法一：延伸交于与，延伸交于．直角中，；中，．由于，所以，于是，故．应选．方法二：过点作，过点作，则由平行线性质可得：，，，∴，故，应选项．点睛：本题考察经过结构协助线，同时利用三角形外角的性质以及平行线的性质成立角之间的关系．7. 如图，在四边形中，动点从点开始沿、、、的路径匀速行进到停止．在这个过程中，的面积随时间的变化关系用图象表示正确的选项是（）．A. B. C. D.【答案】 B【分析】解：当点由点运动到点时，的面积是由小到大；而后点由点运动到点时，的面积是不变的；再由点运动到点时，的面积又由大到小；再察看图形的，故的面积是由小到大的时间应小于的面积又由大到小的时间．应选．点睛：本题考察动点问题的函数图象，函数图象是典型的数形联合，图象应用信息宽泛，经过图象获守信息，不单能够解决生活中的实质问题，还能够提升剖析问题、解决问题的能力．利用图象解决问题时，要点是要理清图象的含义．8. 如图的长方形纸带中，将纸带沿折叠成图，再沿折叠成图，则图中度数是（）．A. B. C. D.【答案】 A【分析】解：由长方形的性质可知，则；在图中，∵，∴；在图中，；在图中，．9. 如图，过边长为的等边的边上一点，作于，为延伸线上一点，当时，连结交边于，则的长为（）．A.B.C.D. 不可以确立【答案】 B【分析】解：过作的平行线交于，∴．∵是等边三角形，∴，，∴是等边三角形，∴．∵，∴．在和中，∵，∴≌（），∴．∵于，是等边三角形，∴，∴，∴．∵，∴．故的长为．点睛：本题考察经过作协助线，结构全等三角形，同时利用等边三角形的性质成立等边三角形边长与之间的关系．10. 如图，点是的中点，于，于，均分，以下结论：①；②；③；④，四个结论中成立的是（）A. ①②B. ①②④C. ①②③D. ①③④【答案】 B【分析】解：过作于，如图，∵，，均分，∴，．在和中，，∴≌（），∴，，；∵点是的中点，∴．在和中，，∴≌（），∴，．∵，∴，①正确；∵，∴，∴，②正确；∵，，④正确；只有时，，∴③不正确．应选．点睛：本题考察经过作垂线，获得两对全等三角形，进而利用全等三角形的性质判断结论中给出的角和线段之间的关系．二、填空题 .11. 已知，，则__________ ．【答案】【分析】解：．故答案为：．点睛：本题考察同底数幂的除法和幂的乘方的性质，这种题型应当先对所求的式子进行变型，进而利用已知条件进一步计算原式的值．12. 以下图的圆面图案是同样半径的圆与圆弧构成的，若向圆面扔掷飞镖，则飞镖落在黑色地区的概率为__________ ．【答案】【分析】计算出黑色地区的面积与整个图形面积的比，利用几何概率的计算方法解答即可：∵ 依据对称的性质知，黑色地区的面积占了整个图形面积的，∴ 飞镖落在黑色地区的概率为。

1
若分式
2
下面四个图案由我国传统文化中的
3
若4
点
5
在数轴上表示不等式组6
已知平行四边形
7
小朱要到距家8
已知，
9
若直线
10
如图，正方形
11
分解因式：
12
若某凸多边形的每个外角均为13
若不等式
14
如图，菱形15
若关于
16
如图，
17
请回答下列各题：18
如图，在
19
分式计算：
20
如图，点
21
某学校总务部门计划为数学组采购一批数学圆规和三角板．调查发现，一套三角板比一个圆规贵
22
如图
23
某水果合作社计划装运甲、乙、丙三种水果到外地销售（每辆汽车规定满载，并且只装一种水
24
如图。

2020-2021学年陕西省西安市碑林区铁一中学九年级（上）第二次月考数学试卷一、选择题（共10小题，每小题3分，计30分.每小题只有一一个是符合题意的）1．下列函数是二次函数的是（）A．y＝ax2+bx+c B．y＝2x﹣3C．D．y＝8x2+12．如图是一个水平放置的全封闭物体，则它的俯视图是（）A．B．C．D．3．在锐角△ABC中，若（sin A﹣）2+|﹣cos B|＝0，则∠C等于（）A．60°B．45°C．75°D．105°4．将抛物找y＝2x2向左平移4个单位，再向下平移1个单位得到的抛物找解析式为（）A．y＝2（x﹣4）2+1B．y＝2（x﹣4）2﹣1C．y＝2（x+4）2+1D．y＝2（x+4）2﹣15．如图，D、E分别是△ABC边AB，AC上的点，∠ADE＝∠ACB，若AD＝2，AB＝6，AC ＝4，则AE的长是（）A．1B．2C．3D．46．在Rt△ABC中，∠C＝90°，a、b、c分别为∠A、∠B、∠C所对的边，则下列等式中不正确的是（）A．a＝c sin A B．a＝C．b＝c sin B D．c＝7．二次函数y＝4x2﹣x+1的图象与x轴的交点个数是（）A．1个B．2个C．0个D．无法确定8．对于双曲线，x＞0时，y随x的增大而增大，则k的取值范围为（）A．k＜2B．k≤2C．k＞2D．k≥29．如图，点A，B，C在正方形网格的格点上，则sin∠BAC＝（）A．B．C．D．10．如图，是抛物线y1＝ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标是A（1，3），与x轴的一个交点B（4，0），直线y2＝mx+n（m≠0）与抛物线交于A，B两点，下列结论：①2a+b＝0；m+n＝3；②抛物线与x轴的另一个交点是（﹣1，0）；③方程ax2+bx+c ＝3有两个相等的实数根；④当1＜x＜4时，有y2＜y1；⑤若ax12+b1x＝ax22+bx2，且x1≠x2；则x1+x2＝1．正确个数是（）A．2个B．3个C．4个D．5个二.填空题（每题3分，共18分）11．抛物线y＝2x2+4x+5的对称轴是，顶点坐标是．12．如图，斜坡AB的坡度是1：4，如果从点B测得离地面的铅垂线高度BC是6米，那么斜坡AB的长度是米．13．将抛物线y＝（x﹣2）2+4绕原点旋转180°，所得抛物线的解析式是．14．如图，点A，B在双曲线y＝（x＞0）上，点C在双曲线y＝（x＞0）上，若AC∥y 轴，BC∥x轴，且AC＝BC，则AB的长为．15．若二次函数y＝ax2﹣6ax+c（a＞0）的图象经过A（﹣1，y1），B（2，y2），C（5，y3）三点，则y1，y2，y3的大小关系是．16．如图，在四边形ABCD中，AB＝AD＝AC，∠ABC＝120°，∠ADC＝150°，BC+CD ＝4，则BD的最小值是．三、解答题（共8小题，计72分，解答应写出过程）17．计算：（1）﹣cos45°+（π﹣3.14）0；（2）（﹣1）2020+|﹣2|+tan60°．18．如图，已知矩形ABCD，AC是一条对角线，请用尺规在边AD上确定点E，在边BC上确定点F，使得四边形AFCE是菱形（不写作法，保留作图痕迹）．19．如图，Rt△ABC中，∠C＝90°，点D在BC边上，已知∠ADC＝45°，DC＝6，sin B ＝．（1）求△ABD的面积．（2）求sin∠BAD．20．“传承红色基因，谱写时代新篇”，爱华中学将举办纪念“一二•九”爱国运动合唱比赛．九年级的3个班级独立参賽，每班随机抽取一首红歌作为参赛曲目，其中备选歌曲有A（《长城谣》）、B（《走向复兴》）、C（《东方红》）三首，每首红歌所选班级不限．（1）直接写出1班选到B《走向复兴》）的概率；（2）若1班已选到A（《长城谣》）作为参赛曲目，请利用列表或画树状图的方法求出3个班恰好演唱3首不同曲目的概率．21．为更好筹备“十四运”的召开，小颖及其小组成员将利用所学知识测量一个广告牌的高度EF．在第一次测量中，小颖来回走动，走到点D时，其影子末端与广告牌影子末端重合于点H，其中DH＝1m．随后，组员在直线DF上平放一平面镜，在镜面上做了一个标记，这个标记在直线DF上的对应位置为点G．镜子不动，小颖从点D沿着直线FD后退5m到B点时，恰好在镜子中看到顶端E的像与标记G重合，此时BG＝2m．如图，已知AB⊥BF，CD⊥BF，EF⊥BF，小颖的身高为1.5m（眼睛到头顶距离忽略不计），平面镜的厚度忽略不计．根据以上信息，求广告牌的高度EF．22．我国部分地区雾霾天气趋于严重，环境治理刻不容缓．某电器商场代理销售某种家用空气净化器，其进价是200元/台．经调研发现，其月销售量y（台）与当月售价x（元/台）之间存在一次函数关系．当售价是400元/台时，月销售量为200台；当售价是360元/台时，月销售量为400台．若供货商规定这种空气净化器售价不能低于260元/台，代理销售商每月要完成不低于700台的销售往来．（1）试确定月销售量y（台）与售价x（元/台）之间的函数关系；（2）试求出当售价x（元/台）定为多少时，商场每月销售这种空气净化器所获得的利润W（元）最大？最大利润是多少元？23．如图，在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）交x轴于A、B两点（点A在点B左侧），交y轴于C点，顶点为D点．其中A（﹣1，0），OC＝OB＝3OA．（1）求该抛物线的表达式；（2）在抛物线上A点左侧的部分上存在点P，使得∠BAD＝∠PBA，直接写出点P的坐标；（3）在x轴是否存在点E，y轴是否存在点F，使得以A、D、E、F四点为顶点的四边形是平行四边形？若存在，求出点E的坐标，若不存在，请说明理由．24．如图1，点C是线段AB上一点，将CA绕点C顺时针旋转90°得到CE，将CB绕点C 旋转，使点B的对应点D落在CE上，连接BE、AD并延长AD交E于点F．（1）求证：AF⊥BE；（2）连接CF，猜想AF，EF，CF存在的等量关系，并证明你猜想的结论；（3）如图2，延长AB到G，使BG＝CB，将线段BG沿直线BE上下平移，平移后的线段记为B'G'，若∠ABE＝60°，当CB'+CG'的值最小时，请求出tan∠G'CG的值．。

2018-2019学年七年级（上）月考数学试卷一、选择题（共10小题，每小题3分，满分30分）1．在有理数1，0，，﹣3中，是负数的为（）A．1 B．0 C．﹣3 D．2．下列四个几何体中，左视图为长方形的是（）A．B．C．D．3．据统计，2018年春节运输总人数为3200000000人，将3200000000用科学记数法表示为（）A．0.32×1010B．3.2×1010C．3.2×109D．32×1084．下面关于五棱柱的说法错误的是（）A．有15条棱B．有10个顶点C．有15个顶点D．有7个面5．下列等式计算正确的是（）A．﹣3﹣2＝﹣1 B．﹣5+4＝9 C．0×（﹣2）＝0 D．﹣32＝96．如图，是正方体的一个平面展开图，在这个正方体中，与“爱”字所在面相对的面上的汉字是（）A．我B．伟C．祖D．国7．已知（x﹣2）2与|y+3|互为相反数，则x﹣y的值为（）A．5 B．﹣5 C．1 D．﹣18．用一个平面去截一个六棱柱，截面的形状不可能是（）A．三角形B．五边形C．七边形D．九边形9．如图是由一些相同的小正方体构成的立体图形分别从正面、左面、上面看到的形状图，那么构成这个立方体图形的小正方体有（）个．A．5 B．6 C．7 D．810．若a为有理数，则下列说法正确的是（）A．﹣a＜0 B．|a|＞0 C．a2+1＞0 D．＝1二、填空题（共6小题，每小题3分，满分18分）11．下列有理数﹣3，0，﹣，2中，最小的数是．12．笔尖在纸上快速滑动写出一个又一个字，用数学知识可以理解为．13．若m，n互为相反数，a，b互为倒数，则2（m+n）﹣3ab＝．14．一个小立方块的六个面分别标有字母A，B，C，D，E，F，从三个不同的方向看到的情形如图所示，则字母C的对面是．15．已知有理数a在数轴上的位置如图，则a+|a﹣1|＝．16．如图，一个长方体的表面展开图中四边形ABCD是正方形，则原长方体的体积是．三、解答题（共6小题，满分52分）17．计算题（1）（﹣15）﹣（﹣23）﹣（+35）+117（2）（﹣1）×÷（﹣0.25）÷（﹣8）（3）（﹣1+）÷（﹣）（4）﹣24﹣（﹣9）÷×（﹣）×|﹣5|18．一个几何体由几个大小相同的小立方块搭成，从上面观察这个几何体，看到的形状如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，请画出从正面、左面看到的这个几何体的形状图．19．某检修小组从A地出发，在东西向的马路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中七次行驶纪录如下．（单位：km）（1）求收工时，检修小组在A地的何方向？距离A地多远？（2）在第几次纪录时距A地最远？（3）若汽车行驶每千米耗油0.4升，问从A地出发，检修结束后再回到A地共耗油多少升？20．有若干个数，第一个记为a1，第二个记为a2，第三个记为a3…．若a1＝﹣，从第2个数起，每个数都等于“1与它前面那个数的差的倒数”．（1）计算a2，a3，a4的值．（2）根据以上计算结果，直接写出a1998，a2006的值．21．已知有一个长为5cm，宽为3cm的长方形，若以这个长方形的一边所在的直线为轴，将它旋转一周，请分别求出所得的几何体的表面积和体积．22．A、B、C三点在数轴上，点A表示的数是﹣4，从点A出发向右平移7个单位长度得到点B．（1）求出点B表示的数，画一条数轴并在数轴上标出点A和点B；（2）若此数轴在一张纸上，将纸沿某一条直线对折，此时B点与表示数﹣1的点刚好重合，折痕与数轴有一个交点D，求点D表示的数的相反数（原卷无此问）；（3）在数轴上有一点C，点C到点A和点B的距离之和为11，求点C所表示的数；（4）A、B从初始位置分别以1单位长度/s和2单位长度/s的速度同时向左运动，是否存在t的值，使t秒后点B到﹣2的距离与点A到原点距离相等？若存在请求出t的值；若不存在，请说明理由．参考答案与试题解析一．选择题（共10小题）1．在有理数1，0，，﹣3中，是负数的为（）A．1 B．0 C．﹣3 D．【分析】根据负数的定义，找出这四个数中的负数即可．【解答】解：在1，0，，﹣3，这四个数中，是负数的数是﹣3，故选：C．2．下列四个几何体中，左视图为长方形的是（）A．B．C．D．【分析】左视图是从左边看所得到的图形，依此即可求解．【解答】解：A、圆柱的左视图是长方形，故选项正确；B、圆台的左视图是梯形，故选项错误；C、圆锥的左视图是三角形，故选项错误；D、球的左视图是圆，故选项错误．故选：A．3．据统计，2018年春节运输总人数为3200000000人，将3200000000用科学记数法表示为（）A．0.32×1010B．3.2×1010C．3.2×109D．32×108【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n 的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：3200000000＝3.2×109．故选：C．4．下面关于五棱柱的说法错误的是（）A．有15条棱B．有10个顶点C．有15个顶点D．有7个面【分析】利用五棱柱的特征即可得到答案．【解答】解：五棱柱有15条棱，10个顶点，7个面．故选：C．5．下列等式计算正确的是（）A．﹣3﹣2＝﹣1 B．﹣5+4＝9 C．0×（﹣2）＝0 D．﹣32＝9【分析】根据各个选项中的式子可以计算出正确的结果，从而可以解答本题．【解答】解：∵﹣3﹣2＝﹣5，故选项A错误；∵﹣5+4＝﹣1，故选项B错误；∵0×（﹣2）＝0，故选项C正确；∵﹣32＝﹣9，故选项D错误；故选：C．6．如图，是正方体的一个平面展开图，在这个正方体中，与“爱”字所在面相对的面上的汉字是（）A．我B．伟C．祖D．国【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．【解答】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，“我”与“大”是相对面，“伟”与“祖”是相对面，“爱”与“国”是相对面．故选：D．7．已知（x﹣2）2与|y+3|互为相反数，则x﹣y的值为（）A．5 B．﹣5 C．1 D．﹣1【分析】根据相反数的概念列出算式，根据非负数的性质求出x、y，根据有理数的减法法则计算，得到答案．【解答】解：∵（x﹣2）2与|y+3|互为相反数，∴（x﹣2）2+|y+3|＝0，则x﹣2＝0，y+3＝0，解得，x＝2，y＝﹣3，则x﹣y＝2+3＝5，故选：A．8．用一个平面去截一个六棱柱，截面的形状不可能是（）A．三角形B．五边形C．七边形D．九边形【分析】六棱柱有8个面，用平面去截六棱柱时最多与8个面相交得八边形，最少与三个面相交得三角形．因此截面的形状可能是：三角形、四边形、五边形、六边形、七边形、八边形．【解答】解：用平面去截一个六棱柱，得的截面可能为三角形、四边形、五边形、六边形、七边形、八边形，不可能为九边形．故选：D．9．如图是由一些相同的小正方体构成的立体图形分别从正面、左面、上面看到的形状图，那么构成这个立方体图形的小正方体有（）个．A．5 B．6 C．7 D．8【分析】易得这个几何体共有2层，由俯视图可得第一层正方体的个数，由主视图和左视图可得第二层正方体的个数，相加即可．【解答】解：由从上面看到的图形易得最底层有4个正方体，第二层有1个正方体，那么共有4+1＝5（个）正方体．故选：A．10．若a为有理数，则下列说法正确的是（）A．﹣a＜0 B．|a|＞0 C．a2+1＞0 D．＝1【分析】根据有理数的绝对值的非负性、偶次方的非负性解答．【解答】解：当a＜0时，﹣a＞0，A错误；|a|≥0，B错误；∵a2≥0，∴a2+1＞0，C正确；＝±1，D错误；故选：C．二．填空题（共6小题）11．下列有理数﹣3，0，﹣，2中，最小的数是﹣3 ．【分析】根据有理数的大小比较的法则分别进行比较即可．【解答】解：∵﹣3＜﹣＜0＜2，∴最小的数是﹣3；故答案为：﹣3．12．笔尖在纸上快速滑动写出一个又一个字，用数学知识可以理解为点动成线．【分析】利用点动成线，线动成面，面动成体，进而得出答案．【解答】解：笔尖在纸上快速滑动写出一个又一个字，用数学知识解释为点动成线．故答案为：点动成线13．若m，n互为相反数，a，b互为倒数，则2（m+n）﹣3ab＝﹣3 ．【分析】根据互为相反数的两个数的和等于0可得m+n＝0，互为倒数的两个数的积等于1可得ab＝1，然后进行计算即可得解．【解答】解：∵m，n互为相反数，∴m+n＝0，∵a，b互为倒数，∴ab＝1，∴2（m+n）﹣3ab＝2×0﹣3×1＝﹣3．故答案为：﹣3．14．一个小立方块的六个面分别标有字母A，B，C，D，E，F，从三个不同的方向看到的情形如图所示，则字母C的对面是A．【分析】根据与A相邻的四个面上的数字确定即可．【解答】解：由图可知，A相邻的四个面上的字母是B、D、E、F，所以，字母C的对面是字母A．故答案为：A．15．已知有理数a在数轴上的位置如图，则a+|a﹣1|＝ 1 ．【分析】先根据a在数轴上的位置确定出a的符号，再根据绝对值的性质把原式进行化简即可．【解答】解：由数轴上a点的位置可知，a＜0，∴a﹣1＜0，∴原式＝a+1﹣a＝1．故答案为：1．16．如图，一个长方体的表面展开图中四边形ABCD是正方形，则原长方体的体积是12cm3．【分析】利用正方形的性质以及图形中标注的长度得出AB＝AE＝4cm，进而得出长方体的长、宽、高进而得出答案．【解答】解：∵四边形ABCD是正方形，∴AB＝AE＝4cm，∴立方体的高为：（6﹣4）÷2＝1（cm），∴EF＝4﹣1＝3（cm），∴原长方体的体积是：3×4×1＝12（cm3）．故答案为：12cm3．三．解答题（共6小题）17．计算题（1）（﹣15）﹣（﹣23）﹣（+35）+117（2）（﹣1）×÷（﹣0.25）÷（﹣8）（3）（﹣1+）÷（﹣）（4）﹣24﹣（﹣9）÷×（﹣）×|﹣5|【分析】（1）减法转化为加法，再进一步计算可得；（2）除法转化为乘法，约分可得答案；（3）除法转化为乘法，再利用乘法分配律计算可得；（4）根据有理数的混合运算顺序和运算法则计算可得．【解答】解：（1）原式＝﹣15+23﹣35+117＝﹣50+140＝90；（2）原式＝﹣××（﹣4）×（﹣）＝﹣1；（3）原式＝（﹣+）×（﹣24）＝﹣10+27﹣4＝13；（4）原式＝﹣16﹣（﹣9）××（﹣）×5＝﹣8﹣8＝﹣16．18．一个几何体由几个大小相同的小立方块搭成，从上面观察这个几何体，看到的形状如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，请画出从正面、左面看到的这个几何体的形状图．【分析】由已知条件可知，从正面看有2列，每列小正方形数目分别为3，4；从左面看有2列，每列小正方形数目分别为4，1．据此可画出图形．【解答】解：如图所示：．19．某检修小组从A地出发，在东西向的马路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中七次行驶纪录如下．（单位：km）（1）求收工时，检修小组在A地的何方向？距离A地多远？（2）在第几次纪录时距A地最远？（3）若汽车行驶每千米耗油0.4升，问从A地出发，检修结束后再回到A地共耗油多少升？【分析】（1）把所有行驶记录相加，再根据正数和负数的意义解答；（2）分别写出各次记录时距离A地的距离，然后判断即可；（3）把所有行驶记录的绝对值相加，再乘以0.4计算即可得解．【解答】解：（1）﹣4+7﹣9+8+6﹣5﹣2＝1答：在A地的东面1km处（2）第一次距A地|﹣4|＝4千米；第二次：|﹣4+7|＝3千米；第三次：|﹣4+7﹣9|＝6千米；第四次：|﹣4+7﹣9+8|＝2千米；第五次：|﹣4+7﹣9+8+6|＝8千米；第六次：|﹣4+7﹣9+8+6﹣5|＝3千米；第七次：|﹣4+7﹣9+8+6﹣5﹣2|＝1千米第5次记录是离A地最远（3）从出发到收工汽车行驶的总路程：|﹣4|+|+7|+|﹣9|+|+8|+|+6|+|﹣5|+|﹣2|+|1|＝42（km）从出发到收工共耗油：42×0.4＝16.8（升）．答：从出发到收工共耗油16.8．20．有若干个数，第一个记为a1，第二个记为a2，第三个记为a3…．若a1＝﹣，从第2个数起，每个数都等于“1与它前面那个数的差的倒数”．（1）计算a2，a3，a4的值．（2）根据以上计算结果，直接写出a1998，a2006的值．【分析】（1）首先根据已知求得a2，a3，a4的值即可；（2）由上面的结果，然后找到这组数的循环规律即可求解．【解答】解：（1）∵a1＝﹣，∴a2＝＝，a3＝＝3；a4＝＝﹣；（2）由上面计算得出：，3，﹣每3个数循环一次．1998÷3＝666，则a1998＝a3＝3，2006÷3＝668…2，则a2006＝a2＝．21．已知有一个长为5cm，宽为3cm的长方形，若以这个长方形的一边所在的直线为轴，将它旋转一周，请分别求出所得的几何体的表面积和体积．【分析】以不同的边为轴旋转一周，可以得到底面半径为3cm，高为5cm，或者得到底面半径为5cm，高为3cm的圆柱体，分别求出结果即可．【解答】解：（1）以长为5cm的边为轴旋转一周：表面积：π×32×2+2π×3×5＝48πcm2，；体积：π×32×5＝45πcm3，（2）以宽为3cm的边为轴旋转一周：表面积：π×52×2+2π×5×3＝80πcm2，；体积：π×52×3＝75πcm3，答：所得的几何体的表面积和体积为48πcm2，45πcm3或80πcm2，75πcm3，22．A、B、C三点在数轴上，点A表示的数是﹣4，从点A出发向右平移7个单位长度得到点B．（1）求出点B表示的数，画一条数轴并在数轴上标出点A和点B；（2）若此数轴在一张纸上，将纸沿某一条直线对折，此时B点与表示数﹣1的点刚好重合，折痕与数轴有一个交点D，求点D表示的数的相反数（原卷无此问）；（3）在数轴上有一点C，点C到点A和点B的距离之和为11，求点C所表示的数；（4）A、B从初始位置分别以1单位长度/s和2单位长度/s的速度同时向左运动，是否存在t的值，使t秒后点B到﹣2的距离与点A到原点距离相等？若存在请求出t的值；若不存在，请说明理由．【分析】（1）根据数轴上两点间的距离公式，可求出点B表示的数，然后在数轴上标出点A和点B即可；（2）根据对称可知点D到﹣1和3的距离相等，可求点D表示的数为：（﹣1+3）÷2＝1，进而求出点D表示的数的相反数为：﹣1；（3）分两种情况讨论：①当E点在A点的左边，②当E点在B点的右边，然后利用数轴上两点间的距离公式即可解答；（4）由t秒后点B到﹣2的距离与点A到原点距离相等，列出一元一次方程即可．【解答】解：（1）﹣4+7＝3，所以点B表示的数为3，将A、B两点标在数轴上如下图：（2）（﹣1+3）÷2＝1，则折痕与数轴有一个交点D表示的数为1，1的相反数为﹣1；（3）∵AB＝7，点E到点A和点B的距离之和为11，∴点E应在线段AB的外，分两种情况：①当E点在A点的左边，设E点表示数为x，∵|EA|＝|x﹣（﹣4）|＝﹣x﹣4，|EB|＝|x﹣3|＝3﹣x，∴（﹣x﹣4）+（3﹣x）＝11，解得：x＝﹣6，所以此时E点所表示的数为：﹣11，②当E点在B点的右边，设E点表示数为x，∵|EA|＝|x﹣（﹣4）|＝x+4，|EB|＝|x﹣3|＝x﹣3，∴（x+4）+（x﹣3）＝11，解得：x＝5，所以此时E点所表示的数为：5，故若点E到点A和点B的距离之和为11，则点E所表示的数为：﹣6或5；（4）存在．理由：t秒时A点运动了t个单位长度，运动到﹣4﹣t的位置，B点运动了2t个单位长度，运动到3﹣2t的位置，因为此时点B到﹣2的距离和点A到原点距离相等，所以①3﹣2t+2＝4+t，解得：t＝，②﹣2﹣3+2t＝4+t；解得t＝9．故当t＝或9s时，点B到﹣2的距离与点A到原点距离相等．。