2014年国家公务员考试行测答题技巧：十字交叉法的运用推广

在前面一篇文章里我们已经初步介绍过如何利用十字交叉法来解决增长率的问题，可以通过简单的判断来得出正确答案，而前面讲的主要的是一步观察就可以排除另外三个选项，得出正确答案，如果这个选项的设置不能一次性排除该如何进一步的解决呢?难道这个时候必须计算吗?这肯定是不需要的，不然不等于前面做的全是无用功，接下来中公教育专家进一步的来介绍资料分析中十字交叉法的应用。

在化学里两种溶液混合，如果两种溶液的量是完全一样的，那么我们知道他们混合之后的溶液浓度肯定就是两种溶液浓度的平均值，进一步的我们可以得出，如果一种溶液偏多，那么溶液浓度肯定是平均值接近溶液量比较多的浓度，同样的，整体的增长率介于部分增长率之间，并且是平均值偏向比重大的那个部分的增长率。

接下来我们来看一道例题。

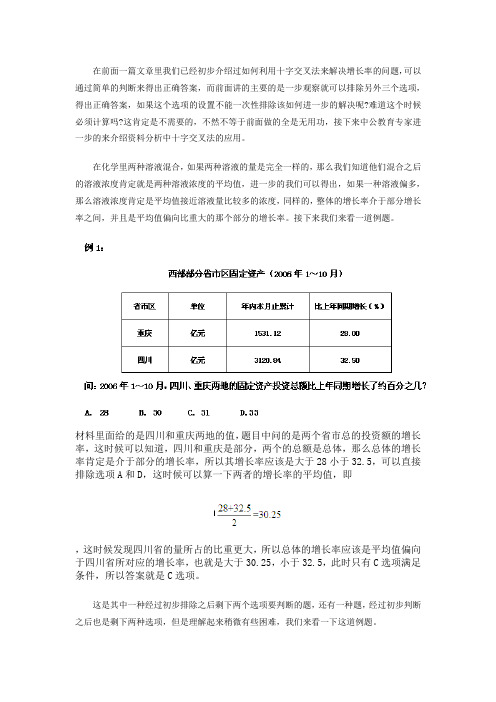
材料里面给的是四川和重庆两地的值，题目中问的是两个省市总的投资额的增长率，这时候可以知道，四川和重庆是部分，两个的总额是总体，那么总体的增长率肯定是介于部分的增长率，所以其增长率应该是大于28小于32.5，可以直接排除选项A和D，这时候可以算一下两者的增长率的平均值，即，这时候发现四川省的量所占的比重更大，所以总体的增长率应该是平均值偏向于四川省所对应的增长率，也就是大于30.25，小于32.5，此时只有C选项满足条件，所以答案就是C选项。

这是其中一种经过初步排除之后剩下两个选项要判断的题，还有一种题，经过初步判断之后也是剩下两种选项，但是理解起来稍微有些困难，我们来看一下这道例题。

例 2. 2008年，某省农产品进出口贸易总额为7.15亿美元，比上年增长25.2%。

其中，出口额为5.02亿美元，增长22.1%;进口额为2.13亿美元，增长33.2%。

问：2008年，该省农产品外贸顺差比上年增长了( )。

A.5%B.15%C.25%D.35%这是国考真题，这题目拿到之后就感觉要算非常困难，如果再不了解顺差什么意思，这种题目基本就可以说根本没有办法做了，所以一些常识性的概念还是要了解一下的，接下来我们来分析一下这道题。

在近几年的行测资料分析部分，往往会涉及到部分和整体的增长率，此时，十字交叉就能成功的解答此类问题。

十字交叉的原理我们在这就不详细的讲解了，红麒麟公考专家提醒你，在行测资料分析使用十字交叉，一般应用于求整体（部分）的增长率或者是求比重的试题中，且要活学活用。

一、十字交叉最浅显应用资料分析的试题往往会涉及到三个指标，两个部分、一个整体，我们依据十字交叉可以得到，整体的增长率必然处于部分增长率之间，此时，比较仁慈的考官，就会在设置选项的时候，让我们能够很容易的排除三个选项，直接得到答案，来看个试题。

******************************************************************************* ******【例1】2008年1~8月，公路客运量比上年同期增长（）。

A．6.9% B．7.4% C．7.9% D．11.7% 整体：1~9月公路客运量；部分：1~8月公路客运量增长11.4%;9月公路客运量增长7.4%；整体的在7.4%~11.4%之间，选C。

******************************************************************************* ******二、十字交叉稍变态应用虽说，整体的增长率处于部分的增长率之间，但是有的时候，试题往往给出的选项，只允许我们排除其中的两个，剩下的也无法排除，此时就要稍稍分析一下基期各部分占整体的比重的大小，来分析整体的增长率到底是偏向哪个部分，即可以将剩余的两个选项，排除掉一个，剩下的一个就是正确答案。

在这肯定注意到，为什么要分析基期的比重，而不是末期的比重呢?因为在这里面涉及了增长率，这就暗含着增长量这个等式，我们具体来看一下。

******************************************************************************* ******整体：末期增长率：r，基期值：R；部分：末期增长率a、b，基期值：A、B；等量关系：A×a+B×b=R×r，A×a+B×b=（A+B）×r；变形：A：B=（r-b）：（a-r）。

行测备考：十字交叉法的应用在加权平均数的相关题型中，由于数量关系复杂，列方程做比较困难，十字交叉法能轻松解决这一问题。

十字交叉法经常运用于浓度、比重、人口、平均分等问题的求解，同时也可以运用于某些较为复杂的问题中。

在数学运算及资料分析中经常用到，达到行测考场上的“秒杀”。

下面我们首先学习下十字交叉法的原理。

十字交叉法使用时要注意几点：第一点：用来解决两者之间的比例关系问题。

第二点：得出比例关系是基数的比例关系。

第三点：总均值放中央，右侧对角线上，大数减小数。

下面我们通过例题来看一下十字交叉法在浓度问题中的应用。

【例1】有100克溶液，第一次加入20克水，溶液的浓度变成50%;第二次再加入80克浓度为40%的同种溶液，则溶液的浓度变为( )A. 45%B. 47%C. 48%D. 46%【解析】本题相当于是120克50%的溶液与80克40%的溶液混合，我们利用“十字交叉法”，把选项代入到其中，很明显只有D选项46%得出的比例等于120:80=3:2.【例2】红酒桶中有浓度为68%的酒，绿酒桶中有浓度为48%的酒，若每个酒桶中取若干混合后，酒浓度为52%;若每个酒桶中取酒的数量比原来都多12 升，混合后的酒浓度为53.2%。

第一次混合时，红酒桶中取的酒是( )。

A.17.8 升B.19.2 升C.22.4 升D.36.3 升【解析】运用“十字交叉法”，易知第一次混合前的质量比为1:4，所以假设第一次分别取x，4x升，再用十字交叉得到第二次混合前的质量比为13:37，所以(x+12):(4x+12)=13:37，得到x=19.2，选择B。

【例3】烧杯中装了100克浓度为10%的盐水，每次向该烧杯中加入不超过14克浓度为50%的盐水，问最少加多少次之后，烧杯中的盐水浓度能达到25%?(假设烧杯中盐水不会溢出)( )A.6B. 5C. 4D. 3解析：运用“十字交叉法”，易知所以至少要加60克，每次最多14克，至少5次。

⾏测资料分析技巧：⼗字交叉法 任何⼀场考试取得成功都离不开每⽇点点滴滴的积累，下⾯由店铺⼩编为你精⼼准备了“⾏测资料分析技巧：⼗字交叉法”，持续关注本站将可以持续获取更多的考试资讯！⾏测资料分析技巧：⼗字交叉法 ⼗字交叉法主要解决的就是⽐值的混合问题，在公务员考试的过程中，资料分析部分解题经常⽤的⼀种解题⽅法。

它应⽤起来快速、准确、⽅便，为我们考试中秒杀题⺫提供了很⼤的助⼒。

那么接下来跟⼤家⼀起来学习⼗字交叉法。

⼀、⼗字交叉法概述 ⼗字交叉法是解决⽐值混合问题的⼀种⾮常简便的⽅法。

这⾥需要⼤家理解“⽐值”“混合”这两个概念。

⽐值：满⾜C/D的形式都可以看成是⽐值;混合：分⼦分⺟具有可加和性。

平均数问题、浓度问题、利润问题、增⻓率问题、⽐重等混合问题，都可以⽤⼗字交叉法来解决。

⼆、⼗字交叉法的模型 在该模型中，需要⼤家掌握以下⼏个知识点： 1、a和b为部分⽐值、r为整体⽐值、A和B为实际量 2、交叉作差时⼀定要⽤⼤数减去⼩数，保证差值是⼀个正数，避免出现错误。

这⾥假定a>b 3、实际量与部分⽐值的关系 实际量对应的是部分⽐值实际意义的分⺟。

如：平均分=总分/⼈数，实际量对应的就是相应的⼈数;浓度=溶质/溶液，实际量对应的就是相应的溶液质量;增⻓率=增⻓量/基期值，实际量对应的就是相应的基期值。

4、在这⾥边有三组计算关系 (1)第⼀列和第⼆列交叉作差等于第三列 (2)第三列、第四列、第五列的⽐值相等 (3)第1列的差等于第三列的和 三组计算关系是我们应⽤⼗字交叉法解题的关键，⼀定要记住并且灵活应⽤。

三、四种考查题型 1、求a，即已知总体⽐值、第⼆部分⽐值、实际量之⽐，求第⼀部分⽐值。

例某班有⼥⽣30⼈，男⽣20⼈。

期中的数学考试成绩如下，全班总的平均分为76，其中男⽣的平均分为70。

求全班⼥⽣的平均分为多少? 解析：平均分=总分/⼈数，是⽐值的形式。

此题中，男⽣的平均分和⼥⽣的平均分混合成了全班的平均分，是⽐值的混合问题，可以⽤⼗字交叉法来解题。

2014国家公务员考试行测:神奇的十字交叉法行测考试是一种倾向性测试，是一种非精确性测试，因此在考试当中不需要按照常规的方法来做题目，按常规列方程等等必然会做题导致时间紧张。

尤其是在数学运算中，更是需要更多的技巧来快速的把正确答案选出来，十字交叉法作为一种替代方程法的快速解题方法，中公教育专家建议考生在考试中灵活应用。

首先来看该方法的应用环境：十字交叉法主要是解决混合平均问题，已知总体或部分的平均量，一共涉及五个量，若题中已知其中四个量，对应其位置，变可以求出五个量中的任意一个量。

中公教育专家在此具体说明：应用一：平均分问题若：已知一个班级，男生人数为x人，平均分为A，女生人数为y人，平均分为B，求这个班级的总体平均分。

(A>B)【实战例题1】某学校对其120名学生进行随机抽查体能测验，平均分是73分，其中男生的平均分是75分，女生的平均分是63分，男生比女生多多少人？A.70B.80C.60D.85男生人数 x 75 73-63 x73 ------- = ----女生人数（120-x） 63 75-73 120-x解得，x=100 所以100-20=80人应用二：溶液问题若：已知一瓶溶液的浓度为A%，另外一瓶的溶液浓度为B%，分别取x和y份进行混合，求得到的溶液浓度为多少。

(A>B)一瓶子： x A% ?-B% x? ----- = ----另外一瓶子：y B% A%-? y【实战例题2】已知在浓度为90%的甲瓶中取40g溶液，在浓度为60%的乙瓶中取20g溶液，进行混合，得到的溶液的浓度为多少？A.75%B.80%C.85%D.90%甲瓶： 40 90% x-60% 40x ----- = ----乙瓶： 20 60% 90%-x 20解得：x=80%应用三：利润问题若：已知某商品的利润率为A%，售出x份，同一商品若利润率为B%，售出y份，求售出所有商品总的利润率为多少。

(A>B)该商品售出量x A ?-B x? ----- = ----该商品售出量y B A-? y【实战例题3】有一批商品，按照50%的利润定价，结果只售出70%后，剩下的商品决定打折出售，这样获得的全部利润是原来能获得利润的82%。

公务员行政职业能力测验考试每道题目平均做题时间约为50秒，时间紧，出题范围广，是考生公认的难度较大的考试。

而行测考试中的数量关系模块由于计算较多，难度较大成为众多考生的梦魇，因此必须转化思维，利用一些解题技巧来简化计算，提高解题速度。

十字交叉法在处理数学运算中的“加权平均问题”时可以明显简化运算，提高运算速度，本文就详细介绍一下十字交叉法的应用。

一、十字交叉法简介当数学运算题最终可以通过下式解出解出，我们就称这类问题为“加权平均问题”。

Aa+Bb=(A+B)r 此式可变化为A/B=(r-b)/(a-r)对于上式这种式子我们可以采用十字交叉的方法来计算，如下所示：A：a r-b\ /r =>A/B=(r-b)/(a-r)/ \B：b a-r二、适用题型十字交叉法最初在浓度问题上应用广泛，但在实际计算过程中，十字交叉法并没有将浓度问题有所简化，而是在以下几种题型中有更广泛的应用，解题速度也有明显提高。

1、数量分别为A与B的人口，分别增长a与b，总体增长率为r。

2、A个男生平均分为a，B个女生平均分为b，总体平均分为r。

3、农作物种植问题，A亩新品种的产量为a，B亩原来品种的产量为b，平均产量为r。

当然还有其他类似的问题，这类问题本质上都是两个不同浓度的东西混合后形成了一个平均浓度，这类问题都可以运用十字交叉法快速解题。

三、真题解析例1、某市现有70万人，如果5年后城镇人口增加4%，农村人口增加5.4%，则全市人口将增加4.8%，那么这个市现有城镇人口（）A、30万B、31.2万C、40万D、41.6万解析：城镇人口：4% 0.6% x\ /4.8%/ \农村人口：5.4% 0.8% 70-x所以0.6%/0.8%= x/（70-x），解得x=30，所以答案为A。

例2、某班男生比女生人数多80％，一次考试后，全班平均成绩为75分，而女生的平均分比男生的平均分高20％，则此班女生的平均分是（）。

A.84分B.85分C.86分D.87分解析：男生：x 1.2x-75 1.8\ /75/ \女生：1.2 x 75-x 1所以有（1.2x-75） /（75-x）=1.8，解得x=70，所以女生平均分为70×1.2=84，答案为A。

公考十字交叉法技巧公考就像一场激烈的战斗，而十字交叉法就像是我们手中的一件秘密武器。

这方法可神奇啦，就像一把万能钥匙，能打开很多公考题目中的难题之锁。

咱们先来看看十字交叉法在浓度问题中的应用。

比如说，有两种不同浓度的盐水，一种浓度高，一种浓度低，要把它们混合成一个特定浓度的盐水。

这就好比把两个不同口味的果汁混在一起，想要调出一个刚刚好的新口味。

如果我们知道了两种盐水的质量和浓度，就可以用十字交叉法轻松算出混合后盐水的质量比例。

这就像是把两种果汁的量按照一定比例混合起来，这个比例就藏在十字交叉法的计算里。

你说神奇不神奇？再说说在平均数问题里的应用吧。

想象有两个班级，一个班级平均分高，一个班级平均分低，现在把这两个班级的学生合在一起算一个新的平均分。

这就像是把两堆不同大小的果子混在一起，然后算平均每个果子的大小。

十字交叉法呢，就能帮我们算出这两个班级学生数量的比例关系。

这就好像是找到了一个天平，能精准地衡量出两边的分量。

那这十字交叉法到底怎么用呢？其实很简单。

就拿前面的浓度问题来说，我们把两种盐水的浓度写在左边，混合后的浓度写在中间，然后交叉相减，得到的差值之比就是两种盐水质量的反比。

这就像玩一个数字游戏，按照规则走，答案就自然而然地出来了。

在平均数问题里也是一样的道理，把两个班级的平均分写在左边，混合后的平均分写在中间，交叉相减得到的差值之比就是两个班级人数的反比。

我们来举个具体的例子吧。

有A盐水浓度为30%，B盐水浓度为10%，混合后浓度为20%。

我们就按照十字交叉法来做，30%和10%写在左边，20%写在中间，30% - 20% = 10%，20% - 10% = 10%，这两个差值是相等的，所以A盐水和B盐水的质量之比就是1:1。

你看，是不是很简单？就像我们把不同颜色的积木按照一定的规则摆放，就能得出一个好看的造型一样。

十字交叉法在公考里可是相当实用的。

很多考生看到那些复杂的数量关系题就头疼，感觉像走进了一个迷宫，找不到出口。

十字交叉法是数学运算及资料分析中经常用到的一种解题方法，熟练运用可以大大提高各位考生在考场上的解题速度。

在平时的复习过程中应作为一个专题加以强化练习，以期达到行测考场上的“秒杀”。

十字交叉法最先是从溶液混合问题衍生而来的。

若有两种质量分别为A与B的溶液，其浓度分别为a与b，混合后浓度为r，则由溶质质量不变可列出下式Aa+Bb=(A+B)r，对上式进行变形可得A/B=r-b/a-r，在解题过程中一般将此式转换成如下形式：注意在交叉相减时始终是大的值减去小的值，以避免发生错误。

十字交叉法不仅仅可用于溶液混合问题，也可以应用于两部分混合增长率问题、平均分数、平均年龄等问题。

只要能符合Aa+Bb=(A+B)r这个式子的问题均可应用十字交叉法，交叉相减后的比值为对应原式中的A和B的比值。

例1 甲容器中有浓度为4%的盐水150克，乙容器中有某种浓度的盐水若干，从乙中取出450克盐水，放入甲中混合成浓度为8.2%的盐水。

问乙容器中盐水的浓度是多少?A.9.6%B.9.8%C.9.9%D.10%【解析】A。

【例2】某市现有70万人口，如果5年后城镇人口增加4%，农村人口增加5.4%，则全市人口将增加4.8%，那么这个市现有城镇人口()。

A.30万B.31.2万C.40万D.41.6万【解析】A。

【例3】(2011国考-76)某单位共有A.B.C.三个部门，三部门人员平均年龄分别为38岁，24岁，42岁，A和B两部门人员平均年龄为30岁，B和C两部门人员平均年龄为34岁，该单位全体人员的平均年龄为多少岁?A.34B.36C.35D.37【解析】C除了在数学运算中可以用到十字交叉法，在一些资料分析的题目中也可以运用十字交叉法，例如：【例4】(2011年917联考)2010年1~6月，全国电信业务收入总量累计完成14860.7亿元，比上年同期增长21.4%;电信主营业务收入累计完成4345.5亿元，比上年同期增长5.9%。

行测什么时候用十字交叉法公务员行测考试数学运算这部分, 经常要用到十字交叉法. 虽然很多里书和网页上写了很多关于十字交叉法, 但是目前还很少有人对什么情况下可以用十字交叉法来快速解题作出具体的叙述. 大多数只是针对某些问题给出解题方法. 对于十字交叉法具体的原理还没有做进一步详细的说明, 即使作了描述, 也比较抽象, 比如什么加权平均等. 为了使得对能否用十字交叉法作出迅速的判断, 我们将在本文里面就其中的原理作出简单明了的阐述以及给出判断的表达式, 然后给出具体的例子来说明它的应用以及相关的练习.希望大家看过本文之后不再对十字交叉法感到束手无策!!我们先给出十字交叉法的原理, 就是什么情况下我们就可以用十字交叉法.如果题目中给出两个平行的情况A, B, 满足条件a, b ; 然后A 和B 按照某种条件混合在一起形成的情况C, 满足条件c. 而且可以表示成如下的表达式. 那么这个时候就可以用十字交叉法. 判断式: A*a+B*b=(A+B)*c=C*c用十字交叉法表示:A a c-bc A/B=(c-b)/(a-c).B b a-c我们常见利用十字交叉法的情形有: 溶液混合问题, 增长率问题, 收益率问题, 平均数问题等.【例1】一杯含盐15％的盐水200克，要使盐水含盐20%，应加盐（ ）克。

A.14.5B.10 C .12.5 D.1520% , 200/x= (100%-20%)/(20%-15%)=80/5x 100% 20%-15%解出x=12.5克.【例2】一块试验田，以前这块地所种植的是普通水稻。

现在将该试验田的1/3种上超级水稻，收割时发现该试验田水稻总产量是以前总产量的1.5倍。

如果普通水稻的产量不变，则超级水稻的平均产量与普通水稻的平均产量之比是（）。

A. 5∶2B. 4∶3C. 3∶1D. 2∶1【解析】假设超级水稻的产量是x, 普通水稻的产量是1; 超级水稻是1/3, 普通水稻是2/3; 产量分别是x, 1; 那么混合就是1,产量是1.5,满足1/3*x+2/3*1=(1/3+2/3)*1.5, 所以可以利用十字交叉法.1/3 x 1.5-11.5 , (1/3)/ (2/3)=(1.5-1)/(x-1.5). 解出x=2.5, 比是2.5:1=5:2.2/3 1 x-1.5【例3】在一次法律知识竞赛中，甲机关20人参加，平均80分，乙机关30人参加，平均70分，问两个机关参加竞赛的人总平均分是多少?A．76 B．75 C．74 D．73【解析】假设总平均成绩是x, 满足20*80+30*70=(20+30)*x,所以可以用十字交叉法做.20 80 x-70x , 20/ 30=( x-70)/ 80-x). 解出x=74分.30 70 80-x【例4】某市现有人口70万, 如果5年后城镇人口增加4%, 农村人口增加5.4%, 则全市人口将增加4.8%, 那么这个市现有城镇人口多少万?A.30万B.31.2万C.40万D.41.6万【解析】假设现有城镇人口x万, 农村人口70-x万,满足: 4%*x+5.4%*(70-x)=(x+70-x)*4.8%所以可以用十字交叉法.x 4% 5.4% -4.8%4.8% , x/ (70-x)=(5.4% -4.8%)/ (4.8%-4%). 解出x=30.70-x 5.4% 4.8%-4%练习1.一批商品，按期望获得50%的利润来定价，结果只销掉70%的商品，为了尽快把剩下的商品全部卖出，商店决定按定价打折扣出售，这样所获得的全部利润是原来期望利润的82%，则打了多少折出售？( )A. 八折B. 八五折C. 九折D. 九五折2. 把浓度为20％、30％和50％的某溶液混合在一起，得到浓度为36％的溶液50升。

2014年山东公考行测数量关系备考之十字交叉2014年山东省公务员考试将在6月下旬举行，相对于2013年来说，时间推迟了将近3个月，这就意味着考生的备考时间增加了三个月，在2014年，山东省采用的命题形式依然是独立命题，这是继2012年脱离联考之后的，第三次独立命题，试题的形式应该会继承2013年的形式，难度应该会有所上升，这对于我们备考来说，一定要熟练的掌握相关基础知识，并且熟悉命题者的出题思维，灵活的解答试题。

十字交叉，是解答行测数量关系问题的一种方法，这种方法主要应用在解答混合问题里面，比如溶液的混合，也就是解答浓度问题，不过从近两年山东省公务员考试的试题来看，对于十字交叉的考查，主要集中在平均数问题上面，这类问题，我们只要分析出部分以及整体，就能快速的逃入到十字交叉的公式，进而解答试题。

【山东2013-60】某单位共有职工72人，年底考核平均分数为85分。

根据考核分数，90分以上的职工评为优秀职工。

已知优秀职工的平均分数为92分，其他职工的平均分数是80分，问优秀职工的人数是多少?A.12B.24C.30D.42【答案】C【解析】本题考查的是十字交叉。

根据题意，假设优秀职工的人数为x，非优秀职工的人数为y，则依据十字交叉原理有：x 92 85-80=585y 80 92-85=7从而有x/y=5/7，那么x的数值一定被5整除，结合选项，只有C选项符合。

【山东2012-53】某单位依据笔试成绩招录员工，应聘者中只有1/4被录取。

被录取的应聘者平均分比录取分数线高6分，没有被录取的应聘者平均分比录取分数线低10分，所有应聘者的平均分是73分。

问录取分数线是多少分?A. 80B. 79C. 78D. 77【答案】B【解析】本题考查的是十字交叉。

根据题意，假设录取分数线是x分，则被录取的平均分为x+6，没有被录取的平均分为x-10。

则依据十字交叉原理有：1/4 x+6 83-x733/4 x-10 x-67从而有录取/未录取=(83-x)/(x-67)=1/3，解得x=79。