基于粗糙集扩展模型的维修级别分析决策研究
- 格式:pdf
- 大小:297.27 KB
- 文档页数:4

基于粗糙集的汽车故障诊断研究本文是将粗糙集理论与汽车故障检测技术结合起来,可以分析诊断信号与故障类型之间的关系,从而对了解汽车故障机理,缩短维修时间,延长汽车的运营周期、减少和预防事故起到积极的推动作用。
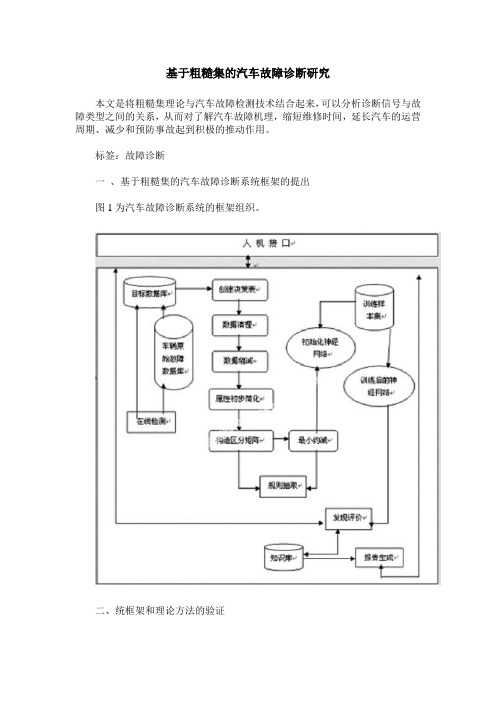
标签:故障诊断一、基于粗糙集的汽车故障诊断系统框架的提出图1为汽车故障诊断系统的框架组织。
二、统框架和理论方法的验证由于汽车故障的产生主要是由于零件之间的自然磨损或异常磨损、零件与有害物质接触造成的腐蚀、零件在长期交变载荷下的疲劳、在外载荷及温度残余内应力下的变形、非金属零件及电器元件的老化、偶然的损伤等原因造成的。
当某处发生故障时,必然使原有供油状态发生变化,燃油流动的压力和流速等参数也会产生相应的改变,反映在压力波形上将导致波形形态和波形参数值的变化,因此通过对压力波形的分析,可以提取足够的特征信息,判别系统的工作状态,从而达到诊断系统故障的目的。
1.数据准备本文将五档手动变速器三档振动信号经小波包分解在各频带能量序列作为学习样本,并直接输入目标数据库。
2.数据离散化2.1模糊c一均值聚类在模糊c一均值聚类方法中,每一个数据点按照一定的模糊隶属度隶属于某一聚类中心。
每种条件属性分为三类,模糊c一均值聚类迭代46次后,求得的三个聚敛中心点和依此取得的断点值如表1。
表1模糊c一均值法聚类求得的中心点和断点三、粗糙集属性的提取1.决策表的建立以模糊c一均值法的聚类结果离散原始数据,建立决策表,记为决策系统Sl。
各属性值以0, 1, 2代替,如属性值在(0,Cut-pointl ]间记为0,依此类推。
表2决策表S12.数据缩减和属性初步简化根据构建车辆故障诊断数据挖掘系统,利用知识的充分性理论对决策表进行简化,消去决策表中的重复信息。
3.建立区分矩阵,得出约简对决策表S1, S2和S3建立区分矩阵。
由区分矩阵,经区分函数析取计算后,可得到最小约简。
分为三类后,利用最小约简也能达到很高分类精度和分类质量。



基于粗糙集理论的不确定信息系统及其决策研究随着云计算、大数据等新兴信息技术的广泛应用,各领域的数据急剧增长,这其中结构化数据仍然是数据的主要表现形式之一。
在这些数据中往往含有大量冗余的与不确定性数据,从而导致模式分类的处理能力与决策的辨识能力的降低。
区间值型数据与直觉模糊型数据作为信息的不确定与不充分的表现形式是两种重要的结构化数据。
如何从这两类不确定数据中发现有价值的信息和规律为管理者提供决策参考,仍然是管理决策科学领域中的研究热点之一。
粗糙集理论作为数据挖掘领域中的重要方法之一,其最显著的优点是在于不需要提供解决问题所需要的数据以外的先验知识,只要面向数据本身提供的信息,就可以实现对数据的分类与决策规则的获取等任务。
该理论已经被成功地应用于机器学习、数据挖掘、决策分析等诸多领域。
经典的粗糙集模型是建立在等价关系基础之上的,要求相对较为严格,处理不确定性数据存在着局限性。
因此,经典粗糙集模型的各种扩充对于不确定信息系统的知识约简与决策规则的获取具有极其重要的意义。
本文以粗糙集为工具,结合国内外的研究现状,较为系统的研究了单粒度与多粒度背景下区间值信息系统与直觉模糊信息系统的属性约简及其决策规则的获取问题,同时面向交通事故因素关联分析问题构造了一种群决策属性粗糙集模型并加以应用。
本文的主要创新性工作如下:(1)分析了现有的容差关系在区间值聚类中的不足,本文构建了一种模糊等价关系,基于此关系分别从单粒度与多粒度视角建立了区间值信息系统的粗糙集模型,给出分辨矩阵、属性约简的判定定理及其属性约简的方法,基于模糊等价关系定义了区间值决策系统上的决策规则置信度因子,给出了决策规则的支持定理及其决策规则的获取方法。
(2)分别从单粒度与多粒度角度建立了直觉模糊信息系统的粗糙集模型。
定义了直觉模糊信息系统上的偏序关系及其分辨矩阵,给出了有效的属性约简方法。
基于直觉模糊决策系统的分类质量给出了相对属性约简的计算方法,研究了相对属性重要度以及序决策规则的提取方法,建立了直觉模糊信息系统的乐观多粒度与悲观多粒度两种模型,分析了相应的性质及其与单粒度模型的联系与区别,给出了基于多粒度序关系的决策规则置信度因子及其决策规则的获取方法。

面向不确定信息系统的粗糙集扩展模型研究粗糙集理论是由波兰学者Pawlak提出的一种进行数据分析的新型工具,已被成功运用于数据挖掘、模式识别以及决策分析等领域。
经典的粗糙集理论建立在等价关系的基础上,可以处理有限的知识分辨能力引起的不确定性问题,但对数据本身的不确定性缺乏相应的处理机制。
因此,面对海量的不确定性数据,通过扩展粗糙集理论来研究不确定信息系统的知识获取,具有重要的理论意义和应用价值。
本文针对信息的不完备和模糊性,以知识约简和决策规则获取为目的,对不确定环境下的粗糙集扩展模型及其应用进行了系统的研究。
主要内容如下:1)针对特征优势关系在对象分类方面的不足,提出一种改进的特征优势关系,并给出不完备序信息系统的粗糙决策模型,与已有模型的对比分析结果表明,在近似分类精度和近似分类质量方面,改进后的粗糙决策模型都要优于已有的粗糙决策模型。
最后,为简化获取的决策规则,利用改进后的特征优势关系,提出基于区分矩阵的知识约简方法。
2)在集值序信息系统中,定义一种δ-优势关系来进行对象的分类,并给出集值序信息系统的不确定性度量;基于δ-优势关系的粗糙集扩展模型,研究了集值序决策系统的知识约简和决策规则获取;另外,依据对象间的不同优势程度,在集值序信息系统定义一种不依赖于任何未知参数的模糊优势关系,并提出基于模糊优势关系的模糊区分矩阵,对此去模糊化处理后,获得了集值序信息系统的知识约简。
3)在集值序信息系统的基础上,研究了决策属性值为模糊性概念的集值序模糊决策系统的粗糙决策问题。
首先将优势关系粗糙集模型推广至模糊情形,然后,基于模糊决策集的下、上近似,给出集值序模糊决策系统下、上近似约简的定义,结合下、上近似协调集的判定定理,提出了基于区分矩阵的下、上近似约简方法,并提取出简化的模糊决策规则。
4)在直觉模糊信息系统中引入优势关系,提出一种基于优势关系的直觉模糊多属性决策方法;对粗糙集模型进行了直觉模糊环境下的扩展,并给出直觉模糊粗糙集的不确定性度量;针对含有多个直觉模糊决策值的直觉模糊决策系统,提出基于区分矩阵的分布约简和分配约简方法。
粗糙集理论在设备故障诊断中的应用研究引言:设备故障诊断一直是工业生产中的重要环节,它能够帮助企业及时发现和解决设备故障,提高生产效率和产品质量。
而粗糙集理论作为一种有效的数据分析方法,近年来在设备故障诊断中得到了广泛的应用。
本文将探讨粗糙集理论在设备故障诊断中的应用研究,并分析其优势和不足之处。
一、粗糙集理论概述粗糙集理论是由波兰学者Zdzisław Pawlak于1982年提出的,它是一种基于信息粗糙度的数据分析方法。
该理论通过将数据集分为不同的等价类,来实现数据的分类和决策。
粗糙集理论的主要思想是在不完备和不确定的信息条件下,通过寻找数据集中的重要属性和规则,来进行有效的决策和分类。
二、粗糙集理论在设备故障诊断中的应用1. 数据预处理设备故障诊断需要大量的数据支持,而这些数据往往存在噪声和冗余。
粗糙集理论可以通过数据预处理的方法,去除噪声和冗余,提取出数据集中的重要特征。
例如,可以通过粗糙集理论中的属性约简方法,选择出对设备故障诊断具有重要意义的属性,从而减少数据集的维度,提高诊断的准确性。
2. 特征选择设备故障诊断中,特征选择是一个关键的问题。
传统的特征选择方法往往依赖于领域专家的经验,而粗糙集理论可以通过分析数据集中的属性依赖关系,自动选择出对设备故障诊断具有重要意义的特征。
这种基于数据的特征选择方法,能够避免主观因素的干扰,提高诊断的准确性和可靠性。
3. 故障诊断模型构建在设备故障诊断中,构建准确可靠的故障诊断模型是非常重要的。
粗糙集理论可以通过分析数据集中的属性依赖关系,构建出针对不同故障类型的故障诊断模型。
例如,可以通过粗糙集理论中的近似集合方法,将数据集中的故障样本划分为不同的等价类,从而得到不同故障类型的特征集合,进而构建出相应的故障诊断模型。
三、粗糙集理论在设备故障诊断中的优势1. 适应不完备和不确定的信息设备故障诊断中,数据往往存在不完备和不确定的情况,而粗糙集理论正是基于这种情况下的数据分析方法。
a decision analysis method based on roughset -回复问题:决策分析中的粗糙集方法是什么?它的步骤是什么?引言:在现代社会中,决策逐渐成为各个领域中的重要环节。
为了实现有效的决策,研究者们提出了各种不同的方法和技术。
其中,基于粗糙集的决策分析方法为决策制定者提供了一种直观且有效的工具。
本文将详细介绍基于粗糙集的决策分析方法的步骤和应用。
一、粗糙集理论概述:粗糙集理论最早由波兰学者Zdzislaw Pawlak于1982年提出,它是一种用于处理不完全和不确定信息的数学工具。
粗糙集理论的核心思想是根据信息的不确定程度,将对象的属性分为精确可确定的部分和模糊不确定的部分。
通过使用“下近似”和“上近似”的概念来描述集合的不确定性程度。
二、决策分析基本步骤:基于粗糙集的决策分析方法通常包括以下步骤:1. 确定决策问题及目标:首先,需要明确决策的具体问题,并清晰定义决策的目标。
例如,某公司要决定使用哪种广告方式提升销售量。
2. 建立决策规则集:收集并整理相关的决策规则。
决策规则是根据已有知识和经验制定的一系列规则,用于将决策目标与决策条件联系起来。
3. 构建决策表:根据收集到的决策规则,建立一个决策表。
决策表是由决策规则的条件与结果组成的表格,用于对决策情况进行归纳和分析。
4. 确定属性重要性:根据问题的具体情况和专家的建议,确定各个属性的重要性。
属性的重要性反映了属性对决策结果的影响程度。
5. 粗糙集约简:利用粗糙集理论中的约简方法,对决策表进行简化。
约简后的决策表可以更好地反映决策规则中的核心信息,减少决策问题的复杂度。
6. 决策推理:根据已经简化的决策表,进行决策推理。
根据决策条件和已知属性,推导出最佳的决策结果。
7. 决策评价:评价决策结果的有效性和准确性。
根据实际情况和决策目标的实现程度,对决策结果进行评估和分析。
8. 反馈和调整:根据评估结果,对决策方法和过程进行反馈和调整。