2017粤教版高中物理必修2第四章《机械能和能源》章末整合
- 格式:doc
- 大小:746.50 KB
- 文档页数:16



第4节 机械能守恒定律新课教学1、推导过程:以做自由落体运动的物体的运动过程为例进行分析分析:小球运动过程中只受到重力的作用,所以依据动能定理 可得:21222121mv mv W G -=① 另外,由重力做功和重力势能变化之间的关系可得: 21mgh mgh W G -= ②由①②可得21222121mv mv -21mgh mgh -= 所以2222112121mv mgh mv mgh +=+ 或2211K P K P E E E E +=+结论:机械能守恒定律2、机械能守恒定律在只有重力做功的情况下,物体的动能和重力势能发生相互转化,而总的机械能保持不变,这个结论叫做机械能守恒定律。
过渡:由学生分析机械能守恒定律成立的条件,并逐渐展开。
3、机械能守恒定律成立的条件只有重力做功(1)只受重力作用;(2)物体受几个力的作用,但只有重力做功;(3)其它的力也做功,但其它力的总功为零;(4)没有任何力做功,物体的能量不会发生变化。
跟踪练习:课本P78/2过渡:在前面分析过的例子中,不仅有动能和重力势能相互转化的情况,也有动能和弹性势能相互转化的情况,后者转化的过程中,机械能是否也是守恒的呢?4、机械能守恒定律的推广若物体运动过程中,不只是只有重力做功,还有弹力做功,或只有弹力做功时,物体的动能和弹性势能相互转化,机械能的总量也是保持不变的。
三、机械能守恒定律的应用1、验证性练习:课本练习 P78/12、应用性练习:课本练习 P78/5四、本课小结ABh 1这节课我们主要以自由落体运动为例,讨论了势能和动能相互转化的情况,并总结出了在只有重力或弹力做功的情况下。
物体的机械能是守恒的结论,同学们课下要认真体会守恒定律的意义,并能够判断定律成立的条件并应用定律求解相关的问题。
五、板书设计第4节 机械能守恒定律1.在只受重力(或弹力)做功的情况下,物体的动能和重力势能(或弹性势能)相互转化,但机械能的总量保持不变.2.数学表达式:1212222121mgh mv mgh mv +=+3.机械能守恒的条件:只有重力做功a 、物体只受重力,不受其他的力。
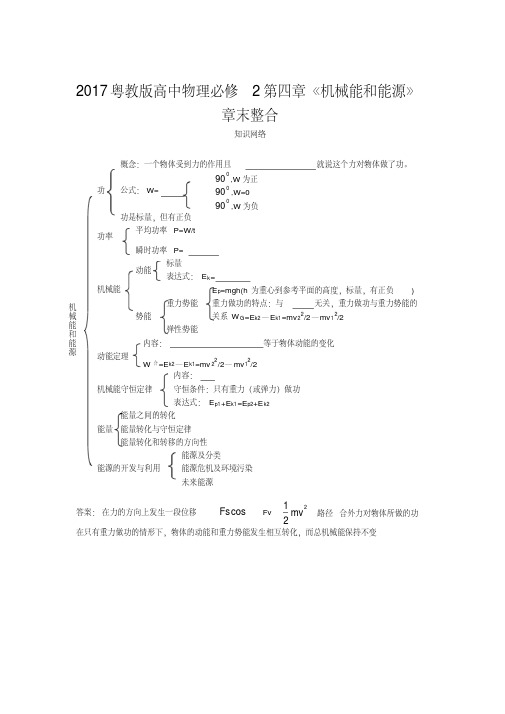


2017粤教版高中物理必修2第四章《机械能和能源》章末整合知识网络答案:在力的方向上发生一段位移 αcos Fs Fv221mv 路径 合外力对物体所做的功 在只有重力做功的情形下,物体的动能和重力势能发生相互转化,而总机械能保持不变090<α,W 为正机械能和能源功概念:一个物体受到力的作用且 就说这个力对物体做了功。
公式:090=α,W=0090>α,W 为负功是标量,但有正负动能标量表达式:E k =机械能重力势能 关系W G =E k2—E k1=mv 22/2—mv 12/2E p =mgh(h 为重心到参考平面的高度,标量,有正负)弹性势能势能 重力做功的特点:与 无关,重力做功与重力势能的动能定理内容: 等于物体动能的变化W 合=E k2—E k1=mv 22/2—mv 12/2能源的开发与利用 能源及分类能源危机及环境污染未来能源能量转化和转移的方向性能量之间的转化 能量转化与守恒定律能量 瞬时功率P=平均功率P=W/t功率表达式:E p1+E k1=E p2+E k2内容:守恒条件:只有重力(或弹力)做功机械能守恒定律专题突破专题一 功的判断与计算1.判断力F 做功的方法(1)看力F 与位移s 的夹角α的大小.若α=90°,则F 不做功;若α<90°,则F 做正功;若α>90°,则F 做负功(或物体克服力F 做功).此法常用于判断恒力做功的情况.(2)看力F 与物体速度v 方向的夹角α的大小.若α=90°,则F 不做功;若α<90°,则F 做正功;若α>90°,则F 做负功.此法常用于曲线运动情况.(3)看物体间是否有能量转化.“功是能量转化的量度”,若有能量转化(增大或减小),则必是有力做功.此法常用于两个相联系的物体做曲线运动的情况.【例1】如图4-1所示,一辆玩具小车静止在光滑的水平导轨上,一个小球用细绳悬挂在车上,由图中位置无初速度释放,则小球在下摆过程中,下列说法正确的是( )图4-1A .绳的拉力对小球不做功B .绳的拉力对小球做正功C .小球所受的合力不做功D .绳的拉力对小球做负功解析:在小球向下摆动的过程中,小车向右运动,绳对小车做正功,小车的动能增加;因为小球和小车组成的系统机械能守恒,且小车的机械能增加,则小球的机械能一定减小,所以绳对小球的拉力做负功.答案:D2.变力做功的计算方法对于功的定义式W =αcos Fs ,其中的F 是恒力,适用于求恒力做功,其中的s 是力F 的作用点发生的位移,α是力F 与位移s 的夹角。
在高中阶段求变力做功问题,既是学生学习和掌握的难点,也是教师教学的难点。
求变力做功的方法很多,比如用动能定理、功率的表达式Pt W =、功能关系、平均值、s F -图像、微元累积法、转换参考系等来求变力做功。
(1)运用功的公式求变力做功 求某个过程中的変力做功,可以通过等效法把求该変力做功转换成求与该変力做功相同的恒力的功,此时可用功定义式W =αcos Fs 求恒力的功,从而可知该変力的功。
等效转换的关键是分析清楚该変力做功到底与哪个恒力的功是相同的。
【例2】人在A 点拉着绳通过一定滑轮吊起质量m=50Kg 的物体,如图1所示,开始绳与水平方向夹角为ο60,当人匀速提起重物由A 点沿水平方向运动m s 2=而到达B 点,此时绳与水平方向成ο30角,求人对绳的拉力做了多少功? 【解析】人对绳的拉力大小虽然始终等于物体的重力,但方向却时刻在变,而已知的位移s 方向一直水平,所以无法利用W =αcos Fs 直接求拉力的功.若转换一下研究对象则不难发现,人对绳的拉力的功与绳对物体的拉力的功是相同的,而绳对物体的拉力则是恒力,可利用W =αcos Fs 求了!设滑轮距地面的高度为h ,则:()s h =-οο60cot 30cot人由A 走到B 的过程中,重物上升的高度h ∆等于滑轮右侧绳子增加的长度,即:οο60sin 30sin hh h -=∆,人对绳子做的功为:()()J J mgs h mg W 73213100013≈-=-=∆⋅=(2)运用动能定理求变力做功动能定理的表述:合外力对物体做功等于物体的动能的改变,或外力对物体做功的代数和等于物体动能的改变。
对于一个物体在某个过程中的初动能和末动能可求,该过程其它力做功可求,那么该过程中変力做功可求。
运用动能定理求变力做功关键是了解哪些外力做功以及确定物体运动的初动能和末动能。
【例3】如图2所示,原来质量为m 的小球用长L 的细线悬挂而静止在竖直位置.用水平拉力F 将小球缓慢地拉到细线与竖直方向成θ角的位置的过程中,拉力F 做功为( ) A. θcos FL B. θsin FL C. ()θcos 1-FL D. ()θcos 1-mgL【解析】很多同学会错选B ,原因是没有分析运动过程,对W=FLcosθ来求功的适用范围搞错,恒力做功可以直接用这种方法求,但变力做功不能直接用此法正确的分析,小球的运动过程是缓慢的,因而任一时刻都可看作是平衡状态,因此F 的大小不断变大,F 做的功是变力功,小球上升过程中只有重力和拉力做功,而整个过程的动能改变为零,可用动能定理求解:0=-'=+K KG F E E W W 所以 ()θcos 1-=-=mgL W W G F ,故D 正确。
(3)运用Pt W =求变力做功涉及到机车的启动、吊车吊物体等问题,如果在某个过程中保持功率P 恒定,随着机车或物体速度的改变,牵引力也改变,要求该过程中牵引力的功,可以通过Pt W =求変力做功。
【例4】质量为5000Kg 的汽车,在平直公路上以60kW 的恒定功率从静止开始启动,速度达到24m/s 的最大速度后,立即关闭发动机,汽车从启动到最后停下通过的总位移为1200m.Gο60ο30图1图2运动过程中汽车所受的阻力不变.求汽车运动的时间.【解析】牵引力是変力,该过程中保持功率P 恒定,牵引力的功可以通过Pt W =来求。
汽车加速运动的时间为1t ,由动能定理得:0F -Pt f 1=⋅s汽车达到最大速度时,牵引力和阻力大小相等,则m f m v F Fv P ⋅== 即mf v P F =可求得汽车加速运动的时间为s s v s Ps F t m f 502412001===⋅=关闭油门后,汽车在阻力作用下做匀减速直线运动至停止,由动量定理得:m mv t -=⋅0F -2f可求得汽车匀减速运动的时间为s s P mv F mv t m f m 48100060245000222=⨯⨯===则汽车运动的时间为:t =t 1+t 2=50s +48s =98s(4)运用功能关系求变力做功做功是能量转化的原因,做功是能量转化的量度,我们可以根据能量转化的情况来判断做功的情况,则给求変力做功提供了一条简便的途径。
运用功能关系求変力做功,关键是分清研究过程中有多少种形式的能转化,即有什么能增加或减少,有多少个力做了功,列出这些量之间的关系。
【例5】一个圆柱形的竖直井里存有一定量的水,井的侧面和底部是密闭的。
在井中固定地插着一根两端开口的薄壁圆管,管和井共轴,管下端未触及井底。
在圆管内有一不漏气的活塞,它可沿圆管上下滑动。
如图3所示,现用卷扬机通过绳子对活塞施加一个向上的力F ,使活塞缓慢向上移动。
已知圆管半径r=0.10m ,井的半径R=2r ,水的密度ρ=1.00×103kg/m 3 ,大气压P 0=1.00×105Pa ,求活塞上升H=9.00m 的过程中拉力所做的功(井和管在水面上及水面下的部分都足够长,不计活塞质量,不计摩擦,重力加速度g=10m/s 2)。
【解析】大气压P 0能够支撑的水柱高度为 m gp h 1000==ρ 从开始提升到活塞至管内外水面高度差为10m 的过程中,活塞始终与水面接触,设活塞上升1h ,管外液面下降2h ,则有:210h h h +=因液体体积不变,有:3122212=-=r R r h h πππ 得 H m h h <==5.74301 此过程拉力为変力,根据功能关系,对于水和活塞这个整体,其机械能的增量等于除重力以外其它力做功。
根据题意,则拉力做功等于水的重力势能的增量,即:图3J h h gh r E W 4211211018.12⨯=+=∆=ρπ 活塞从1h 上升到H 的过程中,液面不变,拉力F 是恒力,02P r F π=,则做功为: J h H P r h H F W 3102121071.4)()(⨯=-=-=π所求拉力所做的总功为:J W W W 4211065.1⨯=+=(5)运用F-S 图像中的面积求变力做功某些求変力做功的问题,如果能够画出変力F 与位移S 的图像,则F-S 图像中与S 轴所围的面积表示该过程中変力F 做的功。
运用F-S 图像中的面积求变力做功的关键是先表示出変力F 与位移S 的函数关系,再在画出F-S 图像。
【例6】用铁锤将一铁钉击入木块,设阻力与钉子进入木板的深度成正比,每次击钉时锤子对钉子做的功相同,已知第一次击后钉子进入木板1cm ,则第二次击钉子进入木板的深度为多少? 【解析】铁锤每次做功都是用来克服铁钉阻力做的功,但摩擦阻力不是恒力,其大小与深度成正比,F=kx ,以F 为纵坐标,F 方向上的位移x 为横坐标,作出F -x 图象,如图4,函数线与x 轴所夹阴影部分面积的值等于F 对铁钉做的功.由于两次做功相等,故有:S 1=S 2(面积) 即:21kx 12=21k(x 2+x 1)(x 2-x 1) 得 cm x 22=所以第二次击钉子进入木板的深度为:cm x x x )12(12-=-=∆(6)运用平均值求变力做功求変力做功可通过s F W ⋅=求,但只有在変力F 与位移S 成正比例、或一次函数关系时,即成线性关系时,221F F F +=才成立。
用平均值求变力做功的关键是先判断変力F 与位移S 是否成线性关系,然后求出该过程初状态的力1F 和末状态的力2F 。
【例7】如图5所示,在盛有水的圆柱形容器内竖直地浮着一块立方体木块,木块的边长为h ,其密度为水的密度ρ的一半,横截面积也为容器截面积的一半,水面高为2h ,现用力缓慢地把木块压到容器底上,设水不会溢出,求压力所做的功。
【解析】木块下降同时水面上升,因缓慢地把木块压到容器底上,所以压力总等于增加的浮力,压力是変力,当木块完全浸没在水中的下降过程压力是恒力。
本题的解法很多,功能关系、F-S 图像法、平均值法等均可求変力做功,现用平均值法求。
木块从开始到完全浸没在水中,设木块下降1x ,水面上升2x 根据水的体积不变,则:图4F x12x 2kx 1kx O 1S 2S 图52212x h x h = 得21x x = 所以当木块下降4h时,木块恰好完全浸没在水中, 1122122)(x x gh x x gh F F ∝=+=∆=ρρ浮所以42211814220424gh h hgh h F F h F W ρρ=+=+== 木块恰好完全浸没在水中经h h h h 45432=-=∆到容器底部,压力为恒力22hgh F ρ=所以42285452gh h h gh h F W ρρ=⋅=∆=故压力所做的功为:42143gh W W W ρ=+=(7)运用微元法求变力做功求変力做功还可以用微元累积法,把整个过程分成极短的很多段,在极短的每一段里,力可以看成是恒力,则可用功的公式求每一段元功,再求每一小段上做的元功的代数和。