人教版数学中考冲刺压轴题《四边形综合》专题训练

中考数学压轴题专项训练：四边形的综合(含答案)2020年数学中考压轴题专项训练：四边形的综合1.如图，四边形ABCD是直角梯形，AD∥BC，AB⊥AD，且AB＝AD+BC，E是DC的中点，连结BE并延长交AD的延长线于G。

1) 证明：因为 AD∥BC，所以∠DGE＝∠XXX，∠GDE＝∠BCE。

又因为 E 是 DC 的中点，即 DE＝CE，所以△DEG≌△CEB（AAS），从而 DG＝BC。

2) 解：当 F 运动到 AF＝AD 时，FD∥BG。

3) 解：结论：FH＝HD。

因为 GE＝BG，又因为△ABG为等腰直角三角形，所以 AE ⊥ BG。

由于 FD∥BG，所以 AE ⊥ FD。

又因为△AFD 为等腰直角三角形，所以 FH＝HD。

2.如图，在矩形ABCD中，过 BD 的中点 O 作 EF⊥BD，分别与 AB、CD 交于点 E、F。

连接 DE、BF。

1) 证明：因为四边形 ABCD 是矩形，所以 AB∥CD。

因此∠DFO＝∠BEO，又因为∠DOF＝∠EOB 且 OD＝OB，所以△DOF≌△BOE（AAS），从而 DF＝BE。

因此四边形BEDF 是平行四边形。

又因为 EF⊥BD，所以四边形 BEDF 是菱形。

2) 解：因为 DM＝AM，DO＝OB，所以 OM∥AB，AB＝2OM＝8.设 DE＝EB＝x，在直角三角形 ADE 中，有 x^2＝4^2+（8﹣x）^2，解得 x＝5.因此 ON＝BE＝5√2.3.(1) 如图1，四边形 EFGH 中，FE＝EH，∠EFG+∠EHG＝180°，点 A，B 分别在边 FG，GH 上，且∠AEB＝∠FEH，求证：AB＝XXX。

2) 如图2，四边形 EFGH 中，FE＝EH，点 M 在边 EH 上，连接 FM，EN 平分∠FEH 交 FM 于点 N，∠ENM＝α，∠FGH＝180°﹣2α，连接 GN，HN。

①找出与 NH 相等的线段，并加以证明。

2022年人教版中考数学一轮复习：四边形综合专项练习题21．如图，已知四边形ABCD是平行四边形，从①AB＝AD，②AC＝BD，③∠ABC＝∠ADC中选择一个作为条件，补充后使四边形ABCD成为菱形，则其选择是（限填序号）．2．如图1，平行四边形纸片ABCD的面积为120，AD＝15．今沿两对角线将四边形ABCD剪成甲、乙．丙、丁四个三角形纸片．若将甲、丙合并（AD、CB重合）形成一个对称图形戊，如图2所示．则图形戊的两条对角线长度之和为．3．如图，菱形ABCD的两条对角线AC，BD交于点O，BE⊥AD于点E，若AC＝8，BD＝6，则BE的长为．4．如图，在▱ABCD中，∠A＝70°，DB＝DC，CE⊥BD于E，则∠BCE＝．5．如图，在菱形ABCD中，AB＝BD，点E、F分别在AB、AD上，且AE＝DF，连接BF与DE交于点H，若CG＝1，则S＝．四边形BCDG6．如图，正方形瓷砖图案是四个全等且顶角为45°的等腰三角形．已知该瓷砖的面积是1m2，则中间小正方形的面积为m2．7．如图所示，在Rt△ABC外作等边△ADE，点E在AB边上，AC＝5，∠ABC＝30°，AD＝3．将△ADE沿AB方向平移，得到△A′D′E′，连接BD′．给出下列结论：①AB＝10；②四边形ADD′A′为平行四边形；③AB平分∠D′BC；④当平移的距离为4时，BD′＝3．其中正确的是（填上所有正确结论的序号）．8．如图，菱形ABCD的对角线AC，BD相交于点O，P为AB边上一动点（不与点A，B重合），PE⊥OA于点E，PF⊥OB于点F，若AB＝4，∠BAD＝60°，则EF的最小值为．9．如图，在正方形ABCD中，点E为BC边上一点，且CE＝2BE，点F为对角线BD上一点，且BF＝2DF，连接AE交BD于点G，过点F作FH⊥AE于点H，若HG＝2cm，则正方形ABCD 的边长为cm．10．把图1中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图2，图3所示的正方形，则图1中菱形的面积为．11．如图，在正方形ABCD内有一点P，若AP＝4，BP＝7，DP＝9，则∠APB的度数为．12．如图是两个边长分别为2a，a的正方形，则△ABC的面积是．13．如图，点P是正方形ABCD内一点，连接AP、BP、DP，若AP＝1，PD＝，∠APB＝135°，则正方形ABCD的面积为．14．如图，正三角形ABC与正方形CDEF的顶点B，C，D三点共线，动点P沿着CA由C向A 运动．连接EP，若AC＝10，CF＝8．则EP的最小值是．15．如图，正方形ABCD中，H为CD上一动点（不含C、D），连接AH交BD于G，过点G作GE⊥AH交BC于E，过E作EF⊥BD于F，连接AE，EH．下列结论：①AG＝EG；②∠EAH＝45°；③BD＝2GF；④GE平分∠FEC．正确的是（填序号）．16．如图，平面内三点A、B、C，AB＝4，AC＝3，以BC为对角线作正方形BDCE，连接AD，则AD的最大值是．17．如图，在正方形ABCD中，点E在对角线AC上，EF⊥AB于点F，EG⊥BC于点G，连接FG，若AB＝8，则FG的最小值为．18．如图，正方形ABCD的边长为2，点E是BC的中点，连接AE与对角线BD交于点G，连接CG并延长，交AB于点F，连接DE交CF于点H，连接AH．以下结论：①CF⊥DE；②＝；③GH＝；④AD＝AH，其中正确结论的序号是．19．如图，矩形ABCD中，对角线AC、BD交于点O，AE⊥BD于E，若∠DAE＝3∠BAE．则的值为．20．将矩形ABCD按如图所示的方式折叠，BE、EG、FG为折痕，若顶点A、C、D都落在点O 处，且点B、O、G在同一条直线上，同时点E、O、F在另一条直线上．（1）的值为．（2）若AD＝4，则四边形BEGF的面积为．参考答案1．解：①∵四边形ABCD是平行四边形，AB＝AD，∴平行四边形ABCD是菱形；②∵四边形ABCD是平行四边形，AC＝BD，∴平行四边形ABCD是矩形；③∵四边形ABCD是平行四边形，∴∠ABC＝∠ADC，因此∠ABC＝∠ADC时，四边形ABCD还是平行四边形；故答案为：①．2．解：如图，连接AD、EF，则可得对角线EF⊥AD，且EF与平行四边形的高相等．∵平行四边形纸片ABCD的面积为120，AD＝1520，∴BC＝AD＝15，EF×AD＝×120，∴EF＝8，又BC＝15，∴则图形戊中的四边形两对角线之和为20+3＝23，故答案为23．3．解：∵四边形ABCD是菱形，∴AO＝CO＝4，BO＝DO＝3，AC⊥BD，∴AD＝＝＝5，＝AD×BE＝×AC×BD，∵S菱形ABCD∴BE＝，故答案为：．4．解：∵四边形ABCD是平行四边形，∴∠BCD＝∠A＝70°，∵DB＝DC，∴∠DBC＝∠BCD＝70°，∵CE⊥BD，∴∠CEB＝90°，∴∠BCE＝20°．故答案为：20°．5．解：过点C作CM⊥GB于M，CN⊥GD，交GD的延长线于N．∵四边形ABCD为菱形，∴AB＝AD＝CD＝BC，∵AB＝BD，∴AB＝BD＝AD＝CD＝BC，∴△ABD为等边三角形，△BCD是等边三角形，∴∠A＝∠BDF＝60°，∠ADC＝60°，在△ADE和△DBF中，，∴△ADE≌△DBF（SAS），∴∠ADE＝∠DBF，∵∠FBC ＝60°+∠DBF ，∠NDC ＝180°﹣（120°﹣∠ADE ）＝60°+∠ADE ，∴∠NDC ＝∠FBC ，在△CDN 和△CBM 中，，∴△CDN ≌△CBM （AAS ），∴CM ＝CN ，在Rt △CBM 与Rt △CDN 中，，∴Rt △CBM ≌Rt △CDN （HL ），∴S 四边形BCDG ＝S 四边形CMGN ．S 四边形CMGN ＝2S △CMG ，∵∠CGM ＝60°，∴GM ＝CG ＝，CM ＝CG ＝，∴S 四边形BCDG ＝S 四边形CMGN ＝2S △CMG ＝2×××＝， 故答案为：．6．解：如图，作大正方形的对角线，作小正方形的对角线并延长交大正方形各边于中点， 设小正方形的边长为xm ， 则大正方形的边长为x +x x ＝（1）xm ， ∵瓷砖的面积是1m 2，∴大正方形的边长为1m ，即（1）x ＝1， 解得x ＝﹣1， ∴中间小正方形的面积为（）2＝3﹣2， 故答案为：3﹣2．7．解：∵∠ACB＝90°，AC＝5，∠ABC＝30°，∴AB＝2AC＝10，故①正确；由平移的性质得：A'D'＝AD，A'D'∥AD，∴四边形ADD′A′为平行四边形，故②正确；当平移的距离为4时，EE'＝4，∴BE'＝AB﹣AE﹣EE'＝10﹣3﹣4＝3，由平移的性质得：∠A'D'E'＝∠A'E'D'＝∠AED＝60°，A'D'＝D'E'＝DE＝AD＝3，∴BE'＝D'E'，∴∠E'BD'＝∠E'D'B＝∠A'E'D'＝30°，∴∠A'D'B＝60°+30°＝90°，∴BD'＝A'D'＝3，故④正确；由④得：当平移的距离为4时，∠E'BD'＝∠ABC＝30°，故③错误；故答案为：①②④．8．解：连接OP，∵四边形ABCD是菱形，∴AC⊥BD，∠CAB＝DAB＝30°，∵PE⊥OA于点E，PF⊥OB于点F，∴∠EOF＝∠OEP＝∠OFP＝90°，∴四边形OEPF是矩形，∴EF＝OP，∵当OP取最小值时，EF的值最小，∴当OP⊥AB时，OP最小，∵AB＝4，∴OB＝AB＝2，OA＝AB＝2，∴S＝OA•OB＝AB•OP，△ABO∴OP＝＝，∴EF的最小值为，故答案为：．9．解：如图，过F作FI⊥BC于I，连接FE，FA，∴FI∥CD，∵CE＝2BE，BF＝2DF，∴设BE＝EI＝IC＝a，CE＝FI＝2a，AB＝3a，∴则FE＝FC＝FA＝a，∴H为AE的中点，∴AH＝HE＝AE＝a，∴AG＝AH+GH＝a+2，∵四边形ABCD是正方形，∴BE∥AD，∴＝＝，∴GE＝AG＝（a+2），∵GE＝HE﹣GH＝a﹣2，∴（a+2）＝a﹣2，解得，a＝，∴AB＝3a＝．故答案为：．10．解：设图1中分成的直角三角形的长直角边为a，短直角边为b，，得，∴图1中菱形的面积为：×4＝48，故答案为48．11．解：∵四边形ABCD为正方形，∴∠ABC＝90°，BA＝BC，∴△BAP绕点A逆时针旋转90°可得△ADE，连接PE，由旋转的性质得，ED＝BP＝7，AE＝AP＝4，∠PBE＝90°，∠AED＝∠APB，∴△APE为等腰直角三角形，∴PE＝AP＝4，∠AEP＝45°，在△PED中，∵PD＝9，ED＝7，PE＝4，∴DE2+PE2＝DP2，∴△PED为直角三角形，∠PED＝90°，∴∠AED＝90°+45°＝135°，∴∠APB＝135°，故答案为：135°．12．解：∵两个正方形的边长分别为2a，a，∴△ABC的的高为：2a+a，底边为：BC＝a，∴△ABC的面积是：（2a+a）•a＝a2．故答案为：a2．13．解：如图，将△APB绕点A逆时针旋转90°得到△AHD，连接PH，过点A作AE⊥DH交DH的延长线于E，∴△APB≌△AHD，∠PAH＝90°，∴PB＝DH，AP＝AH＝1，∠APB＝∠AHD＝135°，∴PH＝AP＝，∠APH＝∠AHP＝45°，∴∠PHD＝90°，∴DH＝＝＝2，∵∠AHD＝135°，∴∠AHE＝45°，∵AE⊥DH，∴∠AHE＝∠HAE＝45°，∴AE＝EH，AH＝AE，∴AE＝EH＝，∴DE＝，∵AD2＝AE2+DE2＝13，∴正方形的面积为13，故答案为：13．14．解：如图，过点E作EP⊥AC，交FC于点G，当EP⊥AC时，EP取得最小值，∵正三角形ABC与正方形CDEF的顶点B，C，D三点共线，∴∠ACB＝60°，∠FCD＝90°，∴∠ACF＝30°，∴∠CGP＝∠EGF＝60°，∵∠F＝90°，∴∠FEG＝30°，设PG＝x，则CG＝2x，∴FG＝CF﹣CG＝8﹣2x，∴EG＝2FG＝2（8﹣2x），∵FG＝EF，∴8﹣2x＝8×，∴x＝4﹣，∴EP＝EG+PG＝2（8﹣2x）+x＝16﹣3x＝4+4．故答案为：4+4．15．解：连接GC，延长EG交AD于点L，∵四边形ABCD为正方形，∴AD∥CB，AD＝CD，∠ADG＝∠CDG＝45°，∵DG＝DG，∴△ADG≌△CDG（SAS），∴AG＝GC，∠HCG＝∠DAG，∵∠HCG+∠GCB＝90°，∴∠DAG+∠GCB＝90°，∵GE⊥AH，∴∠AGL＝90°，∴∠ALG+∠LAG＝90°，∵AD∥CB，∴∠ALG＝∠GEC，∴∠GEC+∠LAG＝90°，∴∠GEC＝∠GCE，∴GE＝GC，∴AG＝EG，故①正确；∵GE⊥AH，∴∠AGE＝90°，∵AG＝EG，∴∠EAH＝45°，故②正确；连接AC交BD于点O，则BD＝2OA，∵∠AGF+∠FGE＝∠GEF+∠EGF＝90°，∴∠AGF＝∠GEF，∵AG＝GE，∠AOG＝∠EFG＝90°，∴△AOG≌△GFE（AAS），∴OA＝GF，∵BD＝2OA，∴BD＝2GF，故③正确．过点G作MN⊥BC于点N，交AD于点M，交BC于点N，∵G是动点，∴GN的长度不确定，而FG＝OA是定值，∴GE不一定平分∠FEC，故④错误；故答案为：①②③．16．解：将△ABD绕点D顺时针旋转90°，得△MCD，如图：由旋转不变性可得：CM＝AB＝4，AD＝MD，且∠ADM＝90°，∴△ADM是等腰直角三角形，∴AD＝AM，AD最大，只需AM最大，而在△ACM中，AM＜AC+CM，∴当且仅当A、C、M在一条直线上，即不能构成△ACM时，AM最大，且最大值为AC+CM ＝AC+AB＝7，此时AD＝AM＝，故答案为：．17．解：连接BE，如图：∵四边形ABCD是正方形，∴∠ABC＝90°，又EF⊥AB于点F，EG⊥BC，∴四边形FBGE是矩形，∴FG＝BE，所以当BE最小时，FG就最小，根据垂线段最短，可知当BE⊥AC时，BE最小，当BE⊥AC时，在正方形ABCD中，△AEB是等腰直角三角形，在Rt△ABE中，根据勾股定理可得2BE2＝AB2＝64，解得BE＝4，∴FG最小为4；故答案为4．18．解：∵四边形ABCD是边长为2的正方形，点E是BC的中点，∴AB＝AD＝BC＝CD＝2，BE＝CE＝，∠DCE＝∠ABE＝90°，∠ABD＝∠CBD＝45°，∴△ABE≌△DCE（SAS），∴∠CDE＝∠BAE，DE＝AE，∵AB＝BC，∠ABG＝∠CBG，BG＝BG，∴△ABG≌△CBG（SAS），∴∠BAE＝∠BCF，∴∠BCF＝∠CDE，又∵∠CDE+∠CED＝90°，∴∠BCF+∠CED＝90°，∴∠CHE＝90°，∴CF⊥DE，故①正确；∵CD＝2，CE＝，由勾股定理得，DE＝＝＝5，＝CD×CE＝DE×CH，∵S△DCE∴CH＝2，∵∠CHE＝∠CBF，∠BCF＝∠ECH，∴△ECH∽△FCB，∴＝，∴＝，∴CF＝5，∴HF＝CF﹣CH＝3，∴＝，故②正确；如图，过点A作AM⊥DE于点M，∵DC＝2，CH＝2，由勾股定理得，DH＝＝＝4，∵∠CDH+∠ADM＝90°，∠DAM+∠ADM＝90°，∴∠CDH＝∠DAM，又∵AD＝CD，∠CHD＝∠AMD＝90°，∴△ADM≌△DCH（AAS），∴CH＝DM＝2，AM＝DH＝4，∴MH＝DM＝2，又∵AM⊥DH，∴AD＝AH，故④正确；∵DE＝5，DH＝4，∴HE＝1，∴ME＝HE+MH＝3，∵AM⊥DE，CF⊥DE，∴∠AME＝∠GHE，∵∠HEG＝∠MEA，∴△MEA∽△HEG，∴＝，∴＝，∴HG＝，故③错误．综上，正确的有：①②④．故答案为：①②④．19．解：∵四边形ABCD是矩形，∴∠BAD＝90°，OA＝AC，OB＝BD，AC＝BD，∴OA＝OB，∴∠OAB＝∠OBA，∵∠DAE＝3∠BAE，∴∠BAE＝×90°＝22.5°，∵AE⊥BD，∴∠OAB＝∠OBA＝90°﹣22.5°＝67.5°，∴∠OAE＝67.5°﹣22.5°＝45°，∴△AOE是等腰直角三角形，∴OA＝OE，设OE＝a，则OB＝OA＝a，∴BE＝OB﹣OE＝（﹣1）a，BD＝2OB＝2a，∴DE＝BD﹣BE＝2a﹣（﹣1）a＝（+1）a，∴＝＝，故答案为：．20．解：（1）由折叠可得，AE＝OE＝DE，CG＝OG＝DG，∴E，G分别为AD，CD的中点，设CD＝2a，AD＝2b，则AB＝OB＝2a，DG＝OG＝CG＝a，BG＝3a，BC＝AD＝2b，∵∠C＝90°，在Rt△BCG中，CG2+BC2＝BG2，∴a2+（2b）2＝（3a）2，∴b＝a，∴＝＝＝，由折叠可得：∠ABE＝∠EBG，∠AEB＝∠BEO，∠DEG＝∠GEO，∵∠AEB＝∠BEO+∠DEG＝∠GEO＝180°，∴∠BEG＝90°，∵∠A＝∠BEG＝90°，∠ABE＝∠EBG，∴△ABE∽△EBG，∴＝＝，故答案为：；（2）∵AD＝BC＝2b＝4，∴b＝2，a＝2，∴AB＝OB＝4，CG＝2，AE＝OE＝2，∴BG＝6，∵∠OBF ＝∠CBG ，由折叠可得∠BOF ＝∠BCG ＝90°， ∴△BOF ∽△BCG ， ∴＝， 即＝，∴OF ＝，∴S 四边形EBFG ＝S △BEG +S △BFG ＝×6×2+×6×＝9． 故答案为：9．。

一、平行四边形真题与模拟题分类汇编（难题易错题）1．如图①，在等腰Rt ABC 中，90BAC ∠=，点E 在AC 上(且不与点A 、C 重合)，在ABC △的外部作等腰Rt CED △，使90CED ∠=，连接AD ，分别以AB ，AD 为邻边作平行四边形ABFD ，连接AF ．()1请直接写出线段AF ，AE 的数量关系；()2①将CED 绕点C 逆时针旋转，当点E 在线段BC 上时，如图②，连接AE ，请判断线段AF ，AE 的数量关系，并证明你的结论；②若25AB =，2CE =，在图②的基础上将CED 绕点C 继续逆时针旋转一周的过程中，当平行四边形ABFD 为菱形时，直接写出线段AE 的长度．【答案】（1）证明见解析；（2）①AF 2AE =②42或22.【解析】【分析】 ()1如图①中，结论：AF 2AE =，只要证明AEF 是等腰直角三角形即可； ()2①如图②中，结论：AF 2AE =，连接EF ，DF 交BC 于K ，先证明EKF ≌EDA 再证明AEF 是等腰直角三角形即可；②分两种情形a 、如图③中，当AD AC =时，四边形ABFD 是菱形.b 、如图④中当AD AC =时，四边形ABFD 是菱形.分别求解即可.【详解】()1如图①中，结论：AF 2AE =．理由：四边形ABFD 是平行四边形，AB DF ∴=，AB AC =，AC DF ∴=，DE EC =，AE EF ∴=，DEC AEF 90∠∠==， AEF∴是等腰直角三角形，AF 2AE ∴=．故答案为AF 2AE =．()2①如图②中，结论：AF 2AE =．理由：连接EF ，DF 交BC 于K ．四边形ABFD 是平行四边形，AB//DF ∴，DKE ABC 45∠∠∴==，EKF 180DKE 135∠∠∴=-=，EK ED =， ADE 180EDC 18045135∠∠=-=-=，EKF ADE ∠∠∴=，DKC C ∠∠=，DK DC ∴=，DF AB AC ==，KF AD ∴=，在EKF 和EDA 中，EK ED EKF ADE KF AD =⎧⎪∠=∠⎨⎪=⎩，EKF ∴≌EDA ，EF EA ∴=，KEF AED ∠∠=，FEA BED 90∠∠∴==，AEF∴是等腰直角三角形，∴=．AF2AE=时，四边形ABFD是菱形，设AE交CD于H，易知②如图③中，当AD AC=+=，===，22EH DH CH2=-=，AE AH EH42AH(25)(2)32=时，四边形ABFD是菱形，易知如图④中当AD AC=-=-=，AE AH EH32222综上所述，满足条件的AE的长为4222【点睛】本题考查四边形综合题、全等三角形的判定和性质、等腰直角三角形的判定和性质、平行四边形的性质、勾股定理等知识，解题的关键是熟练掌握全等三角形的判定和性质，寻找全等的条件是解题的难点，属于中考常考题型．2．已知：在菱形ABCD中，E，F是BD上的两点，且AE∥CF．求证：四边形AECF是菱形．【答案】见解析【解析】【分析】由菱形的性质可得AB∥CD，AB＝CD，∠ADF＝∠CDF，由“SAS”可证△ADF≌△CDF，可得AF＝CF，由△ABE≌△CDF，可得AE＝CF，由平行四边形的判定和菱形的判定可得四边形AECF是菱形．【详解】证明：∵四边形ABCD是菱形∴AB∥CD，AB＝CD，∠ADF＝∠CDF，∵AB＝CD，∠ADF＝∠CDF，DF＝DF∴△ADF≌△CDF（SAS）∴AF＝CF，∵AB∥CD，AE∥CF∴∠ABE＝∠CDF，∠AEF＝∠CFE∴∠AEB＝∠CFD，∠ABE＝∠CDF，AB＝CD∴△ABE≌△CDF（AAS）∴AE＝CF，且AE∥CF∴四边形AECF是平行四边形又∵AF＝CF，∴四边形AECF是菱形【点睛】本题主要考查菱形的判定定理，首先要判定其为平行四边形，这是菱形判定的基本判定.3．在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°.(1)将△ADF绕着点A顺时针旋转90°，得到△ABG(如图①)，求证：△AEG≌△AEF；(2)若直线EF与AB，AD的延长线分别交于点M，N(如图②)，求证：EF2=ME2+NF2；(3)将正方形改为长与宽不相等的矩形，若其余条件不变(如图③)，请你直接写出线段EF，BE，DF之间的数量关系.【答案】（1）证明见解析；（2）证明见解析；（3）EF2=2BE2+2DF2.【解析】试题分析：（1）根据旋转的性质可知AF=AG，∠EAF=∠GAE=45°，故可证△AEG≌△AEF；（2）将△ADF绕着点A顺时针旋转90°，得到△ABG，连结GM．由（1）知△AEG≌△AEF，则EG=EF．再由△BME、△DNF、△CEF均为等腰直角三角形，得出CE=CF，BE=BM，NF=DF，然后证明∠GME=90°，MG=NF，利用勾股定理得出EG2=ME2+MG2，等量代换即可证明EF2=ME2+NF2；（3）将△ADF绕着点A顺时针旋转90°，得到△ABG，根据旋转的性质可以得到△ADF≌△ABG，则DF=BG，再证明△AEG≌△AEF，得出EG=EF，由EG=BG+BE，等量代换得到EF=BE+DF．试题解析：（1）∵△ADF绕着点A顺时针旋转90°，得到△ABG，∴AF=AG，∠FAG=90°，∵∠EAF=45°，∴∠GAE=45°，在△AGE与△AFE中，，∴△AGE≌△AFE（SAS）；（2）设正方形ABCD的边长为a．将△ADF绕着点A顺时针旋转90°，得到△ABG，连结GM．则△ADF≌△ABG，DF=BG．由（1）知△AEG≌△AEF，∴EG=EF．∵∠CEF=45°，∴△BME、△DNF、△CEF均为等腰直角三角形，∴CE=CF，BE=BM，NF=DF，∴a﹣BE=a﹣DF，∴BE=DF，∴BE=BM=DF=BG，∴∠BMG=45°，∴∠GME=45°+45°=90°，∴EG2=ME2+MG2，∵EG=EF ，MG=BM=DF=NF，∴EF2=ME2+NF2；（3）EF2=2BE2+2DF2．如图所示，延长EF交AB延长线于M点，交AD延长线于N点，将△ADF绕着点A顺时针旋转90°，得到△AGH，连结HM，HE．由（1）知△AEH≌△AEF，则由勾股定理有（GH+BE）2+BG2=EH2，即（GH+BE）2+（BM﹣GM）2=EH2又∴EF=HE，DF=GH=GM，BE=BM，所以有（GH+BE）2+（BE﹣GH）2=EF2，即2（DF2+BE2）=EF2考点：四边形综合题4．如图，在正方形ABCD中，E是边AB上的一动点，点F在边BC的延长线上，且=，连接DE，DF，EF. FH平分EFBCF AE∠交BD于点H.⊥；（1）求证：DE DF=：（2）求证：DH DF⊥于点M，用等式表示线段AB，HM与EF之间的数量关系，并（3）过点H作HM EF证明.【答案】（1）详见解析；（2）详见解析；（3）22EF AB HM =-，证明详见解析.【解析】【分析】（1）根据正方形性质， CF AE =得到DE DF ⊥.（2）由AED CFD △△≌，得DE DF =.由90ABC ∠=︒，BD 平分ABC ∠， 得45DBF ∠=︒.因为FH 平分EFB ∠，所以EFH BFH ∠=∠.由于45DHF DBF BFH BFH ∠=∠+∠=︒+∠,45DFH DFE EFH EFH ∠=∠+∠=︒+∠, 所以DH DF =.（3）过点H 作HN BC ⊥于点N ，由正方形ABCD 性质，得222BD AB AD AB =+=.由FH 平分,EFB HM EF HN BC ∠⊥⊥，，得HM HN =.因为4590HBN HNB ∠=︒∠=︒，，所以22sin 45HN BH HN HM ===︒. 由22cos 45DF EF DF DH ===︒，得22EF AB HM =-. 【详解】（1）证明：∵四边形ABCD 是正方形，∴AD CD =，90EAD BCD ADC ∠=∠=∠=︒.∴90EAD FCD ∠=∠=︒.∵CF AE =。

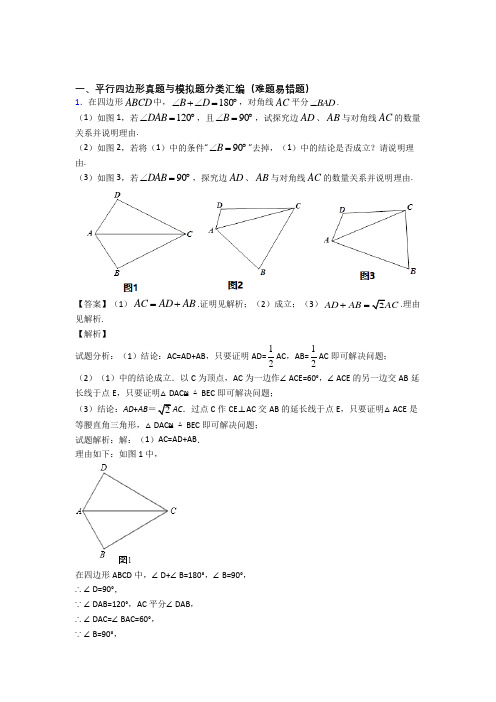
一、平行四边形真题与模拟题分类汇编（难题易错题）1．在四边形ABCD 中，180B D ∠+∠=︒，对角线AC 平分BAD ∠.（1）如图1，若120DAB ∠=︒，且90B ∠=︒，试探究边AD 、AB 与对角线AC 的数量关系并说明理由.（2）如图2，若将（1）中的条件“90B ∠=︒”去掉，（1）中的结论是否成立？请说明理由.（3）如图3，若90DAB ∠=︒，探究边AD 、AB 与对角线AC 的数量关系并说明理由.【答案】（1）AC AD AB =+.证明见解析；（2）成立；（3）2AD AB AC +=.理由见解析. 【解析】试题分析：（1）结论：AC=AD+AB ，只要证明AD=12AC ，AB=12AC 即可解决问题； （2）（1）中的结论成立．以C 为顶点，AC 为一边作∠ACE=60°，∠ACE 的另一边交AB 延长线于点E ，只要证明△DAC ≌△BEC 即可解决问题；（3）结论：AD +AB ＝2AC ．过点C 作CE ⊥AC 交AB 的延长线于点E ，只要证明△ACE 是等腰直角三角形，△DAC ≌△BEC 即可解决问题； 试题解析：解：（1）AC=AD+AB ． 理由如下：如图1中，在四边形ABCD 中，∠D+∠B=180°，∠B=90°， ∴∠D=90°，∵∠DAB=120°，AC 平分∠DAB ， ∴∠DAC=∠BAC=60°， ∵∠B=90°，∴AB＝12AC，同理AD＝12AC．∴AC=AD+AB．（2）（1）中的结论成立，理由如下：以C为顶点，AC为一边作∠ACE=60°，∠ACE的另一边交AB延长线于点E，∵∠BAC=60°，∴△AEC为等边三角形，∴AC=AE=CE，∵∠D+∠ABC=180°，∠DAB=120°，∴∠DCB=60°，∴∠DCA=∠BCE，∵∠D+∠ABC=180°，∠ABC+∠EBC=180°，∴∠D=∠CBE，∵CA=CE，∴△DAC≌△BEC，∴AD=BE，∴AC=AD+AB．（3）结论：AD+AB＝2AC．理由如下：过点C作CE⊥AC交AB的延长线于点E，∵∠D+∠B=180°，∠DAB=90°，∴DCB=90°，∵∠ACE=90°，∴∠DCA=∠BCE，又∵AC平分∠DAB，∴∠CAB=45°，∴∠E=45°．∴AC=CE．又∵∠D+∠ABC=180°，∠D=∠CBE，∴△CDA ≌△CBE ， ∴AD=BE ， ∴AD+AB=AE ．在Rt △ACE 中，∠CAB=45°， ∴AE ＝245ACAC cos ︒＝ ∴2AD AB AC +＝.2．操作与证明：如图1，把一个含45°角的直角三角板ECF 和一个正方形ABCD 摆放在一起，使三角板的直角顶点和正方形的顶点C 重合，点E 、F 分别在正方形的边CB 、CD 上，连接AF ．取AF 中点M ，EF 的中点N ，连接MD 、MN ． （1）连接AE ，求证：△AEF 是等腰三角形； 猜想与发现：（2）在（1）的条件下，请判断MD 、MN 的数量关系和位置关系，得出结论． 结论1：DM 、MN 的数量关系是 ； 结论2：DM 、MN 的位置关系是 ； 拓展与探究：（3）如图2，将图1中的直角三角板ECF 绕点C 顺时针旋转180°，其他条件不变，则（2）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．【答案】（1）证明参见解析；（2）相等，垂直；（3）成立，理由参见解析. 【解析】试题分析：（1）根据正方形的性质以及等腰直角三角形的知识证明出CE=CF ，继而证明出△ABE ≌△ADF ，得到AE=AF ，从而证明出△AEF 是等腰三角形；（2）DM 、MN 的数量关系是相等，利用直角三角形斜边中线等于斜边一半和三角形中位线定理即可得出结论.位置关系是垂直，利用三角形外角性质和等腰三角形两个底角相等性质，及全等三角形对应角相等即可得出结论；（3）成立，连接AE ，交MD 于点G ，标记出各个角，首先证明出MN ∥AE ，MN=AE ，利用三角形全等证出AE=AF ，而DM=AF ，从而得到DM ，MN 数量相等的结论，再利用三角形外角性质和三角形全等，等腰三角形性质以及角角之间的数量关系得到∠DMN=∠DGE=90°．从而得到DM 、MN 的位置关系是垂直.试题解析：（1）∵四边形ABCD 是正方形，∴AB=AD=BC=CD ，∠B=∠ADF=90°，∵△CEF是等腰直角三角形，∠C=90°，∴CE=CF ，∴BC ﹣CE=CD ﹣CF ，即BE=DF ，∴△ABE ≌△ADF ，∴AE=AF ，∴△AEF 是等腰三角形；（2）DM 、MN 的数量关系是相等，DM 、MN 的位置关系是垂直；∵在Rt △ADF 中DM 是斜边AF 的中线，∴AF=2DM ，∵MN 是△AEF 的中位线，∴AE=2MN ，∵AE=AF ，∴DM=MN ；∵∠DMF=∠DAF+∠ADM ，AM=MD ，∵∠FMN=∠FAE ，∠DAF=∠BAE ，∴∠ADM=∠DAF=∠BAE ，∴∠DMN=∠FMN+∠DMF=∠DAF+∠BAE+∠FAE=∠BAD=90°，∴DM ⊥MN ；（3）（2）中的两个结论还成立，连接AE ，交MD 于点G ，∵点M 为AF 的中点，点N 为EF 的中点，∴MN ∥AE ，MN=AE ，由已知得，AB=AD=BC=CD ，∠B=∠ADF ，CE=CF ，又∵BC+CE=CD+CF ，即BE=DF ，∴△ABE ≌△ADF ，∴AE=AF ，在Rt △ADF 中，∵点M 为AF 的中点，∴DM=AF ，∴DM=MN ，∵△ABE ≌△ADF ，∴∠1=∠2，∵AB ∥DF ，∴∠1=∠3，同理可证：∠2=∠4，∴∠3=∠4，∵DM=AM ，∴∠MAD=∠5，∴∠DGE=∠5+∠4=∠MAD+∠3=90°，∵MN ∥AE ，∴∠DMN=∠DGE=90°，∴DM ⊥MN ．所以（2）中的两个结论还成立.考点：1.正方形的性质；2.全等三角形的判定与性质；3.三角形中位线定理；4.旋转的性质．3．如图①，在等腰Rt ABC 中，90BAC ∠=，点E 在AC 上(且不与点A 、C 重合)，在ABC △的外部作等腰Rt CED △，使90CED ∠=，连接AD ，分别以AB ，AD 为邻边作平行四边形ABFD ，连接AF ．()1请直接写出线段AF ，AE 的数量关系；()2①将CED 绕点C 逆时针旋转，当点E 在线段BC 上时，如图②，连接AE ，请判断线段AF ，AE 的数量关系，并证明你的结论；②若25AB =2CE =，在图②的基础上将CED 绕点C 继续逆时针旋转一周的过程中，当平行四边形ABFD 为菱形时，直接写出线段AE 的长度．【答案】（1）证明见解析；（2）①AF 2AE =②42或22.【解析】 【分析】()1如图①中，结论：AF 2AE =，只要证明AEF 是等腰直角三角形即可； ()2①如图②中，结论：AF 2AE =，连接EF ，DF 交BC 于K ，先证明EKF ≌EDA 再证明AEF 是等腰直角三角形即可；②分两种情形a 、如图③中，当AD AC =时，四边形ABFD 是菱形.b 、如图④中当AD AC =时，四边形ABFD 是菱形.分别求解即可.【详解】()1如图①中，结论：AF 2AE =．理由：四边形ABFD 是平行四边形，AB DF ∴=， AB AC =，AC DF ∴=， DE EC =， AE EF ∴=，DEC AEF 90∠∠==， AEF ∴是等腰直角三角形， AF 2AE ∴=．故答案为AF 2AE =．()2①如图②中，结论：AF 2AE=．理由：连接EF ，DF 交BC 于K ． 四边形ABFD 是平行四边形，AB//DF ∴，DKE ABC 45∠∠∴==，EKF 180DKE 135∠∠∴=-=，EK ED =，ADE 180EDC 18045135∠∠=-=-=， EKF ADE ∠∠∴=， DKC C ∠∠=， DK DC ∴=，DF AB AC ==， KF AD ∴=，在EKF 和EDA 中， EK ED EKF ADE KF AD =⎧⎪∠=∠⎨⎪=⎩， EKF ∴≌EDA ，EF EA ∴=，KEF AED ∠∠=，FEA BED 90∠∠∴==，AEF ∴是等腰直角三角形，AF 2AE ∴=．②如图③中，当AD AC =时，四边形ABFD 是菱形，设AE 交CD 于H ，易知EH DH CH 2===22AH (25)(2)32=-=，AE AH EH 42=+=，=时，四边形ABFD是菱形，易知如图④中当AD AC=-=-=，AE AH EH32222综上所述，满足条件的AE的长为4222【点睛】本题考查四边形综合题、全等三角形的判定和性质、等腰直角三角形的判定和性质、平行四边形的性质、勾股定理等知识，解题的关键是熟练掌握全等三角形的判定和性质，寻找全等的条件是解题的难点，属于中考常考题型．4．如图，在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t 秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．（1）求证：AE=DF；（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值，如果不能，说明理由；（3）当t为何值时，△DEF为直角三角形？请说明理由．【答案】（1）见解析；（2）能，t=10；（3）t=152或12.【解析】【分析】（1）利用t表示出CD以及AE的长，然后在直角△CDF中，利用直角三角形的性质求得DF的长，即可证明；（2）易证四边形AEFD是平行四边形，当AD=AE时，四边形AEFD是菱形，据此即可列方程求得t的值；（3）△DEF为直角三角形，分∠EDF=90°和∠DEF=90°两种情况讨论.【详解】解：（1）证明：∵在Rt△ABC中，∠C=90°﹣∠A=30°，∴AB=12AC=12×60=30cm，∵CD=4t，AE=2t，又∵在Rt△CDF中，∠C=30°，∴DF=12CD=2t，∴DF=AE；（2）能，∵DF∥AB，DF=AE，∴四边形AEFD是平行四边形，当AD=AE时，四边形AEFD是菱形，即60﹣4t=2t，解得：t=10，∴当t=10时，AEFD是菱形；（3）若△DEF为直角三角形，有两种情况：①如图1，∠EDF=90°，DE∥BC，则AD=2AE，即60﹣4t=2×2t，解得：t=152，②如图2，∠DEF=90°，DE⊥AC，则AE=2AD，即2t2(604t)=-，解得：t=12，综上所述，当t=152或12时，△DEF为直角三角形.5．在矩形纸片ABCD中，AB=6，BC=8，现将纸片折叠，使点D与点B重合，折痕为EF，连接DF．（1）说明△BEF是等腰三角形；（2）求折痕EF的长．【答案】（1）见解析；（2）.【解析】【分析】（1）根据折叠得出∠DEF=∠BEF，根据矩形的性质得出AD∥BC，求出∠DEF=∠BFE，求出∠BEF=∠BFE即可；（2）过E作EM⊥BC于M，则四边形ABME是矩形，根据矩形的性质得出EM=AB=6，AE=BM，根据折叠得出DE=BE，根据勾股定理求出DE、在Rt△EMF中，由勾股定理求出即可．【详解】（1）∵现将纸片折叠，使点D与点B重合，折痕为EF，∴∠DEF=∠BEF．∵四边形ABCD是矩形，∴AD∥BC，∴∠DEF=∠BFE，∴∠BEF=∠BFE，∴BE=BF，即△BEF 是等腰三角形；（2）过E作EM⊥BC于M，则四边形ABME是矩形，所以EM=AB=6，AE=BM．∵现将纸片折叠，使点D与点B重合，折痕为EF，∴DE=BE，DO=BO，BD⊥EF．∵四边形ABCD是矩形，BC=8，∴AD=BC=8，∠BAD=90°．在Rt△ABE中，AE2+AB2=BE2，即（8﹣BE）2+62=BE2，解得：BE==DE=BF，AE=8﹣DE=8﹣==BM，∴FM=﹣=．在Rt△EMF中，由勾股定理得：EF==．故答案为：．【点睛】本题考查了折叠的性质和矩形性质、勾股定理等知识点，能熟记折叠的性质是解答此题的关键．6．（问题发现）（1）如图（1）四边形ABCD中，若AB=AD，CB=CD，则线段BD，AC的位置关系为；（拓展探究）（2）如图（2）在Rt△ABC中，点F为斜边BC的中点，分别以AB，AC为底边，在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE，连接FD，FE，分别交AB，AC于点M，N．试猜想四边形FMAN的形状，并说明理由；（解决问题）（3）如图（3）在正方形ABCD中，AB=2，以点A为旋转中心将正方形ABCD旋转60°，得到正方形AB'C'D'，请直接写出BD'平方的值．【答案】（1）AC垂直平分BD；（2）四边形FMAN是矩形，理由见解析；（3）16+8或16﹣8【解析】【分析】（1）依据点A在线段BD的垂直平分线上，点C在线段BD的垂直平分线上，即可得出AC 垂直平分BD；（2）根据Rt△ABC中，点F为斜边BC的中点，可得AF=CF=BF，再根据等腰三角形ABD 和等腰三角形ACE，即可得到AD=DB，AE=CE，进而得出∠AMF=∠MAN=∠ANF=90°，即可判定四边形AMFN是矩形；（3）分两种情况：①以点A为旋转中心将正方形ABCD逆时针旋转60°，②以点A为旋转中心将正方形ABCD顺时针旋转60°，分别依据旋转的性质以及勾股定理，即可得到结论．【详解】（1）∵AB=AD，CB=CD，∴点A在线段BD的垂直平分线上，点C在线段BD的垂直平分线上，∴AC垂直平分BD，故答案为：AC垂直平分BD；（2）四边形FMAN是矩形．理由：如图2，连接AF，∵Rt△ABC中，点F为斜边BC的中点，∴AF=CF=BF，又∵等腰三角形ABD和等腰三角形ACE，∴AD=DB，AE=CE，∴由（1）可得，DF⊥AB，EF⊥AC，又∵∠BAC=90°，∴∠AMF=∠MAN=∠ANF=90°，∴四边形AMFN是矩形；（3）BD′的平方为16+8或16﹣8．分两种情况：①以点A为旋转中心将正方形ABCD逆时针旋转60°，如图所示：过D'作D'E⊥AB，交BA的延长线于E，由旋转可得，∠DAD'=60°，∴∠EAD'=30°，∵AB=2=AD'，∴D'E=AD'=，AE=，∴BE=2+，∴Rt△BD'E中，BD'2=D'E2+BE2=（）2+（2+）2=16+8②以点A为旋转中心将正方形ABCD顺时针旋转60°，如图所示：过B作BF⊥AD'于F，旋转可得，∠DAD'=60°，∴∠BAD'=30°，∵AB=2=AD'，∴BF=AB=，AF=，∴D'F=2﹣，∴Rt△BD'F中，BD'2=BF2+D'F2=（）2+（2-）2=16﹣8综上所述，BD′平方的长度为16+8或16﹣8．【点睛】本题属于四边形综合题，主要考查了正方形的性质，矩形的判定，旋转的性质，线段垂直平分线的性质以及勾股定理的综合运用，解决问题的关键是作辅助线构造直角三角形，依据勾股定理进行计算求解．解题时注意：有三个角是直角的四边形是矩形．7．如图，AB 为⊙O 的直径，点E 在⊙O 上，过点E 的切线与AB 的延长线交于点D ，连接BE ，过点O 作BE 的平行线，交⊙O 于点F ，交切线于点C ，连接AC（1）求证：AC 是⊙O 的切线；（2）连接EF ，当∠D= °时，四边形FOBE 是菱形．【答案】（1）见解析；（2）30.【解析】【分析】（1）由等角的转换证明出OCA OCE ∆∆≌，根据圆的位置关系证得AC 是⊙O 的切线. （2）根据四边形FOBE 是菱形，得到OF=OB=BF=EF ，得证OBE ∆为等边三角形，而得出60BOE ∠=︒，根据三角形内角和即可求出答案.【详解】（1）证明：∵CD 与⊙O 相切于点E ，∴OE CD ⊥，∴90CEO ∠=︒，又∵OC BE ，∴COE OEB ∠=∠，∠OBE=∠COA∵OE=OB ，∴OEB OBE ∠=∠，∴COE COA ∠=∠，又∵OC=OC ，OA=OE ，∴OCA OCE SAS ∆∆≌（）， ∴90CAO CEO ∠=∠=︒，又∵AB 为⊙O 的直径，∴AC 为⊙O 的切线；（2）解：∵四边形FOBE 是菱形，∴OF=OB=BF=EF ，∴OE=OB=BE ，∴OBE ∆为等边三角形，∴60BOE ∠=︒，而OE CD ⊥，∴30D ∠=︒．故答案为30．【点睛】本题主要考查与圆有关的位置关系和圆中的计算问题，熟练掌握圆的性质是本题的解题关键.8．如图1，矩形ABCD 中，AB=8，AD=6；点E 是对角线BD 上一动点，连接CE ，作EF ⊥CE 交AB 边于点F ，以CE 和EF 为邻边作矩形CEFG ，作其对角线相交于点H ．（1）①如图2，当点F 与点B 重合时，CE= ，CG= ；②如图3，当点E 是BD 中点时，CE= ，CG= ；（2）在图1，连接BG ，当矩形CEFG 随着点E 的运动而变化时，猜想△EBG 的形状？并加以证明； （3）在图1，CG CE的值是否会发生改变？若不变，求出它的值；若改变，说明理由； （4）在图1，设DE 的长为x ，矩形CEFG 的面积为S ，试求S 关于x 的函数关系式，并直接写出x 的取值范围．【答案】（1）245，185，5，154 ；（2）△EBG 是直角三角形，理由详见解析；（3）34 ；（4）S=34x 2﹣485x+48（0≤x≤325）． 【解析】【分析】（1）①利用面积法求出CE ，再利用勾股定理求出EF 即可；②利用直角三角形斜边中线定理求出CE ，再利用相似三角形的性质求出EF 即可；（2）根据直角三角形的判定方法：如果一个三角形一边上的中线等于这条边的一半，则这个三角形是直角三角形即可判断；（3）只要证明△DCE ∽△BCG ，即可解决问题；（4）利用相似多边形的性质构建函数关系式即可；【详解】（1）①如图2中，在Rt △BAD 中，BD=22AD AB +=10， ∵S △BCD =12•CD•BC=12•BD•CE ， ∴CE=245．CG=BE=2224186()=55-． ②如图3中，过点E 作MN ⊥AM 交AB 于N ，交CD 于M ．∵DE=BE ，∴CE=12BD=5， ∵△CME ∽△ENF ，∴CM EN CE EF=， ∴CG=EF=154， （2）结论：△EBG 是直角三角形．理由：如图1中，连接BH ．在Rt △BCF 中，∵FH=CH ，∴BH=FH=CH ，∵四边形EFGC 是矩形，∴EH=HG=HF=HC ，∴BH=EH=HG ，∴△EBG 是直角三角形．（3）F 如图1中，∵HE=HC=HG=HB=HF ，∴C 、E 、F 、B 、G 五点共圆，∵EF=CG ，∴∠CBG=∠EBF ，∵CD ∥AB ，∴∠EBF=∠CDE ，∴∠CBG=∠CDE ，∵∠DCB=∠ECG=90°，∴∠DCE=∠BCG ，∴△DCE ∽△BCG ， ∴6384CG BC CE DC ===． （4）由（3）可知： 34CG CD CE CB ==， ∴矩形CEFG ∽矩形ABCD ， ∴2264CEFG ABCD S CE CE S CD ==矩形矩形（）， ∵CE 2=（325-x ）2+245）2，S 矩形ABCD =48， ∴S 矩形CEFG =34[（325-x ）2+（245）2]. ∴矩形CEFG 的面积S=34x 2-485x+48（0≤x≤325）． 【点睛】 本题考查相似三角形综合题、矩形的性质、相似三角形的判定和性质、勾股定理、直角三角形的判定和性质、相似多边形的性质和判定等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造相似三角形或直角三角形解决问题，属于中考压轴题．9．已知点O 是△ABC 内任意一点，连接OA 并延长到E ，使得AE=OA ，以OB ，OC 为邻边作▱OBFC ，连接OF 与BC 交于点H ，再连接EF ．（1）如图1，若△ABC为等边三角形，求证：①EF⊥BC；②EF=BC；（2）如图2，若△ABC为等腰直角三角形（BC为斜边），猜想（1）中的两个结论是否成立？若成立，直接写出结论即可；若不成立，请你直接写出你的猜想结果；（3）如图3，若△ABC是等腰三角形，且AB=AC=kBC，请你直接写出EF与BC之间的数量关系．【答案】（1）见解析；（2）EF⊥BC仍然成立；（3）EF=BC【解析】试题分析：（1）由平行四边形的性质得到BH=HC=BC，OH=HF，再由等边三角形的性质得到AB=BC，AH⊥BC，根据勾股定理得到AH=BC，即可；（2）由平行四边形的性质得到BH=HC=BC，OH=HF，再由等腰直角三角形的性质得到AB=BC，AH⊥BC，根据勾股定理得到AH=BC，即可；（3）由平行四边形的性质得到BH=HC=BC，OH=HF，再由等腰三角形的性质和AB=AC=kBC得到AB=BC，AH⊥BC，根据勾股定理得到AH=BC，即可．试题解析：（1）连接AH，如图1，∵四边形OBFC是平行四边形，∴BH=HC=BC，OH=HF，∵△ABC是等边三角形，∴AB=BC，AH⊥BC，在Rt△ABH中，AH2=AB2﹣BH2，∴AH==BC，∵OA=AE，OH=HF，∴AH是△OEF的中位线，∴AH=EF，AH∥EF，∴EF⊥BC，BC=EF，∴EF⊥BC，EF=BC；（2）EF⊥BC仍然成立，EF=BC，如图2，∵四边形OBFC是平行四边形，∴BH=HC=BC，OH=HF，∵△ABC是等腰三角形，∴AB=BC，AH⊥BC，在Rt△ABH中，AH2=AB2﹣BH2=（BH）2﹣BH2=BH2，∴AH=BH=BC，∵OA=AE，OH=HF，∴AH是△OEF的中位线，∴AH=EF，AH∥EF，∴EF⊥BC，BC=EF，∴EF⊥BC，EF=BC；（3）如图3，∵四边形OBFC是平行四边形，∴BH=HC=BC，OH=HF，∵△ABC是等腰三角形，∴AB=kBC，AH⊥BC，在Rt△ABH中，AH2=AB2﹣BH2=（kBC）2﹣（BC）2=（k2-）BC2，∴AH=BH=BC，∵OA=AE，OH=HF，∴AH是△OEF的中位线，∴AH=EF，AH∥EF，∴EF⊥BC，BC=EF，∴EF=BC．考点：四边形综合题．10．倡导研究性学习方式，着力教材研究，习题研究，是学生跳出题海，提高学习能力和创新能力的有效途径．下面是一案例，请同学们认真阅读、研究，完成“类比猜想”的问题．习题如图（1），点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，说明理由．解答：∵正方形ABCD中，AB=AD，∠BAD=∠ADC=∠B=90°，∴把△ABE绕点A逆时针旋转90°至△ADE′，点F、D、E′在一条直线上．∴∠E′AF=90°-45°=45°=∠EAF，又∵AE′=AE，AF=AF∴△AE′F≌△AEF（SAS）∴EF=E′F=DE′+DF=BE+DF．类比猜想：（1）请同学们研究：如图（2），在菱形ABCD中，点E、F分别在BC、CD上，当∠BAD=120°，∠EAF=60°时，还有EF=BE+DF吗？请说明理由．（2）在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B+∠D=180°，∠EAF=∠BAD时，EF=BE+DF吗？请说明理由．【答案】证明见解析．【解析】试题分析：（1）把△ABE绕点A逆时针旋转120°至△ADE′，如图（2），连结E′F，根据菱形和旋转的性质得到AE=AE′，∠EAF=∠E′AF，利用“SAS”证明△AEF≌△AE′F，得到EF=E′F；由于∠ADE′+∠ADC=120°，则点F、D、E′不共线，所以DE′+DF＞EF，即由BE+DF＞EF；（2）把△ABE绕点A逆时针旋转∠BAD的度数至△ADE′，如图（3），根据旋转的性质得到AE′=AE，∠EAF=∠E′AF，然后利用“SAS”证明△AEF≌△AE′F，得到EF=E′F，由于∠ADE′+∠ADC=180°，知F、D、E′共线，因此有EF=DE′+DF=BE+DF；根据前面的条件和结论可归纳出结论．试题解析：（1）当∠BAD=120°，∠EAF=60°时，EF=BE+DF不成立，EF＜BE+DF．理由如下：∵在菱形ABCD中，∠BAD=120°，∠EAF=60°，∴AB=AD，∠1+∠2=60°，∠B=∠ADC=60°，∴把△ABE绕点A逆时针旋转120°至△ADE′，如图（2），连结E′F，∴∠EAE′=120°，∠1=∠3，AE′=AE，DE′=BE，∠ADE′=∠B=60°，∴∠2+∠3=60°，∴∠EAF=∠E′AF，在△AEF和△AE′F中，∴△AEF≌△AE′F（SAS），∴EF=E′F，∵∠ADE′+∠ADC=120°，即点F、D、E′不共线，∴DE′+DF＞EF∴BE+DF＞EF；（2）当AB=AD，∠B+∠D=180°，∠EAF=∠BAD时，EF=BE+DF成立．理由如下：如图（3），∵AB=AD，∴把△ABE绕点A逆时针旋转∠BAD的度数至△ADE′，如图（3），∴∠EAE′=∠BAD，∠1=∠3，AE′=AE，DE′=BE，∠ADE′=∠B，∵∠B+∠D=180°，∴∠ADE′+∠D=180°，∴点F、D、E′共线，∵∠EAF=∠BAD，∴∠1+∠2=∠BAD，∴∠2+∠3=∠BAD，∴∠EAF=∠E′AF，在△AEF和△AE′F中，∴△AEF≌△AE′F（SAS），∴EF=E′F，∴EF=DE′+DF=BE+DF；归纳：在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B+∠D=180°，∠EAF=∠BAD时，EF=BE+DF．考点：四边形综合题．。

2022年人教版中考数学一轮复习：四边形压轴专项练习题1．（1）如图①，点E、F分别在正方形ABCD的边AB、BC上，∠EDF＝45°，连接EF，求证：EF＝AE+FC．（2）如图②，点E，F在正方形ABCD的对角线AC上，∠EDF＝45°，猜想EF、AE、FC的数量关系，并说明理由．2．在▱ABCD中，点M为AB的中点．（1）如图1，若∠A＝90°，连接DM且∠BMD＝3∠ADM，试探究AB与BC的数量关系；（2）如图2，若∠A为锐角，过点C作CE⊥AD于点E，连接EM，∠BME＝3∠AEM，①求证：AB＝2BC；②若EA＝EC，求的值．3．如图，将平行四边形OABC放置在平面直角坐标系xOy内，已知A（3，0），B（0，4）．（Ⅰ）点C的坐标是（，）；（Ⅱ）若将平行四边形OABC绕点O逆时针旋转90°得OFDE，DF交OC于点P，交y 轴于点F，求△OPF的面积；（Ⅲ）在（Ⅱ）的情形下，若再将平行四边形OFDE沿y轴正方向平移，设平移的距离为d，当平移后的平行四边形O'F'D'E′与平行四边形OABC重叠部分为五边形时，设其面积为S，试求出S关于d的函数关系式，并直接写出x的取值范围．4．如图，四边形ABCD中，AD∥BC，∠A＝∠D＝90°，点E是AD的中点，连接BE，将△ABE沿BE折叠后得到△GBE，且点G在四边形ABCD内部，延长BG交DC于点F，连接EF．（1）求证：△EGF≌△EDF；（2）求证：BG＝CD；（3）若点F是CD的中点，BC＝8，求CD的长．5．如图1，正方形ABCD和正方形AEFG，连接DG，BE．（1）[发现]：当正方形AEFG绕点A旋转，如图2，线段DG与BE之间的数量关系是；位置关系是；（2）[探究]：如图3，若四边形ABCD与四边形AEFG都为矩形，且AD＝2AB，AG＝2AE，猜想DG与BE的数量关系与位置关系，并说明理由；（3）[应用]：在（2）情况下，连接GE（点E在AB上方），若GE∥AB，且AB＝，AE＝1，求线段DG的长．6．如图，在等边△ABC中，AB＝6cm，动点P从点A出发以1cm/s的速度沿AB匀速运动．动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动，当点P到达点B时，点P、Q同时停止运动．设运动时间为t（s）．过点P作PE⊥AC于E，连接PQ 交AC边于D．以CQ、CE为边作平行四边形CQFE．（1）当t为何值时，△BPQ为直角三角形；（2）求DE的长；（3）取线段BC的中点M，连接PM，将△BPM沿直线PM翻折，得△B'PM，连接AB'，当t为何值时，AB'的值最小？并求出最小值．7．如图，四边形ABCD是矩形，点E在AB边上，且BC＝BE，连接EC、AC，过点B作BG⊥AC，垂足为G，BG分别交EC、DC于F、H两点．（1）如图1，若BC＝2，∠ECA＝15°，求线段EF的长．（2）如图2，延长AB到M，连接MF，使得∠BMF＝∠FBC，求证：BF+FM＝AC．（3）如图3，在（1）的条件下，点N是线段DC的三等分点，且DN＜CN，点P是线段AD的中点，连接AN，将△ADN绕点D逆时针旋转α°（0≤α≤360）到△A'DN'，连接PA'，NA'，当3NA'﹣PA'取最大值时，请直接写出△A'DH的面积．8．（1）如图1，正方形ABCD和正方形DEFG（其中AB＞DE），连接CE，AG交于点H，请直接写出线段AG与CE的数量关系，位置关系；（2）如图2，矩形ABCD和矩形DEFG，AD＝2DG，AB＝2DE，AD＝DE，将矩形DEFG 绕点D逆时针旋转α（0°＜α＜360°），连接AG，CE交于点H，（1）中线段关系还成立吗？若成立，请写出理由；若不成立，请写出线段AG，CE的数量关系和位置关系，并说明理由；（3）矩形ABCD和矩形DEFG，AD＝2DG＝6，AB＝2DE＝8，将矩形DEFG绕点D 逆时针旋转α（0°＜α＜360°），直线AG，CE交于点H，当点E与点H重合时，请直接写出线段AE的长．9．定义：有一组对边相等且这一组对边所在直线互相垂直的凸四边形叫做“等垂四边形”．（1）如图①，四边形ABCD与四边形AEEG都是正方形，135°＜∠AEB＜180°，求证：四边形BEGD是“等垂四边形”；（2）如图②，四边形ABCD是“等垂四边形”，AD≠BC，连接BD，点E，F，G分别是AD，BC，BD的中点，连接EG，FG，EF．试判定△EFG的形状，并证明；（3）如图③，四边形ABCD是“等垂四边形”，AD＝4，BC＝6，试求边AB长的最小值．10．如图，正方形ABCD和正方形DEFG有公共顶点D．（1）如图1，连接AG和CE，直接写出AG和CE的关系；（2）如图2，连接AE，M为AE中点，连接DM、CG，探究DM、CG的关系，并说明理由；（3）如图3，若AB＝4，DE＝2，直线AG与直线CE交于点P，请直接写出AP的取值范围：．11．在正方形ABCD中，E为边CD上一点（不与点C、D重合），垂直于BE的一条直线MN分别交BC、BE、AD于点M、P、N，正方形ABCD的边长为6．（1）如图1，当点M和点C重合时，若AN＝4，求线段PM的长度；（2）如图2，当点M在边BC上时，判断线段AN、MB、EC之间的数量关系，并说明理由；（3）如图3，当垂足P在正方形ABCD的对角线AC上运动时，连接NB，将△BPN沿着BN翻折，点P落在点P'处，AB的中点为Q，直接写出P'Q的最小值．12．如图，四边形ABCD为矩形，点E为边AB上一点，将△ADE沿DE折叠，点A落在矩形ABCD内的点F处．（1）如图①，若AB＝8，AD＝6，点F恰好落在矩形的对角线BD上，求线段BF的长；（2）如图②，连接BF，若△BEF为等边三角形，求的值；（3）如图③，已知E为AB中点，tan∠ADE＝，连接BF，FC，若△ADE的面积为S，求△BFC的面积．（结果用关于S的代数式表示）13．已知：如图，在矩形ABCD中，对角线AC、BD相交于点O，OE⊥BD交AD边于点E，连接BE．（1）如图1，求证：BD平分∠EBC；（2）如图2，延长EO交BC于点F，当BF＝2AE时，在不添加任何辅助线的情况下，请直接写出图2中所有长度等于CD的线段．14．如图①，在长方形ABCD中，已知AB＝20，AD＝12，动点P从点D出发，以每秒2个单位的速度沿线段DC向终点C运动，运动时间为t秒，连接AP，设点D关于AP的对称点为点E．（1）如图②，射线PE恰好经过点B，试求此时t的值．（2）当射线PE与边AB交于点Q时，①请直接写出AQ长的取值范围：；②是否存在这样的t的值，使得QE＝QB？若存在，请求出所有符合题意的t的值；若不存在，请说明理由．15．【问题提出】如图1，在四边形ABCD中，AD＝CD，∠ABC＝120°，∠ADC＝60°，AB＝2，BC＝1，求四边形ABCD的面积．【尝试解决】旋转是一种重要的图形变换，当图形中有一组邻边相等时，往往可以通过旋转解决问题．（1）如图2，连接BD，由于AD＝CD，所以可将△DCB绕点D顺时针方向旋转60°，得到△DAB'，则△BDB′的形状是．（2）在（1）的基础上，求四边形ABCD的面积．【类比应用】（3）如图3，等边△ABC的边长为2，△BDC是顶角为∠BDC＝120°的等腰三角形，以D为顶点作一个60°的角，角的两边分别交AB于点M，交AC于点N，连接MN，求△AMN的周长．参考答案1．证明：（1）∵四边形ABCD是正方形，∴AB＝BC＝CD＝AD，∠B＝∠C＝∠ADC＝∠DAB＝90°，如图①：延长BA，使AM＝CF，连接MD，在△AMD和△CFD中，，∴△AMD≌△CFD（SAS），∴∠MDA＝∠CDF，MD＝DF，∵∠EDF＝45°，∴∠ADE+∠FDC＝45°，∴∠ADM+∠ADE＝45°＝∠MDE，∴∠MDE＝∠EDF，在△EDF和△EDM中，，∴△EDF≌△EDM（SAS），∴EF＝EM，∵EM＝AM+AE＝AE+CF，∴EF＝AE+CF；（2）EF2＝AE2+CF2，理由如下：如图②，将△CDF绕点D顺时针旋转90°，可得△ADN，由旋转的性质可得DN＝DF，AN＝CF，∠DAN＝∠DCF＝45°，∠CDF＝∠ADN，∴∠CAN＝∠CAD+∠DAN＝90°，∴EN2＝AE2+AN2，∵∠EDF＝45°，∴∠CDF+∠ADE＝45°，∴∠ADE+∠ADN＝45°＝∠NDE＝∠EDF，在△EDF和△EDN中，，∴△EDF≌△EDN（SAS），∴EF＝EN，∴EF2＝AE2+CF2．2．解：（1）BC＝AB，理由如下：∵∠BMD＝3∠ADM，∴∠A+∠ADM＝3∠ADM，∴∠A＝2∠ADM，∵∠A＝90°，∴∠ADM＝45°，∴△ADM是等腰直角三角形，∴AD＝AM，∵四边形ABCD是平行四边形，M是AB中点，∴AD＝BC，AM＝AB，∴BC＝AB；（2）①取CD的中点N，连接MN并延长交CE于F，如图：∵四边形ABCD是平行四边形，M是AB中点，N是CD的中点，∴DN＝CN＝CD＝AB＝AM＝BM，CD∥AB，∴四边形AMND、四边形BCNM是平行四边形，∴MN∥AD∥BC，∴＝，∠AEM＝∠EMF，∠CMF＝∠MCB，∴EF＝CF，∵CE⊥AD于点E，∴MN⊥CE，∴MF是CE的垂直平分线，∴ME＝MC，∴∠EMF＝∠CMF，设∠AEM＝α，则∠EMF＝∠CMF＝∠MCB＝α，∠EMC＝2α，∵∠BME＝3∠AEM，∴∠BME＝3α，∴∠BMC＝∠BME﹣∠EMC＝α，∴∠BMC＝∠MCB＝α，∴BC＝BM＝AB，∴AB＝2BC；②如图：由①知：AB＝2BC，∴CD＝2AD设ED＝x，EC＝y，则EA＝y，AD＝y﹣x，CD＝2（y﹣x），Rt△CDE中，ED2+EC2＝CD2，∴x2+y2＝4（y﹣x）2，化简整理得：3x2﹣8xy+3y2＝0，解得x＝y或x＝y，∵DE＜AE，∴x＝y，∴＝，即＝．3．解：（Ⅰ）∵A（3，0），B（0，4），∴OA＝3，OB＝4，∵四边形OABC是平行四边形，∴BC＝OA＝3，BC∥OA，AB∥OC，∴点C的坐标为：（﹣3，4）；故答案为：﹣3，4；（Ⅱ）由旋转的性质，可得：OD＝OB＝4，OF＝OA＝3，∠ODF＝∠OBA，∠OFD＝∠OAB，∵∠BOD＝90°，∴S△DOF＝OD•OF＝×4×3＝6，DF＝＝＝5，∵AB∥OC，∴∠OBA＝∠BOC，∴∠ODF＝∠BOC，∵∠OFP＝∠DFO，∴△OFP∽△DFO，∴＝（）2＝（）2＝，∴S△OPF＝S△DOF＝×6＝；（Ⅲ）如图，重叠部分为五边形时，F′必须位于点B上方，∵OF＝3，OB＝4，∴d＞1，当点C在D′F′上时，重叠部分不构成五边形，设此时直线D′F′的解析式为y＝x+b，将C（﹣3，4）代入，得4＝×（﹣3）+b，解得：b＝，∴直线D′F′的解析式为y＝x+，令x＝0，得y＝，∴F′（0，），∴OF′＝，∴FF′＝OF′﹣OF＝﹣3＝，∴d＜，∴1＜d＜；∵＝sin∠F′OC＝，∴P′F′＝F′O＝（d+3），同理可得：P′O＝（d+3），∴S△F′P′O＝P′F′•P′O＝×（d+3）×（d+3）＝（d+3）2，∵＝cos∠D′F′O＝，BF′＝d﹣1，∴HF′＝（d﹣1），∵＝sin∠D′F′O＝，∴HB＝HF′＝×（d﹣1）＝（d﹣1），∴S△HBF′＝BF′•HB＝×（d﹣1）×（d﹣1）＝（d﹣1）2，∵OO′＝d，∴O′G＝OO′•sin∠BOC＝d，OG＝OO′•cos∠BOC＝d，∴S△OGO′＝O′G•OG＝×d×d＝d2，∴S＝S△F′P′O﹣S△HBF′﹣S△OGO′＝（d+3）2﹣（d﹣1）2﹣d2＝﹣d2+d+，∴S＝﹣d2+d+（1＜d＜）．4．（1）证明：∵将△ABE沿BE折叠后得到△GBE，∴△ABE≌△GBE，∴∠BGE＝∠A，AE＝GE，∵∠A＝∠D＝90°，∴∠EGF＝∠D＝90°，∵EA＝ED，∴EG＝ED，在Rt△EGF和Rt△EDF中，，∴Rt△EGF≌Rt△EDF（HL）；（2）证明：由折叠性质可得，AB＝BG，∵AD∥BC，∠A＝∠D＝90°，∴四边形ABCD是矩形，∴AB＝CD，∴BG＝DC．（3）解：由折叠可知AB＝GB，由（1）知Rt△EGF≌Rt△EDF，∴GF＝DF，又∵∠C＝90°，AB＝CD，FD＝CF，∴GB＝2GF，BF+GF＝3GF，∵BF2＝BC2+CF2，∴（3GF）2＝64+GF2，∴GF＝2，∴CD＝2GF＝4．5．解：（1）DG＝BE，DG⊥BE，理由如下：∵四边形ABCD和四边形AEFG是正方形，∴AE＝AG，AB＝AD，∠BAD＝∠EAG＝90°，∴∠BAE＝∠DAG，∴△ABE≌△ADG（SAS），∴BE＝DG；如图2，延长BE交AD于Q，交DG于H，∵△ABE≌△DAG，∴∠ABE＝∠ADG，∵∠AQB+∠ABE＝90°，∴∠AQB+∠ADG＝90°，∵∠AQB＝∠DQH，∴∠DQH+∠ADG＝90°，∴∠DHB＝90°，∴BE⊥DG，故答案为：DG＝BE，DG⊥BE；（2）DG＝2BE，BE⊥DG，理由如下：如图3，延长BE交AD于K，交DG于H，∵四边形ABCD与四边形AEFG都为矩形，∴∠BAD＝∠EAG，∴∠BAE＝∠DAG，∵AD＝2AB，AG＝2AE，∴＝＝，∴△ABE∽△ADG，∴＝＝，∠ABE＝∠ADG，∴DG＝2BE，∵∠AKB+∠ABE＝90°，∴∠AKB+∠ADG＝90°，∵∠AKB＝∠DKH，∴∠DKH+∠ADG＝90°，∴∠DHB＝90°，∴BE⊥DG；（3）如图4，（为了说明点B，E，F在同一条线上，特意画的图形）设EG与AD的交点为M，∵EG∥AB，∴∠DME＝∠DAB＝90°，在Rt△AEG中，AE＝1，∴AG＝2AE＝2，根据勾股定理得：EG＝＝，∵AB＝，∴EG＝AB，∵EG∥AB，∴四边形ABEG是平行四边形，∴AG∥BE，∵AG∥EF，∴点B，E，F在同一条直线上，如图5，∴∠AEB＝90°，在Rt△ABE中，根据勾股定理得，BE＝＝＝2，由（2）知，△ABE∽△ADG，∴＝＝，即＝，∴DG＝4．6．解：（1）∵△ABC是等边三角形，∴∠B＝60°，∴当BQ＝2BP时，∠BPQ＝90°，∴6+t＝2（6﹣t），解得：t＝2，即t＝2s时，△BPQ是直角三角形；（2）过P作PK∥BC交AC于K，如图1所示：∵△ABC是等边三角形，∴∠B＝∠A＝60°，AC＝AB＝6cm，∵PK∥BC，∴∠APK＝∠B＝60°，∴∠A＝∠APK＝∠AKP＝60°，∴△APK是等边三角形，∴PA＝PK，∵PE⊥AK，∴AE＝EK，∵AP＝CQ＝PK，∠PKD＝∠DCQ，∠PDK＝∠QDC，∴△PKD≌△QCD（AAS），∴DK＝DC，∴DE＝EK+DK＝（AK+CK）＝AC＝3（cm）；（3）连接AM，AB′，如图2所示：∵BM＝CM＝3，AB＝AC，∴AM⊥BC，∴AM＝＝＝3，∵AB′≥AM﹣MB′，∴AB′≥3﹣3，∴AB′的最小值为3﹣3，此时MP平分∠AMB，则点P到AM、BM的距离相等，∴＝，又∵＝，∴＝＝，∴t＝（6﹣t），解得：t＝9﹣3，即当t为（9﹣3）s时，AB'的值最小，最小值为3﹣3．7．解：（1）如图1，过点F作FK⊥BC于K，∵四边形ABCD是矩形，∴∠ABC＝∠BCD＝90°，∴∠BCE＝∠BEC＝45°，CE＝BC＝2，∵∠ECA＝15°，∴∠BCA＝∠BCE+∠ECA＝60°，∵BG⊥AC，∴∠BGC＝90°，∴∠CBG＝90°﹣∠BCA＝30°，∵FK⊥BC，∴∠CKF＝∠BKF＝90°，∴CK＝FK•tan∠BCE＝FK•tan45°＝FK，BK＝＝＝FK，∵CK+BK＝BC，∴FK+FK＝2，∴FK＝3﹣，∴CF＝FK＝（3﹣）＝3﹣，∴EF＝CE﹣CF＝2﹣（3﹣）＝3﹣3．（2）如图2，延长MF交CD于T，过点T作TP⊥AB于P，∵四边形ABCD是矩形，∴AB∥CD，∠BAD＝∠D＝∠BCD＝90°，∴∠BMF＝∠CTF，∵∠BMF＝∠FBC，∴∠CTF＝∠FBC，∴∠TCF＝∠BCD﹣∠BCE＝90°﹣45°＝45°，∴∠TCF＝∠BCE，在△TCF和△BCF中，，∴△TCF≌△BCF（AAS），∴FT＝BF，∵BG⊥AC，∴∠BGC＝90°，∴∠BCG+∠FBC＝90°，又∵∠BCG+∠ACD＝90°，∴∠FBC＝∠ACD，∵∠BMF＝∠FBC，∴∠BMF＝∠ACD，即∠TMP＝∠ACD，∵TP⊥AB，∴∠APT＝∠MPT＝90°＝∠BAD＝∠D，∴四边形APTD是矩形，∴AD＝PT，在△MTP和△CAD中，，∴△MTP≌△CAD（AAS），即FT+FM＝AC，∴BF+FM＝AC．（3）如图3，以D为圆心，DN、DA为半径作同心圆，∵四边形ABCD是矩形，∴AD∥BC，AD＝BC＝2，∠ADC＝∠BCD＝90°，由（1）得：∠BCA＝60°，∴∠CAD＝∠BCA＝60°，∴CD＝AD•tan∠CAD＝2•tan60°＝6，∵点N是线段DC的三等分点，且DN＜CN，∴DN＝CD＝×6＝2，∵3NA'﹣PA'＝（NA′﹣PA′），∴当3NA'﹣PA'取最大值时，NA′﹣PA′的值最大，∵DA′＝DA＝2，∴＝＝，∵＝＝，∴＝＝，又∵∠A′DN＝∠CDA′，∴△A′DN∽△CDA′，∴＝＝＝，∴A′C＝A′N，∴NA′﹣PA′＝A′C﹣PA′≤PC，当C、P、A′在同一直线上时，NA′﹣PA′的最大值为PC，此时3NA'﹣PA'取最大值，作A′T⊥CD的延长线于T，则A′T∥DP，∴＝＝，设A′T＝x，在Rt△CDP中，PC＝＝＝，∴＝＝，∴A′C＝x，CT＝2x，∴TD＝CT﹣CD＝2x﹣6，在Rt△A′DT中，A′T2+TD2＝A′D2，∴x2+（2x﹣6）2＝（2）2，解得：x＝，∴A′T＝，由（1）知：∠CBG＝30°，∴CH＝BC•tan∠CBG＝2×tan30°＝2，∴DH＝CD﹣CH＝6﹣2＝4，∴S△A′DH＝•DH•A′T＝×4×＝．8．解：（1）如图1，在正方形ABCD和正方形DEFG中，∠ADC＝∠EDG＝90°，∴∠ADE+∠EDG＝∠ADC+∠ADE，即∠ADG＝∠CDE，∵DG＝DE，DA＝DC，∴△GDA≌△EDC（SAS），∴AG＝CE，∠GAD＝∠ECD，∵∠COD＝∠AOH，∴∠AHO＝∠CDO＝90°，∴AG⊥CE，故答案为：相等，垂直；（2）不成立，CE＝2AG，AG⊥CE，理由如下：如图2，由（1）知，∠EDC＝∠ADG，∵AD＝2DG，AB＝2DE，AD＝DE，∴，＝＝，∴＝，∴△GDA∽△EDC，∴＝，即CE＝2AG，∵△GDA∽△EDC，∴∠ECD＝∠GAD，∵∠COD＝∠AOH，∴∠AHO＝∠CDO＝90°，∴AG⊥CE；（3）①当点E在线段AG上时，如图3，在Rt△EGD中，DG＝3，ED＝4，则EG＝5，过点D作DP⊥AG于点P，∵∠DPG＝∠EDG＝90°，∠DGP＝∠EGD，∴△DGP∽△EGD，∴＝，即，∴PD＝，PG＝，则AP＝＝＝，则AE＝AG﹣GE＝AP+GP﹣GE＝+﹣5＝；②当点G在线段AE上时，如图4，过点D作DP⊥AG于点P，∵∠DPG＝∠EDG＝90°，∠DGP＝∠EGD，同理得：PD＝，AP＝，由勾股定理得：PE＝＝，则AE＝AP+PE＝+＝；综上，AE的长为．9．解：（1）如图①，延长BE，DG交于点H，∵四边形ABCD与四边形AEFG都为正方形，∴AB＝AD，AE＝AG，∠BAD＝∠EAG＝90°．∴∠BAE＝∠DAG．∴△ABE≌△ADG（SAS）．∴BE＝DG，∠ABE＝∠ADG．∵∠ABD+∠ADB＝90°，∴∠ABE+∠EBD+∠ADB＝∠DBE+∠ADB+∠ADG＝90°，即∠EBD+∠BDG＝90°，∴∠BHD＝90°．∴BE⊥DG．又∵BE＝DG，∴四边形BEGD是“等垂四边形”．（2）△EFG是等腰直角三角形．理由如下：如图②，延长BA，CD交于点H，∵四边形ABCD是“等垂四边形”，AD≠BC，∴AB⊥CD，AB＝CD，∴∠HBC+∠HCB＝90°∵点E，F，G分别是AD，BC，BD的中点，∴，，EG∥AB，GF∥DC，∴∠BFG＝∠C，∠EGD＝∠HBD，EG＝GF．∴∠EGF＝∠EGD+∠FGD＝∠ABD+∠DBC+∠GFB＝∠ABD+∠DBC+∠C＝∠HBC+∠HCB ＝90°．∴△EFG是等腰直角三角形．（3）延长BA，CD交于点H，分别取AD，BC的中点E，F．连接HE，EF，HF，则，由（2）可知．∴AB最小值为．10．解：（1）AG＝CE且AG⊥CE，理由如下：∵四边形ABCD和四边形DEFG是正方形，∴∠ADC＝∠GDE＝90°，AD＝CD，DG＝DE，∴∠ADG＝∠CDE，∴△ADG≌△CDE（SAS），∴AG＝CE，∵∠ADC＝∠GDE＝90°由旋转可知：AG⊥CE；故答案为：AG＝CE且AG⊥CE；（2）DM、CG的关系是：DM＝CG，且DM⊥CG，理由如下：如图2，延长AD至H，使AD＝DH，连接EH，∵∠GDE＝∠CDH＝90°，∴∠GDE﹣∠CDE＝∠CDH﹣∠CDE，即∠CDG＝∠HDE，∵CD＝DH，GD＝DE，∴△DGC≌△DEH（SAS），∴CG＝EH，∵M是AE的中点，AD＝DH，∴DM是△AEH的中位线，∴DM∥EH，DM＝EH，∴DM＝CG，∵∠GDE＝∠CDH＝90°，∴△DGC绕点逆时针旋转90°到△DEH，∴CG⊥EH，∴DM⊥CG；（3）由（1）可知：直线AG⊥直线CE，∴∠APC＝90°，∴点P在以AC为直径的圆上运动，如图3，当P与F重合时，AP最小，此时A、P、F、G共线，Rt△AGD中，DG＝2，AD＝4，∴AG＝＝2，∴AP＝2﹣2；如图4，当P与F重合时，AP最大，同理得：AP＝2+2，∴AP的取值范围是：2﹣2≤AP≤2+2．故答案为：2﹣2≤AP≤2+2．11．解：（1）∵四边形ABCD是正方形，∴AB＝BC＝CD＝AD＝6，∠D＝∠BCE＝90°，∵BE⊥MN，点M和点C重合，∴MD＝BC＝6，∠DMN+∠BCP＝90°，∠CBE+∠BCP＝90°，∴∠DMN＝∠CBE，在△DMN和△CBE中，，∴△DMN≌△CBE（AAS），∴MN＝BE，∵AN＝4，∴DN＝AD﹣AN＝6﹣4＝2，由勾股定理得：MN＝＝＝2，∴BE＝2，∵∠PBC＝∠CBE，∠CPB＝∠ECB＝90°，∴△PBC∽△CBE，∴＝，∴BP＝＝＝，在Rt△BPM中，由勾股定理得：PM＝＝＝；（2）线段AN、MB、EC之间的数量关系为：AN+EC＝MB，理由如下：过点N作NF⊥BC于N，如图2所示：则四边形ANFB为矩形，∴AN＝BF，NF＝AB＝BC，∵MN⊥BE，∴∠EBC+∠PMB＝90°，∠MNF+∠NMF＝90°，∴∠EBC＝∠MNF，在△EBC和△MNF中，，∴△EBC≌△MNF（ASA），∴FM＝EC，∴MB＝BF+FM＝AN+EC，即AN+EC＝MB；（3）连接BD交AC于点O，如图3所示：则△BPN的直角顶点P在AC上运动，设点P与点C重合时，则点P′与点A重合；设点P与点O重合时，则点P′的落点为O′，∵AO＝OB，∠AOB＝90°，∴∠OAB＝∠BAO′＝45°，当点P在线段CO上运动时，过点P作PG⊥AD于点G，过点P′作P′H⊥AD交DA延长线于点H，连接PD，∵点P在AC上，∴BP＝PD，在△BPC和△DPC中，，∴△BPC≌△DPC（SSS），∴∠CBP＝∠CDP，∵∠CDA＝∠MPB＝90°，∴∠PDN＝∠BMP，∵BC∥AD，∴∠BMP＝∠PND，∴∠PDN＝∠PND，∴PD＝PN，∴BP＝PN，∴∠PNB＝45°，∴∠PNP′＝90°，∴∠P′NH+∠PNG＝90°，∵∠P′NH+∠NP′H＝90°，∠PNG+∠NPG＝90°，∴∠NPG＝∠P′NH，∠PNG＝∠NP′H，由翻折性质得：PN＝P′N，在△PGN和△NHP'中，，∴△PGN≌△NHP'（ASA），∴PG＝NH，GN＝P'H，∵AC是正方形ABCD的对角线，∴∠PAG＝45°，∴△AGP是等腰直角三角形，∴PG＝AG，∴GN＝AH，∴AH＝P'H，∴∠P'AH＝45°，∴∠P'AB＝45°，∴点P'在线段AO'上运动；过点Q作QK⊥AO'，垂足为K，则当P′与K重合时，P'Q最短，∵点Q为AD的中点，∴AQ＝3，在等腰Rt△AKQ中，KQ＝AQ＝×3＝，∴P'Q的最小值为．12．解：（1）如图①中，∵四边形ABCD是矩形，∴∠A＝90°，∴BD＝＝＝10，由翻折的性质可知，DA＝DF＝6，∴BF＝BD﹣DF＝10﹣6＝4．（2）如图②中，∵△EBF是等边三角形，∴EB＝EF，∠BEF＝60°，由翻折的性质可知，EA＝EF，∠AED＝∠FED，∴∠AED＝∠FED＝60°，设AE＝EF＝BE＝m，则AD＝AE＝m，∴AB＝2m，∴＝＝．（3）如图③中，过点F作FT⊥AB于T．设BT＝a．由翻折的性质可知，DE⊥AF，AE＝EF，∵四边形ABCD是矩形，∴∠EAD＝90°，∴∠BAF+∠DAF＝90°，∠DAF+∠ADE＝90°，∴∠BAF＝∠ADE，同法可证∠BAF＝∠BFT，∴tan∠BFT＝tan∠BAF＝tan∠ADE＝，∴FT＝3a，AT＝9a，∴AB＝10a，∴AE＝BE＝5a，AD＝3AE＝15a，∵S△ADE＝×15a×5a＝S，∴a2＝S，∴S△BCF＝×15a×a＝a2＝S．解法二：三角形ADF和三角形BCF加起来等于矩形面积的一半，四边形ADFE面积好求，先求出△AEF的面积，△AEF面积是△ABF的一半．13．证明：（1）∵四边形ABCD是矩形，∴AD∥BC，BO＝DO．又∵OE⊥BE，∴BE＝DE．∴∠EBD＝∠EDB．∵AD∥BC，∴∠EDB＝∠CBD．即BD平分∠EBC．（2）解：长度等于CD的线段有：AE、EO、FO、CF．理由：由（1）知：∠EBO＝∠FBO，在△BEO和△BFO中，，∴△BEO≌△BFO（ASA）．∴OE＝OF，BE＝BF．∵BF＝2AE，∴BE＝2AE．在Rt△ABE中，∵sin∠ABE＝，∴∠ABE＝30°，∵tan∠ABE＝，∴AE＝AB•tan30°＝AB．∵四边形ABCD是矩形，∴AB＝CD，OA＝OB＝OC＝OD．∴AE＝CD．∵∠EBF＝90°﹣∠BAE＝60°，∴△BEF为等边三角形．∴∠EBF＝60°，∴∠EBO＝∠FBO＝∠EBF＝30°．∴∠ABO＝∠ABE+∠EBO＝60°，∴△ABO为等边三角形．∴∠BAO＝∠AOB＝60°，∴∠EAO＝∠EOA＝30°，∴AE＝OE．∵AD∥BC，∴∠OCF＝∠OAE＝30°．∵∠FOC＝∠EOA＝30°，∴∠OCF＝∠FOC．∴OF＝FC．∴OF＝FC＝OE＝AE＝CD．14．解：（1）如图1，∵AB∥CD，∴∠DPA＝∠PAB，由轴对称得：∠DPA＝∠EPA，∴∠EPA＝∠PAB，∴BP＝AB＝20，在Rt△PCB中，由勾股定理得：PC＝＝＝16，∴PD＝4＝2t，∴t＝2；（2）①解法一：如图2，过点P作PH⊥AB于H，过点Q作QG⊥CD于G，∴PH＝QG＝AD＝12，∵∠APQ＝∠PAQ，∴AQ＝PQ，∵PQ2＝PG2+QG2＝PG2+122＝144+PG2，∴AQ2＝144+PG2，∵AQ＝DG＝DP+PG，∴（DP+PG）2＝144+PG2，∵PD＝2t，∴（2t+PG）2＝144+PG2，解得：PG＝，∵AQ＝PD+PG＝2t+＝＝t+，∵t+＝（t﹣）2+2≥2＝12，∴AQ＝t+≥12，由（1）可知：当t＝2时，Q与B重合，此时AQ＝AB＝20，∴12≤AQ≤20；解法二：由（1）可知：当t＝2时，Q与B重合，此时AQ＝AB＝20，如图2，当PQ⊥AB时，E与Q重合，此时AQ＝AD＝12，∴12≤AQ≤20，故答案为：12≤AQ≤20；②存在，分两种情况：当点E在矩形ABCD内部时，如图3，∵QE＝PQ﹣PE＝PQ﹣DP＝PQ﹣2t，∵QE＝QB，PQ＝AQ，∴QB＝AQ﹣2t，∵AQ+BQ＝AB＝20，∴AQ+AQ﹣2t＝20，∴AQ＝10+t，由①可知：AQ＝t+，∴t+＝10+t，解得：t＝3.6；当点E在矩形ABCD的外部时，如图4，∵QE＝PE﹣PQ＝DP﹣PQ＝2t﹣PQ，∵QE＝QB，∴BQ＝2t﹣AQ，∴AB﹣AQ＝2t﹣AQ，∴AB＝2t，∴t＝＝10（此时P与C重合），综上，存在这样的t值，使得QE＝QB，t的值为3.6或10．15．解：（1）∵将△DCB绕点D顺时针方向旋转60°，得到△DAB′，∴BD＝B′D，∠BDB′＝60°，∴△BDB′是等边三角形；故答案为：等边三角形；（2）由（1）知，△BCD≌△B′AD，∴四边形ABCD的面积＝等边三角形BDB′的面积，∵BC＝AB′＝1，∴BB′＝AB+AB′＝2+1＝3，∴S四边形ABCD＝S△BDB′＝；（3）解：将△BDM绕点D顺时针方向旋转120°，得到△DCP，∴△BDM≌△CDP，∴MD＝PD，CP＝BM，∠MBD＝∠DCP，∠MDB＝∠PDC，∵△BDC是等腰三角形，且∠BDC＝120°，∴BD＝CD，∠DBC＝∠DCB＝30°，又∵△ABC等边三角形，∴∠ABC＝∠ACB＝60°，∴∠MBD＝∠ABC+∠DBC＝90°，同理可得∠NCD＝90°，∴∠PCD＝∠NCD＝∠MBD＝90°，∴∠DCN+∠DCP＝180°，∴N，C，P三点共线，∵∠MDN＝60°，∴∠MDB+∠NDC＝∠PDC+∠NDC＝∠BDC﹣∠MDN＝60°，即∠MDN＝∠PDN＝60°，∴△NMD≌△NPD（SAS），∴MN＝PN＝NC+CP＝NC+BM，∴△AMN的周长＝AM+AN+MN＝AM+AN+NC+BM＝AB+AC＝2+2＝4．故△AMN的周长为4．。

冲刺中考压轴真题培优训练：《四边形》1．（2019•抚顺）如图，点E，F分别在正方形ABCD的边CD，BC上，且DE＝CF，点P在射线BC上（点P不与点F重合）．将线段EP绕点E顺时针旋转90°得到线段EG，过点E作GD的垂线QH，垂足为点H，交射线BC于点Q．（1）如图1，若点E是CD的中点，点P在线段BF上，线段BP，QC，EC的数量关系为．（2）如图2，若点E不是CD的中点，点P在线段BF上，判断（1）中的结论是否仍然成立．若成立，请写出证明过程；若不成立，请说明理由．（3）正方形ABCD的边长为6，AB＝3DE，QC＝1，请直接写出线段BP的长．2．（2019•盘锦）如图，四边形ABCD是菱形，∠BAD＝120°，点E在射线AC 上（不包括点A和点C），过点E的直线GH交直线AD于点G，交直线BC于点H，且GH∥DC，点F在BC的延长线上，CF＝AG，连接ED，EF，DF．（1）如图1，当点E在线段AC上时，①判断△AEG的形状，并说明理由．②求证：△DEF是等边三角形．（2）如图2，当点E在AC的延长线上时，△DEF是等边三角形吗？如果是，请证明你的结论；如果不是，请说明理由．3．（2019•无锡）如图，在ABCD中，点E、F分别在边AD、BC上，且DE＝BF，直线EF与BA、DC的延长线分别交于点G，H．求证：（1）△DEH≌△BFG；（2）AG＝CH．4．（2019•朝阳）如图，四边形ABCD是正方形，连接△A C，将ABC绕点A逆时针旋转α得△AEF，连接CF，O为CF的中点，连接OE，OD．（1）如图1，当α＝45°时，请直接写出OE与OD的关系（不用证明）．（2）如图2，当45°＜α＜90°时，（1）中的结论是否成立？请说明理由．（3）当α＝360°时，若AB＝4，请直接写出点O经过的路径长．5．（2019•连云港）问题情境：如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N．判断线段DN、MB、EC之间的数量关系，并说明理由．问题探究：在“问题情境”的基础上．（1）如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ，并延长交边AD于点F．求∠AEF的度数；A N，将APN （2）如图3，当垂足P在正方形ABCD的对角线BD上时，连接△沿着AN翻折，点P落在点P'处，若正方形ABCD的边长为4，AD的中点为S，求P'S的最小值．问题拓展：如图4，在边长为4的正方形ABCD中，点M、N分别为边AB、CD 上的点，将正方形ABCD沿着MN翻折，使得BC的对应边B'C'恰好经过点A，C'N交AD于点F．分别过点A、F作AG⊥MN，FH⊥MN，垂足分别为G、H．若AG＝，请直接写出FH的长．6．（2019•威海）如图，在正方形ABCD中，AB＝10cm，E为对角线BD上一动点，连接AE，CE，过E点作EF⊥AE，交直线BC于点F．E点从B点出发，沿着BD方向以每秒2cm的速度运动，当点E与点D重合时，运动停止．设△BEF 的面积为ycm2，E点的运动时间为x秒．（1）求证：CE＝EF；（2）求y与x之间关系的函数表达式，并写出自变量x的取值范围；（3）求△BEF面积的最大值．7．（2019•重庆）如图，在平行四边形ABCD中，点E在边BC上，连接AE，EM ⊥AE，垂足为E，交CD于点M，AF⊥BC，垂足为F，BH⊥AE，垂足为H，交AF于点N，点P是AD上一点，连接CP．C D＝5，求ACD的面积．（1）若DP＝2AP＝4，CP＝，△（2）若AE＝BN，AN＝CE，求证：AD＝CM+2CE．8．（2019•重庆）在ABCD中，BE平分∠ABC交AD于点E．（1）如图1，若∠D＝30°，AB＝，求ABE的面积；（2）如图2，过点A作AF⊥DC，交DC的延长线于点F，分别交BE，BC于点G，H，且AB＝AF．求证：ED﹣AG＝FC．9．（2019•自贡）（1）如图1，E是正方形ABCD边AB上的一点，连接BD、DE，将∠BDE绕点D逆时针旋转90°，旋转后角的两边分别与射线BC交于点F和点G．①线段DB和DG的数量关系是；②写出线段BE，BF和DB之间的数量关系．（2）当四边形ABCD为菱形，∠ADC＝60°，点E是菱形ABCD边AB所在直线上的一点，连接BD、DE，将∠BDE绕点D逆时针旋转120°，旋转后角的两边分别与射线BC交于点F和点G．①如图2，点E在线段AB上时，请探究线段BE、BF和BD之间的数量关系，写出结论并给出证明；②如图3，点E在线段AB的延长线上时，DE交射线BC于点M，若BE＝1，AB ＝2，直接写出线段GM的长度．10．（2019•台州）我们知道，各个角都相等，各条边都相等的多边形叫做正多边形．对一个各条边都相等的凸多边形（边数大于3），可以由若干条对角线相等判定它是正多边形．例如，各条边都相等的凸四边形，若两条对角线相等，则这个四边形是正方形．（1）已知凸五边形ABCDE的各条边都相等．①如图1，若AC＝AD＝BE＝BD＝CE，求证：五边形ABCDE是正五边形；②如图2，若AC＝BE＝CE，请判断五边形ABCDE是不是正五边形，并说明理由：（2）判断下列命题的真假．（在括号内填写“真”或“假”）如图3，已知凸六边形ABCDEF的各条边都相等．①若AC＝CE＝EA，则六边形ABCDEF是正六边形；（）②若AD＝BE＝CF，则六边形ABCDEF是正六边形．（）11．（2019•天津）在平面直角坐标系中，O为原点，点A（6，0），点B在y 轴的正半轴上，∠ABO＝30°．矩形CODE的顶点D，E，C分别在OA，AB，OB 上，OD＝2．（Ⅰ）如图①，求点E的坐标；（Ⅱ）将矩形CODE沿x轴向右平移，得到矩形C′O′D′E′，点C，O，D，E的对应点分别为C′，O′，D′，E′．设OO′＝t，矩形C′O′D′E′与△ABO重叠部分的面积为S．①如图②，当矩形C′O′D′△E′与ABO重叠部分为五边形时，C′E′，E′D′分别与AB相交于点M，F，试用含有t的式子表示S，并直接写出t的取值范围；②当≤S≤5时，求t的取值范围（直接写出结果即可）．12．（2019•青岛）已知：如图，在四边形ABCD中，AB∥CD，∠ACB＝90°，AB ＝10cm，BC＝8cm，OD垂直平分A C．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为1cm/s；当一个点停止运动，另一个点也停止运动．过点P作PE⊥AB，交BC于点E，过点Q作QF∥AC，分别交AD，OD于点F，G．连接OP，EG．设运动时间为t （s）（0＜t＜5），解答下列问题：（1）当t为何值时，点E在∠BAC的平分线上？（2）设四边形PEGO的面积为S（cm2），求S与t的函数关系式；（3）在运动过程中，是否存在某一时刻t，使四边形PEGO的面积最大？若存在，求出t的值；若不存在，请说明理由；（4）连接OE，OQ，在运动过程中，是否存在某一时刻t，使OE⊥OQ？若存在，求出t的值；若不存在，请说明理由．13．（2019•白银）阅读下面的例题及点拨，并解决问题：例题：如图①，在等边△ABC中，M是BC边上一点（不含端点B，C），N是△ABC的外角∠ACH的平分线上一点，且AM＝MN．求证：∠AMN＝60°．点拨：如图②，作∠CBE＝60°，BE与NC的延长线相交于点△E，得等边BEC，E M．易证：ABM≌△EBM（SAS），可得AM＝EM，∠1＝∠2；又AM＝MN，连接△则EM＝MN，可得∠3＝∠4；由∠3+∠1＝∠4+∠5＝60°，进一步可得∠1＝∠2＝∠5，又因为∠2+∠6＝120°，所以∠5+∠6＝120°，即：∠AMN＝60°．问题：如图③，在正方形A1B1C1D1中，M1是B1C1边上一点（不含端点B1，C1），N是正方形A B C D的外角∠D C H的平分线上一点，且A M＝M N．求证：∠A M N 111111*********＝90°．14．（2019•济宁）如图1，在矩形ABCD中，AB＝8，AD＝10，E是CD边上一点，连接AE，将矩形ABCD沿AE折叠，顶点D恰好落在BC边上点F处，延长AE交BC的延长线于点G．（1）求线段CE的长；（2）如图2，M，N分别是线段AG，DG上的动点（与端点不重合），且∠DMN＝∠DAM，设AM＝x，DN＝y．①写出y关于x的函数解析式，并求出y的最小值；②是否存在这样的点△M，使DMN是等腰三角形？若存在，请求出x的值；若不存在，请说明理由．15．（2019•嘉兴）小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．（1）温故：如图1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC 上，顶点P，N分别在AB，AC上，若BC＝6，AD＝4，求正方形PQMN的边长．（2）操作：能画出这类正方形吗？小波按数学家波利亚在《怎样解题》中的方法进行操作：如图2，任意画△ABC，在AB上任取一点P'，画正方形P'Q'M'N'，使Q'，M'在BC边上，△N'在ABC内，连结BN'并延长交AC于点N，画NM⊥BC 于点M，NP⊥NM交AB于点P，PQ⊥BC于点Q，得到四边形PPQMN．小波把线段BN称为“波利亚线”．（3）推理：证明图2中的四边形PQMN是正方形．（4）拓展：在（2）的条件下，在射线BN上截取NE＝NM，连结EQ，EM（如图3）．当tan∠NBM＝时，猜想∠QEM的度数，并尝试证明．请帮助小波解决“温故”、“推理”、“拓展”中的问题．参考答案1．解：（1）BP+QC＝EC；理由如下：∵四边形ABCD是正方形，∴BC＝CD，∠BCD＝90°，由旋转的性质得：∠PEG＝90°，EG＝EP，∴∠PEQ+∠GEH＝90°，∵QH⊥GD，∴∠H＝90°，∠G+∠GEH＝90°，∴∠PEQ＝∠G，又∵∠EPQ+∠PEC＝90°，∠PEC+∠GED＝90°，∴∠EPQ＝∠GED，在△PEQ和△EGD中，，∴△PEQ≌△EGD（ASA），∴PQ＝ED，∴BP+QC＝BC﹣PQ＝CD﹣ED＝EC，即BP+QC＝EC；故答案为：BP+QC＝EC；（2）（1）中的结论仍然成立，理由如下：由题意得：∠PEG＝90°，EG＝EP，∴∠PEQ+∠GEH＝90°，∵QH⊥GD，∴∠H＝90°，∠G+∠GEH＝90°，∴∠PEQ＝∠G，∵四边形ABCD是正方形，∴∠DCB＝90°，BC＝DC，∴∠EPQ+∠PEC＝90°，∵∠PEC+∠GED＝90°，∴∠GED＝∠EPQ，在△PEQ和△EGD中，，∴△PEQ≌△EGD（ASA），∴PQ＝ED，∴BP+QC＝BC﹣PQ＝CD﹣ED＝EC，即BP+QC＝EC；（3）分两种情况：①当点P在线段BC上时，点Q在线段BC上，由（2）可知：BP＝EC﹣QC，∵AB＝3DE＝6，∴DE＝2，EC＝4，∴BP＝4﹣1＝3；②当点P在线段BC上时，点Q在线段BC的延长线上，如图3所示：同（2）可得：△PEQ≌△EGD（AAS），∴PQ＝DE＝2，∵QC＝1，∴PC＝PQ﹣QC＝1，∴BP＝BC﹣PC＝6﹣1＝5；综上所述，线段BP的长为3或5．2．（1）①解：△AEG是等边三角形；理由如下：∵四边形ABCD是菱形，∠BAD＝120°，∴AD∥BC，AB＝BC＝CD＝AD，AB∥CD，∠CAD＝∠BAD＝60°，∴∠BAD+∠ADC＝180°，∴∠ADC＝60°，∵GH∥DC，∴∠AGE＝∠ADC＝60°，∴∠AGE＝∠EAG＝∠AEG＝60°，∴△AEG是等边三角形；②证明：∵△AEG是等边三角形，∴AG＝AE，∵CF＝AG，∴AE＝CF，∵四边形ABCD是菱形，∴∠BCD＝∠BAD＝120°，∴∠DCF＝60°＝∠CAD，在△AED和△CFD中，，∴△AED≌△CFD（SAS）∴DE＝DF，∠ADE＝∠CDF，∵∠ADC＝∠ADE+∠CDE＝60°，∴∠CDF+∠CDE＝60°，即∠EDF＝60°，∴△DEF是等边三角形；（2）解：△DEF是等边三角形；理由如下：同（1）①得：△AEG是等边三角形，∴AG＝AE，∵CF＝AG，∴AE＝CF，∵四边形ABCD是菱形，∴∠BCD＝∠BAD＝120°，∠CAD＝∠BAD＝60°，∴∠FCD＝60°＝∠CAD，在△AED和△CFD中，，∴△AED≌△CFD（SAS），∴DE＝DF，∠ADE＝∠CDF，∵∠ADC＝∠ADE﹣∠CDE＝60°，∴∠CDF﹣∠CDE＝60°，即∠EDF＝60°，∴△DEF是等边三角形．3．解：（1）∵四边形ABCD是平行四边形，∴AB∥CD，∠B＝∠D，AB＝CD，∴∠G＝∠H，∵∠D＝∠B，∠H＝∠G，DE＝BF，∴△DEH≌△BFG（AAS）；（2）∵△DEH≌△BFG，∴GB＝HD，又∵AB＝CD，∴GB﹣AB＝HD﹣CD，∴AG＝CH．4．解：（1）OE＝OD，OE⊥OD；理由如下：由旋转的性质得：AF＝AC，∠AFE＝∠ACB，∵四边形ABCD是正方形，∴∠ACB＝∠ACD＝∠FAC＝45°，∴∠ACF＝∠AFC＝（180°﹣45°）＝67.5°，∴∠DCF═∠EFC＝22.5°，∵∠FEC＝90°，O为CF的中点，∴OE＝CF＝OC＝OF，同理：OD＝CF，∴OE＝OD＝OC＝OF，∴∠EOC＝2∠EFO＝45°，∠DOF＝2∠DCO＝45°，∴∠DOE＝180°﹣45°﹣45°＝90°，∴OE⊥OD；（2）当45°＜α＜90°时，（1）中的结论成立，理由如下：连接CE，DF，如图所示：在正方形ABCD中，AB＝AD∴AD＝AE∵O为CF的中点，∴OC＝OF∵AF＝AC∴∠ACF＝∠AFC∵∠DAC＝∠EAF∴∠DAC﹣∠DAE＝∠EAF﹣∠DAE∴∠EAC＝∠DAF在△ACE和△AFD中，，∴△ACE≌△AFD（SAS）∴CE＝DF，∠ECA＝∠DFA又∵∠ACF＝∠AFC∴∠ACF﹣∠ECA＝∠AFC﹣∠DFA，∴∠ECO＝∠DFO，在△EOC和△DOF中，，∵EC＝DF，∠ECO＝∠DFO，CO＝FO ∴△EOC≌△DOF（SAS）∴OE＝OD．连接AO，则AO⊥CF，∴∠AOC＝∠ADC＝90°，∴A、C、O、D四点共圆，∴∠AOD＝∠ACD＝45°，同理A、E、O、F四点共圆，∴∠AOE＝∠AFE＝45°，∴∠DOE＝45°+45°＝90°，∴OD⊥OE．（3）连接AO，如图3所示：∵AC＝AF，CO＝OF，∴AO⊥CF，∴∠AOC＝90°，∴点O在以AC为直径的圆上运动，∵α＝360°，∴点O经过的路径长等于以AC为直径的圆的周长，∵AC＝AB＝×4＝8，∴点O经过的路径长为：πd＝8π．5．问题情境：解：线段DN、MB、EC之间的数量关系为：DN+MB＝EC；理由如下：∵四边形ABCD是正方形，∴∠ABE＝∠BCD＝90°，AB＝BC＝CD，AB∥CD，过点B作BF∥MN分别交AE、CD于点G、F，如图1所示：∴四边形MBFN为平行四边形，∴NF＝MB，∴BF⊥AE，∴∠BGE＝90°，∴∠CBF+∠AEB＝90°，∵∠BAE+∠AEB＝90°，∴∠CBF＝∠BAE，在△ABE和△BCF中，，∴△ABE≌△BCF（ASA），∴BE＝CF，∵DN+NF+CF＝BE+EC，∴DN+MB＝EC；问题探究：解：（1）连接AQ，过点Q作HI∥AB，分别交AD、BC于点H、I，如图2所示：∵四边形ABCD是正方形，∴四边形ABIH为矩形，∴HI⊥AD，HI⊥BC，HI＝AB＝AD，∵BD是正方形ABCD的对角线，∴∠BDA＝45°，∴△DHQ是等腰直角三角形，HD＝HQ，AH＝QI，∵MN是AE的垂直平分线，∴AQ＝QE，在Rt△AHQ和Rt△QIE中，，∴Rt△AHQ≌Rt△QIE（HL），∴∠AQH＝∠QEI，∴∠AQH+∠EQI＝90°，∴∠AQE＝90°，∴△AQE是等腰直角三角形，∴∠EAQ＝∠AEQ＝45°，即∠AEF＝45°；（2）连接AC交BD于点O，如图3所示：则△APN的直角顶点P在OB上运动，设点P与点B重合时，则点P′与点D重合；设点P与点O重合时，则点P′的落点为O′，∵AO＝OD，∠AOD＝90°，∴∠ODA＝∠ADO′＝45°，当点P在线段BO上运动时，过点P作PG⊥CD于点G，过点P′作P′H⊥CD 交CD延长线于点H，连接PC，∵点P在BD上，∴AP＝PC，，在△APB和△CPB中，∴△APB≌△CPB（SSS），∴∠BAP＝∠BCP，∵∠BCD＝∠MPA＝90°，∴∠PCN＝∠AMP，∵AB∥CD，∴∠AMP＝∠PNC，∴∠PCN＝∠PNC，∴PC＝PN，∴AP＝PN，∴∠PNA＝45°，∴∠PNP′＝90°，∴∠P′NH+PNG＝90°，∵∠P′NH+∠NP′H＝90°，∠PNG+∠NPG＝90°，∴∠NPG＝∠P′NH，∠PNG＝∠NP′H，由翻折性质得：PN＝P′N，在△PGN和△NHP'中，，∴△PGN≌△NHP'（ASA），∴PG＝NH，GN＝P'H，∵BD是正方形ABCD的对角线，∴∠PDG＝45°，易得PG＝GD，∴GN＝DH，∴DH＝P'H，∴∠P'DH＝45°，故∠P'DA＝45°，∴点P'在线段DO'上运动；过点S作SK⊥DO'，垂足为K，∵点S为AD的中点，∴DS＝2，则P'S的最小值为；问题拓展：解：延长AG交BC于E，交DC的延长线于Q，延长FH交CD于P，如图4：则EG＝AG＝，PH＝FH，∴AE＝5，在Rt△ABE中，BE＝＝3，∴CE＝BC﹣BE＝1，∵∠B＝∠ECQ＝90°，∠AEB＝∠QEC，∴△ABE∽△QCE，∴＝＝3，∴QE＝AE＝，∴AQ＝AE+QE＝，∵AG⊥MN，∴∠AGM＝90°＝∠B，∵∠MAG＝∠EAB，∴△AGM∽△ABE，∴＝，即＝，解得：AM＝，由折叠的性质得：AB'＝EB＝3，∠B'＝∠B＝90°，∠C'＝∠BCD＝90°，∴B'M＝＝，AC'＝1，∵∠BAD＝90°，∴∠B'AM＝∠C'FA，∴△AFC'∽△MAB'，∴＝＝，解得：AF＝，∴DF＝4﹣＝，∵AG⊥MN，FH⊥MN，∴AG∥FH，∴AQ∥FP，∴△DFP∽△DAQ，∴＝，即＝，解得：FP＝，∴FH＝FP＝．6．（1）证明：如图1，过E作MN∥AB，交AD于M，交BC于N，∵四边形ABCD是正方形，∴AD∥BC，AB⊥AD，∴MN⊥AD，MN⊥BC，∴∠AME＝∠FNE＝90°＝∠NFE+∠FEN，∵AE⊥EF，∴∠AEF＝∠AEM+∠FEN＝90°，∴∠AEM＝∠NFE，∵∠DBC＝45°，∠BNE＝90°，∴BN＝EN＝AM，∴△AEM≌△EFN（AAS），∴AE＝EF，∵四边形ABCD是正方形，∴AD＝CD，∠ADE＝∠CDE，∵DE＝DE，∴△ADE≌△CDE（SAS），∴AE＝CE，∴CE＝EF；（2）解：在Rt△BCD中，由勾股定理得：BD＝＝10，∴0≤x≤5，由题意得：BE＝2x，∴BN＝EN＝x，由（1）知：AE＝EF＝EC，分两种情况：①当0≤x≤时，如图1，∵AB＝MN＝10，∴ME＝FN＝10﹣x，∴BF＝FN﹣BN＝10﹣x﹣x＝10﹣2x，∴y＝＝＝﹣2x2+5x；②当＜x≤5时，如图2，过E作EN⊥BC于N，∴EN＝BN＝x，∴FN＝CN＝10﹣x，∴BF＝BC﹣2CN＝10﹣2（10﹣x）＝2x﹣10，∴y＝＝＝2x2﹣5x；综上，y与x之间关系的函数表达式为：；（3）解：①当0≤x≤时，如图1，y＝﹣2x2+5x＝﹣2（x﹣）2+，∵﹣2＜0，∴当x＝时，y有最大值是；②当＜x≤5时，如图2，∴y＝2x2﹣5x＝2（x﹣）2﹣，∵2＞0，∴当x＞时，y随x的增大而增大∴当x＝5时，y有最大值是50；综上，△BEF面积的最大值是50．7．（1）解：作CG⊥AD于G，如图1所示：设PG＝x，则DG＝4﹣x，在Rt△PGC中，GC2＝CP2﹣PG2＝17﹣x2，在Rt△DGC中，GC2＝CD2﹣GD2＝52﹣（4﹣x）2＝9+8x﹣x2，∴17﹣x2＝9+8x﹣x2，解得：x＝1，即PG＝1，∴GC＝4，＝∵DP ＝2AP ＝4，∴AD ＝6，∴△S ACD ×AD ×CG ＝ ×6×4＝12；（2）证明：连接 NE ，如图 2 所示：∵BH ⊥AE ，AF ⊥BC ，AE ⊥EM ，∴∠AEB +∠NBF ＝∠AEB +∠EAF ＝∠AEB +∠MEC ＝90°，∴∠NBF ＝∠EAF ＝∠MEC ，在△NBF 和△EAF 中，，∴△NBF ≌△EAF （AAS ），∴BF ＝AF ，NF ＝EF ，∴∠ABC ＝45°，∠ENF ＝45°，∵∠ANB ＝90°+∠EAF ，∠CEA ＝90°+∠MEC ，∴∠ANB ＝∠CEA ，在△ANB 和△CEA 中，，∴△ANB ≌△CEA （SAS ），∴∠CAE ＝∠ABN ，∵∠NBF ＝∠EAF ，∴∠ABF ＝∠FAC ＝45°∴FC ＝AF ＝BF ，∴∠ANE ＝∠BCD ＝135°，AD ＝BC ＝2AF ，在△ANE 和△ECM 中，，∴△ANE ≌△ECM （ASA ），∴CM＝NE，又∵NF＝NE＝MC，∴AF＝MC+EC，∴AD＝MC+2EC．8．（1）解：作BO⊥AD于O，如图1所示：∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，AB＝CD，∠ABC＝∠D＝30°，∴∠AEB＝∠CBE，∠BAO＝∠D＝30°，∴BO＝AB＝，∵BE平分∠ABC，∴∠ABE＝∠CBE，∴∠ABE＝∠AEB，∴AE＝AB＝，∴△ABE的面积＝AE×BO＝××＝；（2）证明：作AQ⊥BE交DF的延长线于P，垂足为Q，连接PB、PE，如图2所示：∵AB＝AE，AQ⊥BE，∴∠ABE＝∠AEB，BQ＝EQ，∴PB＝PE，∴∠PBE＝∠PEB，∴∠ABP＝∠AEP，∵AB∥CD，AF⊥CD，∴AF⊥AB，∴∠BAF＝90°，∵AQ⊥BE，∴∠ABG＝∠FAP，，在△ABG和△FAP中，∴△ABG≌△AFP（ASA），∴AG＝FP，∵AB∥CD，AD∥BC，∴∠ABP+∠BPC＝180°，∠BCP＝∠D，∵∠AEP+∠PED＝180°，∴∠BPC＝∠PED，在△BPC和△PED中，，∴△BPC≌△PED（AAS），∴PC＝ED，∴ED﹣AG＝PC﹣AG＝PC﹣FP＝FC．9．解：（1）①DB＝DG，理由是：∵∠DBE绕点B逆时针旋转90°，如图1，由旋转可知，∠BDE＝∠FDG，∠BDG＝90°，∵四边形ABCD是正方形，∴∠CBD＝45°，∴∠G＝45°，∴∠G＝∠CBD＝45°，∴DB＝DG；故答案为：DB＝DG；②BF+BE＝BD，理由如下：由①知：∠FDG＝∠EDB，∠G＝∠DBE＝45°，BD＝DG，∴△FDG≌△EDB（ASA），∴BE＝FG，∴BF+FG＝BF+BE＝BC+CG，Rt△DCG中，∵∠G＝∠CDG＝45°，∴CD＝CG＝CB，∵DG＝BD＝BC，即BF+BE＝2BC＝BD；（2）①如图2，BF+BE＝BD，理由如下：在菱形ABCD中，∠ADB＝∠CDB＝∠ADC＝×60°＝30°，由旋转120°得∠EDF＝∠BDG＝120°，∠EDB＝∠FDG，在△DBG中，∠G＝180°﹣120°﹣30°＝30°，∴∠DBG＝∠G＝30°，∴DB＝DG，∴△EDB≌△FDG（ASA），∴BE＝FG，∴BF+BE＝BF+FG＝BG，过点D作DM⊥BG于点M，如图2，∵BD＝DG，∴BG＝2BM，在Rt△BMD中，∠DBM＝30°，∴BD＝2DM．设DM＝a，则BD＝2a，BM＝a，∴BG＝2a，∴＝，∴BG＝BD，∴BF+BE＝BG＝BD；②过点A作AN⊥BD于N，过D作DP⊥BG于P，如图3，Rt△ABN中，∠ABN＝30°，AB＝2，∴AN＝1，BN＝，∴BD＝2BN＝2，∵DC∥BE，∴＝，∵CM+BM＝2，∴BM＝，Rt△BDP中，∠DBP＝30°，BD＝2，∴BP＝3，由旋转得：BD＝BF，∴BF＝2BP＝6，∴GM＝BG﹣BM＝6+1﹣＝．10．（1）①证明：∵凸五边形ABCDE的各条边都相等，∴AB＝BC＝CD＝DE＝EA，在△ABC、△BCD、△CDE、△DEA、EAB中，，∴△ABC≌△BCD≌△CDE≌△DEA≌EAB（SSS），∴∠ABC＝∠BCD＝∠CDE＝∠DEA＝∠EAB，∴五边形ABCDE是正五边形；②解：若AC＝BE＝CE，五边形ABCDE是正五边形，理由如下：在△ABE、△BCA和△DEC中，，∴△ABE≌△BCA≌△DEC（SSS），∴∠BAE＝∠CBA＝∠EDC，∠AEB＝∠ABE＝∠BAC＝∠BCA＝∠DCE＝∠DEC，在△ACE和△BEC中，，∴△ACE≌△BEC（SSS），∴∠ACE＝∠CEB，∠CEA＝∠CAE＝∠EBC＝∠ECB，∵四边形ABCE内角和为360°，∴∠ABC+∠ECB＝180°，∴AB∥CE，∴∠ABE＝∠BEC，∠BAC＝∠ACE，∴∠CAE＝∠CEA＝2∠ABE，∴∠BAE＝3∠ABE，同理：∠CBA＝∠D＝∠AED＝∠BCD＝3∠ABE＝∠BAE，∴五边形ABCDE是正五边形；（2）解：①若AC＝CE＝EA，如图3所示：则六边形ABCDEF是正六边形；假命题；理由如下：∵凸六边形ABCDEF的各条边都相等，∴AB＝BC＝CD＝DE＝EF＝FA，在△AEF、△CAB和△ECD中，，∴△AEF≌△CAB≌△ECD（SSS），如果△AEF、△CAB、△ECD都为相同的等腰直角三角形，则∠F＝∠D＝∠B＝90°，而正六边形的各个内角都为120°，∴六边形ABCDEF不是正六边形；故答案为：假；②若AD＝BE＝CF，则六边形ABCDEF是正六边形；假命题；理由如下：如图4所示：连接AE、AC、CE、BF，，在△BFE和△FBC中，∴△BFE≌△FBC（SSS），∴∠BFE＝∠FBC，∵AB＝AF，∴∠AFB＝∠ABF，∴∠AFE＝∠ABC，在△FAE和△BCA中，，∴△FAE≌△BCA（SAS），∴AE＝CA，同理：AE＝CE，∴AE＝CA＝CE，由①得：△AEF、△CAB、△ECD都为相同的等腰直角三角形，则∠F＝∠D＝∠B＝90°，而正六边形的各个内角都为120°，∴六边形ABCDEF不是正六边形；故答案为：假．11．解：（Ⅰ）∵点A（6，0），∴OA＝6，∵OD＝2，∴AD＝OA﹣OD＝6﹣2＝4，∵四边形CODE是矩形，∴DE∥OC，∴∠AED＝∠ABO＝30°，在Rt△AED中，AE＝2AD＝8，ED＝＝＝4，∵OD＝2，∴点E的坐标为（2，4）；（Ⅱ）①由平移的性质得：O′D′＝2，E′D′＝4∥O′C′∥OB，∴∠E′FM＝∠ABO＝30°，∴在Rt△MFE′中，MF＝2ME′＝2t，FE′＝，ME′＝OO′＝t，D′E′＝＝t，∴△SMFE′＝ME′•FE′＝×t×t＝，∵S矩形C′O′D′E′＝O′D′•E′D′＝2×4＝8，∴S＝S矩形C′O′D′E′﹣△SMFE′＝8﹣，∴S＝﹣②当S＝t2+8，其中t的取值范围是：0＜t＜2；时，如图③所示：O'A＝OA﹣OO'＝6﹣t，∵∠AO'F＝90°，∠AFO'＝∠ABO＝30°，∴O'F＝O'A＝（6﹣t）∴S＝（6﹣t）×（6﹣t）＝，解得：t＝6﹣，或t＝6+（舍去），∴t＝6﹣当S＝5；时，如图④所示：O'A＝6﹣t，D'A＝6﹣t﹣2＝4﹣t，∴O'G＝（6﹣t），D'F＝（4﹣t），∴S＝[（6﹣t）+（4﹣t）]×2＝5，- 35 -∴当≤S≤5时，t的取值范围为≤t≤6﹣．12．解：（1）在Rt△ABC中，∵∠ACB＝90°，AB＝10cm，BC＝8cm，∴AC＝＝6（cm），∵OD垂直平分线段AC，∴OC＝OA＝3（cm），∠DOC＝90°，∵CD∥AB，∴∠BAC＝∠DCO，∵∠DOC＝∠ACB，∴△DOC∽△BCA，∴＝＝，∴＝＝，∴CD＝5（cm），OD＝4（cm），∵PB＝t，PE⊥AB，易知：PE＝t，BE＝t，当点E在∠BAC的平分线上时，+ ＝ + ﹣ ）∵EP ⊥AB ，EC ⊥AC ，∴PE ＝EC ，∴ t ＝8﹣ t ，∴t ＝4．∴当 t 为 4 秒时，点 E 在∠BAC 的平分线上．（2）如图，连接 OE ，PC ．S 四边形 OPEG ＝△S OEG △S OPE △S OEG +（△S OPC △S PCE △S OEC＝ •（4﹣ t ）•3+[ •3•（8﹣ t ）+ •（8﹣ t ）• t ﹣ •3•（8﹣ t ）]＝﹣ t 2+ t +6（0＜t ＜5）．（3）存在．∵S ＝﹣ （t ﹣ ）2+（0＜t ＜5），∴t ＝ 时，四边形 OPEG 的面积最大，最大值为．（4）存在．如图，连接 OQ ．∵OE ⊥OQ ，∴∠EOC +∠QOC ＝90°，∵∠QOC +∠QOG ＝90°，∴∠EOC ＝∠QOG ，∴tan∠EOC ＝tan∠QOG ，∴ ＝ ，∴＝，整理得：5t2﹣66t+160＝0，解得t＝或10（舍弃）∴当t＝秒时，OE⊥OQ．13．解：延长A1B1至E，使EB1＝A1B1，连接EM1C、EC1，如图所示：则EB1＝B1C1，∠EB1M1中＝90°＝∠A1B1M1，∴△EB1C1是等腰直角三角形，∴∠B1EC1＝∠B1C1E＝45°，∵N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点，∴∠M1C1N1＝90°+45°＝135°，∴∠B1C1E+∠M1C1N1＝180°，∴E、C1、N1，三点共线，在△A1B1M1和△EB1M1中，，∴△A1B1M△1≌EB1M1（SAS），∴A1M1＝EM1，∠1＝∠2，∵A1M1＝M1N1，∴EM＝M N，∴∠3＝∠4，∵∠2+∠3＝45°，∠4+∠5＝45°，∴∠1＝∠2＝∠5，∵∠1+∠6＝90°，∴∠5+∠6＝90°，∴∠A1M1N1＝180°﹣90°＝90°．14．解：（1）如图1中，∵四边形ABCD是矩形，∴AD＝BC＝10，AB＝CD＝8，∴∠B＝∠BCD＝90°，由翻折可知：AD＝AF＝10．DE＝EF，设EC＝x，则DE＝EF＝8﹣x．在Rt△ABF中，BF＝＝6，∴CF＝BC﹣BF＝10﹣6＝4，在Rt△EFC中，则有：（8﹣x）2＝x2+42，∴x＝3，∴EC＝3．（2）①如图2中，∵AD∥CG，∴＝，∴＝，∴CG＝6，∴BG＝BC+CG＝16，在Rt△ABG中，AG＝＝8，在Rt△DCG中，DG＝＝10，∵AD＝DG＝10，∴∠DAG＝∠AGD，∵∠DMG＝∠DMN+∠NMG＝∠DAM+∠ADM，∠DMN＝∠DAM，∴∠ADM＝∠NMG，∴△ADM∽△GMN，∴＝，∴＝，∴y＝x2﹣x+10．当x＝4时，y有最小值，最小值＝2．②存在．由题意：∠DMN＝∠DGM．可以推出∠DNM＝∠DMG，推出∠DNM≠∠DMN，所以有两种情形：如图3﹣1中，当MN＝MD时，∵∠MDN＝∠GDM，∠DMN＝∠DGM，∴△DMN∽△DGM，∴＝，∵MN＝DM，∴DG＝GM＝10，∴x＝AM＝8﹣10．如图3﹣2中，当MN＝DN时，作MH⊥DG于H．∵MN＝DN，∴∠MDN＝∠DMN，∵∠DMN＝∠DGM，∴∠MDG＝∠MGD，∴MD＝MG，∵MH⊥DG，∴DH＝GH＝5，由△GHM∽△GBA，可得＝，∴＝，∴MG＝，∴x＝AM＝8﹣＝．综上所述，满足条件的x的值为8﹣10或．15．（1）解：如图1中，∵PN∥BC，∴△APN∽△ABC，∴＝，即＝，解得PN＝．（2）能画出这样的正方形，如图2中，正方形PNMQ即为所求．（3）证明：如图2中，由画图可知∠QMN＝∠PQM＝∠MNP＝∠BM′N′＝90°，∴四边形PNMQ是矩形，MN∥M′N′，B N′△M′∽BNM，∴△∴＝，同理可得：＝，∴＝，∵M′N′＝P′N′，∴MN＝PN，∴四边形PQMN是正方形．（4）解：如图3中，结论：∠QEM＝90°．理由：由tan∠NBM＝＝，可以假设MN＝3k，BM＝4k，则BN＝5k，BQ＝k，BE＝2k，∴＝＝，＝＝，∴＝，∵∠QBE＝∠EBM，∴△BQE∽△BEM，∴∠BEQ＝∠BME，∵NE＝NM，∴∠NEM＝∠NME，∵∠BME+∠EMN＝90°，∴∠BEQ+∠NEM＝90°，∴∠QEM＝90°．。

培优冲刺03四边形压轴题综合1、四边形与翻折的综合2、四边形与旋转的综合3、四边形与新定义的综合4、四边形与中点的综合题型一：四边形与翻折的综合有翻折必有全等，并且是轴对称类型的全等，所以，当四边形压轴题出现翻折或折叠时，一般都是从轴对称类的全等入手思考！【中考真题练】1．（2023•西宁）折叠问题是我们常见的数学问题，它是利用图形变化的轴对称性质解决的相关问题．数学活动课上，同学们以“矩形的折叠”为主题开展了数学活动．【操作】如图1，在矩形ABCD中，点M在边AD上，将矩形纸片ABCD沿MC所在的直线折叠，使点D落在点D′处，MD′与BC交于点N．【猜想】MN＝CN．【验证】请将下列证明过程补充完整：∵矩形纸片ABCD沿MC所在的直线折叠，∴∠CMD＝∠CMD′，∵四边形ABCD是矩形，∴AD∥BC（矩形的对边平行），∴∠CMD＝∠MCN（两直线平行，内错角相等），∴∠CMD′＝∠MCN（等量代换），∴MN＝CN（等角对等边）．【应用】如图2，继续将矩形纸片ABCD折叠，使AM恰好落在直线MD′上，点A落在点A′处，点B落在点B′处，折痕为ME．（1）猜想MN与EC的数量关系，并说明理由；（2）若CD＝2，MD＝4，求EC的长．【分析】【验证】根据折叠的性质得到∠CMD＝∠CMD′，根据矩形的性质推出∠CMD＝∠MCN，则∠CMD′＝∠MCN，根据等腰三角形的判定即可得解；【应用】（1）根据折叠的性质得到∠AME＝∠A′ME，根据矩形的性质推出∠AME＝∠MEN，则∠A′ME＝∠MEN，根据等腰三角形的判定即可得出MN＝EN，结合MN＝CN即可得解；（2）根据矩形的性质、折叠的性质得出∠D＝∠D'＝90°，DC＝D'C＝2，MD＝MD′＝4，设MN＝NC ＝x，则ND′＝4﹣x，根据勾股定理求解即可．【解答】解：【验证】∵矩形纸片ABCD沿MC所在的直线折叠，∴∠CMD＝∠CMD′，∵四边形ABCD是矩形，∴AD∥BC（矩形的对边平行），∴∠CMD＝∠MCN（两直线平行，内错角相等），∴∠CMD′＝∠MCN（等量代换），∴MN＝CN（等角对等边）．故答案为：∠CMD′；∠MCN；两直线平行，内错角相等；∠CMD′＝∠MCN；等角对等边；【应用】（1）EC＝2MN；理由如下：∵由四边形ABEM折叠得到四边形A′B′EM，∴∠AME＝∠A′ME，∵四边形ABCD是矩形，∴AD∥BC（矩形的对边平行），∴∠AME＝∠MEN（两直线平行，内错角相等），∴∠A′ME＝∠MEN，∴MN＝EN（等角对等边），∵MN＝CN，∴MN＝EN＝NC，即EC＝2MN；（2）∵矩形ABCD沿MC所在直线折叠，∴∠D＝∠D'＝90°，DC＝D'C＝2，MD＝MD′＝4，设MN＝NC＝x，∴ND′＝MD′﹣MN＝4﹣x，在Rt△ND′C中，∠D'＝90°，∴ND'2+D'C2＝NC2，∴（4﹣x）2+22＝x2，解得，∴MN＝，∴EC＝2MN＝5．2．（2023•衢州）如图1，点O为矩形ABCD的对称中心，AB＝4，AD＝8，点E为AD边上一点（0＜AE ＜3），连结EO并延长，交BC于点F．四边形ABFE与A′B′FE关于EF所在直线成轴对称，线段B′F交AD边于点G．（1）求证：GE＝GF．（2）当AE＝2DG时，求AE的长．（3）令AE＝a，DG＝b．①求证：（4﹣a）（4﹣b）＝4．②如图2，连结OB′，OD，分别交AD，B′F于点H，K．记四边形OKGH的面积为S1，△DGK的面积为S2，当a＝1时，求的值．【分析】（1）由四边形ABCD是矩形，可得∠GEF＝∠BFE，而四边形ABFE与A′B′FE关于EF所在直线成轴对称，有∠BFE＝∠GFE，故∠GEF＝∠GFE，GE＝GF；（2）过G作GH⊥BC于H，设DG＝x，可知AE＝2x，GE＝AD﹣AE﹣DG＝8﹣3x＝GF，根据点O为矩形ABCD的对称中心，可得CF＝AE＝2x，故FH＝CF﹣CH＝x，在Rt△GFH中，x2+42＝（8﹣3x）2，解得x的值从而可得AE的长为6﹣2；（3）①过O作OQ⊥AD于Q，连接OA，OD，OG，由点O为矩形ABCD的对称中心，EF过点O，可得O为EF中点，OA＝OD，OQ＝AB＝2，证明△GOQ∽△OEQ，得＝，即GQ•EQ＝OQ2，故GQ•EQ＝4，即可得（4﹣a）（4﹣b）＝4；②连接B'D，OG，OB，证明B'F＝DE，OD＝OB＝OB'，可得△DOG≌△B'OG（SSS），∠ODG＝∠OB'G，＝S△OGH，从而△DGK≌△B'GH（ASA），DK＝B'H，GK＝GH，即可证△OGK≌△OGH（SSS），得S△OGK有＝，而∠EGF＝∠DGB'，GE＝GF，GD＝GB'，知EF∥B'D，可得△OKF∽△DKB'，△EGF∽△DGB'，得＝，＝＝＝＝，又△EGF∽△DGB'，有＝，当a＝1时，b＝，即AE＝1，DG＝，即可得＝＝＝＝．【解答】（1）证明：∵四边形ABCD是矩形，∴AD∥BC，∴∠GEF＝∠BFE，∵四边形ABFE与A′B′FE关于EF所在直线成轴对称，∴∠BFE＝∠GFE，∴∠GEF＝∠GFE，∴GE＝GF；（2）解：过G作GH⊥BC于H，如图：设DG＝x，则AE＝2x，∴GE＝AD﹣AE﹣DG＝8﹣3x＝GF，∵∠GHC＝∠C＝∠D＝90°，∴四边形GHCD是矩形，∴GH＝CD＝AB＝4，CH＝DG＝x，∵点O为矩形ABCD的对称中心，∴CF＝AE＝2x，∴FH＝CF﹣CH＝x，在Rt△GFH中，FH2+GH2＝GF2，∴x2+42＝（8﹣3x）2，解得x＝3+（此时AE大于AD，舍去）或x＝3﹣，∴AE＝2x＝6﹣2；∴AE的长为6﹣2；（3）①证明：过O作OQ⊥AD于Q，连接OA，OD，OG，如图：∵点O为矩形ABCD的对称中心，EF过点O，∴O为EF中点，OA＝OD，OQ＝AB＝2，∵GE＝GF，∴OG⊥EF，∴∠GOQ＝90°﹣∠EOQ＝∠QEO，∵∠GQO＝90°＝∠OQE，∴△GOQ∽△OEQ，∴＝，即GQ•EQ＝OQ2，∴GQ•EQ＝4，∵OA＝OD，OQ⊥AD，∴AQ＝DQ＝AD＝4，∴EQ＝AQ﹣AE＝4﹣a，GQ＝DQ﹣GD＝4﹣b，∴（4﹣a）（4﹣b）＝4；②解：连接B'D，OG，OB，如图：∵四边形ABFE与A′B′FE关于EF所在直线成轴对称，∴BF＝B'F，∵点O为矩形ABCD的对称中心，∴BF＝DE，∴B'F＝DE，同理OD＝OB＝OB'，由（1）知GF＝GE，∴B'F﹣GF＝DE﹣GE，即B'G＝DG，∵OG＝OG，∴△DOG≌△B'OG（SSS），∴∠ODG＝∠OB'G，∵DG＝B'G，∠DGK＝∠B'GH，∴△DGK≌△B'GH（ASA），∴DK＝B'H，GK＝GH，∴OD﹣DK＝OB'﹣B'H，即OK＝OH，∵OG＝OG，∴△OGK≌△OGH（SSS），＝S△OGH，∴S△OGK∴S1＝2S△OGK，∴＝，∵∠EGF＝∠DGB'，GE＝GF，GD＝GB'，∴∠GEF＝∠GFE＝∠GDB'＝∠GB'D，∴EF∥B'D，∴△OKF∽△DKB'，△EGF∽△DGB'，∴＝，∵＝，∴＝＝＝＝，∵△EGF∽△DGB'，∴＝，当a＝1时，由①知（4﹣1）×（4﹣b）＝4，∴b＝，∴AE＝1，DG＝，∴GE＝AD﹣AE﹣DG＝，∴＝＝＝＝，∴的值为．3．（2023•烟台）【问题背景】如图1，数学实践课上，学习小组进行探究活动，老师要求大家对矩形ABCD进行如下操作：①分别以点B，C为圆心，以大于BC的长度为半径作弧，两弧相交于点E，F，作直线EF交BC于点O，连接AO；②将△ABO沿AO翻折，点B的对应点落在点P处，作射线AP交CD于点Q．【问题提出】在矩形ABCD中，AD＝5，AB＝3，求线段CQ的长；【问题解决】经过小组合作、探究、展示，其中的两个方案如下：方案一：连接OQ，如图2．经过推理、计算可求出线段CQ的长；方案二：将△ABO绕点O旋转180°至△RCO处，如图3．经过推理、计算可求出线段CQ的长．请你任选其中一种方案求线段CQ的长．【分析】方案一：连接OQ，由翻折的不变性，知AP＝AB＝3，OP＝OB＝2.5，证明△QPO≌△QCO（HL），推出PQ＝CQ，设PQ＝CQ＝x，在Rt△ADQ中，利用勾股定理列式计算求解即可；方案二：将△ABO绕点O旋转180°至△RCO处，证明∠OAQ＝∠R，推出QA＝QR，设CQ＝x，同方案一即可求解．【解答】解：方案一：连接OQ，如图，∵四边形ABCD是矩形，∴AB＝CD＝3，AD＝BC＝5，由作图知BO＝OC＝BC＝2.5，由翻折的不变性，知AP＝AB＝3，OP＝OB＝2.5，∠APO＝∠B＝90°，∴OP＝OC＝2.5，∠QPO＝∠C＝90°，又OQ＝OQ，∴△QPO≌△QCO（HL），∴PQ＝CQ，设PQ＝CQ＝x，则AQ＝3+x，DQ＝3﹣x，在Rt△ADQ中，AD2+QD2＝AQ2.即52+（3﹣x）2＝（3+x）2，解得x＝，∴线段CQ的长为；方案二：将△ABO绕点O旋转180°至△RCO处，如图，∵四边形ABCD是矩形，∴AB＝CD＝3，AD＝BC＝5，由作图知BO＝OC＝BC＝2.5，由旋转的不变性，知CR＝AB＝3，∠BAO＝∠R，∠B＝∠OCR＝90°，则∠OCR+∠OCD＝90°+90°＝180°，∴D、C、R共线，由翻折的不变性，知∠BAO＝∠OAQ，∴∠OAQ＝∠R，∴QA＝QR，设CQ＝x，则QA＝QR＝3+x，DQ＝3﹣x，在Rt△ADQ中，AD2+QD2＝AQ2，即52+（3﹣x）2＝（3+x）2，解得x＝，∴线段CQ的长为．【中考模拟练】1．（2024•天山区校级一模）如图，正方形ABCD边长为1，点E在边AB上（不与A，B重合），将△ADE 沿直线DE折叠，点A落在点A1处，连接A1B，将A1B绕点B顺时针旋转90°得到A2B，连接A1A，A1C，A2C．给出下列四个结论：①△ABA1≌△CBA2；②∠ADE+∠A1CB＝45°；③点P是直线DE上动点，则CP+A1P的最小值为；④当∠ADE＝30°时，△A1BE的面积为．其中正确的结论个数是（）A．1B．2C．3D．4【分析】①正确．根据SAS证明三角形全等即可；②正确．过点D作DT⊥CA1于点T，证明∠ADE+∠CDT＝45°，∠CDT＝∠BCA1即可；③正确．连接PA，AC．因为A，A1关于DE对称，推出PA＝PA1，推出PA1+PC＝PA+PC≥AC＝，可得结论；④错误．过点A1作A1H⊥AB于点H，求出EB，A1H，可得结论．【解答】解：∵四边形ABCD是正方形，∴BA＝BC，∠ABC＝90°，∵∠A1BA2＝∠ABC＝90°，∴∠ABA1＝∠CBA2，∵BA1＝BA2，∴△ABA1≌△CBA2（SAS），故①正确；过点D作DT⊥CA1于点T，∵CD＝DA1，∴∠CDT＝∠A1DT，∵∠ADE＝∠A1DE，∠ADC＝90°，∴∠ADE+∠CDT＝45°，∵∠CDT+∠DCT＝90°，∠DCT+∠BCA1＝90°，∴∠CDT＝∠BCA1，∴∠ADE+∠BCA1＝45°，故②正确；连接PA，AC．∵A，A1关于DE对称，∴PA＝PA1，∴PA1+PC＝PA+PC≥AC＝，∴PA1+PC的最小值为，故③正确；过点A1作A1H⊥AB于点H，∵∠ADE＝30°，∴AE＝A1E＝AD•tan30°＝，∴EB＝AB﹣AE＝1﹣，∵∠A1EB＝60°，∴A1H＝A1E•sin60°＝×＝，∴△A1BE的面积＝×（1﹣）×＝，故④错误；故选：C．2．（2024•曲阜市一模）如图1，菱形纸片ABCD的边长为2，∠ABC＝60°，如图2，翻折∠ABC，∠ADC，使两个角的顶点重合于对角线BD上一点P，EF，GH分别是折痕．设AE＝x（0＜x＜2），给出下列判断：①当x＝1时，DP的长为；②EF+GH的值随x的变化而变化；③六边形AEFCHG面积的最大值是；④六边形AEFCHG周长的值不变．其中正确的是（）A．①②B．①④C．②③④D．①③④【分析】先确定出△ABC是等边三角形，进而判断出△BEF是等边三角形，当x＝1时，求出BP＝BD，即可判断出①正确，再用x表示出EF，BP，DP，GH，然后取x赋予的值，即可求出EF+GH的值，判断出②错误，利用菱形的面积减去两个三角形的面积判断出③错误，利用周长的计算方法即可判定出④正确．【解答】解：∵菱形ABCD的边长为2，∴AB＝BC＝2，∵∠ABC＝60°，∴AC＝AB＝2，BD＝2，由折叠知，△BEF是等边三角形，当x＝1时，则AE＝1，∴BE＝AB﹣AE＝1，由折叠知，BP＝2×＝＝BD，故①正确；如图，设EF与BD交于M，GH于BD交于N，∵AE＝x，∴BE＝AB﹣AE＝2﹣x，∵△BEF是等边三角形，∴EF＝BE＝2﹣x，∴BM＝EM＝×EF＝（2﹣x），∴BP＝2BM＝（2﹣x），∴DP＝BD﹣BP＝2﹣（2﹣x）＝x，∴DN＝DP＝x，∴GH＝2GN＝2×x＝x，∴EF+GH＝2，所以②错误；当0＜x＜2时，∵AE＝x，∴BE＝2﹣x，∴EF＝2﹣x，∴BP＝（2﹣x），∴DP＝x，∴GH＝2×＝x＝DG＝DH，﹣S△BEF﹣S△DGH∴六边形AEFCHG面积＝S菱形ABCD＝×2×2﹣（2﹣x）2﹣x2＝2﹣（x﹣1）2﹣＝﹣（x﹣1）2+，∴当x＝1时，六边形AEFCHG面积最大为，所以③正确，六边形AEFCHG周长＝AE+EF+FC+CH+HG+AG＝x+2﹣x+x+2﹣x+x+2﹣x＝6是定值，所以④正确，即：正确的有①③④，故选：D．3．（2024•辽宁模拟）如图，在矩形ABCD中，AB＝2，，点E为射线BA上一点（点E不与点B 重合），将△BCE沿EC折叠，得到△FCE，点P为线段FC上一点，再将△EFP沿EP折叠，得到△EGP，PG的延长线与边BC相交于点Q．（1）如图1，连接EQ，求证：QB＝QG．（2）如图2，当点E与点A重合时，若点G落在边AD上，连接BF，EC与BF相交于点M，与PQ相交于点N，求MN的长．（3）若点G落在边AD上，且，CE所在直线与AD所在直线相交于点H．①如图3，当点E在线段BA延长线上时，求HG的长；②当点E在线段AB上时，请直接写出HG的长．【分析】（1）根据矩形和折叠的性质证明Rt△EBQ≌Rt△EGQ（HL），即可得QB＝QG；（2）先证明四边形EBQG是矩形，得BQ＝EG＝2，则CQ＝BC﹣BQ＝2﹣2，在RtABC中，由可得∠ACB＝30°，解直角三角形求出CM＝BC•cos30°＝2×＝3，CN＝＝4﹣，即可得MN的长．（3）①过点G作GR⊥BC，垂足为R，则四边形ABRG是矩形．AG＝BR，GR＝AB＝2．在Rt△GQR中，根据勾股定理得QR＝，则，在Rt△EAG中，根据勾股定理得AE ＝1．则EB＝AE+AB＝2+1＝3，证明△EAH∽△EBC．根据相似三角形的性质得，即可求解；②过点G作GR⊥BC，垂足为R，同①的方法即可求解．【解答】（1）证明：∵四边形ABCD是矩形，∴∠B＝90°，由折叠知EG＝EF＝EB，∠EGP＝∠F＝∠B＝90°，∴∠EGQ＝180°﹣∠EGP＝90°，又∵EQ＝EQ，∴Rt△EBQ≌Rt△EGQ（HL），∴QB＝QG；（2）解：∵将△BCE沿EC折叠，得到△FCE，∴EC垂直平分BF．∴∠BMC＝90°，∵四边形ABCD是矩形，∴∠ABC＝∠BAD＝90°，由（1）知∠EGQ＝90°，EG＝EF＝EB＝2，∴四边形EBQG是矩形，∴BQ＝EG＝2，∴CQ＝BC﹣BQ＝2﹣2，在RtABC中，，∴∠ACB＝30°，在Rt△BCM中，CM＝BC•cos30°＝2×＝3，在Rt△CNQ中，CN＝＝4﹣，∴；（3）解：①过点G作GR⊥BC，垂足为R，∴∠GRB＝90°．由（1）得，∴∠DAB＝∠B＝∠GRB＝90°，∴四边形ABRG是矩形．∴AG＝BR，GR＝AB＝2．在Rt△GQR中，，∴，在Rt△EAG中，AE2+AG2＝EG2，∵EG＝EB＝AE+AB＝AE+2，∴，解得AE＝1．∴EB＝AE+AB＝2+1＝3，∵四边形ABRG是矩形，∴AH∥BC．∴△EAH∽△EBC．∴，∴，∴；②过点G作GR⊥BC，垂足为R，同理得，，∴AG＝BQ﹣QR＝﹣＝，在Rt△EAG中，AE2+AG2＝EG2，∵EG＝EB＝AB﹣AE＝2﹣AE，∴AE2+（）2＝（2﹣AE）2，解得AE＝．∴EB＝AB﹣AE＝2﹣＝，∵AH∥BC．∴△EAH∽△EBC．∴，∴，∴AH＝，∴HG＝AH+AG＝+．题型二：四边形与旋转的综合旋转的性质是不改变图形的形状与大小，并且旋转中两对应点与旋转中心连线的三角形是等腰三角形，各等腰三角形间均相似；所以四边形与旋转结合考察的综合题，谨记以下几点：①有旋转就会出现全等三角形、新形成的等腰三角形、新形成的相似三角形、旋转相似必成对！【中考真题练】1．（2023•南充）如图，正方形ABCD中，点M在边BC上，点E是AM的中点，连接ED，EC．（1）求证：ED＝EC；（2）将BE绕点E逆时针旋转，使点B的对应点B′落在AC上，连接MB′．当点M在边BC上运动时（点M不与B，C重合），判断△CMB′的形状，并说明理由．（3）在（2）的条件下，已知AB＝1，当∠DEB′＝45°时，求BM的长．【分析】（1）根据正方形的性质和直角三角形斜边中线的性质可证△EAD≌△EBC（SAS），根据全等三角形的性质即可得证；（2）根据折叠的性质可得根据旋转的性质可得，EB′＝EB，再根据直角三角形斜边的中线的性质可得EB′＝AE＝ME，进一步可得∠AB′M＝90°，可得∠CB′M＝90°，再根据正方形的性质可得∠B′CM＝45°，进一步可得B′M＝B′C，可证△MB′C是等腰直角三角形；（3）延长BE交AD于点F，根据三角形外角的性质可得∠BEB′＝90°，进一步可得∠DEF＝45°，根据△EAD≌△EBC，可得∠AED＝∠BEC，进一步可得∠CEM＝∠DEF＝45°，再证明△CME∽△AMC，根据相似三角形的性质可得CM：AM＝EM：CM，可得，设BM＝x，则CM＝1﹣x，根据勾股定理，AM2＝1+x2，列方程求解即可．【解答】（1）证明：在正方形ABCD中，AD＝BC，∠BAD＝∠ABC＝90°，∵E为AM的中点，∴AE＝BE，∴∠EAB＝∠EBA，∴∠EAD＝∠EBC，在△EAD和△EBC中，，∴△EAD≌△EBC（SAS），∴ED＝EC；（2）解：△CMB′是等腰直角三角形，理由如下：根据旋转的性质可得，EB′＝EB，∵EB＝AE＝ME，∴EB′＝AE＝ME，∴∠EAB′＝∠EB′A，∠EMB′＝∠EB′M，∵∠EAB′+∠EB′A+∠EB′M+∠EMB′＝180°，∴∠AB′M＝90°，∴∠MB′C＝90°，在正方形ABCD中，∠ACB＝45°，∴∠B′MC＝45°，∴B′M＝B′C，∴△CMB′是等腰直角三角形；（3）解：延长BE交AD于点F，如图所示：∵∠BEM＝2∠BAE，∠B′EM＝2∠B′AE，∵∠BAB′＝45°，∴∠BEB′＝90°，∴∠B′EF＝90°，∵∠DEB′＝45°，∴∠DEF＝45°，∵△EAD≌△EBC，∴∠AED＝∠BEC，∵∠AEF＝∠BEM，∴∠CEM＝∠DEF＝45°，∵∠MCA＝45°，∴∠CEM＝∠MCA，又∵∠CME＝∠AMC，∴△CME∽△AMC，∴CM：AM＝EM：CM，∵EM＝AM，∴，在正方形ABCD中，BC＝AB＝1，设BM＝x，则CM＝1﹣x，根据勾股定理，AM2＝1+x2，∴＝（1﹣x）2，解得x＝或x＝2+（舍去），∴BM＝．2．（2023•绍兴）在平行四边形ABCD中（顶点A，B，C，D按逆时针方向排列），AB＝12，AD＝10，∠B为锐角，且sin B＝．（1）如图1，求AB边上的高CH的长；（2）P是边AB上的一动点，点C，D同时绕点P按逆时针方向旋转90°得点C'，D'，①如图2，当C'落在射线CA上时，求BP的长；②当△AC'D'是直角三角形时，求BP的长．【分析】（1）由平行四边形的性质对边相等，和三角函数可求得结果；（2）①由三角形全等和三角形相似可得出结论；②三角形的直角顶点不确定，故要分类讨论，分三种情况讨论，求出结论．【解答】解：（1）在▱ABCD中，BC＝AD＝10，在Rt△BCH中，HC＝BC sin B＝．（2）①如图，作CH⊥BA于点H，由（1）得，BH＝＝＝6，作C'Q⊥BA交BA延长线于点Q，则∠CHP＝∠PQC'＝90°，∴∠C'PQ+∠PC'Q＝90°，∵∠C'PQ+∠CPH＝90°，∴∠PC'Q＝∠CPH，由旋转知PC'＝PC，∴△PQC′≌△CHP（AAS）．设BP＝x，则PQ＝CH＝8，C′Q＝PH＝6﹣x，QA＝PQ﹣PA＝x﹣4．∵C′Q⊥AB，CH⊥AB，∴C′Q∥CH，∴△AQC′∽△AHC，∴，∴，∴x＝，∴BP＝，②由旋转得△PCD≌△PC′D′，CD＝C'D' CD⊥CD'又∵AB∥CD，∴C'D'⊥AB情况一：当以C′为直角顶点时，如图．∵C'D'⊥AB，∴C′落在线段BA延长线上．∵PC⊥PC'，∴PC⊥AB，由（1）知，PC＝8，∴BP＝6．情况二：当以A为直角顶点时，如图，设C'D'与射线BA的交点为T，作CH⊥AB于点H．∵PC⊥PC'，∴∠CPH+∠TPC'＝90°，∵点C，D同时绕点P按逆时针方向旋转90°得点C'，D'，∴∠CPD＝∠C'PD'＝90°，PC＝PD，PC'＝PD'，∴∠CPD＝∠C'PD'，∴△PCD≌△PC'D'（SAS），∴∠PCD＝∠PC'D'，∵AB∥CD，∴∠BPC＝∠PCD＝∠PC'D'，∵∠C'PT+∠CPB＝90°，∴∠C'PT+∠PC'T＝90°，∴∠PTC'＝90°＝∠CHP，∴△CPH≌△PC′T（AAS），∴C′T＝PH，PT＝CH＝8．设C′T＝PH＝t，则AP＝6﹣t，∴AT＝PT﹣PA＝2+t．∵∠C'AD'＝90°，C'D'⊥AB，∴△ATD′∽△C′TA，∴，∴AT2＝C'T⋅TD'，∴（2+t）2＝t（12﹣t），化简得t2﹣4t+2＝0，解得，∴BP＝BH+HP＝8±，情况三：当以D'为直角顶点时，点P落在BA的延长线上，不符合题意．综上所述，BP＝6或8±．②方法二：动静互换：将C、D看成静止的，点A绕P点顺时针旋转90°，∴△APA1是等腰直角三角形，∴A点轨迹是在∠BAE＝45°的射线AE上，当△A1CD为直角三角形时，（i）当∠A1CD＝90°时，∴∠BP1A1＝90°，∴BP1＝＝6；（ii）当点A为直角时，以CD为直径作圆O交AE于点A2、A3.如图所示，则△AOE为等腰直角三角形，∵AO＝8，∴AE＝8，OF＝4，∴A2F＝A3F＝2，AF＝4，∴AA2＝4+2，∴AP2＝4+BP2＝12﹣（4+）＝8﹣，（iii）AA3＝4﹣2，∴AA3＝4﹣，∴BP3＝12﹣（4﹣）＝8+，综上所述：BP＝6或8±．3．（2023•丹东）在△ABC中，∠BAC＝90°，∠ABC＝30°，AB＝6，点D是BC的中点．四边形DEFG 是菱形（D，E，F，G按逆时针顺序排列），∠EDG＝60°，且DE＝2，菱形DEFG可以绕点D旋转，连接AG和CE，设直线AG和直线CE所夹的锐角为α．（1）在菱形DEFG绕点D旋转的过程中，当点E在线段DC上时，如图①，请直接写出AG与CE的数量关系及α的值；（2）当菱形DEFG绕点D旋转到如图②所示的位置时，（1）中的结论是否成立？若成立，请写出证明过程；若不成立，请说明理由；（3）设直线AG与直线CE的交点为P，在菱形DEFG绕点D旋转一周的过程中，当EF所在的直线经过点B时，请直接写出△APC的面积．【分析】（1）由AG＝AD﹣GD＝2﹣2，CE＝CD﹣DE＝2＝AG，即可求解；（2）证明△ADG≌△CDE（SAS），进而求解；（3）证明△BDE、△DGC均为等边三角形，证明A、M、P、G共线，由（1）、（2）知，∠MPC＝60°，即可求解；当B、F重合时，也符合题意，由（1）、（2）知，∠MPC＝60°，则tan∠AEC＝＝＝，在△APC中，用解直角三角形的方法即可求解．【解答】（1）解：AG＝CE，α＝60°，理由：在△ABC中，∠BAC＝90°，∠ABC＝30°，AB＝6，则AC＝AB tan30°＝2，则BC＝2AC＝4，∵点D是BC的中点，则BD＝CD＝AD＝2，则AG＝AD﹣GD＝2﹣2，CE＝CD﹣DE＝2＝AG，在△ACD中，AD＝CD，∠C＝60°，则△ACD为等边三角形，则∠ADC＝60°＝α；（2）（1）的结论成立，理由：证明：延长AG交CD于点T，交CE于点N，∵∠ADG+∠GDC＝60°＝∠GDC+∠CDE，∴∠ADG＝∠CDE，∵AD＝CD，GD＝ED，∴△ADG≌△CDE（SAS），∴AG＝CE，∠DCE＝∠DAN，∵∠ATD＝∠CTN，∴∠ANC＝∠ADC＝60°＝α；（3）解：当B、E、F共线时，如下图，连接AD，根据图形的对称性，当B、E、F共线时，且点D是BC的中点，则F、G、A共线，此时点G、P共点，∵∠EDG＝60°，则∠BDE＝60°，则∠EBC＝∠ECB＝30°，则∠ACG＝30°+60°＝90°则BH＝HD＝DM＝CM＝BC＝，由（1）知△ADC为等边三角形，由（1）、（2）知，∠MPC＝60°，在Rt△ACG中，AC＝2，则CG＝2，则△APC的面积＝AC•GC＝2×2＝2；当B、F重合时，也符合题意，如下图：由（1）、（2）知，∠MPC＝60°，在Rt△AEC中，AC＝2，AE＝AB＝BE＝6﹣2＝4，则tan∠AEC＝＝＝，设AM＝x，则PM＝x，则CM＝＝＝x，而AC2＝AM2+CM2，即12＝3x2+x2，解得：x＝，则△APC的面积＝AM•PC＝x×（x+x）＝；综上，△APC的面积为或2．【中考模拟练】1．（2023•宁阳县一模）如图，Rt△ABE中，∠B＝90°，AB＝BE，将△ABE绕点A逆时针旋转45°，得到△AHD，过D作DC⊥BE交BE的延长线于点C，连接BH并延长交DC于点F，连接DE交BF于点O．下列结论：①DE平分∠HDC；②DO＝OE；③H是BF的中点；④BC﹣CF＝2CE；⑤CD＝HF，其中正确的有（）A．5个B．4个C．3个D．2个【分析】由旋转的性质可得∠DAE＝∠AEB＝45°，AD＝AE＝BE，DH＝BE，AH＝AB，∠ABE＝∠AHD＝90°，通过证明四边形ABCD是矩形，可得AB＝CD＝DH，AD＝BC＝BE，∠BCD＝∠DHE ＝90°，由“HL”可证Rt△DEC≌Rt△DEH，可得HE＝EC，∠AED＝∠DEC＝67.5°，∠CDE＝∠HDE ＝22.5°，可判断①；由角的数量关系和等腰三角形的判定和性质，可判断②③；由相似三角形的判定和性质可得CF＝2HN＝（2﹣）BE，由线段的和差关系可判断④；由∠HFD≠∠HDF，可得HF ≠DH，可判断⑤，即可求解．【解答】解：∵∠ABE＝90°，AB＝BE，∴∠AEB＝∠BAE＝45°，AE＝BE，∵将△ABE绕点A逆时针旋转45°，∴∠DAE＝∠AEB＝45°，AD＝AE＝BE，DH＝BE，AH＝AB，∠ABE＝∠AHD＝90°，∴∠DAB＝∠ABE＝90°，AH＝DH＝AB＝BE，又∵DC⊥BE，∴四边形ABCD是矩形，∴AB＝CD＝DH，AD＝BC＝BE，∠BCD＝∠DHE＝90°，∵DH＝DC，DE＝DE，∴Rt△DEC≌Rt△DEH（HL），∴HE＝EC，∠AED＝∠DEC＝67.5°，∠CDE＝∠HDE＝22.5°，∴DE平分∠HDC，故①正确；∵AB＝AH，∠BAE＝45°，∴∠ABH＝∠AHB＝67.5°，∴∠OHE＝∠OEH＝67.5°，∴OH＝OE，∠DHO＝22.5°＝∠HDO，∴DO＝HO，∴OE＝OD，故②正确；如图，连接CH，∵∠ABH＝67.5°，∴∠CBH＝22.5°，∴∠BFC＝67.5°，∵HE＝EC，∠AEB＝45°，∴∠ECH＝∠EHC＝22.5°，∴∠HBC＝∠HCE，∠FCH＝67.5°，∴BH＝CH，∠FCH＝∠BFC，∴HC＝HF，∴BH＝HF，∴点H是BF的中点，故③正确，如图，过点H作HN⊥BC于N，∴HN∥CD，∴△BHN∽△BFC，∴＝，∴FC＝2HN，∵AE＝BE，AH＝BE，∴HE＝（﹣1）BE＝CE，∵HN⊥BC，∠AEB＝45°，∴HN＝HE＝（﹣1）BE，∴CF＝2HN＝（2﹣）BE，∵BC﹣CF＝BE+CE﹣CF＝BE+（﹣1）BE﹣（2﹣）BE＝2（﹣1）BE，∴BC﹣CF＝2CE，故④正确；∵∠HFD＝180°﹣67.5＝112.5°，∠HDF＝45°，∴∠HFD≠∠HDF，∴HF≠DH，∴HF≠CD，故⑤不合题意，故选：B．2．（2024•永修县一模）在平面直角坐标系中，正方形ABCD的边AD在y轴正半轴上，边BC在第一象限，且A（0，3）、B（5，3），将正方形ABCD绕点A顺时针旋转α（0°＜α＜180°），若点B的对应点B′恰好落在坐标轴上，则点C的对应点C′的坐标为（7，4）或（5，﹣2）或（﹣1，﹣4）．【分析】根据题意画出图形，分3种情况进行讨论：①点B的对应点B′恰好落在x轴正半轴上时，②点B的对应点B′恰好落在y轴负半轴上时，③点B的对应点B′恰好落在x轴负半轴上时，根据旋转的性质，利用全等三角形的判定与性质可得点C的对应点C′的坐标．【解答】解：因为正方形ABCD的边AD在y轴正半轴上，边BC在第一象限，且点A（0，3）、B（5，3），所以画图如下：当正方形ABCD绕点A顺时针旋转α（0°＜α＜180°），①点B的对应点B′恰好落在x轴正半轴上时，如图，∵AB′＝AB＝5，OA＝3，∴OB′＝＝4，∵∠AB′O+∠OAB′＝90°，∠AB′O+∠C′B′E＝90°，∴∠OAB′＝∠C′B′E，在△AB′O和△EB′C′中，，∴△AB′O≌△EB′C′（AAS），∴B′E＝OA＝3，EC′＝OB′＝4，∴OE＝OB′+B′E＝4+3＝7，∴点C的对应点C′的坐标为（7，4）；②点B的对应点B′恰好落在y轴负半轴上时，如图，B′C′＝AB＝BC′＝5，∴点C的对应点C′的坐标为（5，﹣2）；③点B的对应点B′恰好落在x轴负半轴上时，如图，同①可知：△AB′O≌△EB′C′（AAS），∴B′E＝OA＝3，EC′＝OB′＝4，∴OE＝OB′﹣B′E＝4﹣3＝1，∴点C的对应点C′的坐标为（﹣1，﹣4）；综上所述：点C的对应点C′的坐标为（7，4）或（5，﹣2）或（﹣1，﹣4）．故答案为：（7，4）或（5，﹣2）或（﹣1，﹣4）．3．（2024•天津一模）在平面直角坐标系中，O为原点，△OAB是等腰直角三角形，∠OBA＝90°，点A （5，0），点B在第一象限，点P在边OA（点P不与点O，A重合），过点P作PQ⊥OA，交△OAB 的直角边于点Q，将线段QP绕点Q逆时针旋转90°得到线段QM，点P的对应点为M，连接PM．（1）如图①，若点M落在AB上，点B的坐标是（，），点M的坐标是（，）；（2）设△PQM与△OAB重合部分面积为S，OP＝t．①如图②，若重合部分为四边形PQEF，与边AB交于点E，F，试用含t的式子表示S，并直接写出t 的取值范围；②当1≤t≤4时，求S的取值范围．（请直接写出结果即可）【分析】（1）过点B作BG⊥OA于点G，过点M作MN⊥OA于点N，利用等腰直角三角形的性质得到BG＝OG＝，则点B坐标可求；设OP＝x，则PQ＝QM＝x，利用等腰直角三角形的性质，正方形的性质求得线段MN，ON的长度即可得出结论；（2）①当＜t＜时，由（1）知：四边形OQMP为平行四边形，△PQM为等腰直角三角形，利用等﹣S△MEF解答即可；腰直角三角形的性质求得FM，EF的长度，再利用S＝S△PQM②利用分类讨论的思想方法求得当1≤t≤4时，S与t的函数解析式，并求出对应的极值，综合解答过程即可得出结论．【解答】解：过点B作BG⊥OA于点G，过点M作MN⊥OA于点N，如图，∵△OAB是等腰直角三角形，∠OBA＝90°，∴BG＝OG＝GA＝OA．∵点A（5，0），∴OA＝5，∴BG＝OG＝．∴B（，）．设OP＝x，则PQ＝QM＝x，∵PQ⊥OA，QM⊥PQ，∴△PQM为等腰直角三角形，∴PM＝x．∵QM∥PO，OP＝QM，∴四边形OPMQ为平行四边形，∴PM∥OB，∴∠MPA＝∠BOA＝45°，∴△PMA为等腰直角三角形，∴AP＝PM＝2x，∴OA＝OP+PA＝3x＝5，∴x＝．∵PQ⊥OA，QM⊥PQ，MN⊥OA，∴四边形PQMN为矩形，∵PQ＝MQ，∴四边形PQMN为正方形，∴PN＝PQ＝MN＝，∴ON＝．∴M（，）．故答案为：（，）；（，）；（2）①当＜t＜时，如图，∵OP＝t，∴PA＝5﹣t．由（1）知：四边形OQMP为平行四边形，△PQM为等腰直角三角形，∴PQ＝QM＝t，PM＝PQ＝t．∵△PFA为等腰直角三角形，∴PF＝FA＝PA＝（5﹣t），∠PFA＝90°，∴∠MFE＝90°，∴△EFM为等腰直角三角形，∴EF＝FM＝PM﹣PF＝t﹣（5﹣t）＝t﹣，﹣S△MEF∴S＝S△PQM＝PQ•QM﹣EF•FM＝t2﹣＝+t﹣．∴用含t的式子表示S＝+t﹣，t的取值范围为＜t＜．②当1≤t≤时，△PQM与△OAB重合部分面积为△PQM的面积，∴S＝，当t＝1时，S＝，当t＝时，S＝；当＜t＜时，S＝+t﹣＝﹣+，∴当t＝时，S的最大值为；当≤t≤4时，如图，△PQM与△OAB重合部分面积为△PQL的面积，由题意：△PQA，△PQL为等腰直角三角形，PA＝5﹣t，∴PQ＝5﹣t，∴PL＝PQ＝（5﹣t），∴S＝PL•QL＝＝，当t＝时，S＝，当t＝4时，S＝．综上，当1≤t≤4时，S的取值范围≤S≤．题型三：四边形与新定义的综合新定义类问题解题时，一般第一问都会先考察学生对所给新定义的准确理解，所以不需要深入，新定义给什么就用什么即可；新定义第二问一般要结合一个和所给新定义比较接近的一个图形的性质，此时需要把新老知识结合应用，同时思考；新定义最后一问，通常要在两个性质的考点之上拓展延伸，这时就要回归老知识，重点从老知识上来挖掘新定义能带给我们什么！【中考真题练】1．（2023•宁波）定义：有两个相邻的内角是直角，并且有两条邻边相等的四边形称为邻等四边形，相等两邻边的夹角称为邻等角．（1）如图1，在四边形ABCD中，AD∥BC，∠A＝90°，对角线BD平分∠ADC．求证：四边形ABCD 为邻等四边形．（2）如图2，在6×5的方格纸中，A，B，C三点均在格点上，若四边形ABCD是邻等四边形，请画出所有符合条件的格点D．（3）如图3，四边形ABCD是邻等四边形，∠DAB＝∠ABC＝90°，∠BCD为邻等角，连结AC，过B 作BE∥AC交DA的延长线于点E．若AC＝8，DE＝10，求四边形EBCD的周长．【分析】（1）根据邻等四边形定义证明即可；（2）根据邻等四边形定义利用网格即可画图；（3）先证明四边形AEBC是平行四边形，得AE＝BC＝DC，设AE＝BC＝DC＝x，得AD＝DE﹣AE＝10﹣x，过点D作DF⊥BC于点F，得矩形ABFD，得AB＝DF，AD＝BF＝10﹣x，所以CF＝BC﹣BF＝x ﹣（10﹣x）＝2x﹣10，根据勾股定理得82﹣x2＝x2﹣（2x﹣10）2，求出x的值，进而可得四边形EBCD 的周长．【解答】（1）证明：在四边形ABCD中，AD∥BC，∠A＝90°，∴∠ABC＝180°﹣∠A＝90°，∵对角线BD平分∠ADC，∴∠ADB＝∠CDB，∵AD∥BC，∴∠ADB＝∠CBD，∴∠CBD＝∠CDB，∴CD＝CB，∴四边形ABCD为邻等四边形；（2）解：如下3个图，点D′、D、D″即为所求；（3）解：如图3，四边形ABCD是邻等四边形，∴CD＝CB，∵∠DAB＝∠ABC＝90°，∴AD∥BC，∵BE∥AC，∴四边形AEBC是平行四边形，∴EB＝AC＝8，AE＝BC，∴AE＝BC＝DC，设AE＝BC＝DC＝x，∵DE＝10，∴AD＝DE﹣AE＝10﹣x，过点D作DF⊥BC于点F，得矩形ABFD，∴AB＝DF，AD＝BF＝10﹣x，∴CF＝BC﹣BF＝x﹣（10﹣x）＝2x﹣10，在Rt△ABE和Rt△DFC中，根据勾股定理得：BE2﹣AE2＝AB2，CD2﹣CF2＝DF2，∴BE2﹣AE2＝CD2﹣CF2，∴82﹣x2＝x2﹣（2x﹣10）2，整理得x2﹣20x+82＝0，解得x1＝10﹣3，x2＝10+3（不符合题意，舍去），∴CD＝CB＝10﹣3，∴四边形EBCD的周长＝BE+DE+2CD＝8+10+2×（10﹣3）＝38﹣6．2．（2023•常州）对于平面内的一个四边形，若存在点O，使得该四边形的一条对角线绕点O旋转一定角度后能与另一条对角线重合，则称该四边形为“可旋四边形”，点O是该四边形的一个“旋点”．例如，在矩形MNPQ中，对角线MP、NQ相交于点T，则点T是矩形MNPQ的一个“旋点”．（1）若菱形ABCD为“可旋四边形”，其面积是4，则菱形ABCD的边长是2；（2）如图1，四边形ABCD为“可旋四边形”，边AB的中点O是四边形ABCD的一个“旋点”．求∠ACB的度数；（3）如图2，在四边形ABCD中，AC＝BD，AD与BC不平行．四边形ABCD是否为“可旋四边形”？请说明理由．【分析】（1）可推出四边形ABCD是正方形，从而得出结果；（2）连接OC，根据四边形ABCD是“可旋四边形”，O为旋点，可得出OC＝OB＝OA，进一步得出结果；（3）分别作AD和BC的垂直平分线，交于点O，连接OA，OD，OB，OC，可证得△AOC≌△DOB，进而得出∠AOD＝∠BOC，从而得出结果．【解答】解：（1）∵菱形ABCD是“可旋四边形”，∴AC＝BD，∴菱形ABCD是正方形，∴正方形ABCD的边长是2，故答案为：2；（2）如图1，连接OC，∵四边形ABCD是“可旋四边形”，O为旋点，∴OC＝OB，∴∠OCB＝∠OBC，∵OA＝OB，∴OA＝OC，∴∠OAC＝∠OCA，∵∠OAC+∠OCA+∠OBC+∠OCB＝180°，∴2（∠OCA+∠OCB）＝180°，∴∠ACB＝90°；（3）如图2，四边形ABCD是“可旋四边形”，理由如下：分别作AD和BC的垂直平分线，交于点O，连接OA，OD，OB，OC，∴OA＝OD，OC＝OB，∵AC＝BD，∴△AOC≌△DOB（SSS），∴∠AOC＝∠BOD，∴∠AOD＝∠BOC，∴四边形ABCD是“可旋四边形”．3．（2023•淮安）综合与实践定义：将宽与长的比值为（n为正整数）的矩形称为n阶奇妙矩形．（1）概念理解：当n＝1时，这个矩形为1阶奇妙矩形，如图（1），这就是我们学习过的黄金矩形，它的宽（AD）与长（CD）的比值是．（2）操作验证：用正方形纸片ABCD进行如下操作（如图（2））：第一步：对折正方形纸片，展开，折痕为EF，连接CE；第二步：折叠纸片使CD落在CE上，点D的对应点为点H，展开，折痕为CG；第三步：过点G折叠纸片，使得点A、B分别落在边AD、BC上，展开，折痕为GK．试说明：矩形GDCK是1阶奇妙矩形．（3）方法迁移：用正方形纸片ABCD折叠出一个2阶奇妙矩形．要求：在图（3）中画出折叠示意图并作简要标注．（4）探究发现：小明操作发现任一个n阶奇妙矩形都可以通过折纸得到．他还发现：如图（4），点E为正方形ABCD 边AB上（不与端点重合）任意一点，连接CE，继续（2）中操作的第二步、第三步，四边形AGHE的周长与矩形GDCK的周长比值总是定值．请写出这个定值，并说明理由．【分析】（1）将n＝1代入求得结果；（2）延长CG，交BA的延长线于点R，可证得△CDG∽△RAG，从而，可证得ER＝CE，进而设BE＝AE＝1，则AB＝BC＝CD＝AD＝2，ER＝CE＝，进而得出，从而求得DG＝，进一步得出结论；（3）依次对折正方形纸片，折痕为MN；对折矩形ADMN，折痕为EF，将正方形展开；连接CE，折叠纸片，使CD落在CE上，点D落在H点，折痕为CG；过点G折叠纸片，使得点A、B分别落在边AD、BC上，展开，折痕为GK．则矩形GDCK是2阶奇妙矩形；（4）延长CG，交BA的延长线于点R，设AD＝AB＝BC＝CD＝a，设BE＝b，则AE＝a﹣b，同理（2）求得ER＝CE＝，，从而得出AR＝﹣（a﹣b），进而DG＝﹣b，进而表示出四边形CDGK的周长和四边形AGHE的周长，进一步得出结果．【解答】（1）解：当n＝1时，＝，故答案为：；（2）证明：如图1，延长CG，交BA的延长线于点R，∵四边形ABCD是正方形，∴AB∥CD，AB＝BC＝CD＝AD，∠B＝90°，∴∠R＝∠DCG，△CDG∽△RAG，∴，由折叠得，∠GCH＝∠DCG，∴∠R＝∠GCH，∴ER＝CE，设BE＝AE＝1，则AB＝BC＝CD＝AD＝2，ER＝CE＝，∴AR＝ER﹣AE＝，∴，∴DG＝，∴，∴矩形GDCK是1阶奇妙矩形；（3）解：如图2，第一步：对折正方形纸片，折痕为MN；第二步：对折矩形ADMN，折痕为EF，将正方形展开；第三步：连接CE，折叠纸片，使CD落在CE上，点D落在H点，折痕为CG；第四步：过点G折叠纸片，使得点A、B分别落在边AD、BC上，展开，折痕为GK．则矩形GDCK是2阶奇妙矩形；（4）解：如图3，四边形AGHE的周长与矩形GDCK的周长比值是定值，理由如下：延长CG，交BA的延长线于点R，设AD＝AB＝BC＝CD＝a，设BE＝b，则AE＝a﹣b，同理（2）可得：ER＝CE＝，，∴AR＝﹣（a﹣b），∴＝，∴DG＝﹣b，∴四边形CDGK的周长＝2（DG+CD）＝2（+a﹣b），∵EH＝CE﹣CH＝CE﹣CD＝﹣a，∵四边形AGHE的周长＝EH+AE+AG+GH＝（﹣a）+（a﹣b）+AG+DG＝﹣a+a﹣b+a ＝+（a﹣b），∴四边形AGHE的周长与矩形GDCK的周长比值是．【中考模拟练】1．（2024•泰兴市一模）【定义呈现】有两个内角分别是它们对角的两倍的四边形叫做倍对角四边形．其中，这两个内角称为倍角．例如：如图1，在四边形ABCD中，∠A＝2∠C，∠D＝2∠B，那么我们就叫这个四边形是倍对角四边形，其中∠A，∠D称为倍角．【定义理解】如图1，四边形ABCD是倍对角四边形，且∠A，∠D是倍角．求∠B+∠C的度数；【拓展提升】如图2，四边形BDEC是倍对角四边形，且∠DEC，∠BDE是倍角，延长BD、CE交于点A．在BC下方作等边△BCF，延长FC、DE交于点G．若AB＝AC，BC＝2，FG＝kAB，四边形BDEC 的周长记为l．（1）用k的代数式表示l；（2）如图3，把题中的“AB＝AC”条件舍去，其它条件不变．①求证：CE＝EG；②探究是否为定值．如果是定值，求这个定值，如果不是，请说明理由．【分析】【定义理解】由四边形内角和定理可得出答案；【拓展提升】（1）证明△ECG是等边三角形，得出CE＝CG，则可得出答案；（2）①由等边三角形的性质证出∠ECG＝∠G，则可得出答案；②延长GD、FB交于点H，同①可证：DH＝DB，BD+DE+CE＝DH+DE+EG＝HG，证明△ABC∽△FGH，得出，则可得出结论．【解答】【定义理解】解：∵∠A+∠B+∠C+∠D＝360°，又∵∠A＝2∠C，∠D＝2∠B，∴2∠C+∠B+∠C+2∠B＝360°，∴3∠B+3∠C＝360°，∴∠B+∠C＝120°；【拓展提升】（1）解：∵AB＝AC，∴∠ABC＝∠ACB，又∵四边形BDEC是倍对角四边形，∴∠ABC+∠ACB＝120°，。

《四边形的综合》专题训练一．选择题1．如图，在四边形ABCD中，对角线AC，BD相交于点O，添加下列条件后仍不能判定四边形ABCD是平行四边形的是（）A．AD∥BC，AO＝CO B．AD＝BC，AO＝OCC．AD＝BC，CD＝AB D．S△AOD＝S△COD＝S△BOC2．如图，在菱形ABCD中，CE⊥AD于点E，sin D＝，AE＝2，则AC的长为（）A．8B．2C．2D．23．如图，菱形ABCD中，过顶点C作CE⊥BC交对角线BD于E点，已知∠A ＝134°，则∠BEC的大小为（）A．23°B．28°C．62°D．67°4．在▱ABCD中，AB＜BC，对角线AC的垂直平分线交AD于点E，连结CE，若▱ABCD的周长为20cm，则△CDE的周长为（）A．20cm B．40cm C．15cm D．10cm5．如图，在Rt△ABC中，∠B＝90°，∠BAC＝30°，AC＝6，将△ABC沿BC 向右平移得到△DEF．若四边形ACFD的面积等于6，则平移的距离等于（）A．2B．3C．2D．46．如图，在一个三角形的纸片（△ABC）中，∠C＝90°，将这个纸片沿直线DE剪去一个角后变成一个四边形ABED，则图中∠1+∠2的度数为（）A．180°B．90C．270°D．315°7．如图，在正方形ABCD中，顶点A，B，C，D在坐标轴上，且B（2，0），以AB为边构造菱形ABEF，将菱形ABEF与正方形ABCD组成的图形绕点O 逆时针旋转，每次旋转45°，则第2020次旋转结束时，点F2020的坐标为（）A．（﹣2，2）B．（﹣2，﹣2）C．（2，﹣2）D．（﹣2，﹣2）8．如图，在矩形ABCD中，AB＝4，BC＝6，过对角线交点O作EF⊥AC交AD 于点E，交BC于点F，则DE的长是（）A．1B．C．2D．9．如图，在正方形ABCD中，E是BC的中点，F是CD上一点，AE⊥EF．有下列结论：①∠BAE＝30°；②射线FE是∠AFC的角平分线；③CF＝CD；④AF＝AB+CF．其中正确结论的个数为（）A．1 个B．2 个C．3 个D．4 个10．如图，在Rt△ABC中，∠BAC＝90°，∠ACB＝45°，AB＝2，点P为BC上任意一点，连结PA，以PA，PC为邻边作平行四边形PAQC，连结PQ，则PQ的最小值为（）A．2B．C．2D．411．如图，已知菱形ABCD的顶点A（0，﹣1），∠DAC＝60°．若点P从点A 出发，沿A→B→C→D→A…的方向，在菱形的边上以每秒0.5个单位长度的速度移动，则第2020秒时，点P的坐标为（）A．（2，0）B．（，0）C．（﹣，0）D．（0，1 ）12．如图，点M是矩形ABCD的边BC，CD上的点，过点B作BN⊥AM于点P，交矩形ABCD的边于点N，连接DP．若AB＝6，AD＝4，则DP的长的最小值为（）A．2B．C．4D．5二．填空题13．如图是由6个形状、大小完全相同的菱形组成的网格，菱形的顶点称为格点，已知菱形的一个角（∠O）为60°，点A，B，C都在格点上，则sin∠ABC的值是．14．如图，正八边形和正五边形按如图方式拼接在一起，则∠ABC的度数为．15．如图，▱ABCD中，点E为边BC上一点，连接AE、DE，若AE＝AD，ED ＝EC＝6，tan∠DEC＝2tan∠C，则AE的长为．16．在矩形ABCD中，AC、BD交于点O．过点O作OE⊥BD交射线BC于点E，若BE＝2CE，AB＝3，则AD的长为．17．如图，在平面直角坐标系xOy中，已知点A（，0），B（1，1）．若平移点B到点D，使四边形OADB是平行四边形，则点D的坐标是．18．如图，矩形ABCD中，AB＝6，BC＝8，M是AB边上的一点，且AM＝2，点P在矩形ABCD所在的平面上，且∠BPD＝90°，则PM的最大值为．19．如图，在正方形ABCD中，AB＝a，点E，F在对角线BD上，且∠ECF＝∠ABD，将△BCE绕点C旋转一定角度后，得到△DCG，连接FG．则下列结论：①∠FCG＝∠CDG；②△CEF的面积等于；③FC平分∠BFG；④BE2+DF2＝EF2；其中正确的结论是．（填写所有正确结论的序号）三．解答题20．如图，在矩形ABCD中，点O为对角线AC的中点，过点O作EF⊥AC交BC于点E，交AD于点F，连接AE，CF．（1）求证：四边形AECF是菱形；（2）连接OB，若AB＝8，AF＝10，求OB的长．21．如图，在Rt△ABC中，∠C＝90°，∠ABC＝30°，AC＝3．动点P从点C 出发以每秒1个单位的速度沿CA匀速向终点A运动，同时点Q从点A出发以每秒2个单位的速度沿AB匀速向终点B运动，以PC、PQ为邻边构造平行四边形PQMC，当点P到达点A时，点Q也随之停止运动．设点P的运动时间为t秒．（1）求线段AB的长．（2）当PQ与△ABC的边平行或垂直时，求t的值．（3）设平行四边形PQMC与△ABC重叠部分图形的面积为S，求S与t的函数关系式．（4）以PC为边向左侧做正方形PCEF，当正方形PCEF和平行四边形PQMC 重叠部分的图形是轴对称图形时，直接写出t的取值范围．22．如图1所示，边长为4的正方形ABCD与边长为a（1＜a＜4）的正方形CFEG 的顶点C重合，点E在对角线AC上．【问题发现】如图1所示，AE与BF的数量关系为；【类比探究】如图2所示，将正方形CFEG绕点C旋转，旋转角为α（0＜α＜30°），请问此时上述结论是否还成立？如成立写出推理过程，如不成立，说明理由；【拓展延伸】若点F为BC的中点，且在正方形CFEG的旋转过程中，有点A、F、G在一条直线上，直接写出此时线段AG的长度为．23．问题探究：（1）如图1，∠AOB＝45°，在∠AOB内部有一点P，分别作点P关于边OA、OB的对称点P1，P2顺次连接O，P1，P2，则△OP1P2的形状是三角形．（2）如图2，在△ABC中，AB＝AC，∠BAC＝30°，AD⊥BC于D，AD＝2+，求：△ABC的面积．问题解决：（3）如图3，在四边形ABCD内有一点P，点P到顶点B的距离为10，∠ABC ＝60°，点M、N分别是AB、BC边上的动点，顺次连接P、M、N，使△PMN 在周长最小的情况下，面积最大，问：是否存在这种情况？若存在，请求出△PMN的面积的最大值；若不存在，请说明理由．24．【感知】如图①，BD、CE分别是△ABC的外角平分线，过点A作AM⊥BD于M，AN⊥CE于N，连结MN，易证：MN＝（AB+BC+AC）（不需要证明）．【探究】如图②，若BD、CE分别是△ABC的两个内角的平分线，且AM⊥BD于M，AN⊥CE于N，连结MN．试猜想MN与边AB、AC和BC之间的数量关系，并证明你的结论．【应用】如图③，在四边形ABCD中，∠ABC＝∠ADC＝90°，射线BE平分∠ABC，AM⊥BE于点M，连结MD，延长BC至F，若∠DCF＝∠ACD＝75°，AB＝2，直接写出MD的长度．参考答案一．选择题1．解：若∵AD∥BC，∴∠ADO＝∠CBO，且AO＝CO，∠AOD＝∠BOC，∴△AOD≌△COB（AAS）∴AD＝BC，∴四边形ABCD是平行四边形，故A选项不合题意；若AD＝BC，CD＝AB，∴四边形ABCD是平行四边形，故C选项不合题意；若S△AOD＝S△COD＝S△BOC，∴AO＝CO，BO＝DO，∴四边形ABCD是平行四边形，故D选项不合题意；故选：B．2．解：∵sin D＝，设EC＝4x，CD＝5x，由勾股定理可得：ED＝，∵菱形ABCD，∴AD＝CD，即AE+ED＝CD，可得：2+3x＝5x，解得：x＝1，∴AD＝DC＝5，由勾股定理可得：AC＝，故选：D．3．解：∵菱形ABCD，∠A＝134°，∴∠ABC＝180°﹣134°＝46°，∴∠DBC＝，∵CE⊥BC，∴∠BEC＝90°﹣23°＝67°，故选：D．4．解：∵对角线AC的垂直平分线交AD于点E，∴AE＝CE，∵▱ABCD的周长为20cm，∴AD+DC＝10cm，∴△CDE的周长＝DE+CE+CD＝AE+DE+CD＝AD+CD＝10cm，故选：D．5．解：∵∠B＝90°，∠BAC＝30°，AC＝6，∴BC＝AC＝3，∴AB＝＝＝3，∵将△ABC沿BC向右平移得到△DEF．∴AD＝CF，AD∥CF，∴四边形ADFC是平行四边形，∵四边形ACFD的面积等于6，∴CF×AB＝6，故选：A．6．解：∵∠C＝90°，∴∠A+∠B＝90°，∵∠1+∠A+∠B+∠2＝360°，∴∠1+∠2＝360°﹣90°＝270°，故选：C．7．解：∵点B（2，0），∴OB＝2，∴OA＝2，∴AB＝OA＝2，∵四边形ABEF是菱形，∴AF＝AB＝2，∴点F（2，2），由题意可得每次8旋转一个循环，∴2020÷8＝252…4，∴点F2020的坐标与点F坐标关于原点对称，∴点F2020的坐标（﹣2，﹣2）故选：D．8．解：连接CE，如图所示：∵四边形ABCD是矩形，∴∠ADC＝90°，CD＝AB＝4，AD＝BC＝6，OA＝OC，∵EF⊥AC，设DE＝x，则CE＝AE＝6﹣x，在Rt△CDE中，由勾股定理得：x2+42＝（6﹣x）2，解得：x＝，即DE＝；故选：D．9．解：∵在正方形ABCD中，E是BC的中点，∴AB＝BC，BE＝AB，∴tan A＝＝，∵tan30°＝，∴∠BAE≠30°，故①错误；∵∠B＝∠C＝90°，AE⊥EF，∴∠BAE+∠BEA＝90°，∠BEA+∠CEF＝90°，∴∠BAE＝∠CEF，∴△ABE∽△ECF，∵AB＝2BE＝2CE，∴EC＝2CF，设CF＝a，则EC＝BE＝2a，AB＝4a，∴AE＝a，EF＝a，tan∠CFE＝2，∴tan∠AFE＝＝2，∴∠AFE＝∠CFE，即射线FE是∠AFC的角平分线，故②正确；∵BC＝CD，BC＝2CE＝4CF，∴CF＝CD，故③错误；作EG⊥AF于点G，∵FE平分∠AFC，∠C＝90°，∴EG＝EC，∴EG＝EB，∵∠B＝∠AGE＝90°，在Rt△ABE和Rt△AGE中∴Rt△ABE≌Rt△AGE（HL）∴AB＝AG，又∵CF＝GF，AF＝AG+GF，∴AF＝AB+CF，故④正确，由上可得，②④正确，正确的个数为2，故选：B．10．解：设PQ与AC交于点O，作OP′⊥BC于P′．如图所示：∵在Rt△ABC中，∠BAC＝90°，∠ACB＝45°，AB＝2，∴AC＝2，∵四边形PAQC是平行四边形，∴OA＝OC＝AC＝，∴OP′＝1，当P与P′重合时，OP的值最小，则PQ的值最小，∴PQ的最小值＝2OP′＝2．故选：A．11．解：∵四边形ABCD是菱形，∴AB＝BC＝CD＝DA，OD＝OB，AC⊥BD，∵A（0，﹣1），∴OA＝1，在Rt△AOD中，∵∠AOD＝90°，∠DAC＝60°，∴∠ADO＝30°，∴OD＝OA＝，AD＝2OA＝2，∴OB＝，∴B（，0），∵点P的运动速度为0.5单位长度/秒，∴从点A到点B所需时间＝＝4（秒），∴沿A→B→C→D→A所需的时间＝4×4＝16（秒），∵＝126…4，∴移动到第2020秒和第4秒的位置相同，当P运动到第4秒时点P在点B处，即点P的坐标为（，0），故选：B．12．解：∵BN⊥AM，∴∠APB＝90°，∵AB＝6为定长，则P点的运动轨迹是以AB为直径，在AB上方的半圆，取AB的中点为O，连接OD，OD与半圆的交点P′就是DP长的最小值时的位置，如图所示：∵AB＝6，AD＝4，∴OP′＝OA＝AB＝3，OD＝＝＝5，∴DP′＝OD﹣OP′＝5﹣3＝2，∴DP的长的最小值为2，故选：A．二．填空题（共7小题）13．解：如图，连接EA，EC，设菱形的边长为a，由题意得∠AEF＝30°，∠BEF＝60°，AE＝a，EB＝2a，则AB＝a，∴∠AEC＝90°，∵∠ACE＝∠ACG＝∠BCG＝60°，∴∠ECB＝180°，∴E、C、B共线，在Rt△AEB中，sin∠ABC＝＝＝．故答案为：．14．解：由题意得：正八边形的每个内角都等于135°，正五边形的每个内角都等于108°，故∠BAC＝360°﹣135°﹣108°＝117°，∵AB＝AC，∴∠ABC＝∠ACB＝（180°﹣117°）÷2＝31.5°．故答案为：31.5°．15．解：过点A作AN⊥BC于N，过点D作DF⊥BC于F，如图所示：则四边形ADDFN是矩形，∴AN＝DF，∵四边形ABCD是平行四边形，∴AB＝CD，AD＝BC，AB∥CD，∴∠C＝∠ABN，在△ABN和△DCF中，，∴△ABN≌△DCF（AAS），∴BN＝CF，∵tan∠DEC＝2tan∠C，∴＝2，∴FC＝2EF，∵EC＝6，∴EF＝2，FC＝4，∴AN＝DF＝＝＝4，设AE＝AD＝BC＝x，则BE＝x﹣6，NE＝4+x﹣6＝x﹣2，在Rt△AEN中，AN2+NE2＝AE2，即（4）2+（x﹣2）2＝x2，解得：x＝9，∴AE＝9，故答案为：9．16．解：如图，当点E在BC的延长线上时，∵BE＝2CE，∴BC＝CE，∵OE⊥BD，∴OC＝BC＝CE，∵四边形ABCD是矩形，∴AO＝CO＝BO＝DO，AD＝BC；∴BO＝CO＝BC，∴△BOC是等边三角形，∴∠ACB＝60°∴tan∠ACB＝，∴BC＝＝AD，如图，当点E在线段BC上时，设直线OE与直线AB，CD交于点F，点H，∵AB∥CD，∴，∴AF＝CH，∵AB∥CD，∴△EBF∽△ECH，∴，∴BF＝2CH＝2AF，∴3+AF＝2AF，∴AF＝3＝AB，且OE⊥BD，∴AO＝AB＝AF＝3，∵AO＝BO＝CO＝DO，∴AO＝AB＝BO，∴△ABO是等边三角形，∴∠ABD＝60°，∴tan∠ABD＝，∴AD＝3，故答案为：3或．17．解：∵A（，0），∴OA＝，∵四边形OADB是平行四边形，∴BD＝OA＝，BD∥OA，∵B（1，1），∴D（+1，1），故答案为：（+1，1）．18．解：如图，连接BD，以BD为直径作⊙O，则点P在⊙O上，作OE⊥AD 于E，连接OM，PM，OP．∵OE⊥AD，∴AE＝DE＝4，∵OB＝OD，AE＝DE，∴OE＝AB＝3，∵AM＝2，∴EM＝AE﹣AM＝2，∴OM＝＝＝，∵四边形ABCD是矩形，∴∠BAD＝90°，BC＝AD＝8，∴BD＝＝＝10，∴OP＝OB＝OD＝5，∵PM≤OM+OP，∴PM≤+5，∴PM的最大值为+5，故答案为+5．19．解：∵四边形ABCD是正方形，∴∠ECF＝∠ABD＝45°，∴∠BCE+∠FCD＝45°，∵将△BCE绕点C旋转一定角度后，得到△DCG，∴∠CBE＝∠CDG＝45°，BE＝DG，CE＝CG，∠DCG＝∠BCE，∴∠FCG＝∠ECF＝45°，∴∠FCG＝∠CDG＝45°，故①正确，∵EC＝CG，∠FCG＝∠ECF，FC＝FC，∴△ECF≌△GCF（SAS）∴EF＝FG，∠EFC＝∠GFC，S△ECF＝S△CFG，∴CF平分∠BFG，故③正确，∵∠BDG＝∠BDC+∠CDG＝90°，∴DG2+DF2＝FG2，∴BE2+DF2＝EF2，故④正确，∵DF+DG＞FG，∴BE+DF＞EF，∴S△CEF＜S△BEC+S△DFC，∴△CEF的面积＜S△BCD＝，故②错误；故答案为：①③④三．解答题（共5小题）20．证明：（1）∵O是AC的中点，且EF⊥AC，∴AF＝CF，AE＝CE，OA＝OC，∵四边形ABCD是矩形，∴AD∥BC，∴∠AFO＝∠CEO，在△AOF和△COE中，，∴△AOF≌△COE（AAS），∴AF＝CE，∴AF＝CF＝CE＝AE，∴四边形AECF是菱形；（2）如图，∵AB＝8，AF＝AE＝EC＝10，∴BE＝＝＝6，∴BC＝16，∴AC＝＝＝8，∵AO＝CO，∠ABC＝90°，∴BO＝AC＝4．21．解：（1）在Rt△ABC中，∠ACB＝90°，∠ABC＝30°，AC＝3，∴AB＝2AC＝6；（2）当PQ⊥AB时，∵∠BAC＝90°﹣∠ABC＝60°，∴∠APQ＝90°﹣∠BAC＝30°，由题意得：AQ＝2t，PC＝t，∴AP＝3﹣t，∴3﹣t＝2×2t，解得：t＝；当PQ∥BC时，∠AQP＝∠ABC＝30°，∠APQ＝∠ACB＝90°，∴AQ＝2AP，∴2t＝2（3﹣t），解得：t＝；综上所述，当PQ与△ABC的边平行或垂直时，t的值为秒或秒；（3）分两种情况：①当0＜t≤时，作QG⊥AC于G，如图1所示：则AG＝AQ＝t，QG＝AG＝t，∴S＝平行四边形PQMC＝PC×QG＝t×t＝t2；即S＝t2（当0＜t≤）②当＜t≤3时，如图2所示：∵四边形PQMC是平行四边形，∵PC⊥BC，∴QM⊥BC，∵∠ABC＝30°，∴QH＝BQ＝（6﹣2t）＝3﹣t，∴S＝直角梯形PCHQ的面积＝（3﹣t+t）×t＝t；即S＝t（＜t≤3）；（4）分两种情况：①当PQ∥BC时，正方形PCEF和平行四边形PQMC重叠部分的图形是正方形PCEF，轴对称图形，如图3所示：则∠AQP＝∠ABC＝30°，∠APQ＝∠ACB＝90°，AQ＝2AP，∴2t＝2（3﹣t），解得：t＝；②当正方形PCEF和平行四边形PQMC重叠部分的图形是等腰直角△CPF 时，是轴对称图形；则∠CPF＝45°，作QD⊥AC于D，如图4所示：则AD＝AQ＝t，QD＝AD＝t，∵PQ∥CM，∴∠QPD＝45°，∴△QPD是等腰直角三角形，∴PD＝QD＝t，∵AD+PD+∠PC＝AC，∴t+t+t＝3，解得：t＝6﹣3；综上所述，当正方形PCEF和平行四边形PQMC重叠部分的图形是轴对称图形时，t的取值为或6﹣3．22．【问题发现】解：AE＝BF，理由如下：∵四边形ABCD和四边形CFEG是正方形，∴∠B＝∠CFE＝90°，∠FCE＝∠BCA＝45°，CE＝CF，CE⊥GF，∴AB∥EF，∴＝＝，∴AE＝BF；故答案为：AE＝BF；【类比探究】解：上述结论还成立，理由如下：连接CE，如图2所示∵∠FCE＝∠BCA＝45°，∴∠BCF＝∠ACE＝45°﹣∠ACF，在Rt△CEG和Rt△CBA中，CE＝CF，CA＝CB，∴＝＝，∴△ACE∽△BCF，∴＝＝，∴AE＝BF；【拓展延伸】解：如图3所示：连接CE交GF于H，∵四边形ABCD和四边形CFEG是正方形，∴AB＝BC＝4，AC＝AB＝4，GF＝CE＝CF，HF＝HE＝HC，∵点F为BC的中点，∴CF＝BC＝2，GF＝CE＝2，HF＝HE＝HC＝，∴AH＝＝＝，∴AG＝AH+HG＝+；故答案为：+．23．解：（1）如图1中，△OP1P2是等腰直角三角形．理由：∵点P关于边OA、OB的对称点分别为P1，P2，∴OP＝OP1＝OP2，∠AOP＝∠AOP1，∠BOP＝∠BOP2，∵∠AOB＝45°，∴∠P1OP2＝2（∠AOP+∠BOP）＝90°，∴△OP1P2是等腰直角三角形．故答案为等腰直角．（2）如图2中，在AD上取一点E，使得AE＝EC，连接EC．∵AB＝AC，AD⊥BC，∴∠EAC＝∠BAC＝15°，∵EA＝EC，∴∠EAC＝∠ECA＝15°，∴∠DEC＝∠EAC+∠ECA＝30°，设CD＝BD＝x，则EC＝EA＝2x，DE＝x，∵AD＝2+，∴2x+x＝2+，∴x＝1，∴BC＝2CD＝2，∴S△ABC＝•BC•AD＝×2×（2+）＝2+．（3）如图3中，不存在．理由：∵点P关于AB，BC的对称点分别为M，N，∴PB＝BM＝BN＝10，∠PBA＝∠ABM，∠PBC＝∠CBN，∵∠ABC＝60°，∴∠MBN＝2（∠ABP+∠PBC）＝120°，∴△BNM是顶角为120°，腰长为10的等腰三角形，∴MN为定值，∵PM+PN≥MN，∴当点P落在AB或BC上时，PM+PN＝MN＝定值，此时△PMN不存在，∴△PMN的周长不存在最小值．24．解：【感知】如图①中，设AN的延长线交BC的延长线于K，AM的延长线交CB的延长线于J．∵AM⊥BD，∴∠AMB＝∠BMJ＝90°，∵∠ABM＝∠JBM，∠ABM+∠CAM＝90°，∠JBM+∠J＝90°，∴∠BAM＝∠J，∴BA＝BJ，同法可证：CA＝CK，∴AM＝MJ，AN＝NK，∴MN＝JK＝（JB+BC+CK）＝（AB+BC+AC）．【探究】如图②中，结论：MN＝（AB+AC﹣BC）．理由：延长AM交BC于F，延长AN交BC于G．∵AM⊥BD，∴∠AMB＝∠BMJ＝90°，∵∠ABM＝∠FBM，∠ABM+∠BAM＝90°，∠FBM+∠BFM＝90°，∴∠BAM＝∠BFM，∴BA＝BF，同法可证：CA＝CG，∴AM＝MF，AN＝NG，∴MN ＝FG ＝（BF+CG﹣BC ）＝（AB+AC﹣BC）．【应用】如图③中，延长AM交BC于J，延长AD交BC的延长线于K．由题意∠ACB＝180°﹣∠ACD﹣∠DCF＝30°，∵∠ABC＝90°，AB＝2，∴AC＝2AB＝4，BC ＝AB＝2，同法可证DM JK ＝（AC+BC﹣AC ）＝（4+2﹣2）＝1+．- 31 -。

2020年数学中考压轴题专项训练：四边形的综合1．如图，四边形ABCD是直角梯形，AD∥BC，AB⊥AD，且AB＝AD+BC，E是DC的中点，连结BE并延长交AD的延长线于G．（1）求证：DG＝BC；（2）F是AB边上的动点，当F点在什么位置时，FD∥BG；说明理由．（3）在（2）的条件下，连结AE交FD于H，FH与HD长度关系如何？说明理由．（1）证明：∵AD∥BC，∴∠DGE＝∠CBE，∠GDE＝∠BCE，∵E是DC的中点，即DE＝CE，∴△DEG≌△CEB（AAS），∴DG＝BC．（2）解：当F运动到AF＝AD时，FD∥BG．理由：由（1）知DG＝BC，∵AB＝AD+BC，AF＝AD，∴BF＝BC＝DG，∴AB＝AG，∵∠BAG＝90°，∴∠AFD＝∠ABG＝45°，∴FD∥BG．（3）解：结论：FH＝HD．理由：由（1）知GE＝BG，又由（2）知△ABG为等腰直角三角形，所以AE⊥BG，∵FD∥BG，∴AE⊥FD，∵△AFD为等腰直角三角形，∴FH＝HD．2．如图，在矩形ABCD中，过BD的中点O作EF⊥BD，分别与AB、CD交于点E、F．连接DE、BF．（1）求证：四边形BEDF是菱形；（2）若M是AD中点，联结OM与DE交于点N，AD＝OM＝4，则ON的长是多少？（1）证明：∵四边形ABCD是矩形，∴AB∥CD，∴∠DFO＝∠BEO，∵∠DOF＝∠EOB，OD＝OB，∴△DOF≌△BOE（AAS），∴DF＝BE，∴四边形BEDF是平行四边形，∵EF⊥BD，∴四边形BEDF是菱形．（2）解：∵DM＝AM，DO＝OB，∴OM∥AB，AB＝2OM＝8，∴DN＝EN，ON＝BE，设DE＝EB＝x，在Rt△ADE中，则有x2＝42+（8﹣x）2，解得x＝5，∴ON＝．3．（1）如图1，四边形EFGH中，FE＝EH，∠EFG+∠EHG＝180°，点A，B分别在边FG，GH 上，且∠AEB＝∠FEH，求证：AB＝AF+BH．（2）如图2，四边形EFGH中，FE＝EH，点M在边EH上，连接FM，EN平分∠FEH交FM 于点N，∠ENM＝α，∠FGH＝180°﹣2α，连接GN，HN．①找出图中与NH相等的线段，并加以证明；②求∠NGH的度数（用含α的式子表示）．（1）证明：如图1中，延长BH到M，使得HM＝FA，连接EM．∵∠F+∠EHG＝180°，∠EHG+∠EHM＝180°，∴∠F＝∠EHM，∵AE＝HE，FA＝HM，∴△EFA≌△EHM（SAS），∴EA＝EM，∠FEA＝∠HEM，∵∠EAB＝∠FEH，∴∠FEA+∠BEH＝∠HEM+∠BEH＝∠BEM＝∠FEH，∴∠AEB＝∠BEM，∵BE＝BE，EA＝EM，∴△AEB≌△MEB（SAS），∴AB＝BM，∵BM＝BH+HM＝BH+AF，∴AB＝AF+BH．（2）解：①如图2中，结论：NH＝FN．理由：∵NE平分∠FEH，∴∠FEN＝∠HEN，∵EF＝EH，EN＝EN，∴△ENF≌△ENH（SAS），∴NH＝FN．②∵△ENF≌△ENH，∴∠ENF＝∠ENH，∵∠ENM＝α，∴∠ENF＝∠ENH＝180°﹣α，∴∠MNH＝180°﹣α﹣α＝180°﹣2α，∵∠FGH＝180°﹣2α，∴∠MNH＝∠FGH，∵∠MNH+∠FNH＝180°，∴∠FGH+∠FNH＝180°，∴F，G，H，N四点共圆，∵NH＝NF，∴＝，∴∠NGH＝∠NGF＝∠FGH＝90°﹣α．4．如图，已知△ABC中，∠ACB＝90°，AC＝4，BC＝3，点M、N分别是边AC、AB上的动点，连接MN，将△AMN沿MN所在直线翻折，翻折后点A的对应点为A′．（1）如图1，若点A′恰好落在边AB上，且AN＝AC，求AM的长；（2）如图2，若点A′恰好落在边BC上，且A′N∥AC．①试判断四边形AMA′N的形状并说明理由；②求AM、MN的长；（3）如图3，设线段NM、BC的延长线交于点P，当且时，求CP的长．解：（1）如图1中，在Rt△ABC中，∵∠C＝90°，AC＝4，BC＝3，∴AB＝＝＝5，∵∠A＝∠A，∠ANM＝∠C＝90°，∴△ANM∽△ACB，∴＝，∴＝，∴AM＝．（2）①如图2中，∵NA′∥AC，∴∠AMN＝∠NMA′，由翻折可知：MA＝MA′，∠AMN＝∠NMA′，∴∠MNA′＝∠A′MN，∴A′N＝A′M，∴AM＝A′N，∵AM∥A′N，∴四边形AMA′N是平行四边形，∵MA＝MA′，∴四边形AMA′N是菱形．②连接AA′交MN于O．设AM＝MA′＝x，∵MA′∥AB，∴＝，∴＝，解得x＝，∴AM＝，∴CM＝，∴CA′＝＝＝，∴AA′＝＝＝，∵四边形AMA′N是菱形，∴AA′⊥MN，OM＝ON，OA＝OA′＝，∴OM＝＝＝，∴MN＝2OM＝．（3）如图3中，作NH⊥BC于H．∵NH∥AC，∴＝＝∴＝＝∴NH＝，BH＝，∴CH＝BC﹣BH＝3﹣＝，∴AM＝AC＝，∴CM＝AC﹣AM＝4﹣＝，∵CM∥NH，∴＝，∴＝，∴PC＝1．5．如图，四边形ABCD为平行四边形，AD＝1，AB＝3，∠DAB＝60°，点E为边CD上一动点，过点C作AE的垂线交AE的延长线于点F．（1）求∠D的度数；（2）若点E为CD的中点，求EF的值；（3）当点E在线段CD上运动时，是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．解：（1）如图1中，∵四边形ABCD是平行四边形，∴AB∥CB，∠ADC+∠DAB＝180°，∵∠DAB＝60°，∴∠ADC＝120°．（2）如图1中，作AH⊥CD交CD的延长线于H．在Rt△ADH中，∵∠H＝90°，∠ADH＝60°，AD＝2，∴AH＝AD•sin60°＝，DH＝AD•cos60°＝，∵DE＝EC＝，∴EH＝DH+DE＝2，∴AE＝＝＝，∵CF⊥AF，∴∠F＝∠H＝90°，∵∠AEH＝∠CEF，∴△AEH∽△CEF，∴＝，∴＝，∴EF＝．（3）如图2中，作△AFC的外接圆⊙O，作AH⊥CD交CD的郯城县于H，作OK⊥CD于K，交⊙O于M，作FP∥CD交AD的延长线于P，作MN∥CD交AD的延长线于M，作NQ⊥CD于Q．∵DE∥PF，∴＝，∵AD是定值，∴PA定值最大时，定值最大，观察图象可知，当点F与点M重合时，PA定值最大，最大值＝AN的长，由（2）可知，AH＝，CH＝，∠H＝90°，∴AC＝＝＝，∴OM＝AC＝，∵OK∥AH，AO＝OC，∴KH＝KC，∴OK＝＝，∴MK＝NQ＝﹣，在Rt△NDQ中，DN＝＝＝﹣，∴AN＝AD+DN＝+，∴的最大值＝＝+．6．如图，在边长为2的正方形ABCD中，点P是射线BC上一动点（点P不与点B重合），连接AP、DP，点E是线段AP上一点，且∠ADE＝∠APD，连接BE．（1）求证：AD2＝AE•AP；（2）求证BE⊥AP；（3）直接写出的最小值．（1）证明：∵∠DAE＝∠PAD，∠ADE＝∠APD，∴△ADE∽△APD，∴＝，∴AD2＝AE•AP（2）证明：∵四边形ABCD是正方形，∴AD＝AB，∠ABC＝90°，∴AB2＝AE•AP，∴＝，∵∠BAE＝∠PAB，∴△ABE∽△APB，∴∠AEB＝∠ABP＝90°，∴BE⊥AP．（3）∵△ADE∽△APD，∴＝，∴＝，∵AD＝2，∴DE最小时，的值最小，如图，作△ABE的外接圆⊙O，连接OD，OE，易知OE＝1，OD＝，∴DE≥OD﹣OE＝﹣1，∴DE的最小值为﹣1，∴的最小值＝．7．在正方形ABCD中，点E是BC边上一点，连接AE．（1）如图1，点F为AE的中点，连接CF．已知tan∠FBE＝，BF＝5，求CF的长；（2）如图2，过点E作AE的垂线交CD于点G，交AB的延长线于点H，点O为对角线AC 的中点，连接GO并延长交AB于点M，求证：AM+BH＝BE．解：（1）Rt△ABE中，BF为中线，BF＝5，∴AE＝10，FE＝5，作FP⊥BC于点P，Rt△BFP中，，∴BP＝3，FP＝4，在等腰三角形△BFE中，BE＝2BP＝6，由勾股定理求得，∴CP＝8﹣3＝5，∴；（2）∵∠ACD＝∠BAC＝45°，AO＝CO，∠AOM＝∠COG，∴证明△AMO≌△CGO（ASA），∴AM＝GC，过G作GP垂直AB于点P，得矩形BCGP，∴CG＝PB，∵AB＝PG，∠AEB＝∠H，∠ABE＝∠GPH，∴△ABE≌△GPH（ASA），∴BE＝PH＝PB+BH＝CG+BH＝AM+BH．8．阅读理解：如图1，若一个四边形的两条对角线互相垂直，则称这个四边形为垂美四边形．（1）概念理解：如图2，在四边形ABCD中，AB＝AD，CB＝CD，问四边形ABCD是垂美四边形吗？请说明理由；（2）性质探究：如图1，试在垂美四边形ABCD中探究AB2，CD2，AD2，BC2之间的关系，并说明理由；（3）解决问题：如图3，分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE，连结CE、BG、GE、CE交BG于点N，交AB于点M．已知AC＝，AB＝2，求GE的长．解：（1）如图2，四边形ABCD是垂美四边形；理由如下：连接AC、BD交于点E，∵AB＝AD，∴点A在线段BD的垂直平分线上，∵CB＝CD，∴点C在线段BD的垂直平分线上，∴直线AC是线段BD的垂直平分线，∴AC⊥BD，即四边形ABCD是垂美四边形；（2）猜想结论：AB2+CD2＝AD2+BC2，证明：如图1，在四边形ABCD中，∵AC⊥BD，∴∠AOD＝∠AOB＝∠BOC＝∠COD＝90°，由勾股定理得：AB2+CD2＝AO2+BO2+OD2+OC2AD2+BC2＝AO2+BO2+OD2+OC2∴AB2+CD2＝AD2+BC2，（3）如图3，连接CG，BE，∵∠CAG＝∠BAE＝90°，∴∠CAG+∠BAC＝∠BAE+∠BAC，即∠GAB＝∠CAE，在△GAB和△CAE中，FMNG图 3EDCAB∴△GAB≌△CAE（SSS），∴∠ABG＝∠AEC，∵∠AEC+∠AME＝90°，∴∠ABG+∠BMN＝90°，∴∠BNC＝90°，即BG⊥CE，∴四边形CGEB是垂美四边形，由（2）得：EG2+BC2＝CG2+BE2∵，AB＝2，∴BC＝1，，，∴EG2＝CG2+BE2﹣BC2＝6+8﹣2＝13，∴．9．已知：如图，长方形ABCD中，∠A＝∠B＝∠B＝∠D＝90°，AB＝CD＝4米，AD＝BC＝8米，点M是BC边的中点，点P从点A出发，以1米/秒的速度沿AB方向运动再过点B沿BM方向运动，到点M停止运动，点O以同样的速度同时从点D出发沿着DA方向运动，到点A停止运动，设点P运动的时间为x秒．（1）当x＝2秒时，线段AQ的长是 6 米；（2）当点P在线段AB上运动时，图中阴影部分的面积发生改变吗？请你作出判断并说明理由．（3）在点P，Q的运动过程中，是否存在某一时刻，使得BP＝DQ？若存在，求出点P 的运动时间x的值；若不存在，请说明理由．解：（1）∵四边形ABCD是矩形，∴AD＝BC＝8，∵DQ＝2，∴AQ＝AD﹣DQ＝8﹣2＝6，故答案为6．（2）结论：阴影部分的面积不会发生改变．理由：连结AM，作MH⊥AD于H．则四边形ABMH是矩形，MH＝AB＝4．∵S阴＝S△APM+S△AQM＝×x×4+（8﹣x）×4＝16，∴阴影面积不变；（3）当点P在线段AB上时，BP＝4﹣x，DQ＝x．∵BP＝DQ，∴4﹣x＝x，∴x＝3．当点P在线段BM上时，BP＝x﹣4，DQ＝x．∵BP＝DQ，∴x﹣4＝x，∴x＝6．所以当x＝3或6时，BP＝DQ．10．A，B，C，D是长方形纸片的四个顶点，点E、F、H分别是边AB、BC、AD上的三点，连结EF、FH．（1）将长方形纸片ABCD按图①所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B'、C'、D'，点B'在FC'上，则∠EFH的度数为90°；（2）将长方形纸片ABCD按图②所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B'、C'、D'，若∠B'FC'＝18°，求∠EFH的度数；（3）将长方形纸片ABCD按图③所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B'、C'、D'，若∠EFH＝m°，求∠B'FC'的度数为180°﹣2m°．解：（1）∵沿EF，FH折叠，∴∠BFE＝∠B'FE，∠CFH＝∠C'FH，∵点B′在FC′上，∴∠EFH＝（∠BFB'+∠CFC'）＝×180°＝90°，故答案为：90°；（2）∵沿EF，FH折叠，∴可设∠BFE＝∠B'FE＝x，∠C'FH＝∠CFH＝y，∵2x+18°+2y＝180°，∴x+y＝81°，∴∠EFH＝x+18°+y＝99°；（3）∵沿EF，FH折叠，∴可设∠BFE＝∠B'FE＝x，∠C'FH＝∠CFH＝y，∴∠EFH＝180°﹣∠BFE﹣∠CFH＝180°﹣（x+y），即x+y＝180°﹣m°，又∵∠EFH＝∠EFB'﹣∠B'FC'+∠C'FH＝x﹣∠B'FC'+y，∴∠B'FC'＝（x+y）﹣∠EFH＝180°﹣m°﹣m°＝180°﹣2m°，故答案为：180°﹣2m°．11．勾股定理是数学史上非常重要的一个定理．早在2000多年以前，人们就开始对它进行研究，至今已有几百种证明方法．在欧几里得编的《原本》中证明勾股定理的方法如下，请同学们仔细阅读并解答相关问题：如图，分别以Rt△ABC的三边为边长，向外作正方形ABDE、BCFG、ACHI．（1）连接BI、CE，求证：△ABI≌△AEC；（2）过点B作AC的垂线，交AC于点M，交IH于点N．①试说明四边形AMNI与正方形ABDE的面积相等；②请直接写出图中与正方形BCFG的面积相等的四边形．（3）由第（2）题可得：正方形ABDE的面积+正方形BCFG的面积＝正方形ACHI的面积，即在Rt△ABC中，AB2+BC2＝AC2．（1）证明：∵四边形ABDE、四边形ACHI是正方形，∴AB＝AE，AC＝AI，∠BAE＝∠CAI＝90°，∴∠EAC＝∠BAI，在△ABI和△AEC中，，∴△ABI≌△AEC（SAS）；（2）①证明：∵BM⊥AC，AI⊥AC，∴BM∥AI，∴四边形AMNI的面积＝2△ABI的面积，同理：正方形ABDE的面积＝2△AEC的面积，又∵△ABI≌△AEC，∴四边形AMNI与正方形ABDE的面积相等．②解：四边形CMNH与正方形BCFG的面积相等，理由如下：∵Rt△ABC中，AB2+BC2＝AC2，∴正方形ABDE的面积+正方形BCFG的面积＝正方形ACHI的面积，由①得：四边形AMNI与正方形ABDE的面积相等，∴四边形CMNH与正方形BCFG的面积相等；（3）解：由（2）得：正方形ABDE的面积+正方形BCFG的面积＝正方形ACHI的面积；即在Rt△ABC中，AB2+BC2＝AC2；故答案为：正方形ACHI，AC2．12．在长方形纸片ABCD中，点E是边CD上的一点，将△AED沿AE所在的直线折叠，使点D 落在点F处．（1）如图1，若点F落在对角线AC上，且∠BAC＝54°，则∠DAE的度数为18 °．（2）如图2，若点F落在边BC上，且AB＝6，AD＝10，求CE的长．（3）如图3，若点E是CD的中点，AF的沿长线交BC于点G，且AB＝6，AD＝10，求CG 的长．解：（1）∵四边形ABCD是矩形，∴∠BAD＝90°，∵∠BAC＝54°，∴∠DAC＝90°﹣54°＝36°，由折叠的性质得：∠DAE＝∠FAE，∴∠DAE＝∠DAC＝18°；故答案为：18；（2）∵四边形ABCD是矩形，∴∠B＝∠C＝90°，BC＝AD＝10，CD＝AB＝6，由折叠的性质得：AF＝AD＝10，EF＝ED，∴BF＝＝＝8，∴CF＝BC﹣BF＝10﹣8＝2，设CE＝x，则EF＝ED＝6﹣x，在Rt△CEF中，由勾股定理得：22+x2＝（6﹣x）2，解得：x＝，即CE的长为；（3）连接EG，如图3所示：∵点E是CD的中点，∴DE＝CE，由折叠的性质得：AF＝AD＝10，∠AFE＝∠D＝90°，FE＝DE，∴∠EFG＝90°＝∠C，在Rt△CEG和△FEG中，，∴Rt△CEG≌△FEG（HL），∴CG＝FG，设CG＝FG＝y，则AG＝AF+FG＝10+y，BG＝BC﹣CG＝10﹣y，在Rt△ABG中，由勾股定理得：62+（10﹣y）2＝（10+y）2，解得：y＝，即CG的长为．13．如图，矩形ABCD中，AB＝6cm，AD＝8cm，点P从点A出发，以每秒一个单位的速度沿A→B→C的方向运动；同时点Q从点B出发，以每秒2个单位的速度沿B→C→D的方向运动，当其中一点到达终点后两点都停止运动．设两点运动的时间为t秒．（1）当t＝7 时，两点停止运动；（2）设△BPQ的面积面积为S（平方单位）①求S与t之间的函数关系式；②求t为何值时，△BPQ面积最大，最大面积是多少？解：（1）∵四边形ABCD是矩形，∴AD＝BC＝8cm，AB＝CD＝6cm，∴BC+AD＝14cm，∴t＝14÷2＝7，故答案为7．（2）①当0＜t＜4时，S＝•（6﹣t）×2t＝﹣t2+6t．当4≤t＜6时，S＝•（6﹣t）×8＝﹣4t+24．当6＜t≤7时，S＝（t﹣6）•（2t﹣8）＝t2﹣10t+24．②当0＜t＜4时，S＝•（6﹣t）×2t＝﹣t2+6t＝﹣（t﹣3）2+9，∵﹣1＜0，∴t＝3时，△PBQ的面积最大，最小值为9．当4≤t＜6时，S＝•（6﹣t）×8＝﹣4t+24，∵﹣4＜0，∴t＝4时，△PBQ的面积最大，最大值为8，当6＜t≤7时，S＝（t﹣6）•（2t﹣8）＝t2﹣10t+24＝（t﹣5）2﹣1，t＝7时，△PBQ的面积最大，最大值为3，综上所述，t＝3时，△PBQ的面积最大，最大值为9．14．综合实践：问题情境数学活动课上，老师和同学们在正方形中利用旋转变换探究线段之间的关系探究过程如下所示：如图1，在正方形ABCD中，点E为边BC的中点．将△DCE以点D为旋转中心，顺时针方向旋转，当点E的对应点E'落在边AB上时，连接CE'．“兴趣小组”发现的结论是：①AE'＝C'E'；“卓越小组”发现的结论是：②DE＝CE'，DE⊥CE'．解决问题（1）请你证明“兴趣小组”和“卓越小组”发现的结论；拓展探究证明完“兴趣小组”和“卓越小组”发现的结论后，“智慧小组”提出如下问题：如图2，连接CC'，若正方形ABCD的边长为2，求出CC'的长度．（2）请你帮助智慧小组写出线段CC'的长度．（直接写出结论即可）（1）证明：①∵△DE'C'由△DEC旋转得到，∴DC'＝DC，∠C'＝∠DCE＝90°．又∵四边形ABCD是正方形，∴DA＝DC，∠A＝90°，∴DA＝DC'，∵DE'＝DE'，∴Rt△DAE≌Rt△DC'E′（HL），∴AE'＝C'E'．②∵点E为BC中点，C'E'＝AE'＝CE，∴点E'为AB的中点．∴BE′＝CE，又∵DC＝BC，∠DCE＝∠CBE'＝90°，∴△DCE≌△CBE'（SAS），∴DE＝CE'，∠CDE＝∠E'CB，∵∠CDE+∠DEC＝90°，∴∠E'CB+∠CED＝90°，∴DE⊥CE'．（2）解：如图2中，作C′M⊥CD于M，交AB于N．∵AB∥CD，C′M⊥CD，∴C′M⊥AB，∴∠DMC′＝∠C′NE′＝∠DC′E′＝90°，∴∠MDC′+∠DC′M＝90°，∠DC′M+∠E′CN＝90°，∴∠MDC′＝∠E′C′N，∴△DMC′∽△C′NE′，∴＝＝＝2，设NE′＝x，则AM＝AN＝1+x，C′M＝2x，C′N＝（1+x），∵MN＝AD＝2，∴2x+（1+x）＝2，解得x＝，∴CM＝2﹣（1+）＝，MC＝，∴CC′＝＝＝．15．在△ABC中，AD平分∠BAC交BC于D，∠MDN的两边分别与AB，AC相交于M，N两点，且DM＝DN．（1）如图甲，若∠C＝90°，∠BAC＝60°，AC＝9，∠MDN＝120°，ND∥AB．①写出∠MDA＝90 °，AB的长是18 ．②求四边形AMDN的周长．（2）如图乙，过D作DF⊥AC于F，先补全图乙再证明AM+AN＝2AF．解：（1）①∵AD平分∠BAC，∴∠BAD＝∠CAD＝∠BAC＝30°，∵ND∥AB，∴∠NDA＝∠BAD＝30°，∴∠MDA＝∠MDN﹣∠NDA＝120°﹣30°＝90°，∵∠C＝90°，∠BAC＝60°，∴∠ABC＝30°，∴AC＝AB，∴AB＝2AC＝18，故答案为：90，18；②∵∠ABC＝30°，ND∥AB，∴∠NDC＝30°，又∵∠MDN＝120°，∴∠MDB＝30°，∴∠MAD＝∠NAD＝∠ADN＝∠MBD＝30°，∴BM＝MD，DN＝AN，∵DM＝DN，∴BM＝MD＝DN＝AN，在Rt△ADM中，设MD＝x，则AM＝2x，BM＝MD＝DN＝AN＝x，∵AB＝18，∴3x＝18，∴x＝6，∴AM＝12，MD＝DN＝AN＝6，∴四边形AMDN的周长＝AM+MD+DN+AN＝12+6+6+6＝30；（2）补全图如图乙所示：证明：过点D作DE⊥AB于E，如图丙所示：∵DE⊥AB，DF⊥AC，AD平分∠BAC，∴∠DEM＝∠DFN＝90°，DE＝DF，在Rt△DEA和Rt△DFA中，，∴Rt△DEA≌Rt△DFA（HL），∴AE＝AF，在Rt△DEM和Rt△DFN中，，∴Rt△DEM≌Rt△DFN（HL），∴EM＝FN，∴AM+AN＝AE+EM+AF﹣NF＝2AF．。