可靠性原理与方法大作业
- 格式:pdf
- 大小:5.15 MB
- 文档页数:24

零部件的可靠性设计班级:学号:姓名:文威威摘要:本学期选修了电子设备可靠性工程,对这项科学有了更深的了解,进一步了解了本学科在工业生产和科学研究上的重要性。
据国外有关资料介绍,在船用电子设备的故障原因中,属设计不合理的占40%,电子元器件质量问题约占30%,曲操作和维护引起的故障占1 0 %,由制造工艺引起的故障约占1 0 %;对我国某炮瞄雷达现场故障统计数据分析表明,约有25%以上是山设计不合理所造成的。
引言:在可靠性技术迅速发展的今天,从指标试验评价发展到从指标论证、设计、原材料选择到工艺控制及售后服务的全过程的综合管理和评价,许多产品打出“零失效”的王牌。
产品的可黑性在很大程度上取决于设计的正确性, 而这乂基于零部件的可靠性设计。
零部件的可鼎性设计是以提高产品可靠性为LI的、以概率论与数理统汁理论为基础,综合运用数学、物理、丄程力学、机械工程学、人机工程学、系统工程学、运筹学等多方面的知识来研究机械工程的最佳设计问题。
利用可黑性设讣,可以降低元器件及系统的使用失效率,降低设备的成本,提高设备的可鼎性。
电子设备可靠性设计技术主要包括热设计、降额设汁、动态设计、三防设计、电磁兼容设计、振动与冲击隔离设计等。
正文:国内外的实践经验表明,机械结构的可靠性是由设计决定的,而由制造、安装和管理来保证的。
因此将概率设计理论和可黑性分析与设计方法应用于机械结构设讣中,才能得到既有足够安全可靠性,乂有适当经济性的优化结构。
这样,以估计结构系统可鼎度为LI标的、以概率统讣和随机过程理论为基础的、以各种结构分析技术为工具的多种结构可鼎性分析与设计方法迅速发展oRaize r综述了一次二阶矩法和以一次二阶矩法为基础的现代可靠性分析理论。
赵国藩等建立了广义随机空间内考虑随机变量相关性的结构可靠度实用分析方法,扩大了现有可幕度计算方法的适用范围。
并且贡金鑫和赵国藩还研究了原始空间内的可靠性分析方法,这种方法不需要将非正态随机变量映射或当量正态化为正态随机变量,因而特别适合于当随机变量的概率分布函数不存在显式时可靠度的讣算。

如何提高系统可靠性摘要:系统可靠性是指部件、元件、产品或系统在规定条件下、规定时间内、实现规定功能的能力,它是对系统可靠性的定性评价。
介绍了提高系统可靠性的重要意义。
论述了可靠性设计的重要作用及提高系统可靠性的途径和方法。
关键词:系统可靠性提高方法可靠性特征量是用来表示产品总体可靠性高低的各种可靠性数量指标的总称。
对于产品来说,可靠性问题和人身安全、经济效益密切相关。
因此,研究产品的可靠性问题,显得十分重要.非常迫切.一、提高产品可靠性的意义。
1)提高产品可靠性,可以防止故障和事故障的发生,尤其是避免灾难性的事故发生. 2) 提高产品的可靠性,能使产品总的费用降低.提高产品的可靠性,首先要增加费用,如选用好的元器件,研制部分冗余功能的电路及进行可靠性设计、分析、实验,这些都需要经费。
然而,产品可靠性的提高使得维修费及停机检查损失费大大减小,使总费用降低。
3)提高产品的可靠性,可以减少停机时间,提高产品可用率,一台设备可顶几台用,可以发挥几倍的效益。
4)对于公司来讲,提高产品的可靠性,可以改善公司信誉,增强竞争力,扩大市场份额,从而提高经济效益。
二、提高系统可靠性的途径和方法。
1.构建系统本身固有可靠性。
可靠性工程实质上是对影响系统可靠性的薄弱环节的不断发现和不断改进的过程。
产品的可靠性并不是以此达到的,而时间次逼近的。
设计是决定系统固有可靠性的重要环节,在方案论证阶段,通过可靠性预计,比较不同方案的可靠性水平为最优化方案选择提供依据。
产品可靠性的基础是用于开展可靠性具体设计分析工作的基础数据库,基础数据库式设计经验的总汇,需要导入专家意见和设计经验的基础数据库的完备与否直接决定了开展可靠性设计分析工作的水平。
在构建阶段,需将装置的可靠性设计指标要求值分配到各部件,形成各部件可靠性设计指标要求值。
分配需要结合预计的结果,最终得到相对合理的各部件可靠性指标设计要求值。
2.维修可提高系统的可靠性设备的维修是是设备保持、恢复到或改善其由有关技术文件所规定的技术状态的全部技术和管理活动。



机械可靠性设计实验报告学院:机电学院班级:05021104姓名:张木学号:2011301279题目:齿轮:某种机器的齿轮,按国标规定的方法计算或查线图得到各参量的均值和标准差如下,求齿轮的可靠度。
分析:分别计算齿轮齿面接触疲劳强度的可靠度与齿轮齿根弯曲疲劳强度的可靠度后进行比较,取可靠性较小值作为齿轮的可靠度。
12(34644,519.66),(1,0.033),(1.484,0.1613),(1.68,0.0544)(1.603,0.052889),(1.16,0.03828),2(200,1),(148.75,0.74375),(4,0.02),(2.32,0.0116)(189.8,9.49)(),t A V H F H F n H E F N K K K K K K b mm d mm m mm Z Z N mm Z ββααε============2lim (0.81,0.00405),(0.957,0.004785)(1300,156),(1,0.033),(1.03,0.03399)(1.04,0.3432),(0.92,0.03036),(1,0.033),(1,0.033)H N R V L W X Z N mm Z Z Z Z Z Z βσ=========程序流程图:开始计算齿轮零件的齿面接触和齿根弯曲疲劳强度均值uT1,uT2和标准差sT1,sT2根据公式计算应力的均值ut1,ut2和标准差st1,st2然后根据应力和强度的连结方程计算可靠性系数SM1,SM2计算出可靠度R1,R2比较R1,R2,取较小值结束程序1:基于齿面接触强度的可靠性#include <iostream>#include <cmath>using namespace std;#define PI 3.141592653double fun(double x,double miu,double sigma){return 1/(sqrt(2*PI)*sigma)*exp(-((x-miu)*(x-miu))/2/sigma/sigma);}double integral(double miu,double sigma,double a,double b){double s,h;int i;int N=abs(a-b)/0.001;s=(fun(a,miu,sigma)+fun(b,miu,sigma))/2.0;h=(b-a)/N;for(i=1;i<N;i++)s+=fun(a+i*h,miu,sigma);return(s*h);}double sigmaadd(double sigma_c,double sigma_d){return sqrt(sigma_c*sigma_c+sigma_d*sigma_d);}double sigmacheng(double a,double sigma_a,double b,double sigma_b){returnsqrt(a*a*sigma_b*sigma_b+b*b*sigma_a*sigma_a+sigma_b*sigma_b*sigma_a*sigma_a); }double sigmachu(double a,double sigma_a,double b,double sigma_b){return 1/b*sqrt((a*a*sigma_b*sigma_b+b*b*sigma_a*sigma_a)/(b*b+sigma_b*sigma_b)); }int main(){double kf,sigma_kf,ka,sigma_ka,kv,sigma_kv,khb,sigma_khb;double khx,sigma_khx,b,sigma_b,d1,sigma_d1,sigma_v;double zh,sigma_zh,ze,sigma_ze,zt,sigma_zt,v;double zb,sigma_zb,sigmahlim,sigma_sigmahlim,zn,sigma_zn;double zr,sigma_zr,zv,sigma_zv,zl,sigma_zl,zw,sigma_zw;double zx,sigma_zx,ft,sigma_ft,kx,sigma_kx,result;double x,sigma_x,y,sigma_y,u,c,sigma_c,t,sigma_t,R,sigma_R;ft=34644;sigma_ft=519.66;ka=1;sigma_ka=0.033;kv=1.484;sigma_kv=0.1613;khb=1.68;sigma_khb=0.0544;kx=1.16;sigma_kx=0.03828;b=100;sigma_b=0.5;d1=148.75;sigma_d1=0.74375;zh=2.32;sigma_zh=0.0116;ze=189.8;sigma_ze=9.49;zt=0.81;sigma_zt=0.00405;zb=0.957;sigma_zb=0.004785;sigmahlim=1300;sigma_sigmahlim=156;zn=1;sigma_zn=0.033;zr=1.03;sigma_zr=0.03399;zv=1.04;sigma_zv=0.03432;zl=0.92;sigma_zl=0.03036;zw=1;sigma_zw=0.033;zx=1;sigma_zx=0.033;sigma_y=sigmacheng(zh,sigma_zh,ze,sigma_ze);y=zh*ze; sigma_y=sigmacheng(y,sigma_y,zt,sigma_zt);y=y*zt; sigma_y=sigmacheng(y,sigma_y,zb,sigma_zb); y=y*zb;sigma_x=sigmacheng(ka,sigma_ka,kv,sigma_kv);x=ka*kv; sigma_x=sigmacheng(x,sigma_x,khb,sigma_khb); x=x*khb; sigma_x=sigmacheng(x,sigma_x,kx,sigma_kx);x=x*kx;u=3.5;u=(u+1)/u;sigma_t=sigma_ft*u;t=ft*u;sigma_t=sigmachu(t,sigma_t,b,sigma_b);t=t/b;sigma_t=sigmachu(t,sigma_t,d1,sigma_d1); t=t/d1;sigma_c=sigmacheng(t,sigma_t,x,sigma_x); c=t*x;v=c;c=sqrt(sqrt(c*c-0.5*sigma_c*sigma_c));sigma_c=sqrt(v-sqrt(v*v-0.5*sigma_c*sigma_c));sigma_c=sigmacheng(c,sigma_c,y,sigma_y);c=c*y;sigma_sigmahlim=sigmacheng(sigmahlim,sigma_sigmahlim ,zn,sigma_zn);sigmahlim=sigmahlim*zn;sigma_sigmahlim=sigmacheng(sigmahlim,sigma_sigmahlim ,zr,sigma_zr);sigmahlim=sigmahlim*zr;sigma_sigmahlim=sigmacheng(sigmahlim,sigma_sigmahlim ,zv,sigma_zv);sigmahlim=sigmahlim*zv;sigma_sigmahlim=sigmacheng(sigmahlim,sigma_sigmahlim ,zl,sigma_zl);sigmahlim=sigmahlim*zl;sigma_sigmahlim=sigmacheng(sigmahlim,sigma_sigmahlim ,zw,sigma_zw);sigmahlim=sigmahlim*zw;sigma_sigmahlim=sigmacheng(sigmahlim,sigma_sigmahlim ,zx,sigma_zx);sigmahlim=sigmahlim*zx;R=sigmahlim-c;sigma_R=sigmaadd(sigma_sigmahlim,sigma_c);result=integral(R,sigma_R,0,R+100*sigma_R);cout<<result;return 0;}结果:齿面接触可靠度为0.982475程序2:基于齿根弯曲强度的可靠性#include <iostream>#include <cmath>using namespace std;#define PI 3.141592653double fun(double x,double miu,double sigma){return 1/(sqrt(2*PI)*sigma)*exp(-((x-miu)*(x-miu))/2/sigma/sigma);}double integral(double miu,double sigma,double a,double b){double s,h;int i;int N=abs(a-b)/0.001;s=(fun(a,miu,sigma)+fun(b,miu,sigma))/2.0;h=(b-a)/N;for(i=1;i<N;i++)s+=fun(a+i*h,miu,sigma);return(s*h);}double sigmaadd(double sigma_c,double sigma_d){return sqrt(sigma_c*sigma_c+sigma_d*sigma_d);}double sigmacheng(double a,double sigma_a,double b,double sigma_b){returnsqrt(a*a*sigma_b*sigma_b+b*b*sigma_a*sigma_a+sigma_b*sigma_b*sigma_a*sigma_a); }double sigmachu(double a,double sigma_a,double b,double sigma_b){return 1/b*sqrt((a*a*sigma_b*sigma_b+b*b*sigma_a*sigma_a)/(b*b+sigma_b*sigma_b)); }int main(){double ft,sigma_ft,ka,sigma_ka,kv,sigma_kv;double kfb,sigma_kfb,kx,sigma_kx,b,sigma_b;double mn,sigma_mn,result;double y,x,t,c,R,sigma_y,sigma_x,sigma_t,sigma_c,sigma_R;double yf,sigma_yf,ys,sigma_ys;double ye,sigma_ye,yb,sigma_yb,yst,sigma_yst;double sigmaflim,sigma_sigmaflim,ynt,sigma_ynt;double y1t,sigma_y1t,y2t,sigma_y2t,yx,sigma_yx;ft=34644;sigma_ft=519.66;ka=1;sigma_ka=0.033;kv=1.484;sigma_kv=0.1613;kfb=1.603;sigma_kfb=0.052899;kx=1.16;sigma_kx=0.03828;b=100;sigma_b=0.5;mn=4;sigma_mn=0.02;yf=2.36;sigma_yf=0.07788;ys=1.94;sigma_ys=0.06402;ye=0.715;sigma_ye=0.003575;yb=0.8;sigma_yb=0.004;yst=2.1;sigma_yst=0.0693;sigmaflim=310;sigma_sigmaflim=62;ynt=1;sigma_ynt=0.033;y1t=0.99;sigma_y1t=0.03267;y2t=1.065;sigma_y2t=0.035145;yx=1;sigma_yx=0.033;sigma_y=sigmacheng(yf,sigma_yf,ys,sigma_ys);y=yf*ys;sigma_y=sigmacheng(y,sigma_y,ye,sigma_ye);y=ye*y;sigma_y=sigmacheng(y,sigma_y,yb,sigma_yb); y=y*yb;sigma_x=sigmacheng(ka,sigma_ka,kv,sigma_kv);x=ka*kv;sigma_x=sigmacheng(x,sigma_x,kfb,sigma_kfb); x=x*kfb;sigma_x=sigmacheng(x,sigma_x,kx,sigma_kx);x=x*kx;sigma_t=sigmachu(ft,sigma_ft,b,sigma_b);t=ft/b;sigma_t=sigmachu(t,sigma_t,mn,sigma_mn);t=t/mn;sigma_sigmaflim=sigmacheng(sigmaflim,sigma_sigmaflim ,yst,sigma_yst);sigmaflim=sigmaflim*yst;sigma_sigmaflim=sigmacheng(sigmaflim,sigma_sigmaflim ,ynt,sigma_ynt);sigmaflim=sigmaflim*ynt;sigma_sigmaflim=sigmacheng(sigmaflim,sigma_sigmaflim ,y1t,sigma_y1t);sigmaflim=sigmaflim*y1t;sigma_sigmaflim=sigmacheng(sigmaflim,sigma_sigmaflim ,y2t,sigma_y2t);sigmaflim=sigmaflim*y2t;sigma_sigmaflim=sigmacheng(sigmaflim,sigma_sigmaflim ,yx,sigma_yx);sigmaflim=sigmaflim*yx;sigma_c=sigmacheng(t,sigma_t,y,sigma_y);c=t*y;sigma_c=sigmacheng(t,sigma_t,x,sigma_x);c=t*x;R=sigmaflim-c;sigma_R=sigmaadd(sigma_sigmaflim,sigma_c);result=integral(R,sigma_R,0,R+100*sigma_R);cout<<result;return 0;}结果:齿根弯曲疲劳强度可靠度为0.998602综上:齿轮的可靠度为0.982475。

可靠性原理的应用实例引言可靠性是指系统在特定环境和特定条件下,按照特定要求完成规定功能的能力。
在工程领域中,可靠性的提高是一个非常重要的目标,因为它直接关系到产品的性能和用户的满意度。
可靠性原理是指通过合理的设计和管理,使系统能够在各种不确定条件下保持稳定和正常工作。
本文将介绍几个典型的可靠性原理的应用实例,通过对这些实例的分析和讨论,可以更好地理解可靠性原理的实际应用。
实例一:飞机引擎设计飞机引擎的设计是一个典型的应用可靠性原理的实例。
一个飞机引擎必须在各种恶劣的条件下正常工作,如高温、低温、高海拔等。
为了提高可靠性,飞机引擎设计者通常采用以下措施:•冗余设计:引擎内部的关键组件采用冗余设计,即多个相同或类似的组件并联工作,一旦有一个组件发生故障,其他组件可以继续正常工作,从而保证飞机的安全飞行。
•定期维护:引擎的各个组件需要定期检查和维护,以便发现和修复潜在故障,确保引擎的正常运行。
•故障检测与排除系统:飞机引擎通常配备有故障检测与排除系统,可以实时监测引擎的工作状态,一旦发现故障,及时采取措施进行修复或关闭引擎。
通过以上措施的应用,飞机引擎的可靠性得到了有效提高,保证了飞机的安全和航行的顺利进行。
实例二:电力系统设计电力系统的设计是另一个典型的应用可靠性原理的实例。
电力系统必须保证全天候稳定供电,在面对各种异常情况时仍能正常工作。
为了提高可靠性,电力系统设计者采用以下措施:•分级设计:电力系统分为多级供电,保证一级发生故障时,其他级别的供电系统能够接替工作。
•备用电源:电力系统配备备用电源,如柴油发电机组等,一旦主电源发生故障,备用电源能够及时接替供电,避免供电中断。
•过载保护:电力系统内置过载保护系统,可以在电流超出额定负荷时自动切断电源,避免设备过热,从而提高设备的可靠性。
通过以上措施的应用,电力系统的可靠性得到了提高,确保了电力供应的稳定和可靠。
实例三:软件系统设计软件系统的设计也是一个应用可靠性原理的重要领域。

机械可靠性设计姓名:xxx学号:xxxxxxxxx专业:机械制造及其自动化学校:xxxxxxxxxxx2014 年12 月26 日第三部分系统可靠性1.系统的原理图、功能框图和功能流程图、系统的可靠性框图的区别,举例说明。
答:区别:系统的原理图是反应了系统及其组成单元之间物理上的连接与组合关系;功能框图、功能流程图是反映了系统及其组成单元之间的功能关系;可靠性框图是对于复杂产品的一个或一个以上的功能模式,用方框表示的各组成部分的故障或它们的组合如何导致产品故障的逻辑图;系统的原理图、功能框图及功能流程图是建立可靠性模型的基础。
举例:某链式刀库和机械手系统的原理图功能框图功能流程图系统的可靠性框图2.试以行星轮系的可靠性建模为例,说明行星轮系的工作原理和可靠性框图。
答:主要由行星轮g、中心轮k及行星架H组成。
其中行星轮的个数通常为2~6个。
但在计算传动比时,只考虑1个行星轮的转速,其余的行星轮计算时不用考虑,称为虚约束。
它们的作用是均匀地分布在中心轮的四周,既可使几个行星轮共同承担载荷,以减小齿轮尺寸;同时又可使各啮合处的径向分力和行星轮公转所产生的离心力得以平衡,以减小主轴承内的作用力,增加运转平稳性。
行星架是用于支承行星轮并使其得到公转的构件。
中心轮中,将外齿中心轮称为太阳轮,用符号a表示,将内齿中心轮称为内齿圈,用符号b表示。
二、行星轮系的分类根据行星轮系基本构件的组成情况,可分为三种类型:2K-H型、3K型、K-H-V型。
2K-H型具有构件数量少,传动功率和传动比变化范围大,设计容易等优点,因此应用最广泛。
3K型具有三个中心轮,其行星架不传递转矩,只起支承行星轮的作用。
行星轮系按啮合方式命名有NGW、NW、NN型等。
N表示内啮合,W 表示外啮合,G表示公用的行星轮g。
典型行星齿轮传动机构的基本特性。
行星轮系的可靠性框图简化后轮系传动简图图III 可靠性框图3.以身边的典型民用产品为例,进行FMEA分析,并建立故障树。

练习一1. 设导弹的可靠度为0.85,两枚导弹在射击目标时不是互相统计独立,第一枚未击中第二枚也击不中的概率为0.2,然而第一枚击中,第二枚击中的概率不变,仍旧是0.85,试问两枚导弹至少有一枚击中的概率?解:P A ().=085P B A (|).--=02 P B A (|).=085 P B A (|).-=08 P B A (|).-=015 至少有一枚击中的概率是:P AB P AB P B A ()()()++--注意本题指的是第一枚未击中情况下,第二枚的击中概率会有变化,如果第一枚击中话,则第二枚射击无影响,所以A,B 和AB -是统计独立的,故有:P AB P A P B P AB P A P B ()()()...()()()...=⋅=⨯==⋅=⨯=--0850850722508508501275但A -和B 是统计相关的P AB P A P B A ()()(|)...---==⨯=01508012所以至少击中一枚的概率为它们之和=0.972. 试验一种产品,有98%的判断有缺陷的产品,而4%的概率将好产品认为是有缺陷的,如果对一批试验产品有3%的次品率,问一个产品归为次品而真正是次品的概率是多少? 解: D 表示产品是有缺陷的事件C 表示将产品归为有缺陷事件那么 P(D)=0.03 P(C|D)=0.98 P C D (|)_=0.04 用贝叶斯定理来计算P(D|C) P D C P D P C D P C D P D P C D P D (|)()(|)(|)()(|)()(.)(.)(.)(.)(.)(.).__=+=+=003098098003004097043练习二2.1设有一批零件共100件,其中有5件次品,现从中任取50件,问恰好有一件次品的概率是多少?解:S=“从100件中任取50件”共有多少种抽法,即)!50100(!50!10050100-=C 每一种抽法就是一个事件,即得到总的样品空间数。


金属带线锚钉裂问题分析及解决方案(质量与可靠性工程大作业)目录1. 情况说明2. 锚钉断裂问题介绍3. 鱼骨图分析4. 失效复现5. 失效模式分析6. 改进方案7. 试验确认8. 总结1情况说明带线锚钉是由一种非常小的植入物,用于将缝线固定于骨中。
它通过缝针将线穿过软组织,并打结将软组织固定于锚钉上,使软组织与骨重新连接。
产品由钛合金锚钉、超高分子量聚乙烯线和插入器组成。
适用于肩关节、踝关节、膝关节、髋关节、腕关节、骨盆等软组织损伤修复。
金属带线锚钉产品结构示意图如图1所示。
图1带线锚钉结构图本案例中,某款直径为2.8mm的金属带线锚的在临床使用中出现锚钉断裂情况。
为尽量避免类似情况的再次发生,对于该问题使用质量与可靠性分析工具进行分析。
通过分析希望能找到锚钉断裂原因并给出相应的解决方案。
使得产品的安全性得到提高。
2锚钉断裂问题介绍金属带线锚钉由金属锚钉、聚乙烯缝线、插入器、缝合针组成。
其中金属锚钉由符合GB/T 13810标准规定的TC4钛合金材料制成,表面无着色。
插入器与人体接触部分由符合标准YY/T 0294.1-2016要求的06Cr19Ni10不锈钢制成,缝线由超高分子量聚乙烯纱线编织而成。
锚钉结构如图2所示。
图2金属锚钉示意图锚钉断裂形式如图3所示,金属锚钉在使用中在钉头六方根部出现断裂。
分析螺钉的整个结构可知,钉头六方根部为锚钉一个应力集中点,在锚钉拧入过程中,随着锚钉的拧入扭矩不断增大,并且在这过程中如果有底孔偏小或者皮质骨偏厚等情况会进一步使得旋入扭矩变大,由于锚钉本身强度有限,因此容易出现断裂。
综上初步分析引起锚钉断裂的原因是锚钉强度不够以及非预期的使用。
图3锚钉断面图3鱼骨图分析图4鱼骨图4失效复现为复现临床上锚钉的断裂形式,现对锚钉进行模拟扭断试验。
在一般临床应用中,外科医生施加轴向和扭转组合力将骨螺钉植入体内,参考ASTM F543标准对金属锚钉进静态扭转试验。
实验装置如图5所示,将截取插入器固定与上部三爪卡盘,金属锚钉固定于下部三爪卡盘,确保夹持固定完成后,通过试验机程序控制,轴向施加5N载荷确保锚钉尾部完全进入扳手内。
结构可靠性课程大作业船舶与海洋工程结构安全可靠性分析问题1:请列举三种检查可靠性的方法,并写出每种方法的要点。
哪种方法被广泛用于处理工程问题?为什么?第三水平方法,计算结构或结构组件的精确失效概率。
第二水平方法,通过迭代计算等方法得到近似失效概率,如使用随机变量均值和方差的一次二阶矩法。
第一水平方法,通过使用一系列部分安全系数来提供适当的结构可靠性。
目前工程上广泛采用第一水平方法和第二水平方法。
一阶二次矩法计算较为简便,大多大多情况下精度又可以满足工程要求。
问题2:在工程实践当中,很难用标准正态分布描述所有的变量。
对非标准正态分布的变量,如何用 Hasofer-Lind 可靠性指标处理他们?对非正态随机变量在设计验算点处进行当量正态化,将其转化为当量正态随机变量,然后利用改进的一次二阶矩法计算结构的Hasofer-Lind 可靠性指标。
由于该方法为国际结构安全度联合委员会(JCSS)采用,故又称为JC法,是目前应用最为广泛的可靠度分析方法。
设X为非正态随机变量,其概率密度函数及其分布函数分别为f X(x)、F X(x),将其在设计验算点x?处进行当量正态化处理,转化为当量正态随机变量X′。
记X′对应的概率密度函数及分布函数分别为f X′(x)、F X′(x),那么X和X′的概率密度函数和分布函数应满足以下两个条件。
在设计验算点x?处非正态随机变量X与其当量正态随机变量X′的分布函数值相等,且概率密度函数值也相等。
即F X(x?)=F X′(x?)且f X(x?)=f X′(x?)。
可以求得当量正态变量X′的均值μx′、标准差σx′为μX′=x??Φ?1[F X(x?)]σX′σX′=φ{Φ?1[F X(x?)]}f X(x?)将当量正态化过程与改进的一次二阶矩法相结合,即可得到JC法的计算步骤:1.假定验算点坐标x i?(通常可取x i?=μx i);2.对非正态随机变量X i,计算当量正态变量的均值μX′和标准差σX′,替代原变量的均值和标准差;3.计算方向余弦cosθXi;4.计算可靠性指标β;5.计算新验算点坐标x i?;6.由新的验算点重复步骤2到5,直到前后两次计算出的可靠坐标β之差小于允许误差ε;问题3:图1中有一根梁。
系统可靠性原理习题及答案1、 元件可靠性的定义是什么?规定条件、规定时间、规定功能各是什么含义? 解:元件的可靠性:元件在规定的吋间内、规定条件下完成规定功能的能力。
规定时间:指保修期、使用期和贮存期。
规定条件:即使用条件,主要包括:环境条件、包装条件、贮存条件、维 修条件,操作人员条件等。
规定功能:指元件/系统的用途。
2、 元件的可靠度、故障率和平均寿命各是怎么定义的?解:元件的可靠度:在规定条件下,在时刻t 以前正常工作的概率。
元件故障率:即故障率函数,元件在t 时刻以前正常工作,在t 时刻后单 位时间内发生故障的(条件)概率。
平均寿命:即平均无故障工作时间,也称做首次故障平均时间,是寿命的 期望值。
3、 设某种元件的X=0.001/h,试求解:(1)由这种元件组成的二元件并联系统、两元件串联、2/3 (G)系统的平 均寿命。
解:由题意可知,单个元件的可靠度为Rj(t)=e'M , i=l, 2, 3。
A 、二元件并联: 系统的可靠度为: R p (t)=l-(l-R 1(t))(l-R 2(t))=2e At -e-2At 此时系统的平均寿命为由于 1=0.001/h,故 MITF=1500(h)B 、二元件串联: 系统的可靠度为: Rs(t)=Ri(t)R 2(t)=e 2M此时系统的平均寿命为由于 X=0.001/h,故 MTTF=500(h)C 、2/3 (G)系统: 系统的可靠度为:RG("Rdt)R2(t)R3(t)+⑴ Rdt))R2(t)R3(t)+R 丄⑴⑴ R2(t))R3(t)+R"t)R2(t)⑴也⑴)=3严2严此时系统的平均寿命为由于 D ・001/h,故 MTTF=2500/3 (h)(2) t=100h, 500h,1000h时,由这种元件组成的二元件并联系统、两元件串MTTF= R G (t)dt53e"2Xt 一 2e"3At dt =—32e"At _ e _2At dt =—Z联、2/3 (G )系统的可靠度分别是多少? 解:将各t 值代入⑴中的各可靠度R (t )即可得结果。
AP1000设备冷却水系统建模哈尔滨工程大学核科学与技术学院AP1000设备冷却水系统建模姓名:学号:摘要:本文针对非能动安全先进核电厂AP1000的设备冷却水系统(Component Water System ,CCS)的主要工作方式和工作流程,通过对系统运行过程分析,简述了其不同工作状态下的任务剖面状态,并建立了AP1000设备冷却水系统可靠性框图以及数学模型。
关键词:AP1000设备冷却水系统;任务剖面;可靠性分析;数学模型1.引言AP1000在传统成熟的压水堆核电技术基础上,在设计中采用了非能动的严重事故预防和缓解措施,大大降低了发生人为因素错误的可能性,使AP1000的安全性能得到显著提高的同时也提升了经济竞争力。
本文针对AP1000设备冷却水系统可靠性建模研究,旨在对该系统的各个运行阶段进行可靠性验证,并提出相应数学模型,从而加深对AP1000的理解。
2.设备冷却水系统综述2.1 系统功能设备冷却水系统是一个非安全相关的封闭回路冷却水系统,在放射性系统和外界环境之间起到一个屏障的作用,执行非安全相关的纵深防御功能。
2.2 系统组成设备冷却水系统包括两个相互并联并互为支持的独立系列,包括两台CCS泵、两台CCS换热器、一台CCS膨胀水箱、一台化学加药箱、一台辐射监测器装置和相关的管道、阀门、控制设备和仪表。
设备水系统如图1所示:图12.3 系统不同工况的任务剖面简述如前所述,CCS除安全壳隔离外,不执行任何安全相关的功能,但CCS的设计遵循非安全相关的纵深防御原则。
在系统运行的各个阶段,其工作条件、环境及成功准则如下所述:2.3.1 电厂启动阶段电厂启动是指将反应堆从冷停堆状态带到零功率运行的温度和压力,然后进入功率运行状态,该过程要求两个换料后设备冷却水系统的两个系列都投入运行。
电厂启动阶段的成功准则为:两系列设备冷却水系统都投入运行,同时关闭余热排出泵,四台冷却剂泵(RCP)得到冷却,下泄热交换器设置为温度自动控制模式,同时监测设备冷却水的流量和温度,使之在所要求的范围内。
汽车可靠性设计大作业班级学号姓名汽车可靠性设计大作业一、问题说明钢板弹簧作为影响车辆安全的重要零件之一,既负责传递所有各向力和力矩,还具有弹性元件、减振器和导向机构的特性,是重要的高负荷安全部件。
近年来,国内外学者对钢板弹簧的设计进行了研究。
利用虚拟样机理论,在整车动力学仿真的基础上,对汽车钢板弹簧的结构参数进行了优化设计,并对钢板弹簧进行了有限元分析;利用模糊数学理论和优化设计方法,建立了基于模糊综合评判的汽车钢板弹簧优化设计的数学模型,并探讨了其优化设计方法,分析了弹簧材料、加工工艺、设计参数和使用条件对汽车钢板弹簧疲劳寿命的影响,为钢板弹簧的设计提供了一定的理论依据。
二、已知条件汽车钢板弹簧:材料为AISI4340,几何尺寸为b(50.8,0.886)mm,l(762,1.905)mm,h(20,0.3),载荷为P=(8000,160)N,材料强度r=(585.8,28.3)MPa。
三、输出的结果1. SM=3.56592.3.四、计算的模型强度-材料的均值和方差、应力-几何参数和载荷为随机变量、干涉模型五、程序流程图六、源程序1.当载荷为定值时,求出此时的可靠度global R1 R2 sigma_R1 sigma_R2 a sigma_a zhifanliP=8000;sigma_P=160;l=762;sigma_l=1.905;h=20;sigma_h=0.3;b=50.8;sigma_b=0.886;r=585.8;sigma_r=28.3;a=l/2;sigma_a=sigma_l/2;R2=P*a/l;u=P*a;sigma_u=sqrt(P^2*sigma_a^2+a^2*sigma_P^2+sigma_P^2*sigma_a^2); sigma_R2=(sqrt((u^2*sigma_l^2+l^2*sigma_u^2)/(l^2+sigma_l^2)))/l;R1=P-R2;sigma_R1=sqrt(sigma_P^2+sigma_R2^2);zhifanli=[R1 sigma_R1 R2 sigma_R2];M=R1*a;sigma_M=sqrt(R1^2*sigma_a^2+a^2*sigma_R1^2+sigma_R1^2*sigma_a^2);I=b*h^3/12;c=h/2;g=h^2+sigma_h^2;sigma_g=sigma_h*sqrt(4*h^2+2*sigma_h^2);v=b*g;sigma_v=sqrt(g^2*sigma_b^2+b^2*sigma_g^2+sigma_b^2*sigma_g^2);L=M*6/v;sigma_L=6/v*sqrt((M^2*sigma_v^2+v^2*sigma_M^2)/(v^2+sigma_v^2));SM=(r-L)/(sqrt(sigma_r^2+sigma_L^2))结果说明:在给定载荷作用下,在钢板弹簧中央作用时,钢板弹簧受到的力矩最大,钢板弹簧所受的应力最大,所以此时钢板弹簧的可靠度最低,查表得,此时的可靠度R=0.99999,可靠,所以当该载荷作用在钢板弹簧其他位置时,钢板弹簧也可靠。
第五章作业
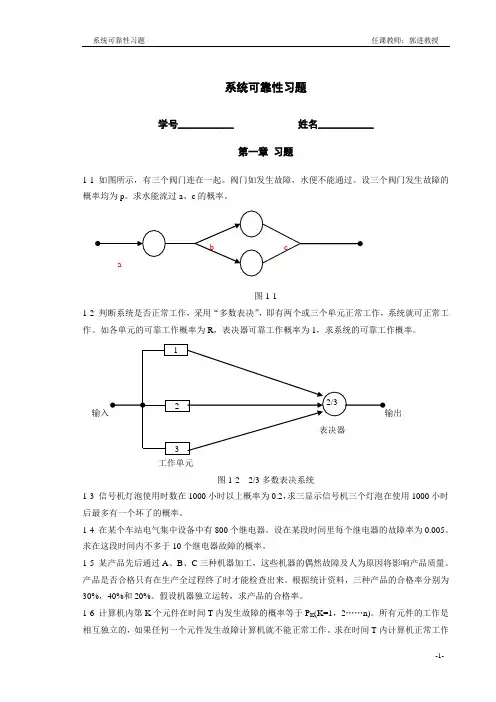
1 画出三个不同单元组成的可维修并联系统的状态转移图并求出状态转移矩阵,假设单元均服从负指数分布,只有一个修理工并且在△t时间内系统出现二次故障的概率为0。
2 设有n根铁索所制成的吊桥,这些铁索中只允许断一根,假定在全n根铁索都安全无事的场合时.各铁索的失效率λ。
,而当有一根铁索断后,剩余铁索的失效率为λ1,试求该桥的可靠度。
第六章作业
1求下列系统的可靠度,表决器的可靠度为1。
各单元可靠度相同且等于R。
若各单元服从负指数分布且失效率为λ,求系统的平均寿命MTTF。
(提示:可用贝叶斯分析法求解)。