模拟退火算法(MATLAB实现)

基于模拟退火算法的任务调度策略优化研究随着人工智能技术的发展，任务调度成为企业管理中的重要问题之一。

针对不同的任务类型和资源瓶颈，企业需要制定适合的任务调度策略。

然而，在现实情况下，制定最优的任务调度策略是非常困难的。

因此，基于模拟退火算法的任务调度策略优化研究，成为了一个备受关注的领域。

一、模拟退火算法概述模拟退火算法（Simulated Annealing, SA）是一种基于概率的全局优化算法。

SA模拟了固体物体在加热冷却过程中的行为，将来自统计物理学的理论和方法应用于解决优化问题。

SA算法是一种可以克服局部极小值陷阱的优化算法，适用于解决有很多局部最优解的、复杂的、大规模的优化问题。

二、任务调度优化问题描述在任务调度优化问题中，假设有n个任务需要完成，并且有m个可用资源可以被分配使用。

每个任务的运行需要特定的资源和时间。

各种资源不能同时处理两个任务。

任务调度问题就是确定如何为每个任务分配资源，以便使任务总运行时间最小。

三、基于模拟退火算法的任务调度优化模拟退火算法是一种全局优化算法。

它适用于解决具有多个极小值的复杂问题。

任务调度优化问题在实际应用中为NP难问题。

利用模拟退火算法进行任务调度优化的基本思想是首先将问题转化为一个数学模型，然后通过模拟退火的过程寻求全局最优解。

具体地，任务调度问题可以表示为一个图论优化问题，其中任务和资源之间的约束可以用一个图G表示。

每个任务和每个可用资源在图G中都表示为一个节点。

如果任务i需要资源j，那么在节点i和节点j之间就会有一条边。

任务调度问题就是要找出图G的最小在连通子图，其保证了所有任务都被完成，同时所有可用资源也被尽可能多地用到。

模拟退火算法的具体流程如下：1.初始化温度T和初始解S0；2.产生一组新解Si，计算函数值E(Si)和E(Si-1)；3.如果E(Si)<E(Si-1)，接受Si作为新的现行解；4.如果E(Si)>E(Si-1)，以一定概率接受Si作为新解；5.降温；6.判断终止条件是否达到。

【文章】matlab带约束模拟退火算法深入探讨和分析matlab带约束模拟退火算法在现代科学和工程领域，优化问题是十分常见的。

而其中，约束优化问题更是一种常见的形式。

为了解决这类问题，人们经过长时间的探索，提出了许多方法，其中模拟退火算法便是一种被广泛应用的优化算法之一。

而在matlab中，带约束的模拟退火算法更是得到了丰富的实现和应用。

本文将从简单到复杂，由浅入深地介绍matlab带约束模拟退火算法，以帮助读者更好地理解和掌握这一优化方法。

1. 什么是模拟退火算法？模拟退火算法是一种基于模拟退火过程的全局优化算法。

它模拟了金属在高温下退火时的物理过程，通过不断降低系统的温度来寻找全局最优解。

在matlab中，模拟退火算法通常通过设置初始温度、终止温度、温度下降率等参数来实现。

2. 为什么需要约束？在实际问题中，许多优化问题都存在着一定的约束条件。

比如工程设计中的材料强度、生产计划中的资源限制等。

如何在求解优化问题时满足这些约束条件便成为了一个重要的问题。

3. matlab带约束模拟退火算法是如何工作的？在matlab中，带约束的模拟退火算法通过引入罚函数、拉格朗日乘子等方法来处理约束条件。

它不仅要寻找全局最优解，还要确保解满足一定的约束条件。

这就需要在温度下降的过程中，不断调整解的位置，以在搜索最优解的同时满足约束条件。

4. 代码实现及应用在matlab中，带约束的模拟退火算法通常通过调用现成的优化工具箱来实现。

我们可以通过设置目标函数、约束条件等参数，来对不同的优化问题进行求解。

可以用该算法来求解工程设计中的优化问题、生产计划中的调度优化问题等。

总结回顾通过本文的介绍，我们对matlab带约束模拟退火算法有了一个较为全面的了解。

我们知道了模拟退火算法是如何工作的，以及在matlab中如何处理带约束的优化问题。

在实际应用中，我们可以根据具体的问题，合理地设置参数和约束条件，来求解复杂的优化问题。

使用matlab实现模拟退火算法标题：使用MATLAB实现模拟退火算法：优化问题的全局搜索方法引言：模拟退火算法（Simulated Annealing）是一种经典的全局优化算法，常用于解决各种实际问题，如组合优化、参数优化、图形分割等。

本文将详细介绍如何使用MATLAB实现模拟退火算法，并介绍其原理、步骤以及代码实现。

1. 模拟退火算法简介模拟退火算法借鉴了金属退火的物理过程，在解空间中进行随机搜索，用于找到全局最优解。

其核心思想是通过接受一定概率的劣解，避免陷入局部极小值，从而实现全局优化。

2. 模拟退火算法步骤2.1 初始参数设置在使用MATLAB实现模拟退火算法之前，我们需要配置一些初始参数，包括起始温度、终止温度、温度衰减系数等。

这些参数的合理设定对算法的效果至关重要。

2.2 初始解的生成在模拟退火算法中，我们需要随机生成一个初始解，作为搜索的起点。

这个初始解可以是随机生成的，也可以是根据问题本身的特性生成的。

2.3 判定条件模拟退火算法需要一个判定条件来决定是否接受新解。

通常我们使用目标函数值的差异来评估新解的优劣。

如果新解更优，则接受；否则，按照一定概率接受。

2.4 温度更新模拟退火算法中最重要的一步是对温度的更新。

温度越高，接受劣解的概率就越大，随着迭代的进行，温度逐渐降低，最终达到终止温度。

2.5 迭代过程在每次迭代中，我们通过随机生成邻近解，计算其目标函数值，并根据判定条件决定是否接受。

同时，根据温度更新的规则调整温度。

迭代过程中，不断更新当前的最优解。

3. MATLAB实现模拟退火算法在MATLAB中，我们可以通过编写函数或使用内置函数来实现模拟退火算法。

具体的实现方法取决于问题的复杂度和求解的要求。

我们需要确保代码的可读性和可复用性。

4. 示例案例：TSP问题求解为了演示模拟退火算法的实际应用，我们将以旅行商问题（Traveling Salesman Problem，TSP）为例进行求解。

模拟退火算法是一种基于物理中退火过程的优化算法，适用于解决全局优化问题。

以下是一个基本的MATLAB模拟退火算法实现示例：
matlab
function SA()
% 参数设置
T = 1000; % 初始温度
alpha = 0.95; % 降温系数
x = rand(1,10); % 初始解
f = @(x) sum(x.^2 - 10*cos(2*pi*x) + 10); % 目标函数
while T > 1e-5
% 随机生成新解
x_new = x + randn(1,10);
% 计算新解的函数值
f_new = f(x_new);
% 计算接受概率
p = exp(-(f_new - f(x))/T);
% 以概率p接受新解，否则拒绝
if rand() < p
x = x_new;
f = f_new;
end
% 降温
T = T*alpha;
end
% 输出最优解和最优值
fprintf('最优解：%f\n', x);
fprintf('最优值：%f\n', f);
end
这个示例中，我们定义了一个目标函数f，它是一个简单的多峰函数。

我们使用一个随机生成的初始解作为初始解x，然后在一个循环中不断生成新的解，并计算其函数值。

我们根据接受概率决定是否接受新解，如果新解更好，则接受；否则，我们以一定的概率接受新解。

在每次迭代中，我们都会降低温度T，直到达到预设的终止条件。

最后，我们输出最优解和最优值。

如何在Matlab中进行模拟退火算法的优化模拟退火算法是一种用于求解复杂问题的全局优化算法。

在Matlab中，我们可以利用其强大的数值计算和优化工具箱来实现模拟退火算法的优化。

本文将介绍如何在Matlab中进行模拟退火算法的优化，并通过一个实际的案例来演示其应用。

一、模拟退火算法简介模拟退火算法是一种启发式的全局优化算法，模拟了固体物体在退火过程中的特性。

其基本原理是通过模拟固体退火过程，逐渐降低系统能量，从而找到全局最优解。

在模拟退火算法中，由于退火过程中存在较高的温度，使算法有机会跳出局部极小值点，因此能够在搜索空间中全面地寻找最优解。

二、Matlab中的模拟退火算法优化函数Matlab提供了优化工具箱，在其中包含了一系列优化函数，其中包括模拟退火算法。

我们可以使用"simulannealbnd"函数来在Matlab中实现模拟退火算法的优化。

三、案例演示：函数最优化假设我们要求解以下函数的最小值：f(x) = x^2 + sin(5x)我们可以使用Matlab中的模拟退火算法优化函数来找到该函数的全局最小值。

1. 定义目标函数首先，我们需要在Matlab中定义目标函数：function y = myfunc(x)y = x.^2 + sin(5*x);2. 编写优化代码接下来，我们可以编写优化代码，利用"simulannealbnd"函数进行模拟退火算法的优化：options = saoptimset('Display','iter','TolFun',1e-6);[x,fval] = simulannealbnd(@myfunc, [-10,10],[],[],options);在上述代码中，"options"用于设置优化选项，"@myfunc"是要优化的目标函数，[-10,10]为变量的取值范围，[]表示无约束条件。

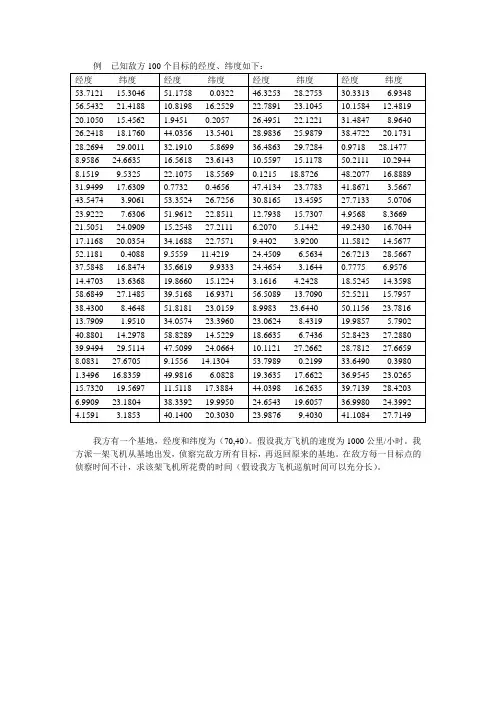
例已知敌方100个目标的经度、纬度如下：我方有一个基地，经度和纬度为（70,40）。

假设我方飞机的速度为1000公里/小时。

我方派一架飞机从基地出发，侦察完敌方所有目标，再返回原来的基地。

在敌方每一目标点的侦察时间不计，求该架飞机所花费的时间（假设我方飞机巡航时间可以充分长）。

这是一个旅行商问题。

我们依次给基地编号为1，敌方目标依次编号为2，3，…，101，最后我方基地再重复编号为102（这样便于程序中计算）。

距离矩阵102102)(⨯=ij d D ，其中ij d 表示表示j i ,两点的距离，102,,2,1, =j i ，这里D 为实对称矩阵。

则问题是求一个从点1出发，走遍所有中间点，到达点102的一个最短路径。

上面问题中给定的是地理坐标（经度和纬度），我们必须求两点间的实际距离。

设B A ,两点的地理坐标分别为),(11y x ，),(22y x ，过B A ,两点的大圆的劣弧长即为两点的实际距离。

以地心为坐标原点O ，以赤道平面为XOY 平面，以0度经线圈所在的平面为XOZ 平面建立三维直角坐标系。

则B A ,两点的直角坐标分别为：)sin ,cos sin ,cos cos (11111y R y x R y x R A )sin ,cos sin ,cos cos (22222y R y x R y x R B 其中6370=R 为地球半径。

B A ,两点的实际距离⎪⎫ ⎛=OBR d OA arccos ， 化简得]sin sin cos cos )(arccos[cos 212121y y y y x x R d +-=。

求解的模拟退火算法描述如下： （1）解空间解空间S 可表为{102,101,,2,1 }的所有固定起点和终点的循环排列集合，即}102,}101,,3,2{),,(,1|),,{(102101211021===ππππππ的循环排列为 S其中每一个循环排列表示侦察100个目标的一个回路，j i =π表示在第i 次侦察j 点，初始解可选为)102,,2,1( ，本文中我们使用Monte Carlo 方法求得一个较好的初始解。

matlab 中的优化算法MATLAB提供了多种优化算法和技术，用于解决各种不同类型的优化问题。

以下是一些在MATLAB中常用的优化算法：1.梯度下降法：梯度下降法是一种迭代方法，用于找到一个函数的局部最小值。

在MATLAB中，可以使用fminunc函数实现无约束问题的梯度下降优化。

2.牛顿法：牛顿法是一种求解无约束非线性优化问题的算法，它利用泰勒级数的前几项来近似函数。

在MATLAB中，可以使用fminunc 函数实现无约束问题的牛顿优化。

3.约束优化：MATLAB提供了多种约束优化算法，如线性规划、二次规划、非线性规划等。

可以使用fmincon函数来实现带约束的优化问题。

4.最小二乘法：最小二乘法是一种数学优化技术，用于找到一组数据的最佳拟合直线或曲线。

在MATLAB中，可以使用polyfit、lsqcurvefit等函数实现最小二乘法。

5.遗传算法：遗传算法是一种模拟自然选择过程的优化算法，用于求解复杂的优化问题。

在MATLAB中，可以使用ga函数实现遗传算法优化。

6.模拟退火算法：模拟退火算法是一种概率搜索算法，用于在可能的解空间中找到全局最优解。

在MATLAB中，可以使用fminsearchbnd函数实现模拟退火算法优化。

7.粒子群优化算法：粒子群优化算法是一种基于群体智能的优化算法，用于求解非线性优化问题。

在MATLAB中，可以使用particleswarm函数实现粒子群优化算法。

以上是MATLAB中常用的一些优化算法和技术。

具体的实现方法和应用可以根据具体问题的不同而有所不同。

Step3：查看已安排路径，发现节点 5 还没有安排车辆，最后第三辆车的路径 为：0-5-0。全部节点安排车辆结束。
通过序贯节约里程法可得三条路径：0-6-3-4-0，0-1-2-0，0-5-0，三条路径的 运行距离分别为：141、138、108，总运行距离为 385。 （2）并行节约里程法
并行节约里程法是指在一次搜索中并行生成全部路径。以上面的算例为例，
第五章 模拟退火算法求解 VRP 问题
讲解标准的车辆路径问题以及节约里程法、模拟退火算法求解 VRP 问题的 Matlab 程序。 Created by Jiannywang@, 20180727
5.1 车辆路径问题（Vehicle Routing Problem,VRP）
车辆路线问题（VRP）最早是由 Dantzig 和 Ramser 于 1959 年首次提出，它 是指一定数量的客户，各自有不同数量的货物需求，配送中心向客户提供货物， 由一个车队负责分送货物，组织适当的行车路线，目标是使得客户的需求得到满 足，并能在一定的约束下，达到诸如路程最短、成本最小、耗费时间最少等目的。
不论哪种合并程序，该算法的前期步骤都是一样的，下面以图 5.1 所示算例
的具体数值来说明。
（1） 给出任意节点对之间的距离，给出所有需求节点的需求量和车辆容量数据；
表 5.1 节点间相互距离
01 2 34 56
0
30 65 67 53 54 28
1
43 72 50 74 53
2
52 27 89 65
车辆容量将多个节点的运输集中到一辆车运输，从而最大程度的节约运输里程，
C-W 算法另一个需要解决的任务就是进行运输任务合并从而实现运输里程的最
大化 节约。
C-W 算法中里程节约的合并过程分为两种：序贯节约里程法和并行节约里程

Matlab技术模拟退火算法随着科学技术的进步和应用领域的扩展，我们对问题的求解和优化的需求也越来越高。

而在这个过程中，模拟退火算法就显得格外重要。

本文将介绍Matlab技术中的模拟退火算法，以及其原理和应用。

一、模拟退火算法简介模拟退火算法（simulated annealing）是一种全局优化算法，它模拟物质从高温状态慢慢冷却至低温状态的过程，通过跳出局部极值，寻找全局最优解。

其基本思路是在搜索空间中随机生成一个解并逐渐改进，以一定的概率接受差解，以避免陷入局部最优解而无法找到全局最优解。

二、模拟退火算法原理模拟退火算法的基本原理源自于固体退火过程。

在固体的退火过程中，随着温度的逐渐下降，原子的运动趋于平稳，达到了最低能量态。

根据固体退火过程的原理，模拟退火算法将其应用在问题的求解过程中。

模拟退火算法主要由三个元素组成：初始温度、降温策略和能量函数。

初始温度决定了搜索空间的范围，温度越高，搜索范围越广。

降温策略决定了温度的降低速度，常见的降温策略有线性降温、指数降温和对数降温等。

能量函数用于评估解的质量，根据问题的性质和目标确定不同的能量函数。

算法的基本流程是：首先，随机生成一个初始解，并将其作为当前解。

随后，通过交换解中的元素、改变解的部分值等操作，产生新的解。

如果新解优于当前解，则接受新解作为当前解；如果新解不优于当前解，则以一定的概率接受差解，以避免陷入局部最优。

重复上述步骤，直到满足终止条件。

三、模拟退火算法在Matlab中的应用Matlab作为一种强大的数学计算工具，提供了丰富的优化算法库。

在Matlab中使用模拟退火算法解决问题，可以通过调用相应的函数实现。

首先，在Matlab中创建一个目标函数，该函数用于评估解的质量。

可以根据不同的问题需求，自定义目标函数。

然后，使用Matlab中的SA函数进行模拟退火算法的实现。

SA函数的参数包括目标函数、初始温度、降温率等。

下面以一个简单的例子来说明模拟退火算法在Matlab中的使用。

else sol_new = sol_current;
end end
用MATLAB实现模拟退火算法
一、0-1背包问题
例：
假设有12件物品，质量分别为2磅、5磅、18磅、3磅、2磅、5磅、 10磅、4磅、11磅、7磅、14磅、6磅，价值分别为5元、10元、13元、 4元、3元、11元、13元、10元、8元、16元、7元、4元，包的最大允 许质量是46磅
tmplist1; %u、v之间的城市移到w后面 end
用MATLAB实现模拟退火算法
一、算法设计步骤
用MATLAB实现模拟退火算法
一、算法设计步骤
% 计算目标函数即内能
E_new = 0; for i = 1 : (amount-1)
E_new = E_new + ... dist_matrix(sol_new(i),sol_new(i+1));
N 结束，输出当
Y
前解
扰动次数
Y
>10000
N
接受新解作为 当前解
N
Y 计算概率与[0,1)随机
数之间的差值
Y
差值大于0
N
扰动：
随机产生 0~1的数
数>0.5
Y
N
二变换法
三变换法
用MATLAB实现模拟退火算法
一、算法设计步骤
用MATLAB实现模拟退火算法
一、算法设计步骤用MBiblioteka TLAB实现模拟退火算法end
%从第一个城市到最后一个城市的距离
E_new = E_new + ... dist_matrix(sol_new(amount),sol_new(1));
用MATLAB实现模拟退火算法

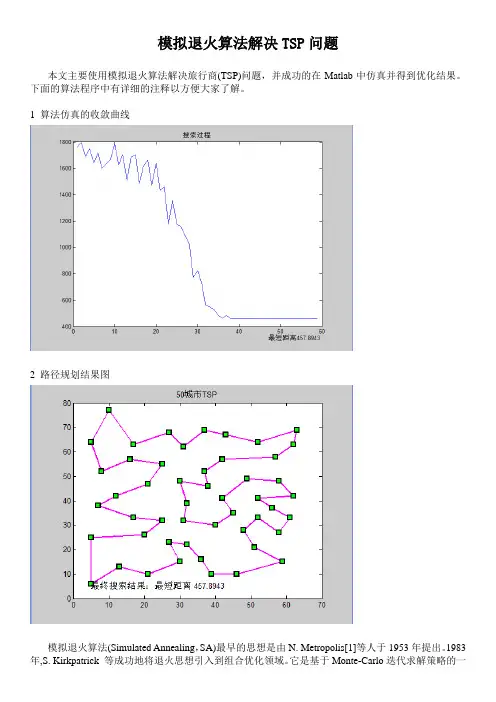
模拟退火算法解决TSP问题本文主要使用模拟退火算法解决旅行商(TSP)问题，并成功的在Matlab中仿真并得到优化结果。

下面的算法程序中有详细的注释以方便大家了解。

1 算法仿真的收敛曲线2 路径规划结果图模拟退火算法(Simulated Annealing，SA)最早的思想是由N. Metropolis[1]等人于1953年提出。

1983 年,S. Kirkpatrick 等成功地将退火思想引入到组合优化领域。

它是基于Monte-Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。

模拟退火算法从某一较高初温出发，伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。

模拟退火算法是一种通用的优化算法，理论上算法具有概率的全局优化性能,目前已在工程中得到了广泛应用，诸如VLSI、生产调度、控制工程、机器学习、神经网络、信号处理等领域。

算法程序：程序分为五部分，下面第一部分是主程序，每个function函数用虚线分开，大家在使用时需要放在不同的.m文件中。

主程序：---------------------------------------------------------------------------------------------------------------------------------- function saclearCityNum=50; %城市个数可分别选30，50，70[dislist,Clist]=tsp(CityNum); %tsp函数中包含城市坐标，dislist是距离矩阵，clist是城市坐标tf=0.01;%最后的温度alpha=0.80;%温度参数L=100*CityNum; %马尔可夫链的长度for i=1:100route=randperm(CityNum);%随机城市序列，即将citynum个城市序列打乱fval0(i)=CalDist(dislist,route);%城市距离之和最优endt0=-(max(fval0)-min(fval0))/log(0.9);%初始温度fval=fval0(100);route_best=route;%最优城市序列fval_best=fval;%城市距离之和最优t=t0;ii=0;%% 搜索开始while t>tf %tf最终温度是while循环的结束条件for i=1:L[fval_after,route_after]=exchange(route,dislist);if fval_after<fvalroute=route_after;fval=fval_after;elseif exp((fval-fval_after)/t)>randroute=route_after;fval=fval_after;endendii=ii+1;drawTSP(Clist,route,fval,ii,0);%作图程序if fval<fval_bestroute_best=route;fval_best=fval;endt=alpha*t;fval_sequence(ii)=fval;enddrawTSP(Clist,route_best,fval_best,ii,1);%作图程序figure(2);plot(1:ii,fval_sequence);%plot the convergence figuretitle('搜索过程');string1=['最短距离',num2str(fval_best)];gtext(string1);end----------------------------------------------------------------------------------------------------------------------------------function [DLn,cityn]=tsp(n)%坐标函数，可根据自己需要修改if n==10city10=[0.4 0.4439;0.2439 0.1463;0.1707 0.2293;0.2293 0.761;0.5171 0.9414;0.8732 0.6536;0.6878 0.5219;0.8488 0.3609;0.6683 0.2536;0.6195 0.2634];%10 cities d'=2.691for i=1:10for j=1:10DL10(i,j)=((city10(i,1)-city10(j,1))^2+(city10(i,2)-city10(j,2))^2)^0.5;endendDLn=DL10;cityn=city10;endif n==30city30=[41 94;37 84;54 67;25 62;7 64;2 99;68 58;71 44;54 62;83 69;64 60;18 54;22 60;83 46;91 38;25 38;24 42;58 69;71 71;74 78;87 76;18 40;13 40;82 7;62 32;58 35;45 21;41 26;44 35;4 50];%30 cities d'=423.741 by D B Fogelfor i=1:30for j=1:30DL30(i,j)=((city30(i,1)-city30(j,1))^2+(city30(i,2)-city30(j,2))^2)^0.5;endendDLn=DL30;cityn=city30;endif n==50city50=[31 32;32 39;40 30;37 69;27 68;37 52;38 46;31 62;30 48;21 47;25 55;16 57;17 63;42 41;17 33;25 32;5 64;8 52;12 42;7 38;5 25; 10 77;45 35;42 57;32 22;27 23;56 37;52 41;49 49;58 48;57 58;39 10;46 10;59 15;51 21;48 28;52 33;58 27;61 33;62 63;20 26;5 6;13 13;21 10;30 15;36 16;62 42;63 69;52 64;43 67];%50 cities d'=427.855 by D B Fogelfor i=1:50for j=1:50DL50(i,j)=((city50(i,1)-city50(j,1))^2+(city50(i,2)-city50(j,2))^2)^0.5; DL50(i,j)=((city50(i,1)-city50(j,1))^2+(city50(i,2)-city50(j,2))^2)^0.5;endendDLn=DL50;cityn=city50;endif n==75city75=[48 21;52 26;55 50;50 50;41 46;51 42;55 45;38 33;33 34;45 35;40 37;50 30;55 34;54 38;26 13;15 5;21 48;29 39;33 44;15 19;16 19;12 17;50 40;22 53;21 36;20 30;26 29;40 20;36 26;62 48;67 41;62 35;65 27;62 24;55 20;35 51;30 50;45 42;21 45;36 6;6 25;11 28;26 59;30 60;22 22;27 24;30 20;35 16;54 10;50 15;44 13;35 60;40 60;40 66;31 76;47 66;50 70;57 72;55 65;2 38;7 43;9 56;15 56;10 70;17 64;55 57;62 57;70 64;64 4;59 5;50 4;60 15;66 14;66 8;43 26];%75 cities d'=549.18 by D B Fogelfor i=1:75for j=1:75DL75(i,j)=((city75(i,1)-city75(j,1))^2+(city75(i,2)-city75(j,2))^2)^0.5; DL75(i,j)=((city75(i,1)-city75(j,1))^2+(city75(i,2)-city75(j,2))^2)^0.5;endendDLn=DL75;cityn=city75;end----------------------------------------------------------------------------------------------------------------------------------function F=CalDist(dislist,s)DistanV=0;n=size(s,2);for i=1:(n-1)DistanV=DistanV+dislist(s(i),s(i+1));endDistanV=DistanV+dislist(s(n),s(1));F=DistanV;-----------------------------------------------------------------------------------function [fval_after,route_after]=exchange(route,d)n=length(d);location1=ceil(n*rand);location2=location1;while location2==location1location2=ceil(n*rand);%the location of two exchanged numberendloc1=min(location1,location2);loc2=max(location1,location2);middle_route=fliplr(route(loc1:loc2));%the part route which has been exchangedroute_after=[route(1:loc1-1) middle_route route(loc2+1:n)];%the after traveling route fval_after=CalDist(d,route_after);end----------------------------------------------------------------------------------function m=drawTSP(Clist,BSF,bsf,p,f)CityNum=size(Clist,1);for i=1:CityNum-1plot([Clist(BSF(i),1),Clist(BSF(i+1),1)],[Clist(BSF(i),2),Clist(BSF(i+1),2)],'ms-', 'LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g');hold on;endplot([Clist(BSF(CityNum),1),Clist(BSF(1),1)],[Clist(BSF(CityNum),2),Clist(BSF(1),2) ],'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g');title([num2str(CityNum),'城市TSP']);if f==0text(5,5,['第 ',int2str(p),' 步',' 最短距离为 ',num2str(bsf)]);elsetext(5,5,['最终搜索结果：最短距离 ',num2str(bsf)]);endhold off;pause(0.05);----------------------------------------------------------------------------------- 结束。

matlab 退火算法退火算法是一种优化算法，常用于求解复杂的优化问题。

它模拟了金属退火的过程，通过不断降低温度来达到减小能量的目标。

退火算法的原理比较简单，但是在实际应用中却能取得很好的效果。

退火算法的基本思想是通过在解空间中搜索，找到能量函数的全局最小值或局部最小值。

这个过程类似于金属被加热后冷却的过程，初始温度很高，然后慢慢降低温度。

在降温的过程中，系统会在解空间中随机选择一个解，并计算其能量值。

如果新的解的能量值比当前解的能量值更小，那么新的解就会被接受。

如果新的解的能量值比当前解的能量值更大，那么新的解有一定的概率被接受。

这个概率与新旧解之间的能量差和当前温度有关。

这样，系统就有了跳出局部最优解的可能性。

退火算法的关键参数包括初始温度、降温速度和停止温度。

初始温度决定了系统开始时的搜索范围，降温速度决定了搜索过程的快慢，停止温度决定了搜索的终止条件。

在实际应用中，选择合适的参数非常重要，不同的参数组合可能导致不同的结果。

退火算法在很多领域都有应用，比如组合优化问题、机器学习和人工智能等。

在组合优化问题中，退火算法可以用来求解旅行商问题、背包问题等。

在机器学习和人工智能领域，退火算法可以用来求解神经网络的权重和阈值。

退火算法的优点是可以避免陷入局部最优解，从而有可能找到全局最优解。

它还可以通过调整参数来控制搜索的速度和精度，具有很强的灵活性。

但是退火算法也存在一些缺点，比如需要事先确定好参数，对问题的建模要求较高。

此外，退火算法的搜索过程是随机的，所以每次运行的结果可能不一样。

总的来说，退火算法是一种强大的优化算法，可以应用于各种复杂的优化问题。

它通过模拟金属退火的过程，不断降低温度来搜索最优解。

退火算法的优势在于能够避免局部最优解，并且具有很强的灵活性。

然而，退火算法也有一些限制，比如需要事先确定好参数，对问题的建模要求较高。

在实际应用中，我们需要根据具体问题的特点和要求，选择合适的退火算法来求解优化问题。

%matlab 程序实现模拟退火算法程序函数求极值（引用后修改，感谢ARMYLAU）%使用模拟退火法求函数f(x,y) = 3*cos(xy) + x + y2的最小值%解：根据题意，我们设计冷却表进度表为：%即初始温度为30%衰减参数为0.95%马可夫链长度为10000%Metropolis的步长为0.02%结束条件为根据上一个最优解与最新的一个最优解的之差小于某个容差。

%使用METROPOLIS接受准则进行模拟, 程序如下%* 日期:2012－11-29%* 作者:steven%*EMAIL:hxs2004@%* 结束条件为两次最优解之差小于某小量function [BestX,BestY]=SimulateAnnealing1clear;clc;%// 要求最优值的目标函数,搜索的最大区间XMAX= 4;YMAX = 4;%冷却表参数MarkovLength = 10000; %// 马可夫链长度DecayScale = 0.95; %// 衰减参数StepFactor = 0.02; %// 步长因子Temperature=30; %// 初始温度Tolerance = 1e-8; %// 容差AcceptPoints = 0.0; %// Metropolis过程中总接受点rnd =rand;% 随机选点初值设定PreX = -XMAX * rand ;PreY = -YMAX * rand;PreBestX = PreX;PreBestY = PreY;PreX = -XMAX * rand ;PreY = -YMAX * rand;BestX = PreX;BestY = PreY;% 每迭代一次退火一次(降温), 直到满足迭代条件为止mm=abs( ObjectFunction( BestX,BestY)-ObjectFunction (PreBestX, PreBestY));while mm > ToleranceTemperature=DecayScale*Temperature;AcceptPoints = 0.0;% 在当前温度T下迭代loop(即MARKOV链长度)次for i=0:MarkovLength:1% 1) 在此点附近随机选下一点p=0;while p==0NextX = PreX + StepFactor*XMAX*(rand-0.5);NextY = PreY + StepFactor*YMAX*(rand-0.5);if p== (~(NextX >= -XMAX && NextX <= XMAX && NextY >= -YMAX && NextY <= YMAX))p=1;endend% 2) 是否全局最优解if (ObjectFunction(BestX,BestY) > ObjectFunction(NextX,NextY))% 保留上一个最优解PreBestX =BestX;PreBestY = BestY;% 此为新的最优解BestX=NextX;BestY=NextY;end% 3) Metropolis过程if( ObjectFunction(PreX,PreY) - ObjectFunction(NextX,NextY) > 0 )%// 接受, 此处lastPoint即下一个迭代的点以新接受的点开始PreX=NextX;PreY=NextY;AcceptPoints=AcceptPoints+1;elsechanger = -1 * ( ObjectFunction(NextX,NextY) - ObjectFunction(PreX,PreY) ) / Temperature ; rnd=rand;p1=exp(changer);double (p1);if p1 > rand %// 不接受, 保存原解PreX=NextX;PreY=NextY;AcceptPoints=AcceptPoints+1;endendendmm=abs( ObjectFunction( BestX,BestY)-ObjectFunction (PreBestX, PreBestY));enddisp('最小值在点:');BestXBestYdisp( '最小值为:{0}');ObjectFunction(BestX, BestY)end****************************************************子函数，目标函数值计算function value=ObjectFunction(x,y)value=3*cos(x*y)+x+y*y;end%使用模拟退火法求函数f(x,y)=sin(x*y)+x^2+y^2的最小值format longXMAX=4; %搜索的最大区间YMAX=4; %搜索的最大区间MarkovLength=10000; %马可夫链长度DecayScale=0.95; %衰减参数0.95StepFactor=0.02; %步长因子Temperature=100; %初始温度Tolerance=1e-8; %容差AcceptPoints=0.0; %Metropolis过程中总接受点PreX=-XMAX*rand; %初始的搜索值PreY=-YMAX*rand; %初始的搜索值PreBestX=PreX; %上一个最优解PreBestY=PreY; %上一个最优解BestX=PreX; %最终解BestY=PreY; %最终解while(1)Temperature=Temperature*DecayScale; %每迭代一次退火一次（降温），直到满足迭代条件为止AcceptPoints=0.0;%在当前温度下迭代（即MARKOV链长度）次for i=0:1:MarkovLengthwhile(1)NextX=PreX+StepFactor*XMAX*(rand-0.5); %在初始点附近随机选下一点NextY=PreY+StepFactor*YMAX*(rand-0.5); %在初始点附近随机选下一点%判断新产生的点是否在规定的最大搜索区间内，若在，则退出循环，不在，继续循环，直到新产生的点在规定的最大搜索区间内if((NextX>=-XMAX && NextX<=XMAX && NextY>=-YMAX &&NextY<=YMAX))break %退出循环endend%判断新产生点与原来最优点哪个更优if(minfunction(BestX,BestY)>minfunction(NextX,NextY))PreBestX=BestX; %保留上一个最优解PreBestY=BestY;BestX=NextX; %新的最优解BestY=NextY;end%接受新产生的点为下一迭代的开始点if(minfunction(PreX,PreY)-minfunction(NextX,NextY)>0)PreX=NextX;PreY=NextY;AcceptPoints=AcceptPoints+1;elsechange=-1*(minfunction(NextX,NextY)-minfunction(PreX,PreY))/Temperature;%不接受，保存原解if(exp(change)>rand)PreX=NextX;PreY=NextY;AcceptPoints=AcceptPoints+1;endendend%结束条件为根据上一个最优解与最新的一个最优解的之差小于某个容差if(~(abs(minfunction(BestX,BestY)-minfunction(PreBestX,PreBestY))>Tolerance)) breakendenda=BestXb=BestYc=minfunction(BestX,BestY)%%%%%%%%%%%%%子程序%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function minf=minfunction(x,y)minf=sin(x*y)+x*x+y*y;%求目标函数的值。

matlab退火算法一、概述退火算法（Simulated Annealing，SA）是一种全局优化算法，它模拟固体物质从高温状态冷却到低温状态的过程。

SA算法最初由Kirkpatrick等人于1983年提出，它是一种启发式算法，可以在搜索空间中寻找全局最优解或近似最优解。

Matlab作为一个强大的数学软件，在优化问题中也有着广泛的应用。

Matlab提供了丰富的工具箱和函数库，其中就包括了SA算法的实现。

本文将从以下几个方面介绍Matlab中的SA算法：原理、实现步骤、函数调用、参数设置和应用实例。

二、原理SA算法是一种基于概率的全局优化算法。

其基本思想是通过模拟物理退火过程，在搜索空间中随机跳跃，并接受劣解以避免陷入局部最优解。

在退火过程中，系统处于一个高温状态时可以接受较差的解，并以较大概率向这些较差解移动。

随着温度逐渐降低，系统逐渐趋向稳定状态，并对较差解的接受率逐渐降低。

当系统达到低温状态时，只接受更优的解，以避免陷入局部最优解。

三、实现步骤SA算法的实现步骤如下：1. 初始化参数。

包括初始温度、终止温度、初始解等。

2. 计算初始解的能量。

3. 进入循环。

在每个循环中，按照一定概率选择一个邻域解，并计算其能量。

4. 判断是否接受邻域解。

如果邻域解更优，则接受该解；否则以一定概率接受该劣解，概率与当前温度和能量差有关。

5. 降低温度。

在每个循环中降低温度，并更新参数。

6. 判断是否满足终止条件。

如果满足，则结束循环；否则返回第3步继续搜索。

四、函数调用Matlab中提供了simulannealbnd函数来实现SA算法。

该函数的调用格式为：[x,fval,exitflag,output] = simulannealbnd(fun,x0,lb,ub,options)其中，fun是目标函数，x0是初始点，lb和ub是变量的上下界限制，options是一个结构体变量，可以设置SA算法的参数和选项。

五、参数设置在使用simulannealbnd函数时，可以通过options结构体来设置SA 算法的参数和选项。

matlab模拟退火算法以matlab模拟退火算法为标题，写一篇文章。

1. 引言模拟退火算法是一种全局优化算法，通过模拟金属退火过程中的晶格结构变化，来搜索问题的最优解。

它广泛应用于组合优化、图论、机器学习等领域。

本篇文章将介绍如何使用matlab实现模拟退火算法，并通过一个简单的例子来演示其应用。

2. 模拟退火算法原理模拟退火算法的核心思想是通过接受较差的解来避免局部最优解，并逐渐降低温度以减小接受较差解的概率。

其基本步骤如下：- 初始化温度和初始解- 在当前温度下，对当前解进行小范围的扰动得到新解- 比较新解与当前解的目标函数值，根据一定的概率选择是否接受新解- 降低温度，重复上述步骤，直到满足停止准则3. matlab实现模拟退火算法在matlab中，我们可以使用内置函数simulannealbnd来实现模拟退火算法。

该函数需要定义目标函数、搜索范围和停止准则等参数。

我们定义一个简单的目标函数，例如求解二元函数f(x,y) = x^2 +y^2的最小值。

我们可以使用matlab的匿名函数来定义目标函数。

```matlabf = @(x) x(1)^2 + x(2)^2;```然后，定义搜索范围，例如x和y的取值范围为[-10, 10]。

```matlablb = [-10, -10];ub = [10, 10];```接着，设置模拟退火算法的参数，包括初始温度、终止温度、退火速率等。

```matlaboptions = optimoptions('simulannealbnd');options.InitialTemperature = 100;options.FunctionT olerance = 1e-6;options.TemperatureFcn = @temperatureexp;options.AnnealingFcn = @annealingboltz;```调用simulannealbnd函数来运行模拟退火算法，并返回最优解和目标函数值。

matlab模拟退火算法工具箱原理概述及解释说明1. 引言1.1 概述模拟退火算法是一种元启发式算法，用于在优化问题中寻找全局最优解。

该算法受到自然界中固体物体冷却过程的启发，通过随机搜索和接受次优解的方式，在搜索空间中逐渐降低温度来达到寻找最优解的目标。

Matlab模拟退火算法工具箱是一个集成了多种模拟退火算法的算法库，旨在帮助研究者和工程师解决各种优化问题。

本文将对Matlab模拟退火算法工具箱进行原理概述，并详细解释其功能和使用方法，以及应用场景和技巧。

1.2 文章结构本文将分为五个部分进行阐述。

首先是引言部分，介绍文章的背景和整体结构。

其次是Matlab模拟退火算法工具箱原理部分，包括对模拟退火算法概述、算法原理解析以及工具箱功能的介绍。

第三部分是Matlab模拟退火算法工具箱的应用场景，包括解决优化问题、参数调优与搜索空间探索等方面。

接着是Matlab 模拟退火算法工具箱的使用方法与技巧，详细说明安装与设置环境、建立模型与参数设定以及运行与结果分析等方面。

最后是结论与展望部分，对全文进行总结并展望未来的研究方向。

1.3 目的本文旨在向读者全面介绍Matlab模拟退火算法工具箱的原理和功能，使其能够理解和应用该工具箱来解决各类优化问题。

通过对应用场景的举例和使用方法与技巧的详细说明，希望读者能够掌握该工具箱的使用，并在实际问题中提取更准确、更高效的优化解。

最后，为了推进该领域的研究，还将提出一些可能的研究方向和展望。

2. Matlab模拟退火算法工具箱原理2.1 模拟退火算法概述模拟退火算法（Simulated Annealing）是一种基于统计物理学中固体退火原理的全局优化算法。

它模拟金属在高温下冷却过程中的晶格结构演变，通过随机搜索和接受恶化解以避免陷入局部最优解，并最终找到全局最优解。

2.2 算法原理解析模拟退火算法的主要原理是通过引入一个控制参数“温度”来控制搜索过程。

在初始阶段，温度较高，搜索范围较广，能够灵活地跳出局部最优解。

matlab simulated_annealing 函数的使用在 MATLAB 中，simulated_annealing 函数是用于模拟退火算法的优化函数。

它可以帮助我们寻找一个函数的全局最小值（或最大值），即找到使目标函数取值最小（或最大）的参数。

下面是使用 simulated_annealing 函数的一般步骤：1. 定义目标函数。

首先，需要定义需要进行优化的目标函数。

这个函数可以是任意 MATLAB 函数，只要它接受参数并返回一个标量值。

2. 设置算法参数。

使用 optimoptions 函数来创建一个 options对象，用于设置模拟退火算法的参数。

例如，可以设置初始温度、退火率、最大迭代次数等。

3. 调用 simulated_annealing 函数。

使用 simulated_annealing 函数来运行模拟退火算法。

需要传递目标函数和 options 对象作为参数。

下面是一个简单的示例，说明如何使用 simulated_annealing 函数：```matlab% 定义目标函数objective = @(x) x(1)^2 + x(2)^2;% 创建 options 对象options = optimoptions('simulannealbnd', 'MaxIterations', 1000);% 调用 simulated_annealing 函数x0 = [1, 1]; % 初始参数值[xmin, fmin] = simulated_annealing(objective, x0, [], [], options);```在这个示例中，目标函数是简单的二次函数（x1^2 + x2^2），我们的目标是找到使其最小化的参数值。

options 对象中设置了最大迭代次数为 1000。

初始参数值 x0 设置为 [1, 1]，即优化过程的起点。

运行 simulated_annealing 函数后，返回最优参数值 xmin 和最小目标函数值 fmin。