当前位置：文档之家 › 传热学(4)-数值解法概要

传热学(4)-数值解法概要

  • 格式：ppt
  • 大小：1.40 MB
  • 文档页数：50

下载文档原格式

  / 50

合集下载

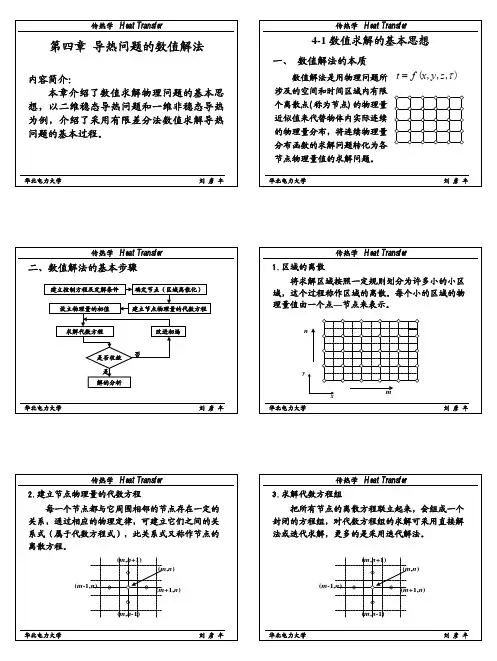
传热学-第四章

传热学-第四章

其中aij、bi为常数，且aij0。改写为显函数形式：
假设
an1t1 an2t2 anjt j anntn bn
t ,, t t ,, t t ,, t
k 1
0 1 1 1 2 1
t ,, t

0 n 1 n 2 n k n
1 t1 b1 a12t2 a1 j t j a1ntn a11 1 t2 b2 a21t1 a2 j t j a2 ntn a22 1 tn bn an1t1 anj t j an ( n 1)tn 1 ann k k 1 max ti ti
13
（1）内部节点温度差分方程 内部节点 n所代表的控制容积在 i 时刻的热平衡： dU 如果节点n的温度对时间的变化率 采用向前差分，热平衡方程式可写成
A
t
i n 1
t t t t t A Ax c x x
i n i n 1 i n
1
（ 3 ） 求解域离散化：用与坐标轴平行的网络线将 所涉及的空间和时间区域划分成有限个子区域，将网 络线的交点作为节点 , 每个节点就代表以它为中心的 子区域（元体或称为控制容积），节点温度就代表子 区域的温度； （4）建立节点温度代数方程组； （ 5 ） 求解节点温度代数方程组，得到所有节点的 温度值； （ 6 ） 对计算结果进行分析，若不符合实际情况， 则修正上述步骤，重复进行计算，直到满意为止。 目前常用的数值解法主要有：有限差分法、有限 元法、边界元法等。其中有限差分法比较成熟，应用 广泛。下面主要介绍有限差分法的基本原理。
3. 节点温度差分方程组的求解方法
线性代数方程组的求解方法有消元法、矩阵求逆 法、迭代法等，这里仅简单介绍在导热的数值计算中 常用的迭代法中的两种： (1) 简单迭代法 (2) 高斯-塞德尔迭代法

传热学的数值解法

传热学的数值解法

导热问题的数值求解方法数值解法的基本思想是用空间和时间区域内有限个离散点（称为节点）上温度的近似值，代替物体内实际的连续温度分布，然后由导热方程和边界条件推导出各节点温度间的相互关系的代数方程组（称为离散方程），求解此方程组，得到节点上的温度值，此即物体中温度场的解。

只要节点分布的足够稠密，数值解就有足够的精度。

求解导热问题的数值方法有有限差分法及有限元法，近几年又发展了边界元法和有限分析法。

数值方法适用于求解各种导热问题，不管物体的几何形状有多复杂，不管线性或非线性问题，都能使用。

由于计算机的飞速发展，计算技术软件发展也很快，数值方法的的地位越来越重要。

1 数值求解的基本思路及稳态导热内节点离散方程的建立一、 解法的基本思路1、基本思路：数值解法的求解过程可用框图4-1表示。

由此可见：1）物理模型简化成数学模型是基础；2）建立节点离散方程是关键；3）一般情况微分方程中，某一变量在某一坐标方向所需边界条件的个数等于该变量在该坐标方向最高阶导数的阶数。

二、稳态导热中位于计算区域内部的节点离散方程的建立方法1、基本方法方法：①泰勒级数展开法；②热平衡法。

1）泰勒级数展开法如图4-3所示，以节点(m,n)处的二阶偏导数为例，对节点(m+1,n)及(m-1,n)分别写出函数t 对(m,n)点的泰勒级数展开式：对(m+1,n)：+∂∂∆+∂∂∆+∂∂∆+∂∂∆+=+444333,222,,,12462x t x x t x x t x x t x t t n m n m n m n m （a ）对（m-1,n ）：+∂∂∆+∂∂∆-∂∂∆+∂∂∆-=-444333,222,,,12462x t x x t x x t x x t xt t n m n m n m n m （b ）（a ）+（b ）得： +∂∂∆+∂∂∆+=+-+444,222,,1,1122x t x x t x t t t n m n m n m n m 变形为n m x t,22∂∂的表示式得：n m x t,22∂∂)(0222,1,,1x x t t t nm n m n m ∆+∆+-=-+ 上式是用三个离散点上的值计算二阶导数n m x t ,22∂∂的严格表达式，其中：)(02x ∆―― 称截断误差，误差量级为2x ∆在数值计算时，用三个相邻节点上的值近似表示二阶导数的表达式即可，则相应的略去)(02x ∆。

第21次课-数值解法概述

第21次课-数值解法概述

传热学数值方法概述非常不幸的是：虽然我们能从数学给出描述流动及传热问题的一般的微分方程，但却不能一般地给出它的解。

这就是造成我们理论和实践脱节的根本原因，也正因为如此，才导致我们在流体力学、传热学中所针对的研究对象常常是理想的或简单问题。

因为只有引入理想流体或简单问题这样一些假定，可以使上述复杂的方程得到大大的简化，以致于我们在数学上能构求解它们。

一、传热数值计算概述 1、通用偏微分方程 基于质量守恒、动量守恒和能量守恒以及过程变量连续性假说的一组相互耦合的偏微分方程组可以写成如下通式：ϕϕϕϕρτρϕS x x x u jj i i +∂∂Γ∂∂=∂∂+∂∂)(，（s Y T u u u ,,,,,1321=ϕ）我们可以说这样一组基于质量、动量和能量守恒的基本方程，在配以适当的边界条件即可适合于任何流动及传热问题。

但是接下来的问题是，也是最为关键的问题是我们如何求解这组相互耦合的强非线性偏微分方程组。

即如何由这样一组方程获得它的解：),,,(321x x x τϕϕ=在编制计算程序时，我们只需要写出一个求解方程的通用程序，对不同意义的φ就可以重复使用这个Γ上述通用微分方程中的四项分别是不稳态项、对流项、扩散项以及源项。

因变量可以代表各种不同的物理量，如化学组外的质量分量、焓或温度、速度分量、湍流功能或湍流的长度尺度。

与此相应，对于这些变量中的每一个都必须给相对应的扩散系数Γ以及源项S 赋以适当的意义。

2、单向与双向的坐标所谓双向坐标就是指如果在一个坐标上的一个给定位置处的条件，受该位置两侧条件变化影响的坐标。

而如果在一个坐标上的一个给定位置处的条件，只受该位置一侧条件变化的影响，这样的坐标就是单向坐标。

通常，空间坐标是双向坐标，时间坐标则是单向坐标。

但空间坐标有时也可以作为单向坐标。

对流是一种单向过程，而扩散则具有双向效应。

当流量很大时，对流作用远远大于扩散作用，因而空间坐标就近于单向坐标了。

传热学4-导热数值解法基础2013

传热学4-导热数值解法基础2013
第四章 导热数值解法基础
求解导热问题的三种基本方法
方法：理论分析法、数值计算法、实验法
三种方法的基本求解过程

理论分析方法：在理论分析的基础上，直接 对导热微分方程在给定的定解条件下进行积 分，这样获得的解称之为分析解，或理论解
数值计算法
把原来在时间和空间连续的物理量的场，用
有限个离散点上的值的集合来代替，通过求
N (i,j+1)
y y W (i-1,j) (i, j) (i+1,j) E
P
(i,j-1) S x x
y
o
x
ti 1, j ti 1, j ti , j ti 1, j ti 1, j ti , j t 2x x x x i , j
qw
x y
2x x 2
y x
4ti, j 2ti 1, j ti, j 1 tm,n 1

qw qvi, j

(2) 外部角点
qw
y ti 1, j ti, j x ti, j 1 ti, j 2 x 2 y y x x y qw qw qvi, j 0 2 2 2 2
区域离散的概念：
控制容积、网格线、节点、界面线、步长
N
网格线
控制体
节点(i,j)
j
二维矩形域内 稳态无内热源， 常物性导热问 题. 对研究区域进 行离散。 △x,△y,△τ 为空间和时间 步长。
y
y M
x
x
i
网格划分
节点: 网格线交点. 控制容积: 节点代表的区 域 ,其边界位于两点之间. 界面: 控制容积的边界. 网格划分方法: A: 先确定节点，后定界面；

传热学—第4章 热传导问题的数值解法

传热学—第4章 热传导问题的数值解法
(k ) t max
⎧a11t1 + a12 t2 + a13t3 = b1 ⎪ ⎨a21t1 + a22 t2 + a23t3 = b2 ⎪a t + a t + a t = b 33 3 3 ⎩ 31 1 32 2
假定初场
⎧ (1) ⎪t1 = ⎪ ⎪ Jacobi ⎨t(1) = 2 ⎪ ⎪ (1) ⎪t3 = ⎩
4.1.1 4 1 1 基本思想 把原来在时间、空间坐标系中连续的物理量的场， 用有限个离散点上的值的集合来代替，通过求解按 定方 建 起来 关 值 代数方程 来获 一定方法建立起来的关于这些值的代数方程，来获 得离散点上被求物理量的值。 这些离散点上被求物理量值的集合称为该物理量 的数值解。
4.1.1 基本思想
λ Δy
Δx = Δy 时： tm −1,n
+ tm+1,n + tm,n+1 + tm,n−1 − 4tm,n = 0
tm ,n
1 = ( tm−1,n + tm+1,n + tm,n+1 + tm ,n−1 ) 4
与Taylor级数法相比，热平衡法物理意义明显。
4.3.1 边界节点离散方程的建立
4-2 内部节点离散方程的建立
4.2.1 4 2 1 Taylor级数展开法
4-2 内部节点离散方程的建立 内部节点离散方程的建
∂ 2t ∂x 2
=
m ,n
tm+1 n − 2tm ,n + tm −1 n 1, 1, Δx 2
控制方程
∂ 2t ∂ 2t + =0 ∂x 2 ∂y 2
∂ 2t ∂y 2

传热学课件第四章 导热问题数值解法基础

传热学课件第四章 导热问题数值解法基础

i , j
t x

t i 1 , j t i , j x
0 x
2.一阶导级的向后差分表达式：舍去<2>式△x2后各项，则有：
i , j
t x

t i , j t i 1 , j x
0 x
第一节 建立离散方程的方法
二、泰勒级数展开法（有限差分法）
k 2 k 1
对 流 h t f t1 A
k k


显式
△x
C.内能增量△u：
u c
x 2
A t1
k

k 1
t1 /
k

△x/2
k hx
据热平衡A+B=C并整理得：
k f
t 2 t1
k

t
t1
k

1 2

c

x
2
t1

k 1
LP
△y
t i 1 , j t i , j x
t i , j 1 t i , j y

y 2
x 2
1
BP

1
x 2
y 2
EP h t f t i , j
△x
1
FP h t f t i , j
t x
t
2
2
x i , j 2!
2

t x
3
x i , j 3!
3
3.一阶导级的中心差分表达式：<1>-<2>式且忽略后项，则有：
i , j
t x

传热学(4)-数值解法


w y
tm1,n tm,n x
同理：通过界面 e,n,s 传导给节点 （ m,n ）的热流量也可求得
t m 1, n t m, n e y x t m, n 1 t m, n s x y
n x
t m, n 1 t m, n y
（3）边界元法
边界元法是在有限元法之后发展起来的一种较精确有效的工程数值分析方法 。 又称边界积分方程-边界元法。它以定义在边界上的边界积分方程为控制方程， 通过对边界分元插值离散，化为代数方程组求解。它与基于偏微分方程的区域 解法相比，由于降低了问题的维数，而显著降低了自由度数，边界的离散也比 区域的离散方便得多，可用较简单的单元准确地模拟边界形状，最终得到阶数 较低的线性代数方程组。
（2）有限元法
有限元方法的基础是变分原理和加权余量法，其基本求解思想是把计算域划分 为有限个互不重叠的单元，在每个单元内，选择一些合适的节点作为求解函数 的插值点，将微分方程中的变量改写成由各变量或其导数的节点值与所选用的 插值函数组成的线性表达式 ，借助于变分原理或加权余量法，将微分方程离 散求解。
对单元体 (m,n). 根据能量守恒定律可知：
e w n s 0
其中，规定：导入元体（ m,n ）的热流量为 正；导出元体（ m,n ）的热流量为负。
说明： ① 上述分析与推导是在笛卡儿坐标系中进 行的； ② 热平衡法概念清晰，过程简捷； ③ 热平衡法与建立微分方程的思路与过程 一致，但不同的是前者是有限大小的单元体， 后者是微元体。
表示未明确写出的 级数余项中的Δ X 的最低阶数为2
根据导热问题的控制方程 ( 导热微1,n 2tm,n tm1,n tm,n1 2tm,n tm,n1 0 2 2 x y

传热学第四章


k及k+1表示迭代次数；
t
(k) max
—第k次迭代得到的最大值
华北电力大学
刘彦丰
传热学 Heat Transfer
4-3 一维非稳态导热问题的数值求解
在非稳态导热问题中，不但需要对空间区域进 行离散，还需要对时间变量进行离散，接下来以一 个一维非稳态导热问题为例，重点介绍对非稳态项 的离散方法，以及不同离散方法对计算带来的影响 等。
n
y
m
x
华北电力大学
刘彦丰
传热学 Heat Transfer 2.建立节点物理量的代数方程
每一个节点都与它周围相邻的节点存在一定的 关系，通过相应的物理定律，可建立它们之间的关 系式（属于代数方程式），此关系式又称作节点的 离散方程。
(m,n+1)
(m,n)
(m-1,n)
(m+1,n)
华北电力大学
(m,n-1)
h,tf
0 q=0 H x
华北电力大学
刘彦丰
传热学 Heat Transfer
二、数学描述
华北电力大学
∂2t ∂x 2
+
∂2t ∂y 2
+
Φ& λ
=
0
x=0 x=H y=0
−
∂t ∂x
=
0
−
λ
∂t ∂x
=
h(t
−tf
)
−
∂t ∂y
=
0
y =W
−
λ
∂t ∂y
=
h(t
−tf
)
刘彦丰
传热学 Heat Transfer
tm,n+1 −tm,n ∆y
(m,n+1)

传热学课件：第四章 数值解法


（2）高斯—赛德尔迭代法
①选初值；
②一次次的直接计算t1，t2，…，tn ，注意计算tn 时， tn前面的温度全部用新值代替。如知道t1后， 求t2时，用t1代替原设的初值。
例题：有一正方形截面，边界长为1m，边 界上的温度已知，求t1，t2，t3，t4。
解（1）列节点方程式
100℃
500℃
12
3 4 100℃
100℃
迭代法
n
t1
t2
t3
t4
0
300
300
200
200
1
275 268.75 168.75 159.38
2 259.38 254.69 154.69 152.35
3 252.35 251.26 151.18 150.61
4 250.61 250.31 150.31 150.15
由(a)可得：
cw 1 说明热源与管子中心不重合。
由(a)、(b)可得：
将(c)代入(b)可得：
从而只能选正号，所以有： 等温线为一圆。
2 具有偏心空腔的圆柱体
由于是稳定导热，从而流过每一等温面的热流量是 相同的
对于等温面 1
y0
h2 h1
ε
对于等温面 2
热阻： 但h1和h2是未知的
2. 间接法（迭代法）经过有限次的迭代，求出近似解， 对于计算机来说，存储量较少。
松弛法（余数调节法）
高斯—赛德尔迭代法
（1）松弛法 ①设初值； ②求R1，R2，…，Rn，找Rmax；(余数) ③如设R4为最大，改变t4，使R4 ≈0，t4=t4+R4/4： ④重新计算有关节点的余数；
⑤重复步骤③ ④ ，直到全部余数为零。

传热学-第四章-热传导问题的数值解法


23
判断迭代是否收敛的准则：
迭代次数，表示第k次迭代
Monday, March 30, 2020
表示第k次迭代所得计算域内的最大值 当有温度t接近于零的时，选此准则较好
24
例题：
Monday, March 30, 2020
25
Monday, March 30, 20day, March 30, 2020
27
1. 一维非稳态导热的数值求解： 第三类边界条件下，常物性、无内热源无 限大平壁的一维非稳态导热问题为例。
1) 求解域的离散
2) 节点温度差分方程的建立
运用热平衡法可以建立非稳态导热物体内部节点和 边界节点温度差分方程。
Monday, March 30, 2020
29
➢ 两点结论：
(a) 任意一个内部节点n在(i+1)时刻的温度都可以由该节点及 其相邻节点(n-1) 、(n+1)在i 时刻的温度由上式直接求出，不必联 立求解方程组，这是显式差分格式的优点。这样就可以从初始温 度出发依次求出各时刻的节点温度；
(b) 必须满足显式差分格式的稳定性条件，即
物理意义:
15
§4-3 边界节点离散方程的建立及代数方程的求解
第一类边界条件：已知全部边界的温度，作为已知值加入到内节点的离散方程中， 组成封闭的代数方程组，直接求解。
n=N
封闭
(m,n+1)
第二类边界条件或第三类边界 条件：部分边界温度未知。
不封闭
w (m-1,n)
n e
(m,n) s
(m,n-1)
(m+1,n)
y
n=1
m=1
m
x
m=M
Monday, March 30, 2020
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（3）建立节点物理量的代数方程（离散方程） 节点上物理量的代数方程称离散方程。其 过程如下： • 首先划分各节点的类型； • 其次，建立节点离散方程； • 最后，代数方程组的形成。 对节点 (m,n) 的代数方程，当 △x=△y 时， 有：
tm , n 1 (tm 1,n tm 1,n tm ,n 1 tm ,n 1) 4
t t 2 0 2 x y
2 2
（2）区域离散化（确立节点）
用一系列与坐标轴平行的网格线把求 解区域划分成若干个子区域，用网格线的 交点作为需要确定温度值的空间位置，称 为节点 ( 结点 ) ，节点的位置用该节点 在两个方向上的标号 m ， n 表示。 相邻两节点间的距离称步长。 如图 (b) 所示。
（2）有限元法
有限元方法的基础是变分原理和加权余量法，其基本求解思想是把计算域划分 为有限个互不重叠的单元，在每个单元内，选择一些合适的节点作为求解函数 的插值点，将微分方程中的变量改写成由各变量或其导数的节点值与所选用的 插值函数组成的线性表达式 ，借助于变分原理或加权余量法，将微分方程离 散求解。
h1t f
（a）
x
三、 基本概念：控制容积、网格线、节点、界 面线、步长
N
(m,n)
n
y
y M
二维矩 形域内 稳态无 内热源， 常物性 的导热 问题
x
x
（b）
m
如图（a）所示二维矩形域内无内热源、稳态、 常物性的导热问题采用数值解法的步骤如下：
（1）建立控制方程及定解条件 针对图示的导热问题，它的控制方程（即 导热微分方程）为：
分析解法与数值解法的异同点： • 相同点：根本目的是相同的，即确定 ① t=f(x,y,z) ；② Q g ( x, y, z, ) 。 • 不同点：数值解法求解的是区域或时间、空 间坐标系中离散点的温度分布代替连续的温度 场；分析解法求解的是连续的温度场的分布特 征，而不是分散点的数值。
• 数值解法的实质 对物理问题进行数值解法的基本思路可以概括 为：把原来在时间、空间坐标系中连续的物理量的 场，如导热物体的温度场等，用有限个离散点上的 值的集合来代替，通过求解按一定方法建立起来的 关于这些值的代数方程，来获得离散点上被求物理 量的值。该方法称为数值解法。 这些离散点上被求物理量值的集合称为该物理 量的数值解。
（1）有限差分法
（2）有限元方法
（3）边界元方法
（1）有限差分法
基本思想是把连续的定解区域用有限个离散点构成的网格来代替， 这些离散点 称作网格的节点；把连续定解区域上的连续变量的函数用在网格上定义的离散 变量函数来近似；把原方程和定解条件中的微商用差商来近似， 积分用积分和 来近似，于是原微分方程和定解条件就近似地代之以代数方程组，即有限差分 方程组 ， 解此方程组就可以得到原问题在离散点上的近似解。然后再利用插值 方法便可以从离散解得到定解问题在整个区域上的近似解。
第四章 导热问题数值解基础
1 、重点内容：
① 掌握导热问题数值解法的基本思路；
② 利用热平衡法和泰勒级数展开法建立
节点的离散方程。 2 、掌握内容：数值解法的实质。 3 、了解内容：了解非稳态导热问题的两 种差分格式及其稳定性。
求解导热问题实际上就是对导热微分方程在 定解条件下的积分求解，从而获得分析解。随着 计算机技术的迅速发展，对物理问题进行离散求 解的数值方法发展得十分迅速，这些数值解法主 要有以下几种：
4-1 导热问题数值求解的基本思想及内部节点离散方程的建立
一、物理问题的数值求解过程
建立控制方程及定解条件 确定节点（区域离散化）
设立温度场的迭代初值
建立节点物理量的代数方程
求解代数方程
改进初场
是否收敛 是 解的分析
否
二、 例题条件
y
二维矩形域内稳态无内热 源，常物性的导热问题
h3 t f
t0
h2 t f
2 ）非线性代数方程组：代数方程一经建立， 其中各项系数在整个求解过程中不断更新。 3 ）是否收敛判断：是指用迭代法求解代数方 程是否收敛，即本次迭代计算所得之解与上一 次迭代计算所得之解的偏差是否小于允许值。
（6） 解的分析
通过求解代数方程，获得物体中 量，热应力及热变形等。因此，对于数值分 析计算所得的温度场及其它物理量应作详细 分析，以获得定性或定量上的结论。
（3）边界元法
边界元法是在有限元法之后发展起来的一种较精确有效的工程数值分析方法 。 又称边界积分方程-边界元法。它以定义在边界上的边界积分方程为控制方程， 通过对边界分元插值离散，化为代数方程组求解。它与基于偏微分方程的区域 解法相比，由于降低了问题的维数，而显著降低了自由度数，边界的离散也比 区域的离散方便得多，可用较简单的单元准确地模拟边界形状，最终得到阶数 较低的线性代数方程组。
（4） 设立迭代初场 代数方程组的求解方法有直接解法与迭 代解法，传热问题的有限差分法中主要采用 迭代法。采用迭代法求解时，需对被求的温 度场预先设定一个解，这个解称为初场，并 在求解过程中不断改进。
（5） 求解代数方程组 求解时遇到的问题： ① 线性； ② 非线性； ③ 收敛性等。 如图 （ b ），除 m=1 的左边界上各节点的 温度已知外，其余 (M-1)N 个节点均需建立 离散方程，共有 (M-1)N 个方程，则构成一 个封闭的代数方程组。 1 ）线性代数方程组：代数方程一经建立， 其中各项系数在整个求解过程中不再变化；
四、 建立离散方程的常用方法： (1) Taylor（泰勒）级数展开法； (2) 多项式拟合法；
(3) 控制容积积分法；
(4) 控制容积平衡法(也称为热平衡法)
(1) 泰勒级数展开法
根据泰勒级数展开式，用节点(m,n)的温度tm,n
来表示节点(m+1,n)，而温度tm+1,n
t x 2 2t tm1,n tm,n x x m,n 2 x 2 x3 3t 3 6 x m,n x 4 4t 4 24 x m,n
用节点(m,n)的温度tm,n来表示节点(m-1,n)的