传热学-第四章22
- 格式:ppt
- 大小:1.07 MB
- 文档页数:28

4. 非稳态导热4.1 知识结构1. 非稳态导热的特点;2. (恒温介质、第三类边界条件)一维分析解求解方法(分离变量,特解叠加)及解的形式(无穷级数求和);3. 解的准则方程形式,各准则(无量纲过余温度、无量纲尺度、傅里叶准则、毕渥准则)的定义式及其物理涵义; 4. 查诺谟图求解方法;5. 多维问题的解(几个一维问题解(无量纲过余温度)的乘积);6. 集总参数法应用的条件和解的形式;7. 半无限大物体的非稳态导热。
4.2 重点内容剖析4.2.1 概述在设备启动、停车、或间歇运行等过程中,温度场随时间发生变化,热流也随时间发生变化,这样的过程称为非稳态导热。
一.过程特点分类1. 周期性非稳态导热(比较复杂,本书不做研究) 如地球表面受日照的情况 (周期为24小时)对于内燃机气缸壁受燃气冲刷的情况,周期为几分之一秒,温度波动只在很浅的表层,一般作为稳态处理。
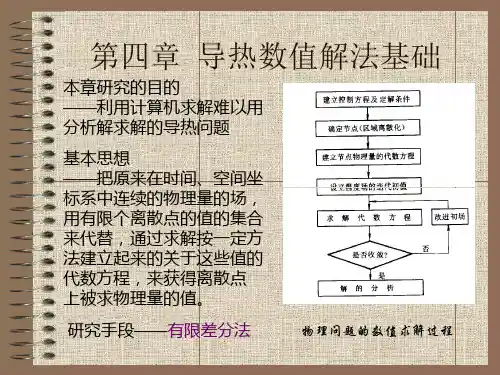
2. 非周期性非稳态导热:(趋于稳态的过程,非稳态 稳态) 例子:如图4-1,一个无限大平板,初始温度均匀,某一时刻左壁面突然受到一恒温热源的加热,分析平壁内非稳态温度场的变化过程: (1) 存在两个阶段初始阶段:温度变化到达右壁面之前(如曲线A-C-D ),右侧不参与换热,此时物体内分为两个区间,非稳态导热规律控制区A-C 和初始温度区C-D 。
正规状况阶段:温度变化到达右壁面之后,右侧参与换热,初始温度分布的tx1t 0t ABCDEF图4-1 非稳态导热过程的温度变化影响逐渐消失。
(2) 热流方向上热流量处处不等因为物体各处温度随时间变化而引起内能的变化,在热量传递路径中,一部分热量要用于(或来源于)这些内能,所以热流方向上的热流量处处不等。
二. 研究任务1. 确定物体内部某点达到预定温度所需时间以及该期间所需供给或取走的热量,以便合理拟定加热和冷却的工艺条件,正确选择传热工质;2. 计算某一时刻物体内的温度场及温度场随时间和空间的变化率,以便校核部件所承受的热应力,并根据它制定热工设备的快速启动与安全操作规程。








第四章 流动沸腾液体在管道或回路中流动时,产生的沸腾现象称为流动沸腾。
这种流动可能是外力强制形成,也可能是回路内的流体的密度差引起的自然循环。
由于流动沸腾中伴随着各种类型的汽液两相流动,所以比池内沸腾更复杂。
目前还无法对流动沸腾过程进行解析求解,研究的途径主要是实验。
§4-1 流型与沸腾工况流动沸腾的特点:1). 由于管道的沿途加热和液体蒸发,汽液两相流的流型会发生一系列的变化。
2). 随着容积流量的增大,流体逐步加速使压力降增大,而引起系统压力的下降,饱和温度也随之降低,这反过来对流型和沸腾产生影响。
因此,对沿加热管的流动沸腾,需分段进行分析计算。
3). 工程上,加热管的配置有竖直和水平两种典型方式(倾斜布置管道处于二者之间)。
在这两种情况下的流动和沸腾特性有明显的差别,一般分开研究。
一、竖直管内流动沸腾的流型和换热工况如图,是典型的竖直管内流动沸腾的流型和换热工况。
当单相流体从下部进入加热管后,①一开始,加热壁上尚不具备成核条件,这时流动为单相流,换热工况为液体的单相对流换热(A区)。
②随着液体被加热,温度升高,逐步使壁面上的某些开始满足成核条件,开始出现小汽泡。
当汽泡长大到一定尺寸后,脱离壁面进入主流,在汽泡刚开始产生的阶段,液体核心区的温度高低于对应的主流压力下的饱和温度,使脱离壁面而后的小汽泡很快在过冷的液体中凝结,加速液体升温,使换热增强。
这时的换热工况为流动过冷沸腾,其流型是泡状流(B区)。
③当液体的主流温度达到饱和温度后,进入主流的汽泡不再凝结,换热进入饱和沸腾工况。
④随着液体中汽泡数量的不断增加,小汽泡之间发生碰撞与合并,开始出现较大的汽团或称弹状大汽泡,其流型由泡状流演变为弹状流动(仍为饱和沸腾)。
⑤随着液体的进一步汽化,含汽量的增加,两相流型转变为环状流,即汽相在管中心区,而液相附着于管壁上。
⑥随着液层的变薄,壁面上的沸腾逐渐被抑制,汽化转变为汽液分界面上的蒸发,换热工况由饱和沸腾逐步变为强制对流蒸发。
《传热学(第四版)》第四章复习题答案1.试简要说明对导热问题进行有限差分数值计算的基本思想与步骤。
答:基本思想:把原来在时间、空间坐标系中连续的物理量的场,用有限个离散点上的值的集合来代替,通过求解按一定方法建立起来的关于这些值的代数方程,来获得离散点上被求物理量的值。
这些离散点上被求物理量值的集合称为该物理量的数值解。
步骤:①建立控制方程及定解条件;②区域离散化;③建立物理量的代数方程;④用迭代法求解时,设立迭代初场;⑤求解代数方程组;⑥解的分析。
2.试说明用热平衡法对节点建立温度离散方程的基本思想。
答:对以节点所代表的元体用傅立叶定律直接写出其能量守恒表达式,得到以元体为研究对象的传热代数方程。
3.推导导热微分方程的步骤和过程与用热平衡法建立节点温度离散方程的过程十分相似,为什么前者得到的是精确描写,而由后者解出的却是近似解。
答:因为微分方程的研究对象是微元体,而用热平衡法建立的节点温度离散方程的研究对象是元体。
微分方程的微元体可以达到无限小,从而可准确描述物体内任一点的连续函数。
而热平衡法对有限大小元体内的分布函数用节点处的值代替,从而得到近似解,不能得到准确解。
4.第三类边界条件边界节点的离散方程,也可用将第三类边界条件表达式中的一阶导数用差分公式来建立。
试比较这样建立起来的离散方程与用热平衡法建立起来的离散方程的异同与优劣。
答:由教材P175 式(a),(b)可得:在x方向上有:ðt ðx |m,n≈t m+1,n−t m,nΔxðt ðx |m,n≈t m,n−t m−1,nΔx同理在y方向上有:ðt ðy |m,n≈t m,n+1−t m,nΔyðt ðy |m,n≈t m,n−t m,n−1Δy从而可得:−λðtðx|m,n≈−λt m+1,n−t m,n∆x=ℎ(t f−t m,n)t m,n=t m,n−1−ℎΔxλt f+ℎΔxλt m,n⇒(1−ℎΔxλ)t m,n=t m,n−1−ℎΔxλt f其它式子可类似导出。