遥感图像处理实验报告_图像的频率域滤波处理

遥感图像处理实验报告《遥感图像处理实验报告》摘要：本实验利用遥感技术获取了一幅卫星图像，通过图像处理技术对图像进行了处理和分析。

实验结果表明，遥感图像处理技术在地理信息系统、环境监测、城市规划等领域具有重要的应用价值。

引言：遥感图像处理是利用遥感技术获取的图像进行数字化处理和分析，以获取有用的地理信息和环境数据的过程。

本实验旨在通过对遥感图像的处理和分析，探讨遥感图像处理技术在实际应用中的作用和意义。

实验方法：1. 获取卫星图像：选择一幅特定区域的卫星图像作为实验对象，确保图像质量和分辨率满足处理要求。

2. 图像预处理：对原始图像进行预处理，包括去噪、增强、几何校正等操作，以提高图像质量和准确性。

3. 图像分析：利用遥感图像处理软件对图像进行分类、特征提取、变化检测等分析，获取地理信息和环境数据。

4. 结果展示：将处理后的图像结果进行展示和分析，对图像处理技术的应用效果进行评估。

实验结果：经过处理和分析，得到了一幅清晰的遥感图像，并从中提取了有用的地理信息和环境数据。

通过图像分类和特征提取，可以准确地识别出不同地物类型，如建筑物、植被、水体等；通过变化检测，可以发现地表的变化情况，如城市扩张、土地利用变化等。

这些信息对于地理信息系统、环境监测、城市规划等领域具有重要的应用价值。

结论：遥感图像处理技术在地理信息系统、环境监测、城市规划等领域具有重要的应用价值，通过对遥感图像的处理和分析，可以获取丰富的地理信息和环境数据，为相关领域的决策和规划提供重要的支持。

在未来的研究中，可以进一步探讨遥感图像处理技术的改进和应用，以满足不同领域的需求。

遥感数字图像处理教程实习报告《数字图像处理》课程实习报告（ 2011 - 2012学年第 1 学期）专业班级：地信09-1班姓名：梁二鹏学号：310905030114指导老师：刘春国----------------------------------------------实习成绩：教师评语：教师签名：年月日实习一：图像彩色合成实习一、实验目的在学习遥感数字图像彩色合成基础上，应用所学知识，基于遥感图像处理软件ENVI进行遥感数字图像彩色合成。

二、实验内容彩色合成：利用TM图像can_tmr.img，实现灰度图像的密度分割、多波段图像的真彩色合成、假彩色合成和标准假彩色合成。

三、实验步骤1、显示灰度图像主要步骤：1、打开ENVI4.7,单击FILE菜单，在下拉菜单中选择open image file 选项，然后在弹出的对话框中选择can_tmr.img文件，单击打开。

2、在可用波段列表对话框中，选中某一波段图像，选中gray scale单选按钮，单击LOAD BAND按钮，显示一幅灰度图像。

3、在可用波段列表对话框中，选择其他某一波段图像，进行显示。

4、利用可用波段列表中的display按钮，同时有多个窗口显示多个波段图像。

5、链接显示。

利用图像窗口tool菜单下的link子菜单link display实现多图像的链接显示。

如图所示：红色方框。

6、使用tool菜单下的Cursor Location/value和pixel Locator功能在确定像素的值和位置。

2、伪彩色合成的主要步骤：1、打开ENVI4.7,单击FILE菜单，在下拉菜单中选择open image file 选项，然后在弹出的对话框中选择can_tmr.img 文件，单击打开。

2、在可用波段列表对话框中，选中gray scale单选按钮，单击LOAD BAND 按钮3、在#1 TM BAND1:CAN_TMR.IMG对话框中，单击菜单栏上的OVERLAY 菜单，在下拉菜单中选择DENSITY SLICE…按钮，在弹出的对话框中选择任意一个波段名称，4、在弹出的对话框中显示系统默认的密度分割，通过定义MIN和max的值可以定义需要分割的密度范围，通过EDIT RANGE ,deleted range，clear ranges 三个按钮可以对默认的分割进行修改，待修改完毕后，单击APPLY按钮，即可显示修改后的效果。

用c,,语言编程实现遥感图像处理实习报告C语言基础编程实习报告（2011～2012学年第2学期）实习名称：认识实习分项名称：C语言基础编程系别：计算机与通信工程系专业：测控（1）班学号：姓名：实习地点：学校机房3楼实习时间：8月23日～8 月26日实习成绩：指导教师：严光银翟勇涛西南交通大学峨眉校区2012年8 月26 日一．实习目的和要求实习目的:1、巩固C语言编程基础知识2、熟练C语言调试中的常见错误及处理办法3、加强C语言综合编程能力训练4、熟练掌握C语言程序上机调试过程5、学会编写C语言程序解决简单计算题、字符串处理问题、日期和时间处理问题、高精度数处理等问题6、提高外文资料阅读理解的能力。

要求：1.电子文档建立一个文件夹，名称为：学号姓名C基础如：学号为20106900，姓名为李四，则，文件夹名称：20106900李四C 基础①C基础编程（10个C程序）文件名格式：学号姓名简拼_题目编号A.c如：题号为1001，则文件名为：20106900LS_1001A.c②C强化编程（共10道，至少选做4道题）文件名格式：学号姓名简拼_题目编号B.c③实习报告电子文档：学号姓名C 基础.doc④改正错误分析示例中的错误2.实习报告（打印稿）二．实习方式和安排方式：上课与上机安排：三. 实习内容(一)C基础编程（选做6题）在杭电OJ成功提交的题目数:6在杭电OJ未成功提交的题目编号:无提交的电子文档中包含的C程序数:6从6道基础编程题中任选2道比较满意的题目,写出详细解题报告如下: ***************************第1题start***************************** （1）题目解析题目编号1108问题描述编写程序计算2个整数a、b的最小公倍数。

输入数据输入数据输入2个整数a和b，中间用空格间隔。

输出要求对于每次读入的一对整数，输出最小公倍数的结果。

每个结果以回车结束。

遥感图像处理实验报告遥感图像处理实验报告引言：遥感图像处理是一门应用广泛的技术，它通过获取、分析和解释地球表面的图像数据，为地质勘探、环境监测、农业发展等领域提供了重要的支持。

本实验旨在探索遥感图像处理的基本方法和技术，以及其在实际应用中的价值和意义。

一、图像预处理图像预处理是遥感图像处理的第一步，它主要包括图像的去噪、增强和几何校正等操作。

在本实验中，我们使用了一张卫星图像作为样本，首先对图像进行了去噪处理，采用了中值滤波算法，有效地去除了图像中的椒盐噪声。

接着，我们对图像进行了增强处理，采用了直方图均衡化算法，使得图像的对比度得到了显著提高。

最后，我们进行了几何校正，通过对图像进行旋转和缩放，使得图像的几何形状与实际地理位置相符合。

二、图像分类图像分类是遥感图像处理的关键步骤之一，它通过对图像中的像素进行分类，将其划分为不同的地物类型。

在本实验中，我们使用了监督分类方法，首先选择了一些具有代表性的样本像素，然后通过训练分类器，将这些样本像素与不同的地物类型进行关联。

接着，我们对整个图像进行分类，将图像中的每个像素都划分为相应的地物类型。

最后，我们对分类结果进行了验证，通过与实地调查结果进行对比，验证了分类的准确性和可靠性。

三、图像融合图像融合是遥感图像处理的一项重要技术，它可以将多个不同波段或分辨率的图像融合成一幅高质量的图像。

在本实验中，我们选择了两幅具有不同波段的卫星图像，通过波段归一化和加权平均的方法，将这两幅图像融合在一起。

融合后的图像不仅保留了原始图像的颜色信息，还具有更高的空间分辨率和光谱分辨率，可以提供更全面和准确的地物信息。

四、图像变化检测图像变化检测是遥感图像处理的一项关键任务，它可以通过对多幅图像进行比较，检测出地表发生的变化情况。

在本实验中，我们选择了两幅具有不同时间的卫星图像，通过差异图像法和指数变化检测法，对这两幅图像进行了变化检测。

通过对比差异图像和变化指数图，我们可以清晰地看到地表发生的变化，如城市扩张、植被变化等，为城市规划和环境监测提供了重要的参考依据。

遥感图像处理实验报告（2013 —2014 学年第1学期）实验名称：图像的频率域滤波处理实验时间：实验地点：指导教师：专业班级：姓名：学号：一：实验目的1：掌握滤波器在程序语言中的定义算法2：理解图像的频率域与空间域之间的区别与联系3：在频率域对图像进行处理，达到平滑（低通滤波）与锐化（高通滤波）的目的二：实验内容1：在Matlab中定义滤波器2：对图像进行频率域处理3：对频率域的处理结果，结合第3次实验（空间域处理）结果进行对比，给出评价三：实验代码及Matlab使用心得（注释中）%清屏，清除工作空间，关闭所有绘图窗口clc;clear all;close all;%读取图像，并建立一个窗口，显示原始图像I = imread('C:\Users\浮生\Desktop\大三\Matlab\data\lena.png', 'png')figure(1)imshow(I)title('原始图像')%图像傅立叶变换%fft(X)函数的作用是，返回矩阵X的【二维离散傅立叶变换】结果%fft()函数采用快速傅立叶变换算法，运算结果的行列数与被变换矩阵的规格相同F = fft2(I);%fftshift()函数的功能则是把FFT的DC分量移动到频谱矩阵的中心%在直观上，就是把低频信息移到矩阵中心，便于直观观看图像的频谱F = fftshift(F);%由于FFT的运算结果的数值跨幅过大%直接显示的话只能看到一个小亮点%为了显示的直观，我们需要自行定义灰度显示幅度%在本例中，我们定义显示幅度为0-50000figure(2);imshow(abs(real(F)), [0 50000]);title('频率域图像')%%%%%%定义滤波器之前的准备工作%%%%%[m n] = size(I);%读取图像的规格p = m/2;%定义两个计数器p和qq = n/2;%用以控制滤波器的遍历过程image = zeros(m,n);%%%%%%截止频率为50的理想低通滤波器%%%%%%%低通滤波器，即让频率高于阈值的信号值为0，而在阈值之下的所有信号保持原样%反映在图像操作中，将去除高频信息，达到平滑的效果lowpass_50 = F;for u = 1:mfor v = 1:nif sqrt((u-p)^2 + (v-q)^2) < 50%什么也不做;elselowpass_50(u, v) = 0;endendend%显示频率域图像figure(3);imshow(abs(real(lowpass_50)), [0 50000]);title('频率域图像截止频率为50的理想低通滤波器');%傅立叶逆运算反算图像image = ifftshift(lowpass_50);%还原矩阵image = ifft2(image);%傅立叶逆运算image = abs(real(image));%复数取实部%显示处理结果图像figure(4);imshow(image, []);title('处理结果截止频率为50的理想低通滤波器')%%%%%%截止频率为100的理想低通滤波器%%%%%%lowpass_100 = F;for u = 1:mfor v = 1:nif sqrt((u-p)^2 + (v-q)^2) < 100%什么也不做;elselowpass_100(u, v) = 0;endendend%显示频率域图像figure(5);imshow(abs(real(lowpass_100)), [0 50000]);title('频率域图像截止频率为100的理想低通滤波器'); %傅立叶逆运算反算图像image = ifftshift(lowpass_100);%还原矩阵image = ifft2(image);%傅立叶逆运算image = abs(real(image));%复数取实部%显示处理结果图像figure(6);imshow(image, []);title('处理结果截止频率为100的理想低通滤波器')%%%%%%截止频率为50的理想高通滤波器%%%%%% highpass_50 = F;for u = 1:mfor v = 1:nif sqrt((u-p)^2 + (v-q)^2) < 50highpass_50(u, v) = 0;else%什么也不做;endendend%显示频率域图像figure(7);imshow(abs(real(highpass_50)), [0 50000]);title('频率域图像截止频率为50的理想高通滤波器');%傅立叶逆运算反算图像image = ifftshift(highpass_50);%还原矩阵image = ifft2(image);%傅立叶逆运算image = abs(real(image));%复数取实部%显示处理结果图像figure(8);imshow(image, []);title('处理结果截止频率为50的理想高通滤波器')%%%%%%截止频率为100的理想高通滤波器%%%%%% highpass_100 = F;for u = 1:mfor v = 1:nif sqrt((u-p)^2 + (v-q)^2) < 100highpass_100(u, v) = 0;else%什么也不做;endendend%显示频率域图像figure(9);imshow(abs(real(highpass_100)), [0 50000]);title('频率域图像截止频率为100的理想高通滤波器');%傅立叶逆运算反算图像image = ifftshift(highpass_100);%还原矩阵image = ifft2(image);%傅立叶逆运算image = abs(real(image));%复数取实部%显示处理结果图像figure(10);imshow(image, []);title('处理结果截止频率为100的理想高通滤波器')%%%%%%截止频率为50的巴特沃斯低通滤波器%%%%%% for u = 1:m,for v = 1:nD=sqrt((u-p)^2 + (v-q)^2);Butterworth(u,v)=1/(1+D/50)^(2*2);endend%显示频率域图像figure(11);imshow(abs(real(Butterworth)), []);title('频率域图像截止频率为50的巴特沃斯低通滤波器'); %傅立叶逆运算反算图像image = F.*Butterworth;image = ifftshift(image);image = abs(ifft2(image));%显示处理结果图像figure(12);imshow(image, []);title('处理结果截止频率为50的巴特沃斯低通滤波器')%%%%%%截止频率为50的高斯低通滤波器%%%%%%for u=1:m,for v=1:nD=sqrt((u-p)^2 + (v-q)^2);Gaussian(u,v)=exp(-D^2/(2*50^2));endend%显示频率域图像figure(13);imshow(abs(real(Gaussian)), []);title('频率域图像截止频率为50的高斯低通滤波器'); %傅立叶逆运算反算图像image = F.*Gaussian;image = ifftshift(image);image = abs(ifft2(image));%显示处理结果图像figure(14);imshow(image, []);title('处理结果截止频率为50的高斯低通滤波器');四：实验结果（仅列一例）五：实验心得1：相较空域滤波，频率域滤波的算法复杂度更高。

一、实验名称遥感图像频率域增强处理二、实验目的对图像数据采用各种图形增强算法，提高图像的目视效果，方便人工目视解译、图像分类中的样本选取等，方便以后的图像解译。

学会使用ENVI软件对遥感影像进行分析增强处理，初步掌握各种图像增强方法，并对其结果进行比较，观察增强效果。

三、实验原理FFT Filtering（Fast Fourier Transform Filtering 快速傅立叶变换滤波）可以将图像变换成为显示不同空间频率成分的合成输出图像。

正向的FFT 生成的图像能显示水平和垂直空间上的频率成分。

图像的平均亮度值显示在变换后图像的中心。

远离中心的像元代表图像中增加的空间频率成分。

这一滤波能被设计为消除特殊的频率成分，并能进行逆向变换。

四、数据来源本次实验所用数据来自于国际数据服务平台；landsat4-5波段30米分辨率TM第三波段影像，投影为WGS-84，影像主要为山西省大同市恒山地区，中心纬度：38.90407 中心经度：113.11840。

五、实验过程1、正向FFT滤波加载影像，在ENVI主菜单栏中选择Filters →FFT Filtering →Forward FFT。

出现Forward FFT Input File对话框，选择要进行滤波的文件，点击ok。

在Forward FFT Parameters对话框中选择输出文件名及位置。

点击ok开始FFT计算。

2、图像平滑1）定义FFT滤波器在ENVI主菜单栏中选择Filters →FFT Filtering →Filter Definition。

将出现Filter Definition选择对话框。

Filter_Yype →Circular Pass。

定义相关参数。

选择输出路径，apply构建FFT滤波器。

2）反向FFT变换选择Filter →FFT Filtering →Inverse FFT，出现Inverse FFT Input File对话框。

遥感图象的频率增强与多光谱增强一、实验目的：学习并掌握遥感图象频率域增强的原理与方法，理解频率域增强的意义。

学习和掌握主成分变换，缨帽变换和色彩变换的基本原理与方法，理解三种变换方法处理的效果及意义二、实验内容：频率域平滑频率域锐化主成分变换缨帽变换色彩变换三、实验原理与方法：频率域增强的方法的基本过程：将空间域图象通过傅立叶变换为频率域图象，然后选择合适的滤波器频谱成分进行增强，再经过傅立叶逆变换变回空间域，得到增强后的图象。

K-L变换是离散（Karhunen-Loeve）变换的简称，又被称作主成分变换。

它是对某一多光谱图像X，利用K-L变换矩阵A进行线性组合，而产生一组新的多光谱图像Y，表达式为Y=AX对图像中每一个像元矢量逐个乘以矩阵A，便得到新图像中每一个像元矢量。

A的作用是给多波段的像元亮度加权系数，实现线性变换。

由于变换前各波段之间有很强的相关性，经过K-L变换组合，输出图像Y的各分量yi之间将具有最小的相关性，这就是变换矩阵A 的作用K-T变换是Kauth-Thomas变换的简称，也称缨帽变换。

这种变换也是一种线性组合变换，其变换公式为：Y＝BX彩色变换实际上就是根据人眼对色彩的分辨力远远大于对灰度的分辨力，将RGB色彩系统和IHS色彩系统相互转化来提高图像被人眼感知的效果四、实验步骤：（省略）实验原图：傅立叶变换图Butterworth滤波器处理Butterworth 高通滤波器Butterworth 低通滤波器Ideal滤波器Ideal 低通滤波器Ideal 高通滤波器Ideal 低通滤波器处理Ideal 高通滤波器处理Butterworth 高通滤波器处理Butterworth低通滤波器处理实验原图主成分正变换后图像实验原主成分处理后再经逆变换处理后图像实验原图缨帽变换后图像原RGB图像HIS图像五、结果分析和讨论：1．比较滤波处理前后的图像，分析低通滤波和高通滤波处理的效果1)经过高通滤波器处理后的图像，图像被锐化，边缘出现抖动现象，2)经过低通滤波处理后的图像，可以有效的消除噪声，由于高频部分含有大量边缘信息，导致边缘损失，图像边缘模糊。

实验五遥感图像处理实验目的：通过上机操作，了解空间增强、辐射增强、频率域增强等几种遥感图象增强处理的过程和方法，加深对遥感图象增强处理的理解。

通过上机操作，初步掌握遥感信息融合的方法，深入理解遥感信息融合在信息解译中的意义。

实验内容：ENVI中进行直方图的交互式拉伸、卷积滤波处理、频率域滤波FFT。

多光谱数据与高分辨率全色数据的融合。

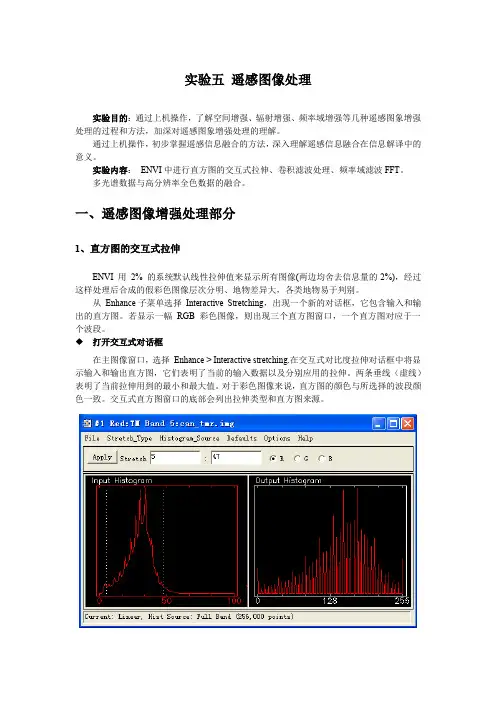
一、遥感图像增强处理部分1、直方图的交互式拉伸ENVI 用2% 的系统默认线性拉伸值来显示所有图像(两边均舍去信息量的2%)，经过这样处理后合成的假彩色图像层次分明、地物差异大，各类地物易于判别。

从Enhance子菜单选择Interactive Stretching，出现一个新的对话框，它包含输入和输出的直方图。

若显示一幅RGB 彩色图像，则出现三个直方图窗口，一个直方图对应于一个波段。

打开交互式对话框在主图像窗口，选择Enhance > Interactive stretching.在交互式对比度拉伸对话框中将显示输入和输出直方图，它们表明了当前的输入数据以及分别应用的拉伸。

两条垂线（虚线）表明了当前拉伸用到的最小和最大值。

对于彩色图像来说，直方图的颜色与所选择的波段颜色一致。

交互式直方图窗口的底部会列出拉伸类型和直方图来源。

注意：要把任何拉伸或直方图变化自动地应用于你的图像，选择Options > Auto Apply: On.◆浏览数据细节要浏览当前的DN值和指定DN值的像元数、直方图以及累积直方图，可以在直方图内按住鼠标左键并拖放随之产生的白色十字交叉指针。

◆设置拉伸参数要更改最小和最大拉伸值，在任意一条垂直虚线上点击鼠标左键，然后拖曳到一个新位置。

或在对话框顶部的文本框中输入所需值。

当选择任意一条线时，当前的DN、像元数、该单位DN 的像元百分比以及累积百分比，显示在输入的直方图上。

当指定最小和最大值时，输入所需要的实际值（例如，最小值37，最大值68 ）或数据的百分比（例如，最小值“2%”，最大值“98%”）。

遥感图像处理实验报告（2013 —2014 学年第1学期）实验名称：图像的空间域滤波处理实验时间：实验地点：指导教师：专业班级：姓名：学号：一：实验目的掌握Matlab编程语言的基本语法掌握Matlab中imread()、imfilter()、imshow()、mat2gray()、等相关函数的用法及意义通过Matlab程序语言完成图像的空间域滤波处理，以达成边缘检测的目的二：实验内容在Matlab中，分别运用经典一阶梯度、Robert算子、Sobel算子、Prewitt算子及Laplacian 算子进行目标图像的边缘检测，互相对比实验结果，分析差异三：实验平台Windows 7 Ultimate SP1Matlab 2012b四：实验代码及Matlab使用心得（注释中）%清空工作空间clc;%清屏clear all;%关闭所有绘图窗口close all;%定义一个矩阵I 用来存储待处理图像,用imread()函数读取的数据格式为unit8I = imread('C:\Users\Administrator\Desktop\Matlab\data\barbara.png');%创建一个绘图窗口，并显示原图像figure(1);imshow(I);title('原图');%把unit8格式数据转换为doulbe格式，以便滤波计算I = double(I);%%%%%%%%%%%%%%%%%%%%%%%%%%%%经典一阶梯度%%%%%%%%%%%%%%%yjtdx = [0 0 0;-1 1 0;0 0 0];yjtdy = [0 -1 0;0 1 0;0 0 0];%imfilter()函数为一个滤波函数%其中有两个参数，外加一系列附加指令%如下中的I 代表被处理图像%yjtdx 代表滤波器%'replicate'是一个附加指令，因为处理过的数据，可能会超出原图像数据大小的上下限%这个附加指令令超出上下限的数据为最接近上下限的数据ImageYjtdx = imfilter(I, yjtdx, 'replicate');ImageYjtdy = imfilter(I, yjtdy, 'replicate');%将x与y方向上的处理结果进行几何平均，作为处理结果ImageYjtd= sqrt(ImageYjtdx.^2 + ImageYjtdy.^2);%figure()函数创建一个绘图窗口figure(2);%绘制处理后的图像%在用imshow()函数显示图像时要注意，因为现在的处理结果是double类型的，而不是unit8类型%而imshow()在显示图像时，只有unit8类型的矩阵图像数据可以直接输入直接显示%而对于double类型的矩阵，imshow()认为其灰度空间是从0到1，而不是从0-256或其它%也就是说，对于double类型的矩阵，imshow()函数不知道矩阵所代表的图像的灰度级数是多少%这时就需要用mat2gray()函数对double型矩阵做归一化，所谓归一化，就是把原矩阵中的数据%映射至0-1的数据空间中，这时，经m at2gray()函数处理过的矩阵，其中所有元素都在0-1范围内%再用imshow()函数进行显示，才可得到正常的显示结果imshow(mat2gray(ImageYjtd));title('经典一阶梯度处理结果'); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%Robert算子%%%%%%%%%%%%%%%%% Robert1 =[-1 0 0;0 1 00 0 0];Robert2 =[0 -1 0;1 0 00 0 0];ImageRobert1 = imfilter(I, Robert1, 'replicate');ImageRobert2 = imfilter(I, Robert2, 'replicate');ImageRobert = sqrt(ImageRobert1.^2 + ImageRobert2.^2);figure(3);imshow(mat2gray(ImageRobert));title('Robert算子处理结果'); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%Sobel算子%%%%%%%%%%%%%%%%%% Sobel1 = [1 2 1;0 0 0;-1 -2 -1];Sobel2 = [-1 0 1;-2 0 2;-1 0 1];ImageSobel1 = imfilter(I, Sobel1, 'replicate');ImageSobel2 = imfilter(I, Sobel2, 'replicate');ImageSobel = sqrt(ImageSobel1.^2 + ImageSobel2.^2);figure(4);imshow(mat2gray(ImageSobel));title('Sobel算子处理结果'); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%Prewitt算子%%%%%%%%%%%%%%%%% Prewitt1 = [-1 -1 -1;0 0 0;1 1 1];Prewitt2 = [-1 0 1;-1 0 1;-1 0 1];ImagePrewitt1 = imfilter(I, Prewitt1, 'replicate');ImagePrewitt2 = imfilter(I, Prewitt2, 'replicate');ImagePrewitt = sqrt(ImagePrewitt1.^2 + ImagePrewitt2.^2);figure(5);imshow(mat2gray(ImagePrewitt));title('Prewitt算子处理结果'); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%Laplacian算子%%%%%%%%%%%%%%%% Laplacian = [0 -1 0;-1 4 -1;0 -1 0];ImageLaplacian = imfilter(I, Laplacian, 'replicate');%滤波结果中可能出现负数，因此需要用abs()函数取绝对值ImageLaplacian = abs(ImageLaplacian);figure(6);imshow(mat2gray(ImageLaplacian));title('Laplacian算子处理结果'); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%五：实验结果（仅列一例）六：实验心得1：Matlab部分Matlab是一个命令行式的、解释式的程序语言，学习难度低，在矩阵和数字处理上处速度也很快，有时间我会继续学习2：滤波算子部分1）：Laplacian算子对噪声比较敏感，图像颗粒感较强时得到的处理结果很差，在几乎没有噪声的图像中，Laplacian算子的处理结果却出奇的好。

《遥感原理》实验报告实验名称：遥感图像处理专业：地理信息科学学号：姓名：指导老师：1、实验目的（1）了解彩色的基本特性和相互关系；掌握三原色及其互补色，掌握加色法；（2）学习掌握图像直方图变化与图像亮度变化的关系；掌握图像线性拉伸的方法和过程；（3）理解遥感图像彩色合成的基本原理；掌握选用不同的合成方案产生不同的合成效果的方法，从而达到突出不同目标地物的目的；（4）了解空间滤波的操作过程和空间滤波对图像产生的效果；（5）了解并掌握K-L变换的过程和方法；进一步理解K-L变换产生的处理效果和处理意义；（6）了解和掌握缨帽变换的过程和处理效果；（7）了解和掌握彩色空间变换的过程和方法。

2、实验材料Photoshop CS6、ENVI5.1、CAI软件和光盘文件3、实验内容与过程3.1 遥感图像的光学合成原理彩色的基本特性：明度、色调和饱和度为彩色的基本特性。

明度是指色彩的明亮程度，是人眼对光源或物体明亮程度地感觉，彩色光亮度越高，人眼感觉就越明亮，即有较高的明度。

明度的高低取决于光源光强及物体表面对光的反射率。

色调是色彩彼此相互区分的特性，色调取决于光源的光谱组成和物体表面的光谱反射特性。

饱和度是色彩纯洁性，取决于物体表面反射光谱的选择性程度，反射性光谱越窄，即光谱的选择性越强，彩色的饱和度就越高。

明度、色调和饱和度三者的关系可以用颜色立体来表述。

非彩色，即黑白色只用明度描述，不使用色调、饱和度。

红橙黄绿青蓝紫各种颜色组成彩图。

在遥感上，彩色图比非彩色图较易识别地物。

白色、黑色和各种灰色组成黑白图象，当物体对可见光的各个波长的反射无选择性时，表现为黑色或灰色。

3.2 遥感图像的线性拉伸打开ENVI>点击菜单栏的“Custom Stretch”按钮>选择”Linear”等进行线性拉伸；或者直接在菜单栏上选择“Linear”“Linear2%”“Linear5%”原图：线性拉伸后：Linear:Linear 1%:当拉伸效果为1%时，显示效果得到了很大改善。