下载文档原格式
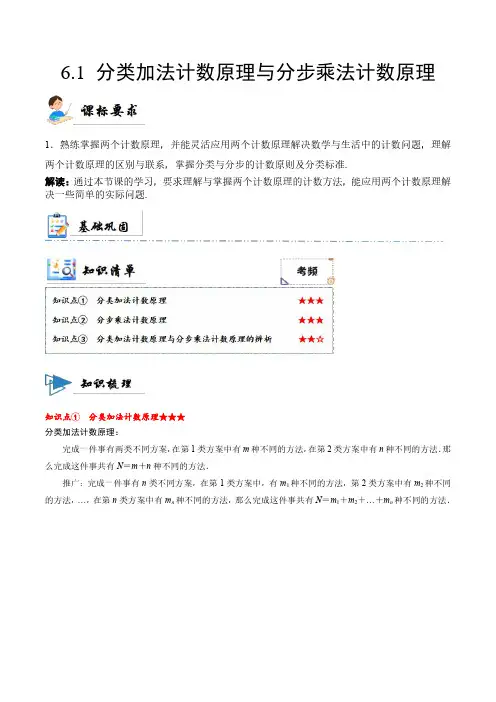
分类加法与分类乘法计数原理一．基础知识１．分类加法与分步乘法计数原理（１）分类加法计数原理完成一件事有两类不同方案，在第一类方案中有ｍ种不同的方法，在第二类方案中有ｎ种不同的方法，那么完成这件事共有Ｎ＝ｍ＋ｎ种不同方法（２）分步乘法计数原理完成一件事需要两个步骤，做第一步有ｍ种不同的方法，做第二步有ｎ种不同的方法，那么完成这件事共有Ｎ＝ｍ⨯ｎ种不同方法２．分清两个计数原理的区别（１）分类加法计数原理是“分类”，分步乘法计数原理是“分步”（２）分类加法计数原理中每类方法中的每一种方法都能独立完成一件事；分步乘法计数原理中每种方法都只能做这件事的一步，不能独立完成这件事二．考点练习１．在所有的两位数中，个位上的数字大于十位上的数字的两位数共有Ａ．４５Ｂ．５０Ｃ．３６Ｄ．３５２．将２名教师４名学生分成两个小组，分别安排到甲，乙两地参加社会实践活动，每个小组由一名教师和两名学生组成，不同的安排方案有Ａ．１２Ｂ．１０Ｃ．９Ｄ．８３．集合Ｐ＝｛x，１｝，Ｑ＝｛y，１,２｝，其中x，y∈｛１,２，３，···，９｝，且Ｐ⊆Ｑ，把满足上述条件的一对有序整数对（x，y）作为一个点的坐标，则这样的点的个数有Ａ．９Ｂ．１４Ｃ．１５Ｄ．２１４．已知两条异面直线a，ｂ上分别有５个点和８个点，则这１３个点可以确定不同的平面的个数Ａ．４０Ｂ．１６Ｃ．１３Ｄ．１０５．从集合｛１,２，３，···，１０｝中任意选出三个不同的数，使它们成等比数列，这样的等比数列的个数是Ａ．３Ｂ．４Ｃ．６Ｄ．８６．用０,１,２，···，９十个数字，可以组成有重复数字的三位数的个数是Ａ．２４３Ｂ．２５２Ｃ．２６１Ｄ．２７９７．从０,２中选一个数字，从１,３,５中选两个数字，组成无重复数字的三位奇数的个数为Ａ．２４Ｂ．１８Ｃ．１２Ｄ．６８．有不同颜色的四件上衣和不同颜色的三条长裤，如果一条长裤与一件上衣配成一套，则不同的配法种数有９．若三角形的三边均为整数，其中一边长为４，另外两边为ｂ，ｃ，且满足ｂ≤４≤ｃ，则这样的三角形有个１０．已知集合Ｍ=｛－３，－２，－１,０，１,２｝，Ｐ（a，ｂ）表示平面上的点（a，ｂ∈Ｍ，则（１）Ｐ可表示平面上不同的点的个数是（２）Ｐ可表示平面上第二象限的点的个数是（３））Ｐ可表示不在直线y＝x的点的个数是１１．已知集合Ｍ=｛－３，－２，－１,０，１,２｝，Ｐ（a ，ｂ）若a ，ｂ，ｃ∈Ｍ，则 （１）y ＝2++ax bx c 表示的不同的二次函数的个数是（２））y ＝2++ax bx c 表示的开口向下的不同的二次函数的个数是 １２．如果一个三位正整数如“123a a a ”满足123<>a a a ，则称这样的三位数为凸数，（如１２０,４６４,２６５），那么所有的凸数的个数是１３．上海某区政府召集５家企业的负责人开年终总结经验交流会，其中甲企业有２人到会，其余４家企业各有１人到会，会上推选３人发言，则这３人来自３家不同企业的可能情况的种数为１４．满足a ，ｂ∈｛－１,０，１,２｝，，且关于x 的方程2+2+ax x b ＝０有实数解的有序数对（a ，ｂ）的个数为１５．我们把各为数字之和为６的四位数称为“六合数”（如２０１３是“六合数”），则“六合数”中首位为２的共有 个三.参考答案１—７ ＣＡＢＣＤＢＢ ８．１２ ９．１０ １０．３６,６,３０,１１．１８０,７２,１２． ２４０,１３． １６,１４． １３,１５． １５。
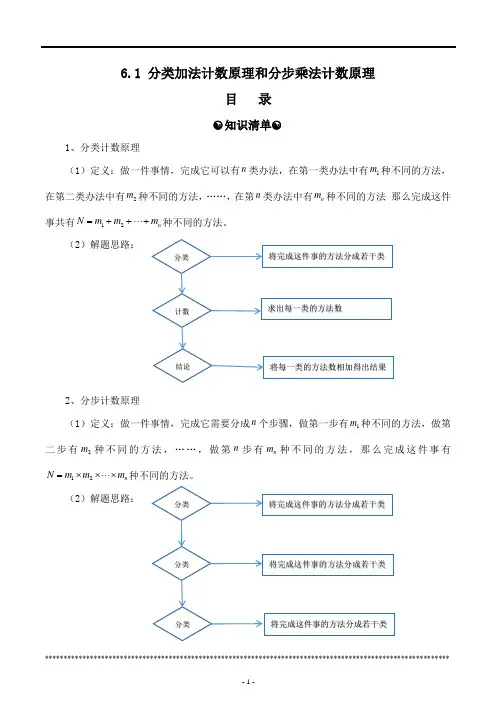
6.1 分类加法计数原理和分步乘法计数原理目 录☯知识清单☯1、分类计数原理（1）定义：做一件事情，完成它可以有n 类办法，在第一类办法中有1m 种不同的方法，在第二类办法中有2m 种不同的方法，……，在第n 类办法中有n m 种不同的方法 那么完成这件事共有12n N m m m =++⋅⋅⋅+种不同的方法。
（2）解题思路：2、分步计数原理（1）定义：做一件事情，完成它需要分成n 个步骤，做第一步有1m 种不同的方法，做第二步有2m 种不同的方法，……，做第n 步有n m 种不同的方法，那么完成这件事有12n N m m m =⨯⨯⋅⋅⋅⨯种不同的方法。
（2）解题思路：分类计数 结论 将完成这件事的方法分成若干类求出每一类的方法数将每一类的方法数相加得出结果分类 分类 分类将完成这件事的方法分成若干类将完成这件事的方法分成若干类将完成这件事的方法分成若干类（3）分步两个条件：①步骤互相独立，互不干扰②步与步确保连续，逐步完成3、两个计数原理的关系（1）两个计数原理的联系与区别分类加法计数原理分步乘法计数原理相同点用来计算完成一件事的方法种类不同点分类完成，类类相加，关键是“分类”分步相乘，步步相乘，关键是“分步”分类完成一件事，每类办法中的每种方法都能独立完成这件事情，要注意“类”与“类”之间的独立性和并列性。
分类计数原理可利用“并联”电路来理解。
分步完成一件事，并且只有各个步骤都完成才算完成这件事，要注意“步”与“步”之间的连续性。
分步计数原理可利用“串联”电路来理解。
运用加法运算运用乘法运算注意点类类独立，不重不漏步步相依，步骤完整（2）利用两个计数原理解决应用问题的一般思路：①弄清完成一件事是做什么；②确定是先分类后分步，还是先分步后分类；③弄清分步、分类的标准是什么；④类要做到不重不漏。
☯典型例题☯母题1：分类计算原理1.设椭圆22xa＋22yb＝1的焦点在y轴上，其中a∈{1，2，3，4，5}，b＝{1，2，3，4，5，6，7}，则满足上述条件的椭圆个数为( )A．20 B．24 C．12 D．112.如图所示，由连接正八边形的三个顶点而组成的三角形中与正八边形有公共边的三角形有________个.3.算盘是中国古代的一项重要发明．现有一种算盘(如图1)，共两档，自右向左分别表示个位和十位，档中横以梁，梁上一珠拨下，记作数字5，梁下五珠，上拨一珠记作数字1(如图2中算盘表示整数51)．如果拨动图1算盘中的三枚算珠，可以表示不同整数的个数为( )A．16B．15C．12D．10分类计数原理解题思路1.根据题目特点恰当选择一个分类标准。
