人教版九年级数学第二十二章《二次函数》解答题专题复习 (46)(含解析)

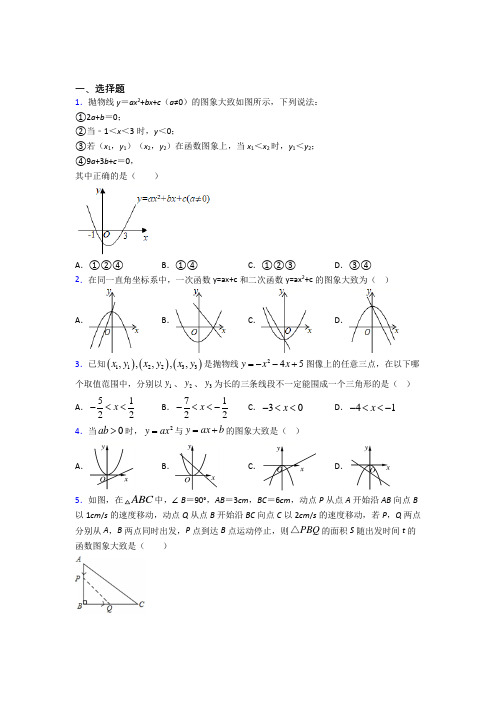
人教版九年级数学第二十二章二次函数综合复习一、选择题（本大题共10道小题）1. 抛物线与x轴交于点(－1，0)和(3，0)，与y轴交于点(0，－3)，则此抛物线的解析式为()A．y＝x2＋2x＋3 B．y＝x2－2x－3C．y＝x2－2x＋3 D．y＝x2＋2x－32.若抛物线y＝x2－2x＋3不动，将平面直角坐标系．．．．．．．．xOy先沿水平方向向右平移1个单位，再沿铅直方向向上平移3个单位，则原抛物线图象的解析式应变为( ) A. y＝(x－2)2＋3 B. y＝(x－2)2＋5C. y＝x2－1D. y＝x2＋43. （2020·深圳）二次函数y＝ax2＋bx＋c(a≠0)的顶点坐标为(－1，n)，其部分图象如图所示，以下结论错误．．的是（）A．abc＞0 B．4ac－b2＜0C．3a＋c＞0 D．关于x的方程ax2＋bx＋c＝n＋1无实数根4. 如图，抛物线y=ax2+bx+c(a≠0)与x轴交于点(-3，0)，其对称轴为直线x=-.结合图象分析下列结论:①abc>0;②3a+c>0;③当x<0时，y随x的增大而增大;④一元二次方程cx2+bx+a=0的两根分别为x1=-，x2=;⑤<0;⑥若m，n(m<n)为方程a(x+3)·(x-2)+3=0的两个根，则m<-3，n>2，其中正确的结论有()A .3个B .4个C .5个D .6个5.已知二次函数y ＝ax 2＋bx ＋c 的图象如图所示，则以下结论同时成立的是( )A.⎩⎨⎧abc>0，b2－4ac<0 B .⎩⎨⎧abc<0，2a ＋b>0 C.⎩⎨⎧abc>0，a ＋b ＋c<0 D.⎩⎨⎧abc<0，b2－4ac>06. （2020•湘西州）已知二次函数y ＝ax 2+bx +c 图象的对称轴为x ＝1，其图象如图所示，现有下列结论：①abc ＞0，②b ﹣2a ＜0，③a ﹣b +c ＞0，④a +b ＞n （an +b ），（n ≠1），⑤2c ＜3b ．正确的是（ ）A ．①③B ．②⑤C ．③④D ．④⑤7. 二次函数y ＝ax 2＋bx ＋c 的部分图象如图所示，顶点为D(－1，2)，与x 轴的一个交点A 在点(－3，0)和(－2，0)之间，有以下结论：①b 2－4ac ＜0；②a ＋b ＋c ＜0；③c －a ＝0；④一元二次方程ax 2＋bx ＋c －2＝0有两个相等的实数根．其中正确的结论有( )A ．1个B ．2个C ．3个D ．4个8. 矩形ABCD 的两条对称轴为坐标轴，点A 的坐标为(2，1)，一张透明纸上画有一个点和一条抛物线，平移透明纸，使这个点与点A 重合，此时抛物线的函数解析式为y ＝x2，再次平移这张透明纸，使这个点与点C 重合，则此时抛物线的函数解析式变为( ) A ．y ＝x2＋8x ＋14 B ．y ＝x2－8x ＋14C ．y ＝x2＋4x ＋3D ．y ＝x2－4x ＋39. 根据下列表格中的对应值，判断方程ax 2＋bx ＋c ＝0(a ≠0)的一个根x 的取值范围是( )A.1.23＜x ＜1.24B ．1.24＜x ＜1.25C ．1.25＜x ＜1.26D ．1＜x ＜1.2310. 如图，抛物线y ＝12x 2－7x ＋452与x 轴交于点A ，B ，把抛物线在x 轴及其下方的部分记作C 1，将C 1向左平移得到C 2，C 2与x 轴交于点B ，D ，若直线y ＝12x ＋m 与C 1，C 2共有3个不同的交点，则m 的取值范围是( )A ．－458＜m ＜－52B ．－298＜m ＜－12C ．－298＜m ＜－52D ．－458＜m ＜－12二、填空题（本大题共8道小题）11.已知抛物线y ＝2(x －1)2上有两点(x 1，y 1)，(x 2，y 2)，且1＜x 1＜x 2，则y 1与y 2的大小关系是________．12.某厂今年一月份新产品的研发资金为a元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年三月份新产品的研发资金y(元)关于x的函数解析式为y＝__________.13.某商店从厂家以每件21元的价格购进一批商品，该商品可以自行定价，若每件商品的售价为a元，则可卖出(350－10a)件．但物价部门限定每件商品加价不能超过进价的40%，若商店想获得最大利润，则每件商品的价格应定为________元．14. 抛物线y＝12(x＋3)2－2是由抛物线y＝12x2先向________(填“左”或“右”)平移________个单位长度，再向________(填“上”或“下”)平移________个单位长度得到的.15. 已知A(0，3)，B(2，3)是抛物线y＝－x2＋bx＋c上两点，该抛物线的顶点坐标是________．16.二次函数y＝－x2＋6x－5的图象开口________，对称轴是________，顶点坐标是________；与x轴的两个交点坐标分别是________，与y轴的交点坐标是_____ ___；在对称轴左侧，即x________时，y随x的增大而________，在对称轴右侧，即x________时，y随x的增大而________，当x＝________时，y有最________值为________；抛物线y＝－x2＋6x－5是由抛物线y＝－x2向________(填“左”或“右”)平移________个单位长度，再向________(填“上”或“下”)平移________个单位长度得到的．17.顶点坐标是(2，0)，且与抛物线y＝－3x2的形状、开口方向都相同的抛物线的解析式为________．18.已知函数y＝ax2＋c的图象与函数y＝－3x2－2的图象关于x轴对称，则a＝______ __，c＝________．三、解答题（本大题共4道小题）19.已知二次函数y1＝ax2＋bx＋c(ab≠0)的图象经过点(0，－1)，顶点为A(－2，－5)．(1)求该二次函数的解析式；(2)把二次函数在第三象限内的部分图象记为图象G，若直线y2＝n与图象G有且仅有1个交点，求n的取值范围．20. 如图所示，抛物线y＝ax2－5x＋4a与x轴相交于点A，B，且过点C(5，4)．(1)求a的值和该抛物线顶点P的坐标；(2)若Q是横轴上方抛物线上的点，且S△QAB＝S△P AB，求点Q的坐标．21.如图，排球运动员站在O处练习发球，将球从点O正上方2米的点A处发出，把球看成点，其运行的高度y(米)与运行的水平距离x(米)满足解析式y＝a(x－6)2＋h.已知球网与点O的水平距离为9米，高度为2.43米，球场的边界距点O的水平距离为18米．(1)当h＝2.6时，求y与x之间的函数解析式；(2)当h＝2.6时，球能否越过球网？球会不会出界？请说明理由；(3)若球一定能越过球网，又不出边界，则h的取值范围是多少？22. 在平面直角坐标系中，设二次函数y1＝(x＋a)(x－a－1)，其中a≠0.(1)若函数y1的图象经过点(1，－2)，求函数y1的表达式；(2)若一次函数y2＝ax＋b的图象与y1的图象经过x轴上同一点，探究实数a，b满足的关系式；(3)已知点P(x0，m)和Q(1，n)在函数y1的图象上．若m<n，求x0的取值范围．人教版九年级数学第二十二章二次函数综合复习-答案一、选择题（本大题共10道小题）1. 【答案】B[解析] 由抛物线与x轴交于点(－1，0)和(3，0)，设此抛物线的解析式为y＝a(x＋1)(x－3)．又因为抛物线与y轴交于点(0，－3)，把x＝0，y＝－3代入y＝a(x＋1)(x－3)，得－3＝a(0＋1)(0－3)，即－3a＝－3，解得a＝1，故此抛物线的解析式为y＝(x ＋1)(x－3)＝x2－2x－3.故选B.2. 【答案】C 【解析】由抛物线y＝x2－2x＋3得y＝(x－1)2＋2.保持抛物线不动，将平面直角坐标系先沿水平方向向右平移1个单位，其实质相当于抛物线向左平移1个单位，再将平面直角坐标系向上平移3个单位，则相当于抛物线向下平移3个单位，根据抛物线平移规律：左加右减，上加下减，可得新的抛物线解析式为y＝(x－1＋1)2＋2－3＝x2－1.3. 【答案】C【解析】根据抛物线开口向下，得到a＜0，对称轴为直线x＝－b2a＝－1，知b＝2a＜0，抛物线与y轴交于正半轴，c＞0，∴abc＞0，故选项A正确；根据抛物线与x轴有两个交点，∴b2－4ac＞0，即4ac－b2＜0，故选项B正确；当x＝1时，y＝a＋b＋c＜0，又∵b＝2a，∴3a＋c＜0，∴选项C错误；∵抛物线开口向下，顶点为（－1，n），∴函数有最大值n，即抛物线y＝ax2＋bx＋c与直线y ＝n＋1无交点，一元二次方程ax2＋bx＋c＝n＋1无实数根，选项D正确；而要选择结论错误．．的，因此本题选C．4. 【答案】C[解析]①由图象可知a<0，b<0，c>0，∴abc>0，故①正确;②由于对称轴是直线x=-，∴a=b.∵图象与x轴的一个交点是(-3，0)，∴另一个交点是(2，0)，把(2，0)代入解析式可得4a+2b+c=0，∴6a+c=0，∴3a+c=-3a，∵a<0，∴-3a>0，∴3a+c>0，故②正确;③由图象可知当-<x<0时，y随x的增大而减小，∴当x<0时，y随x的增大而增大是错误的;④一元二次方程ax2+bx+c=0的两根为x1=-3，x2=2，∴一元二次方程cx2+bx+a=0的两根分别为x1=-，x2=，正确;⑤由图象顶点的纵坐标大于0可知，>0，∴<0，正确;⑥若m，n(m<n)为方程a(x+3)(x-2)+3=0的两个根，则a(x+3)(x-2)=-3，由图象可知，当y=-3时，m<-3，n>2，⑥正确，综上，正确的结论有5个，故选C.5. 【答案】C[解析] 由图象可知，当x＝1时，y＜0，∴a＋b＋c＜0；∵二次函数图象与x轴有两个交点，∴b2－4ac>0；∵二次函数图象与y轴的交点在y轴负半轴上，∴c＜0；∵二次函数图象开口向上，∴a＞0；∵对称轴－b2a＞0，a＞0，∴b＜0.∴abc＞0.故选C.6. 【答案】D【解析】本题主要考查了图象与二次函数系数之间的关系，二次函数y＝ax2+bx+c 系数符号由抛物线开口方向、对称轴和抛物线与y轴的交点、抛物线与x轴交点的个数确定．①由图象可知：a＜0，b＞0，c＞0，abc＜0，故此选项错误；②当x ＝﹣2时，y ＝4a ﹣2b +c ＜0，即b ﹣2a ＞>0，故此选项错误；③当x =-1时，y =a -b +c ＜0，故此选项错误；④当x ＝1时，y 的值最大．此时，y ＝a +b +c ，而当x ＝n 时，y ＝an 2+bn +c ，所以a +b +c ＞an 2+bn +c ，故a +b ＞an 2+bn ，即a +b ＞n （an +b ），故此选项正确．⑤当x ＝3时函数值小于0，y ＝9a +3b +c ＜0，且x1，即a，代入得9（）+3b +c ＜0，得2c ＜3b ，故此选项正确；故④⑤正确．因此本题选 D ．7. 【答案】B8. 【答案】A[解析] 因为矩形ABCD 的两条对称轴为坐标轴，所以矩形ABCD关于坐标原点成中心对称．因为A ，C 是矩形对角线上的两个点，所以点A ，C 关于原点对称，所以点C 的坐标为(－2，－1)，所以抛物线向左平移了4个单位长度，向下平移了2个单位长度，所以平移后抛物线的函数解析式为y ＝(x ＋4)2－2＝x2＋8x ＋14.故选A.9. 【答案】B10. 【答案】C【解析】 如图．∵抛物线y ＝12x 2－7x ＋452与x 轴交于点A ，B ，∴B (5，0)，A (9，0)．∴抛物线C 1向左平移4个单位长度得到C 2，∴平移后抛物线的解析式为y ＝12(x －3)2－2.当直线y ＝12x ＋m 过点B 时，有2个交点， ∴0＝52＋m ，解得m ＝－52；当直线y ＝12x ＋m 与抛物线C 2只有一个公共点时，令12x ＋m ＝12(x －3)2－2，∴x 2－7x ＋5－2m ＝ 0，∴Δ＝49－20＋8m ＝0，∴m ＝－298，此时直线的解析式为y＝12x －298，它与x 轴的交点为(294，0)，在点A 左侧，∴此时直线与C 1，C 2有2个交点，如图所示．∴当直线y ＝12x ＋m 与C 1，C 2共有3个不同的交点时，－298＜m ＜－52.二、填空题（本大题共8道小题）11. 【答案】y 1<y 2 [解析] ∵抛物线的解析式是y ＝2(x －1)2， ∴其对称轴是直线x ＝1，抛物线的开口向上， ∴在对称轴右侧，y 随x 的增大而增大．又∵抛物线y ＝2(x －1)2上有两点(x 1，y 1)，(x 2，y 2)，且1＜x 1＜x 2，∴y 1<y 2. 12. 【答案】a(1＋x)213. 【答案】28 [解析] 设商店所获利润为y 元．根据题意，得y ＝(a －21)(350－10a)＝－10a 2＋560a －7350＝－10(a －28)2＋490， 即当a ＝28时，可获得最大利润．又21×(1＋40%)＝21×1.4＝29.4，而28<29.4，所以a ＝28符合要求． 故商店应把每件商品的价格定为28元，此时可获得最大利润．14.【答案】左 3 下 2 [解析] 抛物线y ＝12x 2的顶点坐标为(0，0)，而抛物线y ＝12(x ＋3)2－2的顶点坐标为(－3，－2)，所以把抛物线y ＝12x 2先向左平移3个单位长度，再向下平移2个单位长度，就得到抛物线y ＝12(x ＋3)2－2.15. 【答案】(1，4)【解析】∵A(0，3)、B(2，3)，两点纵坐标相同，∴A 、B两点关于直线x ＝1对称，∴抛物线的对称轴是直线x ＝1，即－b2×（－1）＝1，解得b ＝2，∵当x ＝0时，y ＝3，∴c ＝3，∴抛物线的解析式为y ＝－x 2＋2x ＋3，当x ＝1时，y ＝－x 2＋2x ＋3＝－12＋2×1＋3＝4，∴抛物线的顶点坐标是(1，4).16. 【答案】向下 直线x ＝3 (3，4) (1，0)，(5，0) (0，－5) ＜3 增大 ＞3 减小 3 大 4 右 3 上 417. 【答案】y ＝－3(x －2)218. 【答案】32三、解答题（本大题共4道小题）19. 【答案】解：(1)∵二次函数y 1＝ax 2＋bx ＋c(ab≠0)的图象的顶点为A(－2，－5)， ∴y 1＝a(x ＋2)2－5. 又∵图象经过点(0，－1)， ∴－1＝a(0＋2)2－5，解得a ＝1， ∴y 1＝(x ＋2)2－5＝x 2＋4x －1.(2)结合图象，知直线y ＝n 与图象G 有且仅有1个交点时，n ＝－5或－1≤n ＜0.20. 【答案】解：(1)把(5，4)代入y ＝ax 2－5x ＋4a ，得25a －25＋4a ＝4，解得a ＝1. ∴该抛物线的解析式为y ＝x 2－5x ＋4. ∵y ＝x 2－5x ＋4＝⎝ ⎛⎭⎪⎫x －522－94，∴顶点P 的坐标为⎝ ⎛⎭⎪⎫52，－94. (2)∵S △QAB ＝S △PAB ，∴点Q 和点P 到横轴的距离相等， 即它们纵坐标的绝对值相等． 由(1)可知点P 的纵坐标是－94， ∴点Q 的纵坐标是94.令x 2－5x ＋4＝94，解得x ＝5±3 22.∴点Q 的坐标为(5－3 22，94)或(5＋3 22，94)．21. 【答案】解：(1)当h ＝2.6时，y ＝a(x －6)2＋2.6.因为点A(0，2)在抛物线上，所以2＝a(0－6)2＋2.6，解得a ＝－160， 所以y 与x 之间的函数解析式为y ＝－160(x －6)2＋2.6. (2)球能越过球网且会出界．理由：当x＝9时，y＝－160(9－6)2＋2.6＝2.45＞2.43，所以球能越过球网；当x＝18时，y＝－160(18－6)2＋2.6＝－2.4＋2.6＝0.2＞0，所以球会出界．(3)把x＝0，y＝2代入y＝a(x－6)2＋h，得a＝2－h 36，所以y＝2－h36(x－6)2＋h.当x＝9时，y＝2－h36(9－6)2＋h＝2＋3h4＞2.43.①当x＝18时，y＝2－h36(18－6)2＋h＝8－3h≤0.②由①②解得h≥8 3.22. 【答案】【思维教练】由图象过点(1，－2)，将其带入y1的函数表达式中，解方程即可；(2)由y1＝(x＋a)(x－a－1)可得出y1过x轴上的两点的坐标，然后分两种情况讨论即可；(3)先求出y1＝(x＋a)(x－a－1)的对称轴，根据开口向上的二次函数，离对称轴越近，函数值越小即可得解．解：(1)∵函数y1＝(x＋a)(x－a－1)图象经过点(1，－2)，∴把x＝1，y＝－2代入y1＝(x＋a)(x－a－1)得，－2＝(1＋a)(－a)，(2分)化简得，a2＋a－2＝0，解得，a1＝－2，a2＝1，∴y1＝x2＋x－2；(4分)(2)函数y1＝(x＋a)(x－a－1)图象在x轴的交点为(－a，0)，(a＋1，0)，①当函数y2＝ax＋b的图象经过点(－a，0)时，把x＝－a，y＝0代入y2＝ax＋b中，得a2＝b；(6分)②当函数y2＝ax＋b的图象经过点(a＋1，0)时，把x＝a＋1，y＝0代入y2＝ax＋b中，得a2＋a＝－b；(8分)(3)∵抛物线y1＝(x＋a)(x－a－1)的对称轴是直线x＝－a＋a＋12＝12，m<n，∵二次项系数为1，∴抛物线的开口向上，∴抛物线上的点离对称轴的距离越大，它的纵坐标也越大，∵m<n，∴点Q离对称轴x＝12的距离比P离对称轴x＝12的距离大，(10分)∴|x0－12|<1－12，∴0<x0<1.(12分)。

第二十二章 二次函数一、选择题（每题3分，共24分）1．下列各式中，y 是x 的二次函数的是（ ）A ．y =1x 2B ．y =x 2+1x +1C ．y =2x 2−1D ．y =x 2−12．下列抛物线中，与y =−3x 2+1抛物线形状、开口方向完全相同，且顶点坐标为(−1,2)的是（ ）A ．y =−3(x +1)2+2B ．y =−3(x−1)2+2C ．y =3(x +1)2+2D ．y =−3(x +1)2+23．在平面直角坐标系中，将二次函数y =3x 2的图象向下平移3个单位长度，所得函数的解析式为（ ）A ．y =3x 2−1B ．y =3x 2+1C ．y =3x 2−3D ．y =3x 2+34．若A (−1,y 1)，B (1,y 2)，C (4,y 3)三点都在二次函数y =−(x−2)2+k 的图象上，则y 1，y 2，y 3的大小关系为（ ）A ．y 1<y 2<y 3B ．y 1<y 3<y 2C ．y 3<y 1<y 2D ．y 3<y 2<y 15．二次函数y =−x 2−2x +c 2−2c 在−3≤x ≤2的范围内有最小值为−5，则c 的值（ ）A ．3或−1B ．−1C ．−3或1D ．36．已知二次函数y =x 2−3x +m （m 为常数）的图象与x 轴的一个交点为(1,0)，则关于x 的一元二次方程x 2−3x +m =0的两实数根是（ ）A ．x 1=0，x 2=−1B ．x 1=1，x 2=2C ．x 1=1，x 2=0D ．x 1=1，x 2=37．如图（1）是一个横断面为抛物线形状的拱桥，当水面在l 时，拱顶（拱桥洞的最高点）离水面3m ，水面宽6m ．如图（2）建立平面直角坐标系，则抛物线的解析式是（ ）A ．y =−13x 2B ．y =13x 2C ．y =−3x 2D ．y =3x 28．如图，已知经过原点的抛物线y =a x 2+bx +c(a ≠0)的对称轴是直线x =−1，下列结论中：①ab >0，②a +b +c >0，③当−2<x <0时y <0.正确的个数是（ ）A．0个B．1个C．2个D．3个二、填空题（每题4分，共20分）9．抛物线y=−3(x−1)2−2的对称轴是直线 ．10．若y=(m−2)x m2−2+x−3是关于x的二次函数．则m的值为 ．11．抛物线y=a x2+bx+c(a≠0)的部分图象如图所示，与x轴的一个交点为(3,0)，对称轴为直线x=1，则当y≤0时，x的取值范围是 ．12．如图，要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端A点安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为2m处达到最高，高度为5m，水柱落地处离池中心距离为6m，则水管的长度OA是 m．13．如图，在平面直角坐标中，抛物线y=a x2+bx(a>0)和直线y=kx(k>0)交于点O和点A，则不等式a x2 +bx<kx的解集为 ．三、解答题（共56分）14．如图所示，二次函数y=a x2+bx+c(a≠0)的图保与x轴相交于A，B两点，其中点A的坐标为(−1，0)，M(2，9)为抛物线的顶点.（1）求抛物线的函数表达式.（2）求△MCB的面积.15．如图所示，在平面直角坐标系中，二次函数y=a x2+4x−3的图象的顶点是A，与x轴交于B，C两点，与y轴交于点D.点B的坐标是(1，0).（1）求A，C两点的坐标，并根据图象直接写出当y>0时x的取值范围.（2）平移该二次函数的图象，使点D恰好落在点A的位置上，求平移后的图象所对应的二次函数的表达式. 16．已知，一个铝合金窗框如图所示，所使用的铝合金材料长度为18m．设AB长为xm，窗户的总面积为Sm2．（1）求S关于x的函数表达式．（2）若AB的长不能低于2m，且AB＜BC，求此时窗户总面积S的最大值和最小值．17．第十九届亚运会在杭州隆重举办，政府鼓励全民加强体育锻炼，李明在政府的扶持下投资销售一种进价为每件50元的乒乓球拍．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：y=−10x+900．（1）设月利润为W（元），求W关于x的函数表达式．（2）销售单价定为每件多少元时，所得月利润最大？最大月利润为多少元？（3）若物价部门规定这种乒乓球拍的销售单价不得超过75元，李明想使获得的月利润不低于3000元，求销售单价x的取值范围．18．如图，二次函数y=a x2+bx+c的图象交x轴于A(−1，0)，B(2，0)，交y轴于C(0，−2).（1）求二次函数的解析式；（2）若点M为该二次函数图象在第四象限内一个动点，求点M运动过程中，四边形ACMB面积的最大值；（3）点P在该二次函数图象的对称轴上，且使|PB−PC|最大，求点P的坐标。

九年级数学上册第二十二章二次函数考点总结单选题1、若y=（m＋1）x m2−6m−5是二次函数，则m= （）A．－1B．7C．－1或7D．以上都不对答案：B分析：令x的指数为2，系数不为0，列出方程与不等式解答即可．由题意得：m2-6m-5=2；且m+1≠0；解得m=7或-1；m≠-1，∴m=7，故选：B．小提示：利用二次函数的定义，二次函数中自变量的指数是2；二次项的系数不为0．2、已知抛物线y=x2+bx+c与x轴的两个交点之间的距离为6，对称轴为x=3，则抛物线的顶点P关于x轴对称的点P′的坐标是（）A．(3,9)B．(3,−9)C．(−3,9)D．(−3,−9)答案：A分析：根据抛物线y＝x2+bx+c与x轴两个交点间的距离为6．对称轴为直线x＝3，可以得到b、c的值，然后即可得到该抛物线的解析式，再将函数解析式化为顶点式，即可得到点P的坐标，然后根据关于x轴对称的点的特点横坐标不变，纵坐标互为相反数，即可得到点P关于x轴的对称点的坐标．解：设抛物线y＝x2+bx+c与x轴两个交点坐标为（x1，0），（x2，0），∵抛物线y＝x2+bx+c与x轴两个交点间的距离为6，对称轴为直线x＝3，∴（x1﹣x2）2＝（x1+x2）2﹣4x1x2＝36，−b=3，2×1∴（﹣b）2﹣4×c＝36，b＝﹣6，解得：c＝0，∴抛物线的解析式为y＝x2﹣6x＝（x﹣3）2﹣9，∴顶点P的坐标为（3，﹣9），∴点P关于x轴的对称点的坐标是（3，9），故选：A．小提示：本题考查抛物线与x轴的交点、二次函数的性质、关于x轴对称的点的坐标特点，解答本题的关键是求出点P的坐标，利用二次函数的性质解答．3、已知a是不为0的常数，函数y＝ax和函数y＝﹣ax2+a在同一平面直角坐标系内的图象可以是（）A．B．C．D．答案：C分析：根据题意分a>0,a<0两种情况讨论，结合函数图象即可求解．解：A.正比例函数中a<0，二次函数开口向上，−a>0，与y轴的交点在y轴正半轴，则a>0，矛盾，故A 不正确；B.正比例函数中a>0，二次函数开口向上，−a>0，与y轴的交点在y轴正半轴，则a>0，矛盾，故B不正确；C.正比例函数中a>0，二次函数开口向下，−a<0，与y轴的交点在y轴正半轴，则a>0，故C正确；D. .正比例函数中a<0，二次函数开口向下，−a<0，与y轴的交点在y轴正半轴，则a>0，矛盾，故D不正确；故选C小提示：本题考查了正比例函数与二次函数的图象的性质，掌握正比例函数与二次函数的图象的性质是解题的关键．4、如图，已知开口向下的抛物线y =ax 2+bx +c 与x 轴交于点(−1,0)对称轴为直线x =1．则下列结论：①abc >0；②2a +b =0；③函数y =ax 2+bx +c 的最大值为−4a ；④若关于x 的方数ax 2+bx +c =a +1无实数根，则−15<a <0．正确的有（ ）A ．1个B ．2个C ．3个D ．4个答案：C分析：由图象可知，图像开口向下，a ＜0，对称轴为x =1，故−b 2a =1，故b ＞0，且b =−2a ，则2a +b =0 图象与y 轴的交点为正半轴，则c ＞0，由此可知abc ＜0，故①错误，由图象可知当x =1时，函数取最大值，将x =1，代入y =ax 2+bx +c ，中得：y =a +b +c ，计算出函数图象与x 轴的另一交点为（3,0）设函数解析式为：y =a(x −x 1)(x −x 2)，将交点坐标代入得化简得：y =ax 2−2ax −3a ，将x =1，代入可得：y =a −2a −3a =−4a ，故函数的最大值为-4a ，、ax 2+bx +c =a +1变形为：ax 2+bx +c −a −1=0要使方程无实数根，则b 2−4a(c −a −1)<0，将c =-3a ，b =−2a ，代入得：20a 2+4a <0，因为a ＜0，则20a +4>0，则a >−15，综上所述−15<a <0，结合以上结论可判断正确的项． 解：由图象可知，图像开口向下，a ＜0，对称轴为x =1，故−b 2a =1，故b ＞0，且b =−2a ，则2a +b =0故②正确，∵图象与y 轴的交点为正半轴，∴c ＞0，则abc ＜0，故①错误，由图象可知当x =1时，函数取最大值，将x =1，代入y =ax 2+bx +c ，中得：y =a +b +c ，由图象可知函数与x 轴交点为（﹣1,0），对称轴为将x =1，故函数图象与x 轴的另一交点为（3,0），设函数解析式为：y =a(x −x 1)(x −x 2)，将交点坐标代入得：y =a(x +1)(x −3)，故化简得：y =ax 2−2ax −3a ，将x =1，代入可得：y =a −2a −3a =−4a ，故函数的最大值为-4a ，故③正确，ax 2+bx +c =a +1变形为：ax 2+bx +c −a −1=0要使方程无实数根，则b 2−4a(c −a −1)<0，将c =-3a ，b =−2a ，代入得：20a 2+4a <0，因为a ＜0，则20a +4>0，则a >−15，综上所述−15<a <0，故④正确，则②③④正确，故选C ．小提示：本题考查二次函数的一般式，二次函数的交点式，二次函数的最值，对称轴，以及交点坐标掌握数形结合思想是解决本题的关键．5、若y ＝（a ﹣2）x 2﹣3x +2是二次函数，则a 的取值范围是（ ）A ．a ≠2B ．a ＞0C ．a ＞2D ．a ≠0答案：A分析：根据二次函数的二次项系数不为0可得关于a 的不等式，解不等式即得答案．解：由题意得： a −2≠0，则a ≠2．故选：A ．小提示：本题考查了二次函数的定义，属于基础题型，掌握二次函数的概念是关键．6、如图，一抛物线型拱桥，当拱顶到水面的距离为2m 时，水面宽度为4m ．那么水位下降1m 时，水面的宽度为（ ）A ．√6mB ．2√6mC ．(√6−4)mD ．(2√6−4)m答案：B分析：结合已知条件先建立适当的坐标系，然后设出解析式，利用点的坐标求得解析式，再将y=−3代入解析式求得相应的x的值，进而求得答案．解：以拱顶为坐标原点建立坐标系，如图：∴设抛物线解析式为：y=ax2，∵观察图形可知抛物线经过点B(2,−2)，∴−2=a⋅22，∴a=−1，2∴抛物线解析式为：y=−1x2，2∴当水位下降1米后，即当y=−2−1=−3时，有−1x2=−3，2∴x1=√6，x2=−√6，∴水面的宽度为：2√6m．故选：B．小提示：本题考查了二次函数的应用，根据已知条件建立坐标系从而求得二次函数解析式是解决问题的关键．7、某商场降价销售一批名牌衬衫，已知所获利润y（元）与降价x（元）之间的关系是y＝－2x2＋60x＋800，则利润获得最多为（）A．15元B．400元C．800元D．1250元答案：D分析：将函数关系式转化为顶点式，然后利用开口方向和顶点坐标即可求出最多的利润．解：y＝－2x2＋60x＋800＝－2（x－15）2＋1250∵－2＜0故当x＝15时，y有最大值，最大值为1250即利润获得最多为1250元故选：D．小提示：此题考查的是利用二次函数求最值，掌握将二次函数的一般式转化为顶点式求最值是解决此题的关键．8、已知a<−1，点(a−1,y1)，(a,y2)，(a+1,y3)都在函数y=3x2−2的图象上，则（）A．y1<y2<y3B．y1<y3<y2C．y2<y1<y3D．y3<y2<y1答案：D分析：先求出抛物线的对称轴，抛物线y=3x2-2的对称轴为y轴，即直线x=0，图象开口向上，当a＜-1时，a-1＜a＜a+1＜0，在对称轴左边，y随x的增大而减小，由此可判断y1，y2，y3的大小关系．解：∵当a＜-1时，a-1＜a＜a+1＜0，而抛物线y=3x2-2的对称轴为直线x=0，开口向上，∴三点都在对称轴的左边，y随x的增大而减小，∴y1＞y2＞y3．故选：D．小提示：本题考查的是二次函数图象上点的坐标特点，当二次项系数a＞0时，在对称轴的左边，y随x的增大而减小，在对称轴的右边，y随x的增大而增大；a＜0时，在对称轴的左边，y随x的增大而增大，在对称轴的右边，y随x的增大而减小．9、某超市销售一种商品，每件成本为50元，销售人员经调查发现，该商品每月的销售量y（件）与销售单价x （元）之间满足函数关系式y=−5x+550，若要求销售单价不得低于成本，为每月所获利润最大，该商品销售单价应定为多少元？每月最大利润是多少？（）A．90元，4500元B．80元，4500元C．90元，4000元D．80元，4000元答案：B分析：设每月所获利润为w ，按照等量关系列出二次函数，并根据二次函数的性质求得最值即可．解：设每月总利润为w ，依题意得：w =y(x −50)=(−5x +550)(x −50)=−5x 2+800x −27500=−5(x −80)2+4500∵−5<0，此图象开口向下，又x ≥50，∴当x =80时，w 有最大值，最大值为4500元．故选：B ．小提示：本题考查了二次函数在实际生活中的应用，根据题意找到等量关系并掌握二次函数求最值的方法是解题的关键．10、下表中列出的是一个二次函数的自变量x 与函数y 的几组对应值：B ．这个函数的图象与x 轴无交点C ．这个函数的最小值小于-6D ．当x >1时，y 的值随x 值的增大而增大答案：C分析：利用表中的数据，求得二次函数的解析式，再配成顶点式，根据二次函数的性质逐一分析即可判断． 解：设二次函数的解析式为y =ax 2+bx +c ，依题意得：{4a −2b +c =6c =−4a +b +c =−6 ，解得：{a =1b =−3c =−4， ∴二次函数的解析式为y =x 2−3x −4=(x −32)2−254，∵a =1>0，∴这个函数的图象开口向上，故A 选项不符合题意；∵△=b 2−4ac =(−3)2−4×1×(−4)=25>0，∴这个函数的图象与x 轴有两个不同的交点，故B 选项不符合题意；∵a =1>0，∴当x =32时，这个函数有最小值−254<−6，故C 选项符合题意；∵这个函数的图象的顶点坐标为(32，−254)， ∴当x >32时，y 的值随x 值的增大而增大，故D 选项不符合题意；故选：C ．小提示：本题主要考查了待定系数法求二次函数的解析式以及二次函数的性质，利用二次函数的性质解答是解题关键．填空题11、如图，抛物线y =ax 2+bx +c(a ≠0)与x 轴交于点(−1,0)和点(2,0)，以下结论：①abc <0；②4a −2b +c <0；③a +b =0；④当x <12时，y 随x 的增大而减小．其中正确的结论有___________．（填写代表正确结论的序号）答案：①②##②①分析：根据二次函数的对称轴位置和抛物线开口方向确定①③，根据x ＝-2时判定②，由抛物线图像性质判定④．解：①抛物线的对称轴在y 轴右侧，则ab ＜0，而c ＞0，故abc ＜0，故正确；②x ＝-2时，函数值小于0，则4a -2b +c ＜0，故正确；③与x 轴交于点(−1,0)和点(2,0)，则对称轴x =−b 2a =−1+22=−12，故a =b ，故③错误； ④当x <12时，图像位于对称轴左边，y 随x 的增大而减大．故④错误；综上所述，正确的为①②．所以答案是：①②．小提示：本题考查了二次函数的图像和性质，要求熟悉掌握函数与坐标轴的交点、顶点等点坐标的求法，及这些点代表的意义及函数特征．12、如图，抛物线y＝ax2与直线y＝bx+c的两个交点坐标分别为A(﹣3，6)，B(1，3)，则方程ax2﹣bx﹣c＝0的解是_________．答案：x1＝﹣3，x2＝1分析：根据抛物线y＝ax2与直线y＝bx+c的两个交点坐标分别为A（﹣3，6），B（1，3），可得方程ax2＝bx+c的解为x1＝﹣3，x2＝1，即可求解．解：∵抛物线y＝ax2与直线y＝bx+c的两个交点坐标分别为A（﹣3，6），B（1，3），∴方程ax2＝bx+c的解为x1＝﹣3，x2＝1，∴ax2﹣bx﹣c＝0的解是x1＝﹣3，x2＝1，所以答案是：x1＝﹣3，x2＝1．小提示：本题考查了一次函数与抛物线交点问题，理解交点的横坐标即为方程的解是解题的关键．13、已知抛物线y=(x−1)(x−5)与x轴的公共点坐标是A(x1,0),B(x2,0)，则x1+x2=_______．答案：6分析：令y=0，可得(x−1)(x−5)=0，解出即可求解．解：∵抛物线y=(x−1)(x−5)与x轴的公共点坐标是A(x1,0),B(x2,0)，令y=0，则(x−1)(x−5)=0，解得：x1=1,x2=5，∴x1+x2=1+5=6．所以答案是：6．小提示：本题主要考查了二次函数的图象与x轴的交点问题，熟练掌握二次函数的图象和性质是解题的关键．14、如图，某单位的围墙由一段段形状相同的抛物线形栅栏组成，为了牢固，每段栅栏间隔0.2米设置一根立柱（即AB间间隔0.2米的7根立柱）进行加固，若立柱EF的长为0.28米，则拱高OC为_____米答案：0.64分析：根据抛物线，建立直角坐标系，求出抛物线解析式，即可求得OC的长．解：如图，以点C为坐标系原点，OC所在直线为y轴，建立直角坐标系．设抛物线的解析式为y=ax2(a≠0)，由题意可知：点A的横坐标为－0.8，点F的横坐标为－0.6，代入y=ax2(a≠0)，有y F=(−0.6)2a=0.36a，y A=(−0.8)2a=0.64a，点A的纵坐标即为OC的长，∴0.36a＋0.28＝0.64a，解得a＝1，∴抛物线解析式为y=x2，y A=(−0.8)2=0.64，故OC的长为：0.64m．小提示：本题考查根据抛物线构建直角坐标系，解决实际问题，熟练掌握二次函数相关知识点是解题的关键．15、已知函数y=mx2+2mx+1在−3⩽x⩽2上有最大值4，则常数m的值为 __.答案：3或−38分析：分两种情况：m>0和m<0分别求y的最大值即可．解：y=mx2+2mx+1=m(x+1)2+1−m.当m>0时，当x=2时，y有最大值，∴4m+4m+1=4，∴m=3；8当m<0时，当x=−1时，y有最大值，∴m−2m+1=4，∴m=−3，或−3.综上所述：m的值为38或−3.故答案是：38小提示：本题考查了二次函数的最值，熟练掌握二次函数的图象及性质，解题时，注意要分类讨论，以防漏解.解答题16、单板滑雪大跳台是北京冬奥会比赛项目之一，举办场地为首钢滑雪大跳台，运动员起跳后的飞行路线可以看作是抛物线的一部分，建立如图所示的平面直角坐标系，从起跳到着陆的过程中，运动员的竖直高度y （单位：m）与水平距离x（单位：m）近似满足函数关系y=a(x−ℎ)2+k(a<0)．某运动员进行了两次训练．(1)第一次训练时，该运动员的水平距离x与竖直高度y的几组数据如下：y=a(x−ℎ)2+k(a<0)；(2)第二次训练时，该运动员的竖直高度y与水平距离x近似满足函数关系y=−0.04(x−9)2+23.24.记该运动员第一次训练的着陆点的水平距离为d1，第二次训练的着陆点的水平距离为d2，则d1______d2（填“>”“=”或“<”）．答案：(1)23.20 m；y=−0.05(x−8)2+23.20(2)＜分析：（1）先根据表格中的数据找到顶点坐标，即可得出h、k的值，运动员竖直高度的最大值；将表格中除顶点坐标之外的一组数据代入函数关系式即可求出a的值，得出函数解析式；（2）着陆点的纵坐标为t，分别代入第一次和第二次的函数关系式，求出着陆点的横坐标，用t表示出d1和d2，然后进行比较即可．（1）解：根据表格中的数据可知，抛物线的顶点坐标为：(8,23.20)，∴ℎ=8，k=23.20，即该运动员竖直高度的最大值为23.20 m，根据表格中的数据可知，当x=0时，y=20.00，代入y=a(x−8)2+23.20得：20.00=a(0−8)2+23.20，解得：a=−0.05，∴函数关系关系式为：y=−0.05(x−8)2+23.20．（2）设着陆点的纵坐标为t，则第一次训练时，t=−0.05(x−8)2+23.20，解得：x =8+√20(23.20−t )或x =8−√20(23.20−t )，∴根据图象可知，第一次训练时着陆点的水平距离d 1=8+√20(23.20−t )，第二次训练时，t =−0.04(x −9)2+23.24，解得：x =9+√25(23.24−t )或x =9−√25(23.24−t )，∴根据图象可知，第二次训练时着陆点的水平距离d 2=9+√25(23.24−t )，∵20(23.20−t )＜25(23.24−t )，∴√20(23.20−t )＜√25(23.24−t )，∴d 1＜d 2．所以答案是：＜．小提示：本题主要考查了二次函数的应用，待定系数法求函数关系式，设着陆点的纵坐标为t ，用t 表示出d 1和d 2是解题的关键．17、如图，抛物线y =−x 2+bx +c 与x 轴交于A ，B 两点，与y 轴交于C 点，直线BC 方程为y =x −3．(1)求抛物线的解析式；(2)点P 为抛物线上一点，若S △PBC =12S △ABC ，请直接写出点P 的坐标；(3)点Q 是抛物线上一点，若∠ACQ =45°，求点Q 的坐标．答案：(1)y =-x 2+4x -3(2)(3+√52,−1+√52)或(3−√52,−1−√52)或（3+√132,−5+√132）或(3−√132,−5−√132) (3)(72,−54)分析：（1）先根据一次函数解析式求出点B 、C 坐标；再代入y =−x 2+bx +c ，求出b 、c 即可求解；（2）过点A作AN⊥BC于N，过点P作PM⊥BC于M，过点P作PE∥BC，交y轴于E,交抛物线于p1,p2，过点E作EF⊥BC于F，先求出AN=√2，再根据两三角形面积关系，求得PM=√22，从而求得CE=1，则点P是将直线BC向上或向下平移1个单位与抛物线的交点，联立解析式即可求出交点坐标；（3）过点Q作AD⊥CQ于D，过点D作DF⊥x轴于F财富点C作CE⊥DF于E，证△CDE≌△DAD（AAS），得DE=AF，CE=DF，再证四边形OCEF是矩形，得OF=CE，EF=OC=3，然后设DE=AF=n，则CE=DF=OF=n+1，DF=3-n，则n+1=3-n，解得：n=1，即可求出D(2,-2),用待定系数法求直线CQ解析式为y=12x-3，最后联立直线与抛物线解析式，求出交点坐标即可求解．（1）解：对于直线BC解析式y=x-3，令x=0时，y=-3，则C(0,-3)，令y=0时，x=3，则B(3,0)，把B(3,0)，C(0,-3)，分别代入y=−x2+bx+c，得{-9+3b+c=0c=−3，解得：{b=4c=−3，∴求抛物线的解析式为：y=-x2+4x-3；（2）解：对于抛物线y=-x2+4x-3，令y=0，则-x2+4x-3=0，解得：x1=1,x2=3,∴A(1,0)，B(3,0)，∴OA=1，OB=3，AB=2，过点A作AN⊥BC于N，过点P作PM⊥BC于M，如图，∵A (1,0)，B (3,0)，C (0,-3)，∴OB =OC =3，AB =2，∴∠ABC =∠OCB =45°，∴AN =√2，∵S △PBC =12S △ABC ， ∴PM =√22，过点P 作PE ∥BC ，交y 轴于E ，过点E 作EF ⊥BC 于F ，则EF = PM =√22，∴CE =1∴点P 是将直线BC 向上或向下平移1个单位，与抛物线的交点，如图P 1，P 2，P 3，P 4，∵B (3,0)，C (0,-3)，∴直线BC 解析式为：y =x -3，∴平移后的解析式为y =x -2或y =x -4,联立直线与抛物线解析式，得{y =−x 2+4x −3y =x −2 或{y =−x 2+4x −3y =x −4， 解得：{x 1=3+√52y =−1+√52 ，{x 1=3−√52y =−1−√52 ，{x 1=3+√132y =−5+√132 ，{x 1=3−√132y =−5−√132 ，∴P 点的坐标为(3+√52,−1+√52)或(3−√52,−1−√52)或（3+√132,−5+√132）或(3−√132,−5−√132)．（3） 解：如图，点Q 在抛物线上，且∠ACQ =45°，过点Q 作AD ⊥CQ 于D ，过点D 作DF ⊥x 轴于F ，过点C 作CE ⊥DF 于E ，∵∠ADC =90°，∴∠ACD =∠CAD =45°，∴CD =AD ，∵∠E =∠AFD =90°，∴∠ADF =90°-∠CDE =∠DCE ，∴△CDE ≌△DAD （AAS ），∴DE =AF ，CE =DF ，∵∠COF =∠E =∠AFD =90°，∴四边形OCEF 是矩形，∴OF =CE ，EF =OC =3，设DE =AF =n ，∵OA =1，∴CE =DF =OF =n +1∴DF =3-n ，∴n +1=3-n解得：n =1，∴DE =AF =1，∴CE =DF =OF =2，∴D (2,-2),设直线CQ 解析式为y =px -3，把D (2,-2)代入，得p =12,∴直线CQ 解析式为y =12x -3，联立直线与抛物线解析式，得{y =12x −3y =−x 2+4x −3解得：{x 1=72y 1=−54 ，{x 2=0y 2=−3 （不符合题意，舍去）， ∴点Q 坐标为(72,−54). 小提示：本题属二次函数与一次函数综合题目，考查了用待定系数法求函数解析式，一次函数图象平行，全等三角形的判定与性质，矩形的判定与性质，熟练掌握一次函数与二次函数的图象性质是解题的关键．18、跳绳是一项很好的健身活动，如图是小明跳绳运动时的示意图，建立平面直角坐标系如图所示，甩绳近似抛物线形状，脚底B 、C 相距20cm ，头顶A 离地175cm ，相距60cm 的双手D 、E 离地均为80cm ．点A 、B 、C 、D 、E 在同一平面内，脚离地面的高度忽略不计．小明调节绳子，使跳动时绳子刚好经过脚底B 、C 两点，且甩绳形状始终保持不变．(1)求经过脚底B、C时绳子所在抛物线的解析式．(2)判断小明此次跳绳能否成功，并说明理由．答案：(1)y=110x2−90.(2)不成功，理由见解析分析：（1）建立如图所示的坐标系：结合题意可得：D(−30,0),E(30,0),由双手D、E离地均为80cm，可得C 点坐标为：(10,−80),再利用待定系数法求解解析式即可；（2）由175−80=95>80,可得跳绳不过头顶A，从而可得答案．（1）解：建立如图所示的坐标系：结合题意可得：D(−30,0),E(30,0),∵双手D、E离地均为80cm．∴C点坐标为：(10,−80),设抛物线为：y=ax2−80,{0=900a+b−80=100a+b,解得：{a=110b=−90,所以抛物线为y=110x2−90.（2）解：∵y=0.1x²－90，∴顶点为（0，－90）.即跳绳顶点到手的距离是90cm，∵175−90=85>80,∴跳绳不过头顶A，∴小明此次跳绳能不成功．小提示：本题考查的是二次函数的实际应用，理解题意，建立合适的坐标系是解本题的关键．。

九年级数学上册第二十二章二次函数知识点总结归纳完整版单选题1、已知实数a ，b 满足b −a =1，则代数式a 2+2b −6a +7的最小值等于（ ）A ．5B ．4C ．3D ．2答案：A分析：由已知得b =a +1，代入代数式即得a 2-4a +9变形为(a -2)2+5，再根据二次函数性质求解． 解：∵b -a =1，∴b =a +1，∴a 2+2b -6a +7=a 2+2(a +1)-6a +7=a 2-4a +9=(a -2)2+5，∵(a -2)2≥0，∴当a =2时，代数式a 2+2b -6a +7有最小值，最小值为5，故选：A ．小提示：本题考查二次函数的最值，通过变形将代数式化成(a -2)2+5是解题的关键．2、点A （m -1，y 1），B （m ，y 2）都在二次函数y =（x -1）2+n 的图象上．若y 1＜y 2，则m 的取值范围为（）A ．m >2B ．m >32C ．m <1D ．32<m <2答案：B分析：根据y 1＜y 2列出关于m 的不等式即可解得答案．解：∵点A （m -1，y 1），B （m ，y 2）都在二次函数y =（x -1）2+n 的图象上，∴y 1=（m -1-1）2+n =（m -2）2+n ，y 2=（m -1）2+n ，∵y 1＜y 2，∴（m -2）2+n ＜（m -1）2+n ，∴（m-2）2-（m-1）2＜0，即-2m+3＜0，∴m＞3，2故选：B．小提示：本题考查了二次函数图象上点的坐标特征，解题的关键是根据已知列出关于m的不等式．3、抛物线y=x2−x−1经过点（m，3），则代数式m2−m−1的值为（）A．0B．1C．2D．3答案：D分析：将点（m，3）代入代数式中即可得到结果．解：将点（m，3）代入m2−m−1中得，m2−m−1=3，故代数式m2−m−1的值为3，故选：D．小提示：本题考查代数式的值，根据函数图象经过的点求函数解析式，能够掌握属性结合思想是解决本题的关键．4、小明在研究抛物线y=−(x−ℎ)2−ℎ+1（h为常数）时，得到如下结论，其中正确的是（）A．无论x取何实数，y的值都小于0B．该抛物线的顶点始终在直线y=x−1上C．当−1<x<2时，y随x的增大而增大，则ℎ≥2D．该抛物线上有两点A(x1,y1)，B(x2,y2)，若x1<x2，x1+x2<2ℎ，则y1>y2答案：C分析：根据二次函数的对称轴、二次函数图象上点的坐标特征、二次函数的性质，判断即可．解：A．∵y=−(x−ℎ)2−ℎ+1，∴当x=ℎ时，y max=−ℎ+1，当ℎ<1时，y max=−ℎ+1>0，故错误；B．∵抛物线y=−(x−ℎ)2−ℎ+1的顶点坐标为(ℎ，−ℎ+1)，当x=ℎ时，y=−ℎ−1≠−ℎ+1，故错误；C．∵抛物线开口向下，当−1<x<2时，y随x的增大而增大，∴ℎ≥2，故正确；D．∵抛物线上有两点A(x1,y1)，B(x2,y2)，若x1<x2，x1+x2<2ℎ，∴x1+x2<ℎ，∴点A到对称轴的距离大2于点B到对称轴的距离，∴y1<y2，故错误．故选C．小提示：本题考查了二次函数的性质，二次函数图象上点的坐标特征，熟练掌握二次函数的性质是解题的关键．5、根据表格中二次函数y＝ax2+bx+c的自变量x与函数值y的对应值，可以判断方程ax2+bx+c＝0的一个解x 的范围是（）C．1＜x＜1.5D．1.5＜x＜2答案：B分析：利用二次函数和一元二次方程的性质．解：观察表格可知：当x=0.5时，y=-0.5；当x=1时，y=1，∴方程ax2+bx+c=0（a≠0，a，b，c为常数）的一个解x的范围是0.5＜x＜1．故选：B．小提示：本题考查了用图象法求一元二次方程的近似根，解题的关键是找到y由正变为负时，自变量的取值即可．6、某种产品按质量分为10个档次，生产最低档次产品，每件获利润8元，每提高一个档次，每件产品利润增加2元，用同样工时，最低档次产品每天可生产60件，提高一个档次将减少3件．如果用相同的工时生产，总获利润最大的产品是第k档次（最低档次为第一档次，档次依次随质量增加），那么k等于（）A．5B．8C．9D．10答案：C分析：第k档次产品比最低档次产品提高了(k−1)个档次，则数量在60的基础上减少了3(k−1)，每件产品利润在8的基础上增加2(k−1)，据此可求出总利润关系，求出最值即可．解：设总利润为y元，∵第k档次产品比最低档次产品提高了(k−1)个档次，∴每天利润为y=[60−3(k−1)][8+2(k−1)]=−6(k−9)2+864，∴当k=9时，产品利润最大，每天获利864元，故选C．小提示：本题考查了二次函数的实际应用，借助二次函数解决实际问题是本题的关键．7、已知抛物线y=x2+bx+c与x轴的两个交点之间的距离为6，对称轴为x=3，则抛物线的顶点P关于x轴对称的点P′的坐标是（）A．(3,9)B．(3,−9)C．(−3,9)D．(−3,−9)答案：A分析：根据抛物线y＝x2+bx+c与x轴两个交点间的距离为6．对称轴为直线x＝3，可以得到b、c的值，然后即可得到该抛物线的解析式，再将函数解析式化为顶点式，即可得到点P的坐标，然后根据关于x轴对称的点的特点横坐标不变，纵坐标互为相反数，即可得到点P关于x轴的对称点的坐标．解：设抛物线y＝x2+bx+c与x轴两个交点坐标为（x1，0），（x2，0），∵抛物线y＝x2+bx+c与x轴两个交点间的距离为6，对称轴为直线x＝3，∴（x1﹣x2）2＝（x1+x2）2﹣4x1x2＝36，−b=3，2×1∴（﹣b）2﹣4×c＝36，b＝﹣6，解得：c＝0，∴抛物线的解析式为y＝x2﹣6x＝（x﹣3）2﹣9，∴顶点P的坐标为（3，﹣9），∴点P关于x轴的对称点的坐标是（3，9），故选：A．小提示：本题考查抛物线与x轴的交点、二次函数的性质、关于x轴对称的点的坐标特点，解答本题的关键是求出点P的坐标，利用二次函数的性质解答．8、已知a是不为0的常数，函数y＝ax和函数y＝﹣ax2+a在同一平面直角坐标系内的图象可以是（）A．B．C．D．答案：C分析：根据题意分a>0,a<0两种情况讨论，结合函数图象即可求解．解：A.正比例函数中a<0，二次函数开口向上，−a>0，与y轴的交点在y轴正半轴，则a>0，矛盾，故A 不正确；B.正比例函数中a>0，二次函数开口向上，−a>0，与y轴的交点在y轴正半轴，则a>0，矛盾，故B不正确；C.正比例函数中a>0，二次函数开口向下，−a<0，与y轴的交点在y轴正半轴，则a>0，故C正确；D. .正比例函数中a<0，二次函数开口向下，−a<0，与y轴的交点在y轴正半轴，则a>0，矛盾，故D不正确；故选C小提示：本题考查了正比例函数与二次函数的图象的性质，掌握正比例函数与二次函数的图象的性质是解题的关键．9、二次函数y=ax2+bx+c(a≠0)的图像如图所示，则关于x的一元二次方程ax2+bx+c=0的根的情况描述正确的是（）A．有两个相等的实数根B．有两个异号的实数根C．有两个同号的实数根D．有两个无法确定符号的实数根答案：B分析：根据二次函数的图像判断与x轴有两个交点，且在原点两侧，故关于x的一元二次方程ax2+bx+c= 0有两个异号的实数根．解：∵二次函数的图像与x轴有两个交点，且在原点两侧，∴关于x的一元二次方程ax2+bx+c=0有两个异号的实数根，故选：B．小提示：本题考查二次函数图像与一元二次方程根的关系，掌握二次函数y=ax2+bx+c(a≠0)的图像与x 轴有交点的横坐标即为关一元二次方程ax2+bx+c=0的根是解答本题的关键．10、已知抛物线y=2(x−3)2−5，其对称轴是（）A．直线x=−3B．直线x=3C．直线x=−5D．直线x=5答案：B分析：直接根据抛物线的顶点式进行解答即可．解：∵y=2(x−3)2−5，∴抛物线对称轴为直线x=3．故选：B．小提示：本题考查二次函数的性质，解题关键是掌握二次函数图像与系数的关系．填空题11、已知二次函数y=(x−1)2+3，当x＝_______时，y取得最小值．答案：1分析：根据抛物线的顶点坐标和开口方向即可得出答案．解：∵y=(x−1)2+3，∴该抛物线的顶点坐标为(1,3)，且开口方向向上，∴当x=1时，y取得最小值，所以答案是：1．小提示：本题考查二次函数的最值，求二次函数最大值或最小值有三种方法：第一种可有图象直接得出，第二种是配方法，第三种是公式法．12、如图，过点D（1，3）的抛物线y=-x2+k的顶点为A，与x轴交于B、C两点，若点P是y轴上一点，则PC+PD的最小值为____．答案：3√2分析：由两点之间线段最短可知，当D、P、B在同一直线上时就可使PC+PD的值最小，解答即可．解：连接PB，对于抛物线y=-x2+k，对称轴是y轴，∴PC=PB，∴当D、P、B在同一直线上时，PC+PD的值最小，最小值为BD的长，∵抛物线y=-x2+k过点D（1，3），∴把x=1，y=3代入y=-x2+k，解得：k=4，把y=0代入y=-x2+4，解得：x=2或x=-2，所以点B的坐标为（-2，0），所以BD=√(−2−1)2+32=3√2，所以答案是：3√2．小提示：本题考查了抛物线与x轴的交点，轴对称－最短路线问题，找到P点是本题的关键．13、已知实数a、b满足a－b2＝4，则代数式a2－3b2＋a－14的最小值是________．答案：6分析：根据a－b2＝4得出b2=a−4，代入代数式a2－3b2＋a－14中，通过计算即可得到答案．∵a－b2＝4∴b2=a−4将b2=a−4代入a2－3b2＋a－14中得：a2－3b2＋a－14=a2−3(a−4)+a−14=a2−2a−2a2−2a−2=a2−2a+1−3=(a−1)2−3∵b2=a−4≥0∴a≥4当a=4时，(a−1)2−3取得最小值为6∴a2−2a−2的最小值为6∵a2－3b2＋a－14=a2−2a−2∴a2－3b2＋a－14的最小值6所以答案是：6．小提示：本题考查了代数式的知识，解题的关键是熟练掌握代数式的性质，从而完成求解．14、已知二次函数y =−x 2−2x +3，当a ⩽x ⩽12时，函数值y 的最小值为1，则a 的值为_______． 答案：−1−√3##−√3−1分析：先把函数解析式化为顶点式可得当x <−1时，y 随x 的增大而增大，当x >−1时，y 随x 的增大而减小，然后分两种情况讨论：若a ≥−1；若a <−1，即可求解．解：y =−x 2−2x +3=−(x +1)2+4，∴当x <−1时，y 随x 的增大而增大，当x >−1时，y 随x 的增大而减小，若a ≥−1，当a ⩽x ⩽12时，y 随x 的增大而减小， 此时当x =12时，函数值y 最小，最小值为74，不合题意，若a <−1，当x =a 时，函数值y 最小，最小值为1，∴−a 2−2a +3=1，解得：a =−1−√3或−1+√3（舍去）；综上所述，a 的值为−1−√3．所以答案是：−1−√3小提示：本题主要考查了二次函数的图象和性质，熟练掌握二次函数的图象和性质是解题的关键．15、已知二次函数y =ax 2+bx +c(a ≠0)的图像的顶点为(2,−2)，与x 轴交于点(1,0)、(3,0)，根据图像回答下列问题：当x _______时，y 随x 的增大而减小：方程ax 2+bx +c =0的两个根是___________．答案： x ＜2 x 1=1，x 2=3分析：利用开口向上和对称轴以及二次函数与一元二次方程的联系即可得到答案．解（1）∵二次函数图像与x轴的两个交点坐标为（1，0）、（3，0），∴二次函数的对称轴为直线x=2，∵抛物线的开口向上，∴当x＜2时，y随x的增大而减小；（2）∵二次函数图像与x轴的两个交点坐标为（1，0）、（3，0），∴方程ax2+bx+c=0的两个根是x1=1，x2=3．小提示：本题考查了二次函数的图像与性质以及二次函数与一元二次方程的联系，属于常考题型．解答题16、在一条笔直的滑道上有黑、白两个小球同向运动，黑球在A处开始减速，此时白球在黑球前面70cm处．小聪测量黑球减速后的运动速度v（单位：cm/s）、运动距离y（单位：cm）随运动时间t（单位：s）变化的数据，整理得下表．y与运动时间t之间成二次函数关系．(1)直接写出v关于t的函数解析式和y关于t的函数解析式（不要求写出自变量的取值范围）(2)当黑球减速后运动距离为64cm时，求它此时的运动速度；(3)若白球一直．．以2cm/s的速度匀速运动，问黑球在运动过程中会不会碰到白球？请说明理由．答案：(1)v=−12t+10，y=−14t2+10t(2)6cm/s(3)黑、白两球的最小距离为6cm，大于0，黑球不会碰到白球分析：（1）根据黑球的运动速度v与运动时间t之间成一次函数关系，设表达式为v=kt+b，代入两组数值求解即可；根据运动距离y与运动时间t之间成二次函数关系，设表达式为y=at2+bt+c，代入三组数值求解即可；（2）当黑球减速后运动距离为64cm时，代入（1）式中y关于t的函数解析式求出时间t，再将t代入v关于t的函数解析式，求得速度v即可；（3）设黑白两球的距离为w cm，得到w=70+2t−y=14t2−8t+70，化简即可求出最小值，于是得到结论．（1）根据黑球的运动速度v与运动时间t之间成一次函数关系，设表达式为v=kt+b，代入（0，10），（1，9.5）得，{10=b 9.5=k+b ，解得{k=−12b=10，∴v=−12t+10，根据运动距离y与运动时间t之间成二次函数关系，设表达式为y=at2+bt+c，代入（0，0），（1，9.75），（2，19）得{0=c9.75=a+b19=4a+2b，解得{a=−14b=10c=0，∴y=−14t2+10t;（2）依题意，得−14t2+10t=64，∴t2−40t+256=0，解得，t1=8，t2=32；当t1=8时，v=6；当t2=32时，v=−6（舍）；答：黑球减速后运动64cm时的速度为6cm/s．（3）设黑白两球的距离为w cm，w=70+2t−y=14t2−8t+70=14(t−16)2+6，∵14>0，∴当t=16时，w的值最小为6，∴黑、白两球的最小距离为6cm，大于0，黑球不会碰到白球．小提示：本题考查一次函数和二次函数的实际应用，待定系数法求解析式，解决本题的关键是明确题意求出函数表达式．17、已知抛物线y=ax2−4ax+3(a≠0)的图象经过点A(−2,0)，过点A作直线l交抛物线于点B(4,m)．(1)求抛物线的函数表达式和顶点坐标．(2)将抛物线向下平移n(n>0)个单位，使顶点落在直线l上，求m，n的值．答案：(1)y=−14x2+x+3；(2,4)(2)3；2分析：（1）把点A(−2,0)代入y=ax2−4ax+3(a≠0)，求出a的值即可；再运用顶点坐标公式求出顶点坐标即可；（2）把C(4,m)代入y=−14x2+x+3可求出m的值；再运用待定系数法求出直线AB的解析式，从而可求出平移后押物线的顶点坐标，进一步可得结论．（1）将A(−2,0)代入y=ax2−4ax+3得：0=4a+8a+3，解得a=−14，∴抛物线的函数表达式为y=−14x2+x+3，∵−b2a =−12×(−14)=2，4ac−b24a=4×(−14)×3−124×(−14)=4，∴顶点坐标为(2,4)；（2）把C(4,m)代入y=−14x2+x+3得，m =−4+4+3=3，设直线AB 的解析式为y =kx +b ，将A (−2,0)，B (4,3)代入y =kx +b 得{0=−2k +b 3=4k +b， 解得{k =12b =1， ∴直线AB 的解析式为y =12x +1， ∵顶点的横坐标为2，∴把x =2代入y =12x +1得：y =2，∴n =4−2=2．小提示：本题主要考查了运用待定系数法求函数关系式以及二次函数图象的平移，正确理解题意是解答本题的关键．18、戴口罩是阻断呼吸道病毒传播的重要措施之一，某商家对一款成本价为每盒50元的医用口罩进行销售，如果按每盒70元销售，每天可卖出20盒．通过市场调查发现，每盒口罩售价每降低1元，则日销售量增加2盒(1)若每盒售价降低x 元，则日销量可表示为_______盒，每盒口罩的利润为______元．(2)若日利润保持不变，商家想尽快销售完该款口罩，每盒售价应定为多少元？(3)当每盒售价定为多少元时，商家可以获得最大日利润？并求出最大日利润．答案：(1)(20+2x )盒，(20-x ) 元(2)每盒售价应定为60元(3)每盒售价应定为65元时，最大日利润是450元分析：（1）根据题意列出代数式即可；（2）设每盒售价x 元，则每件的销售利润为(x −50)元，日销售量为[20+2(70−x )]件，即可得出关于x 的一元二次方程，解之即可得出x 的值，再结合商家想尽快销售完该款商品，即可求解；（3）设日利润为y ，由（2）列出函数关系式，根据二次函数的性质即可求解．（1）设每盒售价降低x 元，则日销量可表示为(20+2x )盒，每盒口罩的利润为70−50−x =20−x （元）所以答案是：(20+2x)；(20−x)（2）设每盒售价x元，则每件的销售利润为(x−50)元，日销售量为[20+2(70−x)]件，根据题意得，(x−50)[20+2(70−x)]=(70−50)×20解得x1=70,x2=60又∵商家想尽快销售完该款商品，∴x=60．答：每件售价应定为60元；（3）设日利润为y，则y=(x−50)[20+2(70−x)]=−2x2+260x−8000=−2(x−65)2+450∴x=65时，y的最大值为450，即每盒售价应定为65元时，最大日利润是450元．小提示：本题考查了一元二次方程的应用，二次函数的应用，根据题意列出方程和函数关系式是解题的关键．。

人教版九年级上册数学第二十二章二次函数含答案一、单选题(共15题，共计45分)1、把二次函数y=x2﹣4x+1化成y=a（x+m）2+k的形式是（）A.y=（x﹣2）2+1B.y=（x﹣2）2﹣1C.y=（x﹣2）2+3 D.y=（x﹣2）2﹣32、平面直角坐标系中，二次函数y＝ax2+bx+c（a≠0）的图象如图所示，现给出下列结论：①abc＜0；②c+2a＞0；③9a﹣3b+c＝0；④a﹣b≤am2+bm（m为实数）；⑤4ac﹣b2＜0．其中正确结论的个数是（）A.2B.3C.4D.53、二次函数y=ax2+bx+c（a≠0）的部分图象如图,图象过点（-1,0），对称轴为直线x=2,下列结论:①4a+b=0;②9a+c＞3b;③8a+7b+2c＞0;④当x＞-1时,y 的值随x值的增大而增大.其中正确的结论有（）A.1个B.2个C.3个D.4个4、二次函数在下列（）范围内，y随着x的增大而增大．A. B. C. D.5、已知二次函数的图象开口向上，则的取值范围是（）A. B. C. D.6、设函数y=3ax2-2bx+c（a，b，c都为正整数且a-b+c=0），若当x=0与x=1时，都有y＞0，则a+b+c的最小值为（）A.7B.4C.6D.107、如图，抛物线经过A（1，0），B（4，0），C（0，﹣4）三点，点D是直线BC上方的抛物线上的一个动点，连结DC，DB，则△BCD的面积的最大值是（）A.7B.7.5C.8D.98、如图，在等边三角形ABC中，点P是BC边上一动点（不与点B，C重合），连接AP，作射线PD，使∠APD=60°，PD交AC于点D，已知AB=a，设CD=y，BP=x，则y与x函数关系的大致图象是（）A. B. C. D.9、将抛物线绕原点O旋转180°，则旋转后的抛物线的解析式为（）A. B. C. D.10、如图，二次函数（）的图象与轴交于点，其对称轴为直线，若，则下列结论中错误的是（）A. B.C. D.11、将抛物线y=(x-6)2+5的图象向左平移1个单位，再向上平移2个单位得到抛物线的解析式是（）A.y=（x-5）2+7B.y=（x-5）2-3C.y=（x-7）2+7D.y=（x-7）2-312、已知二次函数y=ax2+bx+c，且ac＜0，则它的图象经过( )A.一、二、三象限B.二、三、四象限C.一、三、四象限D.一、二、三、四象限13、如图，一条抛物线与x轴相交于A、B两点，其顶点P在折线C﹣D﹣E上移动，若点C、D、E的坐标分别为（﹣1，4）、（3，4）、（3，1），点B的横坐标的最小值为1，则点A的横坐标的最大值为（）A.1B.2C.3D.414、二次函数的图象如图所示，有下列结论：①，②，③，④ ，⑤其中正确的个数有（）A.1个B.2个C.3个D.4个15、已知关于x的二次函数y=（x﹣h）2+3，当1≤x≤3时，函数有最小值2h，则h的值为（）A. B. 或2 C. 或6 D.2、或6二、填空题(共10题，共计30分)16、某电商销售一款夏季时装，进价40元/件，售价110元/件，每天销售20件，每销售一件需缴纳电商平台推广费用a元（a＞0）．未来30天，这款时装将开展“每天降价1元”的夏令促销活动，即从第1天起每天的单价均比前一天降1元．通过市场调研发现，该时装单价每降1元，每天销量增加4件．在这30天内，要使每天缴纳电商平台推广费用后的利润随天数t（t为正整数）的增大而增大，a的取值范围应为________．17、函数y＝ax2+2ax+m（a＜0）的图象过点（2，0），则使函数的值y＜0成立的x的取值范围是________.18、二次函数y＝x2+bx+c的图象如图所示，则x2+bx+c＝0的两根分别是________．19、如图，抛物线（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，顶点为B．①抛物线与直线y=m+2有且只有一个交点；②若点点、点在该函数图象上，则；③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为；④点A关于直线x=1的对称点为C，点D、E分别在x轴和y轴上，当m=1时，四边形BCDE周长的最小值为,其中正确判断的序号是________20、二次函数，当时，的最小值为1，则的取值范围是________.21、如图，△ABC中，则△BED的最大面积为________.22、已知点（-1，m）、（2，n）在二次函数的图像上，如果m>n，那么a________0（用“>”或“<”连接）．23、抛物线向上平移3个单位长度，得到新抛物线的解析式为________.24、对于二次函数y＝x2﹣2mx﹣3，下列正确的说法是________.①它的图象与x轴有两个公共点；②如果当x≤1时，y随x的增大而减小，则m＝1；③如果将它的图象向左平移3个单位后过原点，则m＝﹣1；④如果当x＝﹣8时的函数值与x＝2020时的函数值相等，则当x＝2012时的函数值为﹣3.25、若函数y=mx2﹣2x+1的图象与x轴只有一个交点，则m=________ ．三、解答题(共5题，共计25分)26、我们知道任何实数的平方一定是一个非负数，即：（a+b）2≥0，且﹣（a+b）2≤0．据此，我们可以得到下面的推理：∵x2+2x+3=（x2+2x+1）+2=（x+1）2+2，而（x+1）2≥0∴（x+1）2+2≥2，故x2+2x+3的最小值是2．试根据以上方法判断代数式3y2﹣6y+11是否存在最大值或最小值？若有，请求出它的最大值或最小值．27、已知二次函数y=x2+mx+n的图象经过点P（﹣3，1），对称轴是直线x=﹣1．（1）求m，n的值；（2）x取什么值时，y随x的增大而减小？28、如图,抛物线与x轴交于A、B两点,与y轴交于点C．（1）分别求出点A、B、C的坐标;（2）设抛物线的顶点为M,求四边形ABMC的面积．29、若二次函数y=ax2+bx+c的图象的顶点是（2，1）且经过点（1，2），求此二次函数解析式．30、已知关于x的一元二次方程x2+2x+=0有实数根，k为正整数．（1）求k的值；（2）当此方程有两个非零的整数根时，将关于x的二次函数y=x2+2x+的图象向下平移9个单位，求平移后的图象的表达式；（3）在（2）的条件下，平移后的二次函数的图象与x轴交于点A，B（点A在点B左侧），直线y=kx+b（k＞0）过点B，且与抛物线的另一个交点为C，直线BC上方的抛物线与线段BC组成新的图象，当此新图象的最小值大于﹣5时，求k的取值范围．参考答案一、单选题(共15题，共计45分)1、D3、B4、C5、A6、C7、C8、C9、D10、B11、A12、D13、B14、D15、C二、填空题(共10题，共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题，共计25分)26、27、29、。

第二十二章《二次函数》解答题专题复习 (44)一、解答题1．如图，在平面直角坐标系中，抛物线y=a（x-1）2-4a（a＞0）交x轴于A、B两点，点A在点B的左边，其顶点为点C，一条开口向下的抛物线经过A、B、D三点，其顶点D在x 轴上方，且其纵坐标为3，连接AC、AD、CD．（1）直接写出A、B两点的坐标；（2）求经过A、B、D三点的抛物线所对应的函数表达式；（3）当△ACD为等腰三角形时，求a的值；（4）将线段AC绕点A旋转90°，若点C的对应点恰好落在（2）中的抛物线上，直接写出a的值．2．如图1在平面直角坐标系中二次函数233y ax bx=++的图象与x轴交于(1,0),(3,0)B C-两点点A为抛物线的顶点F为线段AC中点.（1）求,a b的值；（2）求证：BF AC⊥；（3）以抛物线的顶点A为圆心AF为半径作A点E是圆上一动点点P为EC的中点（如图2）；①当ACE∆面积最大时求PB的长度；②若点M为BP的中点求点M运动的路径长.3．已知y是x的二次函数，该函数的图象经过点A(0，5)、B(1，2)、C(3，2)．（1）求该二次函数的表达式，画出它的大致图象并标注顶点及其坐标； （2）结合图象，回答下列问题： ①当1≤x≤4时，y 的取值范围是 ；②当m≤x≤m+3时，求y 的最大值（用含m 的代数式表示）；③是否存在实数m 、n （m≠n ），使得当m≤x≤n 时，m≤y≤n ？若存在，请求出m 、n ；若不存在，请说明理由．4．如图，二次函数2(1)4y a x =++的图像与x 轴交于A 和B 两点，交y 轴于点(0,3)C ，点C 、D 是二次函数图像上的一对对称点，一次函数的图像经过B 、D ；（1）请直接写出D 点的坐标； （2）求二次函数的解析式；（3）根据图像直接写出使一次函数值大于二次函数值的x 的取值范围； 5．已知一抛物线与x 轴的交点是()2,0A -、B （1，0），且经过点C （2，8）. （1）求该抛物线的解析式； （2）求该抛物线的顶点坐标和对称轴.6．已知二次函数2246y x x =+-，请用配方法求出对称轴方程与该抛物线的顶点坐标． 7．如图1，图形ABCD 是由两个二次函数y 1=kx 2+m （k ＜0）与y 2=ax 2+b （a ＞0）的部分图象围成的封闭图形．已知A （1，0）、B （0，1）、D （0，﹣3）．（1）直接写出这两个二次函数的表达式；（2）判断图形ABCD 是否存在内接正方形（正方形的四个顶点在图形ABCD 上），并说明理由；（3）如图2，连接BC ，CD ，AD ，在坐标平面内，求使得△BDC 与△ADE 相似（其中点C 与点E 是对应顶点）的点E 的坐标 8．先阅读以下材料，然后解答问题：材料：将二次函数2y x 2x 3=-++的图象向左平移1个单位，再向下平移2个单位，求平移后的抛物线的解析式（平移后抛物线的形状不变）．解：在抛物线2y x 2x 3=-++上任取两点A （0，3）、B （1，4），由题意知：点A 向左平移1个单位得到A'（1-，3），再向下平移2个单位得到A"（1-，1）；点B 向左平移1个单位得到B'（0，4），再向下平移2个单位得到B"（0，2）． 设平移后的抛物线的解析式为2y x bx c =-++． 则点A"（1-，1），B"（0，2）在抛物线上．可得：1b c 1{c 2--+==，解得：b 0{c 2==． 所以平移后的抛物线的解析式为：2y x 2=-+． 根据以上信息解答下列问题：将直线y 2x 3=-向右平移3个单位，再向上平移1个单位，求平移后的直线的解析式． 9．如图，抛物线2(0)y ax bxa =+≠交x 轴正半轴于点A ，直线2y x =经过抛物线的顶点M ．已知该抛物线的对称轴为直线2x =，交x 轴于点B ．（1）求,a b 的值．（2）P 是第一象限内抛物线上的一点，且在对称轴的右侧，连接,OP BP ．设点P 的横坐标为m ；①OBP 的面积为S ，用含m 的式子表示S ； ②记SK m=．求K 关于m 的函数表达式及K 的范围． 10．在平面直角坐标系xOy 中，对于点(),P x y 和(),Q x y '，给出如下定义：若123y y y <<，则称点Q 为点P 的“可控变点”．例如，点()1,2的“可控变点”为点()1,2，点()1,3-的“可控变点”为点()1,3--． （1）点()5,2--的“可控变点”坐标为 ；（2）若点P 在函数216y x =-+的图象上，其“可控变点”Q 的纵坐标y '是7，求“可控变点” Q 的横坐标；（3）若点P 在函数()2165y x x a =-+-≤≤的图象上，其“可控变点”Q 的纵坐标y '的取值范围是1616y -≤'≤，直接写出实数a 的值．11．已知二次函数2y x px q +=+图象的顶点M 为直线1122y x =+与1y x m =-+-的交点．（1）用含m 的代数式来表示顶点M 的坐标． （2）当2x ≥时，二次函数2y x px q +=+与1122y x =+的值均随x 的增大而增大，求m 的取值范围．（3）若6m =，当x 取值为13t x t -≤≤+时，二次函数2y =最小值，求t 的取值范围．12．已知直线2721+=x y 与茹x 、y 轴分别相交于B ，A 两点，抛物线c bx ax y ++=2过A ，B 两点，且对称轴为直线3-=x ．（1）求A ，B 两点的坐标，并求抛物线的解析式；（2）若点P 以1个单位/秒的速度从点B 沿x 轴向点O 运动．过点P 作y 轴的平行线交直线AB 于点M ，交抛物线于点N ．设点P 运动的时间为t ，MN 的长度为S ，求S 与t 之间的函数关系式，并求出当t 为何值时，S 取得最大值?（3）设抛物线的对称轴CD 与直线AB 相交于点D ，顶点为C ．问：在（2）条件不变情况下，是否存在一个t 值，使四边形CDMN 是平行四边形?若存在，求出t 的值；若不存在，请说明理由．13．抛物线2y x bx c =-++的图象经过点A ( 1，0)，B (0，5)．（1）求这个抛物线的解析式；（2）设（1）中的抛物线与x轴的另一交点为C，抛物线的顶点为D，试求出BCD△的面积；（3）P是线段OC上的一点，过点P作PH x轴，与抛物线交于H点，若直线BC把PCH△分成面积之比为2:3的两部分，请求出P点的坐标．14．今年在全球大疫情的影响下，人们更加关注身边的空气质量。

2020-2021年九年级数学人教版（上）二次函数期末专题复习（含答案）一、选择题 1. 已知函数y=21x 2-x-12，当函数y 随x 的增大而减小时，x 的取值范围是（ ） A. x ＜1 B. x ＞1 C. x ＞-4 D . -4＜x ＜62. 下列函数关系中，可以看做二次函数y=ax 2+bx +c(a ≠0)模型的是( ) A ．在一定的距离内汽车的行驶速度与行驶时间的关系B ．我国人口年自然增长率1%，这样我国人口总数随年份的关系C ．竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系(不计空气阻力)D ．圆的周长与圆的半径之间的关系．3. 把二次函数2x y =的图象向右平移3个单位长度，得到新的图象的函数表达式是（ ）A. 32+=x y B. 32-=x y C . 2)3(+=x y D. 2)3(-=x y4. 在平面直角坐标系中，将抛物线y ＝x 2－4先向右平移2个单位，再向上平移2个单位，得到的抛物线解析式为( )A ．y ＝(x ＋2)2＋2B ．y ＝(x －2)2－2C ．y ＝(x －2)2＋2D ．y ＝(x ＋2)2－25. 将抛物线y ＝x 2－4x －4向左平移3个单位，再向上平移5个单位，得到抛物线的函数表达式为( )A ．y ＝(x ＋1)2－13B ．y ＝(x －5)2－3C ．y ＝(x －5)2－13D ．y ＝(x ＋1)2－36. 如图，某农场拟建一间矩形奶牛饲养室，打算一边利用房屋现有的墙（墙足够长），其余三边除大门外用栅栏围成，栅栏总长度为50m ，门宽为2m ．若饲养室长为xm ，占地面积为ym 2，则y 关于x 的函数表达式为（ ）A ．yx 2+26x （2≤x ＜52） B ．yx 2+50x （2≤x ＜52） C ．y ＝﹣x 2+52x （2≤x ＜52）D ．yx 2+27x ﹣52（2≤x ＜52）7. 已知二次函数y ＝x 2＋bx ＋c 与x 轴只有一个交点，且图象过A(x 1，m)、B(x 1＋n ，m)两点，则m 、n 的关系为( )A. m ＝12nB. m ＝14nC. m ＝12n 2D. m ＝14n 28. 某同学在用描点法画二次函数y ＝ax 2＋bx ＋c 图象时，列出了下面的表格：A. －11B. －2C. 1D. －59. 二次函数y ＝ax 2＋bx ＋c(a ≠0)的图象如图所示，下列结论：①b<0；②c>0；③a ＋c<b ；④b 2－4ac>0，其中正确的个数是( ) A. 1 B. 2 C. 3 D. 410.已知点A （b ﹣m ，y 1），B （b ﹣n ，y 2），C （b，y 3）都在二次函数y ＝﹣x 2+2bx+c 的图象上，若0＜m ＜n ，则y 1，y 2，y 3的大小关系是（ ）A．y 1＜y 2＜y 3 B ．y 2＜y 3＜y 1 C ．y 3＜y 1＜y 2 D ．y 1＜y 3＜y 211.如图，正方形ABCD 的边长为1，E 、F 分别是边BC 和CD 上的动点（不与正方形的顶点重合），不管E 、F 怎样动，始终保持AE ⊥EF ．设BE=x ，DF=y ，则y 是x 的函数，函数关系式是（ ）A 、1y x =+B 、1y x =-C 、21y x x =-+ D 、21y x x =--12. 已知函数y ＝x 2+x ﹣1，当m ≤x ≤m+2时，y ≤1，则m 的取值范围（ ） A ．m ≥﹣2 B ．﹣2≤m ≤﹣1C ．﹣2≤mD ．m ≤﹣1二、填空题13. 抛物线322--=x y 的开口 ,对称轴是 ,顶点坐标是 ,当x 时, y 随x 的增大而增大, 当x 时, y 随x 的增大而减小.14. 已知函数①y=x 2+1，②y=-2x 2+x ．函数____(填序号)有最小值，当x=____时，该函数的最小值是_______． 15. 若函数是关于x 的二次函数，则a 的值为 ． 16. 关于的方程有两个相等的实数根，则相应二次函数与轴必然相交于 点，此时 ．17. 如图，抛物线y ＝ax 2＋bx ＋c 与x 轴相交于点A ，B(m ＋2，0)，与y 轴相交于点C ，点D 在该抛物线上，坐标为(m ，c)，则点A 的坐标是________．18. 竖直上抛的小球离地高度是它运动时间的二次函数．小军相隔1秒依次竖直向上抛出两个小球．假设两个小球离手时离地高度相同，在各自抛出后1.1秒时到达相同的最大离地高度．第一个小球抛出后t 秒时在空中与第二个小球的离地高度相同，则t ＝________．19. 如图，某中学教学楼前喷水池喷出的抛物线形水柱，其解析式为242y x x =-++，则水柱的最大高度是 米。

2023-2024学年九年级数学上册《第二十二章二次函数的图像和性质》同步练习题含答案(人教版）学校:___________班级：___________姓名：___________考号：___________一、选择题1．下列函数中是二次函数的是（）A．y=1x2B．y=2x+1C．y=12x2+2x3D．y=−4x2+52．二次函数y=x2−2x+3的一次项系数是（）A．1 B．2 C．-2 D．33．在同一平面直角坐标系中作出y=2x2，y=−2x2，y=12x2的图象，它们的共同点是（）A．关于y轴对称，抛物线的开口向上B．关于y轴对称，抛物线的开口向下C．关于y轴对称，抛物线的顶点都是原点D．当x>0时，y随x的增大而减小4．抛物线y＝－2x2＋1的顶点坐标是（）A．（－2，0）B．（0，1）C．（0，－1）D．（－2，0）5．已知A(0，y1)，B(3，y2)为抛物线y=(x−2)2上的两点，则y1与y2的大小关系是（）A．y1>y2B．y1=y2C．y1<y2D．无法确定6．已知抛物线y=−(x−b)2+2b+c（b，c为常数）经过不同的两点(−2−b，m)，(−1+c，m)那么该抛物线的顶点坐标不可能是下列中的（）A．(−2，−7)B．(−1，−3)C．(1，8)D．(2，13)7．关于x的二次函数y=ax2+bx+c图象经过点(1，0)和(0，−2)，且对称轴在y轴的左侧，若t= a−b，则t的取值范围是（）A．−2<t<2B．−2<t<0C．−4<t<0D．−4<t<2 8．抛物线y=ax2+bx+c（a，b，c为常数，a>0）经过(0，0)，(4，0)两点．则下列四个结论正确的有（）①4a+b=0；②5a+3b+2c>0；③若该抛物线y=ax2+bx+c与直线y=−3有交点，则a的取值范围是a≥34；④对于a的每一个确定值，如果一元二次方程ax2+bx+c−t=0（t为常数，t≤0）的根为整数，则t的值只有3个．A．1个B．2个C．3个D．4个二、填空题9．当函数y=(a−1)x a2+1+2x+3是二次函数时，a的值为．10．抛物线y=−12x2+1在y轴的右侧呈趋势（填“上升”或者“下降”）．11．将二次函数y=2x2−8x+13化成y=a(x+ℎ)2+k的形式为. 12．对于二次函数y=−2(x+3)2−1，当x的取值范围是时，y随x的增大而减小．13．点P(m，n)在抛物线y=x2+x+2上，且点P到y轴的距离小于1，则n的取值范围是.三、解答题14．已知抛物线的顶点是(−3，2)，且经过点(1，−14)，求该抛物线的函数表达式．15．指出函数y=−12(x+1)2−1的图象的开口方向、对称轴和顶点，怎样移动抛物线y=-12x2就可以得到抛物线y=−12(x+1)2−116．二次函数图象的对称轴是y轴，最大值为4，且过点A（1，2），与x轴交于B、C两点．求△ABC 的面积．17．如图，已知抛物线y=ax2＋bx−3过点A(−1，0)，B(3，0)点M、N为抛物线上的动点，过点M 作MD∥y轴，交直线BC于点D，交x轴于点E.过点N作NF⊥x轴，垂足为点F（1）求二次函数y=ax2+bx−3的表达式；（2）若M点是抛物线上对称轴右侧的点，且四边形MNFE为正方形，求该正方形的面积；18．在直角坐标系中，设函数y=m(x+1)2+4n（m≠0，且m，n为实数）（1）求函数图象的对称轴.（2）若m，n异号，求证：函数y的图象与x轴有两个不同的交点.（3）已知当x=0，3，4时，对应的函数值分别为p，q，r，若2q<p+r，求证：m<0.参考答案1．D2．C3．C4．B5．A6．B7．A8．C9．-110．下降11．y=2(x−2)2+512．x＞-313．74≤n<414．解：∵抛物线的顶点是(−3，2)∴可设抛物线的函数表达式为y=a(x+3)2+2∵抛物线经过点(1，−14)∴−14=a(1+3)2+2，解得a=−1∴抛物线的函数表达式为y=−(x+3)2+2．15．解：由y=−12(x+1)2−1得到该函数的图象的开口方向向下，对称轴是直线x=-1，顶点坐标是（-1，-1）；∵抛物线y=−12x2的顶点坐标是（0，0）∴由顶点（0，0）向左平移1个单位，再向下平移1个单位得到顶点（-1，-1）∴抛物线y=−12x2向左平移1个单位，再向下平移1个单位就可以得到抛物线y=−12(x+1)2−1．16．解：设该二次函数的表达式为y=ax2+4把点A（1，2）代入y=ax2+4，得a+4=2 解得a=-2∴该二次函数的表达式为y=−2x2+4当y=0时解得x 1=−√2，x 2=√2∴BC =2√2∴S △ABC =12×2√2×2=2√2．17．（1）解：把A(−1，0)，B(3，0)代入y =ax 2+bx −3得：{a −b −3=09a +3b −3=0解得{a =1b =2故该抛物线解析式为：y =x 2−2x −3（2）解：由(1)知，抛物线解析式为：y =x 2−2x −3=(x −1)2−4∴该抛物线的对称轴是x =1，顶点坐标为(1，−4).如图，设点M 坐标为(m ，m 2−2m −3)∴ME =|−m 2+2m +3|∵M 、N 关于x =1对称，且点M 在对称轴右侧∴点N 的横坐标为2−m∴MN =2m −2∵四边形MNFE 为正方形∴ME =MN∴|−m 2+2m +3|=2m −2分两种情况：①当−m 2+2m +3=2m −2时，解得：m 1=√5，m 2=−√5（不符合题意，舍去） 当m =√5时，正方形的面积为(2√5−2)2=24−8√5；②当−m2+2m+3=2−2m时，解得：m3=2+√5，m4=2−√5(不符合题意，舍去) 当m=2+√5时，正方形的面积为(2+2√5)2=24+8√5；综上所述，正方形的面积为24−8√5或24+8√5.18．（1）解：∵函数y=m(x+1)2+4n（m≠0，且m，n为实数）∴函数图象的对称轴为x=−1（2）证明：令y=0，则0=m(x+1)2+4n即(x+1)2=−4nm∵ m，n异号>0∴−4nm∴一元二次方程有两个不相等的实数根，即函数y的图象与x轴有两个不同的交点；（3）证明：由题可知p=m+4n，q=16m+4n，r=25m+4n，∵2q−(p+r)=2(16m+4n)−(m+4n+25m+4n)=6m<0∴m<0.。

九年级数学上册第二十二章二次函数知识点梳理单选题1、已知点A（－2，y1），B（1，y2），C（3，y3）在二次函数y=−2x2图象上，则y1，y2，y3的大小关系是（）A．y1<y3<y2B．y1<y2<y3C．y2<y1<y3D．y3<y1<y2答案：D分析：分别计算出自变量为-2、-1和3的函数值，然后比较函数值的大小．解：∵点A（-2，y1），B（1，y2），C（3，y3）在二次函数y=-2x2图象上，∴y1=-2×4=-8；y2=-2×1=-2；y3=-2×9=-18，∴y3＜y1＜y2．故选：D．小提示：本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．2、已知抛物线y=x2+kx−k2的对称轴在y轴右侧，现将该抛物线先向右平移3个单位长度，再向上平移1个单位长度后，得到的抛物线正好经过坐标原点，则k的值是（）A．−5或2B．−5C．2D．−2答案：B分析：根据二次函数图象左加右减，上加下减的平移规律进行解答即可．解：函数y=x2+kx−k2向右平移3个单位，得：y=(x−3)2+k(x−3)−k2；再向上平移1个单位，得：y=(x−3)2+k(x−3)−k2+1，∵得到的抛物线正好经过坐标原点∴0=(0−3)2+k(0−3)−k2+1即k2+3k−10=0解得：k=−5或k=2∵抛物线y=x2+kx−k2的对称轴在y轴右侧∴x=−k＞02∴k＜0∴k=−5故选：B．小提示：此题主要考查了函数图象的平移，要求熟练掌握平移的规律：左加右减，上加下减．3、在同一平面直角坐标系中，函数y=ax2+bx与y＝ax＋b的图象不可能是( )A．B．C．D．答案：D分析：根据二次函数与一次函数的图象与性质进行判断即可．解：当a>0，b>0时，y=ax2+bx的开口上，与x轴的一个交点在x轴的负半轴，y=ax+b经过第一、二、三象限，且两函数图象交于x的负半轴，无选项符合；当a>0，b<0时，y=ax2+bx的开口向上，与x轴的一个交点在x轴的正半轴，y=ax+b经过第一、三、四象限，且两函数图象交于x的正半轴，故选项A正确，不符合题意题意；当a<0，b>0时，y=ax2+bx的开口向下，与x轴的一个交点在x轴的正半轴，y=ax+b经过第一、二、四象限，且两函数图象交于x的正半轴，C选项正确，不符合题意；当a<0，b<0时，y=ax2+bx的开口向下，与x轴的一个交点在x轴的负半轴，y=ax+b经过第二、三、四象限，B选项正确，不符合题意；只有选项D的两图象的交点不经过x轴，故选D.小提示：本题考查二次函数与一次函数图象的性质，解题的关键是根据a、b与0的大小关系进行分类讨论．4、在平面直角坐标系中，若抛物线y=2(x+5)(x−3)经一次变换后得到抛物线y=2(x+3)(x−5)，则这个变换可以是（）A．向左平移2个单位B．向右平移2个单位C．向上平移8个单位D．向下平移8个单位答案：B分析：先将两解析式化成顶点式，然后根据平移前后的两抛物线的顶点坐标即可解答．解：y=2（x+5）（x-3）=2x2+4x-30=2（x+1）2-32，顶点坐标是（-1，-32）．y=2（x+3）（x-5）=2x2-4x-30=2（x-1）2-32，顶点坐标是（1，-32）．所以将抛物线y=2（x+5）（x-3）向右平移2个单位长度得到抛物线y=2（x+3）（x-5）．故选：B．小提示：本题主要考查了二次函数图像与平移变换，掌握平移的规律“左加右减，上加下减”是解答本题的关键．5、如图，已知抛物线y=ax2+bx−2的对称轴是x=−1，直线l∥x轴，且交抛物线于点P(x1,y1),Q(x2,y2)，下列结论错误．．的是（）A．b2>−8a B．若实数m≠−1，则a−b<am2+bmC．3a−2>0D．当y>−2时，x1⋅x2<0答案：C分析：先根据抛物线对称轴求出b=2a，再由抛物线开口向上，得到a>0，则b2+8a=4a2+8a>0由此即可判断A；根据抛物线开口向上在对称轴处取得最小值即可判断B；根据当x=1时，y=a+b−2<0，即可判断C；根据y>−2时，直线l与抛物线的两个交点分别在y轴的两侧，即可判断D．解：∵抛物线y=ax2+bx−2的对称轴是x=−1，∴−b=−1，2a∴b=2a，∵抛物线开口向上，∴a>0，∴b2+8a=4a2+8a>0，∴b2>−8a，故A说法正确，不符合题意；∵抛物线开口向下，抛物线对称轴为直线x=-1，∴当x=-1时，y=a−b−2，最小值∴当实数m≠−1，则a−b−2<am2+bm−2，∴当实数m≠−1时，a−b<am2+bm，故B说法正确，不符合题意；∵当x=1时，y=a+b−2<0，∴a+2a-2＜0，即3a-2＜0，故C说法错误，符合题意；∵y>−2，∴直线l与抛物线的两个交点分别在y轴的两侧，∴x1⋅x2<0，故D说法正确，不符合题意；故选C．小提示：本题主要考查了根据二次函数的图象去判断式子符号，二次函数的系数与图象之间的关系等等，熟知二次函数的相关知识是解题的关键．6、二次函数y=x2+2x+2的图象的对称轴是（）A．x=−1B．x=−2C．x=1D．x=2答案：A分析：将二次函数y=x2+2x+2写成顶点式，进而可得对称轴．解：∵y=x2+2x+2=(x+1)2+1．∴二次函数y=x2+2x+2的图象的对称轴是x=−1．故选A．小提示：本题考查了二次函数的性质，将一般式转化为顶点式是解题的关键．7、某商场降价销售一批名牌衬衫，已知所获利润y（元）与降价x（元）之间的关系是y＝－2x2＋60x＋800，则利润获得最多为（）A．15元B．400元C．800元D．1250元答案：D分析：将函数关系式转化为顶点式，然后利用开口方向和顶点坐标即可求出最多的利润．解：y＝－2x2＋60x＋800＝－2（x－15）2＋1250∵－2＜0故当x＝15时，y有最大值，最大值为1250即利润获得最多为1250元故选：D．小提示：此题考查的是利用二次函数求最值，掌握将二次函数的一般式转化为顶点式求最值是解决此题的关键．8、抛物线y=ax2+bx+c经过点(−1,0)、(3,0)，且与y轴交于点(0,−5)，则当x=2时，y的值为（）A．−5B．−3C．−1D．5答案：A分析：先利用待定系数法求出抛物线解析式，再求函数值即可．解：∵抛物线y=ax2+bx+c经过点(−1,0)、(3,0)，且与y轴交于点(0,−5)，∴{c=−5a−b+c=09a+3b+c=0，解方程组得{c=−5 a=53b=−103，∴抛物线解析式为y=53x2−103x−5，当x=2时，y=53×4−103×2−5=−5．故选择A．小提示：本题考查待定系数法求抛物线解析式，和函数值，掌握系数法求抛物线解析式方法和函数值求法是解题关键．9、如图，等腰Rt△ABC与矩形DEFG在同一水平线上，AB=DE=2,DG=3，现将等腰Rt△ABC沿箭头所指方向水平平移，平移距离x是自点C到达DE之时开始计算，至AB离开GF为止．等腰Rt△ABC与矩形DEFG的重合部分面积记为y，则能大致反映y与x的函数关系的图象为（）A．B．C．D．答案：B分析：根据平移过程，可分三种情况，当0≤x<1时，当1≤x<3时，当3≤x≤4时，利用直角三角形的性质及面积公式分别写出各种情况下y与x的函数关系式，再结合函数图象即可求解．过点C作CM⊥AB于N，DG=3，在等腰Rt△ABC中，AB=2，∴CN=1，①当0≤x<1时，如图，CM=x，∴PQ=2x，∴y=12⋅PQ⋅CM=12×2x⋅x=x2，∴0≤x<1，y随x的增大而增大；②当1≤x<3时，如图，∴y=S△ABC=12×2×1=1，∴当1≤x<3时，y是一个定值为1；③当3≤x≤4时，如图，CM=x−3，∴PQ=2(x−3)，∴y=12AB⋅CN−12PQ⋅CM=12×2×1−12×2×(x−3)2=1−(x−3)2,当x=3，y=1，当3<x<4，y随x的增大而减小，当x=4，y=0，结合ABCD选项的图象，故选：B．小提示：本题考查了动点函数问题，涉及二次函数的图象及性质，能够准确理解题意并分情况讨论是解题的关键．10、如图，在正方形ABCD中，AB=4，点P从点A出发沿路径A→B→C向终点C运动，连接DP，作DP的垂直平分线MN与正方形ABCD的边交于M，N两点，设点P的运动路程为x，△PMN的面积为y，则下列图象能大致反映y与x函数关系的是（）A．B．C．D．答案：A分析：分点P在AB和BC上两种情况，分别求出MN和PF长，利用面积公式求解．解：（1）如图，当0≤x≤4时，点P在AB上，过点N作NE⊥AD于点E，设MN与PD交于点F，∴NE=DC=AD，则PD=√PA2+AD2=√x2+42=√x2+16，又∵MN垂直平分PD，∴PF=12PD=12√x2+16，∴∠MDF+∠FMD=∠MNE+∠FME=90°，∴∠MNE=∠PDA，在△MNE和△PDA中，{∠A=∠NEMAD=EN∠PDA=∠MNE∴△APD≌△EMN，∴PD=MN=√x2+16，∴y=12MN⋅PF=12√x2+16⋅12√x2+16=14x2+4 ,（2）如图，当4＜x≤8时，点P在BC上，过点N作NE⊥CD于点E，设MN交PD于点F，则PD=√PC2+CD2=√(8−x)2+16 ,∴PF=12√(8−x)2+16用（1）的方法得MN=√(8−x)2+16,y=12√(8−x)2+16⋅12√(8−x)2+16=14(x−8)2+4，故y={14x2+4(0≤x≤4)14(x−8)2+4(4＜x≤8)故选择A．小提示：本题考查分段函数，解决问题的关键是根据点P的位置确定自变量的取值范围得出函数解析式．填空题11、抛物线y=3−x2位于y轴左侧的部分是______的．（填“上升”或“下降”）答案：上升分析：根据二次函数图象的性质解答即可．解：∵二次项系数-1<0，∴抛物线开口向下，∵对称轴是直线y=0，∴抛物线y=3−x2位于y轴左侧的部分是上升的．所以答案是：上升．小提示：本题考查了二次函数图象的性质，熟练掌握二次函数y=ax2+k的性质是解答本题的关键．对于二次函数y=ax2+k (a，k为常数，a≠0)，当a>0时，抛物线开口向上，在对称轴的左侧y随x的增大而减小，在对称轴的右侧y随x的增大而增大；当a<0时，抛物线开口向下，在对称轴的左侧y随x的增大而增大，在对称轴的右侧y随x的增大而减小．12、如图，平行四边形ABCD中，AB=4，点D的坐标是(0，8)，以点C为顶点的抛物线经过x轴上的点A，B，则此抛物线的解析式为__________________．答案：y=−2x2+16x−24分析：根据平行四边形的性质得到CD=AB=4，即C点坐标为(4,8)，进而得到A点坐标为(2,0)，B点坐标为(6,0)，利用待定系数法即可求得函数解析式．∵四边形ABCD为平行四边形∴CD=AB=4∴C点坐标为(4,8)∴A点坐标为(2,0)，B点坐标为(6,0)设函数解析式为y=a(x−2)(x−6)，代入C点坐标有8=a(4−2)(4−6)解得a=−2∴函数解析式为y=−2(x−2)(x−6)，即y=−2x2+16x−24故答案为y=−2x2+16x−24．小提示：本题考查了平行四边形的性质，和待定系数法求二次函数解析式，问题的关键是求出A点或B点的坐标．13、如图，二次函数y=ax2+bx+c的部分图象与y轴的交点为（0，3），它的对称轴为直线x=1，则下列结论中：①c=3；②2a+b=0；③8a-b+c>0；④方程ax2+bx+c=0的其中一个根在2，3之间，正确的有_______（填序号）．答案：①②④分析：由二次函数y=ax2+bx+c的部分图象与y轴的交点为（0，3），即可判断①；由抛物线的对称轴为直线x=1，即可判断②；抛物线与x轴的一个交点在-1到0之间，抛物线对称轴为直线x=1，即可判断④，由抛物线开口向下，得到a<0，再由当x=-1时，a−b+c<0，即可判断③．解：∵二次函数y=ax2+bx+c的部分图象与y轴的交点为（0，3），∴c=3，故①正确；∵抛物线的对称轴为直线x=1，∴−b=1，即2a+b=0，故②正确；2a∵抛物线与x轴的一个交点在-1到0之间，抛物线对称轴为直线x=1，∴抛物线与x轴的另一个交点在2到3之间，故④正确；∵抛物线开口向下，∴a<0，∵当x=-1时，a−b+c<0，∴a−b+c+7a<0即8a−b+c<0，故③错误，所以答案是：①②④．小提示：本题主要考查了二次函数图像的性质，解题的关键在于能够熟练掌握二次函数图像的性质．14、如图，一位篮球运动员投篮，球沿抛物线y=−0.2x2+x+2.25运行，然后准确落入篮筐内，已知篮筐的中心离地面的高度为3.05m，则他距篮筐中心的水平距离OH是_________m．答案：4分析：将y=3.05代入y=−0.2x2+x+2.25中可求出x，结合图形可知x=4，即可求出OH．解：当y=3.05时，−0.2x2+x+2.25=3.05，解得：x=1或x=4，结合图形可知：OH=4m，所以答案是：4小提示：本题考查二次函数的实际应用：投球问题，解题的关键是结合函数图形确定x的值．15、如图，一次足球训练中，一球员从球门正前方将球射向球门，球射向球门的路线呈抛物线，当球飞行的水平距离为6米时，球达到最高点，此时球离地面3米，当足球下落到离地面53米时，足球飞行的水平距离为__________米．答案：10分析：设抛物线的解析式为y=a(x−6)2+3，代入原点，确定解析式为y=−112x2+x，当y=53米时，求得x的值即可．设抛物线的解析式为y=a(x−6)2+3，代入原点，得：0=a(0−6)2+3，解得a=−112，∴抛物线的解析式为y=−112x2+x，当y=53米时，−112x2+x=53，解得x=10，x=2（舍去），足球飞行的水平距离为10米，所以答案是：10．小提示：本题考查了抛物线的解析式，已知函数值求自变量值，熟练掌握待定系数法是解题的关键．解答题16、李大爷每天到批发市场购进某种水果进行销售，这种水果每箱10千克，批发商规定：整箱购买，一箱起售，每人一天购买不超过10箱；当购买1箱时，批发价为8.2元/千克，每多购买1箱，批发价每千克降低0.2元．根据李大爷的销售经验，这种水果售价为12元/千克时，每天可销售1箱；售价每千克降低0.5元，每天可多销售1箱．(1)请求出这种水果批发价y（元/千克）与购进数量x（箱）之间的函数关系式；(2)若每天购进的这种水果需当天全部售完，请你计算，李大爷每天应购进这种水果多少箱，才能使每天所获利润最大？最大利润是多少？答案：(1)y=−0.2x+8.4(1≤x≤10且x为整数)．(2)李大爷每天应购进这种水果7箱，获得的利润最大，最大利润是140元．分析：（1）根据题意列出y=8.2−0.2(x−1)，得到结果．（2）根据销售利润=销售量×（售价-进价），利用（1）结果，列出销售利润w与x的函数关系式，即可求出最大利润．（1）解：由题意得y=8.2−0.2(x−1)=−0.2x+8.4∴批发价y与购进数量x之间的函数关系式是y=−0.2x+8.4(1≤x≤10，且x为整数)．（2）解：设李大爷销售这种水果每天获得的利润为w元则w=[12−0.5(x−1)−y]⋅10x=[12−0.5(x−1)−(−0.2x+8.4)]⋅10x=−3x2+41x∵a=−3<0∴抛物线开口向下∵对称轴是直线x=416∴当1≤x≤41时，w的值随x值的增大而增大6∵x为正整数，∴此时，当x=6时，w=138最大当41≤x≤10时，w的值随x值的增大而减小6∵x为正整数，∴此时，当x=7时，w=140最大∵140>138∴李大爷每天应购进这种水果7箱，获得的利润最大，最大利润是140元．小提示：本题考查了二次函数的性质在实际生活中的应用，最大销售利润的问题常利用二次函数的增减性来解答，解题关键是理解题意，确定变量，建立函数模型，然后结合实际选择最优方案进行解决．17、某服装店以每件30元的价格购进一批T恤，如果以每件40元出售，那么一个月内能售出300件，根据以往销售经验，销售单价每提高1元，销售量就会减少10件，设T恤的销售单价提高x元．（1）服装店希望一个月内销售该种T恤能获得利润3360元，并且尽可能减少库存，问T恤的销售单价应提高多少元？（2）当销售单价定为多少元时，该服装店一个月内销售这种T恤获得的利润最大？最大利润是多少元？答案：（1）2元；（2）当服装店将销售单价50元时，得到最大利润是4000元分析：（1）根据题意，通过列一元二次方程并求解，即可得到答案；（2）设利润为M元，结合题意，根据二次函数的性质，计算得利润最大值对应的x的值，从而得到答案．（1）由题意列方程得：（x＋40-30）（300-10x）＝3360解得：x1＝2，x2＝18∵要尽可能减少库存，∴x2＝18不合题意，故舍去∴T恤的销售单价应提高2元；（2）设利润为M 元，由题意可得：M ＝（x ＋40-30）（300-10x ）＝-10x 2＋200x ＋3000＝−10(x −10)2+4000 ∴当x ＝10时，M 最大值＝4000元 ∴销售单价：40＋10＝50元∴当服装店将销售单价50元时，得到最大利润是4000元．小提示：本题考查了一元二次方程、二次函数的知识；解题的关键是熟练掌握一元二次方程、二次函数的性质，从而完成求解．18、在平面直角坐标系中，设二次函数y =−12(x −2m )2+3−m （m 是实数）． (1)当m =2时，若点A (8,n )在该函数图象上，求n 的值．(2)小明说二次函数图象的顶点在直线y =−12x +3上，你认为他的说法对吗？为什么？(3)已知点P(a +1,c)，Q(4m −5+a,c)都在该二次函数图象上，求证：c ≤138．答案：(1)-7 (2)对，理由见解析 (3)见解析分析：（1）把m =2，点A （8，n ）代入解析式即可求解；（2）由抛物线解析式，得顶点是（2m ，3-m ），把x ＝2m 代入y =−12x +3，求出y 值与3-m 比较，若相等则即可判断小明说法正确，否则说法错误；（3）由点P （a +1，c ），Q （4m -5+a ，c ）的纵坐标相同，即可求得对称轴为直线x =a+1+4m−5+a2=a +2m -2，即可得出a +2m -2=2m ，求得a =2，得到P （3，c ），代入解析式即可得到 c =-12（3-2m ）2+3-m ＝-2m 2+5m -32＝-2(m -54)2+138，根据二次函数的性质即可证得结论．(1)解：当m ＝2时，y =-12（x -4）2+1 ∵A （8，n ）在函数图象上， ∴n =-12（8-4）2+1=-7(2)解：由题意得，顶点是（2m，3-m）当x＝2m时，y=-12×2m+3=-m+3∴顶点（2m，3-m）在直线y=-12x+3上(3)证明：∵P（a+1,c），Q（4m-5+a，c）都在二次函数的图象上∴对称轴是直线x=a+1+4m-5+a2=a+2m-2∴a+2m-2＝2m，∴a＝2，∴P（3，c），把P（3，c）代入抛物线解析式，得∴c=-12（3-2m）2+3-m＝-2m2+5m-32＝-2(m-54)2+138，∵-2<0，∴c有最大值为138，∴c≤138．小提示：本题考查了二次函数图象与系数的关系，二次函数图象上点的坐标特征，二次函数的性质，熟练掌握二次函数的性质是解题的关键．。

人教版九年级上册数学第二十二章二次函数解答题专题训练1．如图，已知抛物线26y ax bx +＝＋经过A (-1,0)，B (3,0)两点，C 是抛物线与y 轴的交点．(1)求抛物线的解析式；(2)点P (m ，n )在平面直角坐标系的第一象限内的抛物线上运动，设△PBC 的面积为S 求S 关于m 的函数解析式(指出自变量m 的取值范围)和S 的最大值．2．综合与探究：如图，在平面直角坐标系中，二次函数2y x bx c =++的图象经过点70,4A ⎛⎫- ⎪⎝⎭，点11,4B ⎛⎫ ⎪⎝⎭．(1)求此二次函数的解析式；(2)当22x -≤≤时，求二次函数2y x bx c =++的最大值和最小值；(3)点P 为此函数图象上任意一点，其横坐标为m ，过点P 作PQ x ∥轴，点Q 的横坐标为21m -+．已知点P 与点Q 不重合，且线段PQ 的长度随m 的增大而减小．求m 的取值范围；3．次函数22y ax bx =++的图象交x 轴于点A （－1，0），B （4，0），两点，交y 轴于点C ，动点M 从点A 出发，以每秒2个单位长度的速度沿AB 方向运动，过点M 作MN ⊥x 轴交直线BC 于点N ，交抛物线于点D ，连接AC ，设运动的时间为t 秒．(1)求二次函数22y ax bx =++的表达式；(2)连接BD ，当32t =时，求⊥DNB 的面积；(3)在直线MN 上存在一点P ，当⊥PBC 是以⊥BPC 为直角的等腰直角三角形时，求此时点P 的坐标．4．如图抛物线232y ax x c =++(a ≠0)与x 轴交于A 、B 两点，与y 轴交于点C ，抛物线的对称轴交x 轴于点D ，若点A 坐标为(﹣2,0)，点C 坐标为(0,4)．(1)求抛物线的解析式；(2)在抛物线的对称轴上是否存在点P ，使△PCD 是以CD 为腰的等腰三角形？如果存在，请用尺规在图1中作出这样的点P ，并直接写出P 点的坐标；如果不存在，请说明理由；(3)点E 是线段BC 上的一个动点，过点E 作x 轴的垂线与抛物线相交于点F ，当点E 运动到什么位置时，四边形CDBF 的面积最大？求出四边形CDBF 的最大面积及此时E 点的坐标．5．如图，抛物线212y x bx c =-++与x 轴交于()1,0A -，B 两点，与y 轴交于点()0,2C ，连接BC ．(1)求抛物线的解析式．(2)点P 是第三象限抛物线上一点，直线PE 与y 轴交于点D ，BCD △的面积为12，求点P 的坐标．(3)在（2）的条件下，若点E 是线段BC 上点，连接OE ，将OEB 沿直线OE 翻折得到OEB '△，当直线EB '与直线BP 相交所成锐角为45︒时，求点B '的坐标．6．如图，直线3y x =-交x 轴于点B ，交y 轴于点A ，抛物线24y ax x c =++经过点A ，B ，顶点为点C ．(1)求抛物线的解析式及点C 的坐标．(2)将抛物线24y ax x c =++向下平移m 个单位长度，点C 的对应点为D ，连接AD ，BD ，若2ABD S =，求m 的值．7．如图，抛物线23y ax bx =++与x 轴交于点()3,0A ，与y 轴交于点B ，点C 在直线AB 上，过点C 作CD x ⊥轴于点()1,0D ，将ACD △沿CD 所在直线翻折，使点A 恰好落在抛物线上的点E 处．(1)求抛物线解析式；(2)连接BE ，求BCE 的面积；(3)拋物线上是否存在一点P ，使PEA BAE ∠=∠？若存在，求出P 点坐标；若不存在，请说明理由．8．如图，抛物线2412y ax ax a =--与x 轴交于A 、B 两点（点A 点B 点的左边），与y 轴交于点C ．直线l 与抛物线交于A 、D 两点，与y 轴交于点E ，点D 的坐标为(4,3)．(1)求抛物线的解析式与A 、B 两点坐标；(2)若点P 是抛物线上的点且在直线l 上方，连接PA 、PD ，求当PAD △面积最大时点P 的坐标及该面积的最大值；(3)若点Q 是y 轴上的点，且45ADQ ∠=︒，求点Q 的坐标．9．如图，已知抛物线 24y x =- 与 x 轴交于点 A ，B （点 A 位于点 B 的左侧），C 为顶点，直线 y x m =+ 经过点 A ，与 y 轴交于点 D ．(1)求线段 AD 的长；(2)沿直线 AD 方向平移该抛物线得到一条新拋物线，设新抛物线的顶点为 C，若点 C 在反比例函数 3y x =- 的图象上．求新抛物线对应的函数表达式．10．如图，抛物线的顶点为C (1，9)，与x 轴交于A ，B (4，0)两点．(1)求抛物线的解析式；(2)抛物线与y 轴交点为D ，求BCD S △．11．如图，抛物线y =-x 2+bx +c 与x 轴交于A (2，0)，B (-6，0)两点．(1)求该抛物线的解析式；(2)若抛物线交y 轴于C 点，在该抛物线的对称轴上是否存在点Q ，使得QAC 的周长最小？若存在，求出Q 点的坐标；若不存在，请说明理由．(3)在坐标平面内是否存在一点P ，使得Q 、B 、A 、P 围成的图形是平行四边形，若存在，直接写出点P 的坐标；若不存在，请说明理由．12．已知二次函数()20y ax bx c a =++≠的图象与x 轴相交于点A 和点()10B ,，与y 轴相交于点()0,3C ，抛物线的对称轴是直线1x =-．(1)求二次函数的表达式及A 点的坐标；(2)D 是抛物线的顶点，点E 在抛物线上，且与点C 关于抛物线的对称轴对称，直线BE 交对称轴于点F ，试判断四边形CDEF 的形状，并说明理由．13．如图，已知抛物线212y x bx c =-++与坐标轴分别交于点A (0，8)、B (8，0)和点E ，动点C 从原点O 开始沿OA 方向以每秒1个单位长度移动，动点D 从点B 开始沿BO 方向以每秒1个单位长度移动，动点C 、D 同时出发，当动点D 到达原点O 时，点C 、D 停止运动．(1)直接写出抛物线的解析式：(2)求CED 的面积S 与D 点运动时间t 的函数解析式；当t 为何值时，CED 的面积最大？最大面积是多少？14．如图，抛物线()23202y ax x a =--≠的图像与x 轴交于A 、B 两点，与y 轴交于C 点，已知点B 坐标为()4,0．(1)求该抛物线相应的函数表达式；(2)判断ABC的形状，并说明理由．15．如图，抛物线2=-++的图像过点A(3，0)，对称轴为直线1y x bx cx=，交y轴于点C，点C关于抛物线对称轴的对称点为B．若点P(0，m)，在y轴正半轴上运动，点Q为抛物线一动点，且在第四象限，连接PQ交x轴于点E，连接BE．(1)求抛物线的解析式(2)当m=1.5时，且满足以P、O、E三点构成三角形与BCP相似，求PBE的面积．(3)当以点B、P、E为顶点的三角形为等腰直角三角形时，写出点P的坐标，点Q坐标．16．如图，二次函数y＝ax2＋bx＋c(a≠0)的图象交x轴于A、B两点，交y轴于点D，点B的坐标为(3，0)，顶点C的坐标为(1，4)．(1)求二次函数的解析式；(2)点P是直线BD上的一个动点，过点P作x轴的垂线，交抛物线于点M，当点P在第一象限时，求线段PM长度的最大值；(3)在抛物线上是否存在点Q，且点Q在第一象限，使⊥BDQ中BDQ的坐标；若不存在，请说明理由．17．如图，抛物线22y x x c =-+的顶点A 在直线l ：5y x =-上．(1)求抛物线的解析式及顶点A ；(2)设抛物线与y 轴交于点B ，与x 轴交于点C ，D （C 点在D 点的左侧），判断⊥ABD 的形状；(3)直线l 与x 轴交于点E ，点P 在射线AE 上运动，当PDE △与PAB △的面积相差为2时，利用备用图，求出此时点P 的坐标．18．如图，在平面直角坐标系中，过点()0,4A 、()5,9B 两点的抛物线的顶点C 在x 轴正半轴上．(1)求抛物线的解析式；(2)求点C 的坐标；(3)(),P x y 为线段AB 上一点，14x ≤≤，作PM y ∥轴交抛物线于点M ，求PM 的最大值与最小值．19．如图所示，抛物线y ＝ax 2＋bx ﹣3与x 轴交于A （﹣1，0），B （3，0）两点，与y 轴交于点C ，点M 是抛物线的顶点．(1)求抛物线的解析式及顶点M 的坐标；(2)如图，直线BC 下方的抛物线上有一点D ，过点D 作DE ⊥BC 于点E ，作DF 平行x 轴交直线BC 于点F ，求⊥DEF 周长的最大值．20．在平面直角坐标系xOy 中，已知抛物线2212125555y x mx m m =-+-+-，点A ，B ，C 都在抛物线上，AB∥x 轴，∠ABC ＝135°，且AB ＝4．(1)抛物线的顶点坐标为 （用含m 的代数式表示）；(2)求⊥ABC 的面积；(3)已知M （0，－4）、N （4，－4），若抛物线2212125555y x mx m m =-+-+-与线段MN 恰有一个公共点，求m 的取值范围．答案1．(1)2246y x x =-++ (2)2327324S m ⎛⎫=--+ ⎪⎝⎭(0＜m ＜3)，当m =32时，△PBC 的面积取得最大值，最大值为274 2．(1)274y x x =+- (2)最小值为-2，最大值为174(3)13m < 3．(1)213222y x x =-++ (2)2DNB S =△(3)P （1，－1）或（3，3）4．(1)213442y x x =-++ (2)(3,8)或(3,﹣5)或(3,5)(3)当t ＝4时，四边形CDBF 的最大面积为26，此时E (4,2)5．(1)213222y x x =-++； (2)P （−3，−7）；(3)B '的坐标为⎝⎭或⎛ ⎝⎭．6．(1)243y x x =-+-，(2,1)C (2)23或1037．(1)2y x 2x 3=-++(2)2(3)存在，()2,3或()4,5-8．(1)抛物线的解析式为：2134y x x =-++，A 点坐标为（-2,0），B 点坐标为（6,0）(2)PAD △的面积最大值为274，P 151,4⎛⎫ ⎪⎝⎭ (3)Q 的坐标为（0，133）或（0，-9） 9．(1)AD =(2)新抛物线对应的函数表达式为：268y x x =-+或222y x x -=-． 10．(1)y =-x 2+2x +8；(2)S △BCD =6．11．(1)2412y x x =--+(2)存在，Q (-2，8)(3)存在，(6，8)或(-2，-8)或(-10，8)12．(1)223y x x =--+，()30A -,； (2)四边形CDEF 是菱形，理由见解析． 33．(1)y =-12x 2+3x +8(2)S =-12t 2+5t ，当t =5时，CED 的面积最大，最大面积是252 14．(1)213222y x x =--(2)直角三角形，理由见解析 15．(1)2y x 2x 3=-++(2)3或7532(3)(0，2)，2,2-) 16．(1)y ＝﹣x 2＋2x ＋3 (2)94(3)存在，(1，4)或(2，3)17．(1)223y x x =--，顶点A （1，－4），(2)⊥ABD 为直角三角形，理由见解析(3)（4，－1）或（2，－3）． 18．(1)()22y x =-(2)()2,0(3)最大值是254，最小值是419．(1)y ＝x 2﹣2x ﹣3，（1，﹣4）(2)944+20．(1)（m ，2m －5）(2)2 (3)12m =或559215m --559215m ++。

一、选择题1．抛物线y ＝ax 2+bx +c （a ≠0）的图象大致如图所示，下列说法：①2a +b ＝0；②当﹣1＜x ＜3时，y ＜0；③若（x 1，y 1）（x 2，y 2）在函数图象上，当x 1＜x 2时，y 1＜y 2；④9a +3b +c ＝0，其中正确的是（ ）A ．①②④B ．①④C ．①②③D ．③④ 2．在同一直角坐标系中，一次函数y=ax+c 和二次函数y=ax 2+c 的图象大致为（ ） A ． B ． C ． D ． 3．已知()()()112233,,,,,x y x y x y 是抛物线245y x x =--+图像上的任意三点，在以下哪个取值范围中，分别以1y 、2y 、3y 为长的三条线段不一定能围成一个三角形的是（ ） A ．5122x -<< B ．7122x -<<- C ．30x -<< D ．41x -<<- 4．当0ab >时，2y ax =与y ax b =+的图象大致是（ ）A ．B ．C ．D ． 5．如图，在ABC 中，∠B ＝90°，AB ＝3cm ，BC ＝6cm ，动点P 从点A 开始沿AB 向点B 以1cm /s 的速度移动，动点Q 从点B 开始沿BC 向点C 以2cm /s 的速度移动，若P ，Q 两点分别从A ，B 两点同时出发，P 点到达B 点运动停止，则PBQ △的面积S 随出发时间t 的函数图象大致是（ ）A ．B ．C ．D ． 6．抛物线2(2)3y x =-+的对称轴是（ ）A ．直线2x =-B ．直线3x =C ．直线1x =D ．直线2x = 7．在平面直角坐标系中抛物线2y x =的图象如图所示，已知点A 坐标为(1，1)，过点A 作1//AA x 轴交抛物线于点A ，过点1A 作12//A A OA 交抛物线于点2A ，过点2A 作23//A A x 轴交抛物线于点3A 过点3A 作34//A A OA 交抛物线于点4A ，……则点2020A 的坐标为（ ）A ．(1011， 21011)B ．(-1011， 21011)C ．(-1010， 21011)D ．(1010， 21011)8．已知二次函数()()2y x p x q =---，若m ，n 是关于x 的方程()()20x p x q ---=的两个根，则实数m ，n ，p ，q 的大小关系可能是（ ） A ．m ＜p ＜q ＜nB ．m ＜p ＜n ＜qC ．p ＜m ＜n ＜qD ．p ＜m ＜q ＜n9．抛物线2(3)y a x k =++的图象如图所示．已知点()15,A y -，()22,B y -，()36.5,C y -三点都在该图象上，则1y ，2y ，3y 的大小关系为（ ）A ．123y y y >>B ．321y y y >>C ．213y y y >>D ．231y y y >> 10．如图是抛物线y 1＝ax 2+bx +c （a ≠0）图象的一部分，抛物线的顶点坐标是A （1，3），与x 轴的一个交点B （4，0），直线y 2＝mx +n （m ≠0）与抛物线交于A 、B 两点．下列结论：①2a +b ＝0；②abc ＞0；③方程ax 2+bx +c ＝3有两个相等的实数根；④抛物线与x 轴的另一个交点是（﹣1，0）；⑤当1＜x ＜4时，有y 2＜y 1；⑥a +b ≥m （am +b ）（m 实数）其中正确的是（ ）A ．①②③⑥B ．①③④C ．①③⑤⑥D ．②④⑤ 11．抛物线()2512y x =--+的顶点坐标为（ ）A ．()1,2-B ．()1,2C ．()1,2-D ．()2,1 12．关于抛物线223y x x =-+-，下列说法正确的是（ ）A ．开口方向向上B ．顶点坐标为()1,2-C ．与x 轴有两个交点D ．对称轴是直线1x =-13．把函数2(1)2y x =-+图象向右平移1个单位长度，平移后图象的函数解析式为（ ） A ．22y x =+B ．2(1)1y x =-+C ．2(2)2y x =-+D ．2(1)3y x =-+ 14．抛物线y=2(x －1)2－3向左平移3个单位长度，此时抛物线的对称轴是直线（ ）A ．x =－3B ．x =－1C ．x =－2D ．x =4 15．在西宁市中考体考前，某初三学生对自己某次实心球训练的录像进行分析，发现实心球飞行高度y （米）与水平距离x （米）之间满足函数解析式y 112=-x 223+x 53+，由此可知该生此次实心球训练的成绩为（ ）A ．6米B ．8米C ．10米D ．12米 二、填空题16．如图，在平面直角坐标系中，抛物线2y x x 2=--分别交y 轴，x 轴于点A ，B ，动点E 在抛物线上，EF x ⊥轴，交直线AB 于点F ．则EF 的长为______（用含字母x 的式子来表示）．17．已知抛物线2y x bx c =++的部分图象如图所示，当0y <时，x 的取值范围是______．18．将抛物线2y x 向上平移1个单位，再向左平移2个单位后，得到的抛物线的顶点坐标是__________．19．已知抛物线243y x x =-+与x 轴相交于点A ，B （点A 在点B 左侧），顶点为M 平移该抛物线，使点M 平移后的对应点M '落在x 轴上，点B 平移后的对应点B '落在y 轴上，则平移后的抛物线解析式为______．20．抛物线23y x =先向上平移1个单位，再向左平移1个单位，所得的抛物线为________21．如图是二次函数2(0)y ax bx c a =++≠图象的一部分，有下列4个结论：①0abc >；②240b ac ->；③关于x 的方程20ax bx c ++=的两个根是12x =-，23x =；④关于x 的不等式20ax bx c ++>的解集是2x >-．其中正确的结论是___________．22．小明从如图所示的二次函数()20y ax bx c a =++≠图象中，观察得出了下面五条信息：①32a b =；②240b ac -=；③ 0ab >；④0a b c ++<；⑤20b c +>．你认为正．确．信息的有_______________．（请填序号）23．抛物线y ＝x 2+2x-3与x 轴的交点坐标为____________________．24．如图，将抛物线y=−12x 2平移得到抛物线m ．抛物线m 经过点A （6，0）和原点O ，它的顶点为P ，它的对称轴与抛物线y=−12x 2交于点Q ，则图中阴影部分的面积为______．25．设A （－3，y 1），B （－2，y 2），C （12，y 3）是抛物线y ＝（x+1）2－m 上的三点，则y 1，y 2，y 3的大小关系为_______．（用“＞”连接）26．若函数21y mx x =++的图象与x 轴只有一个公共点，则m 的值是_______．参考答案三、解答题27．如图，已知抛物线y ＝ax 2+bx +c （a ≠0）经过A （﹣1，0），B （3，0），C （0，﹣3）三点，直线l 是抛物线的对称轴．（1）求抛物线的函数解析式；（2）在抛物线的对称轴上是否存在一点M ，使得△ACM 的周长最短？若存在，求点M 的坐标；若不存在，请说明理由．28．某超市经销一种销售成本为每件40元的商品．据市场调查分析，如果按每件50元销售，一周能卖出500件；若销售单价每涨1元，每周销量就减少10件．设每件涨价(0)x x ≥元．（1）写出一周销售量y （件）与x （元）的函数关系式．（2）设一周销售获得毛利润w 元，写出w 与x 的函数关系式，并确定当x 在什么取值范围内变化时，毛利润w 随x 的增大而增大．（3）超市扣除销售额的20%作为该商品的经营费用，为使得纯利润（纯利润=毛利润－经营费用）最大，超市对该商品售价为______元，最大纯利润为______元．29．如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有一道篱笆的长方形花圃，设花圃的宽AB 为x 米，面积为y 平方米．（1）求y 与x 的函数关系式及自变量x 的取值范围；（2）若墙的最大可用长度为9米，求此时当AB 为多少米时长方形花圃的面积最大，最大面积是多少？30．有这样一个问题：探究函数243y x x =-+的图象与性质．小丽根据学习函数的经验，对函数243y x x =-+的图象与性质进行了探究．下面是小丽的探究过程，请补充完整：（1）函数243y x x =-+的自变量x 的取值范围是_______．（2）如图，在平面直角坐标系xOy 中，画出了函数243y x x =-+的部分图象，用描点法将这个函数的图象补充完整；（3）对于上面的函数243y x x =-+，下列四个结论：①函数图象关于y 轴对称；②函数既有最大值，也有最小值；③当2x >时，y 随x 的增大而增大，当2x <-时，y 随x 的增大而减小；④函数图象与x 轴有2个公共点．所有正确结论的序号是_____．（4）结合函数图象，解决问题：若关于x 的方程243x x k -+=有4个不相等的实数根，则k的取值范围是____．。

九年级数学上册第二十二章二次函数知识点总结归纳单选题1、定义：我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”．如图，在正方形OABC 中，点A (0,2)，点C (2,0)，则互异二次函数y =(x −m )2−m 与正方形OABC 有交点时m 的最大值和最小值分别是（ ）A ．4，-1B ．5−√172，-1C ．4，0D ．5+√172，-1 答案：D分析：分别讨论当对称轴位于y 轴左侧、位于y 轴与正方形对称轴x =1之间、位于直线x =1和x =2之间、位于直线x =2右侧共四种情况，列出它们有交点时满足的条件，得到关于m 的不等式组，求解即可． 解：由正方形的性质可知：B （2,2）；若二次函数y =(x −m )2−m 与正方形OABC 有交点,则共有以下四种情况:当m ≤0时，则当A 点在抛物线上或上方时，它们有交点，此时有{m ≤0m 2−m ≤2， 解得：−1≤m <0；当0<m ≤1时，则当C 点在抛物线上或下方时，它们有交点，此时有{0<m ≤1(2−m )2−m ≥0， 解得：0<m ≤1；当1<m ≤2时，则当O 点位于抛物线上或下方时，它们有交点，此时有{1<m ≤2m 2−m >0， 解得：1<m ≤2；当m >2时，则当O 点在抛物线上或下方且B 点在抛物线上或上方时，它们才有交点，此时有{m >2m 2−m ≥0(2−m )2−m ≤2 ，解得：2<m≤5+√17；2，−1．综上可得：m的最大值和最小值分别是5+√172故选：D．小提示：本题考查了抛物线与正方形的交点问题，涉及到列一元一次不等式组等内容，解决本题的关键是能根据图像分析交点情况，并进行分类讨论，本题综合性较强，需要一定的分析能力与图形感知力，因此对学生的思维要求较高，本题蕴含了分类讨论和数形结合的思想方法等．2、如图，二次函数y=ax2+bx+c的图象关于直线x=1对称，与x轴交于A(x1,0)，B(x2,0)两点，若−2< x1<−1，则下列四个结论：①3<x2<4，②3a+2b>0，③b2>a+c+4ac，④a>c>b．正确结论的个数为（）A．1个B．2个C．3个D．4个答案：B分析：根据二次函数的对称性，即可判断①；由开口方向和对称轴即可判断②；根据抛物线与x轴的交点已经x=-1时的函数的取值，即可判断③；根据抛物线的开口方向、对称轴，与y轴的交点以及a－b＋c＜0，即可判断④．∵对称轴为直线x=1，-2<x1<-1，∴3＜x2＜4，①正确，∵−b= 1，2a∴b=- 2а，∴3a＋2b= 3a-4a= -a，∵a＞0，∴3a+2b<0，②错误；∵抛物线与x轴有两个交点，∴b2 - 4ac > 0，根据题意可知x=-1时，y<0，∴a－b＋c<0，∴a＋c<b，∵a＞0，∴b=-2a<0，∴a＋c<0，∴b2 -4ac > a+ c，∴b2＞a＋c＋4ac，③正确；∵抛物线开口向上，与y轴的交点在x轴下方，∴a＞0，c<0，∴a>c，∵a-b＋c<0，b=-2a，∴3a+c<0，∴c<-3a，∴b=–2a，∴b＞c，以④错误；故选B小提示：本题主要考查图象与二次函数系数之间的关系，解题的关键是掌握数形结合思想的应用，注意掌握二次函数图象与系数的关系，掌握二次函数的对称性．3、抛物线y＝x2+3上有两点A（x1，y1），B（x2，y2），若y1＜y2，则下列结论正确的是( )A．0≤x1＜x2B．x2＜x1≤0C．x2＜x1≤0或0≤x1＜x2D．以上都不对答案：D分析：根据二次函数图象及性质，即可判定．∵抛物线y＝x2+3开口向上，在其图象上有两点A（x1，y1），B（x2，y2），且y1＜y2，∴|x1|＜|x2|，∴0≤x1＜x2，或x2＜x1≤0，或x2＞0，x1≤0且x2+x1＞0，或x2＜0，x1＞0且x2+x1＜0，故选：D．小提示：本题考查了二次函数的图象及性质，熟练掌握和运用二次函数的图象及性质是解决本题的关键．4、如图，某公司准备在一个等腰直角三角形ABC的绿地上建造一个矩形的休闲书吧PMBN，其中点P在AC上，点NM分别在BC，AB上，记PM=x，PN=y，图中阴影部分的面积为S，若NP在一定范围内变化，则y与x，S与x满足的函数关系分别是（）A．反比例函数关系，一次函数关系B．二次函数关系，一次函数关系C．一次函数关系，反比例函数关系D．一次函数关系，二次函数关系答案：D分析：先求出AM=PM，利用矩形的性质得出y=﹣x+m，最后利用S=S△ABC－S矩形PMBN得出结论．设AB=m（m为常数）．在△AMP中，∠A=45°，AM⊥PM，∴△AMP为等腰直角三角形，∴AM=PM，又∵在矩形PMBN中，PN=BM，∴x+y=PM+PN=AM+BM=AB=m，即y=﹣x+m，∴y与x成一次函数关系，∴S =S △ABC －S 矩形PMBN =12m 2-xy =12m 2-x （﹣x +m ）=x 2-mx +12m 2， ∴S 与x 成二次函数关系．故选D ．小提示：本题考查了一次函数的实际应用及二次函数的实际应用，解题的关键是掌握根据题意求出y 与x 之间的函数关系式．5、二次函数y =x 的图象经过的象限是（ ）A ．第一、二象限B ．第一、三象限C ．第二、四象限D ．第三、四象限答案：A分析：由抛物线解析式可得抛物线开口方向及顶点坐标，进而求解．∵y =x 2， ∴抛物线开口向上，顶点坐标为（0，0），∴抛物线经过第一，二象限．故选：A ．小提示：本题考查二次函数的性质，解题关键是掌握二次函数图象与系数的关系．6、关于x 的方程ax 2+bx +c =0有两个不相等的实根x 1、x 2，若x 2=2x 1，则4b −9ac 的最大值是（ ）A ．1B ．√2C ．√3D ．2答案：D分析：根据一元二次方程根与系数的关系，求得两根之和和两根之积，再根据两根关系，求得系数的关系，代入代数式，配方法化简求值即可．解：由方程ax 2+bx +c =0有两个不相等的实根x 1、x 2可得，a ≠0，x 1+x 2=−b a ，x 1x 2=c a ∵x 2=2x 1，可得3x 1=−b a ，2x 12=c a ，即2(−b 3a )2=c a 化简得9ac =2b 2 则4b −9ac =−2b 2+4b =−2(b 2−2b)=−2(b −1)2+2故4b −9ac 最大值为2故选D小提示：此题考查了一元二次方程根与系数的关系，涉及了配方法求解代数式的最大值，根据一元二次方程根与系数的关系得到系数的关系是解题的关键．7、已知抛物线y=x2+kx−k2的对称轴在y轴右侧，现将该抛物线先向右平移3个单位长度，再向上平移1个单位长度后，得到的抛物线正好经过坐标原点，则k的值是（）A．−5或2B．−5C．2D．−2答案：B分析：根据二次函数图象左加右减，上加下减的平移规律进行解答即可．解：函数y=x2+kx−k2向右平移3个单位，得：y=(x−3)2+k(x−3)−k2；再向上平移1个单位，得：y=(x−3)2+k(x−3)−k2+1，∵得到的抛物线正好经过坐标原点∴0=(0−3)2+k(0−3)−k2+1即k2+3k−10=0解得：k=−5或k=2∵抛物线y=x2+kx−k2的对称轴在y轴右侧∴x=−k＞02∴k＜0∴k=−5故选：B．小提示：此题主要考查了函数图象的平移，要求熟练掌握平移的规律：左加右减，上加下减．8、在同一平面直角坐标系中，函数y=ax2+bx与y＝ax＋b的图象不可能是( )A．B．C．D．答案：D分析：根据二次函数与一次函数的图象与性质进行判断即可．解：当a>0，b>0时，y=ax2+bx的开口上，与x轴的一个交点在x轴的负半轴，y=ax+b经过第一、二、三象限，且两函数图象交于x的负半轴，无选项符合；当a>0，b<0时，y=ax2+bx的开口向上，与x轴的一个交点在x轴的正半轴，y=ax+b经过第一、三、四象限，且两函数图象交于x的正半轴，故选项A正确，不符合题意题意；当a<0，b>0时，y=ax2+bx的开口向下，与x轴的一个交点在x轴的正半轴，y=ax+b经过第一、二、四象限，且两函数图象交于x的正半轴，C选项正确，不符合题意；当a<0，b<0时，y=ax2+bx的开口向下，与x轴的一个交点在x轴的负半轴，y=ax+b经过第二、三、四象限，B选项正确，不符合题意；只有选项D的两图象的交点不经过x轴，故选D.小提示：本题考查二次函数与一次函数图象的性质，解题的关键是根据a、b与0的大小关系进行分类讨论．9、已知二次函数y=mx2−4m2x−3（m为常数，m≠0），点P(x p,y p)是该函数图象上一点，当0≤x p≤4时，y p≤−3，则m的取值范围是（）A．m≥1或m<0B．m≥1C．m≤−1或m>0D．m≤−1答案：A分析：先求出抛物线的对称轴及抛物线与y轴的交点坐标，再分两种情况：m>0或m<0，根据二次函数的性质求得m的不同取值范围便可．解：∵二次函数y=mx2−4m2x−3，∴对称轴为x=2m，抛物线与y轴的交点为(0,−3)，∵点P(x p,y p)是该函数图象上一点，当0≤x p≤4时，y p≤−3，∴①当m>0时，对称轴x=2m>0，此时，当x=4时，y≤−3，即m⋅42−4m2⋅4−3≤−3，解得m≥1；②当m<0时，对称轴x=2m<0，当0≤x≤4时，y随x增大而减小，则当0≤x p≤4时，y p≤−3恒成立；综上，m的取值范围是：m≥1或m<0．故选：A．小提示：本题考查了二次函数的性质，关键是分情况讨论．10、如图，某涵洞的截面是抛物线形，现测得水面宽AB＝1.6m，涵洞顶点O与水面的距离CO是2m，则当水位上升1.5m时，水面的宽度为（）A．0.4mB．0.6mC．0.8mD．1m答案：C分析：根据题意可建立平面直角坐标系，然后设函数关系式为y=ax2，由题意可知A(−0.8,−2)，代入求解函数解析式，进而问题可求解．解：建立如图所示的坐标系：设函数关系式为y=ax2，由题意得：A(−0.8,−2)，∴−2=0.8×0.8×a，，解得：a=−258∴y=−25x2，8x2，当y=-0.5时，则有−0.5=−258解得：x=±0.4，∴水面的宽度为0.8m；故选C．小提示：本题主要考查二次函数的应用，熟练掌握二次函数的应用是解题的关键．填空题11、已知抛物线y=x2−x−1与x轴的一个交点为(m,0)，则代数式−3m2+3m+2022的值为______．答案：2019分析：先将点（m，0）代入函数解析式，然后求代数式的值即可得出结果．解：将（m，0）代入函数解析式得，m2-m-1=0，∴m2-m=1，∴-3m2+3m+2022=-3（m2-m）+2022=-3+2022=2019．所以答案是：2019．小提示：本题考查了二次函数图象上点的坐标特征及求代数式的值，解题的关键是将点（m，0）代入函数解析式得到有关m的代数式的值．12、如图，在平面直角坐标系中，抛物线y=−x2+2mx+m−2（m为常数，且m>0）与直线y＝2交于A、B两点．若AB＝2，则m的值为______．答案：√21−12分析：设A（x1，2），B（x2，2），抛物线y=−x2+2mx+m−2中，令y=2，得x2−2mx−m+4=0，利用根与系数关系求得AB，可建立关于m的方程并解出即可．解：设A（x1，2），B（x2，2），抛物线y=−x2+2mx+m−2中，令y=2，得：−x2+2mx+m−2=2，即：x2−2mx−m+4=0∴x1+x2=2m,x1x2=−m+4，∴AB=|x2−x1|=√(x2+x1)2−4x1x2=√(2m)2−4(−m+4)=2，∴m2+m−5=0，解得：m1=√21−12,m2=−√21−12(舍去)，所以答案是：√21−12．小提示：本题考查了抛物线与x轴的交点、二次函数与一元二次方程的关系、二次函数图象上点的坐标特征，熟练掌握这三个知识点的综合应用是解题关键．13、平移二次函数的图象，如果有一个点既在平移前的函数图象上，又在平移后的函数图象上，我们把这个点叫做“关联点”．现将二次函数y=x2+2x+c（c为常数）的图象向右平移得到新的抛物线，若“关联点”为(1,2)，则新抛物线的函数表达式为_______．答案：y=(x−3)2−2分析：将（1，2）代入y=x2+2x+c，解得c=-1，设将抛物线y=x2+2x-1=（x+1）2-2，向右平移m个单位，则平移后的抛物线解析式是y=（x+1-m）2-2，然后将（1，2）代入得到关于m的方程，通过解方程求得m的值即可．解：将（1，2）代入y=x2+2x+c，得12+2×1+c=2，解得c=-1．设将抛物线y=x2+2x-1=（x+1）2-2，向右平移m个单位，则平移后的抛物线解析式是y=（x+1-m）2-2，将（1，2）代入，得（1+1-m）2-2=2．整理，得2-m=±2．解得m1=0（舍去），m2=4．故新抛物线的表达式为y=（x-3）2-2．故答案是：y=(x−3)2−2．小提示：本题主要考查了二次函数图象与几何变换，二次函数图象上点的坐标特征以及待定系数法确定函数关系式，解题的关键是理解“关联点”的含义．14、如图是一个横断面为抛物线形状的拱桥，当水面在正常水位的情况下，拱顶（拱桥洞的最高点）离水面2m，水面宽4m．则当水位下降m=________时，水面宽为5m？答案：1.125分析：以抛物线的顶点为原点建立坐标系，则可以设函数的解析式是y=ax2，然后求得水面与抛物线的交点坐标，利用待定系数法求解抛物线的解析式，再利用点的坐标特点即可求解．解：如图，建立如下的坐标系：水面与抛物线的交点坐标是（-2，-2），(2,−2)，设函数的解析式是y=ax2，则4a=-2，解得a=−12，则函数的解析式是y=−12x2．当水面宽为5米时，把x=52代入抛物线的解析式可得：y=12×(52)2=258=3.125,∴3.125−2=1.125（米），所以答案是：1.125．小提示：本题考查了待定系数法求二次函数的解析式，二次函数的性质，建立合适的平面直角坐标系，求得水面与抛物线的交点是解题的关键．15、根据物理学规律，如果不考虑空气阻力，以40m/s的速度将小球沿与地面成30°角的方向击出，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间的函数关系是ℎ=−5t2+20t，当飞行时间t为___________s时，小球达到最高点．答案：2分析：将函数关系式转化为顶点式即可求解．根据题意，有ℎ=−5t2+20t=−5(t−2)2+20，当t=2时，ℎ有最大值．所以答案是：2．小提示：本题考查二次函数解析式的相互转化及应用，解决本题的关键是熟练二次函数解析式的特点及应用．解答题16、某公司电商平台，在2021年五一长假期间，举行了商品打折促销活动，经市场调查发现，某种商品的周销售量y（件）是关于售价x（元/件）的一次函数，下表仅列出了该商品的售价x，周销售量y，周销售利润W（元）的三组对应值数据．（2）若该商品进价a（元/件），售价x为多少时，周销售利润W最大？并求出此时的最大利润；（3）因疫情期间，该商品进价提高了m（元/件）（m>0），公司为回馈消费者，规定该商品售价x不得超过55（元/件），且该商品在今后的销售中，周销售量与售价仍满足（1）中的函数关系，若周销售最大利润是4050元，求m的值．答案：（1）y=−3x+300；（2）售价60元时，周销售利润最大为4800元；（3）m=5分析：（1）①依题意设y=kx+b，解方程组即可得到结论；（2）根据题意得W=(−3x+300)(x−a)，再由表格数据求出a=20，得到W=(−3x+300)(x−20)=−3(x−60)2+4800，根据二次函数的顶点式，求出最值即可；（3）根据题意得W=−3(x−100)(x−20−m)(x⩽55)，由于对称轴是直线x=60+m2>60，根据二次函数的性质即可得到结论．解：（1）设y=kx+b，由题意有{40k+b=180 70k+b=90，解得{k=−3b=300，所以y关于x的函数解析式为y=−3x+300；（2）由（1）W=(−3x+300)(x−a)，又由表可得：3600=(−3×40+300)(40−a)，∴a=20，∴W=(−3x+300)(x−20)=−3x2+360x−6000=−3(x−60)2+4800．所以售价x=60时，周销售利润W最大，最大利润为4800；（3）由题意W=−3(x−100)(x−20−m)(x⩽55)，其对称轴x=60+m2>60，∴0<x⩽55时上述函数单调递增，所以只有x=55时周销售利润最大，∴4050=−3(55−100)(55−20−m)．∴m=5．小提示：本题考查了二次函数在实际生活中的应用，重点是掌握求最值的问题．注意：数学应用题来源于实践，用于实践，在当今社会市场经济的环境下，应掌握一些有关商品价格和利润的知识，总利润等于总收入减去总成本，然后再利用二次函数求最值．17、“八婺”菜场指导菜农生产和销售某种蔬菜，提供如下信息：①统计售价与需求量的数据，通过描点（图1），发现该蔬菜需求量y1（吨）关于售价x（元/千克）的函数图象可以看成抛物线，其表达式为y1=ax2+ c，部分对应值如表：221．③1~7月份该蔬菜售价x1（元/千克），成本x2（元/千克）关于月份t的函数表达式分别为x1=12t+2，x2=1 4t2−32t+3，函数图象见图2．请解答下列问题：(1)求a，c的值．(2)根据图2，哪个月出售这种蔬菜每千克获利最大？并说明理由．(3)求该蔬菜供给量与需求量相等时的售价，以及按此价格出售获得的总利润．答案：(1)a=−15,c=9(2)在4月份出售这种蔬菜每千克获利最大，见解析(3)该蔬菜供给量与需求量相等时的售价为5元/千克，按此价格出售获得的总利润为8000元分析：（1）运用待定系数法求解即可；（2）设这种蔬菜每千克获利w元，根据w=x售价−x成本列出函数关系式，由二次函数的性质可得结论；（3）根据题意列出方程，求出x的值，再求出总利润即可．（1）把{x=3,y=7.2，{x=4,y=5.8代入y需求=ax2+c可得{9a+c=7.2,①16a+c=5.8.②②-①，得7a=−1.4，解得a=−15，把a=−15代入①，得c=9，∴a=−15,c=9．（2）设这种蔬菜每千克获利w元，根据题意，有w=x售价−x成本=12t+2−(14t2−32t+3)，化简，得w=−14t2+2t−1=−14(t−4)2+3，∵−14<0,t=4在1≤t≤7的范围内，∴当t=4时，w有最大值．答：在4月份出售这种蔬菜每千克获利最大．（3）由y供给=y需求，得x−1=−15x2+9，化简，得x2+5x−50=0，解得x1=5,x2=−10（舍去），∴售价为5元/千克．此时，y供给=y需求=x−1=4（吨）=4000（千克），把x=5代入x售价=12t+2，得t=6，把t=6代入w=−14t2+2t−1，得w=−14×36+2×6−1=2，∴总利润=w⋅y=2×4000=8000（元）．答：该蔬菜供给量与需求量相等时的售价为5元/千克，按此价格出售获得的总利润为8000元．小提示：此题主要考查了函数的综合应用，结合函数图象得出各点的坐标，再利用待定系数法求出函数解析式是解题的关键．18、一隧道内设双行公路，隧道的高MN为6米．下图是隧道的截面示意图，并建立如图所示的直角坐标系，它是由一段抛物线和一个矩形CDEF的三条边围成的，矩形的长DE是8米，宽CD是2米．（1）求该抛物线的解析式；（2）为了保证安全，要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离．若行车道总宽度PQ （居中，两边为人行道）为6米，一辆高3.2米的货运卡车（设为长方形）靠近最右边行驶能否安全？请写出判断过程；（3）施工队计划在隧道门口搭建一个矩形“脚手架”ABHG ，使H 、G 两点在抛物线上，A 、B 两点在地面DE 上，设GH 长为n 米，“脚手架”三根木杆AG 、GH 、HB 的长度之和为L ，当n 为何值时L 最大，最大值为多少？ 答案：（1）y=-14x 2+4；（2）能安全通过，见解析；（3）n=4时，L 有最大值，最大值为14分析：（1）根据题意和函数图象，可以设出抛物线的解析式，然后根据抛物线过点F 和点M 即可求得该抛物线的解析式；（2）先求出抛物线的解析式，再根据题意判断该隧道能通过的车辆的最高高度，便可判断该车辆能安全通过．（3）射出H 的坐标，用n 表示出L ，利用二次函数的性质求解即可．解：（1）由题意得M （0，4），F （4，0）可设抛物线的解析式为y=ax 2+4，将F （4，0）代入y=ax 2+4中，得a=-14， ∴抛物线的解析式为y=-14x 2+4； （2）当x=3，y=74， 74+2-12=3.25>3.2，∴能安全通过； （3）由GH=n ，可设H （n 2，−n 216+4），∴GH+GA+BH=n+（−n 216+4）×2+2×2=−18n 2+n +12，∴L=−18n 2+n +12，∵a ＜0，抛物线开口向下，∴当n=-b=4时，L有最大值，最大值为14．2a小提示：本题考查了二次函数的实际应用，解题的关键是要注意自变量的取值范围必须使实际问题有意义．。

人教版九年级上册数学第二十二章二次函数含答案一、单选题(共15题，共计45分)1、若二次函数的图象的顶点在第一象限，且经过点(0，1)和(-1，0)，则的值的变化范围是( )A. B. C. D.2、已知函数y=（k﹣3）x2+2x+1的图象与x轴有交点，则k的取值范围是（）A.k≤4且k≠3B.k＜4且k≠3C.k＜4D.k≤43、已知点，，都在函数的图象上，则，，的大小关系是（）A. B. C. D.4、下列函数式中，是二次函数的是（）A.y=B.y=x 2﹣C.y= x 2D.y=﹣5x+35、如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其中部分图象如图所示，下列结论错误的是（）A.4ac＜b 2B.方程ax 2+bx+c=0的两个根是x1=﹣1，x2=3； C.当y＞0时，x的取值范围是﹣1≤x＜3 D.当x＜0时，y随x增大而增大6、在平面直角坐标系中，如果抛物线y＝2x2不动，而把x轴、y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是( )A. y＝2( x－2) 2 + 2B. y＝2( x + 2) 2－2C. y＝2( x－2) 2－2 D. y＝2( x + 2) 2 + 27、直角坐标平面上将二次函数y=x2﹣2的图象向左平移1个单位，再向上平移1个单位，则其顶点为（）A.（0，0）B.（1，﹣1）C.（0，﹣1）D.（﹣1，﹣1）8、关于二次函数的说法，正确的是( )A.最大值为-4B.最小值为-4C.最大值为-8D.最小值为-89、下列函数中，当x>0时，y随x的增大而减小的是（）A. B. C. D.10、对于函数y=﹣2（x﹣m）2的图象，下列说法不正确的是（）A.开口向下B.对称轴是x=mC.最大值为0D.与y轴不相交11、关于二次函数y=ax2+bx+c的图象有下列命题：①当c=0时，函数的图象经过原点；②当c＞0，且函数的图象开口向下时，方程ax2+bx+c=0必有两个不相等的实根；③函数图象最高点的纵坐标是；④当b=0时，函数的图象关于y轴对称．其中正确命题的个数是（）A.1个B.2个C.3个D.4个12、在下列函数关系式中，二次函数的是（）A. B. C. D.13、下列函数是二次函数的是（）A.y=3x+1B.y=ax 2+bx+cC.y=x 2+3D.y=（x﹣1）2﹣x 214、二次函数y=2x2﹣8x+m满足以下条件：当﹣2＜x＜﹣1时，它的图象位于x 轴的下方；当6＜x＜7时，它的图象位于x轴的上方，则m的值为（）A.8B.﹣10C.﹣42D.﹣2415、烟花厂为扬州烟花三月经贸旅游节特别设计制作一种新型礼炮，这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是，若这种礼炮在点火升空到最高点处引爆，则从点火升空到引爆需要的时间为（）A.3sB.4sC.5sD.6s二、填空题(共10题，共计30分)16、如图，一男生推铅球，铅球行进高度（米）与水平距离（米）之间的关系是，则铅球推出距离________米．17、已知二次函数的图象的顶点在第三象限，且经过点，，则的取值范围为________.18、二次函数y=（x﹣1）2+2的顶点坐标为________．19、已知抛物线（）经过点，且顶点在第一象限.有下列三个结论：①②③.把正确结论的序号填在横线上________.20、某种商品每件进价为20元，调查表明：在某段时间内，若以每件x元（20≤x≤40，且x为整数）出售，可卖出（40﹣x）件，若要使利润最大，则每件商品的售价应为________元.21、请写出一个图象的对称轴为y轴，开口向下，且经过点（1，﹣2）的二次函数解析式，这个二次函数的解析式可以是________．22、已知抛物线y=ax2+bx+c的顶点为D（﹣1，3），与x轴的一个交点在（﹣3，0）和（﹣2，0）之间，其部分图象如图，则以下结论：①b2- 4ac＞0；②c﹣a=3；③a+b+c＜0；④方程ax2+bx+c=m（m≥2）一定有实数根；其中正确的结论为________．23、为响应“足球进校园”的号召，我县教体局在今年 11 月份组织了“县长杯”校园足球比赛．在某场比赛中，一个球被从地面向上踢出，它距地面的高t 表示，其中 t(s)表示足球被踢出后经过的时度 h(m)可用公式 h＝﹣5t2+v(m/s)是足球被踢出时的速度，如果足球的最大高度到 20m，那么足球被间，v踢出时的速度应达到________m/s．24、如图，二次函数y=ax2+bx+c（a≠0）的图象过原点O，且该图象的对称轴是直线x=，若函数值y＞0．则x取值范围是________ ．25、如图，是二次函数y=ax2-x+a2-4的图象，则a的值是________.三、解答题(共5题，共计25分)26、已知函数y=2x2-(3-k)x+k2-3k-10的图象经过原点，试确定k的值。

第二十二章《二次函数》解答题专题复习 (48)一、解答题1．已知二次函数y＝x2－22mx＋m2＋m－1（m为常数）．（1）求证：不论m为何值，该二次函数的图像与x轴总有两个公共点；（2）将该二次函数的图像向下平移k（k＞0）个单位长度，使得平移后的图像经过点（0，－2），则k的取值范围是．2．若二次函数y=ax2+bx+c（a≠0）中，函数值y与自变量x的部分对应值如表：x…-2-1012…y…0-2-204…（1）求该二次函数的表达式；（2）当y≥4时，求自变量x的取值范围．3．如图，抛物线y=ax2+bx+c经过两个确定点A、B，其中A为顶点，B为抛物线与y轴的交点．(1)由抛物线的性质可知，该抛物线还经过一个确定点C，请写出找点C的方法(不要求画图)；(2)若A(1，4)、B(0，3)，求抛物线的解析式．4．已知二次函数y=﹣x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（－1，0），与y轴的交点为（0，3）．（1）求此二次函数的解析式；（2）结合函数图象，直接写出当y≤﹣1时x的取值范围．5．已知，在以O为原点的直角坐标系中，抛物线的顶点为A（1，4），且经过点B（2，3），与x轴交于C、D两点．（1）求直线OB的函数表达式和该抛物线的函数表达式；（2）如图1，点P是x轴上方的抛物线上一动点，过点P作直线PF⊥x轴于点F，交直线OB于点E．若PE=3EF，求出P点的横坐标；（3）如图2，点M是抛物上的一个动点，且在直线OB的上方，过点M作x轴的平行线与直线OB交于点N，T是抛物线对称轴上一点，当MN最大且△MDT周长最小时，直接写出T的坐标．6．在平面直角坐标系中，一次函数y=x+3的图象与x轴交于点A，二次函数y=x2+mx+n的图象经过点A．（1）当m=4时，求n的值；（2）设m=﹣2，当﹣3≤x≤0时，求二次函数y=x2+mx+n的最小值；（3）当﹣3≤x≤0时，若二次函数﹣3≤x≤0时的最小值为﹣4，求m、n的值．7．如图，抛物线y=ax2+c（a＞0）经过梯形ABCD的四个顶点，梯形的底AD在x轴上，其中A（﹣2，0），B（﹣1，﹣3）．（1）求抛物线的解析式；（2）点M为y轴上任意一点，当点M到A、B两点的距离之和为最小时，求此时点M的坐标．8．如图，已知直线y=x与抛物线y=1x2交于A、B两点．2（1）求交点A 、B 的坐标；（2）记一次函数y=x 的函数值为y 1，二次函数y =12x 2的函数值为y 2．若y 1＞y 2，求x 的取值范围；（3）在该抛物线上存在几个点，使得每个点与AB 构成的三角形为等腰三角形？并求出不少于3个满足条件的点P 的坐标．9．在平面直角坐标系xOy 中，抛物线y ＝x 2﹣2x ﹣3与x 轴相交于A ，B （点A 在点B 的左边），与y 轴相交于C ． （1）求直线BC 的表达式．（2）垂直于y 轴的直线l 与直线BC 交于点N （x 1，y 1），与抛物线相交于点P （x 2，y 2），Q （x 3，y 3）．若x 1＜x 2＜x 3，结合函数图象，求x 1+x 2+x 3的取值范围．10．在平面直角坐标系xOy 中，抛物线212c y x x b =++经过点A （0，2）和B （1，32）．（1）求该抛物线的表达式；（2）已知点C 与点A 关于此抛物线的对称轴对称，点D 在抛物线上，且点D 的横坐标为4，求点C 与点D 的坐标；（3）在（2）的条件下，将抛物线在点A ，D 之间的部分（含点A ，D ）记为图象G ， 如果图象G 向下平移t （t ＞0）个单位后与直线BC 只有一个公共点，求t 的取值范围．xO y11．如图，在△ABC 中，∠B=90°，AB=5cm ，BC=7cm ．点P 从点A 开始沿AB 边向点B 以1cm/s 的速度移动，点Q 从点B 开始沿BC 边向点C 以2cm/s 的速度移动．（1）如果P 、Q 分别从A 、B 同时出发，那么几秒后，△PBQ 的面积等于4cm2？（2）如果P 、Q 分别从A 、B 同时出发，那么几秒后，PQ 的长度等于5cm ？（3）如果P 、Q 分别从A 、B 同时出发，△PBQ 的面积能否等于8cm 2？说明理由．由此思考：△PBQ 的面积最多为多少cm 2？12．如图1，抛物线C 1：y ＝ax 2+k 的顶点A （0，﹣2），且过点（2，0），点B 的坐标为（1，0），直线AB 交抛物线C 1于另一点C ．（1）抛物线的解析式为 ； （2）求点C 的坐标：（3）如图2，将抛物线C 1向下平移m （m ＞0）个单位得到抛物线C ，且抛物线C 的顶点为P ，交x 轴负半轴于点M ，交射线BC 于点N ，NQ ⊥x 轴于点Q ，当NP 平分∠MNQ 时，求m 的值．13．如图，点A （﹣2，0），点C （﹣1，0），点A 、C 关于原点O 的对称点分别为点B 、D ．线段AB 沿y 轴向下平移2m （m ＞0）个单位长度，得到线段A 1B 1，抛物线y ＝12ax 2+bx+2过点A 1，B 1． （1）当m ＝1时，a ＝ ； （2）求a 与m 之间的关系式；（3）线段CD 沿y 轴向下平移2n （n ＞0）个单位长度，得到线段C 1D 1，抛物线y ＝ax 2+bx+2过点C 1，D 1．①a ＝ ；（用含n 的式子来表示）m 与n 之间的关系式为 ．②点P （x ，0）在x 轴上，当△PC 1B 1为等腰直角三角形时，直接写出点P 的坐标．14．如图，二次函数23y x x m =-++的图象与x 轴的一个交点为(4,0)B ，另一个交点为A ，且与y 轴相交于C 点（1）则m =_________；C 点坐标为___________；（2）在直线BC 上方的抛物线上是否存在一点M ，使得它与B ，C 两点构成的三角形面积最大，若存在，求出此时M 点坐标；若不存在，请简要说明理由． （3）P 为抛物线上一点，它关于直线BC 的对称点为Q ①当四边形PBQC 为菱形时，求点P 的坐标；②点P 的横坐标为(04)t t <<，当t =________时，四边形PBQC 的面积最大． 15．如图，在直角坐标系中，点A 的坐标为（－2，0），连结OA ，将线段OA 绕原点O 顺时针旋转120°，得到线段OB . （1）求点B 的坐标；（2）求经过A 、O 、B 三点的抛物线的解析式；（3）在（2）中抛物线的对称轴上是否存在点C ，使△BOC 的周长最小？若存在，求出点C 的坐标；若不存在，请说明理由.（4）如果点P 是（2）中的抛物线上的动点，且在x 轴的下方，那么△PAB 是否有最大面积？若有，求出此时P 点的坐标及△PAB 的最大面积；若没有，请说明理由.16．矩形OABC 的顶点A(－8，0)，C(0，6)，点D 是BC 边上的中点，抛物线y ＝ax 2＋bx 经过A ，D 两点，如图所示.(1)求点D 关于y 轴的对称点D′的坐标及a ，b 的值；(2)将抛物线y ＝ax 2＋bx 向下平移，记平移后点A 的对应点为A 1，点D 的对应点为D 1，当抛物线平移到某个位置时，恰好使得点O 是y 轴上到A 1，D 1两点距离之和OA 1＋OD 1最短的一点，求平移后的抛物线解析式.17．如图，已知抛物线23y ax bx =++经过点()1,0A -和点()3,0B ，点C 为抛物线与y轴的交点．()1求抛物线的解析式；()2若点E 为直线BC 上方抛物线上的一点，请求出BCE 面积的最大值．()3在()2条件下，是否存在这样的点()0,D m ，使得BDE 为等腰三角形？如果有，请直接写出点D 的坐标；如果没有，请说明理由．18．如图，已知抛物线y=﹣x 2+2x+3与x 轴交于A ，B 两点（点A 在点B 的左边），与y 轴交于点C ，连接BC ．（1）求A ，B ，C 三点的坐标；（2）若点P 为线段BC 上一点（不与B ，C 重合），PM ∥y 轴，且PM 交抛物线于点M ，交x 轴于点N ，当△BCM 的面积最大时，求△BPN 的周长；（3）在（2）的条件下，当△BCM 的面积最大时，在抛物线的对称轴上存在一点Q ，使得△CNQ 为直角三角形，求点Q 的坐标．19．如图，E 是正方形ABCD 的边AB 上的动点，但始终保持EF ⊥DE 交BC 于点F ． （1）求证：△ADE ∽△BEF ；（2）若正方形的边长为4，设AE=x ，BF=y ，求y 与x 之间的函数解析式； （3）当x 取何值时，y 有最大值？并求出这个最大值．x2+mx+2与x轴交于A、B两点，与y轴交于点C，抛物线的对称20．如图，抛物线y=﹣12交x轴于点D．轴直线x=32（1）求m的值；（2）在抛物线的对称轴上找出点P，使△PCD是以CD为腰的等腰三角形，直接写出P点的坐标；（3）点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，与x轴相交于点H，连接CF、BF、OE，当四边形CDBF的面积最大时，请你说明四边形OCFE的形状．【答案与解析】一、解答题1．（1）证明见解析；（2）k ≥34. （1）根据判别式的值得到△=（2m －1）2 ＋3＞0，然后根据判别式的意义得到结论； （2）把（0，－2）带入平移后的解析式，利用配方法得到k= (m+12)²+34，即可得出结果.（1）证：当y =0时 x 2－mx ＋m 2＋m －1＝0∵b 2－4ac ＝（－m ）2－4（m 2＋m －1） ＝8m 2－4m 2－4m ＋4 ＝4m 2－4m ＋4 ＝（2m －1）2 ＋3＞0∴方程x 2－mx ＋m 2＋m －1＝0有两个不相等的实数根∴二次函数y ＝x 2－mx ＋m 2＋m －1图像与x 轴有两个公共点（2）解：平移后的解析式为: y ＝x 2－mx ＋m 2＋m －1-k,过(0,-2), ∴-2=0-0+m²+m-1-k, ∴k= m²+m+1=(m+12)²+34,∴k ≥34. 【点睛】本题考查了二次函数图象与几何变换以及图象与x 轴交点个数确定方法，能把一个二次三项式进行配方是解题的关键．2．（1）22y x x =+-；（2）x≤﹣3或x≥2. （1）根据表格的数据可得抛物线的对称轴是直线x=12-，设出抛物线的顶点式212y a x k ⎛⎫=++ ⎪⎝⎭，再代入两组数据进行求解即可；（2）由（1）可得抛物线图象开口向上，求得当y=4时x 的值，根据抛物线的图象性质即可得到x 的取值范围.解：（1）根据表中可知：点（﹣1，﹣2）和点（0，﹣2）关于对称轴对称， 即抛物线的对称轴是直线x=12-， 设二次函数的表达式是212y a x k ⎛⎫=++ ⎪⎝⎭， 把点（﹣2，0）和点（0，﹣2）代入得：2212021022a k a k ⎧⎛⎫-++=⎪ ⎪⎪⎝⎭⎨⎛⎫⎪++=- ⎪⎪⎝⎭⎩，解得：a=1，k=94-， 则该二次函数的表达式为2219224y x x x ⎛⎫=+-=+- ⎪⎝⎭ （2）∵1＞0，∴抛物线的图象开口向上， 当y=4时，y=x 2+x ﹣2=4， 解得：x=﹣3或2，则当y≥4时，自变量x 的取值范围是x≤﹣3或x≥2. 【点睛】本题主要考查二次函数图象的性质，解此题的关键在于根据题意利用待定系数法确定函数关系式，再根据抛物线的图象性质进行解答. 3．(1)见解析；(2)y=-x 2+2x+3． (1)根据二次函数的性质即可得到结论； (2)根据待定系数法即可求得二次函数的解析式．解：(1)过点A 作直线MN ⊥x 轴，作点B 关于直线MN 的对称点C ， 则点C 即为所求；(2)∵A 为顶点，∴设抛物线的解析式为：y=a(x-1)2+4， 把B(0，3)代入得，3=a(0-1)2+4， 解得a=-1， ∴y=-(x-1)2+4，即抛物线的解析式为：y=-x 2+2x+3． 【点睛】本题考查了待定系数法求二次函数的解析式，轴对称的性质，熟练掌握待定系数法求函数的解析式是解题的关键．4．（1）y ＝﹣x 2+2x+3（2）当1 （1）利用待定系数法求抛物线解析式；（2）先计算出y =－1对应的自变量的值，然后结合图象，写出y ≤﹣1所对应的自变量的范围即可．（1）把（－1，0）和（0，3）代入y =﹣x 2+bx +c 得：103b c c --+=⎧⎨=⎩，解得：23b c =⎧⎨=⎩，所以抛物线解析式为y =﹣x 2+2x +3；（2）当y =－1时，﹣x 2+2x +3=－1，解得：x 1=1x 2=1x ≤1x ≥1y ≤﹣1．【点睛】本题考查了抛物线与x 轴的交点：把求二次函数y =ax 2+bx +c （a ，b ，c 是常数，a ≠0）与x 轴的交点坐标问题转化解关于x 的一元二次方程即可求得交点横坐标．也考查了二次函数的性质．5．(1) y=x 2﹣2x+5；(2) P 点的横坐标为4; (3) T 的坐标为（1，3）． （1）由B 点坐标利用待定系数法可求直线OB 解析式，利用顶点式可求得抛物线解析式； （2）设P （x ，x 2-2x+5），则可表示出E 点坐标，由PE=3EF 可得到方程解答即可； （3）当M 与B 关于抛物线的对称轴对称时，MN 最大，进而得出T 的坐标． （1）设直线OB 解析式为y=kx ，由题意可得3=2k ，解得k=1.5， ∴直线OB 解析式为y=1.5x ， ∵抛物线顶点坐标为（1，4）， ∴可设抛物线解析式为y=a （x ﹣1）2+4， ∵抛物线经过B （2，3）， ∴3=a+4，解得a=1， ∴抛物线为y=x 2﹣2x+5；（2）设P （x ，x 2﹣2x+5），E 点坐标为（x ，1.5x ）， ∵PE=3EF ， ∴x 2﹣2x+5=4×1.5x ，解得：14x =24x =P 点的横坐标为4．（3）当M 与B 关于抛物线的对称轴对称时，MN 最大，此时B 与N 重合， 此时M 的坐标为（0，3），当MT 垂直对称轴时，△MDT 周长最小， 此时T 的坐标为（1，3）． 【点睛】本题为二次函数的综合应用，涉及待定系数法及方程思想等知识点．在（1）中注意待定系数的应用步骤，在（2）中利用P 、E 的横坐标相等是解题的关键，本题考查知识点较多，。